2020高考数学专题复习专题9平面解析几何第64练抛物线练习理

专题9.5 抛物线1.（2020·全国高考真题（理））已知A 为抛物线C :y 2=2px （p >0）上一点，点A 到C 的焦点的距离为12，到y 轴的距离为9，则p =（ ） A ．2 B ．3 C ．6 D ．9【答案】C 【解析】设抛物线的焦点为F ，由抛物线的定义知||122A p AF x =+=，即1292p=+，解得6p.故选：C.2．（2020·北京高三二模）焦点在x 轴的正半轴上，且焦点到准线的距离为4的抛物线的标准方程是（ ） A ．x 2＝4y B ．y 2＝4x C ．x 2＝8y D ．y 2＝8x【答案】D 【解析】根据题意，要求抛物线的焦点在x 轴的正半轴上， 设其标准方程为22(0)y px p =>， 又由焦点到准线的距离为4，即p ＝4， 故要求抛物线的标准方程为y 2＝8x ， 故选：D.3.（全国高考真题）设F 为抛物线2:4C y x =的焦点，曲线()0ky k x=>与C 交于点P ，PF x ⊥轴，则k =（ ）A ．12B ．1C ．32D ．2【答案】D 【解析】由抛物线的性质可得(1,2)221kP y k ⇒==⇒=，故选D. 4．（2020·全国高考真题（文））设O 为坐标原点，直线2x =与抛物线C ：22(0)y px p =>交于D ，E 两点，若OD OE ⊥，则C 的焦点坐标为（ ） A ．1,04⎛⎫⎪⎝⎭B ．1,02⎛⎫ ⎪⎝⎭C ．(1,0)D ．(2,0)练基础【答案】B 【解析】因为直线2x =与抛物线22(0)y px p =>交于,E D 两点，且OD OE ⊥， 根据抛物线的对称性可以确定4DOx EOx π∠=∠=，所以()2,2D ，代入抛物线方程44p =，求得1p =，所以其焦点坐标为1(,0)2， 故选：B.5.（2019·四川高三月考（文））若抛物线22y px =的准线为圆2240x y x ++=的一条切线，则抛物线的方程为（ ） A.216y x =- B.28y x =-C.216y x =D.24y x =【答案】C 【解析】∵抛物线22y px =的准线方程为x=2p-，垂直于x 轴． 而圆2240x y x ++=垂直于x 轴的一条切线为4x =-， 则42p=，即8p =． 故抛物线的方程为216y x =． 故选：C ．6.（2019·北京高考真题（文））设抛物线y 2=4x 的焦点为F ，准线为l .则以F 为圆心，且与l 相切的圆的方程为__________． 【答案】(x -1)2+y 2=4. 【解析】抛物线y 2=4x 中，2p =4，p =2， 焦点F （1,0），准线l 的方程为x =-1， 以F 为圆心，且与l 相切的圆的方程为 (x -1)2+y 2=22,即为(x -1)2+y 2=4.7.（2019·山东高三月考（文））直线l 与抛物线22x y =相交于A ，B 两点，当AB 4=时，则弦AB 中点M 到x 轴距离的最小值为______. 【答案】32【解析】由题意，抛物线22x y =的焦点坐标为（0，12），根据抛物线的定义如图，所求d=111A B AF BF 113M 2222A B AB M ++--==≥= 故答案为：32． 8.（2021·沙湾县第一中学（文））设过抛物线y 2＝4x 的焦点F 的直线交抛物线于A ，B 两点，且直线AB 的倾斜角为4π，则线段AB 的长是____，焦点F 到A ，B 两点的距离之积为_________.【答案】8 8 【分析】由题意可得直线AB 的方程为1y x =-，然后将直线方程与抛物线方程联立方程组，消去y 后，利用根与系数的关系，结合抛物线的定义可求得答案 【详解】解：由题意得(1,0)F ，则直线AB 的方程为1y x =-，设1122(,),(,)A x y B x y ，由241y x y x ⎧=⎨=-⎩，得2610x x -+=， 所以12126,1x x x x +==， 所以12628AB x x p =++=+=，因为11221,122=+=+=+=+p pAF x x BF x x ， 所以()()1212121116118AF BF x x x x x x ⋅=+⋅+=+++=++=， 故答案为：8，89．（2021·全国高三专题练习）已知抛物线顶点在原点，焦点在坐标轴上，又知此抛物线上的一点(),3A m -到焦点F 的距离为5，则m 的值为__________；抛物线方程为__________. 【答案】答案见解析 答案见解析 【分析】由于抛物线的开口方向未定，根据点(),3A m -在抛物线上这一条件，抛物线开口向下，向左、向右均有可能，以此分类讨论，利用焦半径公式列方程可得p 的值，根据点(),3A m -在抛物线上可得m 的值. 【详解】根据点(),3A m -在抛物线上，可知抛物线开口向下，向左、向右均有可能， 当抛物线开口向下时，设抛物线方程为22x py =-（0p >）， 此时准线方程为2py =，由抛物线定义知(3)52p --=，解得4p =.所以抛物线方程为28x y ，这时将(),3A m -代入方程得m =±当抛物线开口向左或向右时，可设抛物线方程为22y ax （0a ≠），从p a =知准线方程为2ax =-，由题意知()25232am am⎧+=⎪⎨⎪-=⎩，解此方程组得11192a m =⎧⎪⎨=⎪⎩，22192a m =-⎧⎪⎨=-⎪⎩，33912a m =⎧⎪⎨=⎪⎩，44912a m =-⎧⎪⎨=-⎪⎩，综合（1）、（2）得92m =，22y x =； 92m =-，22y x =-；12m =，218y x =； 12m =-，218y x =-；m =±28xy .故答案为：92，92-，12，12-，±22y x =，22y x =-，218y x =，218y x =-，28x y .10.（2019·广东高三月考（理））已知F 为抛物线2:4T x y =的焦点，直线:2l y kx =+与T 相交于,A B 两点.()1若1k =，求FA FB +的值；()2点(3,2)C --，若CFA CFB ∠=∠，求直线l 的方程.【答案】（1）10（2）3240x y +-= 【解析】（1）由题意，可得()0,1F ，设221212,,,44x x A x B x ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭，联立方程组224y kx x y=+⎧⎨=⎩，整理得2480x kx --=，则124x x k +=，128x x =-，又由22121144x x FA FB +++=+()2121222104x x x x +-=+=.（2）由题意，知211,14x FA x ⎛⎫=- ⎪⎝⎭，222,14x FB x ⎛⎫=- ⎪⎝⎭，()3.3FC =--， 由CFA CFB ∠=∠，可得cos ,cos ,FA FC FB FC =又2114x FA =+，2214x FB =+，则FA FC FB FC FA FC FB FC =， 整理得()1212420x x x x ++-=，解得32k =-， 所以直线l 的方程为3240x y +-=.1．（2021·吉林长春市·高三（理））已知M 是抛物线24y x =上的一点，F 是抛物线的焦点，若以Fx 为始边，FM 为终边的角60xFM ∠=，则FM 等于（ ） A ．2 B C ．D ．4【答案】D 【分析】设点200,4y M y ⎛⎫ ⎪⎝⎭，取()1,0a =，可得1cos ,2FM a <>=，求出20y 的值，利用抛物线的定义可求练提升得FM 的值. 【详解】设点()00,M x y ，其中2004y x =，则()1,0F ，2001,4y FM y ⎛⎫=- ⎪⎝⎭，取()1,0a =，则211cos ,2y FM a FM a FM a-⋅<>===⋅⎛，可得4200340480y y -+=，因为20104y ->，可得204y >，解得2012y =，则20034y x ==，因此，014MF x=+=. 故选：D.2.（2017·全国高考真题（文））过抛物线2:4C y x =的焦点F 的直线交C 于点M （在x 轴上方），l 为C 的准线，点N 在l 上且MNl ⊥，则点M 到直线NF 的距离为（）A. B. D.【答案】A 【解析】设直线l 与x 轴相交于点P ，与直线MN 相交于点Q ，(1,0)F ，设||||MN MF m ==，因为||2,30PF NQM =∠=，所以||4,||2QF QM m ==， 所以42m m +=，解得：4m =，设00(,)M x y ，由焦半径公式得：014x +=， 所以03x=，0y =，所以sin sin 42NP MNF NFP NF ∠=∠===，所以点M 到直线NF 的距离为||sin 4NM MNF ⋅∠=⋅=3．（2020·广西南宁三中其他（理））已知抛物线28C y x =：的焦点为F ，P 是抛物线C 的准线上的一点，且P 的纵坐标为正数，Q 是直线PF 与抛物线C 的一个交点，若PQ =，则直线PF 的方程为（ ）A ．20x y --=B ．20x y +-=C ．20x y -+=D ．20x y ++=【答案】B 【解析】过Q 点作QH PM ⊥于H ，因为PQ =，由抛物线的定义得PQ =，所以在Rt PQH ∆中，4PQH π∠=，所以4PFM π∠=，所以直线PF 的斜率为1k =-，所以直线PF 的方程为()()012y x -=--， 即20x y +-=， 故选B.4.（2020·浙江高三月考）如图，已知抛物线21:4C y x =和圆222:(1)1C x y -+=，直线l 经过1C 的焦点F ，自上而下依次交1C 和2C 于A ，B ，C ，D 四点，则AB CD ⋅的值为（ ）A ．14B ．12C ．1D ．2【答案】C 【解析】因为抛物线21:4C y x =的焦点为(1,0)F ，又直线l 经过1C 的焦点F ，设直线:(1)l y k x =-，由24(1)y x y k x ⎧=⎨=-⎩得2222(24)0k x k x k -++=， 设1122(,),(,)A x y B x y ，则121=x x由题意可得：1111=-=+-=AB AF BF x x ， 同理2=CD x ，所以12cos01︒⋅=⋅⋅==AB CD AB CD x x . 故选C5．【多选题】（2022·全国高三专题练习）已知抛物线21:C y mx =与双曲线222:13y C x -=有相同的焦点，点()02,P y 在抛物线1C 上，则下列结论正确的有（ ）A ．双曲线2C 的离心率为2B ．双曲线2C 的渐近线为y x = C ．8m =D ．点P 到抛物线1C 的焦点的距离为4【答案】ACD 【分析】由双曲线方程写出离心率、渐近线及焦点，即可知A 、B 、C 的正误，根据所得抛物线方程求0y ，即知D 的正误. 【详解】双曲线2C 的离心率为2e ==，故A 正确；双曲线2C 的渐近线为y =，故B 错误； 由12,C C 有相同焦点，即24m=，即8m =，故C 正确； 抛物线28y x =焦点为()2,0，点()02,P y 在1C 上，则04y =±，故()2,4P 或()2,4P -，所以P 到1C 的焦点的距离为4，故D 正确． 故选：ACD ．6．【多选题】（2021·海南鑫源高级中学）在下列四个命题中，真命题为（ ）A ．当a 为任意实数时，直线(a -1)x -y +2a +1=0恒过定点P ，则过点P 且焦点在y 轴上的抛物线的标准方程是243x y =B ．已知双曲线的右焦点为(5，0)，一条渐近线方程为2x -y =0，则双曲线的标准方程为221205x y -= C ．抛物线y =ax 2(a ≠0)的准线方程14y a=-D ．已知双曲线2214x y m +=，其离心率()1,2e ∈，则m 的取值范围(-12，0)【答案】ACD 【分析】求出直线定点设出抛物方程即可判断A ；根据渐近线方程与焦点坐标求出,a b 即可判断B ；根据抛物线方程的准线方程公式即可判断C ；利用双曲线离心率公式即可判断D ． 【详解】对A 选项，直线(a -1)x -y +2a +1=0恒过定点为()2,3P -，则过点P 且焦点在y 轴上的抛物线的标准方程设为22x py =，将点()2,3P -代入可得23p =，所以243x y =，故A 正确；对B 选项，知5,2bc a==，又22225a b c +==，解得225,20a b ==，所以双曲线的标准方程为221520x y -=，故B 错； 对C 选项，得21x y a =，所以准线方程14y a=-，正确；对D 选项，化双曲线方程为2214x y m-=-，所以()1,2e =，解得()12,0m ∈-，故正确．故选：ACD7．（2021·全国高二课时练习）已知点M 为抛物线2:2(0)C y px p =>上一点，若点M 到两定点(,)A p p ，,02p F ⎛⎫⎪⎝⎭的距离之和最小，则点M 的坐标为______．【答案】,2p p ⎛⎫⎪⎝⎭【分析】过点M 作抛物线准线的垂线，垂足为B ，根据抛物线的定义可得||||MF MB =， 易知当A ，B ，M 三点共线时||MB MA +取得最小值且为||AB ，进而可得结果. 【详解】过点M 作抛物线准线的垂线，垂足为B ，由抛物线的定义，知点M 到焦点,02p F ⎛⎫⎪⎝⎭的距离与点M 到准线的距离相等，即||||MF MB =，所以||||||||MF MA MB MA +=+， 易知当A ，B ，M 三点共线时，||MB MA +取得最小值， 所以min 3(||||)||2p MF MA AB +==，此时点M 的坐标为,2p p ⎛⎫⎪⎝⎭． 故答案为：2p p ⎛⎫⎪⎝⎭，8．（2021·全国高二课时练习）抛物线()220y px p =>的焦点为F ，已知点A ，B 为抛物线上的两个动点，且满足120AFB ∠=︒，过弦AB 的中点M 作抛物线准线的垂线MN ，垂足为N ，则MN AB的最大值为______.【分析】设=AF a ，=BF b ，根据中位线定理以及抛物线定义可得()12MN a b =+，在AFB △中，由余弦定理以及基本不等式可得)AB a b ≥+，即可求得MN AB 的最大值．【详解】设=AF a ，=BF b ，作AQ 垂直抛物线的准线于点Q ，BP 垂直抛物线的准线于点P .由抛物线的定义，知AF AQ =，BF BP =.由余弦定理得()2222222cos120AB a b ab a b ab a b ab =+=︒=++=+-.又22a b ab +⎛⎫≤ ⎪⎝⎭，∴()()()()22221344a b ab a b a b a b +-≥+-+=+，当且仅当a b =时，等号成立，∴)AB a b ≥+，∴()1a b MN AB +≤=MN AB9．（2020·山东济南外国语学校高三月考）抛物线C ：22y x =的焦点坐标是________；经过点()4,1P 的直线l 与抛物线C 相交于A ，B 两点，且点P 恰为AB 的中点，F 为抛物线的焦点，则AF BF +=________.【答案】1,02⎛⎫⎪⎝⎭9【解析】抛物线C ：22y x =的焦点1,02F ⎛⎫⎪⎝⎭． 过A 作AM ⊥准线交准线于M ，过B 作BN ⊥准线交准线于N ，过P 作PK ⊥准线交准线 于K ，则由抛物线的定义可得AM BN AF BF +=+． 再根据P 为线段AB 的中点，119(||||)||4222AM BN PK +==+=， ∴9AF BF +=，故答案为：焦点坐标是1,02⎛⎫ ⎪⎝⎭，9AF BF +=．10.（2019·四川高考模拟（文））抛物线C ：()220x py p =>的焦点为F ，抛物线过点(),1P p .（Ⅰ）求抛物线C 的标准方程与其准线l 的方程；（Ⅱ）过F 点作直线与抛物线C 交于A ，B 两点，过A ，B 分别作抛物线的切线，证明两条切线的交点在抛物线C 的准线l 上.【答案】（Ⅰ）抛物线的标准方程为24x y =，准线l 的方程为1y =-；（Ⅱ）详见解析. 【解析】（Ⅰ）由221p p =⨯，得2p =，所以抛物线的标准方程为24x y =，准线l 的方程为1y =-.（Ⅱ）根据题意直线AB 的斜率一定存在，又焦点()0,1F ，设过F 点的直线方程为1y kx =+，联立241x yy kx ⎧=⎨=+⎩，得，2440x kx --=. 设()11,A x y ，()22,B x y ，则124x x k +=，124x x =-.∴()22221212122168x x x x x x k +=+-=+.由214y x =得，1'2y x =，过A ，B 的抛物线的切线方程分别为 ()()1112221212y y x x x y y x x x ⎧-=-⎪⎪⎨⎪-=-⎪⎩， 即21122211241124y x x x y x x x ⎧=-⎪⎪⎨⎪=-⎪⎩，两式相加，得()()2212121148y x x x x x =+-+，化简，得()221y kx k =-+，即()21y k x k =--， 所以，两条切线交于点()2,1k -，该点显然在抛物线C 的准线l ：1y =-上.1．（2021·全国高考真题）抛物线22(0)y px p =>的焦点到直线1y x =+，则p =（ ） A ．1 B ．2 C ．D ．4【答案】B 【分析】首先确定抛物线的焦点坐标，然后结合点到直线距离公式可得p 的值. 【详解】抛物线的焦点坐标为,02p ⎛⎫ ⎪⎝⎭，其到直线10x y -+=的距离：d == 解得：2p =(6p =-舍去). 故选：B.2．（2021·天津高考真题）已知双曲线22221(0,0)x y a b a b-=>>的右焦点与抛物线22(0)y px p =>的焦点重合，抛物线的准线交双曲线于A ，B 两点，交双曲线的渐近线于C 、D 两点，若|CD AB ．则双曲线的离心率为（ ） A B C ．2D ．3练真题【答案】A 【分析】设公共焦点为(),0c ，进而可得准线为x c =-，代入双曲线及渐近线方程，结合线段长度比值可得2212a c =，再由双曲线离心率公式即可得解. 【详解】设双曲线22221(0,0)x y a b a b-=>>与抛物线22(0)y px p =>的公共焦点为(),0c ，则抛物线22(0)y px p =>的准线为x c =-，令x c =-，则22221c ya b-=，解得2b y a =±，所以22b AB a =, 又因为双曲线的渐近线方程为b y x a =±，所以2bcCD a=，所以2bc a c ，所以222212a cbc =-=，所以双曲线的离心率ce a== 故选：A.3．（2020·北京高考真题）设抛物线的顶点为O ，焦点为F ，准线为l ．P 是抛物线上异于O 的一点，过P 作PQ l ⊥于Q ，则线段FQ 的垂直平分线（ ）． A ．经过点O B ．经过点P C ．平行于直线OP D ．垂直于直线OP【答案】B 【解析】如图所示：．因为线段FQ 的垂直平分线上的点到,F Q 的距离相等，又点P 在抛物线上，根据定义可知，PQ PF =，所以线段FQ 的垂直平分线经过点P .故选：B.4.（2021·全国高考真题）已知O 为坐标原点，抛物线C ：22y px =(0p >)的焦点为F ，P 为C 上一点，PF 与x 轴垂直，Q 为x 轴上一点，且PQ OP ⊥，若6FQ =，则C 的准线方程为______. 【答案】32x =-【分析】先用坐标表示P Q ，，再根据向量垂直坐标表示列方程，解得p ，即得结果. 【详解】抛物线C ：22y px = (0p >)的焦点,02p F ⎛⎫⎪⎝⎭,∵P 为C 上一点，PF 与x 轴垂直， 所以P 的横坐标为2p，代入抛物线方程求得P 的纵坐标为p ±, 不妨设(,)2pP p ,因为Q 为x 轴上一点，且PQ OP ⊥，所以Q 在F 的右侧， 又||6FQ =， (6,0),(6,)2pQ PQ p ∴+∴=- 因为PQ OP ⊥，所以PQ OP ⋅=2602pp ⨯-=, 0,3p p >∴=，所以C 的准线方程为32x =-故答案为：32x =-.5．的直线过抛物线C ：y 2=4x 的焦点，且与C 交于A ，B 两点，则AB =________．【答案】163【解析】∵抛物线的方程为24y x =，∴抛物线的焦点F 坐标为(1,0)F ，又∵直线AB 过焦点F AB 的方程为：1)y x =- 代入抛物线方程消去y 并化简得231030x x -+=， 解法一：解得121,33x x ==所以12116||||3|33AB x x =-=-= 解法二：10036640∆=-=> 设1122(,),(,)A x y B x y ，则12103x x +=, 过,A B 分别作准线1x =-的垂线，设垂足分别为,C D 如图所示.12||||||||||11AB AF BF AC BD x x =+=+=+++1216+2=3x x =+故答案为：1636．（2020·浙江省高考真题）如图，已知椭圆221:12x C y +=，抛物线22:2(0)C y px p =>，点A 是椭圆1C 与抛物线2C 的交点，过点A 的直线l 交椭圆1C 于点B ，交抛物线2C 于M （B ，M 不同于A ）．（Ⅰ）若116=p ，求抛物线2C 的焦点坐标； （Ⅱ）若存在不过原点的直线l 使M 为线段AB 的中点，求p 的最大值．【答案】（Ⅰ）1(,0)32；【解析】 （Ⅰ）当116=p 时，2C 的方程为218y x =，故抛物线2C 的焦点坐标为1(,0)32；（Ⅱ）设()()()112200,,,,,,:A x y B x y M x y I x y m λ=+，由()22222222220x y y my m x y mλλλ⎧+=⇒+++-=⎨=+⎩， 1200022222,,222m m my y y x y m λλλλλλ--∴+===+=+++， 由M 在抛物线上，所以()222222244222m pm mp λλλλλ=⇒=+++， 又22222()220y pxy p y m y p y pm x y mλλλ⎧=⇒=+⇒--=⎨=+⎩， 012y y p λ∴+=，2101022x x y m y m p m λλλ∴+=+++=+，2122222mx p m λλ∴=+-+.由2222142,?22x y x px y px ⎧+=⎪⇒+=⎨⎪=⎩即2420x px +-=12x p ⇒==-222221822228162p p p m p p p λλλλλ+⇒-=+⋅=++≥+，18p ≥，21160p ≤，p ≤ 所以，p，此时A . 法2：设直线:(0,0)l x my t m t =+≠≠，()00,A x y .将直线l 的方程代入椭圆221:12x C y +=得：()2222220m y mty t +++-=，所以点M 的纵坐标为22M mty m =-+.将直线l 的方程代入抛物线22:2C y px =得：2220y pmy pt --=，所以02M y y pt =-，解得()2022p m y m+=，因此()220222p m xm+=，由220012x y +=解得22212242160m m p m m ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭，所以当m t ==p .。

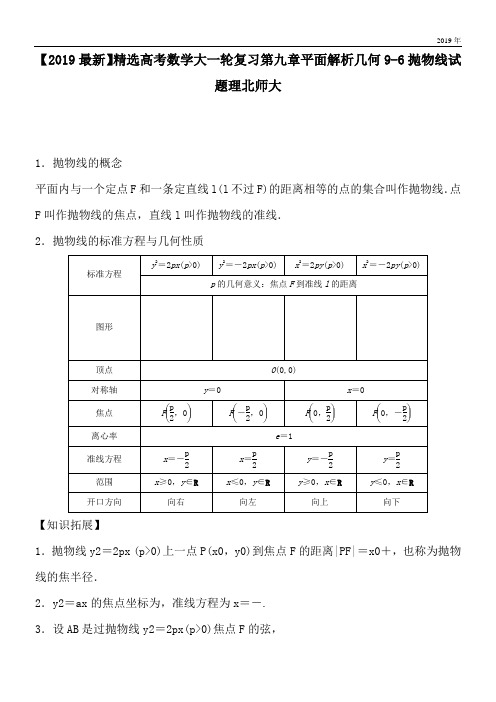
【2019最新】精选高考数学大一轮复习第九章平面解析几何9-6抛物线试题理北师大1．抛物线的概念平面内与一个定点F和一条定直线l(l不过F)的距离相等的点的集合叫作抛物线．点F叫作抛物线的焦点，直线l叫作抛物线的准线．2．抛物线的标准方程与几何性质【知识拓展】1．抛物线y2＝2px (p>0)上一点P(x0，y0)到焦点F的距离|PF|＝x0＋，也称为抛物线的焦半径．2．y2＝ax的焦点坐标为，准线方程为x＝－.3．设AB是过抛物线y2＝2px(p>0)焦点F的弦，若A(x1，y1)，B(x2，y2)，则(1)x1x2＝，y1y2＝－p2.(2)弦长|AB|＝x1＋x2＋p＝(α为弦AB的倾斜角)．(3)以弦AB为直径的圆与准线相切．(4)通径：过焦点垂直于对称轴的弦，长等于2p，通径是过焦点最短的弦．【思考辨析】判断下列结论是否正确(请在括号中打“√”或“×”)(1)平面内与一个定点F和一条定直线l的距离相等的点的轨迹一定是抛物线．( ×)(2)方程y＝ax2(a≠0)表示的曲线是焦点在x轴上的抛物线，且其焦点坐标是(，0)，准线方程是x＝－.( ×)(3)抛物线既是中心对称图形，又是轴对称图形．( ×)(4)AB为抛物线y2＝2px(p>0)的过焦点F(，0)的弦，若A(x1，y1)，B(x2，y2)，则x1x2＝，y1y2＝－p2，弦长|AB|＝x1＋x2＋p.( √)1．(2016·四川)抛物线y2＝4x的焦点坐标是( )A．(0,2) B．(0,1)C．(2,0) D．(1,0)答案D解析∵对于抛物线y2＝ax，其焦点坐标为，∴对于y2＝4x，焦点坐标为(1,0)．2．(2016·张掖一诊)过抛物线y2＝4x的焦点的直线l交抛物线于P(x1，y1)，Q(x2，y2)两点，如果x1＋x2＝6，则|PQ|等于( )A．9 B．8 C．7 D．6答案B解析抛物线y2＝4x的焦点为F(1,0)，准线方程为x＝－1.根据题意，可得|PQ|＝|PF|＋|QF|＝x1＋1＋x2＋1＝x1＋x2＋2＝8.3．设抛物线y2＝8x的准线与x轴交于点Q，若过点Q的直线l与抛物线有公共点，则直线l的斜率的取值范围是( )A. B．[－2,2]C．[－1,1] D．[－4,4]答案C解析Q(－2,0)，设直线l的方程为y＝k(x＋2)，代入抛物线方程，消去y整理得k2x2＋(4k2－8)x＋4k2＝0，由Δ＝(4k2－8)2－4k2·4k2＝64(1－k2)≥0，解得－1≤k≤1.4．(教材改编)已知抛物线的顶点是原点，对称轴为坐标轴，并且经过点P(－2，－4)，则该抛物线的标准方程为________________．答案y2＝－8x或x2＝－y解析设抛物线方程为y2＝2px(p≠0)或x2＝2py(p≠0)．将P(－2，－4)代入，分别得方程为y2＝－8x或x2＝－y.5．(2017·合肥月考)已知抛物线y2＝2px(p>0)的准线与圆x2＋y2－6x－7＝0相切，则p的值为________．答案2解析抛物线y2＝2px(p>0)的准线为x＝－，圆x2＋y2－6x－7＝0，即(x－3)2＋y2＝16，则圆心为(3,0)，半径为4.又因为抛物线y2＝2px(p>0)的准线与圆x2＋y2－6x－7＝0相切，所以3＋＝4，解得p＝2.题型一抛物线的定义及应用例1 设P是抛物线y2＝4x上的一个动点，若B(3,2)，则|PB|＋|PF|的最小值为________．答案4解析如图，过点B作BQ垂直准线于点Q，交抛物线于点P1，则|P1Q|＝|P1F|.则有|PB|＋|PF|≥|P1B|＋|P1Q|＝|BQ|＝4.即|PB|＋|PF|的最小值为4.引申探究1．若将本例中的B点坐标改为(3,4)，试求|PB|＋|PF|的最小值．解由题意可知点(3,4)在抛物线的外部．∵|PB|＋|PF|的最小值即为B，F两点间的距离，∴|PB|＋|PF|≥|BF|＝42＋22＝＝2，即|PB|＋|PF|的最小值为2.2．若将本例中的条件改为：已知抛物线方程为y2＝4x，直线l的方程为x－y＋5＝0，在抛物线上有一动点P到y轴的距离为d1，到直线l的距离为d2，求d1＋d2的最小值．解由题意知，抛物线的焦点为F(1,0)．点P到y轴的距离d1＝|PF|－1，所以d1＋d2＝d2＋|PF|－1.易知d2＋|PF|的最小值为点F到直线l的距离，故d2＋|PF|的最小值为＝3，所以d1＋d2的最小值为3－1.思维升华与抛物线有关的最值问题，一般情况下都与抛物线的定义有关．由于抛物线的定义在运用上有较大的灵活性，因此此类问题也有一定的难度．“看到准线想焦点，看到焦点想准线”，这是解决抛物线焦点弦有关问题的重要途径．(2016·××市铁一中学模拟)已知点P是抛物线y2＝－8x上一点，设P到此抛物线准线的距离是d1，到直线x＋y－10＝0的距离是d2，则d1＋d2的最小值是( )A. B．2 C．6 D．3答案C解析∵抛物线方程是y2＝－8x，∴抛物线的焦点为F(－2,0)，准线方程是x＝2(如图)，∴d1＋d2的最小值是焦点F到直线x＋y－10＝0的距离，即(d1＋d2)min＝＝6.题型二抛物线的标准方程和几何性质命题点1 求抛物线的标准方程例2 已知双曲线C1：－＝1(a>0，b>0)的离心率为2.若抛物线C2：x2＝2py(p>0)的焦点到双曲线C1的渐近线的距离为2，则抛物线C2的方程为( ) A ．x2＝y B ．x2＝y C ．x2＝8y D ．x2＝16y答案 D解析 ∵－＝1的离心率为2， ∴＝2，即＝＝4，∴＝3，＝.x2＝2py(p>0)的焦点坐标为，－＝1的渐近线方程为y ＝±x，即y ＝±x.由题意得＝2，∴p＝8.故C2的方程为x2＝16y.命题点2 抛物线的几何性质例3 已知抛物线y2＝2px(p>0)的焦点为F ，A(x1，y1)，B(x2，y2)是过F 的直线与抛物线的两个交点，求证： (1)y1y2＝－p2，x1x2＝； (2)＋为定值；(3)以AB 为直径的圆与抛物线的准线相切． 证明 (1)由已知得抛物线焦点坐标为(，0)． 由题意可设直线方程为x ＝my ＋，代入y2＝2px ， 得y2＝2p ，即y2－2pmy －p2＝0.(*)则y1，y2是方程(*)的两个实数根，所以y1y2＝－p2. 因为y ＝2px1，y ＝2px2，所以yy ＝4p2x1x2， 所以x1x2＝＝＝. (2)＋＝＋1x2＋p 2＝.因为x1x2＝，x1＋x2＝|AB|－p，代入上式，得＋＝＝(定值)．(3)设AB的中点为M(x0，y0)，分别过A，B作准线的垂线，垂足为C，D，过M作准线的垂线，垂足为N，则|MN|＝(|AC|＋|BD|)＝(|AF|＋|BF|)＝|AB|.所以以AB为直径的圆与抛物线的准线相切．思维升华(1)求抛物线标准方程的常用方法是待定系数法，其关键是判断焦点位置、开口方向，在方程的类型已经确定的前提下，由于标准方程只有一个参数p，只需一个条件就可以确定抛物线的标准方程．(2)在解决与抛物线的性质有关的问题时，要注意利用几何图形的形象、直观的特点来解题，特别是涉及焦点、顶点、准线的问题更是如此．(1)(2016·全国乙卷)以抛物线C的顶点为圆心的圆交C于A，B两点，交C的准线于D，E两点．已知|AB|＝4，|DE|＝2，则C 的焦点到准线的距离为( )A．2 B．4 C．6 D．8(2)(2016·昆明三中、玉溪一中统考)抛物线y2＝2px(p>0)的焦点为F，已知点A、B 为抛物线上的两个动点，且满足∠AFB＝120°.过弦AB的中点M作抛物线准线的垂线MN，垂足为N，则的最大值为( )A. B．1 C. D．2答案(1)B (2)A解析(1)不妨设抛物线C：y2＝2px(p>0)，则圆的方程可设为x2＋y2＝r2(r>0)，如图，又可设A(x0,2)，D，点A(x0,2)在抛物线y2＝2px上，∴8＝2px0，①点A(x0,2)在圆x2＋y2＝r2上，∴x＋8＝r2，②点D在圆x2＋y2＝r2上，∴5＋2＝r2，③联立①②③，解得p＝4，即C的焦点到准线的距离为p＝4，故选B.(2)设|AF|＝a，|BF|＝b，分别过A、B作准线的垂线，垂足分别为Q、P，由抛物线的定义知，|AF|＝|AQ|，|BF|＝|BP|，在梯形ABPQ中，2|MN|＝|AQ|＋|BP|＝a＋b.|AB|2＝a2＋b2－2abc os 120°＝a2＋b2＋ab＝(a＋b)2－ab.又ab≤()2，所以(a＋b)2－ab≥(a＋b)2－(a＋b)2＝(a＋b)2，得到|AB|≥(a＋b)，所以≤＝，即的最大值为.题型三直线与抛物线的综合问题命题点1 直线与抛物线的交点问题例4 已知抛物线C：y2＝8x与点M(－2,2)，过C的焦点且斜率为k的直线与C交于A、B两点．若·＝0，则k＝________.答案2解析抛物线C的焦点为F(2,0)，则直线方程为y＝k(x－2)，与抛物线方程联立，消去y化简得k2x2－(4k2＋8)x＋4k2＝0.设点A(x1，y1)，B(x2，y2)．则x1＋x2＝4＋，x1x2＝4，所以y1＋y2＝k(x1＋x2)－4k＝，y1y2＝k2[x1x2－2(x1＋x2)＋4]＝－16.因为·＝(x1＋2，y1－2)·(x2＋2，y2－2)＝(x1＋2)(x2＋2)＋(y1－2)(y2－2)＝x1x2＋2(x1＋x2)＋y1y2－2(y1＋y2)＋8＝0，将上面各个量代入，化简得k2－4k＋4＝0，所以k＝2.命题点2 与抛物线弦的中点有关的问题例5 (2016·全国丙卷)已知抛物线C：y2＝2x的焦点为F，平行于x轴的两条直线l1，l2分别交C于A，B两点，交C的准线于P，Q两点．(1)若F在线段AB上，R是PQ的中点，证明：AR∥FQ；(2)若△PQF的面积是△ABF的面积的两倍，求AB中点的轨迹方程．(1)证明由题意知，F，设l1：y＝a，l2：y＝b，则ab≠0，且A，B，P，Q，R.记过A，B两点的直线为l，则l的方程为2x－(a＋b)y＋ab＝0.由于F在线段AB上，故1＋ab＝0.记AR的斜率为k1，FQ的斜率为k2，则k1＝＝＝＝－＝－b＝＝k2.所以AR∥FQ.(2)解设过AB的直线为l，设l与x轴的交点为D(x1,0)，则S△ABF＝|b－a||FD|＝|b－a|，S△PQF＝.由题意可得|b－a|＝，所以x1＝1，x1＝0(舍去)．设满足条件的AB的中点为E(x，y)．当AB与x轴不垂直时，由kAB＝kDE可得＝(x≠1)．而＝y，所以y2＝x－1(x≠1)．当AB与x轴垂直时，E与D重合，此时E点坐标为(1,0)，所以，所求轨迹方程为y2＝x－1(x≠1)．思维升华(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要用到根与系数的关系．(2)有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点．若过抛物线的焦点，可直接使用公式|AB|＝x1＋x2＋p，若不过焦点，则必须用一般弦长公式．(3)涉及抛物线的弦长、中点、距离等相关问题时，一般利用根与系数的关系采用“设而不求”、“整体代入”等解法．提醒：涉及弦的中点、斜率时一般用“点差法”求解．(2016·北京东××区质检)已知抛物线C：y2＝2px(p>0)的焦点为F，直线y＝4与y轴的交点为P，与C的交点为Q，且|QF|＝|PQ|.(1)求C的方程；(2)过F的直线l与C相交于A、B两点，若AB的垂直平分线l′与C相交于M、N两点，且A、M、B、N四点在同一圆上，求l的方程．解(1)设Q(x0,4)，代入y2＝2px，得x0＝.所以|PQ|＝，|QF|＝＋x0＝＋.由题设得＋＝×，解得p＝－2(舍去)或p＝2.所以C的方程为y2＝4x.(2)依题意知l与坐标轴不垂直，故可设l的方程为x＝my＋1(m≠0)．代入y2＝4x，得y2－4my－4＝0.设A(x1，y1)，B(x2，y2)，则y1＋y2＝4m，y1y2＝－4.故AB的中点为D(2m2＋1,2m)，|AB|＝|y1－y2|＝4(m2＋1)．又l′的斜率为－m，所以l′的方程为x＝－y＋2m2＋3.将上式代入y2＝4x，并整理得y2＋y－4(2m2＋3)＝0.设M(x3，y3)，N(x4，y4)，则y3＋y4＝－，y3y4＝－4(2m2＋3)．故MN的中点为E(＋2m2＋3，－)，|MN|＝ |y3－y4|＝，由于MN垂直平分AB，故A，M，B，N四点在同一圆上等价于|AE|＝|BE|＝|MN|，从而|AB|2＋|DE|2＝|MN|2，即4(m2＋1)2＋(2m＋)2＋(＋2)2＝，化简得m2－1＝0，解得m＝1或m＝－1.所求直线l的方程为x－y－1＝0或x＋y－1＝0.7．直线与圆锥曲线问题的求解策略典例(12分)已知抛物线C：y＝mx2(m>0)，焦点为F，直线2x－y＋2＝0交抛物线C 于A，B两点，P是线段AB的中点，过P作x轴的垂线交抛物线C于点Q.(1)求抛物线C的焦点坐标；(2)若抛物线C上有一点R(xR,2)到焦点F的距离为3，求此时m的值；(3)是否存在实数m，使△ABQ是以Q为直角顶点的直角三角形？若存在，求出m的值；若不存在，请说明理由．思维点拨(3)中证明·＝0.规范解答解(1)∵抛物线C：x2＝y，∴它的焦点F(0，)．[2分](2)∵|RF|＝yR ＋，∴2＋＝3，得m ＝.[4分](3)存在，联立方程⎩⎪⎨⎪⎧ y ＝mx2，2x －y ＋2＝0，消去y 得mx2－2x －2＝0，依题意，有Δ＝(－2)2－4×m×(－2)>0⇒m>－.[6分]设A(x1，mx)，B(x2，mx)，则(*)∵P 是线段AB 的中点，∴P(，)，即P(，yP)，∴Q(，)．[8分]得＝(x1－，mx －)，＝(x2－，mx －)，若存在实数m ，使△ABQ 是以Q 为直角顶点的直角三角形，则·＝0，即(x1－)·(x2－)＋(mx －)(mx －)＝0，[10分]结合(*)化简得－－＋4＝0，即2m2－3m －2＝0，∴m＝2或m ＝－，而2∈(－，＋∞)，－∉(－，＋∞)．∴存在实数m ＝2，使△ABQ 是以Q 为直角顶点的直角三角形．[12分]解决直线与圆锥曲线的位置关系的一般步骤：第一步：联立方程，得关于x 或y 的一元二次方程；第二步：写出根与系数的关系，并求出Δ>0时参数范围(或指出直线过曲线内一点)； 第三步：根据题目要求列出关于x1x2，x1＋x2(或y1y2，y1＋y2)的关系式，求得结果；第四步：反思回顾，查看有无忽略特殊情况．1．(2017·昆明质检)已知抛物线C 的顶点是原点O ，焦点F 在x 轴的正半轴上，经过F 的直线与抛物线C 交于A 、B 两点，如果·＝－12，那么抛物线C 的方程为( )A．x2＝8y B．x2＝4yC．y2＝8x D．y2＝4x答案C解析由题意，设抛物线方程为y2＝2px(p>0)，直线方程为x＝my＋，联立消去x得y2－2pmy－p2＝0，设A(x1，y1)，B(x2，y2)，则y1＋y2＝2pm，y1y2＝－p2，得·＝x1x2＋y1y2＝(my1＋)(my2＋)＋y1y2＝m2y1y2＋(y1＋y2)＋＋y1y2＝－p2＝－12⇒p＝4，即抛物线C的方程为y2＝8x.2．已知抛物线y2＝2px(p>0)，过其焦点且斜率为1的直线交抛物线于A、B两点，若线段AB的中点的纵坐标为2，则该抛物线的准线方程为( )A．x＝1 B．x＝－1C．x＝2 D．x＝－2答案B解析∵y2＝2px(p>0)的焦点坐标为(，0)，∴过焦点且斜率为1的直线方程为y＝x－，即x＝y＋，将其代入y2＝2px，得y2＝2py＋p2，即y2－2py－p2＝0.设A(x1，y1)，B(x2，y2)，则y1＋y2＝2p，∴＝p＝2，∴抛物线的方程为y2＝4x，其准线方程为x＝－1.3．(2016·上饶四校联考)设抛物线C：y2＝3px(p>0)的焦点为F，点M在C上，|MF|＝5，若以MF为直径的圆过点(0,2)，则抛物线C的方程为( )A．y2＝4x或y2＝8xB．y2＝2x或y2＝8xC．y2＝4x或y2＝16xD．y2＝2x或y2＝16x答案C解析∵抛物线C：y2＝3px(p>0)的焦点为F(，0)，∴|OF|＝，∵以MF为直径的圆过点(0,2)，设A(0,2)，连接AF，AM，可得AF⊥AM，在Rt△AOF 中，|AF|＝，∴sin∠OAF＝＝，根据抛物线的定义，得直线AO切以MF为直径的圆于点A，∴∠OAF＝∠AMF，可得在Rt△AMF中，sin∠AMF＝＝，∵|MF|＝5，|AF|＝，∴ ＝，整理得4＋＝，解得p＝或p＝，∴C的方程为y2＝4x或y2＝16x.4．已知抛物线y2＝2px(p>0)的焦点弦AB的两端点坐标分别为A(x1，y1)，B(x2，y2)，则的值一定等于( )A．－4 B．4C．p2 D．－p2答案A解析①若焦点弦AB⊥x轴，则x1＝x2＝，∴x1x2＝；∴y1＝p，y2＝－p，∴y1y2＝－p2，∴＝－4.②若焦点弦AB不垂直于x轴，可设AB的直线方程为y＝k(x－)，联立y2＝2px，得k2x2－(k2p＋2p)x＋＝0，则x1x2＝.∴y1y2＝－p2.故＝－4.5．(2016·江西南昌第一次模拟)已知抛物线C：y2＝8x的焦点为F，准线为l，P是l上一点，Q是线段PF与C的一个交点，若|FP|＝3|QF|，则|QF|等于( )A. B. C．3 D．2答案A解析如图所示，过点Q作QM⊥l，设l与x轴交于点K，由抛物线定义知，|MQ|＝|QF|，由△PMQ∽△PKF，得|MQ|：|KF|＝|PQ|∶|PF|＝2∶3，所以|QF|＝|MQ|＝|KF|＝×4＝，故选A.6．抛物线y2＝4x的焦点为F，点P(x，y)为该抛物线上的动点，若点A(－1,0)，则的最小值是( )A. B. C. D.223答案B解析抛物线y2＝4x的准线方程为x＝－1，如图，过P作PN垂直直线x＝－1于N，由抛物线的定义可知|PF|＝|PN|，连接PA，在Rt△PAN中，sin∠PAN＝，当＝最小时，sin∠PAN最小，即∠P AN最小，即∠PAF最大，此时，PA为抛物线的切线，设PA的方程为y＝k(x＋1)，联立得k2x2＋(2k2－4)x＋k2＝0，所以Δ＝(2k2－4)2－4k4＝0，解得k＝±1，所以∠PAF＝∠NPA＝45°，|PF|＝＝cos∠NPA＝，故选B.|PA|7．设F为抛物线C：y2＝3x的焦点，过F且倾斜角为30°的直线交C于A，B两点，则|AB|＝________.答案12解析焦点F的坐标为，方法一直线AB的斜率为，所以直线AB的方程为y＝，即y＝x－，代入y2＝3x，得x2－x＋＝0.设A(x1，y1)，B(x2，y2)，则x1＋x2＝，所以|AB|＝x1＋x2＋p＝＋＝12.方法二由抛物线焦点弦的性质可得|AB|＝＝＝12.8．已知抛物线C：y2＝2px(p>0)的准线为l，过M(1,0)且斜率为的直线与l相交于点A，与C的一个交点为B，若＝，则p＝________.答案2解析如图，由AB的斜率为，知∠α＝60°，又＝，∴M为AB的中点．过点B作BP垂直准线l于点P，则∠ABP＝60°，∴∠BAP＝30°，∴|BP|＝|AB|＝|BM|.∴M为焦点，即＝1，∴p＝2.9．已知椭圆E的中心在坐标原点，离心率为，E的右焦点与抛物线C：y2＝8x的焦点重合，A，B是C的准线与E的两个交点，则|AB|＝________.答案6解析抛物线y2＝8x的焦点为(2,0)，准线方程为x＝－2.设椭圆方程为＋＝1(a>b>0)，由题意，c＝2，＝，可得a＝4，b2＝16－4＝12.故椭圆方程为＋＝1.把x＝－2代入椭圆方程，解得y＝±3.从而|AB|＝6.10.设直线l与抛物线y2＝4x相交于A，B两点，与圆(x－5)2＋y2＝r2(r>0)相切于点M，且M为线段AB的中点．若这样的直线l恰有4条，则r的取值范围是________________．答案(2,4)解析如图，设A(x1，y1)，B(x2，y2)，M(x0，y0)，则⎩⎪⎨⎪⎧ y21＝4x1，y22＝4x2，两式相减，得(y1＋y2)(y1－y2)＝4(x1－x2)．当l 的斜率k 不存在时，符合条件的直线l 必有两条．当k 存在时，x1≠x2，则有·＝2，又y1＋y2＝2y0，所以y0k ＝2.由CM⊥AB，得k·＝－1，即y0k ＝5－x0，因此2＝5－x0，x0＝3，即M 必在直线x ＝3上．将x ＝3代入y2＝4x ，得y2＝12，则有－2<y0<2.因为点M 在圆上，所以(x0－5)2＋y ＝r2，故r2＝y ＋4<12＋4＝16.又y ＋4>4(为保证有4条，在k 存在时，y0≠0)，所以4<r2<16，即2<r<4.11．(2016·沈阳模拟)已知过抛物线y2＝2px(p>0)的焦点，斜率为2的直线交抛物线于A(x1，y1)，B(x2，y2)(x1<x2)两点，且|AB|＝9.(1)求该抛物线的方程；(2)O 为坐标原点，C 为抛物线上一点，若＝＋λ，求λ的值．解 (1)直线AB 的方程是y ＝2(x －)，与y2＝2px 联立，从而有4x2－5px ＋p2＝0. 所以x1＋x2＝，由抛物线定义得|AB|＝x1＋x2＋p＝＋p＝9，所以p＝4，从而抛物线方程为y2＝8x.(2)由于p＝4，则4x2－5px＋p2＝0，即x2－5x＋4＝0，从而x1＝1，x2＝4，于是y1＝－2，y2＝4，从而B(4,4)．设C(x3，y3)，则＝(x3，y3)＝(1，－2)＋λ(4,4)＝(4λ＋1,4λ－2)．又y＝8x3，即[2(2λ－1)]2＝8(4λ＋1)，整理得(2λ－1)2＝4λ＋1，解得λ＝0或λ＝2.12．设P，Q是抛物线y2＝2px(p>0)上相异两点，P，Q到y轴的距离的积为4，且·＝0.(1)求该抛物线的标准方程；(2)过点Q的直线与抛物线的另一交点为R，与x轴的交点为T，且Q为线段RT的中点，试求弦PR长度的最小值．解(1)设P(x1，y1)，Q(x2，y2)，∵·＝0，则x1x2＋y1y2＝0.又点P，Q在抛物线上，∴y＝2px1，y＝2px2，代入得·＋y1y2＝0，y1y2＝－4p2，∴|x1x2|＝＝4p2.又|x1x2|＝4，∴4p2＝4，p ＝1，∴抛物线的标准方程为y2＝2x.(2)设直线PQ 过点E(a,0)且方程为x ＝my ＋a ，联立方程组⎩⎪⎨⎪⎧ x ＝my ＋a ，y2＝2x ，消去x 得y2－2my －2a ＝0，∴①设直线PR 与x 轴交于点M(b,0)，则可设直线PR 的方程为x ＝ny ＋b ，并设R(x3，y3)，同理可知，②由①②可得＝.由题意得，Q 为线段RT 的中点，∴y3＝2y2，∴b＝2a.又由(1)知，y1y2＝－4，代入①，可得－2a ＝－4，∴a＝2，∴b＝4，y1y3＝－8，∴|PR|＝|y1－y3|＝·y1＋y32－4y1y3＝2·≥4.当n ＝0，即直线PR 垂直于x 轴时，|PR|取最小值4.13.如图，由部分抛物线：y2＝mx ＋1(m>0，x≥0)和半圆x2＋y2＝r2(x≤0)所组成的曲线称为“黄金抛物线C”，若“黄金抛物线C”经过点(3,2)和(－，)．(1)求“黄金抛物线C”的方程；(2)设P(0,1)和Q(0，－1)，过点P 作直线l 与“黄金抛物线C”相交于A ，P ，B 三点，问是否存在这样的直线l ，使得QP 平分∠AQB？若存在，求出直线l 的方程；若不存在，说明理由．解 (1)∵“黄金抛物线C”过点(3,2)和(－，)，∴r2＝(－)2＋()2＝1,4＝3m ＋1，∴m＝1.∴“黄金抛物线C”的方程为y2＝x ＋1(x≥0)和x2＋y2＝1(x≤0)．(2)假设存在这样的直线l ，使得QP 平分∠AQB，显然直线l 的斜率存在且不为0， 设直线l ：y ＝kx ＋1，联立消去y ，得k2x2＋(2k －1)x ＝0，∴xB＝，yB ＝，即B(，)，∴kBQ＝，联立⎩⎪⎨⎪⎧ y ＝kx ＋1，x2＋y2＝1，消去y ，得(k2＋1)x2＋2kx ＝0，∴xA＝－，yA ＝，即A(－，)，∴kAQ＝－，∵QP 平分∠AQB，∴kAQ＋kBQ ＝0，∴－＝0，解得k ＝－1±，由图形可得k ＝－1－应舍去，∴k＝－1，∴存在直线l ：y ＝(－1)x ＋1，使得QP 平分∠AQB.。

1抛物线的定义：平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹叫做抛物线，定点F 叫做抛物线的焦点，定直线l 叫做抛物线的准线． 2抛物线的图形和性质：①顶点是焦点向准线所作垂线段中点。

②焦准距：FK p =③通径：过焦点垂直于轴的弦长为2p 。

④顶点平分焦点到准线的垂线段：2p OF OK ==。

⑤焦半径为半径的圆：以P 为圆心、FP 为半径的圆必与准线相切。

所有这样的圆过定点F 、准线是公切线。

⑥焦半径为直径的圆：以焦半径 FP 为直径的圆必与过顶点垂直于轴的直线相切。

所有这样的圆过定点F 、过顶点垂直于轴的直线是公切线。

⑦焦点弦为直径的圆：以焦点弦PQ 为直径的圆必与准线相切。

所有这样的圆的公切线是准线。

3抛物线标准方程的四种形式：，，px y px y 2222-==。

，py x py x 2222-== 4抛物线px y 22=的图像和性质：①焦点坐标是：⎪⎭⎫⎝⎛02，p ，②准线方程是：2p x -=。

③焦半径公式：若点),(00y x P 是抛物线px y 22=上一点，则该点到抛物线的焦点的距离（称为焦半径）是：02p PF x =+， ④焦点弦长公式：过焦点弦长121222p pPQ x x x x p =+++=++ ⑤抛物线px y 22=上的动点可设为P ),2(2y py 或2(2,2)P pt pt 或P px y y x 2),(2=其中一般情况归纳：抛物线的定义：例1：点M 与点F (－4，0)的距离比它到直线l ：x －6=0的距离4.2，求点M 的轨迹方程． 分析：点M 到点F 的距离与到直线x =4的距离恰好相等，符合抛物线定义．例2：斜率为1的直线l 经过抛物线y 2=4x 的焦点，与抛物线相交于点A 、B ，求线段A 、B 的长．分析：这是灵活运用抛物线定义的题目．基本思路是：把求弦长AB 转化为求A 、B 两点到准线距离的和．解：如图8－3－1，y 2=4x 的焦点为F (1，0)，则l 的方程为y =x －1．由⎩⎨⎧+==142x y x y 消去y 得x 2－6x +1=0． 设A (x 1，y 1)，B (x 2，y 2) 则x 1+x 2=6． 又A 、B 两点到准线的距离为A '，B '，则()()()8262112121=+=++=+++='+'x x x x B B A A点评：抛物线的定义本身也是抛物线最本质的性质，在解题中起到至关重要的作用。

第7讲 抛物线[基础题组练]1．(2019·高考全国卷Ⅱ)若抛物线y 2＝2px (p >0)的焦点是椭圆x 23p ＋y 2p＝1的一个焦点，则p ＝( )A ．2B ．3C ．4D ．8解析：选D.由题意，知抛物线的焦点坐标为⎝ ⎛⎭⎪⎫p2，0，椭圆的焦点坐标为(±2p ，0)，所以p2＝2p ，解得p ＝8，故选D. 2．若点A ，B 在抛物线y 2＝2px (p >0)上，O 是坐标原点，若正三角形OAB 的面积为43，则该抛物线方程是( )A ．y 2＝233xB ．y 2＝3x C ．y 2＝23xD ．y 2＝33x 解析：选A.根据对称性，AB ⊥x 轴，由于正三角形的面积是43，故34AB 2＝43，故AB ＝4，正三角形的高为23，故可设点A 的坐标为(23，2)，代入抛物线方程得4＝43p ，解得p ＝33，故所求抛物线的方程为y 2＝233x .故选A. 3．(2019·甘肃张掖诊断)过抛物线y 2＝4x 的焦点的直线l 交抛物线于P (x 1，y 1)，Q (x 2，y 2)两点，如果x 1＋x 2＝6，则|PQ |＝( )A ．9B ．8C ．7D ．6解析：选B.抛物线y 2＝4x 的焦点为F (1，0)，准线方程为x ＝－1.根据题意可得，|PQ |＝|PF |＋|QF |＝x 1＋1＋x 2＋1＝x 1＋x 2＋2＝8.故选B.4．(2019·昆明调研)过抛物线C ：y 2＝2px (p ＞0)的焦点F 且倾斜角为锐角的直线l 与C 交于A ，B 两点，过线段AB 的中点N 且垂直于l 的直线与C 的准线交于点M ，若|MN |＝|AB |，则l 的斜率为( )A.13B.33C.32D ．1解析：选B.设抛物线的准线为m ，分别过点A ，N ，B 作AA ′⊥m ，NN ′⊥m ，BB ′⊥m ，垂足分别为A ′，N ′，B ′.因为直线l 过抛物线的焦点，所以|BB ′|＝|BF |，|AA ′|＝|AF |.又N 是线段AB 的中点，|MN |＝|AB |，所以|NN ′|＝12(|BB ′|＋|AA ′|)＝12(|BF |＋|AF |)＝12|AB |＝12|MN |，所以∠MNN ′＝60°，则直线MN 的倾斜角为120°.又MN ⊥l ，所以直线l 的倾斜角为30°，斜率是33.故选B. 5．(2019·合肥模拟)已知直线y ＝k (x ＋2)(k ＞0)与抛物线C ：y 2＝8x 相交于A ，B 两点，F 为C 的焦点．若|FA |＝2|FB |，则k ＝( )A.13B.23C.23D.223解析：选D.设抛物线C ：y 2＝8x 的准线为l ，易知l ：x ＝－2， 直线y ＝k (x ＋2)恒过定点P (－2，0)，如图，过A ，B 分别作AM ⊥l 于点M ，BN ⊥l 于点N ，由|FA |＝2|FB |，知|AM |＝2|BN |， 所以点B 为线段AP 的中点，连接OB ， 则|OB |＝12|AF |，所以|OB |＝|BF |，所以点B 的横坐标为1， 因为k ＞0，所以点B 的坐标为(1，22)， 所以k ＝22－01－（－2）＝223.故选D.6．抛物线C ：y 2＝2px (p >0)的焦点为F ，点O 是坐标原点，过点O ，F 的圆与抛物线C 的准线相切，且该圆的面积为36π，则抛物线的方程为________．解析：设满足题意的圆的圆心为M . 根据题意可知圆心M 在抛物线上， 又因为圆的面积为36π，所以圆的半径为6，则|MF |＝x M ＋p 2＝6，即x M ＝6－p2，又由题意可知x M ＝p 4，所以p 4＝6－p2，解得p ＝8.所以抛物线方程为y 2＝16x . 答案：y 2＝16x7．设抛物线C ：y 2＝4x 的焦点为F ，过点(－2，0)且斜率为23的直线与C 交于M ，N 两点，则FM →·FN →＝________．解析：设M (x 1，y 1)，N (x 2，y 2)．由已知可得直线的方程为y ＝23(x ＋2)，即x ＝32y －2，由⎩⎪⎨⎪⎧y 2＝4x ，x ＝32y －2得y 2－6y ＋8＝0. 由根与系数的关系可得y 1＋y 2＝6，y 1y 2＝8，所以x 1＋x 2＝32(y 1＋y 2)－4＝5，x 1x 2＝（y 1y 2）216＝4，因为F (1，0)，所以FM →·FN →＝(x 1－1)·(x 2－1)＋y 1y 2＝x 1x 2－(x 1＋x 2)＋1＋y 1y 2＝4－5＋1＋8＝8.答案：88．(一题多解)(2018·高考全国卷Ⅲ)已知点M (－1，1)和抛物线C ：y 2＝4x ，过C 的焦点且斜率为k 的直线与C 交于A ，B 两点．若∠AMB ＝90°，则k ＝________．解析：法一：由题意知抛物线的焦点为(1，0)，则过C 的焦点且斜率为k 的直线方程为y＝k (x －1)(k ≠0)，由⎩⎪⎨⎪⎧y ＝k （x －1），y 2＝4x ，消去y 得k 2(x －1)2＝4x ，即k 2x 2－(2k 2＋4)x ＋k 2＝0，设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝2k 2＋4k 2，x 1x 2＝1.由⎩⎪⎨⎪⎧y ＝k （x －1），y 2＝4x ，消去x 得y 2＝4⎝ ⎛⎭⎪⎫1k y ＋1，即y 2－4k y －4＝0，则y 1＋y 2＝4k，y 1y 2＝－4，由∠AMB ＝90°，得MA →·MB →＝(x 1＋1，y 1－1)·(x 2＋1，y 2－1)＝x 1x 2＋x 1＋x 2＋1＋y 1y 2－(y 1＋y 2)＋1＝0，将x 1＋x 2＝2k 2＋4k 2，x 1x 2＝1与y 1＋y 2＝4k，y 1y 2＝－4代入，得k ＝2.法二：设抛物线的焦点为F ，A (x 1，y 1)，B (x 2，y 2)，则⎩⎪⎨⎪⎧y 21＝4x 1，y 22＝4x 2，所以y 21－y 22＝4(x 1－x 2)，则k ＝y 1－y 2x 1－x 2＝4y 1＋y 2，取AB 的中点M ′(x 0，y 0)，分别过点A ，B 作准线x ＝－1的垂线，垂足分别为A ′，B ′，又∠AMB ＝90°，点M 在准线x ＝－1上，所以|MM ′|＝12|AB |＝12(|AF |＋|BF |)＝12(|AA ′|＋|BB ′|)．又M ′为AB 的中点，所以MM ′平行于x 轴，且y 0＝1，所以y 1＋y 2＝2，所以k ＝2.答案：29．已知抛物线y 2＝2px (p >0)的焦点为F ，A 是抛物线上横坐标为4，且位于x 轴上方的点，A 到抛物线准线的距离等于5，过A 作AB 垂直于y 轴，垂足为B ，OB 的中点为M .(1)求抛物线的方程；(2)若过M 作MN ⊥FA ，垂足为N ，求点N 的坐标． 解：(1)抛物线y 2＝2px 的准线为x ＝－p2，于是4＋p2＝5，所以p ＝2.所以抛物线方程为y 2＝4x . (2)因为点A 的坐标是(4，4)， 由题意得B (0，4)，M (0，2)． 又因为F (1，0)，所以k FA ＝43，因为MN ⊥FA ，所以k MN ＝－34.又FA 的方程为y ＝43(x －1)，①MN 的方程为y －2＝－34x ，②联立①②，解得x ＝85，y ＝45，所以点N 的坐标为⎝ ⎛⎭⎪⎫85，45. 10．已知过抛物线y 2＝2px (p >0)的焦点，斜率为22的直线交抛物线于A (x 1，y 1)，B (x 2，y 2)(x 1<x 2)两点，且|AB |＝9.(1)求该抛物线的方程；(2)O 为坐标原点，C 为抛物线上一点，若OC →＝OA →＋λOB →，求λ的值．解：(1)由题意得直线AB 的方程为y ＝22·⎝ ⎛⎭⎪⎫x －p 2，与y 2＝2px 联立，消去y 有4x 2－5px ＋p 2＝0， 所以x 1＋x 2＝5p4.由抛物线定义得|AB |＝x 1＋x 2＋p ＝5p4＋p ＝9，所以p ＝4，从而该抛物线的方程为y 2＝8x . (2)由(1)得4x 2－5px ＋p 2＝0， 即x 2－5x ＋4＝0， 则x 1＝1，x 2＝4，于是y 1＝－22，y 2＝42，从而A (1，－22)，B (4，42)，设C (x 3，y 3)， 则OC →＝(x 3，y 3)＝(1，－22)＋λ(4，42) ＝(4λ＋1，42λ－22)．又y 23＝8x 3，所以[22(2λ－1)]2＝8(4λ＋1)， 整理得(2λ－1)2＝4λ＋1， 解得λ＝0或λ＝2.[综合题组练]1．(2019·重庆六校联考)已知双曲线C 1：x 2a 2－y 2b2＝1(a ＞0，b ＞0)的离心率为2，若抛物线C 2：x 2＝2py (p ＞0)的焦点到双曲线C 1的渐近线的距离为2，则抛物线C 2的方程是( )A ．x 2＝16yB ．x 2＝8y C ．x 2＝833yD ．x 2＝1633y解析：选A.因为双曲线C 1：x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的离心率为2，所以c a ＝2，即a 2＋b 2a 2＝4，所以b 2a 2＝3.因为双曲线的渐近线方程为bx ±ay ＝0，抛物线C 2：x 2＝2py (p ＞0)的焦点⎝ ⎛⎭⎪⎫0，p 2到双曲线的渐近线的距离为2，所以⎪⎪⎪⎪⎪⎪a ·p 2a 2＋b2＝2，解得p ＝8，所以抛物线C 2的方程是x 2＝16y .2．(2019·湖南郴州模拟)如图，过抛物线y 2＝2px (p ＞0)的焦点F 的直线交抛物线于点A ，B ，交其准线l 于点C ，若|BC |＝2|BF |，且|AF |＝3，则此抛物线的方程是( )A ．y 2＝9x B ．y 2＝6x C ．y 2＝3xD ．y 2＝3x解析：选C.设A ，B 在准线l 上的射影分别为A 1，B 1，如图，由于|BC |＝2|BF |＝2|BB 1|，则直线AB 的斜率为3，故|AC |＝2|AA 1|＝2|AF |＝6， 从而|BF |＝1，|AB |＝4， 故p |AA 1|＝|CF ||AC |＝12，即p ＝32， 从而抛物线的方程为y 2＝3x ，故选C.3．(2019·广东六校第一次联考)抛物线y ＝2x 2上有一动弦AB ，中点为M ，且弦AB 的长为3，则点M 的纵坐标的最小值为( )A.118 B.54 C.32D ．1 解析：选A.由题意设A (x 1，y 1)，B (x 2，y 2)，M (x 0，y 0)，直线AB 的方程为y ＝kx ＋b .由题意知y 0≥b ＞0，联立得⎩⎪⎨⎪⎧y ＝kx ＋b y ＝2x 2，整理得2x 2－kx －b ＝0，Δ＝k 2＋8b ＞0，x 1＋x 2＝k 2，x 1x 2＝－b2，则|AB |＝1＋k2k 24＋2b ，点M 的纵坐标y 0＝y 1＋y 22＝x 21＋x 22＝k 24＋b .因为弦AB 的长为3，所以1＋k2k 24＋2b ＝3，即(1＋k 2)(k 24＋2b )＝9，故(1＋4y 0－4b )(y 0＋b )＝9，即(1＋4y 0－4b )(4y 0＋4b )＝36.由基本不等式得，(1＋4y 0－4b )＋(4y 0＋4b )≥2（1＋4y 0－4b ）（4y 0＋4b ）＝12，当且仅当⎩⎪⎨⎪⎧b ＝18y 0＝118时取等号，即1＋8y 0≥12，y 0≥118，点M 的纵坐标的最小值为118，故选A.4．已知直线y ＝a 交抛物线y ＝x 2于A ，B 两点．若该抛物线上存在点C ，使得∠ACB 为直角，则实数a 的取值范围为________．解析：如图，设C (x 0，x 20)(x 20≠a )，A (－a ，a )，B (a ，a )， 则CA →＝(－a －x 0，a －x 20)，CB →＝(a －x 0，a －x 20)．因为CA ⊥CB ，所以CA →·CB →＝0，即－(a －x 20)＋(a －x 20)2＝0，(a －x 20)(－1＋a －x 20)＝0， 所以x 20＝a －1≥0，所以a ≥1. 答案：[1，＋∞)5．(应用型)(2019·湖南六校联考)已知抛物线的方程为x 2＝2py (p >0)，其焦点为F ，点O 为坐标原点，过焦点F 作斜率为k (k ≠0)的直线与抛物线交于A ，B 两点，过A ，B 两点分别作抛物线的两条切线，设两条切线交于点M .(1)求OA →·OB →；(2)设直线MF 与抛物线交于C ，D 两点，且四边形ACBD 的面积为323p 2，求直线AB 的斜率k .解：(1)设直线AB 的方程为y ＝kx ＋p 2，A (x 1，y 1)，B (x 2，y 2)，由⎩⎪⎨⎪⎧x 2＝2py ，y ＝kx ＋p 2，得x 2－2pkx －p 2＝0，则⎩⎪⎨⎪⎧x 1＋x 2＝2pk ，x 1·x 2＝－p 2，所以y 1·y 2＝p 24， 所以OA →·OB →＝x 1·x 2＋y 1·y 2＝－34p 2.(2)由x 2＝2py ，知y ′＝x p，所以抛物线在A ，B 两点处的切线的斜率分别为x 1p ，x 2p ，所以直线AM 的方程为y －y 1＝x 1p(x －x 1)，直线BM 的方程为y －y 2＝x 2p (x －x 2)，则可得M ⎝⎛⎭⎪⎫pk ，－p 2.所以k MF ＝－1k，所以直线MF 与AB 相互垂直．由弦长公式知，|AB |＝k 2＋1|x 1－x 2|＝k 2＋1·4p 2k 2＋4p 2＝2p (k 2＋1)， 用－1k代替k 得，|CD |＝2p ⎝ ⎛⎭⎪⎫1k 2＋1，四边形ACBD 的面积S ＝12·|AB |·|CD |＝2p 2⎝ ⎛⎭⎪⎫2＋k 2＋1k 2＝323p 2，解得k 2＝3或k 2＝13，即k ＝±3或k ＝±33. 6．(创新型)(2019·武汉调研)已知抛物线C ：x 2＝2py (p ＞0)和定点M (0，1)设过点M 的动直线交抛物线C 于A ，B 两点，抛物线C 在A ，B 处的切线的交点为N .(1)若N 在以AB 为直径的圆上，求p 的值；(2)若△ABN 的面积的最小值为4，求抛物线C 的方程． 解：设直线AB ：y ＝kx ＋1，A (x 1，y 1)，B (x 2，y 2)， 将直线AB 的方程代入抛物线C 的方程得x 2－2pkx －2p ＝0， 则x 1＋x 2＝2pk ，x 1x 2＝－2p .①(1)由x 2＝2py 得y ′＝x p ，则A ，B 处的切线斜率的乘积为x 1x 2p 2＝－2p， 因为点N 在以AB 为直径的圆上，所以AN ⊥BN ， 所以－2p＝－1，所以p ＝2.(2)易得直线AN ：y －y 1＝x 1p (x －x 1)，直线BN ：y －y 2＝x 2p(x －x 2)，联立，得⎩⎪⎨⎪⎧y －y 1＝x1p（x －x 1），y －y 2＝x2p （x －x 2），结合①式，解得⎩⎪⎨⎪⎧x ＝pk ，y ＝－1，即N (pk ，－1)．|AB |＝1＋k 2|x 2－x 1|＝1＋k 2（x 1＋x 2）2－4x 1x 2＝1＋k24p 2k 2＋8p ，点N 到直线AB 的距离d ＝|kx N ＋1－y N |1＋k 2＝|pk 2＋2|1＋k2， 则△ABN 的面积S △ABN ＝12·|AB |·d ＝p （pk 2＋2）3≥22p ，当k ＝0时，取等号，因为△ABN 的面积的最小值为4，所以22p ＝4，所以p ＝2，故抛物线C 的方程为x 2＝4y .。

线练习理编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（江苏专用）2018版高考数学专题复习专题9 平面解析几何第64练抛物线练习理）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（江苏专用）2018版高考数学专题复习专题9 平面解析几何第64练抛物线练习理的全部内容。

物线练习理训练目标熟练掌握抛物线的定义及几何性质,能利用定义、几何性质解决有关问题．训练题型(1)求抛物线方程；（2）利用定义、几何性质求最值、参数范围、弦长等．解题策略(1)利用定义进行转化；(2）掌握关于弦长、焦半径的重要结论；（3)恰当运用函数与方程思想、数形结合思想.1．,焦点在x轴上，若曲线C经过点P(1,3)，则其焦点到准线的距离为________．2．已知抛物线C：y2＝8x的焦点为F,准线为l，P是l上一点，Q是直线PF与C的一个交点．若错误!＝4错误!，则QF＝____________.3．已知抛物线C：y2＝4x,顶点为O，动直线l:y＝k(x＋1）与抛物线C交于A,B两点，则错误!·错误!的值为________．4．(2016·长春一模）过抛物线y2＝2px(p＞0)的焦点F且倾斜角为120°的直线l与抛物线在第一、四象限分别交于A、B两点，则错误!＝________。

5．(2016·无锡模拟)如图,过抛物线y2＝2px(p＞0）的焦点F的直线l依次交抛物线及其准线于点A,B，C,若BC＝2BF，且AF＝3,则抛物线的方程是______________．6．(2016·黑龙江哈尔滨三中一模）直线l与抛物线C:y2＝2x交于A，B两点，O为坐标原点．若直线OA，OB的斜率k1，k2满足k1k2＝23,则l过定点________．7．（2016·常州模拟）如图，抛物线C：y2＝2px（p＞0)的焦点为F，A为抛物线C上的点，以F为圆心，错误!为半径的圆与直线AF在第一象限的交点为B，∠AFO＝120°,A在y轴上的投影为N，则∠ONB＝________.8．已知抛物线x2＝4y上有一条长为6的动弦AB，则AB的中点到x轴的最短距离为________．9．(2016·福建质检)过抛物线y2＝2px(p＞0）的焦点作倾斜角为30°的直线l与抛物线交于P,Q两点，分别过P，Q两点作PP，QQ1垂直于抛线物的准线于P1,Q1，若PQ＝2,则四边形PP1Q1Q1的面积是________．10．（2016·镇江模拟）已知过拋物线y2＝4x的焦点F的直线交该抛物线于A，B两点，O是坐标原点,AF＝2，则BF＝______，△OAB的面积是________．11．如图是抛物线形拱桥，当水面在l时，拱顶离水面2米，水面宽4米．水位下降1米后，水面宽________米．12．（2016·石家庄质量检测二）设抛物线C：y2＝4x的焦点为F，过F的直线l与抛物线交于A，B两点，M为抛物线C的准线与x轴的交点．若tan∠AMB＝2错误!，则AB＝________. 13．过抛物线y2＝4x的焦点F作直线交抛物线于A，B两点,若AB＝8，AF＜BF，则BF＝________。

解析几何（6）抛物线1、已知抛物线2:2C y x =，过原点作两条互相垂直的直线分别交C 于,A B 两点（,A B 均不与坐标原点重合），则抛物线的焦点F 到直线AB 距离的最大值为( ) A ．2 B ．3 C ．32D ．4 2、抛物线2?y x =上一点到直线240x y --=的距离最短的点的坐标是()A.()2,4B. 11,24⎛⎫ ⎪⎝⎭C. 39,24⎛⎫ ⎪⎝⎭D.()1,13、已知直线1:4360l x y -+=和直线2:1l x =-,抛物线24y x =上一动点P 到直线1l 和直线2l 的距离之和的最小值是( ) A.3716 B. 3 C.115D. 24、设抛物线24y x =上一点P 到此抛物线准线的距离为1d ,到直线:34120l x y ++=的距离为2d ,则12d d +的最小值为( ) A. 3?B.165 C. 185D. 45、抛物线2y x =-上的一点到直线4380x y +-=的距离的最小值是( )A.75B.85C.43D.3?6、直线l 与抛物线2:2C y x =交于,A B 两点, O 为坐标原点,若直线,OA OB 的斜率12k k ，满足1223k k =,则直线l 过定点( ) A.(-3,0) B.(0,-3) C.(3,0) D.(0,3)7、已知抛物线2:4C y x =的焦点为F ,过点 F 作斜率为1的直线l 交抛物线 C 于,?P Q 两点,则11PF QF+ 的值为( ) A.12 B. 78C. 1D. 28、直线l 与抛物线22016y x =交于,A B 两点, O 为坐标原点,若2015OA OB ⋅=-u u u r u u u r,则直线l 可能过定点( )A.(504,0)B.(1008,0)C.(2015,0)D.(2016,0)9、直线l 与抛物线2:2C y x =交于,A B 两点，O 为坐标原点，若直线,OA OB 的斜率12,k k 满足1223k k =，则直线l 过定点（ ） A. (3,0)B. (0,3)C. (3,0)-D.(0,3)-10、过抛物线2(0)y mx m =>焦点的直线l 与抛物线交于,A B 两点,以AB 为直径的圆的方程为22(4)(2)25x y -+-=,则m =( ) A.2B.4C.2或4D.1011、抛物线()220y px p =>的焦点为F ，已知点A ，B 为抛物线上的两个动点，且满足120AFB ∠=o．过弦AB 的中点M 作抛物线准线的垂线MN ，垂足为N ，则MN AB的最大值为（ ）AB ．1 D 12、抛物线2:2(0)C y px p =>的焦点为,F A 是C 上一点，若A 到F 的距离是A 到y 轴距离的两倍，且三角形OAF 的面积为1（O 为坐标原点），则P 的值为（ ） A.1B.2C.3D.413、已知抛物线2:C y x =，过C 的焦点的直线与C 交于A ，B 两点。

(江苏专用)2018版高考数学专题复习专9平面解析几何第64练高考大题突破练圆锥曲线练习文■ ■1. (2015 -重庆)如图，椭圆W+2=l(a>b>0)的左，右焦点分别为凡尽过尺的直线交a b椭圆于只0两点，且必丄朋.⑴若彤=2+花，恋=2-迈，求椭圆的标准方程：⑵若PR = PQ、求椭圆的离心率e.2. (2016 •四川)已知椭圆E j+$=l(a>b>0)的一个焦点与短轴的两个端点是正三角形的三个顶点，点彳萌，在椭圆5±.(1) 求椭圆尸的方程：(2) 设不过原点0且斜率为*的直线2与椭圆厅交于不同的两点儿B,线段月万的中点为"，直线购与椭圆疋交于C、D.证明：•曲•yfD.3. (2016 •四川)已知椭圆氏芝+圣=l(a>Q0)的两个焦点与短轴的一个端点是直角三角a b形的三个顶点，直线去尸一x+3与椭圆E有且只有一个公共点7：(1) 求椭圆疋的方程及点2■的坐标：(2) 设0是坐标原点，直线F平行于0T,与椭圆f■交于不同的两点儿5,且与直线/交于点只证明：存在常数久，使得Pf= APA-PB,并求人的值.・・y V4. (2015 -江苏)如图，在平而直角坐标系灿冲，已知椭圆-+£=1(&>b>0)的藹心率为a o申，且右焦点尸到直线厶*=一兰的距离为3.Z C(1) 求椭圆的标准方程：(2) 过尸的直线与椭圆交于儿万两点，线段丽的垂直平分线分别交直线』和曲于点只G若PC=2AB,求宜线M的方程.答案精析——圆锥曲线1. 解⑴由椭圆的定义，有2&=朋+出=(2+住)+ (2—迈)=4,故a=2・设椭圆的半焦距为c,由已知朋丄出，得2C=RE=7P E+M=-\/ 2+^2 2+ 2-^/2 2=2^3，即c=©从而二7=1.故所求椭圆的标准方程为f+/=l.(2)连结応0,由椭圆的定义,有PF"PF：=2a、QFd QF：=2a・从而由朋=PQ= PFAQFt、有QF、=X-2P玖・又由朋丄P2 PF、= PQ、知QF尸乜PF、、因此，4a-2PR=£pR,得朋=2(2-住)乩从而啟=2a-朋=2&—2(2—花)&=2(£-1)&・由〃丄啟，知/近+顷=尺忙—(2c)因此亠逻坯a 2a= ~2—^2 ~~^2—1 ~=寸9_6 边=& -羽・2. ⑴解由已知，a=2b,R C・■又椭圆W+2=l(a>b>0)过点a b棚,另，13 4故［了+牙=1，解得b~=l・所以椭圆疋的方程是|+/=1.(2)证明设直线2的方程为缶H0),月⑴，如，駅疋，比).R+y==i>, . ^由方程组$ 得才+2e*+2/zf — 2=0,①［尸$+也，方程①的判别式为4 =4亦一4(2/—2), 由4>0,即2—怎>0,解得一£<也<£・由①得及+上=一2皿上北=2/—2・又yfA・.妇討=t ［（及一龙）'+（H 一北）J =猪［（山+龙）=—4-Y J.Y：］5 . 5=—jliif — 4（2zn —2）］ =^-（2 —zzf）・所以MA・MB=MC・MD・■ ■3. ⑴解由已知，a=£b,则椭圆疋的方程为寿+£=1・由方程组＜厉+g_l'.y=--v+3,得3A;-12.Y+18-262=0.①方程①的判别式为4 =24（歹一3）,由4=0,得U=3,此时方程①的解为x=2,歼R・■V y所以椭圆疋的方程为才+寸=1，点7的坐标为（2, 1）.（2）证明由已知可设直线T的方程为卩=$+加（亦0）,直线01/方程为y=—芬所以"点坐标为（一皿=7（2~zzf）・4y=**+皿所以尸点坐标为(2—寻，1+割.8 .PP设点儿万的坐标分别为礼s必),Bld yt)・3”+4znx+4方—12=0.②方程②的判别式为4 =16(9—2/),由4＞0,解得-甕＜应＜哮.所以刊=4h-y同理PB=^2~-4nf—1234 故存在常数人=了使得Pf= APA・PB.所以PA • PB-Vi + -V：由方程组・■6 + 3~b可得4m由②得及+上=一"4/zf —123=_310 .4. 解⑴由题意，得£=芈且c+?=3,解得 a=yj29 c=l,则 b=l 9 所以椭圆的标准方程为专+y=i.（2）当ABLx 轴时，AB=©又CP=3、不合题意.当？15与x 轴不垂直时，设直线曲的方程为y=kCv —l ）,yj, 5（x :,北）, 将直线月万的方程代入椭圆方程，得（1 + 2尸）£ 一 4&・+ 2 （尸一 1） = 0,Q 的坐标为（希’去）’且AB=p x z —xi :4- yz —yt =p 1 + F X z —X\~" 护 1+F二 1 + 2尸•若k=0,则线段曲的垂直平分线为y 轴，与直线』平行，不合题意. 从而&H0,故宜线比的方程为 卄悬一治-澄7），因为 PC=2AB.2 3尸+1 小+尸_ 4也 1+片 所以I" 1+2左 〜1 + 2片解得&=±1・此时直线曲的方程为y=x-l 或y=—x+l ・则尸点的坐标为（一2 从而PC=- 3#+1 寸1+尸k 1 + 2 戸 *5F+2 k 1+ 2#。

2024届高考数学复习：精选好题专项（抛物线）练习[基础巩固]一、选择题1．抛物线y＝14x2的焦点到其准线的距离为()A．1 B．2C．12D．182．已知抛物线y2＝2px(p>0)的准线经过点(－1，1)，则该抛物线的焦点坐标为() A．(－1，0) B．(1，0)C．(0，－1) D．(0，1)3．动点M到点F(2，1)的距离和到直线l：3x＋4y－10＝0的距离相等，则动点M的轨迹为()A．抛物线B．直线C．线段D．射线4．若抛物线y2＝2px的焦点与双曲线x23－y2＝1的右焦点重合，则p的值为()A．－4 B．4C．－2 D．25．[2022ꞏ全国乙卷(文)，6] 设F为抛物线C：y2＝4x的焦点，点A在C上，点B(3，0)，若|AF|＝|BF|，则|AB|＝()A.2 B．22C．3 D．326．若抛物线y2＝2px(p>0)的焦点是椭圆x23p＋y2p＝1的一个焦点，则p＝()A．2 B．3C．4 D．87.如图，过抛物线y2＝2px(p>0)的焦点F的直线依次交抛物线及准线于点A，B，C，若|BC|＝2|BF|，且|AF|＝4，则抛物线的方程为()A．y2＝8x B．y2＝4xC．y2＝2x D．y2＝x8．设坐标原点为O ，抛物线y 2＝2x 与过焦点的直线交于A ，B 两点，则OA → ꞏOB →等于( )A ．34B ．－34C ．3D ．－39．已知抛物线y 2＝2px (p >0)的焦点为F ，准线为l ，过点F 的直线交抛物线于A ，B 两点，过点A 作准线l 的垂线，垂足为E ，当A 点坐标为(3，y 0)时，△AEF 为正三角形，则此时△OAB 的面积为( )A ．433 B ．3C ．233D ．33二、填空题10．[2021ꞏ新高考Ⅰ卷]已知O 为坐标原点，抛物线C ：y 2＝2px (p ＞0)的焦点为F ，P 为C 上一点，PF 与x 轴垂直，Q 为x 轴上一点，且PQ ⊥OP ，若|FQ |＝6，则C 的准线方程为________．11．[2023ꞏ全国乙卷(理)]已知点A ()1，5 在抛物线C ：y 2＝2px 上，则A 到C 的准线的距离为________．12．已知直线y ＝kx ＋2与抛物线y 2＝8x 有且只有一个公共点，则k 的值为________．[强化练习]13．(多选)[2023ꞏ新课标Ⅱ卷]设O 为坐标原点，直线y ＝－3 (x －1)过抛物线C ：y 2＝2px (p >0)的焦点，且与C 交于M ，N 两点，l 为C 的准线，则( )A ．p ＝2B ．|MN |＝83C ．以MN 为直径的圆与l 相切D ．△OMN 为等腰三角形 14．抛物线有如下光学性质：过焦点的光线经抛物线反射后得到的光线平行于抛物线的对称轴；反之，平行于抛物线对称轴的入射光线经抛物线反射后必过抛物线的焦点．已知抛物线y 2＝4x 的焦点为F ，一条平行于x 轴的光线从点M (3，1)射出，经过抛物线上的点A 反射后，再经抛物线上的另一点B 射出，则△ABM 的周长为( )A ．7112 ＋26 B ．9＋26C ．9＋10D ．8312 ＋2615．已知抛物线C ：y 2＝2px (p >0)的焦点为F ，准线为l ，抛物线C 有一点P ，过点P 作PM ⊥l ，垂足为M ，若等边△PMF 的面积为43 ，则p ＝________．16．过抛物线y 2＝2px (p >0)的焦点F 作倾斜角为60°的直线，与抛物线分别交于A ，B两点(点A 在x 轴上方)，则|AF ||BF | ＝________.参考答案1．B y ＝14 x 2可化为x 2＝4y ，则焦点到准线的距离为12 ×4＝2.2．B ∵y 2＝2px 的准线为x ＝－p 2 ，又准线过点(－1，1)，∴－p2 ＝－1，∴p ＝2，故其焦点坐标为(1，0).3．B ∵F (2，1)在直线l ：3x ＋4y －10＝0上，∴动点M 的轨迹为过点F 且与直线l 垂直的直线．4．B ∵x 23 －y 2＝1的右焦点为(2，0)，∴p2 ＝2，p ＝4.5．B 由已知条件，易知抛物线y 2＝4x 的焦点为F (1，0)，准线方程为x ＝－1.又B (3，0)，则|AF |＝|BF |＝2.不妨设点A 在第一象限，则A (x 0，2x 0 ).根据抛物线的定义可知x 0－(－1)＝2，所以x 0＝1，所以A (1，2)，所以|AB |＝（1－3）2＋（2－0）2 ＝22 .故选B.6．D 由题意，知抛物线的焦点坐标为⎝⎛⎭⎫p 2，0 ，椭圆的焦点坐标为(±2p ，0)，所以p 2 ＝2p ，解得p ＝8，故选D.7．B如图，分别过点A ，B 作准线的垂线，交准线于点E ，D ，设准线与x 轴交于点G ，设|BF |＝a ，则由已知得|BC |＝2a ，由定义得|BD |＝a ，故∠BCD ＝30°，在Rt △ACE 中，∵|AF |＝4，|AC |＝4＋3a ，∴2|AE |＝|AC |，∴4＋3a ＝8，从而得a ＝43 ，∵AE ∥FG ，∴FG AE ＝CF AC ，即p 4 ＝48 ，得p ＝2.∴抛物线方程为y 2＝4x .故选B.8．B 当AB 与x 轴垂直时，A ⎝⎛⎭⎫12，1 ，B ⎝⎛⎭⎫12，－1 ，OA → ꞏOB → ＝12 ×12 ＋1×(－1)＝－34 ；当AB 与x 轴不垂直时，设l ：y ＝k ⎝⎛⎭⎫x －12 ， 由⎩⎪⎨⎪⎧y ＝k ⎝⎛⎭⎫x －12，y 2＝2x ，得k 2x 2－(k 2＋2)x ＋k 24 ＝0 设A (x 1，y 1)，B (x 2，y 2)由韦达定理得x 1＋x 2＝k 2＋2k 2 ，x 1x 2＝14 ，∴OA → ꞏOB →＝x 1x 2＋y 1y 2＝x 1x 2＋k 2⎝⎛⎭⎫x 1－12 ⎝⎛⎭⎫x 2－12 ＝(1＋k 2)x 1x 2－12 k 2(x 1＋x 2)＋k 24 ＝－34 . 9．A 不妨设点A 在第一象限，如图所示，过点F 作AE 的垂线，垂足为H ，由题知当A 的坐标为(3，y 0)时△AEF 为正三角形，此时H 为AE 的中点，|AE |＝3＋p 2 ，|EH |＝p ，∴2p ＝3＋p2 ，解得p ＝2，∴y 2＝4x ，A (3，23 )，F (1，0)，∴k AF ＝3 ，直线AF 的方程为y ＝3 (x －1)，代入抛物线方程得3(x －1)2＝4x .设A (x 1，y 1)，B (x 2，y 2)，解得x 1＝3，x 2＝13 ，此时y 1＝23 ，y 2＝－233 ，∴S △AOB ＝S △OFB ＋S △OF A ＝12 ×1×⎝⎛⎭⎫233＋23 ＝433 ，故选A. 10．x ＝－32答案解析：抛物线C ：y 2＝2px (p >0)的焦点F ⎝⎛⎭⎫p 2，0 ，∵P 为C 上一点，PF 与x 轴垂直，所以P 的横坐标为p2 ，代入抛物线方程求得P 的纵坐标为±p ，不妨设P (p2 ，p )，因为Q 为x 轴上一点，且PQ ⊥OP ，所以Q 在F 的右侧， 又∵|FQ |＝6，∴Q (6＋p 2 ，0)，∴PQ →＝(6，－p )因为PQ ⊥OP ，所以PQ → ꞏOP →＝p 2 ×6－p 2＝0， ∵p >0，∴p ＝3，所以C 的准线方程为x ＝－32 . 11.94答案解析：将点A 的坐标代入抛物线方程，得5＝2p ，于是y 2＝5x ，则抛物线的准线方程为x ＝－54 ，所以A 到准线的距离为1－⎝⎛⎭⎫－54 ＝94. 12．0或1答案解析：由⎩⎪⎨⎪⎧y ＝kx ＋2，y 2＝8x ， 得k 2x 2＋(4k －8)x ＋4＝0， 若k ＝0，满足题意；若k ≠0，则Δ＝(4k －8)2－4×4k 2＝0，得k ＝1.综上得k ＝0或k ＝1.13．AC 由题意，易知直线y ＝－3 (x －1)过点(1，0).对于A ，因为直线经过抛物线C 的焦点，所以易知焦点坐标为(1，0)，所以p2 ＝1，即p ＝2，所以A 选项正确．对于B ，不妨设M (x 1，y 1)，N (x 2，y 2)，x 1<x 2，联立方程得⎩⎨⎧y ＝－3（x －1）y 2＝4x，消去y并整理得3x 2－10x ＋3＝0，解得x 1＝13 ，x 2＝3.所以M (13 ，233 )，N (3，－23 )，所以由两点间距离公式可得|MN |＝（3－13）2－（－23－233）2 ＝163 ，故B 选项错误．对于C ，由以上分析易知，l 的方程为x ＝－1，以MN 为直径的圆的圆心坐标为(53 ，－233)，半径r ＝12 |MN |＝83 ＝53 ＋1，所以以MN 为直径的圆与l 相切，故C 选项正确． 对于D ，由两点间距离公式可得|MN |＝163 ，|OM |＝133 ，|ON |＝21 ，故D 选项错误．综上，选AC.14．B 令y ＝1，得x ＝14 ，即A ⎝⎛⎭⎫14，1 . 由抛物线的光学性质可知AB 经过焦点F ，设直线AB 的方程为y ＝k (x －1)，代入y 2＝4x .消去y ，得k 2x 2－2(k 2＋2)x ＋k 2＝0.则x A x B ＝1，所以x B ＝1x A＝4.|AB |＝x A ＋x B ＋p ＝254 .将x ＝4代入y 2＝4x 得y ＝±4，故B (4，－4). 故|MB |＝（4－3）2＋（－4－1）2 ＝26 .故△ABM 的周长为|MA |＋|MB |＋|AB |＝⎝⎛⎭⎫3－14 ＋26 ＋254 ＝9＋26 .故选B. 15．2答案解析：设准线l 和x 轴交于N 点，PM 平行于x 轴，∠PMF ＝∠MFN ＝60°，由抛物线的定义得到|NF |＝p ，故|MF |＝2p ，故34 (2p )2＝43 ，∴p ＝2.16．3答案解析：如图所示，由题意得准线l ：x ＝－p2 .作AC ⊥l 于点C ，BD ⊥l 于点D ，BH ⊥AC 于点H ，则|AF |＝|AC |，|BF |＝|BD |，|AH |＝|AC |－|BD |＝|AF |－|BF |，因为在Rt △AHB 中，∠HAB ＝60°，所以cos 60°＝|AH ||AB | ＝|AF |－|BF ||AF |＋|BF |，即12 (|AF |＋|BF |)＝|AF |－|BF |，得|AF ||BF | ＝3.。

2020届高考数学压轴必刷题专题09平面解析几何(文理合卷)1．【2019年全国新课标2理科11】设F为双曲线C：1（a＞0，b＞0）的右焦点，O为坐标原点，以OF为直径的圆与圆x2+y2＝a2交于P，Q两点．若|PQ|＝|OF|，则C的离心率为（）A．B．C．2 D．【解答】解：如图，由题意，把x代入x2+y2＝a2，得PQ，再由|PQ|＝|OF|，得，即2a2＝c2，∴，解得e．故选：A．2．【2018年新课标1理科11】已知双曲线C：y2＝1，O为坐标原点，F为C的右焦点，过F的直线与C的两条渐近线的交点分别为M，N．若△OMN为直角三角形，则|MN|＝（）A．B．3 C．2D．4【解答】解：双曲线C：y2＝1的渐近线方程为：y，渐近线的夹角为：60°，不妨设过F （2，0）的直线为：y，则：解得M（，），解得：N（），则|MN|3．故选：B．3．【2018年新课标2理科12】已知F1，F2是椭圆C：1（a＞b＞0）的左、右焦点，A是C的左顶点，点P在过A且斜率为的直线上，△PF1F2为等腰三角形，∠F1F2P＝120°，则C的离心率为（）A．B．C．D．【解答】解：由题意可知：A（﹣a，0），F1（﹣c，0），F2（c，0），直线AP的方程为：y（x+a），由∠F1F2P＝120°，|PF2|＝|F1F2|＝2c，则P（2c，c），代入直线AP：c（2c+a），整理得：a＝4c，∴题意的离心率e．故选：D．4．【2018年新课标3理科11】设F1，F2是双曲线C：1（a＞0．b＞0）的左，右焦点，O是坐标原点．过F2作C的一条渐近线的垂线，垂足为P，若|PF1||OP|，则C的离心率为（）A．B．2 C．D．【解答】解：双曲线C：1（a＞0．b＞0）的一条渐近线方程为y x，∴点F2到渐近线的距离d b，即|PF2|＝b，∴|OP|a，cos∠PF2O，∵|PF1||OP|，∴|PF1|a，在三角形F1PF2中，由余弦定理可得|PF1|2＝|PF2|2+|F1F2|2﹣2|PF2|•|F1F2|COS∠PF2O，∴6a2＝b2+4c2﹣2×b×2c4c2﹣3b2＝4c2﹣3（c2﹣a2），即3a2＝c2，即a＝c，∴e，故选：C．5．【2018年天津理科07】已知双曲线1（a＞0，b＞0）的离心率为2，过右焦点且垂直于x轴的直线与双曲线交于A，B两点．设A，B到双曲线的同一条渐近线的距离分别为d1和d2，且d1+d2＝6，则双曲线的方程为（）A． 1 B． 1C． 1 D． 1【解答】解：由题意可得图象如图，CD是双曲线的一条渐近线y，即bx﹣ay＝0，F（c，0），AC⊥CD，BD⊥CD，FE⊥CD，ACDB是梯形，F是AB的中点，EF3，EF b，所以b＝3，双曲线1（a＞0，b＞0）的离心率为2，可得，可得：，解得a．则双曲线的方程为：1．故选：C．6．【2017年新课标1理科10】已知F为抛物线C：y2＝4x的焦点，过F作两条互相垂直的直线l1，l2，直线l1与C交于A、B两点，直线l2与C交于D、E两点，则|AB|+|DE|的最小值为（）A．16 B．14 C．12 D．10【解答】解：如图，l1⊥l2，直线l1与C交于A、B两点，直线l2与C交于D、E两点，要使|AB|+|DE|最小，则A与D，B，E关于x轴对称，即直线DE的斜率为1，又直线l2过点（1，0），则直线l2的方程为y＝x﹣1，联立方程组，则y2﹣4y﹣4＝0，∴y1+y2＝4，y1y2＝﹣4，∴|DE|•|y1﹣y2|8，∴|AB|+|DE|的最小值为2|DE|＝16，方法二：设直线l1的倾斜角为θ，则l2的倾斜角为θ，根据焦点弦长公式可得|AB||DE|∴|AB|+|DE|，∵0＜sin22θ≤1，∴当θ＝45°时，|AB|+|DE|的最小，最小为16，故选：A．7．【2017年新课标3理科10】已知椭圆C：1（a＞b＞0）的左、右顶点分别为A1，A2，且以线段A1A2为直径的圆与直线bx﹣ay+2ab＝0相切，则C的离心率为（）A．B．C．D．【解答】解：以线段A1A2为直径的圆与直线bx﹣ay+2ab＝0相切，∴原点到直线的距离a，化为：a2＝3b2．∴椭圆C的离心率e．故选：A．8．【2017年上海16】在平面直角坐标系xOy中，已知椭圆C1：1和C2：x21．P为C1上的动点，Q为C2上的动点，w是的最大值．记Ω＝{（P，Q）|P在C1上，Q在C2上，且w}，则Ω中元素个数为（）A．2个B．4个C．8个D．无穷个【解答】解：椭圆C1：1和C2：x21．P为C1上的动点，Q为C2上的动点，可设P（6cosα，2sinα），Q（cosβ，3sinβ），0≤α，β＜2π，则6cosαcosβ+6sinαsinβ＝6cos（α﹣β），当α﹣β＝2kπ，k∈Z时，w取得最大值6，则Ω＝{（P，Q）|P在C1上，Q在C2上，且w}中的元素有无穷多对．另解：令P（m，n），Q（u，v），则m2+9n2＝36，9u2+v2＝9，由柯西不等式（m2+9n2）（9u2+v2）＝324≥（3mu+3nv）2，当且仅当mv＝9nu，取得最大值6，显然，满足条件的P、Q有无穷多对，D项正确．故选：D．9．【2016年新课标2理科11】已知F1，F2是双曲线E：1的左，右焦点，点M在E上，MF1与x轴垂直，sin∠MF2F1，则E的离心率为（）A．B．C．D．2【解答】解：由题意，M为双曲线左支上的点，则丨MF1丨，丨MF2丨，∴sin∠MF2F1，∴，可得：2b4＝a2c2，即b2＝ac，又c2＝a2+b2，可得e2﹣e0，e＞1，解得e．故选：A．10．【2016年浙江理科07】已知椭圆与双曲线C2：y2＝1（n＞0）的焦点重合，e1，e2分别为C1，C2的离心率，则（）A．m＞n且e1e2＞1 B．m＞n且e1e2＜1C．m＜n且e1e2＞1 D．m＜n且e1e2＜1【解答】解：由题意可得m2﹣1＝n2+1，即m2＝n2+2，又m＞1，n＞0，则m＞n，由e12•e22••＝11，则e1•e2＞1．故选：A．11．【2016年新课标3理科11】已知O为坐标原点，F是椭圆C：1（a＞b＞0）的左焦点，A，B 分别为C的左，右顶点．P为C上一点，且PF⊥x轴，过点A的直线l与线段PF交于点M，与y轴交于点E．若直线BM经过OE的中点，则C的离心率为（）A．B．C．D．【解答】解：由题意可设F（﹣c，0），A（﹣a，0），B（a，0），设直线AE的方程为y＝k（x+a），令x＝﹣c，可得M（﹣c，k（a﹣c）），令x＝0，可得E（0，ka），设OE的中点为H，可得H（0，），由B，H，M三点共线，可得k BH＝k BM，即为，化简可得，即为a＝3c，可得e．另解：由△AMF∽△AEO，可得，由△BOH∽△BFM，可得，即有即a＝3c，可得e．故选：A．12．【2015年新课标2理科11】已知A，B为双曲线E的左，右顶点，点M在E上，△ABM为等腰三角形，顶角为120°，则E的离心率为（）A．B．2 C．D．【解答】解：设M在双曲线1的左支上，且MA＝AB＝2a，∠MAB＝120°，则M的坐标为（﹣2a，a），代入双曲线方程可得，1，可得a＝b，c a，即有e．故选：D．13．【2015年浙江理科05】如图，设抛物线y2＝4x的焦点为F，不经过焦点的直线上有三个不同的点A，B，C，其中点A，B在抛物线上，点C在y轴上，则△BCF与△ACF的面积之比是（）A．B．C．D．【解答】解：如图所示，抛物线的准线DE的方程为x＝﹣1，过A，B分别作AE⊥DE于E，交y轴于N，BD⊥DE于D，交y轴于M，由抛物线的定义知BF＝BD，AF＝AE，则|BM|＝|BD|﹣1＝|BF|﹣1，|AN|＝|AE|﹣1＝|AF|﹣1，则，故选：A．14．【2014年新课标1理科10】已知抛物线C：y2＝8x的焦点为F，准线为l，P是l上一点，Q是直线PF 与C的一个交点，若4，则|QF|＝（）A．B．3 C．D．2【解答】解：设Q到l的距离为d，则|QF|＝d，∵4，∴|PQ|＝3d，∴不妨设直线PF的斜率为2，∵F（2，0），∴直线PF的方程为y＝﹣2（x﹣2），与y2＝8x联立可得x＝1，∴|QF|＝d＝1+2＝3，故选：B．15．【2014年新课标2理科10】设F为抛物线C：y2＝3x的焦点，过F且倾斜角为30°的直线交C于A，B两点，O为坐标原点，则△OAB的面积为（）A．B．C．D．【解答】解：由y2＝2px，得2p＝3，p，则F（，0）．∴过A，B的直线方程为y（x），即x y．联立，得4y2﹣12y﹣9＝0．设A（x1，y1），B（x2，y2），则y1+y2＝3，y1y2．∴S△OAB＝S△OAF+S△OFB|y1﹣y2|．故选：D．16．【2014年上海理科17】已知P1（a1，b1）与P2（a2，b2）是直线y＝kx+1（k为常数）上两个不同的点，则关于x和y的方程组的解的情况是（）A．无论k，P1，P2如何，总是无解B．无论k，P1，P2如何，总有唯一解C．存在k，P1，P2，使之恰有两解D．存在k，P1，P2，使之有无穷多解【解答】解：P1（a1，b1）与P2（a2，b2）是直线y＝kx+1（k为常数）上两个不同的点，直线y＝kx+1的斜率存在，∴k，即a1≠a2，并且b1＝ka1+1，b2＝ka2+1，∴a2b1﹣a1b2＝ka1a2﹣ka1a2+a2﹣a1＝a2﹣a1，①×b2﹣②×b1得：（a1b2﹣a2b1）x＝b2﹣b1，即（a1﹣a2）x＝b2﹣b1．∴方程组有唯一解．故选：B．17．【2013年浙江理科09】如图F1、F2是椭圆C1：y2＝1与双曲线C2的公共焦点，A、B分别是C1、C2在第A．B．C．D．【解答】解：设|AF1|＝x，|AF2|＝y，∵点A为椭圆C1：y2＝1上的点，∴2a＝4，b＝1，c；∴|AF1|+|AF2|＝2a＝4，即x+y＝4；①又四边形AF1BF2为矩形，∴，即x2+y2＝（2c）212，②由①②得：，解得x＝2，y＝2，设双曲线C2的实轴长为2m，焦距为2n，则2m＝|AF2|﹣|AF1|＝y﹣x＝2，2n＝2c＝2，∴双曲线C2的离心率e．故选：D．18．【2012年浙江理科08】如图，F1，F2分别是双曲线C：（a，b＞0）的在左、右焦点，B是虚轴的端点，直线F1B与C的两条渐近线分别交于P，Q两点，线段PQ的垂直平分线与x轴交于点M．若|MF2|＝|F1F2|，则C的离心率是（）A．B．C．D．【解答】解：线段PQ的垂直平分线MN，|OB|＝b，|OF1|＝c．∴k PQ，k MN．直线PQ为：y（x+c），两条渐近线为：y x．由，得Q（）；由得P．∴直线MN为，令y＝0得：x M．又∵|MF2|＝|F1F2|＝2c，∴3c＝x M，∴3a2＝2c2解之得：，即e．故选：B．19．【2012年天津理科08】设m，n∈R，若直线（m+1）x+（n+1）y﹣2＝0与圆（x﹣1）2+（y﹣1）2＝1相切，则m+n的取值范围是（）A．[1，1] B．（﹣∞，1]∪[1，+∞）C．[2﹣2，2+2] D．（﹣∞，2﹣2]∪[2+2，+∞）【解答】解：由圆的方程（x﹣1）2+（y﹣1）2＝1，得到圆心坐标为（1，1），半径r＝1，∵直线（m+1）x+（n+1）y﹣2＝0与圆相切，∴圆心到直线的距离d1，整理得：m+n+1＝mn，设m+n＝x，则有x+1，即x2﹣4x﹣4≥0，∵x2﹣4x﹣4＝0的解为：x1＝2+2，x2＝2﹣2，∴不等式变形得：（x﹣2﹣2）（x﹣2+2）≥0，解得：x≥2+2或x≤2﹣2，则m+n的取值范围为（﹣∞，2﹣2]∪[2+2，+∞）．故选：D．20．【2010年新课标1理科12】已知双曲线E的中心为原点，P（3，0）是E的焦点，过P的直线l与E相交于A，B两点，且AB的中点为N（﹣12，﹣15），则E的方程式为（）A．B．C．D．【解答】解：由已知条件易得直线l的斜率为k＝k PN＝1，设双曲线方程为，A（x1，y1），B（x2，y2），则有，两式相减并结合x1+x2＝﹣24，y1+y2＝﹣30得，从而k 1即4b2＝5a2，又a2+b2＝9，解得a2＝4，b2＝5，故选：B．21．【2010年浙江理科08】设F1、F2分别为双曲线的左、右焦点．若在双曲线右支上存在点P，满足|PF2|＝|F1F2|，且F2到直线PF1的距离等于双曲线的实轴长，则该双曲线的渐近线方程为（）A．3x±4y＝0 B．3x±5y＝0 C．4x±3y＝0 D．5x±4y＝0【解答】解：依题意|PF2|＝|F1F2|，可知三角形PF2F1是一个等腰三角形，F2在直线PF1的投影是其中点，由勾股定理知可知|PF1|＝24b根据双曲定义可知4b﹣2c＝2a，整理得c＝2b﹣a，代入c2＝a2+b2整理得3b2﹣4ab＝0，求得∴双曲线渐近线方程为y＝±x，即4x±3y＝0故选：C．22．【2019年新课标1理科16】已知双曲线C：1（a＞0，b＞0）的左、右焦点分别为F1，F2，过F1的直线与C的两条渐近线分别交于A，B两点．若，•0，则C的离心率为．【解答】解：如图，∵，且•0，∴OA⊥F1B，则F1B：y，联立，解得B（，），则，，∴4c2，整理得：b2＝3a2，∴c2﹣a2＝3a2，即4a2＝c2，∴，e．故答案为：2．23．【2019年浙江15】已知椭圆1的左焦点为F，点P在椭圆上且在x轴的上方．若线段PF的中点在以原点O为圆心，|OF|为半径的圆上，则直线PF的斜率是．【解答】解：椭圆1的a＝3，b，c＝2，e，设椭圆的右焦点为F'，连接PF'，线段PF的中点A在以原点O为圆心，2为半径的圆，连接AO，可得|PF'|＝2|AO|＝4，设P的坐标为（m，n），可得3m＝4，可得m，n，由F（﹣2，0），可得直线PF的斜率为．故答案为：．24．【2018年新课标3理科16】已知点M（﹣1，1）和抛物线C：y2＝4x，过C的焦点且斜率为k的直线与C交于A，B两点．若∠AMB＝90°，则k＝．【解答】解：∵抛物线C：y2＝4x的焦点F（1，0），∴过A，B两点的直线方程为y＝k（x﹣1），联立可得，k2x2﹣2（2+k2）x+k2＝0，设A（x1，y1），B（x2，y2），则x1+x2，x1x2＝1，∴y1+y2＝k（x1+x2﹣2），y1y2＝k2（x1﹣1）（x2﹣1）＝k2[x1x2﹣（x1+x2）+1]＝﹣4，∵M（﹣1，1），∴（x1+1，y1﹣1），（x2+1，y2﹣1），∵∠AMB＝90°，∴•0∴（x1+1）（x2+1）+（y1﹣1）（y2﹣1）＝0，整理可得，x1x2+（x1+x2）+y1y2﹣（y1+y2）+2＝0，∴1+242＝0，即k2﹣4k+4＝0，∴k＝2．故答案为：225．【2018年浙江17】已知点P（0，1），椭圆y2＝m（m＞1）上两点A，B满足2，则当m＝时，点B横坐标的绝对值最大．【解答】解：设A（x1，y1），B（x2，y2），由P（0，1），2，可得﹣x1＝2x2，1﹣y1＝2（y2﹣1），即有x1＝﹣2x2，y1+2y2＝3，又x12+4y12＝4m，即为x22+y12＝m，①x22+4y22＝4m，②①﹣②得（y1﹣2y2）（y1+2y2）＝﹣3m，可得y1﹣2y2＝﹣m，解得y1，y2，则m＝x22+（）2，即有x22＝m﹣（）2，即有m＝5时，x22有最大值4，即点B横坐标的绝对值最大．故答案为：5．26．【2018年上海12】已知实数x1、x2、y1、y2满足：x12+y12＝1，x22+y22＝1，x1x2+y1y2，则的最大值为．【解答】解：设A（x1，y1），B（x2，y2），（x1，y1），（x2，y2），由x12+y12＝1，x22+y22＝1，x1x2+y1y2，可得A，B两点在圆x2+y2＝1上，且•1×1×cos∠AOB，即有∠AOB＝60°，即三角形OAB为等边三角形，AB＝1，的几何意义为点A，B两点到直线x+y﹣1＝0的距离d1与d2之和，显然A，B在第三象限，AB所在直线与直线x+y＝1平行，可设AB：x+y+t＝0，（t＞0），由圆心O到直线AB的距离d，可得21，解得t，即有两平行线的距离为，即的最大值为，故答案为：．27．【2018年北京理科14】已知椭圆M：1（a＞b＞0），双曲线N：1．若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点，则椭圆M的离心率为；双曲线N的离心率为．【解答】解：椭圆M：1（a＞b＞0），双曲线N：1．若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点，可得椭圆的焦点坐标（c，0），正六边形的一个顶点（，），可得：，可得，可得e4﹣8e2+4＝0，e∈（0，1），解得e．同时，双曲线的渐近线的斜率为，即，可得：，即，可得双曲线的离心率为e2．故答案为：；2．28．【2017年江苏13】在平面直角坐标系xOy中，A（﹣12，0），B（0，6），点P在圆O：x2+y2＝50上．若20，则点P的横坐标的取值范围是．【解答】解：根据题意，设P（x0，y0），则有x02+y02＝50，（﹣12﹣x0，﹣y0）•（﹣x0，6﹣y0）＝（12+x0）x0﹣y0（6﹣y0）＝12x0+6y+x02+y02≤20，化为：12x0﹣6y0+30≤0，即2x0﹣y0+5≤0，表示直线2x﹣y+5＝0以及直线上方的区域，联立，解可得x0＝﹣5或x0＝1，结合图形分析可得：点P的横坐标x0的取值范围是[﹣5，1]，故答案为：[﹣5，1]．29．【2017年新课标2理科16】已知F是抛物线C：y2＝8x的焦点，M是C上一点，FM的延长线交y轴于点N．若M为FN的中点，则|FN|＝．【解答】解：抛物线C：y2＝8x的焦点F（2，0），M是C上一点，FM的延长线交y轴于点N．若M为FN的中点，可知M的横坐标为：1，则M的纵坐标为：，|FN|＝2|FM|＝26．故答案为：6．30．【2017年北京理科14】三名工人加工同一种零件，他们在一天中的工作情况如图所示，其中A i的横、纵坐标分别为第i名工人上午的工作时间和加工的零件数，点B i的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数，i＝1，2，3．（1）记Q i为第i名工人在这一天中加工的零件总数，则Q1，Q2，Q3中最大的是．（2）记p i为第i名工人在这一天中平均每小时加工的零件数，则p1，p2，p3中最大的是．【解答】解：（1）若Q i为第i名工人在这一天中加工的零件总数，Q1＝A1的纵坐标+B1的纵坐标；Q2＝A2的纵坐标+B2的纵坐标，Q3＝A3的纵坐标+B3的纵坐标，由已知中图象可得：Q1，Q2，Q3中最大的是Q1，（2）若p i为第i名工人在这一天中平均每小时加工的零件数，则p i为A i B i中点与原点连线的斜率，故p1，p2，p3中最大的是p2故答案为：Q1，p231．【2016年江苏10】如图，在平面直角坐标系xOy中，F是椭圆1（a＞b＞0）的右焦点，直线y与椭圆交于B，C两点，且∠BFC＝90°，则该椭圆的离心率是．【解答】解法一：设右焦点F（c，0），将y代入椭圆方程可得x＝±a±a，可得B（a，），C（a，），由∠BFC＝90°，可得k BF•k CF＝﹣1，即有•1，化简为b2＝3a2﹣4c2，由b2＝a2﹣c2，即有3c2＝2a2，由e，可得e2，可得e，解法二：设右焦点F（c，0），将y代入椭圆方程可得x＝±a±a，可得B（a，），C（a，），（a﹣c，），（a﹣c，），•0，则c2a2十b2＝0，因为b2＝a2﹣c2，代入得3c2＝2a2，由e，可得e2，可得e．解法可得FH＝HC a，在直角三角形OHF中，OF2+OH2＝FH2，即有c2a2十b2＝0，因为b2＝a2﹣c2，代入得3c2＝2a2，由e，可得e2，可得e．故答案为：．32．【2016年新课标3理科16】已知直线l：mx+y+3m0与圆x2+y2＝12交于A，B两点，过A，B分别作l的垂线与x轴交于C，D两点，若|AB|＝2，则|CD|＝．【解答】解：由题意，|AB|＝2，∴圆心到直线的距离d＝3，∴3，∴m∴直线l的倾斜角为30°，∵过A，B分别作l的垂线与x轴交于C，D两点，∴|CD|4．故答案为：4．33．【2015年江苏12】在平面直角坐标系xOy中，P为双曲线x2﹣y2＝1右支上的一个动点，若点P到直线x﹣y+1＝0的距离大于c恒成立，则实数c的最大值为．【解答】解：由题意，双曲线x2﹣y2＝1的渐近线方程为x±y＝0，因为点P到直线x﹣y+1＝0的距离大于c恒成立，所以c的最大值为直线x﹣y+1＝0与直线x﹣y＝0的距离，即．故答案为：．34．【2014年新课标2理科16】设点M（x0，1），若在圆O：x2+y2＝1上存在点N，使得∠OMN＝45°，则x0的取值范围是．【解答】解：由题意画出图形如图：点M（x0，1），要使圆O：x2+y2＝1上存在点N，使得∠OMN＝45°，则∠OMN的最大值大于或等于45°时一定存在点N，使得∠OMN＝45°，而当MN与圆相切时∠OMN取得最大值，此时MN＝1，图中只有M′到M″之间的区域满足MN≤1，∴x0的取值范围是[﹣1，1]．35．【2014年浙江理科16】设直线x﹣3y+m＝0（m≠0）与双曲线1（a＞0，b＞0）的两条渐近线分别交于点A，B．若点P（m，0）满足|P A|＝|PB|，则该双曲线的离心率是．【解答】解：双曲线（a＞0，b＞0）的两条渐近线方程为y＝±x，则与直线x﹣3y+m＝0联立，可得A（，），B（，），∴AB中点坐标为（，），∵点P（m，0）满足|P A|＝|PB|，∴3，∴a＝2b，∴b，∴e．故答案为：．36．【2014年上海理科14】已知曲线C：x，直线l：x＝6，若对于点A（m，0），存在C上的点P和l上的Q使得，则m的取值范围为．【解答】解：曲线C：x，是以原点为圆心，2 为半径的圆，并且x P∈[﹣2，0]，对于点A（m，0），存在C上的点P和l上的Q使得，说明A是PQ的中点，Q的横坐标x＝6，∴m∈[2，3]．故答案为：[2，3]．37．【2013年江苏12】在平面直角坐标系xOy中，椭圆C的标准方程为（a＞b＞0），右焦点为F，右准线为l，短轴的一个端点为B，设原点到直线BF的距离为d1，F到l的距离为d2，若d2，则椭圆C的离心率为．【解答】解：如图，准线l：x，d2，由面积法得：d1，若d2，则，整理得a2﹣ab0，两边同除以a2，得（）0，解得．∴e．故答案为：．38．【2013年浙江理科15】设F为抛物线C：y2＝4x的焦点，过点P（﹣1，0）的直线l交抛物线C于两点A，B，点Q为线段AB的中点，若|FQ|＝2，则直线l的斜率等于．【解答】解：由题意设直线l的方程为my＝x+1，联立得到y2﹣4my+4＝0，△＝16m2﹣16＝16（m2﹣1）＞0．设A（x1，y1），B（x2，y2），Q（x0，y0）．∴y1+y2＝4m，∴2m，∴x0＝my0﹣1＝2m2﹣1．∴Q（2m2﹣1，2m），由抛物线C：y2＝4x得焦点F（1，0）．∵|QF|＝2，∴，化为m2＝1，解得m＝±1，不满足△＞0．故满足条件的直线l不存在．故答案为不存在．39．【2012年江苏12】在平面直角坐标系xOy中，圆C的方程为x2+y2﹣8x+15＝0，若直线y＝kx﹣2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，则k的最大值是．【解答】解：∵圆C的方程为x2+y2﹣8x+15＝0，整理得：（x﹣4）2+y2＝1，即圆C是以（4，0）为圆心，1为半径的圆；又直线y＝kx﹣2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，∴只需圆C′：（x﹣4）2+y2＝4与直线y＝kx﹣2有公共点即可．设圆心C（4，0）到直线y＝kx﹣2的距离为d，则d2，即3k2﹣4k≤0，∴0≤k．∴k的最大值是．故答案为：．40．【2012年浙江理科16】定义：曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离，已知曲线C1：y＝x2+a到直线l：y＝x的距离等于曲线C2：x2+（y+4）2＝2到直线l：y＝x的距离，则实数a ＝．【解答】解：圆x2+（y+4）2＝2的圆心为（0，﹣4），半径为，圆心到直线y＝x的距离为2，∴曲线C2：x2+（y+4）2＝2到直线l：y＝x的距离为2．则曲线C1：y＝x2+a到直线l：y＝x的距离等于，令y′＝2x＝1解得x，故切点为（，a），切线方程为y﹣（a）＝x即x﹣y a＝0，由题意可知x﹣y a＝0与直线y＝x的距离为，即解得a或．当a时直线y＝x与曲线C1：y＝x2+a相交，故不符合题意，舍去．故答案为：．41．【2011年浙江理科17】设F1，F2分别为椭圆y2＝1的焦点，点A，B在椭圆上，若5；则点A的坐标是．【解答】解：方法1：直线F1A的反向延长线与椭圆交于点B'又∵由椭圆的对称性，得设A（x1，y1），B'（x2，y2）由于椭圆的a，b＝1，c∴e，F1（，0）．∵|F1A||x1|，|F1B'||x2|，从而有：|x1|＝5|x2|，由于x1，x2，∴x1＞0，x2＞0，即55．①又∵三点A，F1，B′共线，∴（，y1﹣0）＝5（x2，0﹣y2）∴．②由①+②得：x1＝0．代入椭圆的方程得：y1＝±1，∴点A的坐标为（0，1）或（0，﹣1）方法2：因为F1，F2分别为椭圆的焦点，则，设A，B的坐标分别为A（x A，y A），B（x B，y B），若；则，所以，因为A，B在椭圆上，所以，代入解得或，故A（0，±1）．方法k＝tanθ，由，即可得到A（0，±1）．故答案为：（0，±1）．42．【2011年北京理科14】曲线C是平面内与两个定点F1（﹣1，0）和F2（1，0）的距离的积等于常数a2（a＞1）的点的轨迹．给出下列三个结论：①曲线C过坐标原点；②曲线C关于坐标原点对称；③若点P在曲线C上，则△F1PF2的面积不大于a2．其中，所有正确结论的序号是．【解答】解：对于①，由题意设动点坐标为（x，y），则利用题意及两点间的距离公式的得：⇔[（x+1）2+y2]•[（x﹣1）2+y2]＝a4（1）将原点代入验证，此方程不过原点，所以①错；对于②，把方程中的x被﹣x代换，y被﹣y代换，方程不变，故此曲线关于原点对称．②正确；对于③，由题意知点P在曲线C上，则△F1PF2的面积a2sin∠F1PF2，a2，所以③正确．故答案为：②③．43．【2010年上海理科13】如图所示，直线x＝2与双曲线Γ：1的渐近线交于E1，E2两点，记，，任取双曲线上的点P，若（a，b∈R），则a、b满足的一个等式是．【解答】解：依题意可知：E1（2，1），E2（2，﹣1）∴（2a+2b，a﹣b），∵点P在双曲线上∴（a﹣b）2＝1，化简得4ab＝1故答案为4ab＝144．【2010年北京理科14】如图放置的边长为1的正方形P ABC沿x轴滚动．设顶点P（x，y）的轨迹方程是y＝f（x），则f（x）的最小正周期为；y＝f（x）在其两个相邻零点间的图象与x轴所围区域的面积为．【解答】解：从某一个顶点（比如A）落在x轴上的时候开始计算，到下一次A点落在x轴上，这个过程中四个顶点依次落在了x轴上，而每两个顶点间距离为正方形的边长1，因此该函数的周期为4．下面考察P点的运动轨迹，不妨考察正方形向右滚动，P点从x轴上开始运动的时候，首先是围绕A点运动个圆，该圆半径为1，然后以B点为中心，滚动到C点落地，其间是以BP为半径，旋转90°，然后以C为圆心，再旋转90°，这时候以CP为半径，因此最终构成图象如下：故其与x轴所围成的图形面积为．故答案为：4，π+11．【2019年新课标2文科12】设F为双曲线C：1（a＞0，b＞0）的右焦点，O为坐标原点，以OF为直径的圆与圆x2+y2＝a2交于P，Q两点．若|PQ|＝|OF|，则C的离心率为（）A．B．C．2 D．【解答】解：如图，由题意，把x代入x2+y2＝a2，得PQ，再由|PQ|＝|OF|，得，即2a2＝c2，∴，解得e．故选：A．2．【2019年新课标1文科12】已知椭圆C的焦点为F1（﹣1，0），F2（1，0），过F2的直线与C交于A，B两点．若|AF2|＝2|F2B|，|AB|＝|BF1|，则C的方程为（）A．y2＝1 B． 1C． 1 D． 1【解答】解：∵|AF2|＝2|BF2|，∴|AB|＝3|BF2|，又|AB|＝|BF1|，∴|BF1|＝3|BF2|，又|BF1|+|BF2|＝2a，∴|BF2|，∴|AF2|＝a，|BF1|a，在Rt△AF2O中，cos∠AF2O，在△BF1F2中，由余弦定理可得cos∠BF2F1，根据cos∠AF2O+cos∠BF2F1＝0，可得0，解得a2＝3，∴a．b2＝a2﹣c2＝3﹣1＝2．所以椭圆C的方程为：1．故选：B．3．【2018年新课标2文科11】已知F1，F2是椭圆C的两个焦点，P是C上的一点，若PF1⊥PF2，且∠PF2F1＝60°，则C的离心率为（）A．1B．2C．D． 1【解答】解：F1，F2是椭圆C的两个焦点，P是C上的一点，若PF1⊥PF2，且∠PF2F1＝60°，可得椭圆的焦点坐标F2（c，0），所以P（c，c）．可得：，可得，可得e4﹣8e2+4＝0，e∈（0，1），解得e．故选：D．4．【2018年天津文科07】已知双曲线1（a＞0，b＞0）的离心率为2，过右焦点且垂直于x轴的直线与双曲线交于A，B两点．设A，B到双曲线的同一条渐近线的距离分别为d1和d2，且d1+d2＝6，则双曲线的方程为（）A． 1 B． 1C． 1 D． 1【解答】解：由题意可得图象如图，CD是双曲线的一条渐近线y，即bx﹣ay＝0，F（c，0），AC⊥CD，BD⊥CD，FE⊥CD，ACDB是梯形，F是AB的中点，EF3，EF b，所以b＝3，双曲线1（a＞0，b＞0）的离心率为2，可得，可得：，解得a．则双曲线的方程为：1．故选：A．5．【2017年新课标2文科12】过抛物线C：y2＝4x的焦点F，且斜率为的直线交C于点M（M在x轴上方），l为C的准线，点N在l上，且MN⊥l，则M到直线NF的距离为（）A．B．2C．2D．3【解答】解：抛物线C：y2＝4x的焦点F（1，0），且斜率为的直线：y（x﹣1），过抛物线C：y2＝4x的焦点F，且斜率为的直线交C于点M（M在x轴上方），l可知：，解得M（3，2）．可得N（﹣1，2），NF的方程为：y（x﹣1），即，则M到直线NF的距离为：2．故选：C．6．【2017年新课标1文科12】设A，B是椭圆C：1长轴的两个端点，若C上存在点M满足∠AMB＝120°，则m的取值范围是（）A．（0，1]∪[9，+∞）B．（0，]∪[9，+∞）C．（0，1]∪[4，+∞）D．（0，]∪[4，+∞）【解答】解：假设椭圆的焦点在x轴上，则0＜m＜3时，设椭圆的方程为：（a＞b＞0），设A（﹣a，0），B（a，0），M（x，y），y＞0，则a2﹣x2，∠MAB＝α，∠MBA＝β，∠AMB＝γ，tanα，tanβ，则tanγ＝tan[π﹣（α+β）]＝﹣tan（α+β），∴tanγ，当y最大时，即y＝b时，∠AMB取最大值，∴M位于短轴的端点时，∠AMB取最大值，要使椭圆C上存在点M满足∠AMB＝120°，∠AMB≥120°，∠AMO≥60°，tan∠AMO tan60°，解得：0＜m≤1；当椭圆的焦点在y轴上时，m＞3，当M位于短轴的端点时，∠AMB取最大值，要使椭圆C上存在点M满足∠AMB＝120°，∠AMB≥120°，∠AMO≥60°，tan∠AMO tan60°，解得：m≥9，∴m的取值范围是（0，1]∪[9，+∞）故选A．故选：A．7．【2017年新课标3文科11】已知椭圆C：1（a＞b＞0）的左、右顶点分别为A1，A2，且以线段A1A2为直径的圆与直线bx﹣ay+2ab＝0相切，则C的离心率为（）A．B．C．D．【解答】解：以线段A1A2为直径的圆与直线bx﹣ay+2ab＝0相切，∴原点到直线的距离a，化为：a2＝3b2．∴椭圆C的离心率e．故选：A．8．【2016年新课标3文科12】已知O为坐标原点，F是椭圆C：1（a＞b＞0）的左焦点，A，B 分别为C的左，右顶点．P为C上一点，且PF⊥x轴，过点A的直线l与线段PF交于点M，与y轴交于点E．若直线BM经过OE的中点，则C的离心率为（）A．B．C．D．【解答】解：由题意可设F（﹣c，0），A（﹣a，0），B（a，0），设直线AE的方程为y＝k（x+a），令x＝﹣c，可得M（﹣c，k（a﹣c）），令x＝0，可得E（0，ka），设OE的中点为H，可得H（0，），由B，H，M三点共线，可得k BH＝k BM，即为，化简可得，即为a＝3c，可得e．另解：由△AMF∽△AEO，可得，由△BOH∽△BFM，可得，即有即a＝3c，可得e．故选：A．9．【2014年新课标2文科12】设点M（x0，1），若在圆O：x2+y2＝1上存在点N，使得∠OMN＝45°，则x0的取值范围是（）A．[﹣1，1] B．[，] C．[，] D．[，]【解答】解：由题意画出图形如图：点M（x0，1），要使圆O：x2+y2＝1上存在点N，使得∠OMN＝45°，则∠OMN的最大值大于或等于45°时一定存在点N，使得∠OMN＝45°，而当MN与圆相切时∠OMN取得最大值，此时MN＝1，图中只有M′到M″之间的区域满足MN＝1，∴x0的取值范围是[﹣1，1]．故选：A．10．【2014年北京文科07】已知圆C：（x﹣3）2+（y﹣4）2＝1和两点A（﹣m，0），B（m，0）（m＞0），若圆C上存在点P，使得∠APB＝90°，则m的最大值为（）A．7 B．6 C．5 D．4【解答】解：圆C：（x﹣3）2+（y﹣4）2＝1的圆心C（3，4），半径为1，∵圆心C到O（0，0）的距离为5，∴圆C上的点到点O的距离的最大值为6．再由∠APB＝90°可得，以AB为直径的圆和圆C有交点，可得PO AB＝m，故有m≤6，11．【2014年天津文科06】已知双曲线1（a＞0，b＞0）的一条渐近线平行于直线l：y＝2x+10，双曲线的一个焦点在直线l上，则双曲线的方程为（）A． 1 B． 1C． 1 D． 1【解答】解：∵双曲线的一个焦点在直线l上，令y＝0，可得x＝﹣5，即焦点坐标为（﹣5，0），∴c＝5，∵双曲线1（a＞0，b＞0）的一条渐近线平行于直线l：y＝2x+10，∴2，∵c2＝a2+b2，∴a2＝5，b2＝20，∴双曲线的方程为1．故选：A．12．【2011年新课标1文科09】已知直线l过抛物线C的焦点，且与C的对称轴垂直．l与C交于A，B两点，|AB|＝12，P为C的准线上一点，则△ABP的面积为（）A．18 B．24 C．36 D．48【解答】解：设抛物线的解析式为y2＝2px（p＞0），则焦点为F（，0），对称轴为x轴，准线为x∵直线l经过抛物线的焦点，A、B是l与C的交点，∴|AB|＝2p＝12∴p＝6又∵点P在准线上∴DP＝（||）＝p＝6∴S△ABP（DP•AB）6×12＝36故选：C．13．【2011年北京文科08】已知点A（0，2），B（2，0）．若点C在函数y＝x2的图象上，则使得△ABC的面积为2的点C的个数为（）A．4 B．3 C．2 D．1【解答】解：设C（a，a2），由已知得直线AB的方程为，即：x+y﹣2＝0点C到直线AB的距离为：d，有三角形ABC的面积为2可得：|a+a2﹣2|＝2得：a2+a＝0或a2+a﹣4＝0，显然方程共有四个根，可知函数y＝x2的图象上存在四个点（如上面图中四个点C1，C2，C3，C4）使得△ABC的面积为2（即图中的三角形△ABC1，△ABC2，△ABC3，△ABC4）．故选：A．14．【2015年新课标1文科16】已知F是双曲线C：x21的右焦点，P是C的左支上一点，A（0，6）．当△APF周长最小时，该三角形的面积为．【解答】解：由题意，设F′是左焦点，则△APF周长＝|AF|+|AP|+|PF|＝|AF|+|AP|+|PF′|+2≥|AF|+|AF′|+2（A，P，F′三点共线时，取等号），直线AF′的方程为与x21联立可得y2+6y﹣96＝0，∴P的纵坐标为2，∴△APF周长最小时，该三角形的面积为12．故答案为：12．。