小数六年级总复习概念资料(三)式与方程比和比例

复习课:比和比例知识点三：求比值和化简比 知识点四：正比例和反比例的意义和判断方法1、 正比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的比值（商）一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系。

正比例的关系式：k xy=（一定） 2、 反比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系叫做正比例关系。

反比例的关系式：k xy =（一定）3、 判断正、反比例的方法：一找二看三判断（1） 找变量：分析数量关系，确定哪两种量是相关联的量。

（2） 看定量，分析这两种相关联的量，它们之间的关系是商一定还是积一定。

（3） 判断：如果商一定，就成正比例；如果积一定就成反比例；如果商和积都不是定量，就不成比例知识点五：用比例知识解决问题1、按比例分配问题（1）按比例分配应用题：把一个量按照一定的比分配成几部分，求每个部分数量各是多少的应用题叫做按比例分配应用题。

（2）解题方法一般方法：把比转化成为分数，用分数方法解答，即先求出总分数，然后求出各部分量占总量的几分之几，最后按照求一个数的几分之几多少的解题方法，分别求出各部分的量是多少归一法：把比看做分得的分数，先求出各部分的总分数，然后再用“总量÷总份数=平均每份的量（归一）”，再用“一份的量⨯各部分量所对应的份数”，求出各部分的量。

用比例知识解答：首先设未知量为。

再根据题中“已知比等于相对应的量的比”作为等量关系式列出含有x的比例式，再解比例求出x。

2、用正、反比例知识解答应用题的步骤（1）分析数量关系。

判断成什么比例。

（２）找等量关系。

如果成正比例，则按等比找等量关系式；如果成反比例，则按等积找等量关系式。

（３）解比例式。

设未知数为x，并代入等量关系式，得正比例式或反比例式。

（４）解比例。

（５）检验并写出答语。

复习课:比和比例知识点三：求比值和化简比1、 正比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的比值（商）一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系。

正比例的关系式：k xy=（一定） 2、 反比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系叫做正比例关系。

反比例的关系式：k xy =（一定）3、 判断正、反比例的方法：一找二看三判断（1） 找变量：分析数量关系，确定哪两种量是相关联的量。

（2） 看定量，分析这两种相关联的量，它们之间的关系是商一定还是积一定。

（3） 判断：如果商一定，就成正比例；如果积一定就成反比例；如果商和积都不是定量，就不成比例知识点五：用比例知识解决问题 1、 按比例分配问题 （1） 按比例分配应用题：把一个量按照一定的比分配成几部分，求每个部分数量各是多少的应用题叫做按比例分配应用题。

（2） 解题方法一般方法：把比转化成为分数，用分数方法解答，即先求出总分数，然后求出各部分量占总量的几分之几，最后按照求一个数的几分之几多少的解题方法，分别求出各部分的量是多少归一法：把比看做分得的分数，先求出各部分的总分数，然后再用“总量÷总份数=平均每份的量（归一）”，再用“一份的量⨯各部分量所对应的份数”，求出各部分的量。

用比例知识解答：首先设未知量为。

再根据题中“已知比等于相对应的量的比”作为等量关系式列出含有x 的比例式，再解比例求出x 。

2、 用正、反比例知识解答应用题的步骤（1）分析数量关系。

判断成什么比例。

（２）找等量关系。

如果成正比例，则按等比找等量关系式；如果成反比例，则按等积找等量关系式。

（３）解比例式。

设未知数为x ，并代入等量关系式，得正比例式或反比例式。

（４）解比例。

（５）检验并写出答语。

精讲典型题 例题1（1） 一项工程，甲单独做要4天，乙单独做要5天完成，甲和乙的工作效率比是（）：（）（2） 把2米：4厘米化成最简单的整数比是（），比值是（）。

六年级数学《比和比例》知识点一、比的意义和性质1、比的意义两个数相除又叫做两个数的比。

2、比的性质比的前项和后项同时乘上或者除以相同的数（0除外），比值不变。

3、比的应用通过比可以应用一些问题。

二、比例的意义和性质1、比例的意义表示两个比相等的式子叫做比例。

2、比例的性质在一个比例中，组成比例的两个数，叫做比例的项。

在一比例里，两外项的积等于两内项的积。

这叫做比例的基本性质。

3、解比例根据比例的基本性质，如果已知比例中的任何三项，就可以求出这个比例中的另外一个未知项。

这个求未知项的过程，叫做解比例。

三、正比例和反比例1、成正比例的量如果两种量是相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的比值一定，这两种量就叫做成正比例的量。

2、成反比例的量如果两种量是相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量。

3、正比例和反比例的判断方法判断两种量是否成正比例或反比例的方法：一是看这两种相关联的量中相对应的两个数的比值是否一定；二是看这两种量中相对应的两个数的积是否一定。

比的意义：两个量的关系可以用比来表示，我们通常称之为“比”。

定义：在两个量的比中，我们把数量放在前面，单位“1”放在后面，我们称之为前项，后项。

比与除法、分数的关系：比的前项相当于被除数或分子，后项相当于除数或分母，比值相当于商或分数值。

比的性质：比的前项和后项同时乘上或者除以相同的数(0除外)，比值不变。

比例的意义：表示两个比相等的式子叫做比例。

组成比例的四个数叫做比例的项。

两外两项叫做内项，中间两项叫做外项。

如果中间的两项是两个相同的数，这样的比例叫做对称比例。

比例尺的意义：我们把图上距离和实际距离的比叫做比例尺。

我们把比例尺分为放大比例尺和缩小比例尺两种。

缩小比例尺的计算方法：已知实际距离求图上距离，根据公式计算即可；已知图上距离求实际距离根据公式计算即可。

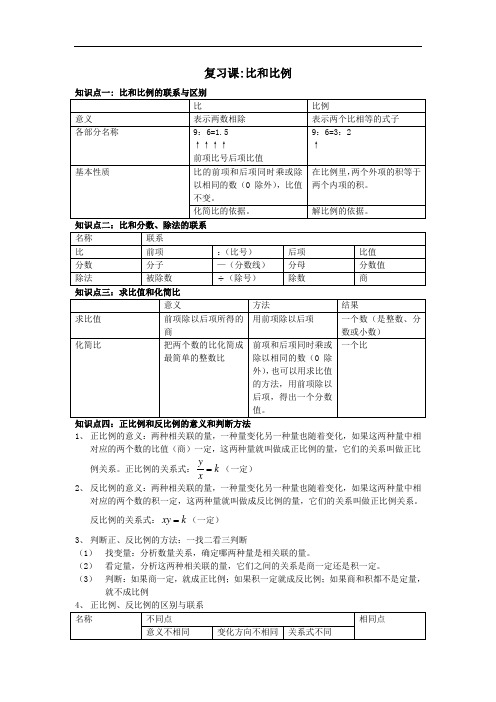
最新小学六年级 __比和比例知识点梳理知识点一 :比和比例的联系与区别比比例意义表示两数相除表示两个比相等的式子各部分名称9：6=1.59： 6=3： 2↑↑↑↑↑前项比号后项比值基本性质比的前项和后项同时乘或除在比例里 ,两个外项的积等于以相同的数（ 0 除外） ,比值不两个内项的积 .变.化简比的依据 .解比例的依据 .知识点二：比和分数、除法的联系名称联系比前项：（比号）后项比值分数分子—（分数线）分母分数值除法被除数（除号）除数商知识点三：求比值和化简比意义方法结果求比值前项除以后项所得的用前项除以后项一个数（是整数、分商数或小数）化简比把两个数的比化简成前项和后项同时乘或一个比最简单的整数比除以相同的数（ 0除外） ,也可以用求比值的方法 , 用前项除以后项 , 得出一个分数值 .知识点四：正比例和反比例的意义和判断方法1、正比例的意义：两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的比值（商）一定 ,这两种量就叫做成正比例的量 ,它们的关系叫做正比例关系.正比例的关系式：y k（一定）x2、反比例的意义：两种相关联的量,一种量变化另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做正比例关系.反比例的关系式：xy k （一定）3、判断正、反比例的方法：一找二看三判断（1）找变量：分析数量关系 ,确定哪两种量是相关联的量 .（2）看定量 ,分析这两种相关联的量 ,它们之间的关系是商一定还是积一定.（3）判断：如果商一定,就成正比例；如果积一定就成反比例；如果商和积都不是定量,就不成比例4、正比例、反比例的区别与联系名称不同点意义不相同变化方向不相同正比例两种量中相对一种量扩大（或应的两个数的缩小）,另一种量比值 , 也就是商也随之扩大（或一定缩小） .反比例两种量中相对一种量扩大（或应的两个数的缩小）,另一种量积一定也随之缩小（或扩大） .相同点关系式不同y两种相关联的xk （一定）量 , 一种量变化另一种量也随着变化xy k （一定）知识点五：用比例知识解决问题1、按比例分配问题（1）按比例分配应用题：把一个量按照一定的比分配成几部分,求每个部分数量各是多少的应用题叫做按比例分配应用题 .（2）解题方法一般方法：把比转化成为分数,用分数方法解答,即先求出总分数,然后求出各部分量占总量的几分之几,最后按照求一个数的几分之几多少的解题方法,分别求出各部分的量是多少归一法：把比看做分得的分数,先求出各部分的总分数,然后再用“总量总份数=平均每份的量（归一）” ,再用“一份的量各部分量所对应的份数”,求出各部分的量.用比例知识解答：首先设未知量为.再根据题中“已知比等于相对应的量的比”作为等量关系式列出含有x 的比例式 ,再解比例求出x.2、用正、反比例知识解答应用题的步骤（1）分析数量关系 .判断成什么比例 .（２）找等量关系 .如果成正比例 ,则按等比找等量关系式；如果成反比例 ,则按等积找等量关系式 .（３）解比例式 .设未知数为 x,并代入等量关系式 ,得正比例式或反比例式 .（４）解比例 .（５）检验并写出答语 .精讲典型题例题 1（ 1）一项工程 ,甲单独做要 4 天,乙单独做要 5天完成 ,甲和乙的工作效率比是（）：（）（ 2）把 2 米： 4 厘米化成最简单的整数比是（）,比值是（） .例题 2汉江码头第一货场有750 吨货物 ,分给两个运输队运到另一货场.甲队有载重 6 吨的汽车6辆,乙队有载重8 吨的汽车 3 量,按两个队的运输能力分配,甲、乙两队各应运货多少吨？巧练考点题1. 请你填一填（ 1） 2.1:0.9 化简成最简单的整数比是（） ,比值是（） . （ 2）甲乙两数的比是 4:5,甲数是乙数的（） ,乙数是甲乙和的（） （ 3）一个最简单的整数比的比值是1.5,这个比是（）（ 4） 4.5 与它的倒数的比是（）（ 5）（） 24= 3=24：（） =（） %8（6）如果 a7= b2( a 、 b 都不为 0),那么 a : b =（）：（）（ 7）除数、被除数的比是 1:3,被除数、除数、商的和是 35,被除数是（）（ 8）一汽车工人加工一批零件 ,如下表每天生产的个数18090 需要的天数（天） 24① 请按每天生产量与需要时间的关系填表.② 这批零件有（）个③ 表中两种量是否成比例： （） ,如果成比例成（）比例 （10）判断一些生活中的实例.①用煤的天数一定 ,每天用煤量与总用煤量（）比例 .②一本书的页数一定 ,已看的页数与没看的页数（）比例③三角形的面积一定 ,三角形的底与高（）比例 .2 判断题（1 ）化简比的结果是一个商 ,可以使小数、分数或整数.（）（2 ）走同一段路 ,甲用1小时 ,乙用1小时 ,甲、乙的速度之比是 5:4. （）5 4（ 3）在一个比例里 ,如果两个外项互为倒数 ,那么两个内项也互为倒数 .（）（ 4）一条道路 ,已修的米数和未修的米数成反比例.（）3 选择题（1）k 5y 且 x 和 y 都不为当 k 一定时 , x 和 y 成（）比例.x,0,A. 成正比例B.成反比例C.不成比例（2）杭州西湖南北长 3.3km, 东西宽 2.8km. 南北长和东西宽的比是（） .A.33km ：28kmB.3.3. ：2.8C.33： 8（3）一个三角形 ,三个内角的度数比是1:4:5,这个三角形是（）A. 锐角三角形B.直角三角形C.钝角三角形（4）在比例尺 1 的地图上 ,量得 A 、 B 两地的距离是 2cm,那么 A 、 B 两地的实际距离100000是（） .A.0.2kmB.2kmC.20km4.解决问题 .（1）药液与水的比是1:1500, 如果倒入药液 20.5g,需要加多少克水呢？（2）从儿童节那天开始,亮亮前七天看书210 页 ,照这样计算 ,这个月亮亮一共看书多少页？。

六年级数学毕业复习_比和比例知识点比和比例知识点---------判断两个量是否成正比例、反比例或不成比例一、写（写出数量关系式）1、根据数量间的关系或公式，写出数量关系式。

如，①宽一定，长方形的面积和长是否成正比例。

根据“长方形的面积=长×宽”得到“宽（一定）长长方形的面积”，因为长方形的面积和长是相关联的量，宽一定，也就是它们的比值一定，所以“宽一定，长方形的面积和长是成正比例”。

②圆锥的体积一定，底面积和高是否成反比例。

根据“底面积×高×31=圆锥的体积”得到“底面积×高=圆锥的体积×3”，因为底面积和高是相关联的量，圆锥的体积一定，“圆锥的体积×3"的结果也一定，就是底面积和高的积一定（底面积×高=圆锥的体积×3（一定）），所以圆锥的体积一定，底面积和高是成反比例。

2、注意：写出的数量关系式，其中的一边（左边）只能有这两个相关联的量，不能有多余的量和数字。

如，“（长＋宽）×2=长方形的周长”的左边就多了×2，长方形的周长”应变为“（长＋宽）=2又如，梯形的上底和下底不变，面积和高。

可以这样写关系式：（a＋b）×h÷2=s→（a＋b）×h÷2÷h=s÷h→（a＋b）÷2 =s÷h→s÷h=（a＋b）÷2，因为上底和下底不变，（a＋b）÷2的结果也是一定的，所以梯形的上底和下底不变，面积和高成正比例。

3、还有些数量之间是无法写关系式的。

如，“小明的身高和跳高的高度成正比例”是无法写出关系式的。

二、看（1、看是否相关联2、看是否能变化3、看是否商（积）一定）1、看是否相关联：也就是一个量变化了，另一个量是否也会随着变化。

如，长方形的面积一定，长和宽就是相关联的量，因为长变化了，宽也会随着变化。

复习课 :比和比例知识点一 :比和比例的联系与区别比比例意义表示两数相除表示两个比相等的式子各部分名称9： 6=9：6=3： 2↑↑↑↑↑前项比号后项比值基本性质比的前项和后项同时乘或除在比例里，两个外项的积等于以相同的数（0 除外），比值两个内项的积。

不变。

化简比的依据。

解比例的依据。

知识点二：比和分数、除法的联系名称联系比前项：（比号）后项比值分数分子—（分数线）分母分数值除法被除数（除号）除数商知识点三：求比值和化简比意义方法结果求比值前项除以后项所得的用前项除以后项一个数（是整数、分商数或小数）化简比把两个数的比化简成前项和后项同时乘或一个比最简单的整数比除以相同的数（ 0除外），也可以用求比值的方法，用前项除以后项，得出一个分数值。

知识点四：正比例和反比例的意义和判断方法1、正比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的比值（商）一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系。

正比例的关系式：y k（一定）x2、反比例的意义：两种相关联的量，一种量变化另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系叫做正比例关系。

反比例的关系式：xy k （一定）3、判断正、反比例的方法：一找二看三判断（1）找变量：分析数量关系，确定哪两种量是相关联的量。

（2）看定量，分析这两种相关联的量，它们之间的关系是商一定还是积一定。

（3）判断：如果商一定，就成正比例；如果积一定就成反比例；如果商和积都不是定量，就不成比例4、正比例、反比例的区别与联系名称不同点意义不相同正比例两种量中相对应的两个数的比值，也就是商一定反比例两种量中相对应的两个数的积一定变化方向不相同关系式不同一种量扩大（或yk （一定）缩小），另一种量x也随之扩大（或缩小）。

一种量扩大（或xy k （一定）缩小），另一种量也随之缩小（或扩大）。

北师大版六年级数学下册总复习——式与方程正比例与反比例正比例和反比例是数学中重要的概念，在解决很多实际问题和数学题目中经常会遇到。

在六年级数学下册总复习中，我们需要掌握正比例和反比例的概念、性质以及解题方法。

1. 正比例关系：正比例关系是指两个变量之间的比例是恒定的，当其中一个变量增加时，另一个变量也随之增加；当其中一个变量减少时，另一个变量也随之减少。

例如：如果一个物体的重量和体积成正比，那么当体积增加时，重量也会增加；当体积减少时，重量也会减少。

正比例关系可以用一个等式来表示：y = kx，其中y和x是两个变量，k称为比例系数。

比例系数k表示两个变量之间的比例关系，是一个常数，永远不会变化。

解题方法：当已知比例关系中的一个变量和比例系数时，可以根据等式求解另一个变量。

如果已知有三个数a、b、c满足比例关系a:b = c:x，可以用等式a/b = c/x来求解x 的值。

2. 反比例关系：反比例关系是指两个变量之间的乘积是恒定的，当其中一个变量增加时，另一个变量会相应地减少；当其中一个变量减少时，另一个变量会相应地增加。

例如：一个车以恒定的速度行驶，在相同的时间内，行驶的距离与速度成反比。

速度越快，行驶的距离越短；速度越慢，行驶的距离越长。

反比例关系可以用一个等式来表示：y = k/x，其中y和x是两个变量，k称为比例系数。

和正比例关系一样，比例系数k是一个常数，永远不会变化。

解题方法：当已知反比例关系中的一个变量和比例系数时，可以根据等式求解另一个变量。

如果已知有三个数a、b、c满足反比例关系a:b = c:x，可以用等式a/b = c/x来求解x的值。

总结：在解决正比例问题时，常用的解题方法是根据已知的比例系数和一个变量求解另一个变量；在解决反比例问题时，常用的解题方法是根据已知的比例系数和一个变量求解另一个变量。