湖北省黄冈中学2017届高三下学期三模文数试题Word版含答案

黄冈市2017年3月高三年级调研考试语文试题本试题卷共10页，22题。

全卷满分150分。

考试用时150分钟。

★祝考试顺利★【注意事项】1．答卷前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用合乎要求的2B铅笔把答题卡上对应题目的答案标号涂黑。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．选考题的作答：先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑。

答案写在答题卡上对应的答题区域内，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

5．考试结束后，请将本试题卷和答题卡一并上交。

第Ⅰ卷阅读题（70分）一、现代文阅读（35分）（一）论述类文本阅读（9分，每小题3分）阅读下面的文字，完成1-3题。

重新体认家庭为社会之本戴志勇近日，央视综合、少儿等频道播出动画剧《郑义门》，呈现了“江南第一家”通过礼法治家、用豆子民主选举家长等方式，对一个成百上千乃至几千人的共同体进行自治的故事。

郑家几百年间出仕为官者无一人因贪墨罢官，让“廉政”成为郑家故事的一个“卖点”。

细节难免艺术虚构，但郑家在历史上是赫赫有名。

其逐渐修订而成的家规168条，放在今日，有很多对个人自我修行仍有实践价值的指引。

但譬如基本不让女性与娘家人走动，族人不得“私藏”一文钱，收支由大家族统一管理等做法，今人恐已难以接受。

尤为值得分析的，是第一集点出的此片主旨：治国必先齐家。

从百年前的“娜拉出走”到今天的肯定家庭，家与国的关系，绕了一大圈，似乎又走回来了。

《大学》将齐家摆在治国之前，首先是因为对治理国家者必须要有极高的要求，而家庭乃是最原本的个人成长与修行场所。

儒家认为，若治国者不能格物致知、正心诚意，必然会心中充满杂念，带来治理困境。

而在家庭中，人首先感受世间最自然的父母养育之情与兄弟手足之爱，有人与人之间基于自然的界限与分寸，自然法奠基于此。

湖北省黄冈市2017届⾼三3⽉份质量数学试题（⽂）含答案黄冈市2017年⾼三年级3⽉份质量检测数学试题（⽂科）⼀、选择题：本⼤题共12个⼩题,每⼩题5分,共60分.在每⼩题给出的四个选项中，只有⼀项是符合题⽬要求的.1.若集合{}02A x x =<<，且A B B = ，则集合B 可能是（）A.{}0 2，B.{}0 1，C.{}0 1 2，，D.{}12.设i 是虚数单位，复数321i z i=-，则复数z 在复平⾯内所对应的点位于（）A.第⼀象限B.第⼆象限C.第三象限D.第四象限3.阅读如图所⽰的程序框图，运⾏相应的程序，输出的S 的值等于（）A.18B.20C.21D.404.某⼀简单⼏何体的三视图如图所⽰，则该⼏何体的外接球的表⾯积是（）A.13πB.16πC.25πD.27π5.下列四个结论：①若0x >，则sin x x >恒成⽴；②命题“若sin 0x x -=，则0x =”的逆否命题为“若0x ≠，则sin 0x x -≠”；③“命题p q ∧为真”是“命题p q ∨为真”的充分不必要条件；④命题“ ln 0x R x x ?∈->，”的否定是“000 ln 0x x x ?∈-<，”.其中正确结论的个数是（） A.1个B.2个C.3个D.4个6.在ABC △中，⾓ A B C ，，的对边分别是 a b c ，，，若 2a A B ==，，则cos B =（）7.已知数据123 n x x x x ，，，…，是某市()*3 n n n N ≥∈，个普通职⼯的年收⼊，设这n 个数据的中位数为x ，平均数为y ，⽅差为z ，如果再加上世界⾸富的年收⼊1n x +，则这1n +个数据中，下列说法正确的是（）A.年收⼊平均数可能不变，中位数可能不变，⽅差可能不变B.年收⼊平均数⼤⼤增⼤，中位数可能不变，⽅差变⼤C.年收⼊平均数⼤⼤增⼤，中位数可能不变，⽅差也不变D.年收⼊平均数⼤⼤增⼤，中位数⼀定变⼤，⽅差可能不变8.过双曲线()222210 0x y a b a b-=>>，的右焦点F 作圆222x y a +=的切线FM （切点为M ），交y 轴于点P ，若M 为线段FP 的中点，则双曲线的离⼼率为（）C.29.函数22ln x x y x=的图象⼤致是（）ABCD10.已知在ABC △中，90ACB ∠=?，3BC =，4AC =，P 是线段AB 上的点，则P 到AC 、BC 的距离的乘积的最⼤值为（）A.3B.2C. D.911.已知数列{}n x 满⾜()*21n n n x x x n N ++=-∈，若11x =，()2 1 0x a a a =≤≠，，且3n n x x +=对于任意正整数n 均成⽴，则数列{}n x 的前2017项和2017S 的值为（） A.672B.673C.1344D.134512.若函数()()()()()3312 112113 114x x x f x x x x x ?-?-≤≤?+=??-+<->??，，或对任意的[]3 2m ∈-，，总有()10f mx fx -+>恒成⽴，则x 的取值范围是（）A.11 23??- ，B.()1 2-，C.41 32??-- ，D.()2 3-，第Ⅱ卷（⾮选择题共90分）⼆、填空题（每题5分，满分20分，将答案填在答题纸上）13.已知两个平⾯向量 a b ，满⾜1a =，2a b -= a 与b的夹⾓为120?，则b =．14.我国古代数学名著《张邱健算经》有“分钱问题”如下：“今有与⼈钱，初⼀⼈与三钱，次⼀⼈与四钱，次⼀⼈与五钱，以次与之，转多⼀钱。

湖北省黄冈市2017年3月高考模拟文科数学试卷一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是满足题目要求的．）1．若集合02{|}A x x =＜＜，且A B B =I ，则集合B 可能是（ ） A ．{0,2}B ．{0,1}C ．{0,1,2}D ．{1}2．设i 是虚数单位，复数32i 1iz =-，则复数z 在复平面内所对应的点位于（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．阅读如图所示的程序框图，运行相应的程序，输出的S 的值等于（ ）A ．18B ．20C ．21D ．404．某一简单几何体的三视图如所示，该几何体的外接球的表面积是（ ）A ．13πB ．16πC ．25πD ．27π5．下列四个结论：①若0x ＞，则sin x x ＞恒成立；②命题“若sin 0x x -=，则0x =”的逆否命题为“若0x ≠，则sin 0x x -≠”； ③“命题p q ∧为真”是“命题p q ∨为真”的充分不必要条件；④命题“x ∀∈R ，ln 0x x -＞”的否定是“x ∃∈R ，ln 0x x -＜”． 其中正确结论的个数是（ ） A ．1个B ．2个C ．3个D ．4个6．ABC △的三内角A 、B 、C 的对边边长分别为a 、b 、c，若a =，2A B =，则cos =B （ ） ABCD7．已知数据1x ，2x ，3x ，…，n x 是上海普通职工n （3n ≥，n ∈*N ）个人的年收入，设这n 个数据的中位数为x ，平均数为y ，方差为z ，如果再加上世界首富的年收入1n x +，则这n +1个数据中，下列说法正确的是（ ）A ．年收入平均数大大增大，中位数一定变大，方差可能不变B ．年收入平均数大大增大，中位数可能不变，方差变大C ．年收入平均数大大增大，中位数可能不变，方差也不变D ．年收入平均数可能不变，中位数可能不变，方差可能不变8．过双曲线22221x y a b+=（0a ＞，0b ＞）的右焦点F 作圆222x y a +=的切线FM （切点为M ），交y 轴于点P ．若M 为线段FP 的中点，则双曲线的离心率是（ ）ABC ．2D9．函数5e x y x x =-的图像大致是（ ）A ．B ．C ．D ．10．已知在ABC △中，90ACB ∠=︒，3BC =，4AC =，P 是线段AB 上的点，则P 到AC ，BC 的距离的乘积的最大值为（ ） A ．3B ．2C．D ．911．已知数列{}n x 满足21||n n n x x x ++=-（*n ∈N ），若11x =，2x a =（1a ≤，0a ≠），且3n n x x +=对于任意正整数n 均成立，则数列{}n x 的前2016项和2016S 的值为（ ） A ．672B ．673C ．1 342D ．1 34412．若函数33(12),(11)21()1(3),(x 11)4x x x f x x x x ⎧--≤≤⎪⎪+=⎨⎪-+-⎪⎩＜或＞对任意的[3,2]m ∈-，总有(1)()0f mx f x -+＞恒成立，则x的取值范围是（ ）A ．11(,)23-B ．(1,2)-C ．41(,)32--D ．(2,3)-二、填空题：本大题共4小题，每题5分，共20分．13．已知两个平面向量r a ，r b 满足||1=r a，|2-r r a b r a 与rb 的夹角为120︒，则||r b =_______． 14．我国古代数学名著《张邱健算经》有“分钱问题”如下：“今有人与钱，初一人与三钱，次一人与四钱，次一人与五钱，以次与之，转多一钱，与讫，还数聚与均分之，人得一百钱，问人几何？”则分钱问题中的人数为_______．15．已知x ，y 满足30030x y x x y -≥⎧⎪-≤⎨⎪+-≥⎩，则目标函数2z x y =-+的最大值为_______．16．关于圆周率π，数学发展史上出现过许多很有创意的求法，如著名的蒲丰实验和查理斯实验．受其启发，我们也可以通过设计下面的实验来估计π的值：先请200名同学，每人随机写下一个都小于1的正实数对(x,y)；再统计两数能与1构成钝角三角形三边的数对（x ，y ）的个数m ；最后再根据统计数m 来估计π的值．假如统计结果是56m =，那么可以估计π≈_______．（用分数表示）三、解答题：本大题共5小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（12分）已知向量(1cos ,1)x ω=+r a，(1,)a x ω=r b （ω为常数且0ω＞），函数()f x =r rg a b 在R 上的最大值为2． （1）求实数a 的值；（2）把函数()y f x =的图象向右平移π6ω个单位，可得函数()y g x =的图象，若()y g x =在π[0,]4上为增函数，求ω的最大值．18．（12分）已知某中学高三文科班学生的数学与地理的水平测试成绩抽样统计如表：x 人数 y ABCA 14 40 10B a 36 b C28834若抽取学生n 人，成绩分为A （优秀），B （良好），C （及格）三个等次，设x ，y 分别表示数学成绩与地理成绩，例如：表中地理成绩为A 等级的共有14401064++=（人），数学成绩为B 等级且地理成绩为C 等级的有8人．已知x 与y 均为A 等级的概率是0.07．（1）设在该样本中，数学成绩的优秀率是30%，求a ，b 的值；（2）已知8a ≥，6b ≥，求数学成绩为A 等级的人数比C 等级的人数多的概率．19．（12分）如图1，以BD 为直径的圆O 经过A ，C 两点，延长DA ，CB 交于P 点，如图2，将PAD 沿线段AB 折起，使P 点在底面ABCD 的射影恰为AD 的中点Q ，1AB BC ==，2BD =，线段PB ，PC 的中点为E ，F ．（1）判断四点A ，D ，E ，F 是否共面，并说明理由；（2）求四棱锥EABCQ ﹣的体积．20．（12分）如图，圆C 与x 轴相切于点T (2,0)，与y 轴正半轴相交于两点M ，N （点M 在点N 的下方），且||3MN =．（Ⅰ）求圆C 的方程；（Ⅱ）过点M 任作一条直线与椭圆22184x y +=相交于两点A ，B ，连接AN 、BN ，求证：ANM BNM ∠=∠．21．（12分）已知函数()(2)ln 23f x x x x =-+-，1x ≥． （1）试判断函数()f x 的零点个数； （2）若函数(1)()()ln a x g x x a x x -=-+在[1,)+∞上为增函数，求整数a 的最大值．（可能要用的数据：ln1.590.46≈；ln1.600.47≈；400419.76≈）请考生在第22，23题中任选一题作答，如果多做，则按多做的第一题计分．作答时请写清题号．[选修4-4：极坐标与参数方程]22．（10分）在直角坐标系xOy 中，曲线C 的参数方程为sin cos sin cos x y αααα=+⎧⎨=-⎩（α为参数）（1）求曲线C 的普通方程；（2）在以O 为极点，x 正半轴为极轴的极坐标系中，直线l πsin()104θ-+=，已知直线l 与曲线C 相交于A ，B 两点，求||AB ．[选修4-5：不等式选讲]23．已知函数|||)|(21f x x a x +=--（a ∈R ）． （Ⅰ）当1a =时，求()2f x ≤的解集；（Ⅱ）若()21f x x ≤+的解集包含集合1[,1]2，求实数a 的取值范围．。

湖北省黄冈市2017年3月高考模拟文科数学试卷一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是满足题目要求的．）1．若集合02{|}A x x =＜＜，且A B B =，则集合B 可能是（ ）A ．{0,2}B ．{0,1}C ．{0,1,2}D ．{1}2．设i 是虚数单位，复数32i 1iz =-，则复数z 在复平面内所对应的点位于（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．阅读如图所示的程序框图，运行相应的程序，输出的S 的值等于（ ） A ．18B ．20C ．21D ．404．某一简单几何体的三视图如所示，该几何体的外接球的表面积是（ ）A ．13πB ．16πC ．25πD ．27π5．下列四个结论：①若0x ＞，则sin x x ＞恒成立；②命题“若sin 0x x -=，则0x =”的逆否命题为“若0x ≠，则sin 0x x -≠”；③“命题p q ∧为真”是“命题p q ∨为真”的充分不必要条件； ④命题“x ∀∈R ，ln 0x x -＞”的否定是“x ∃∈R ，ln 0x x -＜”． 其中正确结论的个数是（ ） A ．1个B ．2个C ．3个D ．4个6．ABC △的三内角A 、B 、C 的对边边长分别为a 、b 、c，若a =，2A B =，则cos =B （ ） A．3B．4C．5D．67．已知数据1x ，2x ，3x ，…，n x 是上海普通职工n （3n ≥，n ∈*N ）个人的年收入，设这n 个数据的中位数为x ，平均数为y ，方差为z ，如果再加上世界首富的年收入1n x +，则这n +1个数据中，下列说法正确的是（ ）A ．年收入平均数大大增大，中位数一定变大，方差可能不变B ．年收入平均数大大增大，中位数可能不变，方差变大C ．年收入平均数大大增大，中位数可能不变，方差也不变D ．年收入平均数可能不变，中位数可能不变，方差可能不变8．过双曲线22221x y a b+=（0a ＞，0b ＞）的右焦点F 作圆222x y a +=的切线FM （切点为M ），交y 轴于点P ．若M 为线段FP 的中点，则双曲线的离心率是（ ）ABC ．2D9．函数5e x y x x =-的图像大致是（ ）A ．B ．C ．D ．10．已知在ABC △中，90ACB ∠=︒，3BC =，4AC =，P 是线段AB 上的点，则P 到AC ，BC 的距离的乘积的最大值为（ ） A ．3B ．2C．D ．911．已知数列{}n x 满足21||n n n x x x ++=-（*n ∈N ），若11x =，2x a =（1a ≤，0a ≠），且3n n x x +=对于任意正整数n 均成立，则数列{}n x 的前2016项和2016S 的值为（ ） A ．672B ．673C ．1 342D ．1 34412．若函数33(12),(11)21()1(3),(x 11)4x x x f x x x x ⎧--≤≤⎪⎪+=⎨⎪-+-⎪⎩＜或＞对任意的[3,2]m ∈-，总有(1)()0f mx f x -+＞恒成立，则x 的取值范围是（ ） A ．11(,)23-B ．(1,2)-C ．41(,)32--D ．(2,3)-二、填空题：本大题共4小题，每题5分，共20分．13．已知两个平面向量a ，b 满足||1=a ，|2|=21-a b ，且a 与b 的夹角为120︒，则||b =_______． 14．我国古代数学名著《张邱健算经》有“分钱问题”如下：“今有人与钱，初一人与三钱，次一人与四钱，次一人与五钱，以次与之，转多一钱，与讫，还数聚与均分之，人得一百钱，问人几何？”则分钱问题中的人数为_______．15．已知x ，y 满足30030x y x x y -≥⎧⎪-≤⎨⎪+-≥⎩，则目标函数2z x y =-+的最大值为_______．16．关于圆周率π，数学发展史上出现过许多很有创意的求法，如著名的蒲丰实验和查理斯实验．受其启发，我们也可以通过设计下面的实验来估计π的值：先请200名同学，每人随机写下一个都小于1的正实数对(x,y)；再统计两数能与1构成钝角三角形三边的数对（x ，y ）的个数m ；最后再根据统计数m 来估计π的值．假如统计结果是56m =，那么可以估计π≈_______．（用分数表示）三、解答题：本大题共5小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（12分）已知向量(1cos ,1)x ω=+a，(1,)a x ω=b （ω为常数且0ω＞），函数()f x =a b 在R 上的最大值为2． （1）求实数a 的值；（2）把函数()y f x =的图象向右平移π6ω个单位，可得函数()y g x =的图象，若()y g x =在π[0,]4上为增函数，求ω的最大值．18．（12分）已知某中学高三文科班学生的数学与地理的水平测试成绩抽样统计如表：若抽取学生n 人，成绩分为A （优秀），B （良好），C （及格）三个等次，设x ，y 分别表示数学成绩与地理成绩，例如：表中地理成绩为A 等级的共有14401064++=（人），数学成绩为B 等级且地理成绩为C 等级的有8人．已知x 与y 均为A 等级的概率是0.07．（1）设在该样本中，数学成绩的优秀率是30%，求a ，b 的值；（2）已知8a ≥，6b ≥，求数学成绩为A 等级的人数比C 等级的人数多的概率．19．（12分）如图1，以BD 为直径的圆O 经过A ，C 两点，延长DA ，CB 交于P 点，如图2，将PAD 沿线段AB 折起，使P 点在底面ABCD 的射影恰为AD 的中点Q ，1AB BC ==，2BD =，线段PB ，PC 的中点为E ，F ．（1）判断四点A ，D ，E ，F 是否共面，并说明理由；（2）求四棱锥EABCQ ﹣的体积．20．（12分）如图，圆C 与x 轴相切于点T (2,0)，与y 轴正半轴相交于两点M ，N （点M 在点N 的下方），且||3MN =．（Ⅰ）求圆C 的方程；（Ⅱ）过点M 任作一条直线与椭圆22184x y +=相交于两点A ，B ，连接AN 、BN ，求证：ANM BNM ∠=∠．21．（12分）已知函数()(2)ln 23f x x x x =-+-，1x ≥． （1）试判断函数()f x 的零点个数； （2）若函数(1)()()ln a x g x x a x x -=-+在[1,)+∞上为增函数，求整数a 的最大值．（可能要用的数据：ln1.590.46≈；ln1.600.47≈；400419.76≈）请考生在第22，23题中任选一题作答，如果多做，则按多做的第一题计分．作答时请写清题号．[选修4-4：极坐标与参数方程]22．（10分）在直角坐标系xOy 中，曲线C 的参数方程为sin cos sin cos x y αααα=+⎧⎨=-⎩（α为参数）（1）求曲线C 的普通方程；（2）在以O 为极点，x 正半轴为极轴的极坐标系中，直线l πsin()104θ-+=，已知直线l 与曲线C 相交于A ，B 两点，求||AB ．[选修4-5：不等式选讲]23．已知函数|||)|(21f x x a x +=--（a ∈R ）． （Ⅰ）当1a =时，求()2f x ≤的解集；（Ⅱ）若()21f x x ≤+的解集包含集合1[,1]2，求实数a 的取值范围．湖北省黄冈市2017年3月高考模拟文科数学试卷答 案一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是满足题目要求的．）1~5．DDBCC 6~10．BBABA 11~12．DA二、填空题（本大题共4小题，每题5分，共20分．请将答案填在答题卡对应题号的位置上．） 13．2 14．195 15．3- 16．7825三、解答题：本大题共5小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．解：（1）π()1cos 2sin()16f x x a x x a ωωω=+++=+++ 因为函数()f x 在R 上的最大值为2， 所以32a +=，故1a =-．（2）由（1）知：π()2sin()6f x x ω=+， 把函数π()2sin()6f x x ω=+的图象向右平移π6ω个单位，可得函数()2sin y g x x ω==． 又∵()y g x =在π[0,]4上为增函数， ∴()g x 的周期2ππT ω=≥，即2ω≤，∴ω的最大值为2． 18．解：（1）由频率=频数总数，得到140.07n=，解得200n =， ∴14280.3200a ++=，解得18a =，∵1428403681034200a b ++++++++=，∴12b =．（2）∵30a b +=，且8a ≥，6b ≥，∴由14281034a b ++++＞，得2a b +＞， (,)a b 的所有结果为(8,22)，(9,21)，(10,20)，(11,19)，(12,18)，(13,17)，(14,16)，(15,15)，(16,14)，(17,12)，(18,12)，(19,20)，(20,10)，(21,9)，(22,8)，(23,7)，(24,6)共17组，其中2a b +＞的有8组，∴数学成绩为A 等级的人数比C 等级的人数多的概率817P =． 19．解：（1）结论：A 、D 、E 、F 四点不共面．理由如下：∵延长DA ，CB 交于P 点， ∴DA 与BC 不平行， 又∵EF BC ∥， ∴EF 与AD 不平行， ∴A 、D 、E 、F 四点共面；（2）由1AB BC ==，2BD =，得60ADB ∠=︒，AD CD =又P 点在底面ABCD 的射影恰为AD 的中点Q ，可得平面PAD ⊥平面ABCD ，且PAD △32PO =， 又E 为线段PB 的中点，∴E 到平面ABCD 的距离为34．122sin60122ABCQ ADB CDB CDO S S S S =+-=⨯︒-︒=△△△．∴13(12334E ABCQ V -=⨯-⨯=20．解：（Ⅰ）设圆C 的半径为r （0r ＞），依题意，圆心坐标为(2,)r ． ∵||3MN =，∴2223()22r =+，解得2254r =， 故圆C 的方程为22525(2)()24x y -+-=． （Ⅱ）把0x =代入方程22525(2)()24x y -+-=，解得1y =或4y =，即点(0,1)M ，(0,4)N ．（1）当AB y ⊥轴时，由椭圆的对称性可知ANM BNM ∠=∠． （2）当AB 与y 轴不垂直时，可设直线AB 的方程为1y kx =+．联立方程22128y kx x y =+⎧⎨+=⎩，消去y 得，2(12)460k x kx ++=﹣. 设直线AB 交椭圆Γ于11(,)A x y 、22(,)B x y 两点， 则122412k x x k -+=+，122612x x k -=+．∴12121212121212443323()0AN BN y y kx kx kx x x x k k x x x x x x -----++=+=+==， ∴ANM BNM ∠=∠． 综上所述，ANM BNM ∠=∠．21．解：（1）由()(2)ln 23f x x x x =-+-，1x ≥，求导2()ln 3f x x x'=-+，（1x ≥）， 则()0f x '＞恒成立，则函数()f x 在[1,)+∞为增函数， 由()(1)1f x f ''≥=，故()(x 2)ln 23f x x x =-+-在[1,)+∞为增函数，又由(1)10f =-＜，(2)10f =＞， ∴函数()f x 在[1,)+∞上有唯一的零点；（2）(1)()()ln a x g x x a x x -=-+，2g ()ln 1a ax x x x '=+-+，在[1,)+∞上恒成立， 由1x =，显然成立，则2(ln 1)1x x a x +≤-在[1,)+∞上恒成立，令2(ln 1)()1x x h x x +=-，(1,)x ∈+∞，则a 小于h x （）的x 在区间(1,)+∞上的最小值，求导2[(2)ln 23]()(1)x x x x h x x -+-'=-，由（1）可知()(x 2)ln 23f x x x =-+-在[1,)+∞为增函数， 故()f x 在[1,)+∞上由唯一的零点m ， 由(1.60)0.012f =，(1.59)0.00860f =-＜则(1.59,1.60)m ∈，()(m 2)ln 230f m m m =-+-=，则23ln 2m m m-=-， 由当(1,m)x ∈，()0h x '＜，()h x 在(1,]m 为减函数，(m,)x ∈+∞，()0h x '＞，()h x 在[m,)+∞为增函数，故当x m =，()h x 有最小值22(ln 1)()12m m mh m m m+==--，令2(0.4,0.41)m t -=∈，则()h x 最小值有，22(2)44123632412364(,) 6.17210041510041m t t m t t -==+-∈++≈-，∴()h x 的最小值大约在61764．～．之间， 故整数a 的最大值为6．22．解：（1）曲线C 的参数方程为sin cos sin cos x y αααα=+⎧⎨=-⎩（α为参数），x ，y 平方相加可得：222x y +=，① （2）直线lsin()104πθ-+=化为普通方程为：10x y -+=，②由②得：1y x =+，③把③带入①得：22210x x +-=，∴1212112x x x x +=⎧⎪⎨=⎪⎩，∴12|||AB x x -=23．【解答】解：（Ⅰ）当1a =时，()|1||21|f x x x =-+-，|1||21()22|f x x x -+-≤⇒≤，上述不等式可化为121122x x x ⎧≤⎪⎨⎪-+-≤⎩或121212x x x ⎧⎪⎨⎪-+-≤⎩＜＜1或11212x x x ≥⎧⎨-+-≤⎩ 解得120x x ⎧≤⎪⎨⎪≥⎩或1122x x ⎧⎪⎨⎪≤⎩＜＜或143x x ≥⎧⎪⎨≤⎪⎩．（3分） ∴102x ≤≤或112x ＜＜或413x ≤≤， ∴原不等式的解集为4{|0}3x x ≤≤．（Ⅱ）∵()|21|f x x ≤-的解集包含1[,1]2，∴当1[,1]2x ∈时，不等式()|21|f x x ≤+恒成立，即|1||22||11|x x x -+-≤+在1[,1]2x ∈上恒成立，∴|1|21||21x x x -+-≤+，即||2x a -≤，∴22x a -≤-≤，∴22x a x -≤≤+在1[,1]2x ∈上恒成立，…（8分） ∴max min (2)(2)x a x -≤≤+，∴512a -≤≤， 所以实数a 的取值范围是5[1,]2-． …（10分）湖北省黄冈市2017年3月高考模拟文科数学试卷解析1．【考点】集合的包含关系判断及应用．【分析】根据A∩B=B，即可判断集合B的范围，可得答案．【解答】解：由题意：集合A={x|0＜x＜2}，∵A∩B=B，∴B⊆A，2．【考点】复数代数形式的乘除运算．【分析】利用复数代数形式的乘除运算化简求得Z所对应点的坐标得答案．【解答】解：∵=，∴复数z在复平面内所对应的点的坐标为（1，﹣1），位于第四象限．3．【考点】循环结构．【分析】算法的功能是求S=21+22+…+2n+1+2+…+n的值，计算满足条件的S值，可得答案．【解答】解：由程序框图知：算法的功能是求S=21+22+…+2n+1+2+…+n的值，∵S=21+22+1+2=2+4+1+2=9＜15，S=21+22+23+1+2+3=2+4+8+1+2+3=20≥15．∴输出S=20.4．【考点】由三视图求面积、体积．【分析】几何体为底面为正方形的长方体，底面对角线为4，高为3．则长方体的对角线为外接球的直径．【解答】解：几何体为底面为正方形的长方体，底面对角线为4，高为3，∴长方体底面边长为2．则长方体外接球半径为r，则2r==5．∴r=．∴长方体外接球的表面积S=4πr2=25π．5．【考点】命题的真假判断与应用．【分析】由函数y=x﹣sinx的单调性，即可判断①；由若p则q的逆否命题：若非q则非p，即可判断②；由复合命题“命题p∧q为真”则p，q都是真，则“命题p∨q为真”，反之不成立，结合充分必要条件的定义即可判断③；由全称命题的否定为特称命题，即可判断④．【解答】解：①由y=x﹣sinx的导数为y′=1﹣cosx≥0，函数y为递增函数，若x＞0，则x＞sinx恒成立，故①正确；②命题“若x﹣sinx=0，则x=0”的逆否命题为“若x≠0，则x﹣sinx≠0”，由逆否命题的形式，故②正确；③“命题p∧q为真”则p，q都是真，则“命题p∨q为真”，反之不成立，则“命题p∧q为真”是“命题p∨q为真”的充分不必要条件，故③正确；④命题“∀x∈R，x﹣lnx＞0”的否定是“∃x0∈R，x0﹣lnx0≤0”，故④不正确．综上可得，正确的个数为3．6．【考点】正弦定理的应用．【分析】通过正弦定理得出sinA和sinB的方程组，求出cosB的值．【解答】解：∵△ABC中，，∴根据正弦定理得∴7．【考点】极差、方差与标准差．【分析】由于数据x1，x2，x3，…，xn是上海普通职工n（n≥3，n∈N*）个人的年收入，设这n个数据的中位数为x，平均数为y，方差为z，如果再加上世界首富的年收入xn+1，我们根据平均数的意义，中位数的定义，及方差的意义，分析由于加入xn+1后，数据的变化特征，易得到答案．【解答】解：∵数据x1，x2，x3，…，xn是上海普通职工n（n≥3，n∈N*）个人的年收入，而xn+1为世界首富的年收入则xn+1会远大于x1，x2，x3，…，xn，故这n+1个数据中，年收入平均数大大增大，但中位数可能不变，也可能稍微变大，但由于数据的集中程序也受到xn+1比较大的影响，而更加离散，则方差变大8．【考点】双曲线的简单性质．【分析】根据OM⊥PF，且FM=PM判断出△POF为等腰直角三角形，推断出∠OFP=45°，进而在Rt△OFM 中求得半径a和OF的关系，进而求得a和c的关系，则双曲线的离心率可得．【解答】解：∵OM⊥PF，且FM=PM∴OP=OF，∴∠OFP=45°∴|0M|=|OF|•sin45°，即a=c•∴e==9．【考点】函数的图象．【分析】利用特殊值法，判断函数的图象即可．【解答】解：当x=﹣1时，y=﹣1+＜0，排除A，C；当x=2时，y=32﹣2e2＞32﹣18＞0，排除D，10【考点】三角形中的几何计算；两点间距离公式的应用．【分析】由题意，以CB和CA建立直角坐标系，可得AB直线方程，P是线段AB上的点，设P（x，y），P到AC，BC的距离的乘积的最大值即为xy的最大值．利用基本不等式求解即可．【解答】解：以CB和CA建立直角坐标系，BC=3，AC=4，即A（0，4），B（3，0）．可得AB直线方程为：4x+3y=12．P是线段AB上的点，设P（x，y），P到AC，BC的距离的乘积的最大值即为xy的最大值．即xy==3，当且仅当4x=3y是取等号．∴P到AC，BC的距离的乘积的最大值为3．11．【考点】数列递推式．【分析】x1=1，x2=a（a≤1，a≠0），可得x3=|x2﹣x1|=|a﹣1|=1﹣a，x1+x2+x3=1+a+（1﹣a）=2；xn+3=xn 对于任意正整数n均成立，可得数列{xn}的周期为3，即可得出．【解答】解：∵x1=1，x2=a（a≤1，a≠0），∴x3=|x2﹣x1|=|a﹣1|=1﹣a，∴x1+x2+x3=1+a+（1﹣a）=2；xn+3=xn对于任意正整数n均成立，∴数列{xn}的周期为3，数列{xn}的前2016项和S2016的值=672×2=1344．12．【考点】函数恒成立问题．【分析】分别讨论当﹣1≤x≤1时，当x＞1或x＜﹣1，f（x）的奇偶性和单调性，可得f（x）为R上的奇函数，且为减函数．由题意可得（m+1）x﹣1＜0，设g（m）=（m+1）x﹣1，m∈[﹣3，2]，由g（﹣3）＜0，g（2）＜0，解不等式即可得到所求范围．【解答】解：当﹣1≤x≤1时，f（x）==﹣=﹣3+，由y=2x在[﹣1，1]递增，可得f（x）在[﹣1，1]递减；且f（﹣x）===﹣f（x），即f（x）为奇函数；当x＞1或x＜﹣1，f（x）=﹣（x3+3x），f（﹣x）=（x3+3x）=﹣f（x），f（x）为奇函数；且f′（x）=﹣（3x2+3）＜0，即有f（x）为递减函数．f（﹣1）=1，f（1）=﹣1，则f（x）为R上的奇函数，且为减函数．则任意的m∈[﹣3，2]，总有f（mx﹣1）+f（x）＞0恒成立，即有f（mx﹣1）＞﹣f（x）=f（﹣x），可得mx﹣1＜﹣x，即为（m+1）x﹣1＜0，设g（m）=（m+1）x﹣1，m∈[﹣3，2]，则g（﹣3）＜0，g（2）＜0，即﹣2x﹣1＜0，3x﹣1＜0，解得﹣＜x＜．13．【考点】平面向量数量积的运算．【分析】根据平面向量的数量积与模长公式，列出方程求出||的值．【解答】解：向量满足，且与的夹角为120°，∴=﹣4•+4=1﹣4×1×||cos120°+4=21，化简得2+||﹣10=0，解得=2或﹣（小于0，舍去）；∴||=2．14．【考点】函数解析式的求解及常用方法．【分析】由题意，意思是：将钱分给若干人，第一人给3钱，第二人给4钱，第三人给5钱，以此类推，每人比前一人多给1钱，分完后，再把钱收回平均分给各人，结果每人分得100钱，问有多少人？是一个等差数列的问题．设人数为n，公差为1，首项为3．求前n项和等于100n，可得答案．【解答】解：设人数为n，公差为1，首项为3．则前n项和．由题意：Sn=100n，即，解得：n=195．15．已知x，y满足，则目标函数z=﹣2x+y的最大值为﹣3．【考点】简单线性规划．【分析】首先画出可行域，利用目标函数等于直线在y轴的截距最大值求z 的最大值．【解答】解：x，y满足的平面区域如图：当直线y=2x+z经过图中的A时，z最大，由得到A（3，3），所以z=﹣2×3+3=﹣3；16．关于圆周率π，数学发展史上出现过许多很有创意的求法，如著名的蒲丰实验和查理斯实验．受其启发，我们也可以通过设计下面的实验来估计π的值：先请200名同学，每人随机写下一个都小于1 的正实数对（x，y）；再统计两数能与1构成钝角三角形三边的数对（x，y）的个数m；最后再根据统计数m来估计π的值．假如统计结果是m=56，那么可以估计π≈．（用分数表示）【考点】模拟方法估计概率．【分析】由试验结果知200对0～1之间的均匀随机数x，y，对应区域的面积为1，两个数能与1构成钝角三角形三边的数对（x，y），满足x2+y2＜1且x，y都小于1，x+y＞1，面积为﹣，由几何概型概率计算公式，得出所取的点在圆内的概率是圆的面积比正方形的面积，二者相等即可估计π的值．【解答】解：由题意，200对都小于l的正实数对（x，y），对应区域的面积为1，两个数能与1构成钝角三角形三边的数对（x，y），满足x2+y2＜1且x，y都小于1，x+y＞1，面积为﹣，因为统计两数能与l 构成钝角三角形三边的数对（x，y）的个数m=56，所以=﹣，所以π=．17．【考点】三角函数的最值；平面向量数量积的运算；三角函数的周期性及其求法；函数y=Asin（ωx+φ）的图象变换．【分析】（1）把向量=（1+cosωx，1），=（1，a+sinωx）（ω为常数且ω＞0），代入函数f（x）=整理，利用两角和的正弦函数化为2sin（ωx+）+a+1，根据最值求实数a的值；（2）由题意把函数y=f（x）的图象向右平移个单位，可得函数y=g（x）的图象，利用y=g（x）在[0，]上为增函数，就是周期≥π，然后求ω的最大值．18．【考点】列举法计算基本事件数及事件发生的概率．【分析】（1）由频率=，能求出a，b的值．（2）由14+a+28＞10+b+34，得a＞b+2，由此利用列举法能求出所求概率．19．【考点】棱柱、棱锥、棱台的体积．【分析】（1）利用三角形中位线定理及BC与AD不平行可得A．D．E、F四点共面；（2）由已知通过求解三角形求得PQ，得到E到底面的距离，再求出四边形ABCQ的面积，代入体积公式求得四棱锥E﹣ABCQ的体积．20.【考点】直线与圆锥曲线的关系；圆的标准方程．【分析】（Ⅰ）设圆C的半径为r（r＞0），依题意，圆心坐标为（2，r），根据|MN|=3，利用弦长公式求得r 的值，可得圆C的方程．（Ⅱ）把x=0代入圆C的方程，求得M、N的坐标，当AB⊥y轴时，由椭圆的对称性可知∠ANM=∠BNM，当AB与y轴不垂直时，可设直线AB的方程为y=kx+1，代入椭圆的方程，利用韦达定理求得KAB+KBN=0，可得∠ANM=∠BNM．21．【考点】利用导数研究函数的单调性；函数零点的判定定理；利用导数研究函数的极值．【分析】（1）求导，由f′（x）＞0则[1，+∞）恒成立，则f（x）在[1，+∞）为增函数，由f（1）=﹣1＜0，f（2）=1＞0，函数f（x）在[1，+∞）上有唯一的零点；（2）求导，分离参数，则a≤在[1，+∞）上恒成立，构造辅助函数，求导，由（1）可知，a 小于h（x）的x在区间（1，+∞）上的最小值，根据函数的单调性，求得函数的h（x）的最小值的取值范围，即可取得整数a的最大值．22．【考点】参数方程化成普通方程；简单曲线的极坐标方程．【分析】（1）把参数方程中的x，y平方相加即可得普通方程；（2）把直线l方程为ρsin（﹣θ）+1=0化为普通方程为：x﹣y+1=0，然后根据弦长公式计算即可．23．【考点】绝对值不等式的解法．【分析】（I）运用分段函数求得f（x）的解析式，由f（x）≤2，即有或或，解不等式即可得到所求解集；（Ⅱ）由题意可得当时，不等式f（x）≤|2x+1|恒成立．即有（x﹣2）max≤a≤（x+2）min．求得不等式两边的最值，即可得到a的范围．。

2017届湖北省黄冈中学高三下学期高考三模数学（文）试题一、单选题1．设集合{}1,2,3,4U =，集合2{|540}A x N x x =∈-+<，则U C A 等于（ ） A. {}1,2 B. {}1,4 C. {}2,4 D. {}1,3,4 【答案】B 【解析】集合{}1,2,3,4U = , 集合{}2{N|540}{N |14A x x x x x =∈-+<=∈<<=,所以{}1,4UA =ð , 故选B.2．复数12z i =+，若复数1z ， 2z 在复平面内的对应点关于虚轴对称，则12z z =（ ） A. 5- B. 5 C. 34i -+ D. 34i -【答案】A【解析】12z ,z 在复平面内的对应点关于虚轴对称，则有22z i =-+，()()12z z 22i i =+-+ 245i =-=- ，故选A.3．某校为了解1000名高一新生的身体生长状况，用系统抽样法（按等距的规则）抽取40名同学进行检查，将学生从进行编号，现已知第18组抽取的号码为443，则第一组用简单随机抽样抽取的号码为（） A. 16 B. 17 C. 18 D. 19 【答案】C【解析】试题分析：第一组用简单随机抽样抽取的号码为，选C ．【考点】系统抽样法4．已知向量()1,2m =- ， ()1,n λ= ，若m n ⊥ ，则2m n + 与m的夹角为（ ） A.23π B. 34π C. 3π D. 4π 【答案】D【解析】依题意，•0m n =，即120λ-+=解得12λ=，故()()()21,22,11,3m n +=-+=，则2m n +与m 的夹角的余弦值cosθ==4πθ=.选D. 5．已知函数()32f x ax bx cx d =+++，若函数()f x 的图象如图所示，则一定有（ ）A. 0,0b c >>B. 0,0b cC. 0,0b c ><D. 0,0b c << 【答案】B【解析】322,'32y a x b xc xd y ax b x c =+++∴=++ , 因为函数32y ax bx cx d =+++ 从左到右先增后减后增，所以二次函数2'32y ax bx c =++ 的图象开口向上， 0a ∴> ，因为函数32y ax bx cx d =+++的极值点都为正，所以2320ax bx c ++= 有两个不同的正根，所以0,03c c a >∴> ， 20,03bb a->< ，故选B.6．设,m n 是空间两条直线， ,αβ是空间两个平面，则下列命题中不正确的是（ ） A. 当n α⊥时，“n β⊥”是“//αβ”的充要条件 B. 当m α⊂时，“m β⊥”是“αβ⊥”的充分不必要条件C. 当m α⊂时，“//n α”是“//m n ”的必要不充分条件D. 当m α⊂时，“n α⊥”是“m n ⊥”的充分不必要条件 【答案】C【解析】当m α⊂ 时，“n α ” ⇒ “m n ”或m 与n 异面“m n ” ⇒ “n α 或n α⊂ ”，所以当m α⊂ 时，“n α ”是 “m n ”的即不必要又不充分条件，故C 错误；当m α⊂ 时，“m β⊥ ” ⇒ “αβ⊥ ” ，“αβ⊥ ”推不出“m β⊥ ”，所以当m α⊂ 时，“m β⊥ ”是 “αβ⊥ ” ，的充分不必要条件，故B 正确；当n α⊥时 ，“n β⊥ ” ⇔ “αβ ” ，所以当n α⊥时 ，“n β⊥ ”是 “αβ ” ，成立的充要条件，故A 正确；当m α⊂ 时，“n α⊥ ” ⇒ “m n ⊥ ” ，“m n ⊥ ”推不出“n α⊥” ，当m α⊂时，“n α⊥”是“m n ⊥”的充分不必要条件,故D 正确，故选C.7．已知双曲线2222:1(1,0)x y C a b a b -=>>的左焦点为F ，第二象限的点M 在双曲线C 的渐近线上，且OM a =，若直线MF 的斜率为ba，则双曲线C 的渐近线方程为（ ）A. y x =±B. 2y x =±C. 3y x =±D. 4y x =± 【答案】A【解析】由题意可知： OPF 是等腰三角形，则： ,22P p P c b bc x y x a a===，点P 在圆上，则： 222P P x y a +=，即： 22222c bc a a ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭，结合222c a b =+整理可得：2222130b b a a ⎛⎫⎛⎫-+= ⎪⎪⎝⎭⎝⎭， 据此可得： 221b a=，双曲线C 的渐近线方程为y x =± .本题选择A 选项.8．若1x y >>， 01a b <<<，则下列各式中一定正确的是（ ） A. x y a b < B. x y a b > C. ln ln x y b a < D. ln ln x yb a> 【答案】A【解析】(01)x y a a =<< 在R 上递减， 1,01x y a b >><<< ，故x ya a < ，再根据幂函数(0)y x αα=> 递增可得y y ab <，所以， x ya b <，故选A.9．若函数()224sin sin 2sin (0)24x f x x x ωπωωω⎛⎫=⋅+-> ⎪⎝⎭在2,23ππ⎡⎤-⎢⎥⎣⎦上是增函数，则ω的取值范围是（ ）A. (]0,1 B. 30,4⎛⎤⎥⎝⎦ C. [)1,+∞ D. 3,4⎡⎫+∞⎪⎢⎣⎭【答案】B【解析】()21c 24?sin cos214?cos2-1422x f x sin x x sin x x πωπωπωωωω⎛⎫-+ ⎪⎛⎫⎝⎭=++-=+ ⎪⎝⎭()21cos22sin x sin x x sin x ωωωω=++= , ,22ππωω⎡⎤∴-⎢⎥⎣⎦是函数含原点的递增区间，又因为函数在2,23ππ⎡⎤-⎢⎥⎣⎦ 上递增，所以][2,,2223ππππωω⎡⎤-⊇-⎢⎥⎣⎦ ，所以得不等式组22{232ππωππω-≤-≤ ，得1{34ωω≤≤ ，又30,04ωω><≤ ， ω 的取值范围是30,4⎛⎤ ⎥⎝⎦，故选B .10．已知中心在坐标原点的椭圆与双曲线有公共焦点，且左、右焦点分别为12,F F ，这两条曲线在第一象限的交点为P ， 12PF F ∆是以1PF 为底边的等腰三角形.若110PF =，记椭圆与双曲线的离心率分别为12,e e ，则12e e ⋅的取值范围是（ ）A. 1,3⎛⎫+∞ ⎪⎝⎭B. 1,5⎛⎫+∞ ⎪⎝⎭C. 1,9⎛⎫+∞ ⎪⎝⎭D. ()0,+∞ 【答案】A【解析】设椭圆和双曲线的半焦距为c ,|PF 1|=m ,|PF 2|=n ,(m >n )， 由于△PF 1F 2是以PF 1为底边的等腰三角形。

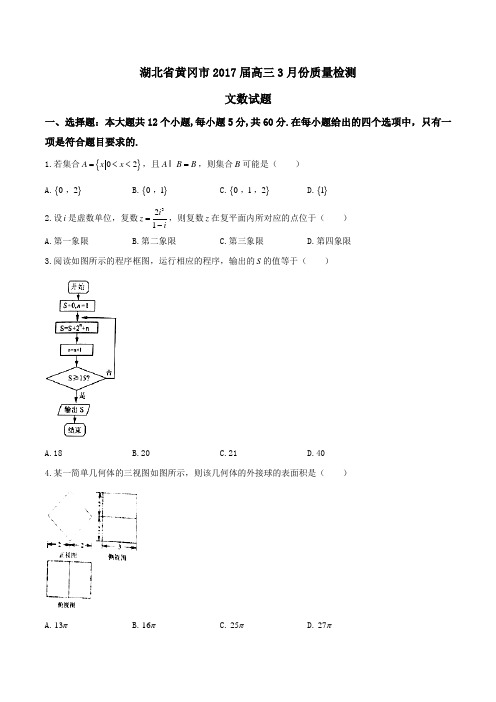
湖北省黄冈市2017届高三3月份质量检测文数试题一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.若集合{}02A x x =<<，且A B B =，则集合B 可能是（ ）A.{}0 2，B.{}0 1，C.{}0 1 2，，D.{}12.设i 是虚数单位，复数321i z i=-，则复数z 在复平面内所对应的点位于（ ） A.第一象限 B.第二象限 C.第三象限 D.第四象限3.阅读如图所示的程序框图，运行相应的程序，输出的S 的值等于（ ）A.18B.20C.21D.404.某一简单几何体的三视图如图所示，则该几何体的外接球的表面积是（ ）A.13πB.16πC.25πD.27π5.下列四个结论：①若0x >，则sin x x >恒成立；②命题“若sin 0x x -=，则0x =”的逆否命题为“若0x ≠，则sin 0x x -≠”；③“命题p q ∧为真”是“命题p q ∨为真”的充分不必要条件；④命题“ ln 0x R x x ∀∈->，”的否定是“000 ln 0x x x ∃∈-<，”.其中正确结论的个数是（ ）A.1个B.2个C.3个D.4个6.在ABC △中，角 A B C ，，的对边分别是 a b c ，，，若 2a A B ==，，则cos B =（ ）7.已知数据123 n x x x x ，，，…，是某市()*3 n n n N ≥∈，个普通职工的年收入，设这n 个数据的中位数为x ，平均数为y ，方差为z ，如果再加上世界首富的年收入1n x +，则这1n +个数据中，下列说法正确的是（ ）A.年收入平均数可能不变，中位数可能不变，方差可能不变B.年收入平均数大大增大，中位数可能不变，方差变大C.年收入平均数大大增大，中位数可能不变，方差也不变D.年收入平均数大大增大，中位数一定变大，方差可能不变 8.过双曲线()222210 0x y a b a b-=>>，的右焦点F 作圆222x y a +=的切线FM （切点为M ），交y 轴于点P ，若M 为线段FP 的中点，则双曲线的离心率为（ ）C.29.函数22ln x x y x=的图象大致是（ ）A B C D10.已知在ABC △中，90ACB ∠=︒，3BC =，4AC =，P 是线段AB 上的点，则P 到AC 、BC 的距离的乘积的最大值为（ ）A.3B.2C. D.911.已知数列{}n x 满足()*21n n n x x x n N ++=-∈，若11x =，()2 1 0x a a a =≤≠，，且3n n x x +=对于任意正整数n 均成立，则数列{}n x 的前2017项和2017S 的值为（ ）A.672B.673C.1344D.134512.若函数()()()()()3312 112113 114x x x f x x x x x ⎧-⎪-≤≤⎪+=⎨⎪-+<->⎪⎩，，或对任意的[]3 2m ∈-，，总有()10f mx fx -+>恒成立，则x的取值范围是（ ） A.11 23⎛⎫- ⎪⎝⎭， B.()1 2-， C.41 32⎛⎫-- ⎪⎝⎭， D.()2 3-，第Ⅱ卷（非选择题 共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.已知两个平面向量 a b ，满足1a =，221a b -=，且a 与b 的夹角为120︒，则b = ．14.我国古代数学名著《张邱健算经》有“分钱问题”如下：“今有与人钱，初一人与三钱，次一人与四钱，次一人与五钱，以次与之，转多一钱。

新联考2016—2017学年第三次联考高三文科数学试题第I 卷 （选择题 共60分）一、选择题：本题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知全集{1,2,3,4,5}A =，{350}B x x =-≤，则A B = =A ．{}1,2B ．513x x ⎧⎫≤≤⎨⎬⎩⎭C ．{}1D ．{}2,3,4,52.已知复数z 满足()124z i i ⋅+-=，则复数z 对应的点Z 位于A ．第一象限B ．第二象限C ．第三象限D ．第四象限3. 已知数列{}n a 为等差数列，531a a =+，且其前10项和10552S =，则1a == A ．12 B ．12- C ．1 D ．144. 元旦晚会，某同学从《默》，《十年》，《父亲》，《李白》四首诗歌中选出两首诗进行表演，则《十年》和父亲的不同时选取的概率为 A ．13 B ．12 C ．23 D ．565．已知方程24y x =表示椭圆，且该抛物线的焦点到直线x m =的距离为4，则m 的值为 A ． 5 B ．-3或5 C ．-2或6 D ．66. 在ABC ∆中，角,,A B C 的对边分别为,,a b c ，已知15,sin 2a b C ===，则边c =7．如图所示，某几何体的三视图是三个边长为1的正方形及每个正方形内一段半径为1，圆心角为90 的圆弧，则该几何体的体积是A ．112π-B ．13π-C ． 16π-D ．124π- 8.下列关系正确的是A. 33441.5 1.7> B.32432234⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭C.3322-->D. ()()31220.70.7>9. 在正四棱锥P ABCD -中，O 为底面ABCD 的中心，2AB PO ==,则异面直线,PC AB 所成角的余弦值为 A．6 B．6．4 D．410.执行右侧的程序框图，如果输入0,1,1x y n ===，则输出的,,x y n 的和为A ．28B ．29C ．52D ．5111. 函数2()ln 4x f x x =-的图像大致是11．抛物线22(0)y px p =>的焦点为F ，过焦点F 倾斜角为3π的直线与抛物线相交于两点,A B 两点，若8AB =，则抛物线的方程为A ．28y x =B ．26y x =C ．24y x =D ． 23y x =12. 已知函数12,012()13sin ,14242x x f x x x π⎧+≤≤⎪⎪=⎨⎪+≤≤⎪⎩，若不等式2()()20f x af x -+<在[]0,4上恒成立，则实数a 取值范围是A ．a >．3a << C ．3a > D．3a <<第II 卷 （非选择题 共90分）本卷包括必考题和选考题两部分.第13---21题为必考题，每个试题考生都必须作答.第22—23题为选考题，考生根据要求作答． 二、填空题:本题共4小题，每题5分.13.某班级的45名学生编号为：1,2,3，…，45，为了采集同学们的身高信息，现采用系统抽样的方法抽取一个容量为5的样本，已知样本中含有编号为5号、23号和41的学生，则样本中剩余两名同学的编号分别为 ．14.在平面直角坐标系xoy 中，已知()()()1,2,9,2,4,,A B C t AC BC -⊥，则实数t 的值为 ．15. 已知函数()sin()(0,0,)f x A x A ωϕωϕπ=+>><，先把()y f x =的图像向左平移3π个单位长度，再将所得的图像横坐标缩短为原来的12，纵坐标不变，得到函数解+析式为2sin y x =，则()y f x =的单调递增区间为 .16.一个小型加工厂用一台机器生产甲、乙两种桶装饮料，生产一桶甲饮料需要白糖4千克，果汁18千克，用时3小时；生产一桶乙饮料需要白糖1千克，果汁15千克，用时1小时.现库存白糖10千克，果汁66千克，生产一桶甲饮料利润为200元，生产一桶乙饮料利润为100元，在使用该机器用时不超过9小时的条件下，生产甲、乙两种饮料之和的最大值为 ．三、解答题：解答应写出文字说明、证明过程或计算步骤． 17.（本小题满分12分）已知数列{}n a 是等差数列，103414,37.a a a a ==+ （1）求通项公式n a ； （2）若22n a n n b a +=-，求数列{}n b 的前n 项和n S ．18. （本小题满分12分）如图，四边形ABCD 是正方形，四边形BDEF 为矩形，2AB BF =,AC BF ⊥，G 为EF 的中点．（1）求证： //CF 平面ADE ,BF ⊥平面ABCD ； （2）若三棱锥F BCD -的的体积为23，求点D 到平面GAB 的距离．19. （本小题满分12分）为了保护青少年眼睛健康，某眼镜经营商对新入学的高一学生视力进行调查，在高一的全体1000名学生中随机抽取了100名学生的体检表，并得到如图所示的频率分布直方图.(1)若直方图中后四组的频数成等差数列，计算高一的全体学生视力在5.0以下的人数，并估计这100名学生视力的中位数（精确到0.1）；（2）视力不小于5.0认为没有近视，低于5.0而高于4.4属于轻微近视，低于4.4属于严重近视.该眼镜经营商对该校高一学生进行送爱心活动，对“严重近视”患者免费配备近视治疗仪，每10人共用一台近视治疗仪，有近视学生可以在该眼镜公司配眼镜.已知每台近视治疗仪的市场价为2000元，每配一副眼镜经营商大约赚100元，试问该校高一年级患有近视的学生在该眼镜公司配眼镜的比例大约多少时，该眼镜经营商在本次活动中不会亏本．20. （本小题满分12分）M N为椭已知椭圆E,圆E上两点，O为坐标原点．（1）求椭圆E的方程；⊥（2）已知OM ON①若直线MN的斜率不存在，求O到直线MN的距离；②当直线MN的斜率为2时，求点O到直线MN的距离.21. （本小题满分12分）已知函数()()()11.xf x x e a x =+--（1）当2a =时，求()y f x =在点()()1,1f 处的切线方程； （2）试讨论函数()()xf xg x e'=的单调性； （3）若当()1,x ∈+∞时，()0f x >恒成立，求a 的取值范围．请考生在第22—23题中任选一题作答，如果多做，则按所做的第一题计分． 22. （本小题满分10分）选修4-4:坐标系与参数方程 在直角坐标系xoy 中，曲线的1C 参数方程为cos 1sin x m y m αα=+⎧⎨=++⎩，（α为参数，m 为常数）．在以坐标原点为极点，x 轴正半轴为极轴的极坐标系中，曲线2C 的极坐标方程为s i n ()23πρθ+=．（1）把曲线2C 化为普通方程；（2）若曲线12,C C 只有一个公共点，求常数m 的值． 23. （本小题满分10分）选修4-5:不等式选讲 已知函数2()4f x x x a =--． （1）当3a =时，解不等式()0f x <；（2）设2()42g x x x =++，不等式()()2g x f x a ≥+恒成立，求实数a 的取值范围．。

湖北省黄冈中学高考数学文科第三轮模拟考试卷新课标 人教版三月检测题本试卷分第Ⅰ卷和第Ⅱ卷两部分，共150 分，考试时间 120 分钟第Ⅰ卷 ( 选择题，共 60 分 )一、选择题：本大题共12 小题，每题5 分，共 60 分，在每题给出的四个选项中，` 只有一项是切合题目要求的 . 1. 设会合 U={(x,y) ｜ x ∈R,y ∈ R},A={(x,y) ｜ 2x-y+m>0},B={(x,y)｜ x+y-n ≤ 0} ，那么点 P(2 ，3) ∈ A ∩ (C U B) 的充要条件是A.m>-1 且 n<5B.m<-1 且 n<5C.m>-1且 n>5D.m<-1 且 n>52. 已知 cos31 °=m,则 sin239 °· tan149 °的值是A. 1 m 2B. 1 m 2C. m 21D.- 1 m 2mm3. 若等比数列a n 中， a 2+a 5+a 11=2,a 5 +a 8+a 14=6, 则 a 2+a 5+a 8 +a 11+a 14 的值为A.8B.大于 8C. 242D. 24031414. 若直线 mx+2ny-4=0(m,n ∈ R)一直均分圆 x 2+y 2-4x-2y-4=0 的周长，则 m ·n 的取值范围是A.(0 ， 1)B.(0 ，1)C.(- ∞， 1)D.(- ∞， 1)5. 设 函数f(x)=1og a x (a>0且a ≠1), 若 f(x ·x ·x · · x2006)=50, 则123f(x 1 2)+f(x2)+f(x2)+ +f(x2) 的值等于2 32006A.2500B.50C.100D.2log a 506. (1-x+x2)(1+x) 6 睁开式中， x 3 项的系数是A.15B.14C.12D.117. 已知平面α∩平面β=异于直线 l 的直线 a ∈α， 异于直线 l 的直线 b ∈β， 且α⊥β， 命题 P ： a ⊥ l ，命题 Q ： a ⊥ b ，则 P 是 Q 的 A. 充足不用要条件B. 必需不充足条件C.充要条件D.既不充足也不用要条件 8. 从 1，2，3， ， 9 这九个数中，随机抽取3 个不一样的数，则这 3 个数的和为偶数的概率是A.2B.4C.11D.109921219. 设 f(x)=1 x2 ，则函数 y=f(x) 的图像对于2 xx1A. 原点对称B.y 轴对称C.x 轴对称D. 直线 y=x 对称10. 已知椭圆的离心率为e ，两焦点分别为F 、F , 抛物线 C 以 F 为极点、 F 为焦点，点 P 为抛121 2物线和椭圆的一个交点，若e ｜ PF 2｜ =｜ PF 1｜ , 则 e 的值为A.1B.2 C.3 D.以上均不对222θ ( 此中 O为原点 ) ，将 AC+CD表示成对于θ的函数f( θ ), 则 f( θ ) 等于 A.2cosθ-cos2 θ B.cos θ +sin θ C.2cos θ (1+cos θ ) D.2sin θ +cos θ-212. 一机器狗每秒钟行进或退后一步，程序设计师让机器狗从行进 3 步，再退后 2 步的规律移动，假如将此机器狗放在数轴的原点，方向正方向，以一步的距离为一个单位长，令P(n)表示第 n 秒机遇器狗所在地点的坐标，且P(0)=0 ，那么以下结论中错误的选项是A. P (3)=3B. P (5)=1C. P (101)=21D. P (103)<P(104)第Ⅱ卷 (非选择题，共90 分 )二、填空题：本大题共 4 小题，每题 4 分，共 16 分， tx 把答案填在题中横线上.13. 已知会合A={x ｜22x -2 x+1 -8=0 ｜ }B={x ｜ x a <x} 若 A B，则实数 a 的取值范围是_________.14. 若半径为R 的球与正三棱柱的各个面相切，则球与正三棱柱的体积比是________.15.三位数中，假如十位上的数字比个位上、百位上的数字都要小，则称这个数为凹数，如524、 317 等都是凹数，那么，各数位上无重复数字的三位凹数共有________个 .16.已知定义在 R 上的函数 y=f(x) 知足以下三个条件：(1)对随意的 x∈ R，都有 f(x+4)=f(x);(2)对随意的 x1， x2∈ R，且 0≤ x1<x2≤ 2, 都有 f(x 1)<f(x 2);(3)函数 y=f(x+2) 的图像对于 y 轴对称 .则 a=f(4.5)，b=f(6.5),c=f(7)从小到大的关系是________.三、解答题：本大题共 6 小题，共74 分，解答应写出文字说明、证明过程或演算步骤.17.( 本小题满分12 分 ) 已知向量m=(1， 1) ，向量 n 与向量 m的夹角为3π, 且m·n=-1.4(1) 求向量 n；(2) 设向量a=(1 ， 0) ，向量 b=(cosx,2cos2(πx)), 此中0<x<2π，若n·a=0,试求｜3 23n+b｜的取值范围.18.( 本小题满分12 分 ) 已知函数f(x)=x3+ax2+bx+c当x=-1时，获得极大值7，当 x=3 时，获得极小值， a 、 b、 c 的值及其极小值.19.( 本小题满分12 分 ) 新上海商业城位于浦东陆家嘴金融贸易区中心地带，它由第一八佰伴、时代广场等18 幢高层商厦， 10000 平方米中心茶园，九座天桥以及600 米长的环形步行街有机构成，座集购物、餐饮、娱乐、休闲、办公于一体的综合性、多功能的现代化商城，此中某一新建商场设有百货部、服饰部和家电部三个经营部，共有190 名售货员，计划全商场日营业额( 指每卖出商品所收到的总金额) 为 60 万元，依据经验，各部商品第 1 万元营业额所售货员人数如表1，每 1 万元营业额所得收益如表2，商场将计划日营业额分派给三个经营部，同时适合安排各部的营业员人数，若商场估计每天的总收益为c(19 ≤ c≤19.7) 万元，商场分派给经营部的日营业额为正整数万元，问这个商场如何分派日营业给三个经营部？各部分别安排多少名售货员？表 1各部每 1 万元营业额所需人数表表 2各部每 1 万元额所得收益表部门人数部门收益百货部5百货部0.3万元服饰部4服饰部0.5万元家电部2家电部0.2万元20.( 本小题满分12 分 ) 如图 , 在三棱柱ABC-A1B1C1中，四边形 A1ABB1是菱形，四边形BCC1B1是矩形， C1B1⊥ AB.(1)求证：平面 C1AB1⊥平面 A1ABB1；(2)求平面 C1 AB1把三棱柱分红两部分的体积比；(3)若 C1B1=3， AB=4，∠ ABB1=60°，求 AC1与平面 BCC1B1所成角的正切值 .21.( 本小题满分 12 分 ) 已知函数 f(x)=x22x 0 ，设正项数列 {a n } 的首项 a 1=2, 前 n项和 S 知足 Sn=f(Sn-1)(n>1, 且 n ∈ N*);n(1) 求 a n 的表达式；(2) 在平面直角坐标系内，直线L n 的斜率为 a n , 且 L n 与曲线 y=x 2 有且仅有一个公共点， L n又与 y 轴交于点 D (0,b* 时，记 d = 1 D n 1D n -1 ，若d n 21d n 2nnn4n2d n 1 ·nC 1+C 2+C 3+ +C n -n<1.22.( 本小题满分1 2为焦点的双曲线C ：x 2 y 2 1上的一点，已知14 分)如图， P 是以 F 、F a2b 2PF 1 · PF 2 =0，且 | PF 1 |=2| PF 2 |.(1) 求双曲线的离心率 e ；(2) 过点 P 作直线分别与双曲线的两渐近线订交于27P 1， P 2 两点，若 OP 1 · OP 2 =-， 2 PP 1 + PP 2 =0，求双曲线 C 的方程 .参照答案一、 1.A 2.B 3.C 4.D 5.C 6.D 7.A8.C 9.B10.C 11.A 12.D二、 13.-2 ≤ a<214.23π15.24016.a<c<b27x y1三、 17.(1) 令 n=(x ，y) ，则2·x 2π1 y2 cos 34x y1x1或 x0即2y2x 1 y0y1，故 n=(-1,0)或n=(0，-1) (2) ∵ a=(1 ，0)n · a=02πxπ∴ n=(0,-1)n+b=x，2cos1cosx, cos x2cos323π2cos2 x πx11cos42x1cos2x cos4π故n b2cos2x3=1+2x 322231cos2x π2x=1+1cos2x -1cos2x3sin2x1cos23222111cos2x3sin2x=1+1cos 2xπ22223∵0<x< 2ππ2xπ5π3333则-1 ≤cos2x π11n b 25故2n b 5 . 32242218. ∵f(x)=x3+ax2+bx+c,∴ f(x)=3x2 +2ax+bf ( 1 ) 0 3 2a b 0a3依题意有 f ( 3)0276a b0b9f ( 1 ) 7-1 a - b c 7 c 2由 f(x)=2x 2 -6x-9<0有:-1<x<3∴f(x)在(-∞ ,-1)递加，(-1，3)递减，(3，+∞)递加故f(x)在x=-1取得极大值，在x=3 获得极大值，在x=3 获得极小值，且f(x)极小值=f(3)=-25.19. 设商场分派给百货部、服饰部、家电部日营业额分别为x、 y、 z 万元 (x 、 y、 z ∈N*)x y z60①3x, 代入①得：z=25+x ∴依题意有：5x4y 2 z 190② 由①、②消去z 得： y=35-c0.3x0.5 y 0.2 z③22c=0.3x+0.53x..x35x0.2 252225 0352x8x10∴ 19≤ c≤19.7∴8≤x ≤ 10而 x,y,z ∈N*∴y或y20 23z29z30故该商场分派营业额及各部售货员人数的方案有两种，分别为：方案 1：部门营业员人数百货部8 40服饰部23 92家电部2958方案 2：部门营业员人数百货部10 50服饰部20 80家电部306020.(1) 四边形 BCC 1B 1 是矩形，∴ C 1B 1 ⊥ B 1B 又∵ C 1B 1 ⊥ AB∴ C 1 B 1⊥面 A 1 ABB 1 而 C 1 B 1∈面 C 1AB 1∴面 C 1AB 1 ⊥画 A 1ABB 1(2) 设三棱柱 ABC-A 1B 1C 1 底面积为 S ，高为 h 则 V 三棱柱 =Sh∵平面 C AB 把三棱柱分红三棱锥A-A B C 和四棱锥 A-BCCB 两部分，而1 ∴V A-A B C = Sh111 111131 1 12V A A 1B 1C 11VA-BCC 1B 1 =Sh故VA BCC 1B 223∴平面 C AB 把三棱柱分红两部分的体积比为1∶ 2.11(3) 过 A 作 AE ⊥ BB 于 E ，连 C 1 E ∵ C 1 B 1 ⊥面 A ABB ∴面 BCCB ⊥面 A ABB故 AE ⊥面 BCCB ∴∠ ACE 为 AC1111111111与面 BCCB 所成的角 . ∵在菱形 A 1ABB 1 中，AB=4，∠ ABB=60°∴△ ABB 为等边三角形， 故 BB=4，AE=2 3.11111在 Rt △C 1 B 1E 中， C 1 B 1=3， B 1E=2，∴ C 1E= 13 , 故在 Rt △AEC 1中，tan ∠AC 1E=AE2 39 .与面 所成角的正切值为 2 39 .C1E13 AC1 BCC1B1 1321.(1) 由 S n =S n2 2S nSn 1 2 , 因此数列S n2 为公差的等差数列，∴1得是以 S n2*2n ,Sn=2n ,a n=S n-Sn-1=4n-2(n ≥ 2), 又 a 1 =2∴ a n =4n-2(n ∈ N ).(2) 设 L n ： y=a n x+b n , 由y a n x b n x2a n xb n0,yx2据题意方程有相等实根，∴△=a 2 40 ，∴ b n =-121 42 2 2 1 2 n a n) )b n44 ( n( n当 n ∈N *时， d n = 1 b nbn 111 ( 2n 1)2 ( 2n 1) 21 2n1,44( 2n 1) 2( 2n 1 )28n 2 2 4n 21 111,∴ Cn=22( 4n 24n 22( 4n1 )1) 12n 1 2n 1∴ c 1 +c 2 +c 3 + +c n -n=n+ 1 11 11 111n3355 72n 1 2n111 1 .2n 122.(1)由PF?PF 0 得 PF PF，即△ F 1 PF 2 为直角三角形 .121 2设|PF 2 | r，则| PF|1=2r, 于是有 (2r) 2 +r 2=4c 2 和 2r-r=2a 5× (2a) 2 =4c 2e= 5 .(2)b e 2 12,可设 P (x 1, 2x 1), p 2 ( x 2 , 2x 2 ), P(x, y),a1则OP ·=x1x 2 +y 1y 2= x 1 x 2 -4 x 1 x 2 =-271x 2 9.①1OP 2x44x 2 - x -2(x 1 - x) x2x 1x 23由PP 2 +2 PP 1 =0 得- 2x 2 - y -2(2x 1 - y)2(2x 1 - x 2 )y3x 2 y 2(2x 1 - x 2 )24(2x 1 - x 2 )222∵点 P(x,y) 在双曲线1上，9a 29b 2=1, 又 b =4a .a 2b 2(2x 1x 2 )2 (2x 1 - x 2 ) 292∴上式为9a 21 . 简化得： x 1x 2=8a9a 2② 由①、②得 222x2y2. a =2进而得 b =2，进而得b =8. 故所求双曲线方程为2 81。

黄冈市2017年高三年级3月份质量检测数学试题（文科）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.若集合错误！未找到引用源。

，且错误！未找到引用源。

，则集合错误！未找到引用源。

可能是（）A.错误！未找到引用源。

B.错误！未找到引用源。

C.错误！未找到引用源。

D.错误！未找到引用源。

2.设错误！未找到引用源。

是虚数单位，复数错误！未找到引用源。

，则复数错误！未找到引用源。

在复平面内所对应的点位于（）A.第一象限B.第二象限C.第三象限D.第四象限3.阅读如图所示的程序框图，运行相应的程序，输出的错误！未找到引用源。

的值等于（）A.18B.20C.21D.404.某一简单几何体的三视图如图所示，则该几何体的外接球的表面积是（）A.错误！未找到引用源。

B.错误！未找到引用源。

C.错误！未找到引用源。

D.错误！未找到引用源。

5.下列四个结论：①若错误！未找到引用源。

，则错误！未找到引用源。

恒成立；②命题“若错误！未找到引用源。

，则错误！未找到引用源。

”的逆否命题为“若错误！未找到引用源。

，则错误！未找到引用源。

”；③“命题错误！未找到引用源。

为真”是“命题错误！未找到引用源。

为真”的充分不必要条件；④命题“错误！未找到引用源。

”的否定是“错误！未找到引用源。

”.其中正确结论的个数是（）A.1个B.2个C.3个D.4个6.在错误！未找到引用源。

中，角错误！未找到引用源。

的对边分别是错误！未找到引用源。

，若错误！未找到引用源。

，则错误！未找到引用源。

（）A.错误！未找到引用源。

B.错误！未找到引用源。

C.错误！未找到引用源。

D.错误！未找到引用源。

7.已知数据错误！未找到引用源。

是某市错误！未找到引用源。

个普通职工的年收入，设这错误！未找到引用源。

个数据的中位数为错误！未找到引用源。

，平均数为错误！未找到引用源。

，方差为错误！未找到引用源。

，如果再加上世界首富的年收入错误！未找到引用源。