华师版七下一元一次方程50道练习题(含答案)
- 格式:doc
- 大小:165.32 KB
- 文档页数:6


华东师大版七年级数学(下)第六章 一元一次方程 单元综合练习(含答案)1.方程2x +3=7的解是( )A .x =5B .x =4C .x =3.5D .x =22.在解方程x -13+x =3x +12时,方程两边同时乘6,去分母后,正确的是( ) A .2x -1+6x =3(3x +1) B .2(x -1)+6x =3(3x +1)C .2(x -1)+x =3(3x +1)D .(x -1)+x =3(x +1)3.若2(a +3)的值与4互为相反数,则a 的值为( )A .-1B .-72C .-5 D.124.已知方程x -2y +3=8,则整式x -2y 的值为( )A .5B .10C .12D .155.某车间有26名工人,每人每天可以生产800个螺钉或1000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,设安排x 名工人生产螺钉,则下面所列方程正确的是( )A .2×1000(26-x )=800xB .1000(13-x )=800xC .1000(26-x )=2×800xD .1000(26-x )=800x6.在如图2018年6月份的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )A .27B .51C .69D .727.书店举行购书优惠活动:①一次性购书不超过100元,不享受打折优惠;②一次性购书超过100元但不超过200元一律打九折;③一次性购书200元以上一律打七折.小丽在这次活动中,两次购书总共付款229.4元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是________元.8.一件服装的标价为300元,打八折销售后可获利60元,则该件服装的成本价是________元.9.若代数式x -5与2x -1的值相等,则x 的值是________.10.王经理到襄阳出差带回襄阳特产——孔明菜若干袋,分给朋友们品尝.如果每人分5袋,还余3袋;如果每人分6袋,还差3袋,则王经理带回孔明菜________袋.11.甲、乙二人在环形跑道上同时同地出发,同向运动.若甲的速度是乙的速度的2倍,则甲运动2周,甲、乙第一次相遇;若甲的速度是乙的速度的3倍,则甲运动32周,甲、乙第一次相遇;若甲的速度是乙的速度的4倍,则甲运动43周,甲、乙第一次相遇……以此探究正常走时的时钟,时针和分针从0点(12点)同时出发,分针旋转________周,时针和分针第一次相遇.12.解方程:(1)5x +2=3(x +2); (2)x 6-30-x 4=5.13.小陈妈妈做儿童服装生意,在六一这一天上午的销售中,某规格童装每件以60元的价格卖出,盈利20%,求这种规格童装每件的进价.14.某停车场的收费标准如下:中型汽车的停车费为12元/辆,小型汽车的停车费为8元/辆.现在停车场共有50辆中、小型汽车,这些车共缴纳停车费480元,中、小型汽车各有多少辆?15.在红城中学举行的“我爱祖国”征文活动中,七年级和八年级共收到征文118篇,且七年级收到的征文篇数地八年级收到的征文篇数的一半还少2篇,求七年级收到的征文有多少篇.16.世界读书日,某书店举办“书香”图书展.已知《汉语成语大词典》和《中华上下五千年》两本书的标价总和为150元,《汉语成语大词典》按标价的50%出售,《中华上下五千年》按标价的60%出售,小明花80元买了这两本书,求这两本书的标价各是多少元.17.某运动员在一场篮球比赛中的技术统计如下表所示:注:表中出手投篮次数和投中次数均不包括罚球.根据以上信息,求本场比赛中该运动员投中2分球和3分球各几个.第六章章末练习答案详解1.D [解析] 2x +3=7,移项、合并得2x =4,解得x =2.故选D.2.B [解析] 方程两边同时乘以6,得2(x -1)+6x =3(3x +1).故选B.3.C [解析] ∵2(a +3)的值与4互为相反数,∴2(a +3)+4=0,∴a =-5.故选C. 4.A [解析] 根据等式的性质1,等式两边同时加上-3,可得x -2y =5.故选A. 5.C [解析] 本题的等量关系是:螺母的总个数是螺钉总个数的2倍.设安排x 名工人生产螺钉,则(26-x)人生产螺母,由题意得1000(26-x)=2×800x.故选C.6.D [解析] 设第一个数为x ,则第二个数为x +7,第三个数为x +14,则这三个数的和为x +x +7+x +14=3x +21=3(x +7).当x =16时,3(x +7)=69;当x =10时,3(x +7)=51;当x =2时,3(x +7)=27,可见任意圈出一竖列上相邻的三个数的和不可能是72.故选D.7.248元或296 [解析] 设第一次购书的原价为x 元,则第二次购书的原价为3x 元.依题意,得①当0<x ≤1003时,x +3x =229.4,解得x =57.35(舍去);②当1003<x ≤2003时,x +910×3x =229.4,解得x =62,此时两次购书原价总和为4x =4×62=248(元);③当2003<x ≤100时,x +710×3x =229.4,解得x =74,此时两次购书原价总和为4x =4×74=296(元).综上可知:小丽这两次购书原价的总和是248元或296元.8.180 [解析] 设该件服装的成本价是x 元,依题意得300×810-x =60,解得x =180.∴该件服装的成本价是180元.9.-4 [解析] 根据题意得x -5=2x -1,解得x =-4.10.3311.1211 [解析] 直接利用时针和分针第一次相遇,则时针比分针少转了一周,再利用分针转动一周60分钟,时针转动一周720分钟,进而得出等式求出答案.设分针旋转x 周后,时针和分针第一次相遇,则时针旋转了(x -1)周,根据题意可得60x =720(x -1),解得x =1211.12.解:(1)去括号,得5x +2=3x +6,移项、合并,得2x =4,解得x =2.(2)去分母,得2x -3(30-x)=60,去括号,得2x -90+3x =60,移项,得2x +3x =60+90,合并同类项,得5x =150,系数化为1,得x =30.13.解:设这种规格童装每件的进价为x 元.根据题意,得(1+20%)x =60,解方程,得x =50.答:这种规格童装每件的进价为50元.14.解:设中型汽车有x辆,则小型汽车有(50-x)辆,根据题意,得12x+8(50-x)=480,解得x=20,所以50-x=30.答:中型汽车有20辆,小型汽车有30辆.15.解:设八年级收到的征文有x篇,则七年级收到的征文有篇,依题意知+x=118,解得x=80,则118-80=38.答:七年级收到的征文有38篇.16.解:设《汉语成语大词典》的标价是x元,则《中华上下五千年》的标价是(150-x)元,根据题意得50%x+60%(150-x)=80,解得x=100,所以150-x=150-100=50.答:《汉语成语大词典》的标价是100元,《中华上下五千年》的标价是50元.17.解:设本场比赛中该运动员投中2分球x个,则投中3分球(22-x)个.依题意得10+2x+3(22-x)=60,解得x=16,所以22-x=22-16=6.答:本场比赛中该运动员投中2分球16个,3分球6个.。

华师大版七年级下册一元一次方程练习题一.选择题(共10小题)1.(2012•铜仁地区)铜仁市对城区主干道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完.设原有树苗x棵,则根据题意列出方程正确的是()A.5(x+21﹣1)=6(x﹣1)B.5(x+21)=6(x﹣1)C.5(x+21﹣1)=6x D.5(x+21)=6x 2.(2012•台湾)如图为制作果冻的食谱,傅妈妈想依此食谱内容制作六人份的果冻.若她加入50克砂糖后,不足砂糖可依比例换成糖浆,则她需再加几小匙糖浆?()A.15 B.18 C.21 D.243.某商品每件的标价是330元,按标价的八折销售时,仍可获利10%,则这种商品每件的进价为()A.240元B.250元C.280元D.300元4.(2011•铜仁地区)小明从家里骑自行车到学校,每小时骑15km,可早到10分钟,每小时骑12km就会迟到5分钟.问他家到学校的路程是多少km?设他家到学校的路程是xkm,则据题意列出的方程是()A.B.C.D.5.(2011•日照)某道路一侧原有路灯106盏,相邻两盏灯的距离为36米,现计划全部更换为新型的节能灯,且相邻两盏灯的距离变为70米,则需更换的新型节能灯有()A.54盏B.55盏C.56盏D.57盏6.(2010•枣庄)如图(1),把一个长为m,宽为n的长方形(m>n)沿虚线剪开,拼接成图(2),成为在一角去掉一个小正方形后的一个大正方形,则去掉的小正方形的边长为()A.B.m﹣n C.D.7.(2010•内江)某品牌服装折扣店将某件衣服按进价提高50%后标价,再打8折(标价的80%)销售,售价为240元.设这件衣服的进价为x元,根据题意,下面所列的方程正确的是()A.x•50%×80%=240 B.x•(1+50%)×80%=240 C.240×50%×80%=x D.x•(1+50%)=240×80% 8.元旦那天,6位朋友均匀地围坐在圆桌旁共度佳节.圆桌半径为60cm,每人离圆桌的距离均为10cm,现又来了两名客人,每人向后挪动了相同的距离,再左右调整位置,使8人都坐下,并且8人之间的距离与原来6人之间的距离(即在圆周上两人之间的圆弧的长)相等.设每人向后挪动的距离为x,根据题意,可列方程()A.B.C.2π(60+10)×6=2π(60+π)×8 D.2π(60﹣x)×8=2π(60+x)×69.(2007•陕西)中国人民银行宣布,从2007年6月5日起,上调人民币存款利率,一年定期存款利率上调到3.06%,某人于2007年6月5日存入定期为1年的人民币5000元(到期后银行将扣除20%的利息锐),设到期后银行应向储户支付现金x元,则所列方程正确的是()A.x﹣5000=5000×3.06% B.x+5000×20%=5000×(1+3.06%)C.x+5000×3.06%×20%=5000×3.06% D.x+5000×3.06%×20%=5000×(1+3.06%)10.(2006•武汉)越来越多的商品房空置是目前比较突出的问题,据国家有关部门统计:2006年第一季度全国商品房空置面积为1.23亿m2,比2005年第一季度增长23.8%,下列说法:①2005年第一季度全国商品房空置面积为亿m2;②2005年第一季度全国商品房空置面积为亿m2;③若按相同增长率计算,2007年第一季度全国商品房空置面积将达到1.23×(1+23.8%)亿m2;④如果2007年第一季度全国商品房空置面积比2006年第一季度减少23.8%,那么2007年第一季度全国商品空置面积与2005年第一季度相同.其中正确的是()A.①,④B.②,④C.②,③D.①,③二.填空题(共6小题)11.(2012•山西)图1是边长为30cm的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知该长方体的宽是高的2倍,则它的体积是_________cm3.12.(2012•眉山)某学校有80名学生,参加音乐、美术、体育三个课外小组(每人只参加一项),这80人中若有40%的人参加体育小组,35%的人参加美术小组,则参加音乐小组的有_________人.13.(2012•鄂尔多斯)某超市在“五一”活动期间,推出如下购物优惠方案:①一次性购物在100元(不含100元)以内,不享受优惠;②一次性购物在100元(含100元)以上,350元(不含350元)以内,一律享受九折优惠;③一次性购物在350元(含350元)以上,一律享受八折优惠.小敏在该超市两次购物分别付款60元和288元.如果小敏把这两次购物改为一次性购物,则应付款____元.14.(2011•昆明)某公司只生产普通汽车和新能源汽车,该公司在去年的汽车产量中,新能源汽车占总产量的10%,今年由于国家能源政策的导向和油价上涨的影响,计划将普通汽车的产量减少10%,为保持总产量与去年相等,那么今年新能源汽车的产量应增加的百分数为_________.15.(2011•德州)长为1,宽为a的矩形纸片(),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为_________.16.(2007•桂林)如图是2004年6月份的日历,如图那样,用一个圈竖着圈住3个数,如果被圈的三个数的和为39,则这三个数中最大的一个为_________.三.解答题(共9小题)17.(2012•梧州)今年5月,在中国武汉举办了汤姆斯杯羽毛球团体赛.在27日的决赛中,中国队占胜韩国队夺得了冠军.某羽毛球协会组织一些会员到现场观看了该场比赛.已知该协会购买了每张300元和每张400元的两种门票共8张,总费用为2700元.请问该协会购买了这两种门票各多少张?18.(2012•无锡)某开发商进行商铺促销,广告上写着如下条款:投资者购买商铺后,必须由开发商代为租赁5年,5年期满后由开发商以比原商铺标价高20%的价格进行回购,投资者可在以下两种购铺方案中做出选择:方案一:投资者按商铺标价一次性付清铺款,每年可以获得的租金为商铺标价的10%.方案二:投资者按商铺标价的八五折一次性付清铺款,2年后每年可以获得的租金为商铺标价的10%,但要缴纳租金的10%作为管理费用.(1)请问:投资者选择哪种购铺方案,5年后所获得的投资收益率更高?为什么?(注:投资收益率=×100%)(2)对同一标价的商铺,甲选择了购铺方案一,乙选择了购铺方案二,那么5年后两人获得的收益将相差5万元.问:甲、乙两人各投资了多少万元?19.(2012•天津)某通讯公司推出了移动电话的两种计费方式(详情见下表).月使用费/元主叫限定时间/分主叫超时费/(元/分)被叫方式一58 150 0.25 免费方式二88 350 0.19 免费设一个月内使用移动电话主叫的时间为t分(t为正整数),请根据表中提供的信息回答下列问题:(Ⅰ)用含有t的式子填写下表:t≤150 150<t<350 t=350 t>350方式一计费/元 58 _________ 108 _________方式二计费/元 88 88 88 _________(Ⅱ)当t 为何值时,两种计费方式的费用相等?(Ⅲ)当330<t <360时,你认为选用哪种计费方式省钱(直接写出结果即可).20.(2011•连云港)根据我省“十二五”铁路规划,连云港至徐州客运专线项目建成后,连云港至徐州的最短客运时间将由现在的2小时18分缩短为36分钟,其速度每小时将提高260km .求提速后的火车速度.(精确到1km/h )21.(2012•淮安)某省公布的居民用电阶梯电价听证方案如下:第一档电量 第二档电量 第三档电量月用电量210度以下,每度价格0.52元 月用电量210度至350度,每度比第一档提价0.05元 月用电量350度以上,每度比第一档提价0.30元例:若某户月用电量400度,则需交电费为210×0.52+(350﹣210)×(0.52+0.05)+(400﹣350)×(0.52+0.30)=230(元)(1)如果按此方案计算,小华家5月份的电费为138.84元,请你求出小华家5月份的用电量;(2)以此方案请你回答:若小华家某月的电费为a 元,则小华家该月用电量属于第几档?22.(2008•郴州)我国政府从2007年起对职业中专在校学生给予生活补贴.每生每年补贴1500元.某市预计2008年职业中专在校生人数是2007年的1.2倍,且要在2007年的基础上增加投入600万元.2008年该市职业中专在校生有多少万人,补贴多少万元?23.(2007•宿迁)某公司在中国意杨之乡﹣﹣宿迁,收购了1600 m 3杨树,计划用20天完成这项任务,已知该公司每天能够精加工杨树50 m 3或者粗加工杨树100 m 3.则:(1)该公司应如何安排精加工、粗加工的天数,才能按期完成任务?(2)若每立方米杨树精加工、粗加工后的利润分别是500元、300元,则该公司加工后的木材可获利多少元?(结果保留两个有效数字)24.(2007•湖州)自选题:如图,正方形ABCD的周长为40米,甲、乙两人分别从A、B同时出发,沿正方形的边行走,甲按逆时针方向每分钟行55米,乙按顺时针方向每分钟行30米.(1)出发后_________分钟时,甲乙两人第一次在正方形的顶点处相遇;(2)如果用记号(a,b)表示两人行了a分钟,并相遇过b次,那么当两人出发后第一次处在正方形的两个相对顶点位置时,对应的记号应是_________.25.(2006•郴州)售货员:“快来买啦,特价鸡蛋,原价每箱14元,现价每箱12元,每箱有鸡蛋30个.”顾客甲:“我店里买了一些这种特价鸡蛋,花的钱比按原价买同样多鸡蛋花的钱的2倍少96元.”乙顾客:“我家买了相同箱数的特价的鸡蛋,结果18天后,剩下的20个鸡蛋全坏了.”请你根据上面的对话,解答下面的问题:(1)顾客乙买的两箱鸡蛋合算吗?说明理由.(2)请你求出顾客甲店里买了多少箱这种特价鸡蛋,假设这批特价鸡蛋的保质期还有18天,那么甲店里平均每天要消费多少个鸡蛋才不会浪费?华师大版七年级下册一元一次方程练习题参考答案与试题解析一.选择题(共10小题)1.(2012•铜仁地区)铜仁市对城区主干道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完.设原有树苗x棵,则根据题意列出方程正确的是()A.5(x+21﹣1)=6(x﹣1)B.5(x+21)=6(x﹣1)C.5(x+21﹣1)=6x D.5(x+21)=6x考点:由实际问题抽象出一元一次方程.分析:设原有树苗x棵,根据首、尾两端均栽上树,每间隔5米栽一棵,则缺少21棵,可知这一段公路长为5(x+21﹣1);若每隔6米栽1棵,则树苗正好用完,可知这一段公路长又可以表示为6(x﹣1),根据公路的长度不变列出方程即可.解答:解:设原有树苗x棵,由题意得5(x+21﹣1)=6(x﹣1).故选A.点评:考查了由实际问题抽象出一元一次方程,本题是根据公路的长度不变列出的方程.“表示同一个量的不同式子相等”是列方程解应用题中的一个基本相等关系,也是列方程的一种基本方法.2.(2012•台湾)如图为制作果冻的食谱,傅妈妈想依此食谱内容制作六人份的果冻.若她加入50克砂糖后,不足砂糖可依比例换成糖浆,则她需再加几小匙糖浆?()A.15 B.18 C.21 D.24考点:一元一次方程的应用.分析:根据六人份需20×6=120克砂糖,尚需120﹣50=70克砂糖,再利用20克砂糖=6小匙糖浆,即可得出答案.解答:解:六人份需20×6=120克砂糖,尚需120﹣50=70克砂糖,又20克砂糖=6小匙糖浆,所求=70÷20×6=21(小匙).故选:C.点评:此题主要考查了实际生活问题的应用,根据标签上所标示的20克砂糖=6小匙糖浆得出答案是解题关键.3.(2012•牡丹江)某商品每件的标价是330元,按标价的八折销售时,仍可获利10%,则这种商品每件的进价为()A.240元B.250元C.280元D.300元考点:一元一次方程的应用.专题:应用题.分析:设这种商品每件的进价为x元,则根据按标价的八折销售时,仍可获利l0%,可得出方程,解出即可.解答:解:设这种商品每件的进价为x元,由题意得:330×0.8﹣x=10%x,解得:x=240,即这种商品每件的进价为240元.故选A.点评:此题考查了一元一次方程的应用,属于基础题,解答本题的关键是根据题意列出方程,难度一般.4.(2011•铜仁地区)小明从家里骑自行车到学校,每小时骑15km,可早到10分钟,每小时骑12km就会迟到5分钟.问他家到学校的路程是多少km?设他家到学校的路程是xkm,则据题意列出的方程是()A.B.C.D.考点:由实际问题抽象出一元一次方程.专题:探究型.分析:先设他家到学校的路程是xkm,再把10分钟、5分钟化为小时的形式,根据题意列出方程,选出符合条件的正确选项即可.解答:解:设他家到学校的路程是xkm,∵10分钟=小时,5分钟=小时,∴+=﹣.故选A.点评:本题考查的是由实际问题抽象出一元一次方程,解答此题的关键是把10分钟、5分钟化为小时的形式,这是此题的易错点.5.(2011•日照)某道路一侧原有路灯106盏,相邻两盏灯的距离为36米,现计划全部更换为新型的节能灯,且相邻两盏灯的距离变为70米,则需更换的新型节能灯有()A.54盏B.55盏C.56盏D.57盏考点:一元一次方程的应用.专题:优选方案问题.分析:可设需更换的新型节能灯有x盏,根据等量关系:两种安装路灯方式的道路总长相等,列出方程求解即可.解答:解:设需更换的新型节能灯有x盏,则70(x﹣1)=36×(106﹣1),70x=3850,x=55,则需更换的新型节能灯有55盏.故选B.点评:本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.注意根据实际问题采取进1的近似数.6.(2010•枣庄)如图(1),把一个长为m,宽为n的长方形(m>n)沿虚线剪开,拼接成图(2),成为在一角去掉一个小正方形后的一个大正方形,则去掉的小正方形的边长为()A.B.m﹣n C.D.考点:一元一次方程的应用.专题:几何图形问题.分析:此题的等量关系:大正方形的面积=原长方形的面积+小正方形的面积.特别注意剪拼前后的图形面积相等.解答:解:设去掉的小正方形的边长为x,则:(n+x)2=mn+x2,解得:x=.故选A.点评:本题考查同学们拼接剪切的动手能力,解决此类问题一定要联系方程来解决.7.(2010•内江)某品牌服装折扣店将某件衣服按进价提高50%后标价,再打8折(标价的80%)销售,售价为240元.设这件衣服的进价为x元,根据题意,下面所列的方程正确的是()A.x•50%×80%=240 B.x•(1+50%)×80%=240 C.240×50%×80%=x D.x•(1+50%)=240×80%考点:由实际问题抽象出一元一次方程.专题:销售问题.分析:等量关系为:标价×8折=240,把相关数值代入即可求得所求的方程.解答:解:这件衣服的标价为x•(1+50%),打8折后售价为x•(1+50%)×80%,可列方程为x•(1+50%)×80%=240,故选B.点评:根据实际售价找到相应的等量关系是解决问题的关键,注意应先算出这件衣服的标价.8.(2008•新疆)元旦那天,6位朋友均匀地围坐在圆桌旁共度佳节.圆桌半径为60cm,每人离圆桌的距离均为10cm,现又来了两名客人,每人向后挪动了相同的距离,再左右调整位置,使8人都坐下,并且8人之间的距离与原来6人之间的距离(即在圆周上两人之间的圆弧的长)相等.设每人向后挪动的距离为x,根据题意,可列方程()A.B.C.2π(60+10)×6=2π(60+π)×8 D.2π(60﹣x)×8=2π(60+x)×6考点:由实际问题抽象出一元一次方程.专题:几何图形问题.分析:首先理解题意找出题中存在的等量关系:8人之间的距离=原来6人之间的距离,根据等量关系列方程即可.解答:解:设每人向后挪动的距离为x,则这8个人之间的距离是:,6人之间的距离是:,根据等量关系列方程得:=.故选A.点评:列方程解应用题的关键是找出题目中的相等关系.9.(2007•陕西)中国人民银行宣布,从2007年6月5日起,上调人民币存款利率,一年定期存款利率上调到3.06%,某人于2007年6月5日存入定期为1年的人民币5000元(到期后银行将扣除20%的利息锐),设到期后银行应向储户支付现金x元,则所列方程正确的是()A.x﹣5000=5000×3.06% B.x+5000×20%=5000×(1+3.06%)C.x+5000×3.06%×20%=5000×3.06% D.x+5000×3.06%×20%=5000×(1+3.06%)考点:由实际问题抽象出一元一次方程.专题:应用题.分析:首先理解题意找出题中存在的等量关系:不扣除利息税的一年本息和=本金+利息=本金×(1+利率),根据此等式列方程即可.解答:解:设到期后银行应向储户支付现金x元,根据等式:不扣除利息税的一年本息和=本金+利息=本金×(1+利率),列方程得x+5000×3.06%×20%=5000×(1+3.06%).故选D.点评:注意本金、利息、利息税、利率之间的关系.10.(2006•武汉)越来越多的商品房空置是目前比较突出的问题,据国家有关部门统计:2006年第一季度全国商品房空置面积为1.23亿m2,比2005年第一季度增长23.8%,下列说法:①2005年第一季度全国商品房空置面积为亿m2;②2005年第一季度全国商品房空置面积为亿m2;③若按相同增长率计算,2007年第一季度全国商品房空置面积将达到1.23×(1+23.8%)亿m2;④如果2007年第一季度全国商品房空置面积比2006年第一季度减少23.8%,那么2007年第一季度全国商品空置面积与2005年第一季度相同.其中正确的是()A.①,④B.②,④C.②,③D.①,③考点:一元一次方程的应用.专题:增长率问题.分析:此题主要是套用有关增长率的公式:基数×(1+增长率)=增长后的面积,理解清题意,分析即可.解答:解:①若设2005年第一季度全国商品房空置面积是x亿m2.根据增长率的意义,得:x(1+23.8%)=1.23,则x=亿m2,正确;②由①知,错误;③根据增长率的意义,正确;④由于增长和降低的基数不相同,故2007年第一季度全国商品空置面积与2005年第一季度不相同,错误.故选D.点评:注意增长和降低的基数,能够根据增长率和降低率正确表示两个量之间的关系.二.填空题(共6小题)11.(2012•山西)图1是边长为30cm的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知该长方体的宽是高的2倍,则它的体积是1000cm3.考点:一元一次方程的应用.分析:设长方体的高为xcm,然后表示出其宽为30﹣4x,利用宽是高的2倍列出方程求得小长方体的高后计算其体积即可.解答:解:长方体的高为xcm,然后表示出其宽为30﹣4x,根据题意得:30﹣4x=2x解得:x=5故长方体的宽为10,长为20cm则长方体的体积为5×10×20=1000cm3.故答案为1000.点评:本题考查了一元一次方程的应用,解题的关键是找到等量关系并列出方程.12.(2012•眉山)某学校有80名学生,参加音乐、美术、体育三个课外小组(每人只参加一项),这80人中若有40%的人参加体育小组,35%的人参加美术小组,则参加音乐小组的有20人.考点:一元一次方程的应用.分析:设参加音乐小组的人数为x,则根据总数为80可得出方程,解出即可得出答案.解答:解:设参加音乐小组的人数为x,则由题意得:80×40%+80×35%+x=80,解得:x=20,即参加音乐小组的有20人.故答案为:20.点评:此题考查了一元一次方程的应用,解答本题可以利用方程求解,也可以运用代数式的知识求解,例如:先求出参加音乐小组的人数所占的比例,然后乘以80即可.13.(2012•鄂尔多斯)某超市在“五一”活动期间,推出如下购物优惠方案:①一次性购物在100元(不含100元)以内,不享受优惠;②一次性购物在100元(含100元)以上,350元(不含350元)以内,一律享受九折优惠;③一次性购物在350元(含350元)以上,一律享受八折优惠.小敏在该超市两次购物分别付款60元和288元.如果小敏把这两次购物改为一次性购物,则应付款304或336元.考点:一元一次方程的应用.分析:要求他一次性购买以上两次相同的商品,应付款多少元,就要先求出两次一共实际买了多少元,第一次购物显然没有超过100元,即是60元.第二次就有两种情况,一种是超过100元但不超过350元一律9折;一种是购物不低于350元一律8折,依这两种计算出它购买的实际款数,再按第三种方案计算即是他应付款数.解答:解:第一次购物显然没有超过100元,即在第二次消费60元的情况下,他的实质购物价值只能是60元.第二次购物消费288元,则可能有两种情况,这两种情况下付款方式不同(折扣率不同):第一种情况:他消费超过100元但不足350元,这时候他是按照9折付款的.设第二次实质购物价值为x元,那么依题意有x×0.9=288,解得:x=320.第二种情况:他消费不低于350元,这时候他是按照8折付款的.设第二次实质购物价值为a元,那么依题意有a×0.8=288,解得:a=360.即在第二次消费288元的情况下,他的实际购物价值可能是320元或360元.综上所述,他两次购物的实质价值为60+320=380或60+360=420,均超过了350元.因此均可以按照8折付款:380×0.8=304(元),420×0.8=336(元),故答案为:304元或336元.点评:此题主要考查了一元一次方程的应用,解题关键是第二次购物的288元可能有两种情况,需要讨论清楚.本题要注意不同情况的不同算法,要考虑到各种情况,不要丢掉任何一种.14.(2011•昆明)某公司只生产普通汽车和新能源汽车,该公司在去年的汽车产量中,新能源汽车占总产量的10%,今年由于国家能源政策的导向和油价上涨的影响,计划将普通汽车的产量减少10%,为保持总产量与去年相等,那么今年新能源汽车的产量应增加的百分数为90%.考点:一元一次方程的应用.分析:这是一道关于和差倍分问题的应用题,设今年新能源汽车的产量应增加的百分数为x%,解这道的关键是根据“为保持总产量与去年相等”,而去年的总量未知,可以设为参数a,就可以表示出去年普通汽车和新能源汽车的产量分别为90%a和10%a,而几年的普通汽车和新能源汽车的产量分别为90%a(1﹣10%)和10%a (1+x%).就可以根据等量关系列出方程.解答:解:设今年新能源汽车的产量应增加的百分数为x%,去年的总产量为a,由题意,得90%a(1﹣10%)+10%a(1+x%)=a,解得:x=90.故答案为:90%.点评:本题考查了一元一次方程的运用.要求学生能熟练地掌握例一元一次方程解应用题的步骤.解一元一次方程的关键是找到等量关系.15.(2011•德州)长为1,宽为a的矩形纸片(),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为或.考点:一元一次方程的应用.专题:操作型.分析:根据操作步骤,可知每一次操作时所得正方形的边长都等于原矩形的宽.所以首先需要判断矩形相邻的两边中,哪一条边是矩形的宽.当<a<1时,矩形的长为1,宽为a,所以第一次操作时所得正方形的边长为a,剩下的矩形相邻的两边分别为1﹣a,a.由1﹣a<a可知,第二次操作时所得正方形的边长为1﹣a,剩下的矩形相邻的两边分别为1﹣a,a﹣(1﹣a)=2a﹣1.由于(1﹣a)﹣(2a﹣1)=2﹣3a,所以(1﹣a)与(2a﹣1)的大小关系不能确定,需要分情况进行讨论.又因为可以进行三次操作,故分两种情况:①1﹣a>2a﹣1;②1﹣a<2a﹣1.对于每一种情况,分别求出操作后剩下的矩形的两边,根据剩下的矩形为正方形,列出方程,求出a的值.解答:解:由题意,可知当<a<1时,第一次操作后剩下的矩形的长为a,宽为1﹣a,所以第二次操作时正方形的边长为1﹣a,第二次操作以后剩下的矩形的两边分别为1﹣a,2a﹣1.此时,分两种情况:①如果1﹣a>2a﹣1,即a<,那么第三次操作时正方形的边长为2a﹣1.∵经过第三次操作后所得的矩形是正方形,∴矩形的宽等于1﹣a,即2a﹣1=(1﹣a)﹣(2a﹣1),解得a=;②如果1﹣a<2a﹣1,即a>,那么第三次操作时正方形的边长为1﹣a.则1﹣a=(2a﹣1)﹣(1﹣a),解得a=.故答案为或.点评:本题考查了一元一次方程的应用,解题的关键是分两种情况:①1﹣a>2a﹣1;②1﹣a<2a﹣1.分别求出操作后剩下的矩形的两边.16.(2007•桂林)如图是2004年6月份的日历,如图那样,用一个圈竖着圈住3个数,如果被圈的三个数的和为39,则这三个数中最大的一个为20.考点:一元一次方程的应用.专题:数字问题.分析:设最大的一个数为x,则最小的数是(x﹣14),中间的数是(x﹣7),相等关系是:三个数的和为39,则可列出方程求解.解答:解:设最大的一个数为x,根据题意列方程得:(x﹣14)+(x﹣7)+x=39,解得x=20.点评:解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.需注意日历上竖列相邻的两个数相隔7.三.解答题(共9小题)17.(2012•梧州)今年5月,在中国武汉举办了汤姆斯杯羽毛球团体赛.在27日的决赛中,中国队占胜韩国队夺得了冠军.某羽毛球协会组织一些会员到现场观看了该场比赛.已知该协会购买了每张300元和每张400元的两种门票共8张,总费用为2700元.请问该协会购买了这两种门票各多少张?考点:一元一次方程的应用.分析:设每张300元的门票买了x张,则每张400元的门票买了(8﹣x)张,根据题意建立方程,求出方程的解就可以得出结论.解答:解:设每张300元的门票买了x张,则每张400元的门票买了(8﹣x)张,由题意,得300x+400(8﹣x)=2700,。
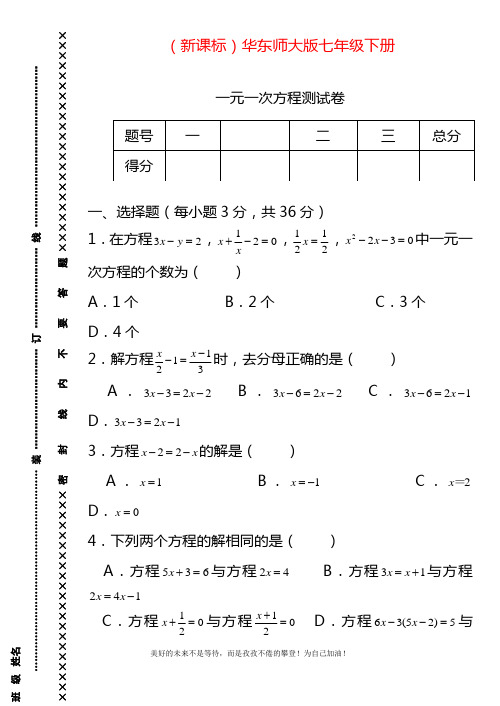
…………………………………………… 装 ………………………… 订 ……………………线 ………………………………………… ×××××××××××××××密封线内不要答题×××××××××××××××××××××× (新课标)华东师大版七年级下册 一元一次方程测试卷 一、选择题(每小题3分,共36分) 1.在方程23=-y x ,021=-+x x ,2121=x ,0322=--x x 中一元一次方程的个数为( ) A .1个 B .2个 C .3个 D .4个 2.解方程3112-=-x x 时,去分母正确的是( ) A .2233-=-x x B .2263-=-x x C .1263-=-x x D .1233-=-x x 3.方程x x -=-22的解是( ) A .1=x B .1-=x C .2=x D .0=x 4.下列两个方程的解相同的是( ) A .方程635=+x 与方程42=x B .方程13+=x x 与方程142-=x x C .方程021=+x 与方程021=+x D .方程5)25(36=--x x 与题号 一 二 三 总分 得分3156=-x x5.A 厂库存钢材为100吨,每月用去15吨;B 厂库存钢材82吨,每月用去9吨。
若经过x 个月后,两厂库存钢材相等,则x 是( )A .3B .5C .2D .46.某种商品的标价为120元,若以九折降价出售,相对于进货价仍获利20%,该商品的进货价为( )。

华师大版七年级数学下册《一元一次方程》单元试卷检测练习及答案解析一、选择题1、在①2x+1;②1+7=15﹣8+1;③;④x+2y=3中,方程共有()A.1个B.2个C.3个D.4个2、下列方程:①;②0.3x=1;③;④x2-4x=3;⑤x=0;⑥x+2y =1.其中,一元一次方程的个数是( )A.2 B.3 C.4 D.53、已知x=﹣5是方程ax﹣3=x﹣a的解,则a的值是()A.﹣2 B.2 C.D.﹣4、若多项式x+2的值为1,则x等于( )A.1 B.-1 C.3 D.-35、若和互为相反数,则的值是A.B.C.D.6、解方程2(x-3)-3(x-4)="5" 时,下列去括号正确的是()A.2x-3-3x+4=5 B.2x-6-3x-4=5C.2x-3-3x-12=5 D.2x-6-3x+12=57、(2014•道外区一模)陈华以8折的优惠价钱买了一双鞋子,节省了20元,那么他买鞋子时实际用了()A.60元B.80元C.100元D.150元8、希望中学九年级1班共有学生49人,当该班少一名男生时,男生的人数恰好为女生人数的一半.设该班有男生x人,则下列方程中,正确的是()A.2(x﹣1)+x=49 B.2(x+1)+x=49C.x﹣1+2x=49 D.x+1+2x=499、某商场购进一批服装,每件进价为200元,由于换季滞销,商场决定将这种服装按标价的六折销售,若打折后每件服装仍能获利20%,则该服装标价是()A.350元B.400元C.450元D.500元10、a※b是新规定的这样一种运算法则:a※b=a+2b,例如3※(﹣2)=3+2×(﹣2)=﹣1.若(﹣2)※x=2+x,则x的值是()A.1 B.5 C.4 D.2二、填空题11、如果3y9﹣2m+2=0是关于y的一元一次方程,则m=________.12、与2的和的3倍等于的2倍与5的和,列出方程为________________.13、若(m-1)x|m|-9=5是一元一次方程,则m的值为______________.14、已知x=1是方程的解,则a=________.15、在梯形面积公式S=(a+b)h中,用 S、a、h表示b,b=________,当S=16,a=3,h=4时,b的值为________.16、小华同学在解方程5x﹣1=()x+3时,发现“括号”处的数字模糊不清,但察看答案可知解为x=2,则“括号”处的数字为________.17、若多项式x-5与2x-1的值相等,则x的值是______.18、湘潭盘龙大观园开园啦!其中杜鹃园的门票售价为:成人票每张50元,儿童票每张30元.如果某日杜鹃园售出门票100张,门票收入共4000元.那么当日售出成人票张.19、已知某校的女生占全体学生人数的52%且比男生多80人.若设这个学校的全体学生人数为x,则可列出方程.20、王大爷用280元买了甲、乙两种药材,甲种药材每千克20元,乙种药材每千克60元,且甲种药材比乙种药材多买了2千克,则甲种药材买了___千克.三、计算题21、解方程:(1)(2)22、解方程:(1)3(x-2)+1=x-5(2x-1)(2)四、解答题23、当x为何值时,式子-3x的值比式子的值大5?24、若方程与的解互为相反数,求k的值.25、为响应“让阅读走进生活”的号召,某中学七年级(1)班的老师为本班学生准备了若干本课外阅读书籍分发给大家,若每人3本还剩10本,若每人4本,则差36本,求本班有多少人,多少本书?26、某车间有16名工人,每人每天可加工甲种零件5个或乙种零件4个.在这16名工人中,一部分人加工甲种零件,其余的加工乙种零件.已知每加工一个甲种零件可获利16元,每加工一个乙种零件可获利24元.若此车间一共获利1 440元,求这一天有几名工人加工甲种零件.27、某学校组织八年级学生参加社会实践活动,若单独租用35座客车若干辆,则刚好坐满;若单独租用55座客车,则可以少租一辆,且余45个空座位.(1)求该校八年级学生参加社会实践活动的人数;(2)已知35座客车的租金为每辆320元,55座客车的租金为每辆400元.根据租车资金不超过1 500元的预算,学校决定同时租用这两种客车共4辆(可以坐不满).请你计算本次社会实践活动所需车辆的租金.参考答案1、B2、B3、C4、B5、B6、D7、B8、A9、B10、C11、412、3(x+2)=2x+513、-114、﹣515、516、317、-418、50.19、0.52x﹣(1﹣0.52)x=80.20、521、(1)x=0(2)x=22、23、x=-124、25、本班有46人,148本书.26、6.27、175人;1440元.答案详细解析【解析】1、试题分析:方程是含有未知数的等式,是等式但不含未知数不是方程,含未知数不是等式也不是方程.解:(1)2x+1,含未知数但不是等式,所以不是方程.(2)1+7=15﹣8+1,是等式但不含未知数,所以不是方程.(3),是含有未知数的等式,所以是方程.(4)x+2y=3,是含有未知数的等式,所以是方程.故有所有式子中有2个是方程.故选B.点评:本题主要考查方程的定义,解决关键在于掌握方程的两个要素:(1)含未知数.(2)要是等式.2、①,右边不是整式,故不是一元一次方程;②0.3x=1,符合定义,是一元一次方程;③,符合定义,是一元一次方程;④x2-4x=3,是高次项的的次数是2,故不是一元一次方程;⑤x=0,符合定义,是一元一次方程;⑥x+2y=1,含有两个未知数,故不是一元一次方程,所以有三个一元一次方程,故选B.【点睛】本题主要考查一元一次方程的定义,熟记定义是解题的关键.3、试题分析:已知x=﹣5是方程ax﹣3=x﹣a的解,即把x=﹣5代入方程即可得到一个关于a的方程,从而求得a的值.解:根据题意得:﹣5a﹣3=﹣5﹣a解得:a=故选:C.点评:解题的关键是根据方程的解的定义,使方程左右两边的值相等的未知数的值是该方程的解.4、根据题意得:x+2=1,解得x=-1.故选B.5、试题解析根据题意得:+=0,去分母得:2x+6+3-3x=0,解得:x=9.故选B.6、试题解析:由原方程去括号,得2x-6-3x+12=5.故选D.7、试题分析:可根据原价﹣实际付的价钱=节省的钱,列等价量关系,其中设原价为x 元,实际付的价钱为x×80%,节省的钱为20元.解:根据题意可得:设鞋子的原价为x元,则:x﹣x×80%=20,解得:x=100,所以买鞋子的实际用了x×80%=80.故选B.点评:本题的等价量关系为:原价﹣折扣价=节省的钱,八折即原价的80%.8、试题分析:利用该班少一名男生时,男生人数恰为女生人数的一半用男生的人数表示出女生的人数,利用女生人数+男生人数=49求解.解:设男生人数为x人,则女生为2(x﹣1),根据题意得:2(x﹣1)+x=49,故选A.点评:本题考查了由实际问题抽象出一元一次方程,解题的关键是找到正确的等量关系.9、试题分析:设该服装标价为x元,根据售价﹣进价=利润列出方程,解出即可.解:设该服装标价为x元,由题意,得0.6x﹣200=200×20%,解得:x=400.故选:B.点评:本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程.10、解:由题意得:﹣2+2x=2+x,解得:x=4,故答案为:C11、【分析】根据一元一次方程的定义解答即可.【详解】∵3y9﹣2m+2=0是关于y的一元一次方程,∴9-2m=1,∴m=4.故答案为:4.【点睛】本题考查了一元一次方程的定义,熟记一元一次方程的定义是解题的关键.12、分析:根据题中的数量关系与相等关系列方程.详解:根据题意得,3(x+2)=2x+5.故答案为3(x+2)=2x+5.点睛:本题考查了列一元一次方程,理解题中的数量关系,注意在相应的位置加上括号,确定运算顺序,根据题中的相等关系列方程.13、试题解析:由题意可得:解得:故答案为:点睛:含有一个未知数,并且未知数的最高次数是的整式方程就是一元一次方程.14、把x=1代入方程得:,去分母得:3a+9=6﹣2+2a,移项合并得:a=﹣5,故答案为:﹣5.【点睛】本题考查了一元一次方程的解的定义,就是能够使方程左右两边相等的未知数的值.15、把b看作是未知数,其余的字母都看作是已知数,解关于b的一元一次方程.去分母得,2S=(a+b)h,去括号得,2S=ah+bh,移项得,hb=2S-ah,因为h>0,系数化为1得,b=.当S=16,a=3,h=4时,b==5.故答案为(1);(2)5.16、解:把x=2代入5x﹣1=()x+3得:10﹣1=2()+3,解得:()=3,故答案为:3.17、根据题意得:x-5=2x-1,解得x=-4.故答案为-4.18、试题分析:设当日售出成人票x张,儿童票(100﹣x)张,可得:50x+30(100﹣x)=4000,解得:x=50.故当日售出成人票50张.故答案为:50.考点:一元一次方程的应用.19、试题分析:设这个学校的全体学生人数为x个,根据女生占全体学生人数的52%且比男生多80人,可列方程0.52x﹣(1﹣0.52)x=80.考点:由实际问题抽象出一元一次方程.20、试题分析:5设买了甲种药材x千克,乙种药材(x﹣2)千克,依题意,得20x+60(x ﹣2)=280,解得:x=5.即:甲种药材5千克.故答案为:5.考点:一元一次方程的应用.21、试题分析:根据一元一次方程的解法:去分母、去括号、移项、合并同类项、系数化为1,解方程即可.试题解析:(1)4(x-1)=1-x4x-4=1-x4x+x=1+45x=5x=1(2)2(2x+1)-(10x+1)=64x+2-10x-1=6-6x=5x=-22、(1)3(x-2)+1=x-5(2x-1)(2)23、试题分析:根据题意列方程,然后解方程即可.试题解析:解:根据题意,得:,解得x=-1.24、分析:分别解得x的值,然后利用相反数的定义列出关于k的方程,通过解方程可以求得k的值.详解:由方程3(x﹣k)=2(x+1)得:x=2+3k,由方程x﹣3(x﹣1)=2﹣(x+1)得:x=2,则2+3k+2=0,∴.点睛:本题考查了一元一次方程的解的定义:使一元一次方程左右两边相等的未知数的值叫做一元一次方程的解.25、试题分析:设本班有x人,则这些课外阅读书的本书表示为3x+10,也可以表示为4x-36,由此联立方程求得答案即可.试题解析:设本班有x人,由题意得3x+10="4x-36"解得:x=46;则3x+10=148本答:本班有46人,148本书.考点:一元一次方程的应用.26、试题分析:等量关系为:加工甲种零件的总利润+加工乙种零件的总利润=1440,把相关数值代入求解即可.试题解析:解:设这一天有x名工人加工甲种零件,则这天加工甲种零件有5x个,乙种零件有4(16﹣x)个.由题意,得16×5x+24×4(16﹣x)=1440,解得x=6.答:这一天有6名工人加工甲种零件.考点:1.一元一次方程的应用;2.经济问题.27、试题分析:设单独租用35座客车需x辆,根据学生的人数相等列出方程进行求解;设租35座客车y辆,则租55座客车(4-y)辆,根据题意列出不等式组求出y的值,然后计算租金.试题解析:(1)设单独租用35座客车需x辆,由题意得,解得x=5.∴35x=35×5=175(人).答:该校八年级参加社会实践活动的人数为175人.(2)设租35座客车y辆,则租55座客车(4-y)辆,由题意得解这个不等式组,得∵y取正整数,∴y=2.∴4-y=2∴320×2+400×2=1440(元).所以本次社会实践活动所需车辆的租金为l 440元.考点:一元一次方程、一元一次不等式组的应用.。

6.2.2.1解一元一次方程(定义及去括号类)★只含有未知数(元),并且含有未知数的式子都是式,未知数的次数都是,这样的方程叫做一元一次方程★解含括号的一元一次方程(1)当方程中含有带括号的式子时,需把括号去掉,方法与有理数运算中的去括号类似;(2)去括号的依据是去括号法则(3)一般步骤:去括号、合并同类项、移项、系数化为1。
一.选择题(共5小题)1.下列方程:①2x2﹣x=6;②y=x﹣7;③;④;⑤;⑥x=3,其中是一元一次方程的有()A.2个B.3个C.4个D.以上答案都不对2.方程3(x+1)=x+1的解是()A.x=﹣1B.x=0C.x=1D.x=23.下列方程的解是x=2的方程是()A.3x+6=0B.C.D.1﹣2x=54.如果方程﹣4x=﹣2与关于x的方程6x﹣2m=9的解互为相反数,则m的值是()A.﹣6B.6C.D.5.已知(a﹣3)x|a﹣2|﹣5=8是关于x的一元一次方程,则a=()A.3或1B.1C.3D.0二.填空题(共5小题)6.若4x2k+3=9是一元一次方程,则k=.7.若x=﹣1是关于x的方程2x﹣m=6的解,则m的值是.8.若方程(k﹣2)x|k|﹣1+7=0是关于x的一元一次方程,则k的值等于.9.方程(2a﹣1)x2+3x+1=4是一元一次方程,则a=.10.若关于x的方程(3a+2)x2+4x b﹣2﹣5=0是一元一次方程,则关于x的方程ax+b=0的解是.三.解答题(共30小题)11.解方程:2x﹣9=5x+3.12.解方程:(1)8﹣x=3x+2;(2).13.解方程:(1)2x+3=11﹣6x;(2)(3x﹣6)=x﹣3.14.解方程:8x=﹣2(x+4).15.解方程:3x﹣2(x+3)=6﹣2x.16.解方程:3(2x﹣1)=4x+3.17.2(x﹣3)=5﹣3(x+1).18.解方程:7x+2(3x﹣3)=20.19.解方程:6(x+)+2=29﹣3(x﹣1)20.解方程:3x﹣7(x﹣1)=3﹣2(x+3).21.解方程:4x﹣6=2(3x﹣1)22.(3x﹣6)=x﹣3.23.解方程:5x﹣2(3﹣2x)=﹣3.24.解方程:4x﹣3=2(x﹣1)25.2(x+8)=3(x﹣1)26.(x+1)﹣2(x﹣1)=1﹣3x.27.解方程:2(x﹣2)﹣3(4x﹣1)=9(1﹣x)28.解方程:7+2x=12﹣2x.29.解方程:(x﹣1)=2﹣(x+2).30.解方程:x﹣1=2(x+1)31.解方程:2﹣2(x﹣1)=3x+4.32.解方程:5x+2=3(x+2)33.34.35.解下列方程:(1)2{3[4(5x﹣1)﹣8]﹣20}﹣7=1;(2)=1;(3)x﹣2[x﹣3(x+4)﹣5]=3{2x﹣[x﹣8(x﹣4)]}﹣2;36.有一位同学在解方程3(x+5)+5[(x+5)﹣1]=7(x+5)﹣1,首先去括号,得3x+15+5x+25﹣5=7x+35﹣1,然后移项,合并同类项,最后求解,你有没有比他更简单的解法?试求解.37.已知y=1是方程2﹣(m﹣y)=2y的解,求关于x的方程m(x﹣3)﹣2=m(2x+5)的解.38.若方程3(2x﹣1)=2﹣3x的解与关于x的方程6﹣2k=2(x+3)的解相同,求k的值.39.已知方程(1﹣m2)x2﹣(m+1)x+8=0是关于x的一元一次方程.(1)求m的值及方程的解.(2)求代数式5x2﹣2(xm+2x2)﹣3(xm+2)的值.40.已知(m﹣3)x|m|﹣2+6=0是关于x的一元一次方程.(1)求m的值;(2)若|y﹣m|=3,求y的值.6.2.2.1解一元一次方程(定义及去括号类)参考答案与试题解析★只含有一个未知数(元),并且含有未知数的式子都是整式,未知数的次数都是1,这样的方程叫做一元一次方程★解含括号的一元一次方程(4)当方程中含有带括号的式子时,需把括号去掉,方法与有理数运算中的去括号类似;(5)去括号的依据是去括号法则(6)一般步骤:去括号、合并同类项、移项、系数化为1。
2022-2023学年华东师大版七年级数学下册《6.2解一元一次方程》同步练习题(附答案)一.选择题1.已知关于x的方程2x﹣a+5=0的解是x=﹣2,则a的值为()A.1B.﹣1C.2D.92.在解方程时,去分母后正确的是()A.5x=15﹣3(x﹣1)B.x=1﹣(3x﹣1)C.5x=1﹣3(x﹣1)D.5x=3﹣3(x﹣1)3.若代数式x﹣的值是2,则x的值是()A.0.75B.1.75C.1.5D.3.54.若x=1是方程(1)2﹣的解,则关于y的方程(2)m(y﹣3)﹣2=m(2y ﹣5)的解是()A.﹣10B.0C.D.45.已知a是任意有理数,在下面各题中结论正确的个数是()①方程ax=0的解是x=1;②方程ax=a的解是x=1;③方程ax=1的解是x=;④方程|a|x=a的解是x=±1.A.0B.1C.2D.36.已知关于x的一元一次方程2023x+m=x﹣2023的解为x=6,则关于y的一元一次方程2023(5﹣y)﹣m=2028﹣y的解为y=()A.y=﹣11B.y=2C.y=10D.y=117.已知关于x的方程2ax﹣b=3x﹣2有无数多个解,则()A.,b=2B.,b=﹣2C.,b=2D.a,b的值不存在二.填空题8.若5x+2与﹣2x+9互为相反数,则x的值为.9.小马在解关于x的一元一次方程=3x时,误将﹣2x看成了+2x,得到的解为x=6,请你帮小马算一算,方程正确的解为x=.10.关于x的方程4x﹣5=3(x﹣1)的解与的解相同,则a的值为.11.“△”表示一种运算符号,其意义是a△b=3a﹣2b,若x△(1△3)=2,则x=.12.已知a,b,c,d为有理数,现规定一种新运算,如,那么当时,则x的值为.13.如果a、b为定值,且关于x的方程,无论k为何值时,它的解总是x =1,那么2a﹣b=.14.已知关于x的一元一次方程+3=2021x+m的解为x=3,那么关于y的一元一次方程+3=2021(1﹣y)+m的解为y=.三.解答题15.解方程:(1)6y+2=3y﹣4;(2).16.解方程:(1)4x﹣2=3﹣x;(2)3(x﹣1)﹣3=0;(3);(4).17.解方程:(1)﹣=﹣1;(2)﹣=2.18.先阅读下列解题过程,然后解答后面两个问题.解方程:|x﹣3|=2.解:当x﹣3≥0时,原方程可化为x﹣3=2,解得x=5;当x﹣3<0时,原方程可化为x﹣3=﹣2,解得x=1.所以原方程的解是x=5或x=1.(1)解方程:|3x﹣2|﹣4=0.(2)解关于x的方程:|x﹣2|=b+119.已知关于x的方程(a﹣2)x|a|﹣1+4b=0为一元一次方程,且该方程的解与关于x的方程的解相同.(1)求a、b的值;(2)在(1)的条件下,若关于y的方程|m﹣1|y+n=a+1+2by有无数解,求m,n的值.20.定义:若关于x的方程ax+b=0(a≠0)的解与关于y的方程cy+d=0(c≠0)的解满足|x﹣y|=m(m为正数),则称方程ax+b=0(a≠0)与方程cy+d=0(c≠0)是“m差解方程”.(1)请通过计算判断关于x的方程2x=5x﹣12与关于y的方程3(y﹣1)﹣y=1是不是“2差解方程”;(2)若关于x的方程x﹣=n﹣1与关于y的方程2(y﹣2mn)﹣3(n﹣1)=m是“m差解方程”,求n的值;(3)若关于x的方程sx+t=h(s≠0),与关于y的方程s(y﹣k+1)=h﹣t是“2m差解方程”,试用含m的式子表示k.参考答案一.选择题1.解:由方程2x﹣a+5=0的解是x=﹣2,故将x=﹣2代入方程得:2×(﹣2)﹣a+5=0,解得:a=1.故选:A.2.解:方程两边都乘以15得,5x=15﹣3(x﹣1).故选:A.3.解:∵代数式x﹣的值等于2,∴x﹣=2,∴3x﹣1﹣x=6,∴x=3.5.故选:D.4.解:先把x=1代入方程(1)得:2﹣(m﹣1)=2×1,解得:m=1,把m=1代入方程(2)得:1×(y﹣3)﹣2=1×(2y﹣5),解得:y=0.故选:B.5.解:①当a≠0时,x=0,错误;②当a≠0时,两边同时除以a,得:x=1,错误;③ax=1,当a≠0时,两边同时除以a,得:x=,错误;④当a=0时,x取全体实数,当a>0时,x=1,当a<0时,x=﹣1,错误.故选:A.6.解:方程2023(5﹣y)﹣m=2028﹣y可变形为2023(y﹣5)+m=(y﹣5)﹣2023.∵关于x的一元一次方程2023x+m=x﹣2023的解为x=6,∴关于(y﹣5)的一元一次方程2023(y﹣5)+m=(y﹣5)﹣2023的解为y﹣5=6,∴y=11,∴关于y的一元一次方程2023(5﹣y)﹣m=2028﹣y的解为y=11.故选:D.7.解:∵2ax﹣b=3x﹣2,∴(2a﹣3)x=b﹣2.∵关于x的方程2ax﹣b=3x﹣2有无数多个解,∴2a﹣3=0且b﹣2=0,∴,b=2,故选:A.二.填空题8.解:根据题意得:(5x+2)+(﹣2x+9)=0,去括号得:5x+2﹣2x+9=0,合并同类项得:3x=﹣11,系数化1得:x=.9.解:当x=6时,=3×6,解得:a=8,∴原方程是=3x,解得:x=3.故答案为:3.10.解:解4x﹣5=3(x﹣1)得x=2,把x=2代入,得则,解得,a=8,故答案为:8.11.解:根据题中的新定义得:x△(1△3)=x△(﹣3)=3x+6=2,移项合并得:3x=﹣4,解得:x=﹣,故答案为:﹣12.解:∵=ad﹣bc,由=22,∴2×7﹣4(x+1)=22,去括号,可得:14﹣4x﹣4=22,移项,可得:﹣4x=22﹣14+4,合并同类项,可得:﹣4x=12,系数化为1,可得:x=﹣3.故答案为:﹣3.13.解:将x=1代入=2+,∴,∴4k+2a=12+1+bk,∴4k﹣bk=13﹣2a,∴k(4﹣b)=13﹣2a,由题意可知:b﹣4=0,13﹣2a=0,∴a=,b=4,∴2a﹣b=13﹣4=9,故答案为:914.解:∵+3=2021+m的解为x=3,∴+3=2021(1﹣y)+m中,1﹣y=x=3,解得:y=﹣2.故答案为:﹣2.三.解答题15.解:(1)移项,得:6y﹣3y=﹣4﹣2;合并同类项,得:3y=﹣6;方程两边同除于3,得:y=﹣2;(2)去分母,得:2(x+1)﹣6=5x﹣1;去括号,得:2x+2﹣6=5x﹣1;移项、合并同类项,得:﹣3x=3;方程两边同除以﹣3,得:x=﹣1.16.解:(1)4x﹣2=3﹣x,移项合并同类项得:5x=5,未知数系数化为1得:x=1;(2)3(x﹣1)﹣3=0,去括号得:3x﹣3﹣3=0,移项合并同类项得:3x=6,未知数系数化为1得:x=2;(3),去分母得:8(2x﹣1)=6(5x+1),去括号得:16x﹣8=30x+6,移项合并同类项得:﹣14x=14,未知数系数化为1得:x=﹣1;(4),去分母得:15﹣10(x﹣7)=6(x+15),去括号得:15﹣10x+70=6x+90,移项合并同类项得:﹣16x=5,未知数系数化为1得:.17.解:去分母,得4(2x﹣1)﹣2(10x+1)=3(2x+1)﹣12,去括号,得8x﹣4﹣20x﹣2=6x+3﹣12,移项,得8x﹣20x﹣6x=3﹣12+4+2,合并,得﹣18x=﹣3,系数化为1,得x=.(2)原方程可变形为:﹣=2,去分母,得30x﹣7(17﹣20x)=42,去括号,得30x﹣119+140x=42,移项,得30x+140x=119+42,合并,得170x=161,系数化为1,得x=.18.解:(1)当3x﹣2≥0时,原方程可化为3x﹣2﹣4=0,解得x=2;当3x﹣2<0时,原方程可化为﹣(3x﹣2)﹣4=0,解得x=﹣.所以原方程的解是x=2或x=﹣.(2)①当b+1<0,即b<﹣1时,原方程无解,②当b+1=0,即b=﹣1时:原方程可化为:x﹣2=0,解得x=2;③当b+1>0,即b>﹣1时:当x﹣2≥0时,原方程可化为x﹣2=b+1,解得x=b+3;当x﹣2<0时,原方程可化为x﹣2=﹣(b+1),解得x=﹣b+1.19.解:(1)∵方程(a﹣2)x|a|﹣1+4b=0为一元一次方程,∴|a|﹣1=1,∴a=±2,∵a﹣2≠0,∴a≠2,∴a=﹣2,∴方程为﹣4x+4b=0,解得x=b,∵方程的解与方程的解相同,∴=1,∴x=1,∴b=1;(2)由题可知方程为|m﹣1|y+n=﹣2+1+2y,∴(|m﹣1|﹣2)y=﹣n﹣1,∵方程有无数解,∴﹣n﹣1=0,|m﹣1|≠2,∴n=﹣1,m≠3或m≠﹣1.20.解:(1)2x=5x﹣12的解为x=4,3(y﹣1)﹣y=1的解为y=2,∵|x﹣y|=|4﹣2|=2,∴关于x的方程2x=5x﹣12与关于y的方程3(y﹣1)﹣y=1是“2差解方程”;(2)方程x﹣=n﹣1的解为x=,方程2(y﹣2mn)﹣3(n﹣1)=m的解为y=,∵两个方程是“m差解方程”,∴|﹣|=m,∴|3+4n|=2,∴n=﹣或n=﹣;(3)方程sx+t=h的解为x=,方程s(y﹣k+1)=h﹣t的解为y=,∵两个方程是“2m差解方程”,∴|﹣|=2m,∴|1﹣k|=2m,∴k=1﹣2m或k=2m+1.。
月 号 姓名 班级一、慧眼识金1.某数的等于4与这个数的的差,那么这个数是 【 】. (A)4 (B)-4 (C)5 (D)-52.若,则的值为 【 】.(A)8 (B)-8 (C)-4 (D)43.若,则①;②;③;④中,正确的有 【 】.(A)1个 (B)2个 (C)3个 (D)4个4.下列方程中,解是的是 【 】.(A) (B) (C) (D)5.下列方程中,变形正确的是 【 】.二、画龙点睛1.在中, 是方程的解. 2.若是的解,则的值是 .3.当 时,代数式与的差为10. 154532113x x -=-4x -a b =1133a b -=-1134a b =3344a b -=-3131a b -=-1x =-2(2)12x --=2(1)4x --=1115(21)x x +=+2(1)2x --=-3443x x -==-(A) 由得232x x +=-(B) 由3=得552x x ==-(C) 由2-得5252x x +==+(D) 由得3510x x x ===,,432x x +-=m 3221x x -=+3010m +x =1(25)2x +1(92)3x +三 考考你的基本功1.解下列方程(1); (2);(3); (4).月 号 姓名 班级一 慧眼识金1.对于“”,下列移项正确的是 【 】.(A) (B) (C) (D)2.某同学在解关于的方程时,误将看作,得到方程的解为,则原方程的解为 【 】.(A) (B) (C) (D)3.小丽的年龄乘以3再减去3是18,那么小丽现在的年龄为 【 】.(A)7岁 (B)8岁 (C)16岁 (D)32岁4.下列方程中,是二元一次方程的是( )A .y=x+2B .x-1y=3 C .y=2-x 2 D .xy=2 5.在下列方程组中,不是二元一次方程组的是( )A .36263325 (3442124657)x y x y x y x y B C D x y x y y z x y -=-=+=+=⎧⎧⎧⎧⎨⎨⎨⎨+=+=+=+=⎩⎩⎩⎩ 6.已知11220x ax y y x by =+=-⎧⎧⎨⎨=-=⎩⎩是方程组的解,则a+b=( ) 76226x x --=-4352x x --=--453x x =+3735y y +=--x y a b +=-x b y a -=-x a y b -=+a x y b -=+a x b y +=-x 513a x -=x -x +2x =-3x =-0x =2x =1x =A .2B .-2C .4D .-4一;画龙点睛1.如果与互为相反数,则的值为 . 2.已知方程是关于的一元一次方程,则 .3.如果成立,则的正数解为 .三 考考你的基本功1.解下列方程 (1) 1111248x x x x -=++ (2) 3142125x x -+=-1)32,20,351,7(2)(3)(4)3217.5 4.2 3.23 1.2y x x y x y x y x y y x x y x y =--==+⎧⎧⎧+=+=⎨⎨⎨+=+=-=⎩⎩⎩月 号 姓名 班级一 慧眼识金1‘下列四组变形中,属于去括号的是( )A.5x+3=0,则5x=-3B.x = 6,则x = 12C.3x-(2-4x)=5,则3x+4x-2=5D.5x=1+4,则5x=52、某同学在方程5x-1=□x+3时,把□处的数字看错了,解得x=-4/3,该同学把□看成了( )154m +14m +m 1(2)60a a x --+=x a =3123x x +=-x 12A.3B.-8C. 8D. -3 3、下列结论:①若a ﹤b ,则a 2c ﹤b 2c ;②若a c ﹥b c ,则a ﹥b ;③若a ﹥b 且若c =d ,则a c ﹥b d ;④若a 2c ﹤b 2c ,则a ﹤b 。
第6章一元一次方程单元测试卷一、选择题(每题3分,共30分)1.下列变形中,不正确的是( )A.若x+a=y+a,则x=yB.若-x=-y,则x=yC.若x-1=y-1,则x=yD.若x2=y2,则x=y2.下列式子是一元一次方程的是( )A.2x+y=5B.x2-4x=3C.x-2=D.=6x-23.已知关于x的方程2x+a-5=0的解是x=2,则a的值为( )A.1B.-1C.9D.-94.下列各组方程的解相同的是( )A.=与x-1=2B.2x(x+1)=x+1与2x+1=0C.-=1与-=10D.x-7=13与x-14=265.图①为一正面白色,反面灰色的长方形纸片.今沿虚线剪开分成甲、乙两长方形纸片,并将甲纸片反面朝上黏贴于乙纸片上,形成一张白、灰相间的长方形纸片,如图②所示.若图②中白色与灰色区域的面积比为8 3,图②纸片的面积为33,则图①纸片的面积为何?( )A. B. C.42 D.446.我们来定义一种运算:=ad-bc.例如=2×5-3×4=-2;再如=3x-2,按照这种定义,当x满足()时,=.A.x=-B.x=-C.x=D.x=7.方程2-=-去分母,得( )A.2-5(3x-7)=-4(x+17)B.40-15x-35=-4x-68C.40-5(3x-7)=-4x+68D.40-5(3x-7)=-4(x+17)8.按如图所示的程序计算,若输入的数为50,则输出的结果为152,要使输出的结果为125,则输入的正整数x的值的个数最多有( )A.0个B.1个C.2个D.3个9.方程x+2=1的解是( )A.x=3B.x=-3C.x=1D.x=-110.学校机房今年和去年共购置了100台计算机,已知今年购置计算机数量是去年购置计算机数量的3倍,则今年购置计算机的数量是( )A.25台B.50台C.75台D.100台二、填空题(每题3分,共24分)11.如果方程(k-1)x|k|+3=0是关于x的一元一次方程,那么k的值是________.12.一艘轮船顺水航行的速度是20海里/时,逆水航行的速度是16海里/时,则水流速度是________海里/时.13.足球比赛的记分规则:胜一场得3分,平一场得1分,负一场得0分,一支球队踢了14场,负了5场,共得19分,那么这支球队胜了________场.14.购买一本书,打八折比打九折少花2元钱,那么这本书的原价是________元.15.一件工作,甲单独做完要用20 h,乙单独做完比甲要多用4 h,设他们一起做x h完成全部工作的,依题意可列方程为________,解得x 的值是________.16.某商场将一款空调按标价的八折出售,仍可获利10%,若该空调的进价为2 000元,则标价为________元.17.小丁在解方程5a-x=13(x为未知数)时,误将-x看成+x,解得方程的解是x=-2,则原方程的解为________.18.在我国明代数学家吴敬所著的《九章算术比类大全》中,有一道数学名题叫“宝塔装灯”,内容为“远望巍巍塔七层,红灯点点倍加增;共灯三百八十一,请问顶层几盏灯?”请你算出塔的顶层有________盏灯.(倍加增指从塔的顶层到底层)三、解答题(19题8分,20~23题每题6分,24、25题每题7分,共46分)19.解下列方程:(1)5x+3=-7x+9; (2)5(x-1)-2(3x-1)=4x-1;(3)-=2+; (4)-=3.20.某篮球运动员去年共参加40场比赛,其中3分球的命中率为0.25,平均每场有12次3分球未投中.问:该运动员去年的比赛中共投中多少个3分球?21.列方程解应用题:把一些图书分给某班学生阅读,若每人分3本,则剩余20本;若每人分4本,则还缺25本,这个班有学生多少人?22.打一份稿件,甲独打需5小时,乙独打需8小时,如果甲先打2小时后,乙加入合打,打完这份稿件还要几小时?23.若A、B两地相距480千米,一列慢车从A地开出,每小时行驶60千米,一列快车从B地开出,每小时行驶65千米.两车同时开出,相向而行,几小时后两车相遇?画线段图:写解题过程:24.为鼓励居民节约用电,某省试行阶梯电价收费制,具体执行方案如下:例如:一户居民七月份用电420度,则需缴电费420×0.85=357(元). 某户居民五、六月份共用电500度,缴电费290.5元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小于400度.问该户居民五、六月份各用电多少度?25.一天,丁浩和妈妈来到“农工商超市”.琳琅满目的商品让人目不暇接.刚巧经理也在旁边,他对丁浩说:“我来考考你,请你帮我算算,该超市上月的营业额为x元.这个月比上个月增长20%,则该超市这个月的营业额为多少元?”丁浩不费吹灰之力说出了答案___________.经理竖起大拇指,又说:“两周前,我用10 000元人民币购进一批货物,很快售完,获利10%,几天后,我又以上次销售额的90%购进同样的货物,由于销路不畅,一件也未售出.两天后,我将商品按照进价的90%售完.在这两次交易中,我是盈利了还是亏损了?”丁浩略加思索就答出来了“”,并算出了盈亏的具体数量: .经理佩服丁浩的同时,又不忘推销商品,接着又说:“我们超市的书最近将有一种会员卡出售.如果花20元钱买一张会员卡后,凭卡购书可以按标价的80%计费,在什么情况下你买卡合算?在什么情况下买卡不合算?”丁浩找出一张纸,将正确结论和解答很快写了下来.经理看了当场就奖励了一本书给丁浩.请你重现丁浩的正确解答过程.妈妈看了好高兴,拿着一袋鲜牛奶,指着“净重500±0.5克”的标志对丁浩说:“这是什么意思?”丁浩看了看,解释道:“.”聪明的你,阅读了上述短文,请你结合平时的数学学习,用简短的文字,说说你的感想:.参考答案一、1.【答案】D解:A.根据等式的两边同时减去相同的数等式成立可得,此选项正确;B.根据等式的两边同时乘相同的数等式成立可得,此选项正确;C.根据等式的两边同时加上相同的数等式成立可得,此选项正确;D.不符合等式的基本性质,故错误.故选D.2.【答案】D3.【答案】A4.【答案】D解:A.第一个方程去分母得:3(x-1)=4,去括号得:3x-3=4,本选项错误;B.第一个方程变形得:2x(x+1)-(x+1)=0,即(x+1)(2x-1)=0,本选项错误;C.第一个方程变形得:-=1,本选项错误;D.第一个方程去分母得:x-14=26,本选项正确,故选D.5.【答案】C解:设题图②中白色区域的面积为8x,则灰色区域的面积为3x,由题意,得8x+3x=33,解得:x=3,所以灰色区域的面积为:3×3=9,所以题图①纸片的面积为:33+9=42.6.【答案】A解:=,可化简为:2-2x=(x-1)-(-4)×,化简可得-2x=3,即x=-.7.【答案】D8.【答案】C解:当3x+2=125时,x=41;当3x+2=41时,x=13;当3x+2=13时,x=,不符合条件.则满足条件的x值是41和13.9.【答案】D10.【答案】C二、11.【答案】-1解:因为方程(k-1)x|k|+3=0是关于x的一元一次方程,所以|k|=1,且k-1≠0,解得k=-1,故答案是:-1.12.【答案】213.【答案】5解:设这支球队胜了x场,由题意,得3x+(14-5-x)×1=19,解得x=5.经检验,符合题意.14.【答案】20解:设原价为x元,由题意得:0.9x-0.8x=2,解得x=20.经检验,符合题意.15.【答案】x=;16.【答案】2750 解:设空调的标价为x元,由题意,得80%x-2 000=2000×10%,解得:x=2 750.经检验,符合题意.17.【答案】x=2解:把x=-2代入5a+x=13得:5a-2=13,解得:a=3;所以原方程是15-x=13,解这个方程得:x=2.18.【答案】3解:设顶层的红灯有x盏,则第六层有2x盏,第五层有4x盏,第四层有8x盏,第三层有16x盏,第二层有32x盏,第一层有64x盏,总共有381盏,列出方程,解方程,即可得解.三、19.解:(1)移项得:5x+7x=9-3,合并同类项得:12x=6,系数化为1得:x=.(2)去括号得:5x-5-6x+2=4x-1,移项、合并同类项得:-5x=2,系数化为1得:x=-.(3)去分母得:3x-(5x+23)=12+2(2x-4),去括号得:3x-5x-23=12+4x-8,移项、合并同类项得:-6x=27,系数化为1得:x=-.(4)原方程可变形为:5x-10-2(x+1)=3,去括号得:5x-10-2x-2=3,移项、合并同类项得:3x=15,系数化为1得:x=5.20.解:设该运动员共出手x个3分球.根据题意,得=12,解得x=640,0.25x=0.25×640=160.答:该运动员去年的比赛中共投中160个3分球.21.解:设这个班有学生x人,由题意,得3x+20=4x-25,解得x=45.经检验,符合题意.答:这个班有学生45人.22.解:设打完这份稿件还要x小时.根据题意,得:×(2+x)+x=1,解得x=.经检验,符合题意.答:打完这份稿件还要小时.23.解:线段图如图,设x小时后两车相遇,根据题意可得: (60+65)x=480,解得:x=3.84.经检验,符合题意.答:3.84小时后两车相遇.24.解:设五月份用电x度,则六月份用电(500-x)度.由题意得500-x>x,所以x<250.当x≤200时,则300≤500-x<400,所以由题意得0.55x+0.6(500-x)=290.5,解得x=190,所以六月份用电310度;当200<x<250时,则250<500-x<300,所以由题意得0.6x+0.6(500-x)=290.5,word版数学此方程无解.综上可得,五月份用电190度,六月份用电310度.分析:本题考查了列一元一次方程解实际问题的运用、分类讨论思想的运用.25.解:x元;盈利了;10元设购书用x元时,买卡与不买卡花钱一样多,则有20+80%x=x,x=100. 购书少于100元时,买卡不合算;购书多于100元时,买卡合算.根据净重500±0.5克,得出这袋牛奶净重在500-0.5=499.5(克)到500+0.5=500.5(克)之间;数学与生活密切相关,数学来源于生活(答案不唯一).11 / 11。
华师大新版七年级下学期《6.2.2 解一元一次方程》同步练习卷一.选择题(共12小题)1.下列方程变形中,正确的是()A.方程3x﹣2=2x+1,移项,得3x﹣2x=﹣1+2B.方程3﹣x=2﹣5(x﹣1),去括号,得3﹣x=2﹣5x﹣1C.方程,未知数系数化为1,得t=1D.方程,去分母,得5(x﹣1)﹣2x=12.若关于x的方程的解为0,则m的值为()A.0B.1C.﹣1D.23.已知关于x的方程2a(x﹣1)=(6﹣a)x+4b有无数个解,那么a+b的值为()A.0B.﹣1C.1D.﹣34.已知a+2=b﹣2==2008,且a+b+c=2008k,那么k的值为()A.4B.C.﹣4D.5.若是方程mx﹣2m+2=0的根,则x﹣m的值为()A.0B.1C.﹣1D.26.将方程去分母:两边同乘以6,得到新的方程是()A.3x﹣9﹣4x﹣2=1B.3x﹣9﹣4x+2=1C.3x﹣9﹣4x﹣2=6D.3x﹣9﹣4x+2=67.规定=ad一bc.若=3,则x=()A.0B.3C.1D.28.定义“*”运算为a*b=ab+2a,若(3*x)+(x*3)=14,则x=()A.﹣1B.1C.﹣2D.29.聪聪在做作业时,不小心把墨水滴在了作业本上,有一道方程题被墨水盖住了一个常数.这个方程是2x﹣,怎么办聪聪想了想,便翻着书后的答案,此方程的解是x=﹣,他很快就计算好了这个常数,你认为这个常数是()A.1B.2C.3D.410.已知关于x的方程4x﹣3m=2的解是x=m,则m的值是()A.2B.﹣2C.D.﹣11.如果方程2x+1=3的解也是方程2﹣=0的解,那么a的值是()A.7B.5C.3D.以上都不对12.要使关于x的方程ax﹣1=x+a无解,则常数a的值应取()A.1B.﹣1C.±1D.0二.填空题(共17小题)13.要使方程a(2x﹣1)=3x﹣2无解,则a=.14.若x=2是关于x的方程的解,则a=.15.已知关于x的方程9x﹣3=kx+14有整数解,那么满足条件的所有整数k=.16.已知关于x的方程2mx﹣6=(m+2)x有正整数解,则整数m的值是.17.对于数a,b,c,d,规定一种运算=ad﹣bc,如=1×(﹣2)﹣0×2=﹣2,那么当=27时,则x=.18.若关于x的方程2x﹣3=1和解互为相反数,则k=.19.已知方程,则代数式3+的值为.20.已知x=﹣2是关于x的方程(1﹣2ax)=x+a的解,则a的值为.21.a,b,c,d为实数,先规定一种新的运算:=ad﹣bc,那么=2009时,x=.22.对任意两个实数a,b,用max(a,b)表示其中较大的数,如max(2,﹣4)=2,则方程的解是.23.关于x的方程kx﹣1=2x的解为正实数,则k的取值范围是.24.a,b,c,d为实数,先规定一种新的运算:=ad﹣bc,那么=2009时,x=.25.在等式3×□﹣2×□=15的两个方格内分别填入一个数,使这两个数是互为相反数且等式成立.则第一个方格内的数是.26.已知关于x的方程有相同的解,那么这个解是.27.定义a*b=ab+a+b,若3*x=31,则x的值是.28.关于x的方程||x﹣2|﹣1|=a恰有三个整数解,则a的值为.29.方程|2001x﹣2001|=2001的解是.三.解答题(共17小题)30.解下列方程(1)2t﹣4=5t+5(2)=1﹣.31.已知关于x的方程6x+2a﹣1=5x和方程4x+2a=7x+1的解相同,求:(1)a的值;(2)代数式(a+3)2012×(2a﹣)2013的值.32.解方程(1)3x=5x﹣4(2)5(x﹣2)=4﹣(2﹣x)(3)=(4).33.解方程:(1)0.7x=0.8x﹣1(2).34.已知是方程的根,(1)求m的值;(2)先化简,再求代数式的值.35.解方程:(1)9x﹣3(x﹣1)=6(2)﹣1=36.解方程:(1)(2).37.解方程:(1)(2)38.解方程:(1)2(x+8)=3x﹣1(2)39.阅读下列文字后,解答问题:我们知道,对于关于x的方程ax=b,当a不等于0时,方程的解为x=;当a 等于0,b也等于0时,所有实数x都能使方程等式成立,也就是说方程的解为全体实数;当a等于0,而b不等于0时,没有任何x能满足方程使等式成立,此时,我们说方程无解.根据上述知识,判断a,b为何值时,关于x的方程a(4x﹣2)﹣3b=8x﹣7的解为全体实数?a,b为何值时,无解.40.解方程:(1)﹣3(x﹣5)=21(2)+1=(3)41.(1)计算:(2)解方程:(3)已知A=4x2﹣4xy+y2,B=x2+xy﹣5y2,求3A﹣B.42.本题共两题:(1)计算1﹣(2﹣3)2×(﹣2)3;(2)解方程:.43.解下列方程:(1)5(x+8)﹣5=2x﹣7;(2).44.解方程:(1)3(2x﹣1)﹣2(1﹣x)=0;(2).45.解下列方程:(1)x+1=1﹣x;(2)=+3.46.解方程:华师大新版七年级下学期《6.2.2 解一元一次方程》同步练习卷参考答案与试题解析一.选择题(共12小题)1.下列方程变形中,正确的是()A.方程3x﹣2=2x+1,移项,得3x﹣2x=﹣1+2B.方程3﹣x=2﹣5(x﹣1),去括号,得3﹣x=2﹣5x﹣1C.方程,未知数系数化为1,得t=1D.方程,去分母,得5(x﹣1)﹣2x=1【分析】根据移项的法则以及去括号的法则、等式的基本性质即可判断.【解答】解:A、方程3x﹣2=2x+1,移项,得3x﹣2x=1+2,选项错误;B、方程3﹣x=2﹣5(x﹣1),去括号,得3﹣x=2﹣5x+5,选项错误;C、方程,未知数系数化为1,得t=,选项错误;D、正确.故选:D.【点评】本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.2.若关于x的方程的解为0,则m的值为()A.0B.1C.﹣1D.2【分析】把x=0代入方程,即可得到一个关于m的方程,即可求得m的值.【解答】解:把x=0代入方程得:=﹣m,解得:m=﹣1.故选:C.【点评】本题考查了方程的解的定义,正确理解定义是关键.3.已知关于x的方程2a(x﹣1)=(6﹣a)x+4b有无数个解,那么a+b的值为()A.0B.﹣1C.1D.﹣3【分析】本方程进行化简,方程有无数个解,则x的系数等于0,且常数项也是0,据此即可求解.【解答】解:去括号得:2ax﹣2a=(6﹣a)x+4b,即(3a﹣6)x=2a+4b,根据题意得:,解得:,则a+b=2﹣1=1.故选:C.【点评】本题考查了方程的解,正确理解方程无解的条件是关键.4.已知a+2=b﹣2==2008,且a+b+c=2008k,那么k的值为()A.4B.C.﹣4D.【分析】将a+2=b﹣2==2008分成a+2=2008①,b﹣2=2008②,c=2008③这3个等式,然后将3式相加即可求得答案【解答】解:由a+2=b﹣2==2008可得,a+2=2008①,b﹣2=2008②,=2008,即c=2×2008③,将①+②+③得,a+b+c=4×2008,∴a+b+c=2008k,中k的值为4.故选:A.【点评】此题主要考查学生对解一元一次方程的理解和掌握,解答此题的关键是将a+2=b﹣2==2008分成3个等式,然后将3式相加问题可解.5.若是方程mx﹣2m+2=0的根,则x﹣m的值为()A.0B.1C.﹣1D.2【分析】把x值代入所给的方程即可求得m的值,进而求得x的值,那么就可求得所给代数式的值.【解答】解:把x=1﹣代入方程得:m(1﹣)﹣2m+2=0,解得:m=1,∴x=0,∴x﹣m=0﹣1=﹣1,故选:C.【点评】是方程的根应适合这个方程.有两个未知数时,应把其中一个当成已知数求解.6.将方程去分母:两边同乘以6,得到新的方程是()A.3x﹣9﹣4x﹣2=1B.3x﹣9﹣4x+2=1C.3x﹣9﹣4x﹣2=6D.3x﹣9﹣4x+2=6【分析】根据等式的基本性质,方程两边同乘以6,再去括号即可得出答案.【解答】解:两边同乘以6,得3(x﹣3)﹣2(2x+1)=6,去括号得,3x﹣9﹣4x﹣2=6.故选:C.【点评】本题考查了一元一次方程的解法和去括号的法则.是基础知识要熟练掌握.7.规定=ad一bc.若=3,则x=()A.0B.3C.1D.2【分析】解答此题的关键是根据规定=ad一bc.若=3时,列方程,然后解方程即可得出答案.【解答】解:如规定=ad一bc,若=3时,可列方程2(x﹣1)﹣(﹣3x)=3,去括号,得2x﹣2+3x=3,移项并合并,得5x=5,系数化为1,得x=1.故选:C.【点评】此题主要考查学生对解一元一次方程的理解和掌握,难度不大,属于基础题.8.定义“*”运算为a*b=ab+2a,若(3*x)+(x*3)=14,则x=()A.﹣1B.1C.﹣2D.2【分析】根据题目定义的运算可得关于x的一元一次方程,求解即可.【解答】解:根据题意(3*x)+(x*3)=14,可化为:(3x+6)+(3x+2x)=14,解得x=1.故选:B.【点评】本题立意新颖,借助新运算,实际考查解一元一次方程的解法.解一元一次方程常见的思路有通分,移项等.9.聪聪在做作业时,不小心把墨水滴在了作业本上,有一道方程题被墨水盖住了一个常数.这个方程是2x﹣,怎么办聪聪想了想,便翻着书后的答案,此方程的解是x=﹣,他很快就计算好了这个常数,你认为这个常数是()A.1B.2C.3D.4【分析】提示:关键在于利用一元一次方程求出未知常数的值.x=﹣是本题的关键,设这个常数为y,由已知条件,把x=﹣代入方程2x﹣y,可以得到2×(﹣)﹣=×(﹣)﹣y,这就转化为解关于y 的一元一次方程了.【解答】解:设这个常数为y,把x=﹣代入方程2x﹣y,得:2×(﹣)﹣=×(﹣)﹣y,解得:y=3,所以这个常数是3,故选:C.【点评】已知方程的解,直接把解代入原方程,可以求其它常数的值,这是方程的解的运用.10.已知关于x的方程4x﹣3m=2的解是x=m,则m的值是()A.2B.﹣2C.D.﹣【分析】此题用m替换x,解关于m的一元一次方程即可.【解答】解:由题意得:x=m,∴4x﹣3m=2可化为:4m﹣3m=2,可解得:m=2.故选:A.【点评】本题考查代入消元法解一次方程组,可将4x﹣3m=2和x=m组成方程组求解.11.如果方程2x+1=3的解也是方程2﹣=0的解,那么a的值是()A.7B.5C.3D.以上都不对【分析】可以分别解出两方程的解,两解相等,就得到关于m的方程,从而可以求出m的值.【解答】解:解方程2x+1=3得:x=1,解方程2﹣=0得:x=a﹣6∴a﹣6=1,解得:a=7,故选:A.【点评】本题解决的关键是能够求解关于x的方程,正确理解方程解的含义.12.要使关于x的方程ax﹣1=x+a无解,则常数a的值应取()A.1B.﹣1C.±1D.0【分析】先将方程变形为ax=b的形式,再根据一元一次方程无解的情况:a=0,b≠0,求得方程ax﹣1=x+a中a的值.【解答】解:将原方程变形为(a﹣1)x=a+1.由已知该方程无解,所以,解得a=1.故a的值应取1.故选:A.【点评】本题考查了一元一次方程解的情况.一元一次方程的标准形式为ax=b,它的解有三种情况:①当a≠0,b≠0时,方程有唯一一个解;②当a=0,b ≠0时,方程无解;③当a=0,b=0时,方程有无数个解.二.填空题(共17小题)13.要使方程a(2x﹣1)=3x﹣2无解,则a=.【分析】先将方程变形为ax=b的形式,再根据一元一次方程无解的情况:a=0,b≠0,求得方程a(2x﹣1)=3x﹣2中a的值.【解答】解:将原方程变形为2ax﹣a=3x﹣2,即(2a﹣3)x=a﹣2.由已知该方程无解,所以,解得a=.故答案为.【点评】本题考查了一元一次方程解的情况.一元一次方程的标准形式为ax=b,它的解有三种情况:①当a≠0,b≠0时,方程有唯一一个解;②当a=0,b ≠0时,方程无解;③当a=0,b=0时,方程有无数个解.14.若x=2是关于x的方程的解,则a=12.【分析】本题把x=2代入方程,看做是关于a的一元一次方程,解答出即可.【解答】解:把x=2代入原方程得,=1﹣a+6,整理得,a=12,故答案为12.【点评】本题主要考查一元一次方程的解,把x的值代入后,原方程就变形为,关于a的一元一次方程,正确解答即可.15.已知关于x的方程9x﹣3=kx+14有整数解,那么满足条件的所有整数k=8、10、﹣8、26.【分析】原方程可化为(k﹣9)x=﹣17,要有整数解则(k﹣9)=±1、±17,由此可得出k的值.【解答】解:原方程可化为(k﹣9)x=﹣17,要有整数解则(k﹣9)=±1、±17,故k=8、10、﹣8、26.【点评】本题考查一元一次方程的解,难度不大,要注意对原方程变形,这样容易得出答案.16.已知关于x的方程2mx﹣6=(m+2)x有正整数解,则整数m的值是3,4,5,8.【分析】首先求出方程2mx﹣6=(m+2)x的解,得出用含m的代数式表示x的式子,然后根据x是正整数,m是整数,即可得出结果.【解答】解:解关于x的方程2mx﹣6=(m+2)x,得:x=.∵x为正整数,∴为正整数,又∵m是整数,∴m﹣2是6的正约数,∴m﹣2=1,2,3,6,∴m=3,4,5,8.【点评】本题主要考查了字母系数的一元一次方程的解法,有一定难度,要注意不要漏解.17.对于数a,b,c,d,规定一种运算=ad﹣bc,如=1×(﹣2)﹣0×2=﹣2,那么当=27时,则x=﹣26.【分析】根据运算规则将=27表示为方程的形式即可求解.【解答】解:根据运算规则:=27可化为:(x+1)(x﹣1)﹣(x﹣1)(x+2)=27,去括号得:﹣1﹣x+2=27,移项合并同类项得:x=﹣26.故填﹣26.【点评】本题考查解一元一次方程的解法;解一元一次方程常见的思路有通分,移项,左右同乘除等.18.若关于x的方程2x﹣3=1和解互为相反数,则k=﹣.【分析】解方程2x﹣3=1就可以求出方程的解,这个解的相反数也是方程的解,根据方程的解的定义,把这个解的相反数代入就可以求出k 的值.【解答】解:首先解方程2x﹣3=1得:x=2;把x=﹣2代入方程,得到:=k+6;解得:k=﹣.故填:﹣.【点评】本题的关键是正确解一元一次方程以及互为相反数的意义.方程的解就是能够使方程左右两边相等的未知数的值.19.已知方程,则代数式3+的值为4.【分析】首先求得x﹣=,代入所求的式子整体代入求解.【解答】解:∵,∴x﹣=代入代数式3+=3+20×=4故答案是4.【点评】本题主要考查了方程的解的定义,正确理解定义是关键.同时考查了整体代入的思想.20.已知x=﹣2是关于x的方程(1﹣2ax)=x+a的解,则a的值为﹣.【分析】根据方程的解的定义,把x=﹣2代入方程,即可得到关于a的方程,即可求解.【解答】解:根据题意得:(1+4a)=﹣2+a,解得:a=﹣故答案是:﹣.【点评】本题主要考查了方程的解的定义,正确解方程是解题的关键.21.a,b,c,d为实数,先规定一种新的运算:=ad﹣bc,那么=2009时,x=.【分析】根据规定的运算,即可把转化为10﹣4(1﹣x),从而解方程即可.【解答】解:根据题意得=10﹣4(1﹣x)=2009,解得:x=.故填.【点评】解决此题的关键是能够根据规定的运算把方程的左边正确转化.22.对任意两个实数a,b,用max(a,b)表示其中较大的数,如max(2,﹣4)=2,则方程的解是x=﹣1.【分析】此题根据题意可以确定=3,然后即可得到一个一元一次方程,解此方程即可求出方程的解.【解答】解:∵max(2,﹣4)=2,∴定=3,∴方程变为:3x=4x+1,解得:x=﹣1.故填:x=﹣1.【点评】本题立意新颖,借助新运算,实际考查解一元一次方程的解法;解一元一次方程常见的过程有去括号、移项、系数化为1等.23.关于x的方程kx﹣1=2x的解为正实数,则k的取值范围是k>2.【分析】先解方程,然后根据解为正实数,可以得到关于k的不等式,从而可以确定出k的范围.【解答】解:∵kx﹣1=2x∴(k﹣2)x=1,解得,x=,∵关于x的方程kx﹣1=2x的解为正实数,∴>0,解得,k>2,故答案为:k>2.【点评】本题考查一元一次方程的解,解题的关键是会解方程,建立相应的不等式.24.a,b,c,d为实数,先规定一种新的运算:=ad﹣bc,那么=2009时,x=.【分析】根据运算规则:=2009,可得方程10﹣4(1﹣x)=2009,解即可.【解答】解:根据题意,得10﹣4(1﹣x)=2009,解得:x=.【点评】本题考查解一元一次方程的解法;解一元一次方程常见的思路有去分母,移项,系数化1等.25.在等式3×□﹣2×□=15的两个方格内分别填入一个数,使这两个数是互为相反数且等式成立.则第一个方格内的数是3.【分析】根据相反数的定义,结合方程计算.【解答】解:设第一个□为x,则第二个□为﹣x.依题意得3x﹣2×(﹣x)=15,解得x=3.故第一个方格内的数是3.故答案为:3.【点评】学会分析,学会总结,学会举一反三是解决此类问题的关键.26.已知关于x的方程有相同的解,那么这个解是x=.【分析】将第一个方程中的a用x表示出来代入第二个方程即可得出答案.【解答】解:由第一个方程得:7x=2a,a=x,将a=x代入第二个方程得:﹣=1,解得:x=.故填x=.【点评】本题考查同解方程的知识,关键是理解同解的定义,难度不大,但很容易出错.27.定义a*b=ab+a+b,若3*x=31,则x的值是7.【分析】先根据题意理解“*”所表示的运算法则,然后再根据此运算法则将3*x=31化为3x+3+x=31,解出即可.【解答】解:由题意得:3*x=31可化为:3x+3+x=31,移项合并得:2x=14,系数化为1得:x=7.故答案为:7.【点评】本题考查解一元一次方程的知识,比较新颖,关键是根据题意列出方程.28.关于x的方程||x﹣2|﹣1|=a恰有三个整数解,则a的值为1.【分析】根据绝对值的性质可得|x﹣2|﹣1=±a,然后讨论x≥2及x<2的情况下解的情况,再根据方程有三个整数解可得出a的值.【解答】解:①若|x﹣2|﹣1=a,当x≥2时,x﹣2﹣1=a,解得:x=a+3,a≥﹣1;当x<2时,2﹣x﹣1=a,解得:x=1﹣a;a>﹣1;②若|x﹣2|﹣1=﹣a,当x≥2时,x﹣2﹣1=﹣a,解得:x=﹣a+3,a≤1;当x<2时,2﹣x﹣1=﹣a,解得:x=a+1,a<1;又∵方程有三个整数解,∴可得:a=﹣1或1,根据绝对值的非负性可得:a≥0.即a只能取1.故答案为1.【点评】本题考查含绝对值的一元一次方程,难度较大,掌握绝对值的性质及不等式的解集的求法是关键.29.方程|2001x﹣2001|=2001的解是x=2或x=0.【分析】解题的关键是去掉绝对值,再计算比较容易了.整体思想:由|x﹣1|=1联想x﹣1=±1,求得x【解答】解:原式=|x﹣1|=1∴x﹣1=1或x﹣1=﹣1∴x=2或x=0故x的解是0或2【点评】本题主要考查的是含有绝对值函数的一元一次方程的一般计算题.难易适中.三.解答题(共17小题)30.解下列方程(1)2t﹣4=5t+5(2)=1﹣.【分析】(1)首先移项,把含t的项移到等号左边,常数项移到等号右边,再合并同类项,最后把t的系数化为1即可;(2)首先乘以6去分母,然后再去括号、移项、合并同类项,最后把y的系数化为1即可.【解答】解:(1)2t﹣4=5t+5,移项得:2t﹣5t=5+4,合并同类项得:﹣3t=9,把t的系数化为1得:t=﹣3;(2)去分母得:2(4y﹣1)=6﹣(2y+5),去括号得:8y﹣2=6﹣2y﹣5,移项得:8y+2y=6﹣5+2,合并同类项得:10y=3,把y的系数化为1得:y=.【点评】此题主要考查了解一元一次方程,解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1.31.已知关于x的方程6x+2a﹣1=5x和方程4x+2a=7x+1的解相同,求:(1)a的值;(2)代数式(a+3)2012×(2a﹣)2013的值.【分析】(1)分别求出两个关于x的方程,根据两个方程的解相同,可得到一个关于a的方程,即可求得a的值;(2)根据同底数的幂的乘法法则即可求得式子的值.【解答】解:(1)由6x+2a﹣1=5x得x=﹣2a+1①由4x+2a=7x+1得x=②,∵关于x的方程6x+2a﹣1=5x和方程4x+2a=7x+1的解相同,∴﹣2a+1=,解得:a=;(2)当a=时,(a+3)2012×(2a﹣)2013=(+3)2012×(2×﹣)2013=()2012×(﹣)2013=[×(﹣)]2012×(﹣)=﹣.【点评】本题主要考查了方程的解的定义,正确利用同底数的幂的运算性质即可求解.32.解方程(1)3x=5x﹣4(2)5(x﹣2)=4﹣(2﹣x)(3)=(4).【分析】各方程去分母,去括号,移项合并,将未知数系数化为1,即可求出解.【解答】解:(1)移项合并得:2x=4,解得:x=2;(2)去括号得:5x﹣10=4﹣2+x,移项合并得:4x=12,解得:x=3;(3)去分母得:18x+6=14+2x,移项合并得:16x=8,解得:x=0.5;(4)方程变形得:=﹣,去分母得:60x﹣30=70x﹣3,移项合并得:10x=﹣27,解得:x=﹣2.7.【点评】此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,求出解.33.解方程:(1)0.7x=0.8x﹣1(2).【分析】(1)移项、合并同类项,然后系数化成1,即可求解;(2)首先去分母、去括号、然后移项、合并同类项,然后系数化成1,即可求解.【解答】解:移项,得:0.7x﹣0.8x=﹣1,则﹣0.1x=﹣1,则x=10;(2)去分母,得:2(3x﹣1)﹣6x=6﹣(4x﹣1),去括号,得:6x﹣2﹣6x=6﹣4x+1移项、合并同类项,得:4x=9,则x=.【点评】本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.注意移项要变号.34.已知是方程的根,(1)求m的值;(2)先化简,再求代数式的值.【分析】(1)把x=﹣代入方程,即可得到一个关于m的方程,解方程即可求得m的值;(2)首先去括号,然后合并同类项即可把式子化简,然后代入m的值计算即可.【解答】解:(1)把代入方程得:﹣=,解得:m=1;(2)原式=﹣m2+m﹣2﹣m+1=﹣m2﹣1把m=1代入,则原式=﹣2.【点评】本题考查了方程的解的定义以及整式的化简求值,正确对整式进行化简是关键.35.解方程:(1)9x﹣3(x﹣1)=6(2)﹣1=【分析】根据等式的性质1“等式的两边加(或减)同一个数(或式子),结果仍相等”和等式的性质2“等式两边乘同一个数,或除以同一个不为0的数,结果仍相等”来解答.【解答】解:(1)去括号得:9x﹣3x+3=6,移项合并同类项得:6x=3,系数化为1得:x=.(2)去分母得:x+1﹣2=4(3x﹣1),去括号得:x+1﹣2=12x﹣4,移项、合并同类项得:﹣11x=﹣3,系数化为1得:.【点评】注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.36.解方程:(1)(2).【分析】(1)方程去括号后,移项合并,将x系数化为1,即可求出解;(2)方程左边第二项变形后,去分母,去括号后,移项合并,将x系数化为1,即可求出解.【解答】解:(1)去括号得:5﹣5x+3=4x﹣3,移项合并得:﹣9x=﹣11,解得:x=;(2)方程变形得:﹣=1,去分母得:4(x﹣3)﹣3(3x+1)=12,去括号得:4x﹣12﹣9x﹣3=12,移项合并得:﹣5x=27,解得:x=﹣.【点评】此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,求出解.37.解方程:(1)(2)【分析】(1)这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.(2)方程两边都含有分数系数,如果直接通分,有一定的难度,但对每一个式子先进行化简、整理为整数形式,难度就会降低.【解答】解:(1)去分母得:4(2x﹣1)﹣3(5x+1)=168,去括号得:8x﹣4﹣15x﹣3=168,移项合并得:﹣7x=175,系数化为1得:得x=﹣25;(2)原方程变形为:﹣=212(10x﹣10)﹣3(5﹣x)=126,∴20x﹣20﹣15+3x=126,23x=161,∴x=7.【点评】本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.第(2)题教会学生对于分数的分子、分母同时扩大或缩小若干倍,值不变.这一性质在今后常会用到.38.解方程:(1)2(x+8)=3x﹣1(2)【分析】(1)直接去括号,化系数为1,得到方程的解即可.(2)带分母的方程,要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.【解答】解:(1)去括号,得2x+16=3x﹣1解得,x=17;(2)去分母,得y﹣20=4y+6,解得,.【点评】本题考查了一元一次方程的解法,去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.39.阅读下列文字后,解答问题:我们知道,对于关于x的方程ax=b,当a不等于0时,方程的解为x=;当a 等于0,b也等于0时,所有实数x都能使方程等式成立,也就是说方程的解为全体实数;当a等于0,而b不等于0时,没有任何x能满足方程使等式成立,此时,我们说方程无解.根据上述知识,判断a,b为何值时,关于x的方程a(4x﹣2)﹣3b=8x﹣7的解为全体实数?a,b为何值时,无解.【分析】根据题意把原方程移项、合并同类项,再根据一次项系数为0和不为0两种情况讨论方程解的情况.【解答】解:原方程可以化为:4(a﹣2)x=2a+3b﹣7,当a﹣2=0且2a+3b﹣7=0,即当a=2,b=1时,方程的解为全体实数;当a﹣2=0而2a+3b﹣7≠0,即a=2,b≠1时,方程无解.【点评】本题考查了一元一次方程解的情况,在解答时要注意一次项系数为0和不为0两种情况,不要漏解.40.解方程:(1)﹣3(x﹣5)=21(2)+1=(3)【分析】(1)去括号,合并同类项,解答即可.(2)先去分母,在方程左右两边同乘以12,化简合并同类项,解答即可.(3)去分母,在方程的左右两边同乘以3,化简解答即可.【解答】解:(1)﹣3(x﹣5)=21,去括号,﹣3x+15=21,解得,x=﹣2;(2),去分母,得4(x﹣4)+12=3(3﹣2x),解得,x=1.3;(3),去分母,得1.5x﹣1﹣5x=1.5,解得,.【点评】去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.41.(1)计算:(2)解方程:(3)已知A=4x2﹣4xy+y2,B=x2+xy﹣5y2,求3A﹣B.【分析】(1)按照有理数混合运算法则计算即可求出结果;(2)首先把方程两边同时乘以6,然后移项、合并同类项,最后化系数为1即可求出结果;(3)直接把A、B两个多项式代入3A﹣B中,然后合并同类项即可解决问题.【解答】解:(1)=﹣1﹣2+=﹣;(2),去分母得:6x﹣3(x﹣1)=12﹣2(x﹣2),∴6x﹣3x+3=12﹣2x+4,∴x=;(3)∵A=4x2﹣4xy+y2,B=x2+xy﹣5y2,∴3A﹣B=3(4x2﹣4xy+y2)﹣(x2+xy﹣5y2)=12x2﹣12xy+3y2﹣x2﹣xy+5y2=11x2﹣13xy+8y2.【点评】第一题考查的有理数的混合运算,对于混合运算的法则应该很熟练;第二题考查的是解一元一次方程,要求学生对于解方程的一般步骤很熟练;第三题考查的整式的加减运算,关键是合并同类项.42.本题共两题:(1)计算1﹣(2﹣3)2×(﹣2)3;(2)解方程:.【分析】(1)考查了实数的计算,解题时要注意运算顺序;(2)这是一个带分母的方程,所以要先去分母,再去括号,最后移项,化系数为1,从而得到方程的解.【解答】解:(1)原式=1﹣1×(﹣8)=1+8=9;(2)去分母得:24﹣4(2x﹣3)=﹣3(x﹣7)去括号得:24﹣8x+12=﹣3x+21移项得:﹣8x+3x=21﹣24﹣12合并同类项得:﹣5x=﹣15系数化为1得:x=3.【点评】实数的计算在解题时要注意运算顺序.去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.43.解下列方程:(1)5(x+8)﹣5=2x﹣7;(2).【分析】(1)是简单的一元一次方程,通过移项,系数化为1即可得到;方程;(2)是较为复杂的去分母,本题方程两边都含有分数系数,如果直接通分,有一定的难度,但对每一个式子先进行化简、整理为整数形式,难度就会降低.【解答】解:(1)去括号得:5x+40﹣5=2x﹣7移项合并同类项得:3x=﹣42,系数化为1得:x=﹣14;(2)去分母得:3(5﹣3x)+6=2(2﹣5x)﹣6x,去括号得:15﹣9x+6=4﹣10x﹣6x,移项合并同类项得:7x=﹣17系数化为1得:.【点评】本题易在去分母、去括号和移项中出现错误,还可能会在解题前产生害怕心理,往往不知如何寻找公分母,怎样合并同类项,怎样化简,所以我们要教会学生分开进行,从而达到分解难点的效果.去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.44.解方程:(1)3(2x﹣1)﹣2(1﹣x)=0;(2).【分析】根据等式的性质1“等式的两边加(或减)同一个数(或式子),结果仍相等”和等式的性质2“等式两边乘同一个数,或除以同一个不为0的数,结果仍相等”来解答.【解答】解:(1)去括号得:6x﹣3﹣2+2x=0,移项合并同类项得:8x=5,系数化为1得:x=;(2)原方程可化为:﹣=,去分母得:4x+8﹣2(3x+4)=2(x﹣1),去括号得:4x+8﹣6x﹣8=2x﹣2,移项合并同类项得:﹣4x=﹣2,系数化为1得:x=.【点评】去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号.本题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍,值不变.这一性质在今后常会用到.45.解下列方程:(1)x+1=1﹣x;(2)=+3.【分析】(1)先移项,再合并同类项,最后化系数为1,从而得到方程的解;(2)方程两边都含有分数系数,如果直接通分,有一定的难度,但对每一个式子先进行化简、整理为整数形式,难度就会降低.【解答】解:(1)移项得:x+x=1﹣1,合并同类项得:2x=0,化系数为1得:x=0;(2)原方程变形为:5x﹣10=2+2x+3,则:3x=15,∴x=5.【点评】本题考查解一元一次方程,解一元一次方程的一般步骤是:去分母、去括号、移项、合并同类项、化系数为1.第(2)题易在去分母、去括号和移项中出现错误,还可能会在解题前产生害怕心理.因为看到小数、分数比较多,学生往往不知如何寻找公分母,怎样合并同类项,怎样化简.第(2)题的另外一个重点是教会学生对于分数的分子、分母同时扩大或缩小若干倍,值不变.这一性质在今后常会用到.46.解方程:【分析】将|x|当作未知数,先去分母,然后移项合并,最后化系数为1可得出|x|的值,继而可得出x的值.【解答】解:去分母得:3|x|﹣1=8,移项合并得:3|x|=9,系数化为1得:|x|=3,∴x1=3,x2=﹣3.【点评】本题考查含绝对值的一元一次方程,难度不大,先解出|x|的值是本题的妙笔.。