桥牌牌型概率大全
- 格式:xls
- 大小:15.50 KB
- 文档页数:1

桥牌精确叫牌体系精确法叫牌体系-开叫摘要1C: 16hcp 以上任何牌型,逼叫1D: 11-15hcp,不保证张数。
1H/1S 11-15hcp,5张以上套1NT:14-16 hcp,平均牌型,允许不好的六张低花,允许有五张高花,或是4441牌型,单张是大牌2C:11-15hcp,6张以上套,或5张以上带一门4张高花(C套不要太差,即AKQJT中有3张)2D:单套高花的阻击叫,视局况而定,有局时套要好,点力集中在套上,无局以干扰为主。
2H:阻击叫,双高,通常5/4,H>=S,6-10P2S: 阻击叫,S+m 5+4,局况不利时保证5+52NT:20-21hcp,平均牌型,允许5张套,允许有五张高花,或是 4441 牌型,单张是大牌3C/3D/3H/3S: 6-10p,通常7张套3NT: AKQ带头7张套,无缺门,旁门至多1张K4C/4D/4H/4S: 6-10p, 通常8张以上套1C开叫1C 1D: 0-7P,任何牌型1H/1S: 8P以上,5张以上套1NT: 8-13P或16P以上平均牌型2C/2D: 8P以上,5张以上套2H/2NT/3C/3D:8 P以上,所叫花色的上一级花色为单张,44412S: 14-15P,均型3H/3S: 4-7P,点基本在套上,7张3NT: AKQ带头7张套,无缺门,旁门至多1张K4C 4-7点点基本在套上 8张4D 4-7点点基本在套上 8张4H 想打4S 想打1C 1D1H/1S /2C/2D 5张套 16-21p1NT 17-19p 均型,或是5332,五张低花2S/3C/3D 22p以上,所叫花色至少为半坚固套F12H 转移2S,可能是H单套22H以上,转移之后叫2NT,24-25或者28点以上,逼局,转移之后3NT,26-273H/3S/4C/4D 22P以上,所叫花色为单张,F1 ,44412NT 22-23p 均型3NT赢敦型1C 1D1H 1S 4-7P, 通常没有三张支持,四张黑桃1NT 4-7p,无三张h支持2C\D 4-7p,五张以上套2H 4-7p,三张支持,简单支持2S\3C\3D 6-7p,五张以上套,且有三张h支持,3H 6-7P, 四张支持,3S\4C\4D 6-7p,四张支持,S\C\D单缺4H TO PLAY1S 大致同上1C 1D1NT 2C stayman,不保证4张高花2D/2H tran to 2H /2S再叫2NT为5332均型 6-7p 邀叫2S 低花 stayman,最少5-5的两门低花,4-7p2NT 转移3C,再加回3D想打。
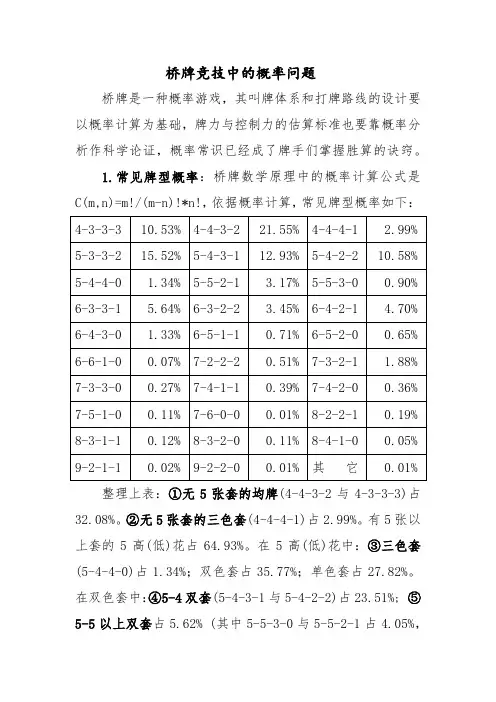
桥牌竞技中的概率问题桥牌是一种概率游戏,其叫牌体系和打牌路线的设计要以概率计算为基础,牌力与控制力的估算标准也要靠概率分析作科学论证,概率常识已经成了牌手们掌握胜算的诀窍。
1.常见牌型概率:桥牌数学原理中的概率计算公式是C(m,n)=m!/(m-n)!*n!,依据概率计算,常见牌型概率如下:整理上表:①无5张套的均牌(4-4-3-2与4-3-3-3)占32.08%。
②无5张套的三色套(4-4-4-1)占2.99%。
有5张以上套的5高(低)花占64.93%。
在5高(低)花中:③三色套(5-4-4-0)占1.34%;双色套占35.77%;单色套占27.82%。
在双色套中:④5-4双套(5-4-3-1与5-4-2-2)占23.51%; ⑤5-5以上双套占5.62% (其中5-5-3-0与5-5-2-1占4.05%,6-5占1.36%,6-6、7-5、7-6等只占0.19%);⑥4-6以上双套占6.83% (其中4-6-3-0与4-6-2-1占6.03%,4-7占0.75%,4-8等只占0.05%)。
在单色套中:⑦5张单套(5-3-3-2)占15.52%;⑧6张单套(6-3-3-1与6-3-2-2)占9.09%;⑨7张以上单套占3.11% (其中7-3-2-1与7-2-2-2和7-3-3-0占2.66%,而8-2、8-3、9-2等只占0.45%)。
以上总概率99.3%的3组9类18种牌型就是本体系所应该(能够)描述的牌型。
2.防守方牌张分配概率:依据机会均等原则,防守方在某一门花色上的牌张分配似乎总是理当趋近于均匀,但桥牌分牌竟必不同于扔硬币,概率测算结果自然会有些异常:牌张数=奇数(3,5,7)时,均匀分配(2-1,3-2,4-3)概率均大于50%,对庄家有利。
牌张数=偶数(4,6,8)时,平均分配概率均小于50%,非均匀分配(3-1,4-2,5-3)概率反而更大,对庄家不利。
唯牌张数=2例外,1-1分配概率52%,2-0分配概率48%。

某一花色牌张分布概率表:
我开始学桥牌时,我的老师就给了我十二条“戒律”要我熟记,告诉我只要严格按此行事,我就最终能成为冠军选手。
下面就是要我熟记的十二条:
1,先出一张A,以便能看一下明手的牌。
2,出最长最强花色的第四张。
3,有连接张的花色不要出小牌。
4,同伴叫过的花色出最大的一张。
5,吃不准时就出将牌。
6,出下家有大牌的花色。
7,出上家弱的花色。
8,永远要回同伴所出的花色。
9,第二家打小牌。
10,第三家打大牌。
11,用更大的牌盖上家的大牌。
12,不要飞掉同伴的大牌。

《桥牌初阶》――东北风整理A、叫牌牌力估算一、一手牌的估算:1. A,K,Q,J在一手牌中的实际点力值是不同的。
它是依随所在套的护张长度而减值的,所以,A单张=3点;K单张=2点;Q双张=1点;J三张=0点2.全手牌是平均牌型时,减1点3.全手牌无A时,减1点。
4.长套从第5张起(含第5张)每长一张就加一点。
有另一5张以上套的,仍按此计算。
5.对伙伴所开叫的主套或副套有所配合时,所配合的套里的Q,和J能加1点。
6.当一手牌对伙伴的高套有所配合时,最少是3张(通常定为将牌的)。
则:边花的副牌,双张的加1点;单张的加2点;缺门的加3点。
(注:持长套将牌的一方的短套边花色不做调整!)二、一手牌的开叫条件:1.一阶5张高花的开叫条件是:(第一,二家)a)12大牌点时,必须要有2.5个大牌防御赢墩!!再加上一个5张以上的高套。
b)10-11大牌点时,除了要有2.5个防御大牌赢墩以外,要再加上一个5张好套,还要有一个4张以上的边花可叫套!(带K,Q的套)并且全手牌要有单,缺花色!c)13大牌点时,只要有一个5张高套,具备2个大牌防御赢墩时就可以开叫了。
注: 1)防御赢墩:A=1个 KQ=1个;AQ=1.5个 AK=2个;K=0.5个。
2)5张好套:是有2个大牌AKQ带头的 5张套。
或是KJ109X 的5张套。
2.草花开叫条件是:a)13-14大牌点的平均型牌,没有4张方片的3张以上套。
(套上带点,如不带点,则开叫3张的方片套)b)同时有4-4低套时要优先开叫草花套。
除非4张草花不占点,先开叫方片套。
c)12大牌点,要有5张以上的草花套。
并要有2.5个大牌防御赢墩。
3. 1方片开叫条件是:a)13-14大牌点,4张以上的方片套。
b)12大牌点,要有5张以上的方片套。
并要有2.5个大牌防御赢墩。
4.同时拥有两套牌时的开叫选择:4.1:a)5-5套,不论高低限,永远优先开叫级别较高的套。
b)6-5套低限牌力时,也要优先选择级别较高的套开叫!即便是较高的套是5张也要先叫它!!c)6-6套同5-5套开叫一样。

桥牌单套打法概率速查表
目录
防守方没有AKQJ时的概率 (2)
防守方有J时的概率 (3)
防守方有Q时的概率 (7)
防守方有K时的概率 (15)
防守方有QJ时的概率 (25)
防守方有A时的概率 (29)
防守方有KJ时的概率 (32)
防守方有AJ时的概率 (42)
防守方有KQ时的概率 (46)
防守方有AQ时的概率 (51)
防守方有KQJ时的概率 (55)
防守方有AK时的概率 (57)
防守方有AQJ时的概率 (60)
防守方有AKJ时的概率 (62)
防守方有AKQ时的概率 (64)
防守方牌张分配概率表 (65)
一手牌的分布概率表 (66)
张定)
张
张
张
张
张
张
张Q飞张
张
张出K时,再出小牌至9飞张)
单套结构打法(总表)第 36 页
出小牌至9,如果9被J吃进,再出
张
张
张。

精确叫牌体系开叫摘要 ( Summary of Opening )1C : 16HCP以上任何牌型, 逼叫1D : 11-15 HCP, 一, 二家保证 4 张以上套, 三, 四家只保证 2 张以上1H/S : 11-15HCP, 5 张以上套, 通常开叫的是手上最长的一门套, 两门一样长时, 选择开叫较高的花色(例外:梅花和高花是6-5, 还是叫高花)1NT : 13-15HCP平均牌型, 允许五张低花(五张高花的5332,如果点力分散也可以开1N)2C : 11-15HCP, 6 张以上套 , 或 5 张以上套带4 张高花2D : 11-15HCP, 4-4-1-4 或 4-4-0-5, 方块单张或缺门2H/2S :阻击叫, 6-10 HCP, 符合二三法则(有局下二,无局下三)2NT : 22-24HCP, 平均牌型,允许5332的平均牌型,允许单张大牌3C/3D/3H/3S : 阻击叫,6-10HCP, 7张套3NT : 赌博性, AKQ 带头 7 张高花套, 无缺门, 旁门至多 1 张 K,整手不超过16P4C/4D/4H/4S :阻击叫, 6-10 HCP, 8 张以上套第一章 1C 开叫及应叫1C:16 HCP以上任意牌型, 逼叫1D:0-7HCP,任意牌型1H/1S:8HCP↑,5张以上套,任意牌型1NT:8-13HCP或16HCP 均型2C/2D:8HCP↑,5张以上套,2H/2S/3C/3D: 8HCP↑,所叫为单张以下的花色,44412NT:14-15HCP,均型3H/3S:4-7HCP,点基本在套上,7张3NT:AKQ领头7张1C--1D : 0 - 7 HCP 开叫人再叫1H/1S/2C/2D:16-21HCP, 5张以上套,不逼叫(NF)1NT:16-18HCP 均型2NT:19-21HCP 均型3NT:25-27HCP 均型2H/2S/3C/3D:22HCP↑ ,所叫花色至少半坚固套,逼叫3H/3S/4C/4D:22HCP↑所叫为单张,逼叫,4441型1C 1D1H 1S:4-7HCP,通常无三张支持1NT:4-7HCP,通常无4张S无3张H支持2C/2D: 4-7HCP, 5张以上套2H: 3 张王牌, 4 - 7 HCP, 简单支持2S/3C/3D:6-7HCP, 5张以上套,且有3张H支持,配显,INV3H:4 张王牌, 6 - 7 HCP, INV3S/4C/4D:SPL,S/C/D单缺 6-7HCP开叫人如果是高限在同伴邀请的时候必须进局,好的17HCP和18-19HCP1S 大致同上1C 1D1NT 2C:Stayman, 询问高花2D:转换叫, 逼开叫人叫 2H,再叫2NT为5332均型6-7HCP INV2H:转换叫, 逼开叫人叫 2S,再叫2NT为5332均型6-7HCP INV2S:最少 5 - 5 的两门低花,4-7HCP2NT:无高花,6-7HCP邀请成局3C/3D:止叫, 6 张以上的梅花, 最多一张大牌4D/4H:TRAN to 4H/4S1C 1D2C/2D:NF, 2D/2H/2S: 4-7HCP,5张以上套,NF2NT:6-7HCP,INV3C/3D: 4-7HCP,正常加叫3D/3H/3S:6-7HCP,6张以上套1C 1D2NT 3C:Stayman, 询问高花3D/3H:TRAN to 3H/3S3S : 低花Stayman3NT:TO PLAY4C :0-4HCP。


精确法叫牌体系开叫摘要1C:16hcp以上任何牌型,逼叫。
1D:11—15hcp,通常保证1张。
1H/1S:11—15hcp,五张以上套。
1NT:14—16hcp,平均牌型,允许5张套,六张低花,单张大牌。
2C:11—15hcp,6张以上套,或5张以上带一门4张高花。
2D:单套高花的阻击叫,保证6张以上。
2H:阻击叫,6—10hcp,双高,通常5/4,H>=S。
2S:阻击叫,S+m 5/4,局况不利时保证55。
2NT:20—21hcp,平均牌型,允许5张套,六张低花,单张大牌。
3C/3D/3H/3S:7—10hcp,7张套。
3NT:AKQ带头7张套,无缺门,旁门至多1张K。
4C/4D:7—10hcp,8张以上套。
4H/4S:to play。
1C开叫1C:16hcp以上任何牌型,逼叫。
1D:0—7P,任何牌型。
1H/1S:8P以上,5张以上套。
1NT:8—13P或16P以上平均牌型。
2C/2D:8P以上,5张以上套。
2H/2NT/3C/3D:8P以上,4441,所叫为单张的下一个花色。
2S:14—15hcp,均型。
3H/3S:4—7hcp,7张套。
4H/4S:4—7hcp,8张套,至少A或K。
3NT:AKQ带头7张套,无缺门,旁门至多一张K。
1C 1D1H/1S:16—21P,5张套。
2C/2D:54以上或6张以上的非均型,均型(允许5张套)叫1NT。
1NT:16—19P,均型。
2H/2S/3C/3D:22P以上,半坚固套,F1。
2NT:22—23P,均型。
3NT:24—26P,均型。
3H/3S/4C/4D:22P+, 4441所叫为单张,F。
,1C 1D2D 2NT:5—7P,寻找高花配1C 1D1H 1S:4—7P,没有3张支持,有4张以上S1NT:4—7P,没有3张H,没有4张S2C/2D:4—7p,5张以上套。
2H:4—7P,3张支持。
2S/3C/3D:6—7P,5张以上套,且有3张H支持,邀叫。

牌游戏中的牌型与概率计算在牌游戏中,牌型和概率计算是非常重要的概念。
牌型是指由一组牌组成的特定形式,而概率计算则是研究某一特定结果出现的可能性。
本文将探讨牌游戏中常见的牌型以及如何计算其概率。
一、顺子顺子是指牌面数字连续的一组牌,如“3、4、5、6、7”。
在扑克牌中,顺子可以由五张连续数字的牌组成。
要计算顺子的概率,我们首先需要确定的是顺子可能出现的总数和所有可能的组合数。
在一副标准的扑克牌中,总共有52张牌。
如果我们要求顺子的长度为5张牌,那么可用的牌的数量将减少至47张。
而顺子可能出现的组合数则是根据长度而定的。
以长度为5的顺子为例,假设我们随机抽取了一张2,那么剩下的4张牌中,需要有3张与之相连的数字才能组成顺子(例如3、4、5)。
由于每个数字有4张牌,所以出现这种情况的可能性为4/47。
接下来,我们需要考虑各种可能的起始牌。
如果我们随机抽取了一张A作为起始牌,则剩下的4张牌只需有3张与之相连的数字。
同样地,这种情况的可能性为4/47。
综合考虑所有可能的起始牌,以及四张牌与之相连的情况,我们可以计算出顺子出现的概率。
具体计算过程相对繁琐,但通过数学方法可以得出大约为4.62%。
二、对子对子是指牌面数字相同的两张牌,如“8、8”。
对于一副标准扑克牌来说,对子的概率计算相对简单。
这是因为对子是牌型中最常见的一种。
在一副标准扑克牌中,每个数字有4张牌,所以对子的可能性为4/52,即约为7.69%。
三、同花同花是指一组牌中的所有花色相同,但数字不一定连续的情况。
同花也是牌型中比较常见的一种,其概率计算也相对简单。
以五张牌的同花为例,我们首先需要确定同花可能出现的组合数。
在一副标准扑克牌中,每种花色有13张牌,所以我们选择5张同花牌的概率为13/52。
接下来,我们需要考虑剩下的两张牌是否与之同花。
由于剩下的两张牌可以是任意花色,所以这两张牌是与同花无关的。
(不适用模型)简单计算后得知,五张同花牌出现的概率约为 4.96%。

桥牌分布概率的原理与滥用由Parsifal发表在桥牌游戏(或曰比赛)中,数学扮演着一个极其重要的角色。
其中,对除自己和明手外另外两家牌型分布的推算是一个非常有趣的课题。
对牌型分布概率有所了解的朋友们很可能会对那些看起来比较复杂的数字感到迷惑不解——例如,1-1分布的概率为什么是52%而2-0分布是48%之类,甚至可能会觉得这个48%是不是四舍五入得来的。
其实,这些数字背后的理论说起来挺简单,更值得注意的是在运用这些数字的时候要万分小心。
所有为我们所熟知的牌型分布概率都是建立在一个条件上的:对所关心的那两家手里的牌我们事先没有获得任何信息,也就是说对那26张牌我们一无所知。
如果在这个条件不能得到满足的情况下机械地运用表格里那些枯燥的数字,误入歧途的可能性是很大的。
我们从最简单的有价值情况入手。
当自己和明手一共持有一套花色的11张的时候,另外2张牌分布的概率是怎么样的呢?由基本的组合理论所得出的结论非常简单:从2张牌中取出0、1和2张的方式各为1、2和1,分别对应2-0、1-1和2-0分布——也就是说,2-0分布和1-1分布的概率皆为2/4=50%.很遗憾,这个结论是不正确的,原因在于它是一个独立事件概率理论,并没有考虑到2张牌之间的相关。
正确的分析方法应该如下:两家暗手一共有26张牌,在零信息的条件下它们为这套花色余下的2张牌提供了26个位置。
第1张牌(这种表达方式并没有人为带来2张牌“地位”上的区别,证明很简单,就是把连乘式两个因子的分子交换一下位置而已)在某一家的概率是显而易见的:13/26.这时分析第2张牌——这时一共余下25个位置:2-0分布对应的情况是第2张牌也在第1张牌所在的一家,一共有12种可能,其概率为12/25;1-1分布对应的情况是第2张牌在另一家,一共有13种可能,其概率为13/25.可见1-1分布的概率比2-2分布大。
具体的数字计算如下(对非严格等式,单独概率保留三位有效数字,总概率保留到小数点后第三位):2-0分布一共有2种情况(根据独立事件组合理论,下同),各自对应概率13/26 *12/25=0.24,总概率为2*0.24=0.48;1-1分布一共也有2种情况,各自对应概率13/26*13/25=0.26,总概率为2*0.26=0.52.3张牌的情况如下:3-0分布一共有2种情况,各自对应概率13/26*12/25*11/24=0.11,总概率为2*0.11=0.22;2-1分布一共有6种情况,各自对应概率13/26*13/25*12/24=0.13,总概率为6*0.13=0.78.4张牌的情况如下:4-0分布一共有2种情况,各自对应概率13/26*12/25*11/24*10/23=0.0478,总概率为2*0.0478=0.096;3-1分布一共有8种情况,各自对应概率13/26*13/25*12/24*11/23=0.0622,总概率为8*0.0622=0.497;2-2分布一共有6种情况,各自对应概率13/26*13/25*12/24*12/23=0.0678,总概率为6*0.0678=0.407.5张牌的情况如下:5-0分布一共有2种情况,各自对应概率13/26*12/25*11/24*10/23*9/22 =0.0196,总概率为2*0.0196=0.039;4-1分布一共有10种情况,各自对应概率13/26*13/25*12/24*11/23*10/22 =0.0283,总概率为10*0.0283=0.283;3-2分布一共有20种情况,各自对应概率13/26*13/25*12/24*12/23*11/22 =0.0339,总概率为20*0.0229=0.678.6张牌的情况如下:6-0分布一共有2种情况,各自对应概率13/26*12/25*11/24*10/23*9/22 *8/21=0.00745,总概率为2*0.00745=0.015;5-1分布一共有12种情况,各自对应概率13/26*13/25*12/24*11/23*10/22 *9/21=0.0121,总概率为12*0.0121=0.145;4-2分布一共有30种情况,各自对应概率13/26*13/25*12/24*12/23*11/22 *10/21=0.0161,总概率为30*0.0161=0.484;3-3分布一共有20种情况,各自对应概率13/26*13/25*12/24*12/23*11/22 *11/21=0.0178,总概率为20*0.0178=0.355.等等等等。
掌握桥牌中的概率比众所周知,数学家和著书人并不一定能成为一个优秀的桥牌手,而一个优秀的桥牌手却必须具有著书人和数学家的某些技能。
桥牌手必须知道桥牌中的概率比,以及如何应用这些概率比。
本书与这套从书中的其余各书略有不同,在本书的开始部分有一定篇幅的理论探讨内容。
我们考虑这部分内容对于从未接触过任何形式的概率比的牌手说来,可能会产生困难。
但是我们认为,先读一读这部分理论内容,然后学习示例,再回过头来看看理论问题,就可以对内容实质获得更为清楚的印象。
概率比的重要性桥牌并不是一种数学游戏,但是桥牌中出现的各种机会都要用到数学。
举一个最简单的例子,AQ飞牌成功的机会为50%。
对于一个花色的各种可能分配,以及对于通过一轮、两轮或三轮硬打下来某一大牌的可能性,也可以作出这种类似的计算。
本书的第一部分主要涉及理论内容,因为假如你不知道和不懂得概率比,则你对于很多牌就不可能作出一个明智的做庄计划。
下面先用一个实际的情况为例。
J 9 78 47 2A K 9 7 4 3西首攻 3K 8 2A K Q JA J T 66 5在两家不叫之后南开叫1。
北应叫2,南跳再叫3NT,成为最后定约。
西首攻3,东用A 得进,并回出一。
西用Q 赢得,并再出而做好这个花色;已经看到是4-3分配。
现在南立即看到了8个赢墩。
并且由于外面只剩下一张,所以他允许丢失1墩或者1墩。
问题在于究竟他应该送掉1墩呢,还是应该计划进行的联合飞(conbination finisse)?为了对上述问题作出准确的回答,你需要知道:要能够迅速回答这类问题,你需要知道:1. 作3-2分配的机会是多少?2. 通过先用10飞,再用J 飞的办法,在中多做出一个赢墩的机会是多少?除与这两个机会有关的数学希望之外,还有一个因素也必须加以考虑。
这就是西用4张作出的首攻。
这个事实使得的平均分配的可能性略为增大。
现在你的直觉和经验可以告诉你,做是较好的机会。
由于这个问题需要涉及概率比,这里暂不多讲,关于具体的概率比以后都要讲到。
桥牌的坐庄技巧下面就让带大家了解下桥牌的坐庄技巧吧。
桥牌的坐庄技巧一、建立长套花色的赢墩:1. 花色的建立:a.当大牌不连接时,朝大牌方向出张。
一张在敌方手中的关键牌,它所在的位置是决定胜负的因素。
如在叫或打牌中你没有得到任何信息的话,则概率如下:单张关键牌有利位置:50%双张关键牌有利位置:25%二张中打对一张:75%三张中打对二张:50%b.一门花色牌张的分配概率:对方持有的牌张分配百分率% 分配百分率% 分配百分率%2张1-1 52 2-0 483张2-1 78 3-0 224张3-1 50 2-2 40 4-0 105张3-2 68 4-1 28 5-0 46张4-2 6-0 48 11 5-2 31 5-1 167张4-3 7-0 62 少于0.5 5-2 31 6-1 7二、飞牌1. 缺少坚强的连接张时,手上出小牌。
2. 有几张大牌时,先用最小的一张大牌飞。
3. 通过叫牌和防守方首攻得到的信息判断飞牌的方向。
4. “八飞九不飞是指庄家和明手在同一门花色中共有8张缺Q时,一般应飞Q,有9张时,不飞,用AK砸Q。
桥牌的坐庄技巧三、投入法:(需先剥光被投入的花色)通过敌方叫牌过程和出牌所得到的信息,判断何时投入谁家,对我方有利,从而可得赢墩。
四、挤压法(要有一个可用来挤压的花色)要记住打牌过程所出的所有牌;要留好明暗手之间的一个桥路。
通过挤压使得防守方被迫让我们做出一个赢墩。
五、剪刀法:(使防守方以后没有进手张)在有将定约中,如果庄家有足够的将牌,但是缺少将牌的A(第一轮控制)。
当首攻人攻出的第一张牌可能是单张时(或双张),要看防守方是否还有边花上的A,如果有而且这个边花你有K(或第二轮控制,单张)时,先打掉这个边花A,再动将牌。
它包括(1)明手将吃;(2)暗手将吃(又名倒打法);(3)交叉将吃。
二、明手将吃的基本思路计算进手张,要保持桥路畅通,使将吃能连续进行,防止在将吃进行中对方获得出牌权,采用调将而破坏将吃法。
三角形中的桥牌概率(3)在《三角形中的桥牌概率(2)》的末尾,我向大家抛出了这样一个问题:一门花色在外面一共有6张牌,3-3分布的组合共有20种可能性,占到总64种组合的31.25%。
但为什么所有的桥牌概率分布表查到的3-3分布概率都是35.53%呢?孰真孰假?在回答这个问题之前,我们先来看问题的简化版:一门花色在外面一共有2张牌,分别是x和y。
按照三角形的理论,1-1分布的组合共有2种可能性,占到总4种可能性的50%。
可是,从桥牌概率分布表查到的1-1分布概率却是52%,这当中的差异到底是什么呢?明明牌都已经发好了呀,要么2-0(或0-2),要么1-1,五五开的事情,这多出来的2%是从哪里来的?答案:50%是“古典概率”,52%是“先验概率”(又名“原始概率”)。
“古典概率”生活在一个非黑即白的世界里。
举例来说,扔个硬币,它掉到地面上的时候,只存在“正面朝上”和“反面朝上”这两种情况。
它绝对不可能最终竖立在地面上,掉出第三种可能性。
而且,当这枚硬币被抛出后,它“正面朝上”和“反面朝上”的机会是均等的。
不存在说硬币某一面的材料是吸铁石,而地面是铁块,永远牢牢地只吸住硬币其中一面落地的情况。
“古典概率”运用到桥牌里时,可以这样理解:当牌发好后、谁都没有看到的时候,假如两个人对一门花色一共持有2张,那这2张牌是1-1分布的可能性的确是50%。
可是,这个50%要被验证的话,必须双方同时把这门花色的牌摊出来才可以。
(或者双方永远都不摊牌也可以,那1-1分布的可能性也依然永远是50%)为什么一定要同步摊牌(或同步不摊牌)呢?因为当一旦只有一个人摊牌、而另一个人还没有摊牌的时候,在那一刹那,第2张牌归属的先决条件就变化了。
它不再属于“古典概率”中非黑即白的世界了,它踩在“古典概率”的肩膀上,进入了“空档原理”的世界。
“空档原理”是什么?我们来讲一个买电影票的故事。
从前,有个电影院,一共有26个座位,左右两个区各占13个座位。
部分定约叫牌1Women's Day有关桥牌定约的统计学概率在1%以上的定约有哪些?其中,部分定约有10个,占34.26%;成局定约有7个,占54.79%;满贯定约有4个,占5.83%,共占94.88%。
在桥牌比赛中,部分定约占所有定约的37.12%。
在16个部分定约中,它们的分布情况如下(转引自一休桥牌博客,样本量131082副牌):1阶花色定约全部加起来只有1.06%,没有第10位2C一个定约多;4阶低花定约排11、12位,都不到1%;排名前十位的是1NT、2S、2H、3S、3H、3D、3C、2D、2NT、2C,这10个部分定约加起来有34.26%,占所有部分定约的92.30%。
1NT、2S、2H在部分定约中举足轻重,1NT作为王者、2S作为大哥、2H作为小弟三者占比16.4%(接近部分定约的半壁江山);3阶花色定约占比13.04%。
两者相加29.44%,占所有部分定约的79.31%。
因此一无将(6.11%)、二、三高花(17.33%)以及三低花(6.00%)是部分定约的主战场。
从总体构成来看,高花部分定约占比18.23%(占部分定约的半壁江山,其中黑桃部分定约10.25%),低花部分定约占比10.97%(不到三分之一),无将部分定约占比7.92%(刚过五分之一)。
从分数来看,低花定约要超过同级高花定约必须多拿2墩,高花定约要超过同级无将定约必须多拿1墩,因此配合良好的高花定约不仅优先于低花定约,也优先于无将定约,因为有将定约往往能比无将定约多拿1至2墩。
定约得墩数统计:定约得9、10、8、11、7、12墩依次占21.37%、21.11%、15.76%、14、79%、9.40%、8.38%,有点像开会排座次。
共计90.81%,其中9墩、10墩像两座山峰一样排在中间,占42.48%。
9墩、10墩定约是部分定约和成局定约混杂的区域,9墩里有成局定约3NT,10墩里有部分定约4C、4D。
7、8、9墩依此占9.40%、15.76%、21.37%,像爬山一样,提示我们叫部分定约要像爬山一样勇攀高峰!高于平均失败率35.28%的8个部分定约及其失败率:定约失败率最高的是3H,其次是3S,再次是2NT,这些可以归因于阻击叫,竞叫,或者为了邀局而导致的冒叫,也说明高花邀叫系统和2NT开叫或2NT应叫可能存在问题,需要改进。
说明:
1、此表根据桥牌网游中的快枪手zr51cf整理和补充完成,希望成为一种共识模式。
免费下载,目的是推广和普及,特别适合桥牌初学者边用边学。
2 、桥牌概率问题
桥牌是讲究概率的。
一个刚学桥牌的人,特别是人文学科的学生特别头疼,这是错误的只需记住几个常见的数字再加上一点点常识就行了。
平均一手牌的大牌点只有7~12点之间,这个数字占53%。
你和明手共有7张牌,对方6张牌3-3分布占36%,2-4分布占48%,绝对平均数占得比例并不高。
当你和明手共有8张牌时,对方2-3分布的概率占68%,1-4分布占28%。
当你和明手共有9张牌时,对方1-3分布占50%,2-2分布占40%,0-4分布占10%;当你和明手共有10张牌时,对方1-2分布占78%,0-3分布占22%
总之,你和明手加起来时奇数时,对方可能是不平均分布;如果是偶数,对方很可能平均分布。
这是你在没有任何线索的情况下的概率。