《自动控制系统计算机仿真》习题参考答案

《控制系统数字仿真》练习题及答案1. 单选题1. 某系统的函数关系式为y=1/（x3-2x+4），绘制x在0至10之间变化的图形，正确的是（）。

A. fplot('1/(x*3-2*x+4)',[0 10])B. fplot('1/(x.^3-2*x+4)',[0 10])C. plot('1/(x.^3-2*x+4)',[0 10])D. plot('1/(x*3-2*x+4)',[0 10])正确答案：B2. 绘制系统零极点图的命令是（）。

A. stepB. pzmapC. rlocusD. sgrid正确答案：B3. 将系统零极点形式变换为传递函数形式的命令是（）。

A. tf2zpB. ss2tfC. ss2zpD. zp2tf正确答案：D4. AUTOCAD的坐标体系，包括世界坐标和（）坐标系。

A. 绝对坐标B. 平面坐标C. 相对坐标D. 用户坐标正确答案：D5. 在MATLAB工作空间中，表示圆周率的特殊变量是（）。

A. piB. ansC. iD. eps正确答案：A6. 下列哪条指令是求矩阵的行列式的值（）。

A. invB. diagC. detD. eig正确答案：C7. 在CAD网络系统中，以下说法不正确的是（）。

A. 设计资料可以共享B. 硬件可以共享C. 电脑文件可以共享D. 可以方便管理设计进度正确答案：C8. i=2; a=2i;b=2*i;c=2*sqrt(-1);程序执行后；a, b, c的值分别是（）。

A. a=4,b=4,c=2.0000iB. a=4,b=2.0000i, c=2.0000iC. a=2.0000i, b=4,c=2.0000iD. a=2.0000i,b=2.0000i,c=2.0000i正确答案：C9. 在循环结构中跳出循环，执行循环后面代码的命令为（）。

A. returnB. breakC. continueD. keyboard正确答案：B10. figure命令的作用是（）。

控制系统计算机仿真（电子工业出版社蒋珉）参考答案说明：1．对于可以用文字或数字给出的情况，直接给出参考答案。

2．对于难以用文字或数字给出的情况，将提供MATLAB程序或Simulink模型。

目录：第 1 章绪论第 2 章连续系统数字仿真的基本算法第 3 章采样控制系统的数字仿真第 4 章控制系统优化设计与仿真第 5 章控制系统仿真建模第 6 章仿真的工程应用实例第 1 章绪论1.1 系统是被研究的对象，模型是对系统的描述，仿真是通过模型研究系统的一种工具或手段。

1.2 数学仿真的基本工具是数字计算机，因此也称为计算机仿真或数字仿真。

将数学模型通过一定的方式转变成能在计算机上实现和运行的数学模型，称之为仿真模型。

1.3 因为仿真是在模型上做试验，是一种广义的试验。

因此，仿真基本上是一种通过试验来研究系统的综合试验技术，具有一般试验的性质。

而进行试验研究通常是需要进行试验设计。

1.4 解析法又称为分析法，它是应用数学推导、演绎去求解数学模型的方法。

仿真法是通过在模型上进行一系列试验来研究问题的方法。

利用解析法求解模型可以得出对问题的一般性答案，而仿真法的每一次运行则只能给出在特定条件下的数值解。

，解析法常常是围绕着使问题易于求解，而不是使研究方法更适合于问题，常常因为存在诸多困难而不能适用。

从原则上讲，仿真法对系统数学模型的形式及复杂程度没有限制，是广泛适用的，但当模型的复杂程度增大时，试验次数就会迅速增加，从而影响使用效率。

1.5 仿真可以应用于系统分析、系统设计、理论验证和训练仿真器等方面。

1.6[]x xx21 01 000 1720 8=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---= y u注：本题答案是用MA TLAB中tf2ss()函数给出的，是所谓“第二能控标准型”(下同)。

1.7[]xx x 310001010001133=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=y u 1.8 25433)(232+++++=s s s s s s G 1.9[])(264.0368.00)()(001)(010*******.0368.1)1(k k y k u k k x x x =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=+ 1.10 仿真模型见praxis1_10_1.mdl ；MA TLAB 程序见praxis1_10_2.m 。

1控制系统计算机仿真试题一、 填空题（每空1分，共20分）1、在自动控制中，常见的数学模型可以分为（ ）模型、（ ）模型和（ ）模型三大类。

2、常用的基本算法可以分为（ ）、（ ）和（ ）三大类。

3、实时数字仿真通常是指把一个（ ）嵌入到一个具有实物模型的实际系统或仿真系统的运行过程中，这就要求仿真模型的时间比例尺必须完全等于原始模型的时间比例尺。

4、采样控制系统是用（ ）或（ ）作为系统的控制器，对连续的被控对象进行控制的一种动态系统。

5、在数学上，解决参数优化问题的途径一般有两条，即（ ）和（ ），并且可以按照一定的评判标准对优化方法进行评价。

6、控制系统参数优化设计中的目标函数一般可以分为两大类，（ ）目标函数和（ ）目标函数。

7、数学建模方法大致分为（ ）建模法、（ ）建模法和（）建模法。

8、在系统辨识中，（）是一种基本的参数估计方法。

9、在衡量作为随机变量的参数估计量的优劣时，通常基于（ ）、（ ）和（ ）三个要求。

二、判断题（每题1分，共10分）1、相邻两个离散时间点的间距h=t k+1－t k 称为计算步长或计算步距。

（ ）2、欧拉法是一种最简单的数值积分算法，由于其精度高，所以在实际中广泛使用。

（ ）3、多步法与单步法相比，要达到相同的精度，计算工作量要少得多。

（ ）4、采样控制系统是既有连续信号又有离散信号的混合系统，系统按采样周期T 重复工作，只有在采样时刻，数字控制器才有输出，完成一次控制作用。

（ ）5、为了克服梯度计算的困难，人们提出了一些不用计算梯度的优化方法，目前应用得较为广泛的是差分方程法。

（ ）6、在仿真寻优中，选择不同的参照对象会得到不同的目标函数。

（ ）7、模型与真实世界之间最重要的关系就是抽象和映射。

映射是建模的基础。

（ ）8、最小二乘法是一种经典的、有效的数据处理方法。

（ ）9、倒立摆系统是一种常见的运用反馈原理来控制一个开环不稳定系统的试验装置。

控制系统计算机辅助设计综合实验指导实验名称：连续与离散系统校正实验，系统可控性与可观性实验，系统的simulink仿真实验陈茜编实验人：苏建聪学号：200830810122班级：08电气工程及其自动化1班信息工程系实验任务书1. 有一个单位负反馈控制系统，如果控制对象的传递函数为设计要求：① 相角裕度≥45°；② 当系统的输入信号是单位斜坡信号时，稳态误差ess ≤0.04。

③ 要求绘制出校正后系统和未校正系统的Bode 图及其闭环系统的单位阶跃响应曲线，并进行对比。

2. 有一个单位负反馈控制系统，如果控制对象的传递函数为：试设计一个串联滞后校正装置。

设计要求：①相角裕度≥45°；② 当系统的输入信号是单位斜坡信号时，稳态误差ess ≤0.04。

③ 要求绘制出校正后系统和未校正系统的Bode 图及其闭环系统的单位阶跃响应曲线，并进行对比。

3. 有一个单位负反馈控制系统，如果控制对象的传递函数为 ()()4+=s s k s G p试设计一个串联超前滞后校正装置，设计要求： ①相角裕度≥45°；② 当系统的输入信号是单位斜坡信号时，稳态误差ess ≤0.04。

③ 要求绘制出校正后系统和未校正系统的Bode 图及其闭环系统的单位阶跃响应曲线，并进行对比。

4. 系统结构图如图所示，其中，采样周期Ts=0.01s ，被控对象()()110+=s s s G ，()s G h 为零阶保持器。

用W 变换法设计一超前校正装置D(z)，使系统相位裕度γ≥50°，校验设计后系统的性能指标。

5. 系统结构图如图所示，其中，采样周期Ts=0.01s ，被控对象1)s(0.2s k )(+=s G ο，()s G h 为零阶保持器。

用对数频率法设计D(z)，使系统开环增益k ≥30(1/s)，截止频率ωc ≥15(1/s),相位裕度γ≥50 °1使 s 11se -1(s)-Tsh T G +≈=，求出未校正系统的开环系统的开环传递函数(s)(s)G G (s)0s =G ,的传递函数模型参数。

3 0 1 0 X 2 3 0 X 2 u 6 6 1 0
解：1）求特征值法，输入命令
计算结果为 可见，矩阵 A 的特征值实部均为负，因此系统稳定。 2）采用李亚普诺夫第二法， 输入命令
计算结果
显然，P 阵的各阶主子式均为正定，系统稳定。 6-2 某单位负反馈系统的开环控制系统的传递函数为
试求该系统状态空间表达式的对角线标准形。 解：输入语句
计算结果
表明该系统状态空间表达式的对角线标准形为
6
3 0 0 7.762 0 2 0 X 9.798 u X 0 0 1 2.872
4-3 求出以下系统的传递函数
11
运行后，计算出
G C (s)
0.3162s 1 0.1044s 1 5.692 s 1 0.04888s 1
于是，校正后的系统开环传递函数为
GC ( s )G ( s )
0.033s 2 0.4206s 1 200 2 0.2782 s 5.741s 1 s (0.1s 1)(0.01s 1)
， 3-5
，
，
已知某系统的闭环传递函数 ( s ) 如下，试用 roots（）命令来判断系统的稳定性。
( s)
解：输入命令
3s 2 2s 5 s 5 2 s 4 4 s 3 5s 2 7 s 6
计算结果如下，系统不稳定
3-6
求复数矩阵 C
1 3i 5 i 7 3i 的转置 C1 与共轭转置 C2。 6 2i 3 2i 4 3i
《自动控制系统计算机仿真》
习题参考答案

长风破浪会有时，直挂云帆济沧海。

住在富人区的她吉林大学智慧树知到“电气工程及其自动化”《控制系统数字仿真》网课测试题答案（图片大小可自由调整）第1卷一.综合考核(共15题)1.在循环结构中跳出循环，执行循环后面代码的命令为()。

A、returnB、breakC、continueD、keyboard正确答案：B2.计算机仿真的发展方向有哪些()。

A、向模型更加准确的方向发展B、向虚拟现实技术C、向高技术智能化、一体化方向发展D、向更加广阔的时空发展正确答案：A,B,C,D3.在CAD命令输入方式中以下不可采用的方式有()。

A、点取命令图标B、在菜单栏点取命令C、用键盘直接输入D、利用数字键输入正确答案：D4.i=2; a=2i;b=2*i;c=2*sqrt（-1）;程序执行后;a, b, c的值分别是()。

A、a=4,b=4,c=2.0000iB、a=4,b=2.0000i,c=2.0000iC、a=2.0000i,b=4,c=2.0000iD、a=2.0000i,b=2.0000i,c=2.0000i 正确答案：C5.根据采样过程的特点，可以将采样分为以下几种类型()。

A、周期采样B、同步采样和非同步采样C、多速采样D、固定采样正确答案：A,B,C6.系统仿真大都采用计算机程序处理和数值计算，由于计算机的字长有限，不同档次的计算机其计算结果的有效值不一致，导致仿真过程出现舍入误差()。

A、错误B、正确正确答案：B7.在保证计算稳定性及计算精度的要求下，尽可能选较小的仿真步长()。

A、错误B、正确正确答案：A8.通常仿真时多采用四阶龙格库塔法，其原因就是这种计算公式的截断误差较小()。

A、错误B、正确正确答案：B9.微分方程能够反映系统内部各状态之间的相互关系，适用于多输入多输出系统。

传递函数是零极点形式和部分分式形式的基础()。

A、错误B、正确正确答案：A10.关于MATLAB语言中，变量的命名错误的是()。

控制系统仿真答案一．选择题二．名词解释及简答题1．系统的三个属性是什么？请解释其具体含义。

答：系统的三个属性：整体性、相关性、隶属性。

整体性：各部分(子系统)不能随意分割。

相关性：各部分(子系统) 以一定的规律或方式相联系，由此决定了其特有的性能。

隶属性：不能清楚的分出系统“内部”与“外部”，常常需要根据研究的问题来确定哪些属于系统的内部因素，哪些属于外部环境，其界限也是随不同的研究目的而变化，将这一特性称之为隶属性。

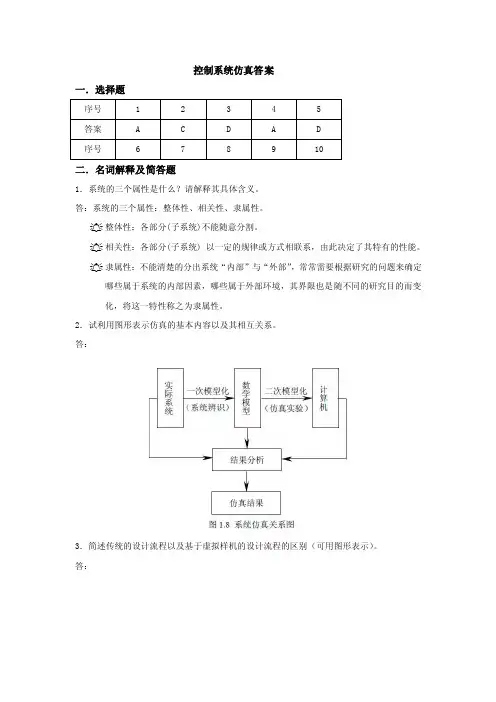
2．试利用图形表示仿真的基本内容以及其相互关系。

答：3．简述传统的设计流程以及基于虚拟样机的设计流程的区别（可用图形表示）。

答：三．判断题，正确的在括号内打“√”，错误的打“╳”，并改正错误结论重新阐述。

1．（√）为了限制所研究问题涉及的范围，一般用系统边界把被研究的系统与系统环境区分开来。

2．（╳）模型按数学模型的形式分为：物理仿真、数学仿真、数学－物理混合仿真或半实物仿真。

改1：按模型的性质分为：物理仿真、数学仿真、数学－物理混合仿真或半实物仿真。

改2：按数学模型的形式分为：连续系统仿真、离散事件系统仿真、离散—连续系统仿真。

3．（√）series函数可以将两个系统按串联方式连接，它即适合于连续时间系统，也适合于离散时间系统。

4．（√）S-函数为Simulink的“系统”函数，它是能够响应Simulink求解器命令的函数，采用非图形化的方法实现一个动态系统。

5．（╳）Matlab在执行运算符的优先级的时候，逻辑运算符“<”的优先级要高于矩阵乘法运算“*”的优先级。

改：Matlab在执行运算符的优先级的时候，逻辑运算符“<”的优先级要低于矩阵乘法运算“*”的优先级。

四、2、main(){float x,money;Scanf(“%f/n”,&x);If(x<50) then money=2.5*xElse if(x>=50 and x<100)Else if (x>=100)Then money=2.5*x*(1-0.2) ;Printf(“money=%f”,money);}五．综合题1．编程实现以下图形绘制。

一、数值计算，编程完成以下各题〔共20分，每题5分〕1、脉冲宽度为d ，周期为T 的矩形脉冲的傅里叶级数如下式描述：)2cos(/)/sin(21[)(1τπππτn T d n T d n T d f n ∑∞=+=当150=n ，41=T d ，2/12/1<<-τ，绘制出函数)(τf 的图形。

解： syms n t;f=((sin(n*pi/4))/(n*pi/4))*cos(2*pi*n*t); s=symsum(f,n,1,150); y=(1+2*s)/4; x=-0.5:0.01:0.5; Y=subs(y,'t',x); plot(x,Y)2、画出函数5505.025.55.15.1cos 5)5(sin )(2x x x x ex x f x +++-=在区间[3,5]的图形，求出该函数在区间[3, 5]中的最小值点m in x 和函数的最小值m in f .解：程序如下 x=3:0.05:5;y=(sin(5*x).^2).*exp(0.05*x.^2)-5*(x.^5).*cos(1.5*x)+1.5*abs(x+5.5)+x.^2.5; mix_where=find(y==min(y)); xmin=x(mix_where); hold on; plot(x,y);plot(xmin,min(y),'go','linewidth',5);str=strcat('(',num2str(xmin),',',num2str(min(y)),')'); text(xmin,min(y),str); Xlabel('x')Ylabel('f(x)')经过运行后得到的图像截图如下：运行后的最小值点m in x =4.6，m in f = -8337.86253、画出函数xe x xf x 5.2cos )(3.02-⋅=-在[1，3]区间的图形，并用编程求解该非线性方程0)(=x f 的一个根，设初始点为20=x .解： x=1:0.02:3; x0=2;y=@(x)(cos(x).^2).*exp(-0.3*x)-2.5*abs(x); fplot(y,[1,3]); Xlabel('x') Ylabel('f(x)')X1=fzero('(cos(x).^2).*exp(-0.3*x)-2.5*abs(x)',x0)运行后求得该方程的一个根为z=0.3256。

一、单选题1、仿真的()很关键，不能太大也不能太小，太大会丢信息，太小会增加计算机仿真的复杂程度.A.采样周期B.时间C.仿真步数D.计算步距正确答案：D2、仿真时间要求涵盖被仿真对象的全部（）过程。

A.扰动B.稳定C.动态D.静态正确答案：C3、衡量控制系统的三个品质指标（）、准确性、快速性。

A.动态性能B.稳态性能C.快速性能D.稳定性正确答案：D4、目标函数的设计过程中除了体现控制品质的要求还需要考虑（）的输出。

A.控制器B.被控对象C.检测变送器D.执行机构正确答案：A5、目标函数中对控制品质的要求一般是通过（）的平方来体现的。

A.测量值B.期望值C.被调量D.偏差正确答案：D6、（）随着搜索维数的增加，其计算量呈指数增加，因此适合于低维空间。

A.遗传算法B.粒子群C.穷举法D.最小二乘法正确答案：C7、（）属于群体智能，思想来源于蚂蚁找食物的过程。

A.粒子群算法B.模糊算法C.蚁群算法D.遗传算法正确答案：C8、遗传算法的第一步是（），种群规模和种群中个体的多样性尤其重要。

A.确定遗传因子B.确定遗传规则C.确定种群个数D.选择初始种群正确答案：D9、()是指给输入扰动加载单位阶跃输入，得到的输出曲线的形式。

A.脉冲曲线B.飞升曲线C.斜波曲线D.加速度曲线正确答案：B10、最小二乘方法适用于对()系统进行辨识。

A.单入单出B.多输入多输出C.单入多输出D.多输入单出正确答案：A11、（）的设计目的在于克服单一的扰动。

A.前馈B.回路C.反馈D.前向通道正确答案：A12、史密斯预估控制特别适合于具有（）特性的被控对象。

A.慢速B.大纯迟延C.稳定D.快速正确答案：B13、大纯迟延特性的被控对象的传递函数中τ表达的是（）。

A.积分时间B.比例系数C.纯迟延时间D.微分时间正确答案：C14、（）是当被控对象的输入发生变化时被控对象的输出要经过τ时间段内才能产生变化。

A.调节时间B.峰值时间C.微分时间D.纯迟延时间正确答案：D15、盲人爬山的路径优化需要解决两个问题。

第一章习题1-1什么是仿真？它所遵循的基本原则是什么？答：仿真是建立在控制理论，相似理论，信息处理技术和计算技术等理论基础之上的，以计算机和其他专用物理效应设备为工具，利用系统模型对真实或假想的系统进行试验，并借助专家经验知识，统计数据和信息资料对试验结果进行分析和研究，进而做出决策的一门综合性的试验性科学。

它所遵循的基本原则是相似原理。

1-2在系统分析与设计中仿真法与解析法有何区别？各有什么特点？答：解析法就是运用已掌握的理论知识对控制系统进行理论上的分析，计算。

它是一种纯物理意义上的实验分析方法，在对系统的认识过程中具有普遍意义。

由于受到理论的不完善性以及对事物认识的不全面性等因素的影响，其应用往往有很大局限性。

仿真法基于相似原理，是在模型上所进行的系统性能分析与研究的实验方法。

1-3数字仿真包括那几个要素？其关系如何？答: 通常情况下，数字仿真实验包括三个基本要素，即实际系统，数学模型与计算机。

由图可见，将实际系统抽象为数学模型，称之为一次模型化，它还涉及到系统辨识技术问题，统称为建模问题；将数学模型转化为可在计算机上运行的仿真模型，称之为二次模型化，这涉及到仿真技术问题，统称为仿真实验。

1-4为什么说模拟仿真较数字仿真精度低？其优点如何？。

答：由于受到电路元件精度的制约和容易受到外界的干扰，模拟仿真较数字仿真精度低但模拟仿真具有如下优点：（1）描述连续的物理系统的动态过程比较自然和逼真。

（2）仿真速度极快，失真小，结果可信度高。

（3）能快速求解微分方程。

模拟计算机运行时各运算器是并行工作的，模拟机的解题速度与原系统的复杂程度无关。

（4）可以灵活设置仿真试验的时间标尺，既可以进行实时仿真，也可以进行非实时仿真。

（5）易于和实物相连。

1-5什么是CAD技术？控制系统CAD可解决那些问题？答：CAD技术，即计算机辅助设计（Computer Aided Design）,是将计算机高速而精确的计算能力，大容量存储和数据的能力与设计者的综合分析，逻辑判断以及创造性思维结合起来，用以快速设计进程，缩短设计周期，提高设计质量的技术。

控制系统数字仿真题库一、填空题1. 定义一个系统时，首先要确定系统的边界；边界确定了系统的范围，边界以外对系统的作用称为系统的输入，系统对边界以为环境的作用称为系统的输出。

2．系统的三大要素为：实体、属性和活动。

3．人们描述系统的常见术语为：实体、属性、事件和活动。

4．人们经常把系统分成四类，它们分别为：连续系统、离散系统、采样数据系统和离散-连续系统。

5、根据系统的属性可以将系统分成两大类：工程系统和非工程系统。

6．根据描述方法不同，离散系统可以分为：离散时间系统和离散事件系统。

7. 系统是指相互联系又相互作用的实体的有机组合。

8．根据模型的表达形式，模型可以分为物理模型和数学模型二大类，其中数学模型根据数学表达形式的不同可分为二种，分别为：静态模型和动态模型。

9、采用一定比例按照真实系统的样子制作的模型称为物理模型，用数学表达式来描述系统内在规律的模型称为数学模型。

10．静态模型的数学表达形式一般是代数方程和逻辑关系表达式等，而动态模型的数学表达形式一般是微分方程和差分方程。

11．系统模型根据描述变量的函数关系可以分类为线性模型和非线性模型。

12 仿真模型的校核是指检验数字仿真模型和数学模型是否一致。

13．仿真模型的验证是指检验数字仿真模型和实际系统是否一致。

14．计算机仿真的三个要素为：系统、模型与计算机。

15．系统仿真的三个基本活动是系统建模、仿真建模和仿真试验。

16．系统仿真根据模型种类的不同可分为：物理仿真、数学仿真和数学-物理混合仿真。

17．根据仿真应用目的的不同，人们经常把计算机仿真应用分为四类，分别为：系统分析、系统设计、理论验证和人员训练。

18．计算机仿真是指将模型在计算机上进行实验的过程。

19. 仿真依据的基本原则是:相似原理。

20. 连续系统仿真中常见的一对矛盾为计算速度和计算精度。

21．保持器是一种将离散时间信号恢复成连续信号的装置。

22．零阶保持器能较好地再现阶跃信号。

解：（1）
1n＝3，根轨迹有3条分支,且均趋于无穷远处；
2实轴上的根轨迹：[-50,0],( 00];
3渐进线： ， ；
4分离点：
求解得： ， （舍去）；
作出根轨迹如图所示：
（2）临界开环增益 为根轨迹与虚轴交点对应的开环增益。
令 ，代入 ，并令其实部、虚部分别为零，即
，
解得： （舍去）
（3）系统处于临界阻尼比 ，相应闭环根位于分离点处，即要求分离点d对应的K值。将s＝d＝-21.3代入幅值条件：
（2）系统的脉冲响应
2-10试简化图2-9中的系统结构图，并求传递函数C(s)/R(s )和C(s)/N(s)。
可求出：
令R（s）＝0，简化结构图如图所示：
所以：
（b）令N（s）＝0，简化结构图如下图所示：
所以：
令R（s）＝0，简化结构图如下图所示
2-12 试用梅逊增益公式求图2-8中各系统信号流图的传递函 数C(s)/R(s)。
其中，T１、Ｔ２和K２为正常数。若要求r(t)=1+ t时，c?
分析：先求出系统的误差传递函数，再利用稳态误差计算公式，根据题目要求确定参数。
解：对方程组进行拉普拉斯变换，可得
按照上面三个公式画出系统的结构图如下：
定义误差函数
所以
令 ，可得 ，因此，当 时，满足条件。
可见，当 第一次为0时， ，所以
根据调节时间 的定义： ，即
，得
所以：
3-5设图3-3是简化的飞行控制系统结构图，试选择参数K１和Kt，使系统ωｎ＝６、ζ＝１。
分析：求出系统传递函数，如果可化为典型二阶环节形式，则可与标准二阶环节相对照，从而确定相应参数。
解 对结构图进行化简如图所示。

自动控制系统习题及答案自动控制系统习题及答案自动控制系统是现代工程领域中的重要学科，它涉及到机械、电子、计算机等多个学科的知识。

掌握自动控制系统的理论和实践对于工程师来说至关重要。

为了帮助学习者更好地理解和应用自动控制系统的知识，下面将介绍一些常见的习题及其答案。

1. 什么是自动控制系统？自动控制系统是一种能够自动地对给定的输入信号进行处理，并产生相应的输出信号以实现特定控制目标的系统。

它由传感器、执行器、控制器和反馈回路等组成。

2. 什么是负反馈控制？负反馈控制是一种常见的控制方式，它通过将输出信号与参考信号进行比较，并根据比较结果调节系统的输入信号，使输出信号逼近参考信号。

这种控制方式能够提高系统的稳定性和鲁棒性。

3. 什么是传递函数？传递函数是描述线性时不变系统输入与输出之间关系的数学函数。

它通常用Laplace 变换表示，可以通过对系统的微分方程进行变换得到。

4. 如何计算传递函数？传递函数可以通过系统的微分方程或状态空间方程进行推导和计算。

对于线性时不变系统，可以使用 Laplace 变换将微分方程转换为代数方程，然后求解得到传递函数。

5. 什么是稳定性？稳定性是指系统在受到扰动时能够保持有限的响应，而不会发生不可控的振荡或发散。

稳定性是自动控制系统设计中一个重要的考虑因素。

6. 如何判断系统的稳定性？系统的稳定性可以通过判断系统的极点位置来确定。

对于连续时间系统，如果所有的极点实部都小于零，则系统是稳定的；对于离散时间系统，如果所有的极点模长都小于1，则系统是稳定的。

7. 什么是根轨迹？根轨迹是描述系统极点随控制参数变化的轨迹。

通过绘制根轨迹可以分析系统的稳定性、动态响应和性能。

8. 什么是频率响应？频率响应是描述系统对不同频率输入信号的响应特性。

通过频率响应可以分析系统的幅频特性、相频特性和相位裕度等。

9. 如何设计 PID 控制器？PID 控制器是一种常用的控制器，它由比例、积分和微分三个部分组成。

第二章2.1x=[15 22 33 94 85 77 60]x(6)x([1 3 5])x(4:end)x(find(x>70))2.2T=[1 -2 3 -4 2 -3] ;n=length(T);TT=T';for k=n-1:-1:0B(:,n-k)=TT.^k;endBtest=vander(T)2.3A=zeros(2,5);A(:)=-4:5L=abs(A)>3islogical(L)X=A(L)2.4A=[4,15,-45,10,6;56,0,17,-45,0]find(A>=10&A<=20)2.5p1=conv([1,0,2],conv([1,4],[1,1]));p2=[1 0 1 1];[q,r]=deconv(p1,p2);cq='商多项式为'; cr='余多项式为';disp([cq,poly2str(q,'s')]),disp([cr,poly2str(r,'s')])2.6A=[11 12 13;14 15 16;17 18 19];PA=poly(A)PPA=poly2str(PA,'s')第三章3.1n=(-10:10)';y=abs(n);plot(n,y,'r.','MarkerSize',20)axis equalgrid onxlabel('n')3.2x=0:pi/100:2*pi;y=2*exp(-0.5*x).*sin(2*pi*x);plot(x,y),grid on;3.3t=0:pi/50:2*pi;x=8*cos(t);y=4*sqrt(2)*sin(t);z=-4*sqrt(2)*sin(t);plot3(x,y,z,'p');title('Line in 3-D Space');text(0,0,0,'origin');xlabel('X'),ylable('Y'),zlable('Z');grid;3.4theta=0:0.01:2*pi;rho=sin(2*theta).*cos(2*theta); polar(theta,rho,'k');3.5[x,y,z]=sphere(20);z1=z;z1(:,1:4)=NaN;c1=ones(size(z1));surf(3*x,3*y,3*z1,c1);hold onz2=z;c2=2*ones(size(z2));c2(:,1:4)=3*ones(size(c2(:,1:4))); surf(1.5*x,1.5*y,1.5*z2,c2); colormap([0,1,0;0.5,0,0;1,0,0]);grid onhold off第四章4.1for m=100:999m1=fix(m/100);m2=rem(fix(m/10),10);m3=rem(m,10);if m==m1*m1*m1+m2*m2*m2+m3*m3*m3 disp(m)endend4.2function[s,p]=fcircle(r)s=pi*r*r;p=2*pi*r;4.3y=0;n=100;for i=1:ny=y+1/i/i;endy4.4s=0;for i=1:5s=s+factor(i);ends4.5sum=0;i=1;while sum<2000sum=sum+i;i=i+1;end;n=i-24.6function k=jcsum(n)k=0;for i=0:nk=k+2^i;end或function k=jcsum1(n)k=0;i=0;while i<=nk=k+2^i;i=i+1;end第五章5.1A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];b=[13,-9,6,0]';x=A\b5.2[U,fmin]=fminsearch('fxyz',[0.5,0.5,0.5])function f=fxyz(u)x=u(1);y=u(2);z=u(3);f=x+y.^2./x/4+z.^2./y+2./z;5.3X=linspace(0,2*pi,50);Y=sin(X);P=polyfit(X,Y,3)AX=linspace(0,2*pi,50);Y=sin(X);Y1=polyval(P,X)plot(X,Y,':O',X,Y1,'-*')5.4x=0:2.5:10;h=[0:30:60]';T=[95,14,0,0,0;88,48,32,12,6;67,64,54,48,41];xi=[0:0.5:10];hi=[0:10:60]';temps=interp2(x,h,T,xi,hi,'cubic');mesh(xi,hi,temps);第六章6.1syms xy=finverse(1/tan(x))6.2syms x yf=1/(1+x^2); g=sin(y);fg=compose(f,g)6.3syms xg=(exp(x)+x*sin(x))^(1/2);dg=diff(g)6.4F=int(int('x*exp(-x*y)','x'),'y')6.5syms xF=ztrans(x*exp(-x*10))6.6a=[0 1;-2 -3];syms sinv(s*eye(2)-a);6.7f=solve('a*x^2+b*x+c')6.8f=solve('x+y+z=1','x-y+z=2','2*x-y-z=1')6.9y=dsolve('D2y+2*Dy+2*y=0','y(0)=1','Dy(0)=0') ezplot(y),grid on6.10a=maple('simplify(sin(x)^2+cos(x)^2);')6.11f=maple('laplace(exp(-3*t)*sin(t),t,s);')6.12syms t xF=sin(x*t+2*t);L=laplace(F)第七章7.17.27.37.47.57.67.7第八章8.1（1）num=[5]; den=[1,2,2];sys=tf(num,den)（2）s = tf('s');H = [5/(s^2+2*s+2) ];H.inputdelay =2（3）h=tf([0.5,0],[1,-0.5,0.5],0.1)8.2num=2*[1,0.5];den=[1,0.2,1.01];sys=tf(num,den)[z,p,k]=tf2zp(num,den);zpk(z,p,k)[A,B,C,D]=tf2ss(num,den);ss(A,B,C,D)8.3num=[1,5]; den=[1,6,5,1]; ts=0.1;sysc=tf(num,den);sysd=c2d(sysc,ts,'tustin')8.4r1=1;r2=2;c1=3;c2=4;[A,B,C,D]=linmod('x84');[num,den]=ss2tf(A,B,C,D);sys=tf(num,den)8.5A=[1,1,0;0,1,0;0,0,2];B=[0,0;1,0;0,-2];n=size(A)Tc=ctrb(A,B);if n==rank(Tc)disp('系统完全能控');elsedisp('系统不完全能控');end第九章9.1num=[2,5,1];den=[1,2,3];bode(num,den);grid on ;figure;nyquist(num,den);9.2num=5*[1,5,6];den=[1,6,10,8];step(num,den);grid on ;figure;impulse(num,den);grid on ;9.3kosi=0.7;wn=6;num=wn^2;den=[1,2*kosi*wn,wn^2];step(num,den);grid on ;figure;impulse(num,den);grid on ;9.4den=[1,2,8,12,20,16,16];[rtab,info]=routh(den)a=rtab(:,1)if all(a>0)disp('系统是稳定的');elsedisp('系统是不稳定的');end9.5num=7*[1,5];den=conv([1,0,0],conv([1,10],[1,1]));[gm,pm,wg,wc]=margin(num,den)第十章10.1ng0=[1]; dg0=10000*[1 0 -1.1772];g0=tf(ng0,dg0); %满足开环增益的为校正系统的传递函数s=kw2s(0.7,0.5) %期望的闭环主导极点ngc=rg_lead(ng0,dg0,s);gc=tf(ngc,1)g0c=tf(g0*gc);rlocus(g0,g0c);b1=feedback(g0,1); %未校正系统的闭环传递函数b2=feedback(g0c,1); %校正后系统的闭环传递函数figure,step(b1,'r--',b2,'b'); grid on %绘制校正前后系统的单位阶跃响应曲线10.2KK=20;s1=-2+i*sqrt(6);a=1ng0=[10];dg0=conv([1,0],[1,4]);g0=tf(ng0,dg0);[ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a);gc=tf(ngc,dgc)g0c=tf(KK*g0*gc);b1=feedback(k*g0,1);b2=feedback(g0c,1);step(b1,'r--',b2,'b');grid on10.3KK=128;s1=-2+i*2*sqrt(3);a=2ng0=[10];dg0=conv([1,0],conv([1,2],[1,8]));g0=tf(ng0,dg0);[ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a);gc=tf(ngc,dgc)g0c=tf(KK*g0*gc);rlocus(g0,g0c);b1=feedback(k*g0,1);b2=feedback(g0c,1);figure,step(b1,'r--',b2,'b');grid on10.4ng0=[1];dg0=conv([1,0,0],[1,5]);g0=tf(ng0,dg0);w=logspace(-3,3);KK=1;Pm=50;[ngc,dgc]=lead4(ng0,dg0,KK,Pm,w);gc=tf(ngc,dgc);g0c=tf(KK*g0*gc);bode(KK*g0,w);hold on,bode(g0c,w);grid on,hold off [gm,pm,wcg,wcp]=margin(g0c)Kg=20*log10(gm)g1=feedback(g0c,1);bode(g1),grid on,[mag,phase,w]=bode(g1);a=find(mag<=0.707*mag(1));wb=w(a(1))max(mag)b=find(mag==max(mag))wr=w(b)10.5KK=40; Pm=50;ng0= KK *[1]; dg0=conv([1,0],conv([1,1],[1,4]));g0=tf(ng0,dg0) ;w=logspace(-2,4);[ngc,dgc]=fg_lead_pm(ng0,dg0,Pm,w)gc=tf(ngc,dgc),g0c=tf(g0*gc);b1=feedback(g0,1); b2=feedback(g0c,1);step(b1,'r--', b2,'b'); grid onfigure, bode(g0,'r--',g0c,'b',w), grid on,[gm,pm,wcg,wcp]=margin(g0c), Km=20*log10(gm)10.6KK=200; bp=0.3; ts=0.7; delta=0.05;ng0=[1];dg0=conv([1,0],conv([0.1,1],conv([0.02 1],conv([0.01,1],[0.005 1]))));g0=tf(ng0,dg0);w=logspace(-4,3);t=[0:0.1:3];[mag,phase]=bode(KK*g0,w);[gm0,pm0,wg0,wc0]=margin(mag,phase,w),gm0=20*log10(gm0)%gm0 = -15.6769%2、确定期望的开环传递函数mr=0.6+2.5*bp;wc=ceil((2+1.5*(mr-1)+2.5*(mr-1)^2)*pi/ts), h=(mr+1)/(mr-1)w1=2*wc/(h+1), w2=h*w1w1=wc/10; w2=25;ng1=[1/w1,1]; dg1=conv([1/w2,1],conv([1,0],[1,0]));g1=tf(ng1,dg1);g=polyval(ng1,j*wc)/polyval(dg1,j*wc); K=abs(1/g); %剪切频率处幅值为1，求K值g1=tf(K*g1)%3、确定反馈环节传递函数h=tf(dg1,ng1); Kh=1/K;h=tf(Kh*h) %期望频率特性的倒特性%4、验算性能指标g2=feedback(KK*g0,h); %校正后，系统的开环传递函数b1=feedback(KK*g0,1); b2=feedback(g2,1);bode(KK*g0,'r--',g2,'b',h,'g',w);grid onfigure,step(b1, 'r--',b2, 'b',t); grid on,[pos,tr,ts,tp]=stepchar(b2,delta)。

控制系统仿真本科中国地质大学开卷参考资料题库及答案
控制系统仿真(专升本)阶段性作业1
总分：100分得分：0分
一、单选题
1. 下列哪个选项不属于Matlab的优点_______。

(4分)
(A) Matlab是一种演算式语言
(B) Matlab程序的执行速度快
(C) Matlab具有强大的矩阵运算能力
(D) Matlab具有功能强大的工具箱
参考答案：A
2. 以下变量名无效的是_______。

(4分)
(A) aa
(B) A_a
(C) 2d
(D) Mm_
参考答案：C
3. 以下命令表示清除Matlab命令窗口内容的是_______。

(4分)
(A) clc
(B) clear all
(C) close all
(D) clear
参考答案：A
4. 关于SIMULINK的说法错误的是_______。

(4分)
(A) SIMULINK的缺省仿真时间长度为10秒
(B) SIMULINK实现了可视化的动态仿真，可以与MATLAB进行数据传递
(C) SIMULINK默认的数值运算方法是ode45
(D) SIMULINK模型的扩展名为mld
参考答案：A
二、多选题
1. 控制系统的仿真涉及到以下哪些学科_______。

(4分)
(A) 控制理论
(B) 计算数学
(C) 计算机技术
(D) 综合性科学
参考答案：A,B,C
2. 计算机数字仿真包括哪些要素_______。

(4分)
(A) 系统。

[Z,P,K]=ss2zp(A,B,C,D);(4%)
[R,P,H]=residue(A,B,C,D);(5%)
计算机仿真习题
一、填空题
1.Matlab的程序文件和simulink的模型文件的扩展名分别是_.m_____、_.mdl___。
2.四阶龙格-库塔法的局部截断误差为___Oh(5)____________。（注：步长用h表示）
3.已知A=[1 2 1;2 3 0;1 0 1];B=[1 2 0;3 5 0;0 1 4],写出下列指令运行的结果：
用 ，
答：
5.设系统的微分方程为 ，y为系统输出量，u为系统输入量，试导出系统的标准状态方程。
答：
令 , (4%)
则有 (8%)
(10%)
三、简答题
1.在连续系统的数字仿真中，有哪几种常用的数值积分法？分别有哪些特点
答：欧拉法和龙格-库塔法.
欧拉法：是显示一步算法，可以自启动，但是精度较低
龙格-库塔法：也是显示一步算法，也可以自启动，四阶龙格-库塔法的精度较高，能满足大多数工程的精度要求。
[A,B,C,D]=tf2ss(num,den); (3%)
[Z,P,K]=tf2zp(num,den); (4%)
[R,P,H]=residue(num,den);(5%)
（2）(5%)
2. , , ,D=0
sys=ss(A,B,C,D);(2%)
[num,den]=ss2tf(A,B,C,D);(3%)
6.计算机仿真的三要素为系统、模型与计算机。
7.matlab中最基本的绘图函数是___plot__________。
二、综合计算题
1.系统结构如下图所示，写出该系统的连接矩阵W和W0.并写出连接矩阵非零元素阵WIJ，其中Gi表示传递函数， 表示反馈系数

2-2.用 matlab 语言求下列系统的状态方程、传递函数、零极点增益、和部分分 式形式的模型参数，并分别写出其相应的数学模型表达式：
(1)
G（s）=
s3 + 7s2 + 24s + 24 s4 +10s3 + 35s2 + 50s + 24
2.25 -5 -1.25 -0.5 4
(2)
.
X
=
（3）部分分式形式的模型参数：编写程序>> A=[2.25 -5 -1.25 -0.5 2.25 -4.25 -1.25 -0.25 0.25 -0.5 -1.25 -1 1.25 -1.75 -0.25 -0.75]；
>> B=[4 2 2 0]'; >> C=[0 2 0 2]; >> D=[0]; >> [num den]=ss2tf(A,B,C,D) >> [R,P,H]=residue(num,den)
指令与控制台指令与控制台指令与控制台指令与控制台角度读角度读角度读角度读出装置出装置出装置出装置转台电子转台电子转台电子转台电子驱动器驱动器驱动器驱动器陀螺陀螺陀螺陀螺力矩器力矩器力矩器力矩器星敏感器星敏感器星敏感器星敏感器地球模拟器地球模拟器地球模拟器地球模拟器指令译码器指令译码器指令译码器指令译码器星光模拟器星光模拟器星光模拟器星光模拟器姿态控制系统电子装置姿态控制系统电子装置姿态控制系统电子装置姿态控制系统电子装置射频敏感器射频敏感器射频敏感器射频敏感器太阳敏感器太阳敏感器太阳敏感器太阳敏感器混合计算机混合计算机混合计算机混合计算机太阳模拟器太阳模拟器太阳模拟器太阳模拟器数字部分数字部分数字部分数字部分接口接口接口接口卫星动力学卫星动力学卫星动力学卫星动力学三轴机械转台三轴机械转台三轴机械转台三轴机械转台模拟部分模拟部分模拟部分模拟部分地球敏感器地球敏感器地球敏感器地球敏感器8888卫星姿态控制仿真试验系统卫星姿态控制仿真试验系统卫星姿态控制仿真试验系统卫星姿态控制仿真试验系统第二章习题第二章习题第二章习题第二章习题21212121思考题思考题思考题思考题