北师大版数学高二必修5第三章4.2、4.3简单线性规划及其应用作业

3.4.2简单的线性规划一、教学目标：1.了解线性规划的意义及线性约束条件、线性目标函数、可行解、可行域、最优解等概念；2.能根据条件建立线性目标函数；3.了解线性规划问题的图解法，并会用图解法求线性目标函数的最大值、最小值.二、教学重、难点：线性规划问题的图解法；寻求线性规划问题的最优解.三、教学过程：（一）复习练习：1．画出下列不等式表示的平面区域：（1）()(233)0x y x y -+-<； （2）|341|5x y +-<．（二）新课讲解：1．引例：设2z x y =+，式中变量,x y 满足条件4335251x y x y x -≤-⎧⎪+≤⎨⎪≥⎩，求z 的最大值和最小值.问题：能否用不等式的知识来解决以上问题？（否）那么，能不能用二元一次不等式表示的平面区域来求解呢？怎样求解？由题意，变量,x y 所满足的每个不等式都表示一个平面区域，不等式组则表示这些平面区域的公共区域。

由图知，原点(0,0)不在公共区域内，当0,0x y ==时，20z x y =+=，即点(0,0)在直线0l ：20x y +=上，作一组平行于0l 的直线l ：2x y t +=，t R ∈，可知：当l 在0l 的右上方时，直线l 上的点(,)x y满足20x y +>，即0t >，而且，直线l 往右平移时，t 随之增大。

由图象可知，当直线l 经过点(5,2)A 时，对应的t 最大，当直线l 经过点(1,1)B 时，对应的t 最小，所以，max 25212z =⨯+=，min 2113z =⨯+=．2．有关概念在上述引例中，不等式组是一组对变量,x y 的约束条件，这组约束条件都是关于,x y 的一次不等式，所以又称为线性约束条件。

2z x y =+是要求最大值或最小值所涉及的变量,x y 的解析式，叫目标函数。

又由于2z x y =+是,x y 的一次解析式，所以又叫线性目标函数.一般地，求线性目标函数在线性约束条件下的最大值或最小值的问题，统称为线性规划问题。

4.3简单线性规划的应用一、非标准1.有5辆6吨的汽车,4辆4吨的汽车,需x辆6吨汽车y辆4吨汽车,要运送最多的货物,完成这项运输任务的线性目标函数为()A.z=6x+4yB.z=5x+4yC.z=x+yD.z=4x+5y答案:A2.已知点(x,y)构成的平面区域如图阴影部分所示,z=mx+y(m为常数)在平面区域内取得最大值的最优解有无数多个,则m的值为()A.-B.C.D.解析:观察平面区域可知直线y=-mx+z与直线AC重合,则-m=k AC==-,解得m=.答案:B3.在“家电下乡”活动中,某厂要将100台洗衣机运往邻近的乡镇,现有4辆甲型货车和8辆乙型货车可供使用,每辆甲型货车运输费用400元,可装洗衣机20台;每辆乙型货车运输费用300元,可装洗衣机10台,若每辆车至少运一次,则该厂所花的最少运输费用为()A.2 000元B.2 200元C.2 400元D.2 800元解析:设需甲型货车x辆,乙型货车y辆,由题意知,作出其可行域如图,描出阴影内部整点及部分边界整点.可知目标函数z=400x+300y,在点A处取最小值z=400×4+300×2=2 200(元).答案:B4.如图,目标函数z=ax-y的可行域为四边形OACB(含边界),若C是该目标函数z=ax-y的最优解,则a的取值范围是()A. B.C. D.解析:最优解为C点,则目标函数表示的直线斜率在直线BC与AC的斜率之间.因为k BC=-,k AC=-,所以a∈.答案:B5.某公司招收男职员x名,女职员y名,x和y需满足约束条件则z=10x+10y 的最大值是()A.80B.85C.90D.95解析:先画出满足约束条件的可行域,如图阴影部分所示.由解得但x∈N,y∈N,结合图知当x=5,y=4时,z max=90,选C.答案:C6.若直线y=2x上存在点(x,y)满足约束条件则实数m的最大值为. 解析:由约束条件作出其可行域如图:由图可知当直线x=m过直线y=2x与x+y-3=0的交点(1,2)时m取得最大值,此时x=m=1. 答案:17.某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元.现该公司至少要生产A类产品50件,B类产品140件,则所需租赁费最少为元.解析:设甲种设备需要生产x天,乙种设备需要生产y天,此时该公司所需租赁费为z元, 则z=200x+300y.又因为即画出该不等式组表示的平面区域,如图阴影部分所示.解即点A(4,5).由z=200x+300y,得直线y=-x+过点A(4,5)时,z=200x+300y取得最小值,为2 300元.答案:2 3008.设不等式组表示的平面区域为D.若指数函数y=a x的图像上存在区域D上的点,则a的取值范围是.解析:画出可行域如图阴影部分,易知a∈(0,1)时不合题意,故a>1.两直线的交点为A(2,9).由图像可知,当y=a x通过该交点A时,a取最大值,∴f(2)=a2=9,∴a=3.故a∈(1,3].答案:(1,3]9.某养鸡场有1万只鸡,用动物饲料和谷物饲料混合喂养.每天每只鸡平均吃混合饲料0.5 kg,其中动物饲料不能少于谷物饲料的.动物饲料每千克0.9元,谷物饲料每千克0.28元,饲料公司每周仅保证供应谷物饲料50 000 kg,问饲料怎样混合,才使成本最低?解:设每周需用谷物饲料x kg,动物饲料y kg,每周总的饲料费用为z元,那么而z=0.28x+0.9y,如图,作出不等式组所表示的平面区域,即可行域.作一组平行直线0.28x+0.9y=t.其中经过可行域内的点A时,z最小,又直线x+y=35 000和直线y=x的交点A.即x=,y=时,饲料费用最低.答:谷物饲料和动物饲料应按5∶1的比例混合,此时成本最低.10.要将两种大小不同的钢板截成A,B,C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:钢板类型A规格B规格C规格规格类型第一种钢板 2 1 1第二种钢板 1 2 3今需要A,B,C三种规格的成品分别为15,18,27块,问各截这两种钢板多少张可得所需的三种规格成品,且使所用钢板张数最少?解:设需截第一种钢板x张,第二种钢板y张,可得且x,y都是整数,求目标函数z=x+y取最小值时的x,y.作可行域如图所示,平移直线z=x+y可知直线经过点,此时x+y=,但都不是整数,所以可行域内的点不是最优解.首先在可行域内打网格,其次描出A附近的所有整点,接着平移直线l:x+y=0,会发现当移至B(3,9),C(4,8)时,即z取得最小值12.故本题有两种截法:第一种截法是截第一种钢板3张、第二种钢板9张;第二种截法是截第一种钢板4张、第二种钢板8张.两种方法最少要截两种钢板共12张.答:截第一种钢板3张、第二种钢板9张,或截第一种钢板4张、第二种钢板8张时,所用钢板张数最少.。

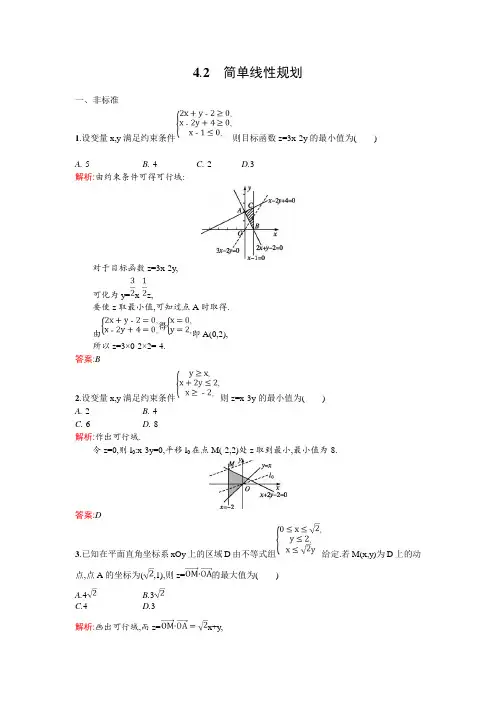
4.2简单线性规划一、非标准1.设变量x,y满足约束条件则目标函数z=3x-2y的最小值为()A.-5B.-4C.-2D.3解析:由约束条件可得可行域:对于目标函数z=3x-2y,可化为y=x-z,要使z取最小值,可知过点A时取得.由即A(0,2),所以z=3×0-2×2=-4.答案:B2.设变量x,y满足约束条件则z=x-3y的最小值为()A.-2B.-4C.-6D.-8解析:作出可行域.令z=0,则l0:x-3y=0,平移l0在点M(-2,2)处z取到最小,最小值为-8.答案:D3.已知在平面直角坐标系xOy上的区域D由不等式组给定.若M(x,y)为D上的动点,点A的坐标为(,1),则z=的最大值为()A.4B.3C.4D.3解析:画出可行域,而z=x+y,∴y=-x+z.令l0:y=-x,将l0平移到过点(,2)时,截距z有最大值,故z max=+2=4.答案:C4.已知x,y满足则点P(x,y)到直线x+y=-2的距离的最小值为()A. B.2C. D.解析:不等式组所表示的可行域如图阴影部分.其中点P(1,1)到直线的距离最短,其最小值为=2,故选B.答案:B5.若点(x,y)位于曲线y=|x-1|与y=2所围成的封闭区域,则2x-y的最小值为.解析:由y=|x-1|=及y=2画出可行域如图阴影部分.令2x-y=z,则y=2x-z,画直线l0:y=2x并平移到过点A(-1,2)的直线l,此时-z最大,即z最小=2×(-1)-2=-4.答案:-46.若变量x,y满足约束条件则z=x+2y的最小值为.解析:根据得可行域如图,根据z=x+2y得y=-,平移直线y=-,在M点z取得最小值.由此时z min=4+2×(-5)=-6.答案:-67.若实数x,y满足则z=3x+2y的最小值为.解析:上述不等式组所表示的可行域如图阴影部分.令t=x+2y,则当直线y=-x+t经过原点O(0,0)时,t取最小值,也即t有最小值为0,则z=3x+2y有最小值为30=1.答案:18.如果实数x,y满足不等式组则(x+2)2+(y+1)2的最小值为.解析:画出不等式组表示的平面区域,如图阴影部分.表示可行域内的点D(x,y)与定点M(-2,-1)间的距离.显然当点P在点A(1,2)时|PM|最小,这时|PM|=3,故(x+2)2+(y+1)2的最小值是18.答案:189.求z=5x-8y的最大值,使式中的x,y满足约束条件解:作出满足不等式组的可行域,如图阴影部分.作直线l0:5x-8y=0,平移直线l0,由图可知,当平移到直线经过A点时,z取最大值.解方程组得A(6,0),所以z max=5×6-8×0=30.10.已知-4≤a-b≤-1,-1≤4a-b≤5,求9a-b的取值范围.解:如图所示,令a=x,b=y,z=9a-b,即已知-4≤x-y≤-1,-1≤4x-y≤5,求z=9x-y的取值范围,画出不等式表示的可行域如图阴影部分.由z=9x-y,得y=9x-z,当直线过点A时z取最大值,当直线过点B时z取最小值.由得A(3,7),由得B(0,1),即z max=9×3-7=20,z min=-1,所以9a-b的取值范围是[-1,20].。

2021年高中数学 3.4.2 简单线性规划课后巩固练习北师大版必修5一、选择题（每小题4分，共16分）1.（2011·山东高考）设变量x,y满足约束条件，则目标函数z=2x+3y+1的最大值为( )（A）11 （B）10 （C）9 （D）8.52.（2011·浙江高考）若实数x,y满足不等式组则3x+4y的最小值是( )（A）13 （B）15 （C）20 （D）283.(2011·贵阳高二检测)若实数x、y满足不等式组则目标函数z=x+y的最大值是( )(A)3 (B)5 (C) (D)74.已知x、y满足不等式组且z=2x+y的最大值是最小值的3倍，则a=( )(A)0 (B) (C) (D)1二、填空题（每小题4分，共8分）5.已知点P（x,y）在不等式组表示的平面区域上运动，则z＝x-y的取值范围是________.6.(2011·湖南高考）设m>1,在约束条件下，目标函数z=x+5y的最大值为4，则m的值为________.三、解答题（每小题8分，共16分）7.已知-1<x+y<4且2<x-y<3，求z=2x-3y的取值范围.8.设变量x，y满足约束条件求z=(x- )2+y2的取值范围.【挑战能力】（10分）设O为坐标原点，A（1,1），若点B（x,y）满足，试求的最大值.答案解析1.【解析】选B.画出平面区域表示的可行域如图所示，由目标函数z=2x+3y+1得直线y=-，当直线过点A （3，1）时，目标函数z=2x+3y+1取得最大值为10，故选B.2.独具【解题提示】先画出可行域，求出区域定点的坐标，通过平移直线3x+4y=0,观察可得.【解析】选A.x+2y-5=0与2x+y-7=0的交点为（3，1），通过直线平移可知（3，1）即为最优解，此时3x+4y 取得最小值13.3.【解析】选D.作可行域如图：y=-x+z,过点A时z取最大值.由得，点A坐标为（5，2）.故z max=5+2=7.4. 【解析】选B.依题意可知a<1.作出可行域如图所示，z=2x+y在A点和B点处分别取得最小值和最大值.由得A(a，a)，由得B(1,1)，∴z max=3，z min=3a.∴a=.5.【解析】可行域为如图阴影部分，其中A（2，0），C（0，1），z=x-y在A处取最大值z=2-0=2,在C处取最小值z=0-1=-1,∴z的取值范围为[-1,2].答案：[-1,2]6.独具【解题提示】画出可行域，观察图形，可知直线y=-过直线的交点时，取最大值.【解析】画出可行域，可知z=x+5y在点（）处取最大值为4，解得m=3.答案：37.【解析】画出可行域(如图)，将目标函数z=2x-3y变形为y=，它表示与y=x平行、截距是-的一族平行直线，当它经过点A时，截距-最大，此时z最小（取不到）；当它经过点B时，截距-最小，此时z最大（取不到）.由⇒A(3,1)由⇒B(1,-2)∴过点A时，z=2×3-3×1=3过点B时，z=2×1-3×(-2)=8∴z=2x-3y的取值范围是(3，8).所以目标函数z=2x-3y的取值范围是(3，8).独具【方法技巧】目标函数z=ax+by的最值与b取值的关系线性目标函数z=ax+by取最大值时的最优解与b的正负有关，当b>0时，最优解是将直线ax+by=0在可行域内向上平移到端点(一般是两直线交点)的位置得到的；当b<0时，则是向下方平移，过可行域的端点时取得的.8.独具【解题提示】目标函数z的几何意义是可行域内的点到点（,0)距离的平方.【解析】由作出可行域，如图阴影部分所示.z=（x-)2+y2表示可行域内的任意一点与点(，0)距离的平方.因此(x-)2+y2的最小值为点(,0)到直线x+2y-1=0距离的平方，则z min=.z的最大值为点(,0)到点A、点B、点D距离平方中的最大值，则由计算知z max=，∴z的取值范围是［, ］. 【挑战能力】【解析】不等式x2+y2-2x-2y+1≥0⇔(x-1)2+(y-1)2≥1先作出不等式组表示的平面区域,如图阴影部分所示.=（1,1）·（x,y）＝x＋y，令z=x+y，化为y=-x+z则将直线y=－x向右上方平移时，z随之增大，当平移至通过可行域内的点B（2,2）时，z最大,∴z max=2+2=4,即的最大值为4.32154 7D9A 続Qw24733 609D 悝30899 78B3 碳A40191 9CFF 鳿" _31261 7A1D 稝35449 8A79 詹B23309 5B0D 嬍37681 9331 錱。

简单线性规划 教学目标一、知识与技能 1.掌握线性规划的意义以及约束条件、目标函数、可行解、可行域、最优解等基本概念;2.运用线性规划问题的图解法，并能应用它解决一些简单的实际问题.二、.过程与方法1.培养学生观察、联想以及作图的能力，渗透集合、化归、数形结合的数学思想，提高学生“建模”和解决实际问题的能力;2.结合教学内容，培养学生学习数学的兴趣和“用数学”的意识，激励学生创新.三、情感,态度与价值观1.通过本节教学着重培养学生掌握“数形结合”的数学思想，尽管侧重于用“数”研究“形”，但同时也用“形”去研究“数”，培养学生观察、联想、猜测、归纳等数学能力;2.结合教学内容，培养学生学习数学的兴趣和“用数学”的意识，激励学生勇于创新.教学重点、难点重点: 简单线性规划问题的求解，线性目标函数的几何意义难点:简单线性规划问题的求解教学过程导入新课师 前面我们学习了二元一次不等式A x+B y+C ＞0在平面直角坐标系中的平面区域的确定方法，请同学们回忆一下.（生回答）推进新课问题提出 设x , y 满足条件求z=2x+y 的最大值和最小值.师 如何将上述不等式组表示成平面上的区域？生 （板演）师 这样，上述问题就转化为：当x 、y 满足上述不等式组时，z 的最大值是多少？ 师 把z=2x+y 变形为2y x z =-+,这是斜率为-2，在y 轴上的截距为z 的直线.当z 变化时可以得到什么样的图形？在上图中表示出来.生 当z 变化时可以得到一组互相平行的直线.（板演）师 由于这些直线的斜率是确定的，因此只要给定一个点〔例如（1，2）〕，就能确定一条直线2y x z =-+，这说明，截距z 可以由平面内的一个点的坐标唯一确定.可以看到直线2y x z =-+与表示不等式组的区域的交点坐标满足不等式组，而且当截距z 最大时，z 取最大值，因此，问题转化为当直线2y x z =-+与不等式组确定的区域有公共点时，可以在区域内找一个点P ，使直线经过P 时截距z 最大.［合作探究］师 诸如上述问题中，不等式组是一组对变量x 、y 的约束条件，由于这组约束条件都是关于x 、y 的一次不等式，所以又可称其为线性约束条件.t=2x+y 是欲达到最大值或最小值所涉及的变量x 、y 的解析式，我们把它称为目标函数.由于t=2x+y 又是关于x 、y 的一次解析式，所以又可叫做线性目标函数.另外注意：线性约束条件除了用一次不等式表示外，也可用一次方程表示.一般地，求线性目标函数在线性约束条件下的最大值或最小值的问题，统称为线性规划问题.例如：我们刚才研究的就是求线性目标函数z=2x+y 在线性约束条件下的最大值和最小值的问题，即为线性规划问题.那么，满足线性约束条件的解（x,y)叫做可行解，由所有可行解组成的集合叫做可行域.在上述问题中，可行域就是阴影部分表示的三角形区域.其中可行解（5，2）和（1，1）分别使目标函数取得最大值和最小值，它们都叫做这个问题的最优解.课堂小结用图解法解决简单的线性规划问题的基本步骤：1.首先，要根据线性约束条件画出可行域（即画出不等式组所表示的公共区域）.2.设t=0，画出直线l 0.3.观察、分析，平移直线l 0，从而找到最优解.4.最后求得目标函数的最大值及最小值.设计意图:这个问题是前两个问题的综合,这样设计,过渡自然,层层递进,学生分组合作探究,讨论做法,重点体现数与形的结合。

基础巩固某人有一栋楼房，室内面积共计，拟分割成两类房间作为旅游客房，大房间每间面积为，可住游客名，每名游客每天住宿费元；小房间每间面积为，可住游客名，每名游客每天住宿费元；装修大房间每间需要元，装修小房间每间需要元．如果他只能筹款元用于装修，且游客能住满客房，他应隔出大房间和小房间各多少间，才能获得最大效益？有一批钢管，长度都是，要截成和两种毛坯，且以这两种毛坯数量之比大于配套，问怎样截最合理？已知甲、乙两煤矿每年的产量分别为万吨和万吨，需经过东车站和西车站两个车站运往外地．东车站每年最多能运万吨煤，西车站每年最多能运万吨煤，甲煤矿运往东车站和西车站的运费价格分别为元吨和元吨，乙煤矿运往东车站和西车站的运费价格分别为元吨和元吨．煤矿应怎样编制调运方案，能使总运费最少？医院用甲、乙两种原料为手术后的病人配营养餐．甲种原料每含单位蛋白质和单位铁质，售价元；乙种原料每含单位蛋白质和单位铁质，售价元．若病人每餐至少需要单位蛋白质和单位铁质．试问：应如何使用甲、乙原料，才能既满足营养，又使费用最省？有一批同规格的钢条，每根钢条有两种切割方式，可截成长度为的钢条根，长度为的钢条根；或截成长度为的钢条根，长度为的钢条根．现长度为的钢条至少需要根，长度为的钢条至少需根，问：如何切割可使钢条用量最省？综合过关制定投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损．某投资人打算投资甲、乙两个项目，根据预测，甲、乙项目可能的最大盈利率分别是和，可能的亏损率分别为和，投资人计划投资金额不超过万元，要求确保可能的资金亏损不超过万元，问投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？某运输公司接受了向抗洪救灾地区每天送至少支援物资的任务．该公司有辆载重的型卡车与辆载重为的型卡车，有名驾驶员，每辆卡车每天往返的次数为型卡车次，型卡车次；每辆卡车每天往返的成本费型为元，型为元．请为公司安排一下，应如何调配车辆，才能使公司所花的成本费最低？若只安排型或型卡车，所花的成本费分别是多少？能力提升某电脑用户计划使用不超过元的资金购买单价分别为元、元的单片软件和盒装磁盘，根据需要，软件至少买片，磁盘至少买盒，则不同的选购方式有多少种？参考答案分析：设大房间间，小房间间，然后列出，的关系式，写出目标函数，即可转化为求目标函数的最值问题．解：设隔出大房间间，小房间间，收益为元，则，满足(\\(＋≤，＋≤，≥，≥，))即(\\(＋≤，＋≤，≥，≥，))＝＋.作出可行域，如图所示的阴影部分．解方程组(\\(＋＝，＋＝，))得点的坐标为(，)．由于点的坐标不是整数，而最优解(，)是整点，所以可行域内点(，)不是最优解．经验证：经过可行域内的整点，且使＝＋取得最大值的整点是()和()，此时＝元，即应隔出小房间间，或大房间间、小房间间，可以获得最大利润．分析：先设出未知数，建立约束条件和目标函数后，再按求最优解是整数解的方法去求．解：设截的根，的根，根据题意，得(\\(＋≤，<，>，>，))且，∈＋.作出可行域，如图中的阴影部分．目标函数为＝＋，作一组平行直线＋＝，经过可行域内的点且和原点距离最远的直线为过()的直线，这时＋＝.由、为正整数，知()不是最优解．在可行域内找整点，使＋＝.可知点()、()、()、()、()均为最优解．即每根钢管截的根，的根，或截的根，的根，或截的根，的根，或截的根，的根，或截的根，的根最合理．解：设甲煤矿向东车站运万吨煤，乙煤矿向东车站运万吨煤，那么总运费＝＋(－)＋＋(－)万元，即＝－－.其中、应满足(\\(≥，≥，－≥，－≥，＋≤，－＋(－(≤.))作出上面的不等式组所表示的平面区域，如图阴影部分所示．。

, [学生用书单独成册])[A.基础达标]1．不等式组⎩⎪⎨⎪⎧（x －y ＋3）（x ＋y ）≥0，－32≤x ≤3表示的平面区域是( )A ．矩形B ．三角形C ．直角梯形D ．等腰梯形解析：选B.不等式组⎩⎪⎨⎪⎧（x －y ＋3）（x ＋y ）≥0－32≤x ≤3⇔⎩⎪⎨⎪⎧x －y ＋3≥0－32≤x ≤3x ＋y≥0或⎩⎪⎨⎪⎧x －y ＋3≤0－32≤x ≤3x ＋y ≤0，那么利用不等式表示的区域可知，得到的区域为三角形，故选B.2．若x ，y ∈R ，且⎩⎪⎨⎪⎧x ≥1，x －2y ＋3≥0，y ≥x ，则z ＝x ＋2y 的最小值等于( )A ．2B ．3C ．5D ．9解析：选B.可行域如图阴影部分所示，则当直线x ＋2y －z ＝0经过点M (1，1)时，z ＝x ＋2y 取得最小值，为1＋2＝3.3．在△ABC 中，三个顶点分别为A (2，4)，B (－1，2)，C (1，0)，点P (x ，y )在△ABC 的内部及其边界上运动，则y －x 的取值范围为( )A ．[1，3]B ．[－3，1]C ．[－1，3]D ．[－3，－1] 解析：选C.先画出三角形区域(如图)，然后转化为一个线性规划问题，求线性目标函数z ＝y －x 的取值范围．由图求出其取值范围是[－1，3]．4．直线2x ＋y ＝10与不等式组⎩⎪⎨⎪⎧x ≥0，y ≥0，x －y ≥－2，4x ＋3y ≤20表示的平面区域的公共点有( )A ．0个B ．1个C ．2个D ．无数个解析：选B.画出可行域如图阴影部分所示．因为直线过(5，0)点，故只有1个公共点(5，0)．5．实数x ，y 满足不等式组⎩⎪⎨⎪⎧y ≥0，x －y ≥0，2x －y －2≥0，则W＝y －1x ＋1的取值范围是( )A.⎣⎡⎦⎤－1，13B.⎣⎡⎦⎤－12，13C.⎣⎡⎭⎫－12，＋∞D.⎣⎡⎭⎫－12，1 解析：选D.画出题中不等式组所表示的可行域如图所示，目标函数W ＝y －1x ＋1表示阴影部分的点与定点A (－1，1)的连线的斜率，由图可知点A (－1，1)与点(1，0)连线的斜率为最小值，最大值趋近于1，但永远达不到1，故－12≤W ＜1.6．如图中阴影部分的点满足不等式组⎩⎪⎨⎪⎧x ＋y ≤5，2x ＋y ≤6，x ≥0，y ≥0.在这些点中，使目标函数z ＝6x ＋8y取得最大值的点的坐标是________．解析：首先作出直线6x ＋8y ＝0，然后平移直线，当直线经过平面区域内的点(0，5)时截距最大，此时z 最大．答案：(0，5)7．已知实数x ，y 满足⎩⎪⎨⎪⎧x ＋2y －5≤0，x ≥1，y ≥0，x ＋2y －3≥0，则yx 的最大值为________．解析：画出不等式组⎩⎪⎨⎪⎧x ＋2y －5≤0，x ≥1，y ≥0，x ＋2y －3≥0对应的平面区域Ω如图阴影部分所示，y x＝y －0x －0表示平面区域Ω上的点P (x ，y )与原点的连线的斜率．A (1，2)，B (3，0)， 所以0≤yx≤2.答案：28．在平面直角坐标系中，若不等式组⎩⎪⎨⎪⎧x ＋y －1≥0，x －1≤0，ax －y ＋1≥0(a 为常数)所表示的平面区域的面积等于2，则a 的值为________．解析：如图所示的阴影部分即为满足不等式组⎩⎪⎨⎪⎧x ＋y －1≥0，x －1≤0的可行域，而直线ax －y ＋1＝0恒过点(0，1)，故可看成直线绕点(0，1)旋转．当a ＞－1时，可行域是一个封闭的三角形区域，由12×(a ＋1)×1＝2得a ＝3.答案：39．如果由约束条件⎩⎪⎨⎪⎧y ≥0，y ≤x ，y ≤2－x ，t ≤x ≤t ＋1所确定的平面区域的面积为S ＝f (t )(0＜t ＜1)，试求f (t )的表达式．解：由约束条件所确定的平面区域是五边形ABCEP (如图)，其面积S ＝f (t )＝S △OPD －S △AOB －S △ECD ，而S △OPD ＝12×1×2＝1，S △OAB ＝12t 2，S △ECD ＝12(1－t )2所以S ＝f (t )＝1－12t 2－12(1－t )2＝－t 2＋t ＋12(0＜t ＜1)．10．已知x ，y 满足约束条件⎩⎪⎨⎪⎧x ≥1，x －3y ≤－4，3x ＋5y ≤30.(1)求目标函数z ＝2x ＋y 的最大值和最小值；(2)求z＝y ＋5x ＋5的取值范围．解：作出可行域如图所示．(1)作直线l ：2x ＋y ＝0，并平移此直线，当平移直线过可行域内的A 点时，z 取最小值；当平移直线过可行域内的B 点时，z 取得最大值．解⎩⎪⎨⎪⎧x ＝1，x －3y ＝－4，得A ⎝⎛⎭⎫1，53. 解⎩⎪⎨⎪⎧x －3y ＝－4，3x ＋5y ＝30，得B (5，3)． 所以z max ＝2×5＋3＝13，z min ＝2×1＋53＝113.(2)z ＝y ＋5x ＋5＝y －（－5）x －（－5），可看作区域内的点(x ，y )与点D (－5，－5)连线的斜率，由图可知，k BD ≤z ≤k CD .因为k BD ＝3－（－5）5－（－5）＝45，k CD ＝275－（－5）1－（－5）＝2615，所以z ＝y ＋5x ＋5的取值范围是⎣⎡⎦⎤45，2615. [B.能力提升]1．设O 为坐标原点，A (1，1)，若点B (x ，y )满足⎩⎪⎨⎪⎧x 2＋y 2－2x －2y ＋1≥0，1≤x ≤2，1≤y ≤2，则OA →·OB →取得最小值时，点B 的个数是( ) A ．1 B ．2C ．3D ．无数个解析：选B.如图，阴影部分为点B (x ，y )所在的区域．因为OA →·OB →＝x ＋y ， 令z ＝x ＋y ，则y ＝－x ＋z .由图可知，当点B 在C 点或D 点时，z 取最小值，故点B 的个数为2. 2.如图所示的坐标平面的可行域内(包括边界)，若使目标函数z ＝ax ＋y (a ＞0)取得最大值的最优解有无穷多个，则a 的值为( )A.14B.35C ．4 D.53解析：选B.由y ＝－ax ＋z 知当－a ＝k AC 时，最优解有无穷多个．因为k AC ＝－35，所以a ＝35. 3．若目标函数z ＝x ＋y ＋1在约束条件⎩⎪⎨⎪⎧x ＋y －2≤0x －y ＋2≤0y ≤n x ≥－3下取得最大值的最优解有无穷多个，则n 的取值范围是________． 解析：先根据⎩⎪⎨⎪⎧x ＋y －2≤0，x －y ＋2≤0，x ≥－3，作出如图所示阴影部分的可行域，欲使目标函数z ＝x ＋y ＋1取得最大值的最优解有无穷多个，需使目标函数对应的直线平移时达到可行域的边界直线x ＋y －2＝0，且只有当n ＞2时，可行域才包含x ＋y －2＝0这条直线上的线段BC 或其他部分．答案：(2，＋∞)4．若实数x ，y 满足⎩⎪⎨⎪⎧x －y ＋1≥0，x ＋y ≥0，x ≤0.则z ＝3x ＋2y 的最小值是________．解析：由不等式组得可行域是以A (0，0)，B (0，1)，C (－0.5，0.5)为顶点的三角形，易知当x ＝0，y ＝0时，z ′＝x ＋2y 取最小值0.所以z ＝3x ＋2y 的最小值是1.答案：15．设m 为实数，若⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫（x ，y ）⎪⎪⎪⎩⎪⎨⎪⎧x －2y ＋5≥03－x ≥0mx ＋y ≥0⊆{(x ，y )|x 2＋y 2≤25}，求m 的取值范围．解：由题意知，可行域应在圆内，如图阴影部分所示，如果－m ＞0，则可行域取到x ＜－5的点，不能在圆内，故－m ≤0，即m ≥0.当mx ＋y ＝0绕坐标原点旋转时，直线过B 点时为边界位置，此时－m ＝－43，所以m ＝43.所以0≤m ≤43.6．实系数一元二次方程x 2＋ax ＋2b ＝0有两个根，一个根在区间(0，1)内，另一个根在区间(1，2)内，求：(1)点(a ，b )对应的区域的面积； (2)b －2a －1的取值范围； (3)(a －1)2＋(b －2)2的值域．解：方程x 2＋ax ＋2b ＝0的两根在区间(0，1)和(1，2)上的几何意义分别是：函数y ＝f (x )＝x 2＋ax ＋2b 与x 轴的两个交点的横坐标分别在区间(0，1)和(1，2)内，由此可得不等式组⎩⎪⎨⎪⎧f （0）＞0，f （1）＜0，f （2）＞0⇔⎩⎪⎨⎪⎧b ＞0，a ＋2b ＋1＜0，a ＋b ＋2＞0.由⎩⎪⎨⎪⎧a ＋2b ＋1＝0，a ＋b ＋2＝0，解得A (－3，1)； 由⎩⎪⎨⎪⎧a ＋b ＋2＝0，b ＝0，解得B (－2，0)； 由⎩⎪⎨⎪⎧a ＋2b ＋1＝0，b ＝0，解得C (－1，0)．所以在如图所示的坐标平面aOb 内，满足约束条件的点(a ，b )对应的平面区域为△ABC (不包括边界)．(1)△ABC 的面积为S △ABC ＝12×|BC |×h ＝12(h 为A 到Oa 轴的距离)．(2)b －2a －1的几何意义是点(a ，b )和点D (1，2)连线的斜率． k AD ＝2－11＋3＝14，k CD ＝2－01＋1＝1.由图可知，k AD ＜b －2a －1＜k CD.所以14＜b －2a －1＜1，即b －2a －1∈⎝⎛⎭⎫14，1.(3)因为(a－1)2＋(b－2)2表示区域内的点(a，b)与定点(1，2)之间距离的平方，所以(a－1)2＋(b－2)2∈(8，17)．。

,[学生用书单独成册])[.基础达标]．不等式组表示的平面区域是( )．矩形．三角形．等腰梯形．直角梯形解析：选.不等式组⇔或，那么利用不等式表示的区域可知，得到的区域为三角形，故选.．若，∈，且则＝＋的最小值等于( )．．．．解析：选.可行域如图阴影部分所示，则当直线＋－＝经过点(，)时，＝＋取得最小值，为＋＝.．在△中，三个顶点分别为(，)，(－，)，(，)，点(，)在△的内部及其边界上运动，则－的取值范围为( )．[，]．[－，]．[－，－]．[－，]解析：选.先画出三角形区域(如图)，然后转化为一个线性规划问题，求线性目标函数＝－的取值范围．由图求出其取值范围是[－，]．．直线＋＝与不等式组表示的平面区域的公共点有( )．个．个．个．无数个解析：选.画出可行域如图阴影部分所示．因为直线过(，)点，故只有个公共点(，)．．实数，满足不等式组则＝的取值范围是( )解析：选.画出题中不等式组所表示的可行域如图所示，目标函数＝表示阴影部分的点与定点(－，)的连线的斜率，由图可知点(－，)与点(，)连线的斜率为最小值，最大值趋近于，但永远达不到，故－≤＜.．如图中阴影部分的点满足不等式组在这些点中，使目标函数＝＋取得最大值的点的坐标是．解析：首先作出直线＋＝，然后平移直线，当直线经过平面区域内的点(，)时截距最大，此时最大．答案：(，)．已知实数，满足则的最大值为．解析：画出不等式组对应的平面区域Ω如图阴影部分所示，＝表示平面区域Ω上的点(，)与原点的连线的斜率．(，)，(，)，所以≤≤.答案：．在平面直角坐标系中，若不等式组(为常数)所表示的平面区域的面积等于，则的值为．解析：如图所示的阴影部分即为满足不等式组的可行域，而直线－＋＝恒过点(，)，故可看成直线绕点(，)旋转．当＞－时，可行域是一个封闭的三角形区域，由×(＋)×＝得＝.答案：．如果由约束条件所确定的平面区域的面积为＝()(＜＜)，试求()的表达式．解：由约束条件所确定的平面区域是五边形(如图)，其面积＝()＝△－△－△，而△＝××＝，△。