下载文档原格式
第二节直线的投影在图学中一般用线段表示直线，图学中讲的直线主要是指中学定义的线段，较少指直线，很少指射线，一般混称为直线。
具体指那种，要具体问题具体分析。
ABabCDc (d)如何求出直线的投影？直线的投影一般仍为直线；当直线垂直于投影面时，其投影积聚为一点，称其在该投影面上具有积聚性。
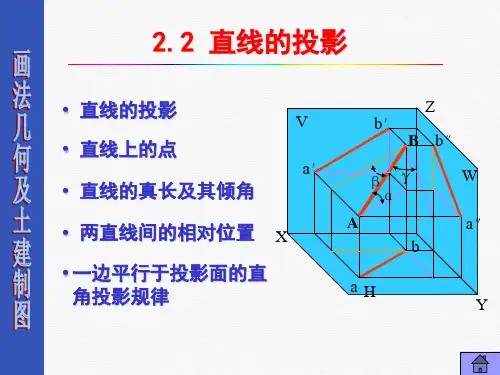
H同面投影——不同的几何元素在同一投影面上的投影一、直线对投影面的各种相对位置1. 一般位置直线——倾斜于三个投影面的直线2. 投影面平行线——仅平行于一个投影面的直线3. 投影面垂直线——垂直于一个投影面的直线后两类统称为特殊位置直线直线与H、V和W三个投影面的夹角称为直线对投影面的倾角αβγ分别用、、表示Xa'abY HWb''Ob'a''ZY b''YZa''bb'BA Va a'XO HW αβγ1.一般位置直线的投影（1）线段在各投影面上的投影长度小于线段的实长。
（2）直线的各投影均倾斜于投影轴αcos AB ab =βcos AB b a =''γcos AB b a =''''细实线粗度：0.2~0.3mm 粗实线粗度：0.5~0.7mm2. 投影面的平行线定义：仅平行于一个投影面的直线，称为投影面平行线。
平行于H面的直线称为水平线平行于V面的直线称为正平线平行于W面的直线称为侧平线aB b'V HAbb''a''YW Oa'XHab'bY Wb''a''ZY Oa'Xγβ（1）水平线1、ab=AB2、反映β、γ实角3、a ’b’//OX 轴a’’b’’//OY W 轴保真的投影与轴的夹角反映空间直线对相应面的倾角。
另外两个投影平行于相应的投影轴。
H XWH VYββb''YZa''bb'B AH Va a'XOWγY WY HZa''bb'aa'Oαb''（2）正平线1、a’b’=AB2、反映α、γ实角3、ab//OX 轴a’’b’’//OZ 轴γY WY HZa''bb'aa'Oαb''正平线Hab'bY Wb''a''ZY Oa'X γβ水平线典型特征及对比（3）侧平线b''YZb’AHVa a'XOW B a''b Wb''Y YHZa''bb'a a'XOαβ1、a’’b’’=AB2、反映α、β实角3、a ’b’//OZ 轴ab//OY H 轴投影面平行线投影性质：投影面平行线在其所平行的投影面上的投影反映线段的实长；与投影轴的夹角反映直线对相应投影面的倾角；线段的另两个投影平行于相应的投影轴，且小于实长。
chenmeihua 《土木建筑制图》 4 投影基本原理4 投影基本原理本章提要：（1）点的投影（2）直线的投影（3）平面的投影（4）直线与平面及两平面的相对位置4 投影基本原理▪4.1 点的投影▪4.2 直线的投影▪4.3 平面的投影▪4.4 直线与平面及两平面的相对位置s'a'b'c'asb cb"s"a" (c")任何形体都是由点、线和平面组成的。
如图所示的三棱锥，既可看成由四个点所构成，又可看成由六条直线或四个平面所构成。
在点、线、面中,点又是组成形体的最基本的几何元素。
所以, 要正确地表达形体(画图), 要正确地理解他人的设计思想(看图), 点的投影规律是必须掌握的基础。
4.1 点的投影4.1 点的投影一、点的两面投影二、点的三面投影与坐标系的关系三、两点的相对位置及重影点采用多面投影过空间点A 的投射线与投影面P 的交点即为点A 在P 面上的投影。
点在一个投影面上的投影不能确定点的空间位置。
1.点在一个投影面上的投影解决办法？ 一、点的两面投影aB 1B 2B 32.两面投影体系的建立及四个分角正立投影面——正面或V 面 水平投影面——水平面或H 面投影轴——OX 轴（V 面与H 面的交线）XO两个投影面互相垂直四个分角3. 两投影面体系中点的投影点A 的水平投影 —— a 点A 的正面投影 —— a 'aAa '空间点用大写字母表示，点的投影用小写字母表示。
a x4.投影面展开HXHVOaaa x xzy向下翻不动A通常不画出投影面的边界5.点的两面投影规律AQ1) aa'⊥OX2) a'a x =Aa , aa x =Aa'点的两面投影规律点的V、H投影连线垂直于OX轴；点的H 投影到OX轴的距离等于空间点到V面的距离, 点的V投影到OX轴的距离等于空间点到H面的距离。
