第4章-面板数据模型与应用
- 格式:ppt
- 大小:1.23 MB
- 文档页数:62


面板数据模型与应用1.面板数据定义panel data的中译:面板数据、桌面数据、平行数据、纵列数据、时间序列截面数据、混合数据(pool data)、固定调查对象数据。
面板数据定义(1)面板数据定义为相同截面上的个体在不同时点的重复观测数据。
(2)称为纵向(longitudinal)变量序列(个体)的多次测量。
面板数据从横截面(cross section)看,是由若干个体(entity, unit, individual)在某一时点构成的截面观测值,从纵剖面(longitudinal section)看每个个体都是一个时间序列。
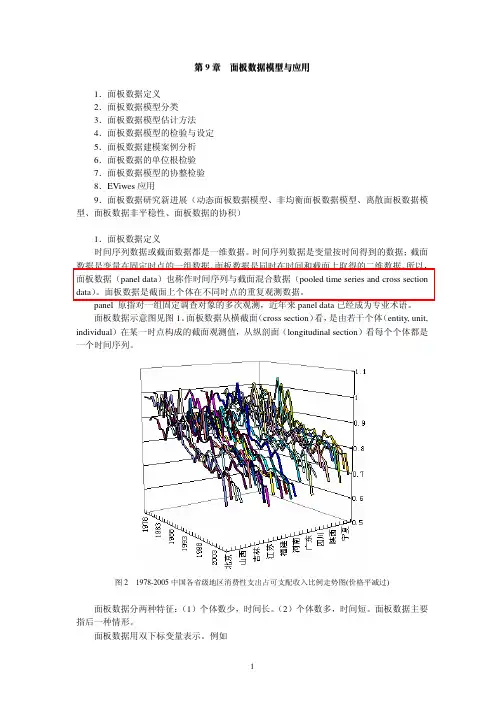
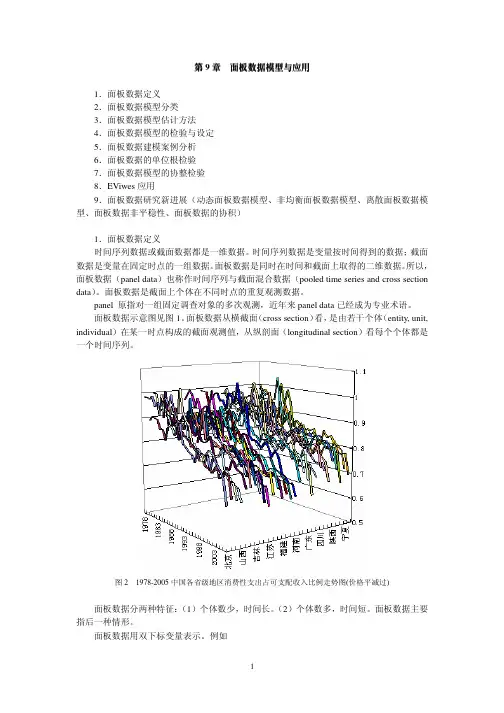
1图1 N=7,T=50的面板数据示意图2面板数据用双下标变量表示。
例如y i t, i = 1, 2, …, N; t = 1, 2, …, Ti对应面板数据中不同个体。
N表示面板数据中含有N个个体。
t对应面板数据中不同时点。
T表示时间序列的最大长度。
若固定t不变,y i ., ( i = 1, 2, …, N)是横截面上的N个随机变量;若固定i不变,y. t, (t = 1, 2, …, T)是纵剖面上的一个时间序列(个体)。
2. 面板数据模型面板数据模型是利用面板数据构建的模型。
面板数据系一组个体在一段时间内的观测值形成的数据集,这里“个体”可以是个人、家庭、企业、行业、地区3或国家(Baltagi,2008)。
1966年,Balestra & Nerlove发表了第一篇利用面板数据模型研究天然气需求估计的论文,此后,面板数据模型这一新的计量分析方法在理论和应用上得到迅速发展,已形成现代计量经济学的一个相对独立的分支。
面板数据模型由于同时使用了截面数据(cross-sectional data)和时间序列数据(time series data),因而可以控制个体的异质性,识别、测量单纯使用这两种数据无法估计的效应;并且具有包含更多的信息、更大的变异和自由度、变量间的共线性也更弱的特性,可得到更精确的参数估计(Hsiao,2003、2008)。



面板数据模型面板数据模型是一种用于描述面板数据结构和分析的统计模型。
它是一种多层次的数据结构,包含了不同时间点和不同个体的观测数据。
面板数据模型广泛应用于经济学、社会学、医学等领域的研究中。
面板数据模型的标准格式如下:1. 面板数据的基本信息:- 面板数据的来源和采集方法;- 面板数据的时间范围和频率;- 面板数据的样本规模和样本特征。
2. 面板数据的变量定义:- 面板数据中所包含的变量名称和含义;- 面板数据中的自变量和因变量的定义;- 面板数据中可能存在的缺失值和异常值处理方法。
3. 面板数据模型的建立:- 面板数据模型的理论基础和假设前提;- 面板数据模型的数学表达式和形式;- 面板数据模型的参数估计方法和模型诊断。
4. 面板数据模型的应用:- 面板数据模型在实际研究中的应用案例;- 面板数据模型的结果解释和推断方法;- 面板数据模型的政策效果评估和预测分析。
5. 面板数据模型的优缺点:- 面板数据模型相比其他统计模型的优势;- 面板数据模型的局限性和应用条件;- 面板数据模型的改进和发展方向。
6. 面板数据模型的软件实现:- 面板数据模型的常用软件工具和编程语言;- 面板数据模型的软件实现步骤和代码示例;- 面板数据模型的软件可视化和结果输出。
总结:面板数据模型是一种强大的分析工具,可以用于描述和分析面板数据结构。
它能够捕捉到时间和个体之间的变化和相关性,为研究者提供了丰富的数据信息。
然而,面板数据模型也存在一些局限性,如样本选择偏差和模型假设的限制等。
因此,在应用面板数据模型时,需要根据具体研究问题和数据特点进行合理的模型选择和分析方法。

面板数据模型面板数据模型,又称固定效应模型,是计量经济学中常用的一种数据分析方法。
它适用于时间序列和截面数据的联合分析,具有较高的灵活性和强大的解释能力。
本文将对面板数据模型的基本原理、应用场景以及估计方法进行介绍,并通过实例说明其实际运用。
第一部分:面板数据模型的基本原理面板数据模型基于以下假设:每个个体(又称单位)在不同时间点都有观测值,并且个体之间的观测值具有相关性。
面板数据模型通常由固定效应模型和随机效应模型两种形式。
固定效应模型假设个体特定的不变因素对观测值产生了影响,这些不变因素可能包括个体的性别、年龄、学历等。
固定效应模型可以通过引入个体固定效应变量来捕捉这些影响因素,并以此来解释观测值的变动。
第二部分:面板数据模型的应用场景面板数据模型在经济学、金融学、社会学等领域得到了广泛的应用。
例如,在经济学中,研究人员可以利用面板数据模型来分析不同国家或地区的经济增长情况,探讨政策对经济发展的影响;在金融学领域,研究人员可以运用面板数据模型来研究股票价格的波动和影响因素。
第三部分:面板数据模型的估计方法面板数据模型有多种估计方法,常见的有固定效应模型估计和随机效应模型估计。
固定效应模型估计通常采用最小二乘法,即通过对个体固定效应进行回归分析来求解模型参数。
随机效应模型估计则假设个体固定效应是误差项的一部分,通过对固定效应进行随机化处理得到模型的估计结果。
实例应用:假设我们需要研究不同地区的教育水平对经济增长的影响,我们可以使用面板数据模型来分析这个问题。
我们收集了10个地区在2010年到2020年的经济增长率和教育水平数据。
我们可以利用固定效应模型来探究教育水平对经济增长的影响。
首先,我们创建一个包含个体固定效应的面板数据模型,并使用最小二乘法来估计参数。
然后,我们通过分析模型的显著性水平、参数估计结果以及模型拟合程度来得出结论。
通过面板数据分析,我们可以发现教育水平对经济增长确实存在显著的正向影响。



面板数据模型引言概述:面板数据模型是一种经济学和统计学中常用的数据分析方法。
它适合于具有时间和个体维度的数据,可以匡助研究人员更好地理解个体之间的关系以及时间的变化趋势。
本文将详细介绍面板数据模型的概念、应用领域、优势和限制,并提供一些实际案例来说明其实际价值。
正文内容:1. 面板数据模型的概念1.1 面板数据模型的定义面板数据模型是一种同时考虑时间和个体维度的数据分析方法。
它将个体的观察结果按照时间顺序罗列,形成一个面板数据集,以便分析个体之间的关系和时间的变化趋势。
1.2 面板数据模型的分类面板数据模型可以分为固定效应模型和随机效应模型。
固定效应模型假设个体之间的差异是固定的,而随机效应模型则允许个体之间的差异是随机的。
2. 面板数据模型的应用领域2.1 经济学领域面板数据模型在经济学领域得到广泛应用。
例如,研究人员可以利用面板数据模型来分析不同国家或者地区的经济增长率、失业率和通货膨胀率之间的关系,以及企业的生产效率和市场竞争程度之间的关系。
2.2 社会科学领域面板数据模型也在社会科学领域具有重要意义。
研究人员可以利用面板数据模型来研究教育、健康、就业等社会问题,并分析个体特征对这些问题的影响。
2.3 金融领域面板数据模型在金融领域的应用也非常广泛。
例如,研究人员可以利用面板数据模型来分析不同股票的收益率之间的关系,以及股票市场的波动与宏观经济指标之间的关系。
3. 面板数据模型的优势3.1 控制个体固定效应面板数据模型可以通过固定效应来控制个体固有的差异,从而更准确地分析个体之间的关系。
3.2 利用时间维度的信息面板数据模型可以利用时间维度的信息,分析个体随时间的变化趋势,更好地理解时间的影响。
3.3 提高数据的效率面板数据模型可以利用面板数据集中的交叉个体和时间信息,提高数据的效率,减少估计的方差。
4. 面板数据模型的限制4.1 数据缺失问题面板数据模型在面对数据缺失问题时可能会浮现一些难点,需要采取一些特殊的处理方法。
面板数据模型初步在经济学研究和实际应用中,经常会遇到时间序列与横截面相结合的二维数据。
例如,在居民家庭消费分析中,会遇到不同省市地区的居民家庭人均消费和居民家庭人均收入的年度时间序列数据;在生产函数分析中,会遇到不同企业的产出、资本、劳动等年度或季度时间序列数据。
这种具有时间序列与横截面信息的二维数据称为面板数据(Panel Data ),也可称为平行数据、时间序列与截面混合数据(Pooled Time Series and Cross Section Data )。
面板数据从横截面上看,是由若干个体,比如个人、家庭、企业或国家等,在某一时间构成的截面观测值,从纵剖面上看每个个体都是一个时间序列。
经典计量经济学在分析实际问题时,只利用了时间序列或截面数据进行建模,在很多情况下是不能满足人们分析问题的需要。
例如,在分析企业生产成本问题,若只选用截面数据,即选择同一时间上不同规模的企业数据作为样本观测,可以分析生产成本与企业规模的关系,但是不能分析技术革新对生产成本的影响;若只采用时间序列数据,即选择某个企业在不同时间上的数据作为样本观测,可以分析生产成本与技术革新的关系,但是不能分析企业规模对生产成本的影响;然而利用面板数据,即在不同的时间上选择不同规模的企业数据作为样本观测,就可以同时分析企业规模和技术革新对生产成本的影响。
因此,面板数据含有更多的信息,能更好构造和检验真实的、复杂的行为模型,同时它还能够增加模型的自由度,降低解释变量之间的多重共线性程度,更高的估计效率,正是由于面板数据具有诸多的优点,Panel Data 模型是近年来非经典计量经济学的一个重要发展之一,在经济学领域得到大量广泛的应用,比如在宏观经济领域,它被广泛应用于经济增长、技术创新、金融、税收政策等领域;在微观经济领域,它被大量应用于就业、家庭消费、入学、市场营销等领域。
但是,由于面板数据自身的特点,Panel Data 模型的设定和估计都存在一定的假设条件,如果应用不当的话,将会产生较大偏误,估计结果与实际相差甚远。