下载文档原格式
《钢结构基本原理》课程教学大纲课程编号：031126 学分：2.5 总学时：43大纲执笔人：罗烈大纲审核人：陈以一一、课程性质与目的《钢结构基本原理》是土木工程、港口航道与海岸工程专业的专业基础课程，属必修课。
钢结构是现代土木工程的基本结构形式之一。
设置本课程的目的，是使学生全面掌握钢结构材料、构件和连接的基础知识，理解钢结构分析的基本原理，为进一步学习各类钢结构与金属结构的设计、制作和建造提供基础。
本课程开设双语教学班。
二、课程基本要求1．了解钢结构的特点、历史、现状及发展前景；2．掌握钢结构材料的基本性能；3．了解钢结构的典型破坏模式、破坏原因和力学分析的基本方法；4．掌握钢结构基本构件及连接的性能、受力分析与设计计算；5．了解钢结构体系的组成原理和典型结构形式的设计要点。
三、课程基本内容1．绪论钢结构的特点及应用；钢结构发展的历史、现状和趋势；钢结构的构件组成和主要结构形式。
2．钢结构材料钢材在单向均匀受拉时的工作性能；钢材在单轴反复应力作用下的工作性能；钢材在复杂应力作用下的工作性能；钢材抗冲击性能及冷弯性能；影响钢材性能的一般因素；钢材的脆性破坏和延性破坏、疲劳破坏和损伤累积破坏；钢结构防护；钢结构用钢材的分类。
3．钢结构的主要破坏形式整体失稳破坏；板件局部失稳与屈曲后强度；强度破坏与塑性重分布；疲劳；脆性断裂及其机理。
4．钢结构的连接连接的主要类型；对接焊缝构造和计算；角焊缝构造和计算；普通螺栓连接构造和计算；高强螺栓连接构造和计算。
5．受拉构件及索受拉构件的强度，净截面概念；截面效率；拉弯构件的截面强度及强度计算准则；轴力和弯矩的相关关系；索的基本力学性质。
6. 轴心受压构件轴心受压构件的强度；轴心受压构件整体稳定的平衡方程及其理论解，长细比概念；影响整体稳定承载力的因素，整体稳定的工程计算方法；实腹式构件与格构式构件；轴心受压构件的局部稳定；防止局部失稳的设计原则和利用屈曲后强度的设计原则；宽厚比概念。
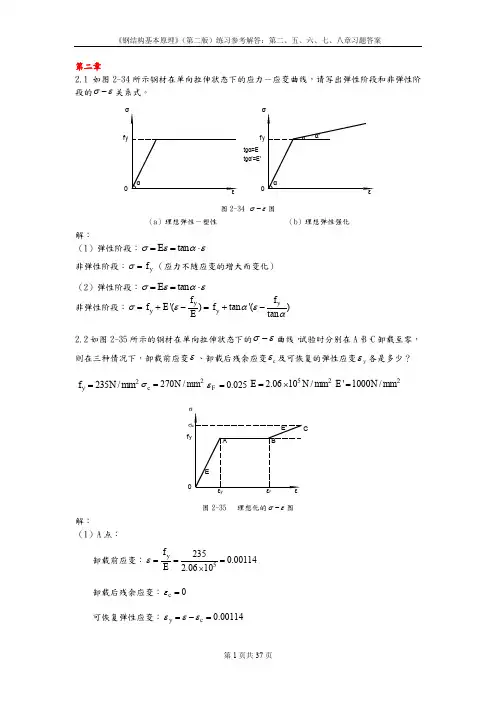
第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。
图2-34 σε-图（a ）理想弹性－塑性（b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化）（2）弹性阶段：tan E σεαε==⋅非弹性阶段：'()tan '()tan y yy y f f f E f E σεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？2235/y f N mm =2270/c N mm σ=0.025F ε=522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解：（1）A 点：卸载前应变：52350.001142.0610y f Eε===⨯卸载后残余应变：0c ε=可恢复弹性应变：0.00114y c εεε=-=tgα'=E'f y 0f y 0tgα=E σf yCσF（2）B 点： 卸载前应变：0.025F εε== 卸载后残余应变：0.02386y c f Eεε=-=可恢复弹性应变：0.00114y c εεε=-=（3）C 点： 卸载前应变：0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变：0.05869cc Eσεε=-=可恢复弹性应变：0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。
同济大学钢结构基本原理(沈祖炎)课后习题答案完全版1. 引言同济大学钢结构基本原理是一门介绍钢结构基本知识和原理的课程。
在学习过程中，课后习题是检验学生掌握程度的重要方式。
本文是同济大学钢结构基本原理(沈祖炎)课后习题的完全版答案。
2. 第一章2.1 选择题1.D2.A3.B4.C5.A2.2 填空题1.拱2.跨度3.支点4.平行5.水平2.3 解答题1.我们可以通过使用方法一和方法二来计算桁架的支反作用力。
方法一使用刚度法，方法二使用Joints法。
具体步骤如下：方法一：–计算桁架的节点刚度矩阵。
–将所有节点刚度矩阵相加得到整个桁架的刚度矩阵。
–构造一个受力平衡的方程组，解得桁架的支反作用力。
方法二：–构造一个支座方程组，解得支座反力。
–通过节点内力平衡，计算出节点的内力。
2.钢结构的主要优点有：–高强度：钢材具有较高的强度和抗拉性能，使得钢结构能够承受较大的荷载。
–轻质：相对于混凝土结构来说，钢结构的自重较轻，可以减少建筑物的结构材料的使用量，降低建筑成本。
–施工速度快：由于钢结构可以在工厂中预制，因此施工速度较快，可以缩短工期，减少施工成本。
–可拆装性好：钢结构可以拆装，便于改建和迁移。
3.塔式起重机是利用强大的垂直支撑能力用高耸的塔架将货物一拉再拉的起重设备。
它是用来适应高空起重和物料搬移的一种机械。
结构上，塔式起重机主要由塔式结构、起升机构、回转机构和顶部配重组成。
其中，塔式结构是起重机的主要承重部分，承担起重机自重和起升机构的荷载。
塔式结构通常使用钢材制作，因为钢材具有较高的强度和抗拉性能，能够承受大的荷载。
此外，塔式起重机的钢结构也具有较好的可拆装性，便于施工和维护。
3. 第二章3.1 选择题1.B2.D3.A4.C5.B3.2 填空题1.核算按简化梁简化支承条件方式2.弹性模量3.建筑结构4.弹性变形5.线弹性3.3 解答题1.三个节点的坐标分别为A(0, 0)，B(0, 4)，C(4, 0)。
H型截面轴心受压柱实验报告学号：姓名：任课老师：实验老师：实验日期：2012年03月30日一、实验目的：1、通过试验掌握钢构件的试验方法，包括试件设计、加载装置设计、测点布置、试验结果整理等方法。
2、通过试验观察十字型截面轴心受压柱的失稳过程和失稳模式。
3、将理论极限承载力和实测承载力进行对比，加深对轴心受压构件稳定系数计算公式的理解。
二、实验原理：1、基本微分方程根据开口薄壁杆件理论，具有初始缺陷的轴心压杆的弹性微分方程为：''''00()0IV IVx EI v v Nv Nx θ-+-=''''00()0IV IV y EI u u Nu Ny θ-+-=''''''''2''''00000()()0IV IV t EI GI Nx Ny r N R ωθθθθθθθθ----++-=2、扭转失稳欧拉荷载H 型截面为双轴对称截面，因其剪力中心和形心重合，有 x 0 y 0 0，代入上式可得：''0()0IV IVx EI v v Nv -+=(a)''0()0IV IV y EI u u Nu -+= (b)''''2''''000()()0IV IV t EI GI r N R ωθθθθθθ---+-=(c)说明H 型双轴对称截面轴心压杆在弹性阶段工作时，三个微分方程是相互独立的，可分别单独研究。
在弹塑性阶段，当研究（a ）式时，只要截面上的产于应力对称与 Y 轴，同时又有00u =和00θ=，则该式将始终和其他两式无关，可单独研究。
这样，压杆将只发生Y 方向的位移，整体失稳呈弯曲变形状态，称为弯曲失稳。
这样，式（b ）也是弯曲失稳，只是弯曲失稳的方向不同而已。
5.1 影响轴心受压稳定极限承载力的初始缺陷有哪些?在钢结构设计中应如何考虑?5.2 某车间工作平台柱高2.6m,轴心受压,两端铰接.材料用I16,Q235钢,钢材的强度设计值2215/d f N mm =.求轴心受压稳定系数ϕ及其稳定临界荷载.如改用Q345钢2310/d f N mm =,则各为多少?解答:查P335附表3-6,知I16截面特性,26.57, 1.89,26.11x y i cm i cm A cm === 柱子两端较接, 1.0x y μμ== 故柱子长细比为 1.0260039.665.7x x xli μλ⨯===,2600 1.0137.618.9y y y l i μλ⨯===因为x y λλ<,故对于Q235钢相对长细比为137.61.48λπ=== 钢柱轧制, /0.8b h ≤.对y 轴查P106表5-4(a)知为不b 类截面。
故由式5-34b得()223212ϕααλλλ⎡=++⎢⎣ ()2210.9650.300 1.48 1.482 1.48⎡=+⨯+⎢⎣⨯ 0.354=(或计算137.6λ=,再由附表4-4查得0.354ϕ=)故得到稳定临界荷载为20.35426.1110215198.7crd d N Af kN ϕ==⨯⨯⨯=当改用Q365钢时,同理可求得 1.792λ=。
由式5-34b 计算得0.257ϕ= (或由166.7λ=,查表得0.257ϕ=)故稳定临界荷载为20.25726.1110310208.0crd d N Af kN ϕ==⨯⨯⨯=5.3 图5-25所示为一轴心受压构件,两端铰接,截面形式为十字形.设在弹塑性范围内/E G 值保持常数,问在什么条件下,扭转屈曲临界力低于弯曲屈曲临界力,钢材为Q235.5.4 截面由钢板组成的轴心受压构件,其局部稳定计算公式是按什么准则进行推导得出的.5.5 两端铰接的轴心受压柱,高10m,截面为三块钢板焊接而成,翼缘为剪切边,材料为Q235,强度设计值2205/d f N mm =,承受轴心压力设计值3000kN (包括自重).如采用图5-26所示的两种截面,计算两种情况下柱是否安全.图5-26 题5.5解答:截面特性计算: 对a)截面:32394112(5002020500260)8500 1.436101212x I mm =⨯⨯⨯+⨯⨯+⨯⨯=⨯ 3384112205005008 4.167101212y I mm =⨯⨯⨯+⨯⨯=⨯ 2250020500824000A mm =⨯⨯+⨯=244.6x i mm ==131.8y i mm==对b)截面:32384112(4002540025212.5)104009.575101212x I mm =⨯⨯⨯+⨯⨯+⨯⨯=⨯ 33841122540040010 2.667101212y I mm =⨯⨯⨯+⨯⨯=⨯ 24002524001024000A mm =⨯⨯+⨯=199.7x i mm ==105.4y i mm==整体稳定系数的计算:钢柱两端铰接,计算长度10000ox oy l l mm == 对a)截面: 1000040.88244.6ox x x l i λ=== 1000075.87131.8ox y y l i λ=== 对b)截面: 1000050.08199.7kx x x l i λ=== 1000094.88105.4ox y y l i λ=== 根据题意,查P106表5-4(a),知钢柱对x 轴为b 类截面,对y 轴为c 类截面.对a)截面:对x 轴:40.880.440x λπ===()223212x x x x ϕααλλλ⎡=++⎢⎣()2210.9650.30.440.4420.44⎡=⨯+⨯+-⎢⨯⎣0.895=(或计算40.88λ=,再由附表4-4查得0.896xϕ)对y 轴:25.870.816y λπ===()223212y y y y ϕααλλλ⎡=++⎢⎣()2210.9060.5950.8160.81620.816⎡=⨯+⨯+⎢⨯⎣0.604=(或计算75.87λ=,再由附表4-5查得0.604yϕ)故取该柱的整体稳定系数为0.604ϕ=对b)截面,同理可求得0.852x ϕ=,0.489y ϕ=,故取该柱截面整体稳定系数为0.489ϕ= 整体稳定验算:对a)截面 0.604240002052971.68 3000 crd d N Af kN kN ϕ==⨯⨯=<不满足。
