课程实践报告_汉诺塔

一、实习背景随着社会竞争的日益激烈，团队协作和综合素质成为职场成功的关键。

为了提升自身的团队协作能力和综合素质，我参加了由我国某知名培训机构举办的汉诺塔素质拓展实习。

本次实习旨在通过汉诺塔这个经典团队协作项目，锻炼我们的逻辑思维、沟通协作和问题解决能力。

二、实习内容1. 项目介绍汉诺塔（又称河内塔）是一个源于印度的古老传说。

传说中，有三位神父，他们需要将64个金盘从一根柱子搬运到另一根柱子上，每次只能移动一个金盘，且大金盘不能放在小金盘上面。

这个传说后来演变为汉诺塔游戏，成为团队协作和素质拓展的经典项目。

2. 实习过程在实习过程中，我们被分成若干个小组，每个小组拥有自己的三根柱子和64个金盘。

我们的任务是按照规则，将所有金盘从一根柱子移动到另一根柱子上。

（1）初始阶段：在培训师的引导下，我们小组进行了初步的讨论和分工。

大家纷纷提出自己的想法，但整体思路并不明确。

在培训师的指导下，我们逐渐明确了目标，并制定了初步的方案。

（2）实践阶段：按照方案，我们开始尝试移动金盘。

在这个过程中，我们遇到了许多困难，如沟通不畅、分工不明确、策略不当等。

我们不断调整策略，优化分工，逐步克服了困难。

（3）总结阶段：在完成了汉诺塔的移动后，我们小组进行了总结。

我们分析了在实习过程中遇到的问题，并提出了改进措施。

同时，我们还与其他小组进行了交流，学习他们的优点，为自己的团队提升提供了借鉴。

三、实习心得1. 团队协作的重要性通过汉诺塔实习，我深刻体会到团队协作的重要性。

在团队中，每个人都要发挥自己的优势，相互配合，共同解决问题。

只有团结一致，才能取得成功。

2. 沟通与协调在实习过程中，我们发现沟通与协调是团队协作的关键。

只有充分沟通，才能确保每个人都能明确自己的任务和责任，避免误解和冲突。

3. 策略与执行力在汉诺塔游戏中，制定合理的策略和执行力至关重要。

我们需要根据实际情况，不断调整策略，确保任务的顺利完成。

4. 耐心与毅力汉诺塔游戏具有一定的难度，需要我们具备耐心和毅力。

一、实验背景汉诺塔问题（Hanoi Tower Problem）是一个经典的递归问题，最早由法国数学家亨利·埃德蒙·卢卡斯（Edouard Lucas）在1883年提出。

该问题涉及三个柱子和一系列大小不同的盘子，初始时所有盘子按照从小到大的顺序叠放在一个柱子上。

问题的目标是按照以下规则将所有盘子移动到另一个柱子上：每次只能移动一个盘子，且在移动过程中，大盘子不能放在小盘子上面。

汉诺塔问题不仅是一个数学问题，也是一个计算机科学问题。

它在算法设计、递归算法分析等领域有着重要的应用价值。

通过解决汉诺塔问题，可以加深对递归算法的理解，同时也能够锻炼逻辑思维和问题解决能力。

二、实验目的1. 理解汉诺塔问题的基本原理和解决方法。

2. 掌握递归算法的设计和应用。

3. 分析汉诺塔问题的复杂度，为实际应用提供参考。

三、实验内容1. 实验环境：Windows操作系统，Python编程语言。

2. 实验步骤：（1）设计一个汉诺塔问题的递归算法。

（2）编写程序实现该算法。

（3）测试算法在不同盘子数量下的运行情况。

（4）分析算法的复杂度。

3. 实验程序：```pythondef hanoi(n, source, target, auxiliary):if n == 1:print(f"Move disk 1 from {source} to {target}")returnhanoi(n-1, source, auxiliary, target)print(f"Move disk {n} from {source} to {target}") hanoi(n-1, auxiliary, target, source)# 测试程序hanoi(3, 'A', 'C', 'B')```4. 实验结果：（1）当盘子数量为3时，程序输出以下移动序列：```Move disk 1 from A to CMove disk 2 from A to BMove disk 1 from C to BMove disk 3 from A to CMove disk 1 from B to AMove disk 2 from B to CMove disk 1 from A to C```（2）当盘子数量为4时，程序输出以下移动序列：```Move disk 1 from A to CMove disk 2 from A to BMove disk 1 from C to BMove disk 3 from A to CMove disk 1 from B to AMove disk 2 from B to CMove disk 1 from A to CMove disk 4 from A to BMove disk 1 from C to BMove disk 2 from C to AMove disk 1 from B to AMove disk 3 from C to BMove disk 1 from A to CMove disk 2 from A to BMove disk 1 from C to BMove disk 4 from B to CMove disk 1 from B to AMove disk 2 from A to CMove disk 1 from A to C```四、实验分析1. 算法复杂度：汉诺塔问题的递归算法具有指数级的复杂度，其时间复杂度为O(2^n)，其中n为盘子的数量。

汉诺塔实验报告
实验目的：
1. 了解汉诺塔问题的基本原理和规则；
2. 探究汉诺塔问题的解法方法；
3. 实现汉诺塔问题的自动解决。

实验器材：
1. 汉诺塔游戏盘；
2. 三个铁柱子；
3. 若干大小不同的木块。

实验步骤：
1. 将汉诺塔游戏盘放在桌子上，将三个铁柱子按照规定放好；
2. 将木块按照大小顺序放在游戏盘上的一个铁柱子上；
3. 学习汉诺塔的规则：第一，每次只能移动一个木块；第二，
大的木块不能在小的木块上面；
4. 准备按照规则玩一次汉诺塔游戏并记录操作步骤；
5. 研究汉诺塔问题的解法方法，探究能否有更高效的解法；
6. 利用编程语言，自编程序实现汉诺塔问题的解决；
实验结果：
通过汉诺塔游戏的实践操作，学生们掌握了汉诺塔问题的基本
原理和规则，学习了汉诺塔问题的解法方法，能够熟练操作解决
汉诺塔问题。

在编制汉诺塔问题的解决程序时，学生们运用了自己的思维和
编程技能，实现了木块的自动移动，大大提高了解决问题的效率。

结论：
汉诺塔问题是一种经典的数学问题，通过实验，我们对汉诺塔
问题有了更为深刻的理解。

实验得到的结果表明，通过编程语言
自编程序能够更为高效地解决问题，这为我们今后学习科学知识提供了很好的借鉴意义。

一、引言汉诺塔，一个古老的数学问题，源自印度的一个传说。

在实训过程中，我深刻体会到了汉诺塔问题的魅力，以及它所蕴含的数学原理和团队协作精神。

以下是我在实训过程中的心得体会。

二、汉诺塔问题概述汉诺塔问题是一个经典的递归问题，描述了三个柱子和若干个大小不同的盘子。

初始时，所有盘子都按照从大到小的顺序放置在第一个柱子上。

要求按照以下规则，将所有盘子移动到第三个柱子上：1. 每次只能移动一个盘子；2. 盘子只能从柱子顶端取出，并且只能放在另一个柱子的顶端；3. 大盘子不能放在小盘子下面。

三、实训过程及心得1. 实训目标本次实训旨在通过解决汉诺塔问题，培养我们的逻辑思维能力、递归算法设计能力以及团队协作精神。

2. 实训过程在实训过程中，我们首先学习了汉诺塔问题的基本概念和递归算法。

接着，我们分组进行实际操作，尝试解决不同层数的汉诺塔问题。

在操作过程中，我们遇到了许多困难，如如何设计递归算法、如何优化算法效率等。

3. 实训心得（1）递归算法的重要性通过实训，我深刻认识到递归算法在解决汉诺塔问题中的重要性。

递归算法能够将复杂的问题分解为更简单的问题，使得问题求解过程更加直观。

在实训过程中，我们通过递归算法成功解决了多层汉诺塔问题。

（2）团队协作精神汉诺塔问题不仅考验个人的逻辑思维能力，还考验团队协作精神。

在实训过程中，我们小组共同探讨、分析问题，互相学习、借鉴，最终成功解决了问题。

这使我认识到，在团队合作中，每个人都应发挥自己的优势，共同为团队目标努力。

（3）算法优化在实训过程中，我们不断尝试优化算法，以提高问题求解效率。

例如，我们可以通过记忆化搜索、动态规划等方法减少重复计算。

这使我认识到，在编程实践中，算法优化是非常重要的。

（4）实践与理论相结合通过实训，我深刻体会到实践与理论相结合的重要性。

在实训过程中，我们不仅学习了汉诺塔问题的理论知识，还通过实际操作巩固了所学知识。

这种实践与理论相结合的学习方式，有助于我们更好地掌握编程技能。

汉诺塔实验报告
一、实验目的：
1、掌握产生式系统解决汉诺塔算法的基本思想。

2、熟悉和掌握问题规约法的原理、实质和规约过程。

3、理解规约图的表示方法。

二、实验原理：
1、在移动盘子时，每次只移动A/B/C柱子上可以移动的盘子中最大的盘子。

2、如果上一次已经移动了某个盘子，则下一次不能继续移动，即：一个盘子不能被连续移动两次。

如：某次操作将1号盘子由A柱子移动到B柱子，那么在选择下一个要移动的盘子时应不在考虑1号盘。

3、当某个可以移动的盘子摆放位置不唯一时要将当前状态入栈，并选择盘子移动前所在的柱子的左侧（同理：反方向选择也可）柱子作为移动的目标柱子。

为提高程序运行过程中的空间利用率，产生式规则在汉诺塔移动过程中依据以上规则自动生成。

三、实验条件：
1、必须要有三个柱子A,B,C。

2、盘子的数量不能太多。

3、应该用自己熟悉的语言写程序。

四、实验步骤：
第一次移动之后：
第二次移动之后：
第三次移动之后：
五、实验内容：
利用c/c++语言编写汉诺塔程序，并实现盘子的移动过程。

六、实验小结：
通过本次实验我掌握了汉诺塔的算法和移动的过程，同时也更好的运用了c++的知识解决了这个问题，在做的过程中确实有不懂的地
方，但是查资料还是解决了，希望自己以后会更好的利用c++/c这们高级程序编写语言。

计算机学院实验报告课程名称：数据结构实验名称：汉诺塔学生姓名：朱孝彬学生学号：20110511001实验日期：2012一、实验目的1．理解数据结构中汉诺塔2．掌握汉诺塔的C++描述。

二、实验内容1．编制汉诺塔的程序。

三、实验步骤1．需求分析本演示程序用C++6.0编写，完成汉诺塔的生成，2．概要设计1）为了实现上述程序功能，需要定义单链表的抽象数据类型：（1）insert3. 源代码#include<stdio.h>#include<stdlib.h>#define MaxSize 30typedef struct{int data[MaxSize];char name;int top;}SqStack;void Move(SqStack * &a,SqStack * &b);int Hanoi(int n,SqStack * &a,SqStack * &b,SqStack * &c); void InitStack(SqStack * &s);int Push(SqStack * &s,int e); /*进栈*/int Pop(SqStack * &s,int &e); /*出栈*/void main(){int n,i;SqStack *a,*b,*c;InitStack(a);InitStack(b);InitStack(c);a->name='A';b->name='B';c->name='C';printf("请输入汉诺塔中圆环的个数n: ");scanf("%d",&n);for(int t=n;t>0;t--)Push(a,t);printf("\n\t假设有三根柱子A、B、C，开始时A柱子上有1~%d环，并且它们是按照从小到大的顺序放在A柱子上的，按照汉诺塔规则，将A柱子上所有环通过B柱子，移动到C柱子的则移动方法为：\n\n",n);i=Hanoi(n,a,b,c);free(a);free(b);free(c);printf("总共需要移动的次数为：%d次\n",i);}void InitStack(SqStack * &s) /*初始化栈*/{s=(SqStack *)malloc(sizeof(SqStack));s->top=-1;}int Push(SqStack * &s,int e) /*进栈*/{if(s->top==MaxSize-1)return 0;s->top++;s->data[s->top]=e;return 1;}int Pop(SqStack * &s,int &e) /*出栈*/{if(s->top==-1)return 0;e=s->data[s->top];s->top--;return 1;}int Hanoi(int n,SqStack * &a,SqStack * &b,SqStack * &c){static int i=0;if(n==1){Move(a,c);i++;}else{Hanoi(n-1,a,c,b);Move(a,c);i++;Hanoi(n-1,b,a,c);}return i;}void Move(SqStack * &a,SqStack * &b){int i;Pop(a,i);printf("\t\t\t%d环-->%c柱子\n",i,b->name); Push(b,i);}实验结果：1.当输入2时，运行结果如下：2. 当输入3时，运行结果如下：3. 当输入4时，运行结果如下：4. 当输入5时，运行结果如下：四、实验总结（结果分析和体会）本次试验中，在解决汉诺塔问题中，结合了最近刚学的栈的知识，并且运用到之前学到的函数的递归的运用，很好的解决了这一类问题。

一、实训背景河内塔，又称汉诺塔，起源于印度的一个古老传说，是一种经典的智力游戏。

在河内塔游戏中，玩家需要将一串大小不一的圆盘从一根柱子移动到另一根柱子上，同时遵守以下规则：1）每次只能移动一个圆盘；2）圆盘只能从上往下移动；3）大盘不能放在小盘上面。

河内塔游戏不仅是一种娱乐方式，更是锻炼思维能力和逻辑推理能力的有效途径。

二、实训目的1. 了解河内塔游戏的起源、规则和玩法。

2. 通过实际操作，掌握河内塔游戏的解题技巧。

3. 培养团队合作精神，提高团队协作能力。

4. 锻炼逻辑思维能力，提高创新能力。

三、实训内容1. 游戏规则介绍河内塔游戏由三根柱子组成，分别为A、B、C柱。

在A柱上放置一串大小不一的圆盘，要求将所有圆盘移动到C柱上，在移动过程中，必须遵循以下规则：（1）每次只能移动一个圆盘；（2）圆盘只能从上往下移动；（3）大盘不能放在小盘上面。

2. 游戏操作步骤（1）将圆盘按照从小到大的顺序依次放在A柱上，形成一个金字塔状；（2）按照规则，将圆盘从A柱移动到B柱或C柱上；（3）重复步骤（2），直到所有圆盘都移动到C柱上。

3. 解题技巧（1）先找出移动圆盘的顺序，即确定每一步应该移动哪个圆盘；（2）分析移动过程中可能出现的错误，如将大盘放在小盘上面等；（3）运用递归思想，将问题分解为更小的子问题。

四、实训过程1. 实训分组将参与实训的学员分成若干小组，每组人数相等，以便进行团队合作。

2. 游戏规则讲解由指导老师向学员讲解河内塔游戏的规则、操作步骤和解题技巧。

3. 游戏实践各小组按照规则进行游戏，尝试移动圆盘，解决问题。

4. 经验分享各小组分享在游戏过程中遇到的问题、解决方法以及心得体会。

5. 总结与反思指导老师对本次实训进行总结，强调河内塔游戏在培养思维能力和团队合作精神方面的作用。

五、实训成果1. 学员们掌握了河内塔游戏的规则和操作步骤；2. 学员们在游戏过程中培养了团队合作精神，提高了团队协作能力；3. 学员们的逻辑思维能力和创新能力得到了锻炼。

一、引言汉诺塔问题是一种经典的递归问题，起源于印度的一个古老传说。

该问题涉及三个柱子和若干个大小不一的盘子，要求按照一定的规则将盘子从第一个柱子移动到第三个柱子。

在解决汉诺塔问题的过程中，我们可以锻炼逻辑思维、递归算法设计以及编程能力。

本报告将详细介绍汉诺塔问题的背景、解决方法、实践过程及心得体会。

二、汉诺塔问题背景汉诺塔问题最早由法国数学家卢卡斯在1883年提出。

传说在古印度有一个名为汉诺塔的庙宇，庙里有一个汉诺塔塔，塔上有64个盘子，每个盘子大小不同，且按照从小到大的顺序叠放。

为了拯救世界，僧侣们需要将所有盘子从第一个柱子移动到第三个柱子，同时每次只能移动一个盘子，且在移动过程中，大盘子不能放在小盘子上面。

三、汉诺塔问题解决方法1. 递归算法汉诺塔问题可以通过递归算法来解决。

递归算法的基本思想是将大问题分解为若干个小问题，然后逐一解决小问题，最终解决大问题。

对于汉诺塔问题，我们可以将其分解为以下三个步骤：（1）将n-1个盘子从第一个柱子移动到第二个柱子；（2）将第n个盘子从第一个柱子移动到第三个柱子；（3）将n-1个盘子从第二个柱子移动到第三个柱子。

递归算法如下：```function hanoi(n, start, end, auxiliary) {if (n == 1) {console.log(`移动盘子1从${start}到${end}`);return;}hanoi(n - 1, start, auxiliary, end);console.log(`移动盘子${n}从${start}到${end}`);hanoi(n - 1, auxiliary, end, start);}```2. 动态规划除了递归算法，我们还可以使用动态规划的方法来解决汉诺塔问题。

动态规划的思想是将问题分解为若干个子问题，然后求解子问题，最后将子问题的解合并成原问题的解。

对于汉诺塔问题，我们可以定义一个二维数组dp[i][j]，表示将i个盘子从第一个柱子移动到第j个柱子的最小移动次数。

1、需求分析
设计任务：
在平面上有三个位置A、B、C，在A位置上有n个大小不等的圆盘、小盘压在大盘上形成圆盘堆。

要求将A位置的N个圆盘通过B位置移动到C位置上，并按同样的顺序叠放。

移动盘子时必须遵循以下规则：
（1）每次只能移动一个盘子
（2）圆盘可以放在A、B、C任何一个塔座上
（3）任何时刻都不能将大圆盘压在小圆盘上
针对任务需求分析：
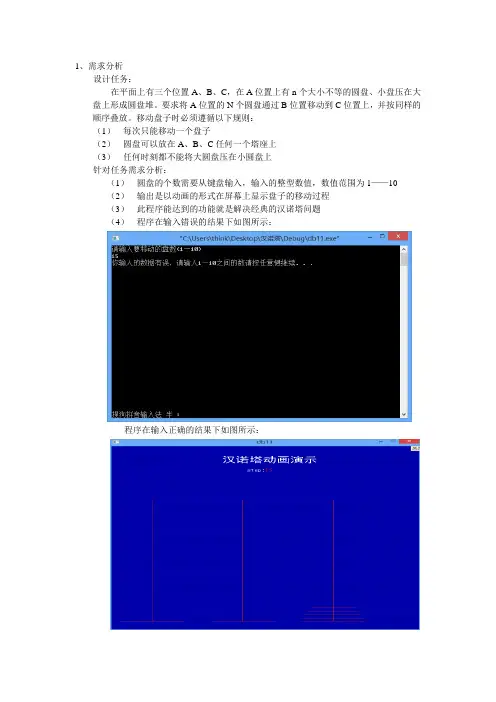
（1）圆盘的个数需要从键盘输入，输入的整型数值，数值范围为1——10
（2）输出是以动画的形式在屏幕上显示盘子的移动过程
（3）此程序能达到的功能就是解决经典的汉诺塔问题
（4）程序在输入错误的结果下如图所示：
程序在输入正确的结果下如图所示：
2、概要设计。