信息的数字化表示

《信息的数字化表示》教学设计教学目标：1、知识与技能：掌握利用数字设备将身边信息数字化的方法，了解信息来源的多样性及实际意义。

2、过程与方法:能根据贴近生活和学习的实际问题分析信息需求，确定所需信息类型和获取方式，能依据主题选取合适的信息内容,能对学习过程和成果进行认真的评价，进一步提升合作学习的能力。

3、情感态度价值观:培养学生的发现、创新与探索能力，实际动手操作能力，培育学生的创新精神、审美能力,展示自我能力知识要点：1、获取数字化声音信息能运行使用附件里的录音机录制声音文件并保存2、获取数字化图像、视频信息（1）能运行摄像头软件获取图像（2）能将BMP文件转化为JPEG文件格式(3）能使用摄像头获取视频文件3、加工处理获取信息（1）能简单加工处理信息。

如用Photoshop、画图软件加工处理等（2）用PowerPoint将获取的信息制作电子作品4、评价量规（1）完成《资料收集情况表》的填写（2）参照评价量规作自我评价教学重点、难点：重点：在了解信息获取的常用渠道基础上,学习使用麦克和摄像头获取身边的信息,将其数字化，并能简单加工处理。

在学习过程中提升合作学习能力。

难点：在获取信息过程中的创新精神和审美能力的培养。

教学设计分析：1、教学内容分析这节课的主要内容信息是数字化表示，能利用麦克、摄像头将生活中的信息转化为数字化信息，并将获得的信息简单加工处理，结合PowerPoint和Photoshop软件制作。

因此本节课的教学内容可分为三大部分：（1）获取数字化信息;（2）简单加工处理信息；(3)交流与评价.第一部分是利用麦克、摄像头获取声音、图像、视频信息。

第二部分是利用计算机中的图像处理软件和媒体制作播放软件等工具打开一些文本、图像、音频和视频等文件,试着将其转换成其他格式的同类型文件，比较这些不同文件格式有些什么特点,最后用PowerPoint制作一个电子作品第三部分是交流与评价：学生完成资料搜集汇总表的填写，根据多渠道获取信息的评价量规作作自我评价,然后通过对获取信息进行设计加工布局及参加活动的积极性进行组内评选，推荐作品，选出优秀作品进行展示,教师点评，评价要点:过程性资料齐全（选题及相关内容设计，资料收集情况表,数字化成果）；能根据实际问题分析需求，所选内容能很好的表现主题；能根据需要选择合理的信息来源，从多渠道获取信息；完成对获得信息的简单加工整理.2、教学对象分析：学生已经了解掌握利用麦克、摄像头获取声音、图像、视频信息,学生能利用图像处理软件Photoshop、媒体制作播放软件简单加工获取的信息。

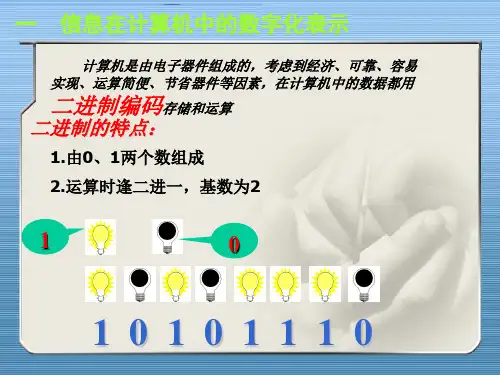
计算机中信息的表示方法计算机要处理的信息是多种多样的，如日常的十进制数、文字、符号、图形、图像和语言等。

但是计算机无法直接“理解”这些信息，所以计算机需要采用数字化编码的形式对信息进行存储、加工、和传送。

信息的数字化表示就是采用一定的基本符号，使用一定的组合规则来表示信息。

计算机中采用的二进制编码，其基本符号是“0”和“1”。

一、进制计数的方法有很多种，在日常生活中我们最常见的是国际上通用的计数方法——十进制计数法。

但是除了十进制外还有其他计数制，如一天24小时，称为24进制，一小时60分钟，称为60进制，这些称为进位计数制。

计算机中使用的是二进制。

这几种进制采用的都是带权计数法，它包含两个基本要素：基数、位权。

基数是一种进位计数制所使用的数码状态的个数。

如十进制有十个数码：0、1、2……7、8、9，因此基数为10。

二进制有两个数码：0和1，因此基数为2。

位权表示一个数码所在的位。

数码所在的位不同，代表数的大小也不同。

如十进制从右面起第一位是个位，第二位是十位，第三位是百位，……。

“个（100）、十（101）、百（102）、千（103）……”就是十进制位的“位权”。

每一位数码与该位“位权”的乘积表示该位数值的大小。

如十进制中9在个位代表9，在十位上代表90。

二进制的表示一般一个长度为n 的二进制数a n-1……a1a0,用科学计数法表示为：a n-1……a1a0= a n-1×2n-1＋……a1×21＋a0×20。

例如，二进制数10101用科学计数法表示：10101=1×24＋0×23＋1×22＋0×21＋1×20。

进制转换在计算机世界中还涉及到八进制、十进制和十六进制。

下面将讲述这几种进制之间的转换。

1．二进制与十进制的转换（1）二进制转十进制方法：“按权展开求和”例：（1011.01）2＝（1×23＋0×22＋1×21＋1×20＋0×2－1＋1×2－2）10＝（8＋0＋2＋1＋0＋0.25）10＝（11.25）10（2）十进制转二进制·十进制整数转二进制数：“除以2取余，逆序输出”例：（89）10＝（1011001）22 892 44 (1)2 22 02 11 02 5 (1)2 2 (1)2 1 00 (1)·十进制小数转二进制数：“乘以2取整，顺序输出”例：(0．625)10= (0．101)20．625X 21．02．八进制与二进制的转换例：将八进制的37．416转换成二进制数：3 7 ．4 1 6011 111 ．100 001 110即：（37．416）8 ＝（11111．10000111）2例：将二进制的10110．0011 转换成八进制：0 1 0 1 1 0 ．0 0 1 1 0 02 6 ．1 4即：（10110．011）2＝（26．14）83．十六进制与二进制的转换例：将十六进制数5DF．9 转换成二进制：5 D F ．90101 1101 1111 ．1001即：（5DF．9）16＝（10111011111．1001）2例：将二进制数1100001.111 转换成十六进制：0110 0001 ．11106 1 ． E即：（1100001．111）2＝（61．E）16二进制的运算：算术运算:加法：0+0=0 ，0+1=1，1+0=1，1+1=10减法：0－0=0，1－0=1，1－1=0，10－1=1乘法：0*0=0，0*1=0，1*0=0，1*1=1位运算与：0 and 0=0 , 0 and 1=0 , 1 and 0=0 , 1 and 1=1或：0 or 0 =0 , 0 or 1=1 , 1 or 0=1 , 1 or 1=1非：not 0=1 , not 1=0异或：0 xor 0=0 , 0 xor 1=1 , 1 xor 0 =1 , 1 xor 1 =0位移运算左移（二进制数k左移n位）：k shl n = k * 2n右移（二进制数k右移n位）：k shr n = k div 2n例：求下列二进制数运算的结果101+101=1010101*11=11111000－11=1011001 shl 2=1001001100110 shr 2 =11001二、计算机中数的表示在普通数字中，用“+”或“—”符号在数的绝对值之前来区分数的正负。

教学案例一：课题：信息的数字化表示――编码教学要求：使学生进一步理解数的编码方式，并能进行数制的转换。

教学重难点：把十进制数转换成二进制数。

教学器材：演示用计算机、数字投影机或计算机教学网络教学过程：1．引言信息时代几乎一切信息都要转换成数字，才能用计算机和通信技术进行传播和交流。

用数字表示各种信息，叫做信息的数字化表示，也叫信息的编码，这是信息技术的重要环节。

这节课我们一起来学习：数的编码方式。

2．十进制和二进制向学生分别介绍十进制数和二进制数的特点。

(1)把十进制整数转换为二进制数因为同学们第一次进行这种运算，所以老师必须一步一步讲清楚，让同学掌握数制转换的方法。

(2)除2取余把一个十进制整数转换为十进制数，只要将这个十进制整数一次又一次地被2除，得到的余数（从最后一次的余数写起）就是用二进制表示的数。

[例1] 把十进制数17转换为二进制数解：∴17（10）＝10001(2)＝(2)让学生练习：11（10）92（10）＝(2)129（10）＝(2)136（10）＝(2)248（10）＝(2)注意：把一个十进制数转换为二进制数，整数部分可以用除2取余法，对于小数部分就用基数2连续去乘它，直到乘积的小数部分等于“0”为止。

如果十进制小数不能用有限位二进制小数表示时，那么可以根据对精度的要求，选取一定的位数。

下面列举两个例子：[例2] 把十进制数123.75转换为二进制数解：十进制数进位0.75×2=1.5 10.5×2=1 1∴123.75＝1111011.11(2)（10）[例3] 把十进制数0.65转换为二进制数解：十进制数进位0.65×2=1.30 10.3×2=0.6 00.6×2=1.2 10.2×2=0.4 00.4×2=0.8 00.8×2=1.6 10.6×2=1.2 1∴0.65（10）＝0.1010011(2)+∈∈是尾数误差,∈<2－7通过上述例子的讲授和学生适应练习（学生练习可以让几个学生到黑板上做，其他学生做在练习本上。

信息的表示信息的数字化表示一、通信的回顾数据通信也许可以追溯到“烽火戏诸候”的典故。

夜晚点火或白天点狼烟表示有敌人入侵，可称为“1”状态，无火或狼烟表示平安无事，称为“0”状态。

通信是从1838年莫尔斯发明电报算起，一个多世纪以来，通信可以大致划分三个阶段：1838年电报开始的通信的初级阶段；1948年香农提出信息论开始的近代通信阶段；80年代以后的光纤通信应用、综合业务数字网的崛起的现代通信阶段。

二、消息、信息、信号1、消息是指有待于传输的语音、图象、图片和文字、数字、数据等。

前者为连续消息（指消息状态连连续消息续变化），后者为离散消息（指消息离散消息状态是可数的或离散的）。

消息为信息的载体。

载体2、信息信息：指消息中包含的有意义的内容。

通信中信息：的信息可以度量，它和消息中某事件发生的不确定性（概率）有关。

信息量：是对消息中所含信息多少的一种度量。

信息量：在信息论中，消息所含的信息量单位是bit （比特）。

3、信号在通信中，消息常用电信号的某个电参量的变化来表示，故信号是与消息一一对应的电量。

这种携带特定消息的电信号通常称为信号。

电信号同时消息也可用非电信号来表示，如磁信号、光信号等，这些信号可以通过一定方式的转换成为电信号。

4、模拟信号和数字信号模拟信号：信号中代表消息的电参量的状态数为无穷多个，在幅度上和时间上连续变化的信号。

这种信号称为模拟信号。

数字信号：相对模拟信号，若代表消息的电参量的状态数为有限个，则称之为数字信号。

相对而言，模拟信号比较适合于传输，数字信号则比较适合于处理。

三、通信系统简介1、通信系统的基本组成（点对点）：发送设备信道接收设备通信：指信息传递的全过程，即信息的传输与交换。

利用电信号来传递信息的方式称为“电通信”，简称为通信。

电通信信道：传递信号的通道。

从概念上讲，信道和电路并不等同，信道一般都是用来表示向某一个方向传送信息的媒体，而一条通信电路则往往包括一条发送信道和一条接收信道。

《信息的数字化表示》教学设计教学过程设计教学环节教师活动学生活动设计意图一、情景导入，激发兴趣（2min）1.情景导入制作好A、B、C、D四张不同的卡纸，分别贴上不同的月份，学生说出自己的生日月份出现在哪几张卡纸上，教师说出他的月份。

学生积极参与到游戏当中，产生浓厚的兴趣和强烈的求知欲。

通过设置情景和悬念，激发学生的学习动机，进而引起学习兴趣。

二、信息的数字化（30min）1.计算机和二进制计算机是基于二进制运行，信息要能够被计算机处理，必须数字化为二进制。

十进制有0~9十个数码，逢十进一；二进制有0、1两个数码，逢二进一；十六进制有0~9、a~f十六个数码，逢十六进一。

活动1：用计算器进行数值转换：2.文字编码在word中，通过【插入】——【符号】，打开符号对话框，通过字符对话框，可以翻译出老师给的数字所代表的文字。

活动2：星座解密向学生介绍文字的编码：在计算机中，为每一个字符都指定一个唯一对应的数字作为编码。

3.二维码的原理先演示用二维码工具如何生成二维码，制作二维码签名。

然后介绍二维码编码的原理。

二维码是图片和文字的混合体，二维码本身是以图形的方式呈现，但编码的是文本信息。

活动4：将生成的二维码签名粘贴到任务文档中，然后上交。

互动：教师展示学生提交的文件，识别其中的二维码，解密学生数字化的文字。

听讲：明确计算机是基于二进制运行的。

通过类比十进制，学习二进制和十六进制。

练习：用计算器进行进制转换。

完成活动2：教师展示一组数字，通过字符对话框查看数字所对应的字符，解密老师的星座听讲:理解文字编码的方式完成活动3。

用二维码工具制作签名。

听讲二维码的原理。

完成活动：将二维码签名插入任务计算机基于二进制，人类习惯的是十进制。

为了兼顾人类和计算机，介绍十六进制。

同时为后面的活动做铺垫。

强调本节课重点：文字的编码。

让学生亲自制作二维码，同时引导学生注意观察和思考生活中新生事物。

文档中。

三、扩展提升（5min)1.图片编码(3min)结合PPT介绍图片的数字化方式。