棱锥的概念和性质.

初中数学复习解谜棱锥与棱柱的性质与计算方法初中数学复习解谜：棱锥与棱柱的性质与计算方法在初中数学学习中，我们学习了许多几何图形的性质与计算方法，其中包括了棱锥和棱柱。

在本文中，我们将探讨这两种几何图形的特点、属性和计算方法。

一、棱锥的性质与计算方法1. 棱锥的定义棱锥是指一个顶点和一组边，其中除了顶点外的其他点都在同一个平面内，而相交的边则相交于一个顶点。

棱锥的顶点称为尖端，该棱锥的底面是一个多边形，而其侧面是由尖端与底面上的各个顶点相连而成的。

2. 棱锥的性质（1）棱锥的底面是一个多边形，其边数决定了棱锥的类型，例如三角棱锥、四边形棱锥等。

（2）棱锥的侧面是由尖端与底面上的各个顶点相连而构成的。

（3）棱锥的高是指从尖端到底面的垂直距离。

3. 棱锥的计算方法（1）棱锥的表面积计算方法公式为：表面积 = 底面积 + 侧面积（2）棱锥的体积计算方法棱锥的体积是指由底面上所有顶点与尖端依次相连而成的三角锥的体积之和。

计算公式为：体积 = 1/3 ×底面积 ×高度二、棱柱的性质与计算方法1. 棱柱的定义棱柱是指底面为一个多边形，而侧面是由底面上的各个顶点与对应顶点相连而成的直线段组成的几何图形。

2. 棱柱的性质（1）棱柱的底面是一个多边形，其边数决定了棱柱的类型，例如三角棱柱、四边形棱柱等。

（2）棱柱的侧面是由底面上的各个顶点与对应顶点相连而构成的。

（3）棱柱的高是指两个并行底面之间的距离。

3. 棱柱的计算方法（1）棱柱的表面积计算方法和。

计算公式为：表面积 = 2 ×底面积 + 侧面积（2）棱柱的体积计算方法棱柱的体积是指由底面上的各个顶点与对应顶点相连而成的所有矩形的体积之和。

计算公式为：体积 = 底面积 ×高度三、棱锥与棱柱的比较1. 相同点棱锥和棱柱都是由底面和侧面组成的几何图形，都有底面积和高度的概念，都可以计算表面积和体积。

2. 不同点（1）形状不同：棱锥的底面是一个多边形，而棱柱的底面也是一个多边形，但是两者的底面形状可以不同。

小学数学知识归纳掌握棱锥和棱锥的性质棱锥是一种常见的几何图形，它由一个底面和多条侧边构成。

在小学数学中，学生需要了解棱锥的性质以及相关的数学知识。

接下来，本文将归纳掌握棱锥的性质，并对相关概念进行解释。

1. 棱锥的定义与性质棱锥是由一个多边形（底面）和一些连接多边形顶点和一个点（顶点）的线段（侧边）所构成的立体图形。

棱锥的侧边数目取决于多边形的边数。

据此可知，棱锥具有以下性质：- 棱锥必定有一个顶点和一个底面，顶点是由侧边所汇聚而成。

- 棱锥的侧边数目与多边形的边数有关。

- 如果棱锥的侧边数目为3，则它是一个三棱锥；如果侧边数目为4，则为四棱锥，以此类推。

2. 棱锥的种类根据底面的形状，棱锥可以分为不同的种类：- 三棱锥：底面是一个三角形，侧边有3条。

- 四棱锥：底面是一个四边形，侧边有4条。

- 五棱锥：底面是一个五边形，侧边有5条。

- 六棱锥：底面是一个六边形，侧边有6条。

- 依此类推，可以有七棱锥、八棱锥等。

3. 与棱锥相关的数学知识在学习棱锥的过程中，学生还需要了解一些与棱锥相关的数学知识，例如：- 底面与侧面：棱锥的底面是由连接顶点的线段所围成的多边形。

与底面相邻的面是侧面，因为它们有一个公共的边。

- 顶点角：顶点角是由侧边所围成的角。

对于一个n棱锥（n > 3），顶点角的个数为n个。

- 高度：棱锥的高度是从顶点到底面的垂直距离。

- 表面积：棱锥的表面积由底面积和所有侧面积之和构成。

- 体积：棱锥的体积可以通过公式V = (1/3) * 底面积 * 高度来计算。

4. 棱锥的应用棱锥是几何学中的重要概念，它在现实生活中有广泛的应用，例如：- 施工业：在建筑和工程领域中，棱锥的概念被应用于设计各种形状的建筑和结构。

- 包装工业：许多包装盒的形状可以近似看作棱锥。

- 地理测量学：地球的地壳形状可用棱锥来近似表示。

- 自然界中的晶体：许多晶体的形状与棱锥相似。

本文对小学数学中的棱锥及其性质进行了归纳与解释。

棱锥的性质及其计算公式棱锥是一种几何体，具有一定的性质和计算公式。

本文将介绍棱锥的性质，并提供相关的计算公式。

首先，棱锥是由一个多边形的底面和一个顶点连接而成的立体图形。

底面可以是任意形状的多边形，而顶点与底面上的各个顶点连线的线段称为棱。

棱锥的侧面是由底面上的各个顶点与顶点连线所围成的三角形。

根据底面的形状不同，可以有正棱锥、直棱锥、斜棱锥等不同类型的棱锥。

棱锥有以下几个重要的性质：1. 底面积：棱锥的底面积可以根据具体的底面形状来计算。

例如，如果底面是一个正多边形，则可以根据正多边形的边长和边数来计算底面积。

若底面面积为A，则底面积公式为：A = (n * s^2) / (4 * tan(π/n))其中，n表示底面多边形的边数，s表示底面边长，π为圆周率。

2. 侧面积：棱锥的侧面积指的是所有侧面三角形的面积之和。

侧面积的计算与底面形状和棱锥的高度有关。

对于任意形状的底面，可以使用海伦公式将侧面积计算为三角形三边长度的函数。

3. 总表面积：棱锥的总表面积等于底面积加上侧面积。

即S = A + L其中，S表示总表面积，A表示底面积，L表示侧面积。

4. 体积：棱锥的体积可以根据底面积和棱锥高度来计算。

体积的计算公式为：V = (A * h) / 3其中，V表示体积，A表示底面积，h表示棱锥的高度。

除了以上的基本性质，棱锥还涉及到一些其他的概念和计算公式：5. 斜高：棱锥的斜高是指从棱锥顶点到底面上一条边的距离。

斜高可以使用勾股定理计算，即斜高^2 = 高^2 + 距离^2其中，高表示棱锥的高度，距离表示从顶点到底面上一条边的垂直距离。

6. 母线：棱锥的母线是由棱锥顶点连接到底面上一条边上的点的线段。

母线的长度可以使用勾股定理计算，即母线^2 = 高^2 + 距离^2其中，高表示棱锥的高度，距离表示从顶点到底面上一条边的垂直距离。

综上所述，棱锥是一种由底面和顶点组成的立体图形，具有多个性质和计算公式。

棱柱与棱锥的概念与性质棱柱与棱锥是几何学中常见的三维图形，它们在数学和物理学等领域有着广泛的应用。

本文将对棱柱与棱锥的概念进行介绍，并探讨它们的性质和特点。

一、棱柱的概念与性质棱柱是由两个平行的多边形底面和它们之间的若干个侧面组成的立体图形。

其中，多边形底面的边数决定了棱柱的名称，例如三角形底面的棱柱称为三棱柱，四边形底面的棱柱称为四棱柱，以此类推。

（1）棱柱的特点在棱柱中，底面和顶面是平行的，并且底面的对应边和顶面的对应边相互平行。

此外，棱柱的侧面由底面的各个顶点和顶面的对应顶点之间的线段组成，这些线段称为棱。

因此，棱柱的名称即为棱的总和。

（2）棱柱的面积和体积棱柱的面积等于底面的面积加上底面与顶面之间的若干个侧面的面积之和。

具体地，棱柱的表面积为：底面积 + 侧面积 = 底面积 + 棱长×棱的数量。

棱柱的体积等于底面的面积乘以棱长。

因此，我们可以用以下公式计算棱柱的体积：体积 = 底面积 ×棱长。

二、棱锥的概念与性质棱锥是由一个多边形底面和它的顶点以及底面的各个顶点之间的直线段组成的立体图形。

与棱柱不同的是，棱锥只有一个底面，而棱柱有两个平行的底面。

（1）棱锥的特点在棱锥中，底面是一个多边形，顶点位于多边形的正上方。

底面的各个顶点与顶点之间的线段称为棱。

同样，棱锥的名称即为棱的总和。

（2）棱锥的面积和体积棱锥的面积等于底面的面积加上底面与顶点之间的若干个侧面的面积之和。

具体地，棱锥的表面积为：底面积 + 侧面积 = 底面积 + 各侧面的面积之和。

棱锥的体积等于底面的面积乘以高，并除以3（三棱锥）或者是高乘以底面积，并除以3（四棱锥）。

因此，我们可以用以下公式计算棱锥的体积：体积 = 底面积 ×高 ÷ 3。

三、棱柱与棱锥的应用棱柱与棱锥在日常生活和工程实践中有着广泛的应用。

例如，在建筑领域，棱柱形状的建筑物如柱子、烟囱等被广泛使用。

同时，棱锥形状的物体如手指、纸锥、礼帽等也是我们常见的物品。

棱锥与棱台的概念棱锥和棱台是几何学中的两个重要概念，它们都属于多面体的一种。

下面我将分别对棱锥和棱台进行详细的介绍。

一、棱锥棱锥是由一个多边形的底面和一个顶点连接底面上各个顶点的直线段所组成的几何体。

棱锥的特点是顶点只有一个，底面是一个多边形，而侧面是由底面上的各个顶点和顶点连线所组成的三角形。

棱锥的侧面数量与底面的边数相等。

棱锥的分类：1. 正棱锥：底面是一个正多边形，且顶点到底面各顶点的距离相等。

2. 斜棱锥：底面是一个任意多边形，且顶点到底面各顶点的距离不相等。

棱锥的性质：1. 棱锥的底面积加上各个侧面的面积之和等于棱锥的表面积。

2. 棱锥的体积等于底面积乘以高再除以3。

二、棱台棱台是由两个平行的多边形底面和连接底面上对应顶点的直线段所组成的几何体。

棱台的特点是顶点和底面上的各个顶点都连成一条直线，且底面和顶面平行。

棱台的侧面是由底面上的各个顶点和顶面上的对应顶点连线所组成的梯形。

棱台的分类：1. 正棱台：底面和顶面都是正多边形，且底面和顶面平行。

2. 斜棱台：底面和顶面都是任意多边形，且底面和顶面平行。

棱台的性质：1. 棱台的底面积加上顶面积加上各个侧面的面积之和等于棱台的表面积。

2. 棱台的体积等于底面积乘以高再除以3。

总结：棱锥和棱台都是由多边形组成的几何体，它们的区别在于棱锥只有一个顶点，而棱台有两个平行的底面。

棱锥的侧面是由底面上的各个顶点和顶点连线所组成的三角形，而棱台的侧面是由底面上的各个顶点和顶面上的对应顶点连线所组成的梯形。

棱锥和棱台的体积都可以通过底面积乘以高再除以3来计算。

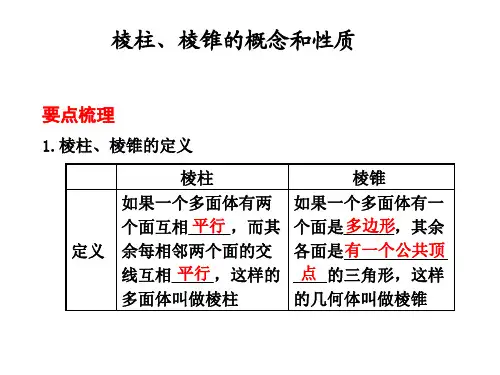
高二数学棱锥基本性质及其应用本周学习内容：棱锥的性质、侧面积公式及体积公式；本周学习重点：棱锥的性质及其应用一、基本概念1. 定义、概念：有一个面是多边形，其余各面是有一个公共顶点的三角形，由这些面构成的几何体叫棱锥。

2. 分类：按底面多边形的数，(底面、侧面、棱、侧棱、顶点、高、斜高)3. 棱锥的性质：1. 平行于底面的截面与底面是相似的多边形；2. 有一个面是多边形，其余各面是三角形，但反之不然。

4. 正棱锥定义：如果一个棱锥的底面是正多边形，并且顶点在底面上的射影是底面的中心，这样的棱锥叫正棱锥。

判断一个棱锥是否是正棱锥必须满足下列两个条件：一是底面是正多边形，二是顶点在底面上的射影是正多边形的中心。

5. 正棱锥的性质：1. 各侧棱相等，各侧面都是全等的等腰三角形，各等腰三角形底边上的高相等，它叫做正棱锥的斜高；2. 棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形；棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形。

6. 棱锥的体积及侧面积：；棱锥的侧面积等各侧面三角形面积之和。

二、相关例题：例1. 判断问题：(1)底面是正多边形的棱锥是正棱锥。

( )(2)所有的侧棱都相等的棱锥是正棱锥。

( )(3)侧面是全等的等腰三角形的棱锥是正棱锥。

( )例2. 如图正四面体ABCD中，E为棱AD的中点，则CE与平面BCD所成角的大小为( C )A. 30°B. 60°C.D.例3.若正三棱锥的侧面积是底面积的2倍，则底面与底面所成的二面角是( D )(A)15° (B)30° (C)45° (D)60°分析：可利用二面角的定义或者说二面角的投影面积公式得到答案例4.正四棱锥的侧棱与底面成45°角，则侧面与底面所成二面角的正弦值为( D )(A)(B)(C)(D)分析：可设棱高为1，通过转化可得顶点在底面的射影到正多边形的距离，进而可得。

七年级有关棱锥的知识点棱锥是一种几何体，由一个多边形的底面和相连的三角形面组成。

在七年级数学学习中，棱锥是一个比较重要的概念，掌握相关知识对于学生来说是非常必要的。

下面我们将介绍有关棱锥的各种知识点。

一、棱锥定义棱锥是一种几何体，由一个多边形的底面和相连的三角形面组成。

底面的任意两点之间都可以用棱线连接起来，并在每条棱线的一端连接一条三角形面，形成一个尖端。

尖端处的三角形面称为棱锥的顶面，连接顶面的每一条棱线都称为棱锥的母线。

棱锥的高是从顶面到底面的垂直距离。

二、棱锥分类1. 正棱锥：当上下底面为正多边形且底面中心与顶点连线垂直时，称其为正棱锥。

2. 锥顶角：将任意一点向顶点作射线，这条射线与棱锥底面相交成角，称为锥顶角。

3. 棱锥的性质：- 棱锥的侧面是由底面上的每一条边与顶面连接而成；- 棱锥的侧面三角形两边之和大于第三边；- 棱锥的底面视情况而定，可以是任何多边形。

三、棱锥图形的测量1. 棱锥体积公式：棱锥的体积可以用下式来计算：V = 1/3 ×底面面积 ×高其中，底面面积指的是棱锥底面所围成的面积大小，高为从顶面到底面的垂直距离。

2. 棱锥侧面积公式：棱锥的侧面积可以用下式来计算：S = 1/2 ×母线 ×母线生成的三角形面积其中，母线指的是棱锥底边的一条边，母线生成的三角形面积指的是以该条母线为斜边的棱锥侧面三角形围成的面积。

综上所述，棱锥是一种基本几何体，在七年级数学的双入口阶段中，掌握棱锥的相关知识点是很重要的。

希望通过本文的介绍，能够帮助学生们更好的理解和掌握棱锥的知识。

计算棱锥的体积与表面积的公式及应用数学是一门抽象而又实用的学科，它贯穿于我们生活的方方面面。

在初中数学中，我们学习了很多基本的几何概念和公式。

今天，我将向大家介绍如何计算棱锥的体积与表面积的公式及应用。

一、棱锥的定义与性质棱锥是由一个多边形的底面和一个顶点连接而成的几何体。

棱锥的性质有很多，其中最重要的是它的底面是一个多边形，而其他的面都是三角形。

这个性质将会在计算棱锥的体积与表面积时发挥重要作用。

二、棱锥的体积计算公式计算棱锥的体积是我们最常见的问题之一。

棱锥的体积公式是：体积 = 底面积×高 ÷ 3。

其中，底面积是底面的面积，高是从顶点到底面的垂直距离。

举个例子来说明。

假设我们有一个底面为正方形的棱锥，边长为a，高为h。

那么，这个棱锥的底面积就是a²，体积就是a² × h ÷ 3。

同样地，如果底面是一个圆形，半径为r，那么棱锥的底面积就是πr²，体积就是πr² × h ÷ 3。

三、棱锥的表面积计算公式计算棱锥的表面积也是我们常常遇到的问题。

棱锥的表面积公式是：表面积 =底面积 + 侧面积。

其中，底面积是底面的面积，侧面积是所有侧面的面积之和。

对于一个底面为正方形的棱锥，边长为a，高为h。

底面积就是a²，侧面积是四个三角形的面积之和，即4 × (1/2 × a × h)。

所以，这个棱锥的表面积就是a² + 4× (1/2 × a × h)。

如果底面是一个圆形，半径为r，那么棱锥的底面积就是πr²，侧面积是所有侧面的面积之和，即(1/2 ×圆周长 ×高)。

所以，这个棱锥的表面积就是πr² + (1/2 ×圆周长 × h)。

四、棱锥的应用棱锥的计算公式在实际生活中有很多应用。

棱柱和棱锥知识点归纳总结棱柱和棱锥是几何学中常见的立体图形，它们都具有特定的几何属性和计算方法。

本文将对棱柱和棱锥的定义、性质和计算方法进行归纳总结。

一、棱柱的定义与性质棱柱是指具有两个平行的底面，并且侧面由若干个连接两个底面相对点的四边形构成的立体图形。

棱柱的侧面都是平行四边形，而底面则可以是任意形状的多边形。

棱柱的性质包括：1. 底面：棱柱有两个相同形状的底面，且底面之间平行。

2. 侧面：棱柱的侧面是若干个平行四边形，且平行四边形两对边相互平行。

3. 高度：棱柱的高度是两个底面之间的垂直距离。

4. 体积：棱柱的体积等于底面面积乘以高度，即V = 底面积 ×高度。

5. 表面积：棱柱的表面积等于底面积加上所有侧面的面积之和。

二、棱锥的定义与性质棱锥是指具有一个底面和一个顶点，并且侧面由底面上的点与顶点相连而成的三角形构成的立体图形。

棱锥的底面可以是任意形状的多边形，而侧面都是三角形。

棱锥的性质包括：1. 底面：棱锥有一个底面，可以是任意形状的多边形。

2. 顶点：棱锥有一个顶点，位于侧面的同一平面上。

3. 侧面：棱锥的侧面是若干个三角形，每个三角形的一个顶点是棱锥的顶点。

4. 高度：棱锥的高度是从顶点向底面垂直引出的线段。

5. 体积：棱锥的体积等于底面积乘以高度再除以3，即V = (底面积×高度) / 3。

6. 表面积：棱锥的表面积等于底面积加上所有侧面的面积之和。

三、棱柱和棱锥的计算方法1. 底面积的计算：棱柱和棱锥的底面积可以根据底面的形状来计算，比如矩形的底面积等于长乘以宽，三角形的底面积等于底边乘以高再除以2。

2. 侧面积的计算：棱柱和棱锥的侧面积可以根据其侧面的形状来计算，比如平行四边形的侧面积等于底边乘以高，三角形的侧面积等于底边乘以高再除以2。

3. 体积的计算：棱柱的体积等于底面积乘以高度，棱锥的体积等于底面积乘以高度再除以3。

通过了解棱柱和棱锥的定义、性质以及计算方法，我们可以更好地理解和运用这两个几何图形。

初中数学知识归纳棱锥的基本概念与性质在初中数学中，我们学习了很多几何形体的知识，其中包括棱锥。

本文将对棱锥的基本概念和性质进行归纳总结。

通过对棱锥的深入了解，我们可以更好地理解和运用这一几何形体。

一、棱锥的定义棱锥是由一个多边形的一个顶点和其他顶点连线所围成的几何体。

这个多边形叫做底面，其他顶点叫做棱锥的顶点，连接底面和顶点的线段叫做棱锥的侧面。

二、棱锥的分类根据棱锥底面的形状，我们可以将棱锥分为不同的类型，比如三角锥、四边形锥、五边形锥等等。

1. 三角锥：棱锥的底面是一个三角形，侧面是由底面的三条边和顶点连接而成的三个三角形。

2. 四边形锥：棱锥的底面是一个四边形，侧面是由底面的四条边和顶点连接而成的四个三角形。

3. 五边形锥：棱锥的底面是一个五边形，侧面是由底面的五条边和顶点连接而成的五个三角形。

以此类推，根据底面形状的不同，我们可以得到不同类型的棱锥。

三、棱锥的性质除了以上的分类，棱锥还有一些基本的性质，它们有助于我们理解和计算棱锥的各个方面。

1. 棱锥的顶角：棱锥的顶点所对应的角叫做棱锥的顶角。

棱锥的顶角可以由顶点和底面上的两个相邻顶点连接线所围成。

2. 棱锥的高：棱锥的高是从顶点到底面上垂直的一条线段。

我们可以通过底面到顶点的长度和顶角的大小来计算棱锥的高。

3. 棱锥的体积：棱锥的体积是指棱锥所包围的三维空间的容积大小。

计算棱锥的体积可以使用公式V=1/3Ah，其中A表示底面的面积，h表示棱锥的高。

四、棱锥的应用棱锥作为几何形体，有着广泛的应用。

以下是一些常见的应用场景：1. 建筑学：许多建筑物的屋顶形状就是棱锥，例如一些教堂或塔楼的尖顶。

2. 地质学：地质学中的山峰或山脉形状可以近似看作棱锥。

3. 工程学：一些锥形状的工程设施，如防波堤或烟囱，也属于棱锥的应用。

通过学习和了解棱锥的基本概念和性质，我们可以更好地应用数学知识来解决与棱锥相关的问题。

同时，这也有助于我们在现实生活中观察和理解棱锥形状的事物。