下载文档原格式
绝密★启用前2019年普通高等学校招生全国统一考试文科数学本试卷共5页。
考试结束后，将本试卷和答题卡一并交回。
注意事项：1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。
2．选择题必须使用2B 铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合={|1}A x x >-，{|2}B x x =<，则A ∩B = A ．(-1，+∞) B ．(-∞，2)C ．(-1，2)D ．∅2．设z =i(2+i)，则z = A ．1+2i B ．-1+2iC ．1-2iD ．-1-2i3．已知向量a =(2，3)，b =(3，2)，则|a -b |= A ．2 B ．2 C ．52D ．504．生物实验室有5只兔子，其中只有3只测量过某项指标，若从这5只兔子中随机取出3只，则恰有2只测量过该指标的概率为A ．23 B ．35 C ．25D ．155．在“一带一路”知识测验后，甲、乙、丙三人对成绩进行预测．甲：我的成绩比乙高．乙：丙的成绩比我和甲的都高． 丙：我的成绩比乙高．成绩公布后，三人成绩互不相同且只有一个人预测正确，那么三人按成绩由高到低的次序为 A ．甲、乙、丙 B ．乙、甲、丙C ．丙、乙、甲D ．甲、丙、乙6．设f (x )为奇函数，且当x ≥0时，f (x )=e 1x -，则当x <0时，f (x )= A ．e 1x --B ．e 1x -+C ．e 1x ---D ．e 1x --+7．设α，β为两个平面，则α∥β的充要条件是 A ．α内有无数条直线与β平行 B ．α内有两条相交直线与β平行 C ．α，β平行于同一条直线 D ．α，β垂直于同一平面 8．若x 1=4π，x 2=43π是函数f (x )=sin x ω(ω>0)两个相邻的极值点，则ω=A ．2B ．32C ．1D ．129．若抛物线y 2=2px （p >0）的焦点是椭圆2213x y p p+=的一个焦点，则p = A ．2 B ．3C ．4D ．8 10．曲线y =2sin x +cos x 在点(π，-1)处的切线方程为A ．10x y --π-=B ．2210x y --π-=C ．2210x y +-π+=D ．10x y +-π+=11．已知a ∈（0，π2），2sin2α=cos2α+1，则sin α= A ．15B ．55C ．33D ．25512．设F为双曲线C：22221x ya b-=（a>0，b>0）的右焦点，O为坐标原点，以OF为直径的圆与圆x2+y2=a2交于P、Q两点．若|PQ|=|OF|，则C的离心率为A ．2B ．3C．2 D ．5二、填空题：本题共4小题，每小题5分，共20分。
2019年高考全国2卷文科数学试题解析1．设集合{1,2,3},{2,3,4}A B ==，则AB =A ．{}123,4，， B ．{}123，， C ．{}234，， D ．{}134，， 【答案】A 【解析】由题意{1,2,3,4}A B =，故选A.2．(1i)(2i)++=A ．1i -B ．13i +C ．3i +D ．33i + 【答案】B3．函数π()sin(2)3f x x =+最小正周期为 A ．4π B ．2π C ． π D ．π2【答案】C【解析】由题意2ππ2T ==，故选C. 4．设非零向量a ，b 满足+=-a b a b ，则A ．a ⊥bB ．=a bC ．a ∥bD ．>a b 【答案】A【解析】由+=-a b a b 平方得222222+⋅+=-⋅+a a b b a a b b ，即0⋅=a b ，则⊥a b ，故选A.5．若1a >，则双曲线2221x y a-=的离心率取值范围是A ．)+∞B ．2)C ．D ．(1,2) 【答案】C6．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为 A ．90π B ．63π C ．42π D ．36π【答案】B【解析】由题意，该几何体是由高为6的圆柱截取一半后的图形加上高为4的圆柱，故其体积为221π36π3463π2V =⋅⋅⋅+⋅⋅=，故选B. 7．设,x y 满足约束条件2+330,2330,30,x y x y y -≤⎧⎪-+≥⎨⎪+≥⎩则2z x y =+的最小值是A ．15-B ．9-C ．1D ．9 【答案】A【解析】绘制不等式组表示的可行域，结合目标函数的几何意义可得函数在点()6,3B --处取得最小值，最小值为min 12315z =--=-．故选A.8．函数2()ln(28)f x x x =--的单调递增区间是A ．(,2)-∞-B ． (,1)-∞C ． (1,)+∞D ． (4,)+∞ 【答案】D9．甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩，老师说：你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩.看后甲对大家说：我还是不知道我的成绩，根据以上信息，则A．乙可以知道四人的成绩B．丁可以知道四人的成绩C．乙、丁可以知道对方的成绩D．乙、丁可以知道自己的成绩【答案】D【解析】由甲的说法可知乙、丙一人优秀一人良好，则甲、丁一人优秀一人良好，乙看到丙结果则知道自己的结果，丁看到甲的结果则知道自己结果，故选D.10．执行下面的程序框图，如果输入的1a=-，则输出的S=A．2 B．3 C．4 D．5【答案】B11．从分别写有1,2,3,4,5的5张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数大于第二张卡片上的数的概率为A．110B．15C．310D．25【答案】D【解析】如下表所示，表中的点的横坐标表示第一次取到的数，纵坐标表示第二次取到的数：总计有25种情况，满足条件的有10种. 所以所求概率为102255=. 12．过抛物线2:4C y x =的焦点F ，3的直线交C 于点M （M 在x 的轴上方），l 为C 的准线，点N 在l 上且MN l ⊥,则M 到直线NF 的距离为A 5B ．2C ． 23D ． 33【答案】C二、填空题，本题共4小题，每小题5分，共20分. 13．函数()2cos sin f x x x =+的最大值为 . 5【解析】2()215f x ≤+=14．已知函数()f x 是定义在R 上函数，当(,0)x ∈-∞时，32()2f x x x =+,则(2)f = .【答案】12【解析】(2)(2)[2(8)4]12f f =--=-⨯-+=.15．长方体的长，宽，高分别为3,2,1，其顶点都在球O 球面上，则球O 的表面积为 . 【答案】14π【解析】球的直径是长方体的体对角线，所以222232114,4π14π.R S R =++===16．ABC △的内角,,A B C 的对边分别为,,a b c ,若2cos cos cos b B a C c A =+,则B = .【答案】π3【解析】由正弦定理可得1π2sin cos sin cos sin cos sin()sin cos 23B B AC C A A C B B B =+=+=⇒=⇒=. 17．（12分）已知等差数列{}n a 的前n 项和为n S ，等比数列{}n b 的前n 项和为n T ，11221,1,2a b a b =-=+=.（1）若335a b +=，求{}n b 的通项公式； （2）若321T =，求3S . 18．（12分）如图，四棱锥P ABCD -中，侧面PAD 为等边三角形且垂直于底面ABCD ,1,90.2AB BC AD BAD ABC ==∠=∠=︒ （1）证明：直线BC ∥平面PAD ;（2）若△PCD 的面积为27，求四棱锥P ABCD -的体积. 19．（12分）海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取100个网箱，测量各箱水产品产量（单位：kg ）, 其频率分布直方图如下：（1）记A 表示事件“旧养殖法的箱产量低于50 kg”，估计A 的概率；（2）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：（3）根据箱产量的频率分布直方图，对这两种养殖方法的优劣进行比较. 附：22()()()()()n ad bc K a b c d a c b d -=++++.K 2=22006266343815.70510010096104⨯⨯-⨯⨯⨯⨯（）≈.由于15.705＞6.635,故有99%的把握认为箱产量与养殖方法有关.（3）箱产量的频率分布直方图表明：新养殖法的箱产量平均值（或中位数）在50 kg 到55 kg 之间，旧养殖法箱产量平均值(或中位数)在45 kg 到50 kg 之间,且新养殖法的箱产量分布集中程度较旧养殖法箱产量分布集中程度高,因此,可以认为新养殖法的箱产量较高且稳定,从而新养殖法优于旧养殖法. 20．（12分）设O 为坐标原点，动点M 在椭圆C 错误!未找到引用源。
学校：____________________ _______年_______班 姓名：____________________ 学号：________- - - - - - - - - 密封线 - - - - - - - - - 密封线 - - - - - - - - -绝密★启用前2019年普通高等学校招生全国统一考试文科数学 全国II 卷本试卷共23小题，满分150分，考试用时120分钟(适用地区：内蒙古/黑龙江/辽宁/吉林/重庆/陕西/甘肃/宁夏/青海/新疆/西藏/海南) 注意事项：1．答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其它答案标号。
回答非选择题时，将答案写在答题卡上。
写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
一、二、 选择题：本题共12小题，每小题5分，共60分。
在每个小题给出的四个选项中， 只有一项是符合题目要求的。
1．已知集合={|1}A x x >-，{|2}B x x =<，则A ∩B = A ．(–1，+∞)B ．(–∞，2)C ．(–1，2)D ．∅2．设z =i(2+i)，则z =A ．1+2iB ．–1+2iC ．1–2iD ．–1–2i3．已知向量a =(2，3)，b =(3，2)，则|a –b |= AB ．2C ．D ．504．生物实验室有5只兔子，其中只有3只测量过某项指标，若从这5只兔子中随机取出3只，则恰有2只测量过该指标的概率为 A ．23 B ．35 C ．25D ．155．在“一带一路”知识测验后，甲、乙、丙三人对成绩进行预测． 甲：我的成绩比乙高．乙：丙的成绩比我和甲的都高．丙：我的成绩比乙高．成绩公布后，三人成绩互不相同且只有一个人预测正确，那么三人按成绩由高到低的次序为 A ．甲、乙、丙 B ．乙、甲、丙C ．丙、乙、甲D ．甲、丙、乙6．设f (x )为奇函数，且当x ≥0时，f (x )=e 1x -，则当x <0时，f (x )=A ．e 1x --B ．e 1x -+C ．e 1x ---D ．e 1x --+ 7．设α，β为两个平面，则α∥β的充要条件是 A ．α内有无数条直线与β平行 B ．α内有两条相交直线与β平行 C ．α，β平行于同一条直线 D ．α，β垂直于同一平面 8．若x 1=4π，x 2=43π是函数f (x )=sin x ω(ω>0)两个相邻的极值点，则ω= A ．2 B ．32 C ．1 D ．129．若抛物线y 2=2px （p >0）的焦点是椭圆2213x y p p+=的一个焦点，则p = A ．2 B ．3 C ．4 D ．8 10．曲线y =2sin x +cos x 在点(π，–1)处的切线方程为A ．10x y --π-=B ．2210x y --π-=C ．2210x y +-π+=D ．10x y +-π+= 11．已知a ∈（0，π2），2sin2α=cos2α+1，则sinα= A ．15BCD12．设F为双曲线C：22221x ya b-=（a>0，b>0）的右焦点，O为坐标原点，以OF为直径的圆与圆x2+y2=a2交于P、Q两点．若|PQ|=|OF|，则C 的离心率为ABC．2 D二、填空题：本题共4小题，每小题5分，共20分。
绝密★启用前2019年普通高等学校招生全国统一考试文科数学本试卷共5页。
考试结束后，将本试卷和答题卡一并交回。
注意事项：1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。
2．选择题必须使用2B 铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合={|1}A x x >-，{|2}B x x =<，则A ∩B = A ．(–1，+∞) B ．(–∞，2)C ．(–1，2)D ．∅2．设z =i(2+i)，则z = A ．1+2i B ．–1+2iC ．1–2iD ．–1–2i3．已知向量a =(2，3)，b =(3，2)，则|a –b |= A ．2B ．2C ．52D ．504．生物实验室有5只兔子，其中只有3只测量过某项指标，若从这5只兔子中随机取出3只，则恰有2只测量过该指标的概率为 A ．23 B ．35 C ．25D ．155．在“一带一路”知识测验后，甲、乙、丙三人对成绩进行预测． 甲：我的成绩比乙高． 乙：丙的成绩比我和甲的都高． 丙：我的成绩比乙高．成绩公布后，三人成绩互不相同且只有一个人预测正确，那么三人按成绩由高到低的次序为 A ．甲、乙、丙 B ．乙、甲、丙C ．丙、乙、甲D ．甲、丙、乙6．设f (x )为奇函数，且当x ≥0时，f (x )=e 1x -，则当x <0时，f (x )=A ．e 1x --B ．e 1x -+C ．e 1x ---D ．e 1x --+7．设α，β为两个平面，则α∥β的充要条件是 A ．α内有无数条直线与β平行 B ．α内有两条相交直线与β平行 C ．α，β平行于同一条直线 D ．α，β垂直于同一平面8．若x 1=4π，x 2=43π是函数f (x )=sin x ω(ω>0)两个相邻的极值点，则ω= A ．2B ．32 C ．1 D ．129．若抛物线y 2=2px （p >0）的焦点是椭圆2213x y p p+=的一个焦点，则p = A ．2 B ．3C ．4D ．810．曲线y =2sin x +cos x 在点(π，–1)处的切线方程为A ．10x y --π-=B ．2210x y --π-=C ．2210x y +-π+=D ．10x y +-π+=11．已知a ∈（0，π2），2sin2α=cos2α+1，则sinα= A ．15B ．55 C ．33D ．25512．设F 为双曲线C ：22221x y a b-=（a >0，b >0）的右焦点，O 为坐标原点，以OF 为直径的圆与圆x 2+y 2=a 2交于P 、Q 两点．若|PQ |=|OF |，则C 的离心率为A ．2B ．3C ．2D ．5二、填空题：本题共4小题，每小题5分，共20分．13．若变量x ，y 满足约束条件23603020x y x y y ⎧⎪⎨⎪⎩+-≥+-≤-≤，，，则z =3x –y 的最大值是___________.14．我国高铁发展迅速，技术先进．经统计，在经停某站的高铁列车中，有10个车次的正点率为0.97，有20个车次的正点率为0.98，有10个车次的正点率为0.99，则经停该站高铁列车所有车次的平均正点率的估计值为___________.△的内角A，B，C的对边分别为a，b，c.已知b sin A+a cos B=0，则B=___________. 15．ABC16．中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图1）.半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美．图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1．则该半正多面体共有________个面，其棱长为_ ________．（本题第一空2分，第二空3分．）三、解答题：共70分。
2019年高考文科数学真题答案（全国2卷）
2019年高考文科数学真题答案（全国2卷）全国二卷适用地区：甘肃、青海、黑龙江、吉林、辽宁、宁夏、新疆、内蒙古、陕西、重庆
2019年高考文科数学真题答案（全国2卷）全国二卷适用地区：甘肃、青海、黑龙江、吉林、辽宁、宁夏、新疆、内蒙古、陕西、重庆
2019年高考文科数学真题答案（全国2卷）
2019年高考文科数学真题答案（全国2卷）
2019年高考文科数学真题答案（全国2卷）全国二卷适用地区：甘肃、青海、黑龙江、吉林、辽宁、宁夏、新疆、内蒙古、陕西、重庆
2019年高考文科数学真题答案（全国2卷）全国二卷适用地区：甘肃、青海、黑龙江、吉林、辽宁、宁夏、新疆、内蒙古、陕西、重庆
2019年高考文科数学真题答案（全国2卷）全国二卷适用地区：甘肃、青海、黑龙江、吉林、辽宁、宁夏、新疆、内蒙古、陕西、重庆。
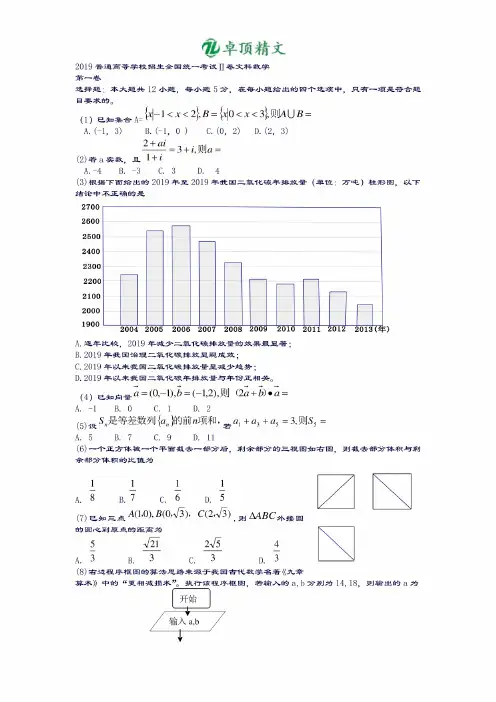
2019普通高等学校招生全国统一考试II卷文科数学第_卷选择题：本大题共124、题，每4、题5分，在每4、题给出的四个选项中，只有一项是符合题目要求的。
⑴已知集合a=M t<x<2},B=H0<x<3},则AU3=A.(-1,3)B.(-1,0)C.(0,2)D.(2,3)2+ai日.顽----—=3+z,贝!J q=(2)若a实数，且1+，A.-4B.-3C.3D.4(3)根据下面给出的2019年至2019年我国二氧化碳年排放量(单位：万吨)柱形图，以下结论中不正确的是C.2019年以来我国二氧化碳排放量呈减少趋势；D.2019年以来我国二氧化碳年排放量与年份正相关。
(4)已知向量"=(O,T)E=(-1,2),则(2a+i)・a=A.-1B.0C.1D.2/[-\、S〃是等差数列}的前〃项和，—％+%+%=3,则S5=A.5B.7C.9D.11(6)—个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为J.£££A.8b.7 c.6 D.5⑺已知三点A(1,O),B(O,g),C(2,73),则AABC夕卜接圆的圆，《到原点的距>离为5恒2^54A.3b.3 C.3 D.3(8)右边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术，执行该程序框图,若输入的a,b分别为14,18,则输出的a为开始输入a,b{a“}丫两——=4(。
4—1),则。
2=(9)已知等比数列4C2_1A.2B.1C.2D.8(10)已知A,B是球0的球面上两点，ZAO3=90°,C为该球面上动点，若三棱锥0_ABC 体积的最大值为36,则球0的表面积为A.367tB.647tC.144冗D. 256兀(11)如图，长方形的边AB=2,BC=1,0是AB的中点，点P沿着边BC,CD,与DA运动，记ZBOP=x，将动点P到两点距离之和表示为函数/■"),贝昕⑴的图像大致为/(x)=ln(l+|x|)-—二，则使得f3)>y(2x-1)成立的x的范围是(12)设函数1+尤("I)(-8,；)U(l,+8)(—；，!)(—8,—：)U(：,+8) A.3 B.3 C.33d.33第二卷填室题：本大题共4个小题，每小题5分己知国数八工)=心'―2工的图像过点(-1,4)，贝此=%+y-5<0,<2x-y-l>0,贝!Jz=2尤+y的最大值为(14)若x,y满足约束条件—2'+1'°‘。
继电高中2019 年普通高等学校招生全国统一考试（全国Ⅱ卷）文科数学1. 设集合A x | x -1 ， B x | x 2 ，则A B( )A. ( 1, )B. ( ,2)C. ( 1,2)D.答案：C解析：A x | x -1 ，B x | x 2 ，∴ A B （1,2）.2. 设 z i(2 i ) ，则z ( )A. 12iB. 1 2iC.1 2iD. 1 2i答案：D解析：因为 z i (2 i ) 1 2i ，所以z 1 2i .r(2,3) r r r3. 已知向量 a ， b (3,2) ，则 a b （）A. 2B. 2C. 5 2D. 50答案：A解答：r r r r由题意知 a b ( 1,1)，所以 a b2 .4.生物实验室有 5只兔子，其中只有 3 只测量过某项指标.若从这 5 只兔子中随机取出 3 只，则恰有2 只测量过该指标的概率为（）2A.33B.52C.51D.5答案：B解答：计测量过的 3 只兔子为1、2、3，设测量过的 2 只兔子为 A 、 B 则 3 只兔子的种类有(1,2,3) (1,2, A) (1,2, B) (1,3, A) (1,3, B) (1,A, B) 2,3, A 2,3, B 2, A, B 3, A, B,则恰好6种，所以其概率为3有两只测量过的有5 .5. 在“一带一路”知识测验后，甲、乙、丙三人对成绩进行预测.甲：我的成绩比乙高 .乙：丙的成绩比我和甲的都高 .丙：我的成绩比乙高 .成绩公布后，三人成绩互不相同且只有一个人预测正确，那么三人按成绩由高到低的次序为（）A．甲、乙、丙B．乙、甲、丙C．丙、乙、甲D．甲、丙、乙答案：A解答：根据已知逻辑关系可知，甲的预测正确，乙丙的预测错误，从而可得结果.6.设f (x)为奇函数，且当x 0 时， f ( x) e x1，则当 x 0 时， f ( x)（）A. e x 1B. e x 1C. e x 1D. e x 1答案：D解答：当 x 0 时， x 0 ， f ( x) e x 1，又 f (x) 为奇函数，有 f ( x) f ( x) e x 1 .7. 设, 为两个平面，则/ / 的充要条件是 ( )A.内有无数条直线与平行B.内有两条相交直线与平行C., 平行于同一条直线D., 垂直于同一平面答案：B解析 :根据面面平行的判定定理易得答案.8. x1 , x2 3f ( x) sin x(0)两个相邻的极值点，则= 4 是函数若 4 A．2B. 3 2C.11D. 2答案：A解答：T 3T= ,所以=2 .由题意可知 2 4 4 2 即9. 若抛物线y2 2 px( p 0) 的焦点是椭圆x2 y2 1 的一个焦点，则p （）3 p pA.2B.3C.4D.8答案：D解析：抛物线 y2 2 px( p 0) 的焦点是(p,0)，椭圆x2y2 1 的焦点是( 2 p ,0) ，2 3 p p∴ p2 p ，∴ p 8 . 210. 曲线 y 2sin x cos x 在点 ( , 1) 处的切线方程为( )A. x y 1 0B. 2x y 2 1 0C. 2x y 2 1 0D. x y 1 0答案：C解析：因为 y 2cos x sin x ，所以曲线 y 2sin x cos x 在点 ( , 1) 处的切线斜率为 2 ，故曲线y 2sin x cos x 在点 ( , 1) 处的切线方程为2x y 2 1 0 .11.已知(0, ) ，2sin 2cos21，则 sin（）2A.155 B.53C.3D.2 55答案： B 解答：(0,2 ) ， 2sin 2cos 214sin cos2cos 2 ，则 2sincostan1 ，所以 cos 1 12 5 ，2tan 25所以 sin1 cos 25 .5C :x 2y212. 设 F 为双曲线 221(a 0,b0)ab的右焦点， 0 为坐标原点， 以 OF 为直径的圆与圆 x 2y2a 2 交于P,Q两点，若PQ OF, 则 C 的离心率为 :A.2B. 3C. 2D. 5 答案： A解析：设 F 点坐标为（ c,0) ，则以 OF 为直径的圆的方程为 （ xc ) 2c 2y 2 ----- ①，222圆的方程 x2 y 2 a2 ----- ②，则① - ②，化简得到x a 2 ，代入②式，求得y ab ，则c c设 P 点坐标为（a2 ,ab) ，Q点坐标为（a2,ab) ，故PQ2ab，又 PQ OF ,则c c c c c2ab2ab c 2 a 2 2 a b ，故e c a2 b2 2a2 .故选c, 化简得到 b ，a a a cA.二、填空题2x 3y 6 0 13. 若变量x, y满足约束条件x y 3 0z 3x y的最大值是.y 2 0则答案：9解答：根据不等式组约束条件可知目标函数z3x y 在3,0处取得最大值为9.14.我国高铁发展迅速，技术先进 . 经统计，在经停某站的高铁列车中，有10 个车次的正点率为 0.97 ，有 20 个车次的正点率为0.98 ，有 10 个车次的正点率为0.99 ，则经停该站的高铁列车所有车次的平均正点率的估计值为.答案：0.98解答：平均正点率的估计值0.97 10 0.98 20 0.99 1040 0.98.15.ABC 的内角A, B,C的对边分别为a,b, c.已知 b sin A a cosB 0 ，则B .答案：34解析：根据正弦定理可得sin B sin A sin AcosB 0,即 sin A sin B cos B 0 ，显然 sin A 0 ，所以 sin B cosB 0 ，故B 3. 416. 中国有悠久的金石文化，印信是金石文化的代表之一. 印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图 1）. 半正多面体是由两种或两种以上的正多边形围成的多面体. 半正多面体体现了数学的对称美. 图 2 是一个棱数为48 的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为 1. 则该半正多面体共有个面，其棱长为.(本题第一空 2 分，第二空 3 分 .)答案：262 1解析：由图 2 结合空间想象即可得到该正多面体有26 个面；将该半正多面体补成正方体后，根据对称性列方程求解.三、解答题17. 如图，长方体ABCD A1B1C1D1的底面ABCD是正方形，点E在棱AA1上， BE⊥ EC1.（ 1）证明：BE平面 EB1C1（ 2）若AE AE1 , AB 3 ,求四棱锥E BB1C1C 的体积.答案：（1）看解析（2）看解析解答：（ 1）证明：因为B1C1C 面 A1 B1 BA ，BE 面 A1B1BA∴ B1C1⊥ BE 又 C1 E B1C1 C1，∴ BE 平面 EB1C1；（ 2）设AA1 2a 则 BE2 9 a2 ， C1E 2 18+a 2 ， C1 B2 9 4a22 =BE 2 C1E 2 ∴ a，∴ 1 1因为 C1B 3 V E BB1C1CSBB1C1Ch 3 6 3=183 318. 已知a n 是各项均为正数的等比数列，a1 2, a3 2a 2 16 .(1)求 a n的通项公式：(2) 设 b n log 2 a n，求数列 b n 的前 n 项和 .答案：（ 1）a n 22 n 1 ；（ 2）n2解答：(1) 已知 a1 2, a3 2a2 16 ，故 a1 q2 2a1q 16 ，求得 q 4 或 q 2 ，又 q 0 ，故q 4 ，则 a n a1q n 1 2 4n 1 22 n 1 .(2) 把 a n代入 b n，求得 b n 2n 1，故数列b n 的前 n 项和为[1(2n 1)]n n 2.219. 某行业主管部门为了解本行业中小企业的生产情况，随机调查了100 个企业，得到这些企业第一季度相对于前一年第一季度产值增长率y 的频数分布表.y 的分组0.20,0 0,0.20 0.20,0.40 0.40,0.60 0.60,0.80 企业数 2 24 53 14 7 （ 1）分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例；（2）求这类企业产值增长率的平均数与标准差的估计值（同一组中的数据用该组区间的中点值为代表） . （精确到 0.01 ）附：748.602 .答案：详见解析解答 :（ 1）这类企业中产值增长率不低于40%的企业比例是14721，100100这类企业中产值负增长的企业比例是2.100（ 2）这类企业产值增长率的平均数是0.10 2 0.10 24 0.30 53 0.50 14 0.70 7 1000.30这类企业产值增长率的方差是0.1022 0.10 0.3020.30 0.3020.50 0.30 20.70 0.30 2100 0.02960.3024 53 14 7 所以这类企业产值增长率的标准差是0.02962 742 8.602 0.172040.17 .100 10020. 已知 F 1 , F 2 是椭圆 C ： x 2 y 21(a 0,b 0) 的两个焦点， P 为 C 上的点， O 为坐标 2 b 2a原点 .（ 1）若 POF 2 为等边三角形，求 C 的离心率；（ 2）如果存在点 P ，使得 PF 1 PF 2 ，且 F 1 PF 2 的面积等于 16 ，求 b 的值和 a 的取值范围 . 答案：详见解析解答 :（ 1）若 POF 2 为等边三角形，则 P 的坐标为c 3x 2 y 2,2 c ，代入方程22 1，可得2a bc 2 3c 2 1，解得 e 2 4 2 3 ，所以 e31 .4a 24b 2uuuuruuuuruuur 2 uuuur 2 4c 2 ， （ 2）由题意可得PF 1PF 2 2a ，因为 PF 1 PF 2 ，所以 PF 1 PF 2uuuruuuur2uuur uuuuruuur uuuur4a24c24b2，所以 PF 1PF 22 PF 1 PF 24c 2，所以 2 PF1PF 2uuur uuuur2SPF 1F 2 1 uuur uuuurb 216b 4 .所以PF 1 PF 2 2b ，所以 2 PF 1 PF 2 ，解得uuuruuuuruuur uuuuruuur uuuuruuur uuuur 2 2，即 a 2 因为 PF 1PF 2 4 PF 1 PF 2 ，即 2a 4 PF 1 PF 2 PF 1 PF 2 ， 所以 a232 ，所以 a 4 2 .21. 已知函数 f ( x) (x 1)ln xx 1.证明：（ 1） f (x) 存在唯一的极值点；（ 2） f (x) 0 有且仅有两个实根，且两个实根互为倒数.答案： 见解析 解答：（ 1） f ( x)ln x 1 (x 0) ，设 g( x) ln x1， g (x) 11 0xx xx 2则 g(x) 在 (0,) 上递增， g(1)1 0 ， g (2) ln2 1 lne1 0 ，2 2所以存在唯一 x 0 (1,2) ，使得 f (x 0 ) g ( x 0 ) 0 ，当 0 xx 0 时， g (x) g ( x 0 ) 0，当 x x 0 时， g( x) g( x 0 ) 0，所以 f ( x) 在 (0, x 0 ) 上递减，在 (x 0 , ) 上递增，所以 f ( x) 存在唯一的极值点 .（ 2）由（ 1）知存在唯一 x 0(1,2) ，使得 f (x 0 ) 0 ，即 ln x 01 ，x 0f (x 0 ) ( x 0 1)ln x 0 x 0 1 ( x 0 1)1x 0 1( x 01) 0 ，x 0x 011 1)( 2)11 13221) e 21 e 23 0 ，f ( 2 )( 2 220 ， f (e )2(ee eee所以函数 f ( x) 在 (0, x 0 ) 上， (x 0 , ) 上分别有一个零点 .设 f ( x 1 )f ( x 2 ) 0， f (1) 2 0 ，则 x 1 1 x 0x 2 ，有 ( x 1 1) ln x 1 x 1 1 0ln x 1x 11，x 1 1(x 2 1) ln x 2 x 2 1 0ln x 2x 2 1 ，x 2 1设 h(x)ln x x 1，当 0x, x 1 时，恒有 h( x) h( 1 ) 0 ，x 1x则 h(x 1 ) h( x 2 ) 0 时，有 x 1x 2 1 .四、选做题（ 2 选 1）22. 在极坐标系中，O 为极点，点M ( 0 , 0 ) ( 0 0) 在曲线 C : =4sin 上，直线 l 过点A(4,0) 且与OM垂直，垂足为P .（ 1）当03时，求0及 l 的极坐标方程；（ 2）当M在C上运动且P在线段OM上时，求P点轨迹的极坐标方程 .答案：（ 1）0 2 3 ， l 的极坐标方程：sin(6) 2 ；（ 2）P点轨迹的极坐标方程为=4cos (4 , ) . 2解析：（ 1）当03 时，0 =4sin 0 4sin 2 3 ，3以 O 为原点，极轴为x轴建立直角坐标系，在直角坐标系中有M ( 3,3) ，A(4,0) ，k OM 3 ，则直线 l 的斜率k 3 ，由点斜式可得直线l ： y 3( x 4) ，化成极坐标方程为3 3sin( ) 2；6（ 2）∵l OM ∴OPA ，则 P 点的轨迹为以OA为直径的圆，此时圆的直角坐标方程2为 ( x 2) 2 y 2 4 ，化成极坐标方程为=4cos ，又 P 在线段OM上，由4sin可4cos得，∴ P 点轨迹的极坐标方程为=4cos ( , ) .4 4 2 23.[ 选修 4-5：不等式选讲 ]已知 f ( x) | x a | x | x 2 | (x a)（ 1）当a 1 时，求不等式 f (x) 0的解集：（ 2）若x( ,1) 时， f ( x)0 ，求 a 得取值范围.答案（1）看解析（2）看解析继电高中- 11 -解答：2x 2 4x 2( x 2),（ 1）当 a1时，f ( x)x 1 x x2 (x1) 2 x 2(1 x 2),2x 2 4x 2( x 1).2x 24x2 0 2 x 2 02x 24x 2解得不等f (x)所以不等式 等价于 或x 或x 21 2x 1式的解集为 x x 2 。
绝密★启用前2019年普通高等学校招生全国统一考试文科数学本试卷共5页。
考试结束后，将本试卷和答题卡一并交回。
注意事项：1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。
2．选择题必须使用2B 铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。
3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。
4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。
5．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合={|1}A x x >-，{|2}B x x =<，则A ∩B = A ．(-1，+∞) B ．(-∞，2)C ．(-1，2)D ．∅2．设z =i(2+i)，则z = A ．1+2i B ．-1+2iC ．1-2iD ．-1-2i3．已知向量a =(2，3)，b =(3，2)，则|a -b |= A ．2 B ．2 C ．52D ．504．生物实验室有5只兔子，其中只有3只测量过某项指标，若从这5只兔子中随机取出3只，则恰有2只测量过该指标的概率为A ．23 B ．35 C ．25D ．155．在“一带一路”知识测验后，甲、乙、丙三人对成绩进行预测．甲：我的成绩比乙高． 乙：丙的成绩比我和甲的都高． 丙：我的成绩比乙高．成绩公布后，三人成绩互不相同且只有一个人预测正确，那么三人按成绩由高到低的次序为 A ．甲、乙、丙 B ．乙、甲、丙C ．丙、乙、甲D ．甲、丙、乙6．设f (x )为奇函数，且当x ≥0时，f (x )=e 1x -，则当x <0时，f (x )= A ．e 1x --B ．e 1x -+C ．e 1x ---D ．e 1x --+7．设α，β为两个平面，则α∥β的充要条件是 A ．α内有无数条直线与β平行 B ．α内有两条相交直线与β平行 C ．α，β平行于同一条直线 D ．α，β垂直于同一平面 8．若x 1=4π，x 2=43π是函数f (x )=sin x ω(ω>0)两个相邻的极值点，则ω= A ．2 B ．32C ．1D ．129．若抛物线y 2=2px （p >0）的焦点是椭圆2213x y p p+=的一个焦点，则p = A ．2 B ．3C ．4D ．8 10．曲线y =2sin x +cos x 在点(π，-1)处的切线方程为A ．10x y --π-=B ．2210x y --π-=C ．2210x y +-π+=D ．10x y +-π+=11．已知a ∈（0，π2），2sin2α=cos2α+1，则sin α= A ．15B ．55C ．33D ．25512．设F 为双曲线C ：22221x y a b-=（a >0，b >0）的右焦点，O 为坐标原点，以OF 为直径的圆与圆x2+y2=a2交于P、Q两点．若|PQ|=|OF|，则C的离心率为A ．2B ．3C．2 D ．5二、填空题：本题共4小题，每小题5分，共20分。
2019年普通高等学校招生全国统一考试文科数学（II 卷）答案详解一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（集合）已知集合={|1}A x x >-，{|2}B x x =<，则A ∩B = A ．(-1，+∞) B ．(-∞，2)C ．(-1，2)D ．∅【解析】={|12}A B x x -<<，即C 答案.【答案】C2．（复数）设z =i (2+i )，则z = A ．1+2i B ．-1+2iC ．1-2iD ．-1-2i【解析】i z 21+-=，则z 的共轭复数为i z 21--=. 【答案】D3．（平面向量）已知向量a =(2，3)，b =(3，2)，则|a -b |= A ．2 B ．2 C ．52D ．50【解析】∵(1,1)a b -=-，∴||2a b -=.【答案】A4．（概率统计）生物实验室有5只兔子，其中只有3只测量过某项指标，若从这5只兔子中随机取出3只，则恰有2只测量过该指标的概率为A ．23 B ．35 C ．25D ．15【解析】从这5只兔子中随机取出3只的所有情况数为35C ，恰有2只测量过该指标的所有情况数为1213C C .所以所求的概率为53251213==C C C P .PS ：可以用列举法进行求解. 设5只兔子的编号为1、2、3、A 、B ，其中1、2、3为测量过某项指标的，A 、B 为未测量过某项指标的. 从这5只兔子中随机取出3只的所有情况有：（1,2,3）、（1,2,A ）、（1,2,B ）、（1,3,A ）、（1,3,B ）、（1,A,B ）、（2,3,A ）、（2,3,B ）、（2,A,B ）、（3,A,B ）, 共10种情况；其中恰有2只测量过该指标的情况有（1,2,A ）、（1,2,B ）、（1,3,A ）、（1,3,B ）、（2,3,A ）、（2,3,B ），共6种情况. 所以所求的概率53106==P . 【答案】B5．（推理）在“一带一路”知识测验后，甲、乙、丙三人对成绩进行预测． 甲：我的成绩比乙高． 乙：丙的成绩比我和甲的都高． 丙：我的成绩比乙高．成绩公布后，三人成绩互不相同且只有一个人预测正确，那么三人按成绩由高到低的次序为 A ．甲、乙、丙 B ．乙、甲、丙C ．丙、乙、甲D ．甲、丙、乙【解析】由题意，可把三人的预测简写成：甲：甲＞乙乙：丙＞乙，且 丙＞甲 丙：丙＞乙因只有一个人预测正确，分别进行假设： 若乙预测正确，则丙预测正确，不符合题意；若丙预测正确，甲预测错误，则有丙＞乙＞甲，那么乙的预测是正确的，不符合题意； 若甲预测正确，丙预测错误，则有甲＞乙＞丙，那么乙的预测是错误的，符合题意. 所以三人按成绩由高到低的次序为 甲＞乙＞丙 .PS ：可以直接用4个答案分别验证题设，快速得出正确答案.【答案】A6．（函数）设f (x )为奇函数，且当x ≥0时，()1xf x e =-，则当x <0时，f (x )=A ．1xe--B ．1xe-+ C ．1xe---D ．1xe--+【解析】设x ＜0，则－x ＞0，则有1)(-=--xex f .∵f (x )为奇函数，∴1)()(-=-=--xe xf x f即1)(+-=-xex fPS ：直接用特殊法. 1)1(-=e f ，则1)1(+-=-e f ，因此可以首先排除答案A 、C ，只有D 答案符合题意.【答案】D7．（立体几何）设α，β为两个平面，则α∥β的充要条件是 A ．α内有无数条直线与β平行 B ．α内有两条相交直线与β平行 C ．α，β平行于同一条直线 D ．α，β垂直于同一平面【解析】通过画图，采用排除法，很容易得到正确答案. 【答案】B8．（三角函数）若x 1=4π，x 2=43π是函数f (x )=sin x ω(ω>0)两个相邻的极值点，则ω= A ．2 B ．32C ．1D ．12【解析】由正弦函数的图像可知，函数f (x )=sin x ω(ω>0)两个相邻的极值点的差值等于函数周期的一半，即函数f (x )=sin x ω(ω>0)的周期πππ=-⨯=)443(2T ，所以22==Tπω. 【答案】A9．（解析几何）若抛物线y 2=2px （p >0）的焦点是椭圆2213x y p p+=的一个焦点，则p = A ．2 B ．3C ．4D ．8【解析】抛物线y 2=2px (p ＞0)的焦点为)0,2(p，并且在x 轴上. 所以椭圆1322=+p y p x 的一个焦点为)0,2(p . 所以有p p22=，得p =8. 【答案】D10．（函数）曲线y =2sin x +cos x 在点(π，-1)处的切线方程为A ．10x y --π-=B ．2210x y --π-=C ．2210x y +-π+=D ．10x y +-π+=【解析】由y =2sin x +cos x 得，y ′=2cos x －sin x ，∴在点(π，-1)处的切线斜率为k =－2.∴切线方程为)(21π--=+x y ，即01212=+-++πy x . 【答案】C11．（三角函数）已知a ∈（0，π2），2sin2α=cos2α+1，则sin α= A ．15B ．55C ．33D ．255【解析】利用三角公式12cos 2sin 2+=αα化简得ααα2cos 2cos sin 4=ααcos sin 2=所以2cot =α，设α所对得边为1，则临边为2，斜边为5，所以55sin =α. 【答案】B12．（解析几何）设F 为双曲线C ：22221x y a b-=（a >0，b >0）的右焦点，O 为坐标原点，以OF 为直径的圆与圆x 2+y 2=a 2交于P 、Q 两点．若|PQ |=|OF |，则C 的离心率为A ．2B ．3C ．2D ．5【解析】如图A12所示. ∵OF 为直径，=PQ OF ，∴PQ 也是直径.，即点P 、Q 的坐标为)2,2(c c .把)2,2(c c 代入222+=x y a 得，222=c a . ∴22=e ，即2=e .图A12【答案】A二、填空题：本题共4小题，每小题5分，共20分。
