2019-2020学年辽宁省大连市普兰店区九年级上学期期末考试数学试卷

大连市 2020 版九年级上学期数学期末考试试卷（II）卷姓名:________班级:________成绩:________一、 选择题（共 30 分） (共 10 题；共 30 分)1. （3 分） (2020 七下·金寨月考) 已知不等①、②、③的解集在数轴上的表示如图所示，则它们的公共部分的解集是（ ）A. B. C. D . 无解2. （3 分） (2019 九上·江北期末) 若 A.，则下列式子一定成立的是（ ）B. C. D. 3.（3 分）(2019 九上·潮南期末) 将抛物线 A. B.C.向左平移 2 个单位后得到新的抛物线的表达式为D. 4. （3 分） (2019 九上·潮南期末) 如图，四边形 ABCD 为 小是（ ）的内接四边形，∠BCD=120°，则∠BOD 的大A. B.第 1 页 共 13 页C. D. 5. （3 分） (2019 九上·潮南期末) 边长为 2 的正方形内接于 A.1 B.2，则的半径是C.D. 6. （3 分） (2019 九上·潮南期末) 方程 A.的左边配成完全平方后所得方程为B.C. D.7. （3 分） (2019 九上·潮南期末) A，B 是上的两点，， 的长是 ，则的度数是A . 30B.C.D.8. （3 分） (2019 九上·潮南期末) 某种植基地 2017 年蔬菜产量为 80 吨，预计 2019 年蔬菜产量达到 100 吨，求蔬菜产量的年平均增长率，设蔬菜产量的年平均增长率为 ，则可列方程为A.B.C.D.9. （3 分） (2019 九上·潮南期末) 如图，将线段 的延长线上，则的大小为绕点 逆时针旋转，得到．若点 在第 2 页 共 13 页A.B.C.D.10. （3 分） (2019 九上·潮南期末) 如图，抛物线的一个交点坐标为，其部分图象如图所示，下列结论：①②方程的两个根是，大而增大．其中正确的个数是的对称轴为直线，与 轴③④当时， 随 增A . 1个 B . 2个 C . 3个 D . 4个二、 填空题（共 24 分） (共 6 题；共 24 分)11. （4 分） (2018 九上·淮安月考) 已知一等腰三角形的底边长和腰长分别是方程 x2﹣3x=4（x﹣3）的两个 实数根，则该等腰三角形的周长是________.12. （4 分） (2019 七上·双台子月考) 已知是数轴上的三个点，且 在 的右侧.点表示的数分别是 1，3，如图所示.若，则点 表示的数是________.13. （4 分） (2019·鄂尔多斯模拟) 下列说法正确的是________．（填写正确说法的序号）①在角的内部，到角的两边距离相等的点在角的平分线上；②一元二次方程 x2﹣3x＝5 无实数根；③的平方根为±4；④了解北京市居民”一带一路”期间的出行方式，采用抽样调查方式；⑤圆心角为 90°的扇形面积是 π，则扇形半径为 2．第 3 页 共 13 页14. （4 分） (2019 七下·呼和浩特期末) 以下四个命题：①的立方根是 ②要调查一批灯泡的使用寿命适宜用抽样调查③两条直线被第三条直线所截同旁内角互补④已知与其内部一点 ,过 点作,作,则.其中假命题的序号为________．15. （4 分） (2017 九上·澄海期末) 抛物线 y=x2+2x+1 的顶点坐标是________．16. （4 分） (2019 九上·潮南期末) 已知正方形中，点 在边 上，，（如图所示）把线段 绕点 旋转，使点 落在直线 上的点 处，则 、 两点的距离为________．三、 解答题（共 18 分） (共 3 题；共 18 分)17. （6 分） (2019 七下·姜堰期中) 已知关于 ， 的二元一次方程组 反数，求 k 的值.的解互为相18. （6 分） (2019 九上·潮南期末) 设二次函数的图象的顶点坐标为，且过点，求这个函数的关系式．19. （6 分） (2019 九上·潮南期末) 在边长为 1 个单位长度的小正方形组成的网格中，建立如图所示的平面直角坐标系是格点三角形（顶点在网格线的交点上）（1） 先作关于原点 成中心对称的△，再把△向上平移 4 个单位长度得到△；（2） △与是否关于某点成中心对称？若是，直接写出对称中心的坐标；若不是，请说明理由．四、 解答题（共 21 分） (共 3 题；共 21 分)20. （7.0 分） (2017·溧水模拟) 综合题:求下列事件概率第 4 页 共 13 页（1） 小杨和小姜住在同一个小区，该小区到苏果超市有 A、B、C 三条路线． ①求小杨随机选择一条路线，恰好是 A 路线的概率； ②求小杨和小姜两人分别随机选择一条路线去苏果超市，恰好两人选择同一条路线的概率． （2） 有 4 位顾客在超市中选购 4 种品牌的方便面．如果每位顾客从 4 种品牌中随机的选购一种，那么 4 位顾 客选购同一品牌的概率是________，至少有 2 位顾客选择的不是同一品牌的概率是________（直接填字母序号）A．B．（ ） 3C．1﹣（ ） 3D．1﹣（ ）3． 21. （7.0 分） (2017·营口) 如图，有四张背面完全相同的纸牌 A、B、C、D，其正面分别画有四个不同的几何图形，将这四张纸牌背面朝上洗匀．（1） 从中随机摸出一张，求摸出的牌面图形是中心对称图形的概率；（2） 小明和小亮约定做一个游戏，其规则为：先由小明随机摸出一张纸牌，不放回，再由小亮从剩下的纸牌中随机摸出一张，若摸出的两张牌面图形都是轴对称图形小明获胜，否则小亮获胜，这个游戏公平吗？请用列表法（或树状图）说明理由（纸牌用 A、B、C、D 表示）．22. （7.0 分） (2012·杭州) 有一组互不全等的三角形，它们的边长均为整数，每个三角形有两条边的长分别为 5 和 7．（1） 请写出其中一个三角形的第三边的长；（2） 设组中最多有 n 个三角形，求 n 的值；（3） 当这组三角形个数最多时，从中任取一个，求该三角形周长为偶数的概率．五、 解答题（共 27 分） (共 3 题；共 27 分)23. （9 分） 已知 y+2 与 x 成正比例，且 x=3 时 y=1．（1） 写出 y 与 x 之间的函数关系式；（2） 求当 x=﹣1 时，y 的值；（3） 求当 y=0 时，x 的值．24. （9.0 分） (2019 九上·潮南期末) 已知内接于以 为直径的，过点 作的切线交 的延长线于点 ，且．第 5 页 共 13 页（1） 求 （2） 在切线的度数； 上截取，连接 ，判断直线 与的位置关系，并证明．25. （9 分） (2019 九上·潮南期末) 如图，已知抛物线 （点 在点 的右侧），与 轴交于点 ．的图象与 轴交于 ， 两点（1） 求直线 的解析式；（2） 点 是直线 下方抛物线上的一点，当的面积最大时，在抛物线的对称轴上找一点 ，使得的周长最小，请求出点 的坐标和点 的坐标；（3） 在（2）的条件下，是否存在这样的点，使得为等腰三角形？如果有，请直接写出点的坐标；如果没有，请说明理由．第 6 页 共 13 页参考答案一、 选择题（共 30 分） (共 10 题；共 30 分)1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、二、 填空题（共 24 分） (共 6 题；共 24 分)11-1、 12-1、 13-1、 14-1、 15-1、 16-1、三、 解答题（共 18 分） (共 3 题；共 18 分)第 7 页 共 13 页17-1、 18-1、19-1、 19-2、四、 解答题（共 21 分） (共 3 题；共 21 分)20-1、 20-2、 21-1、第 8 页 共 13 页21-2、22-1、22-2、 22-3、五、 解答题（共 27 分） (共 3 题；共 27 分)23-1、 23-2、23-3、第 9 页 共 13 页24-1、24-2、第 10 页 共 13 页25-1、25-2、25-3、。

辽宁省2019-2020学年九年级上学期期末数学试题A卷姓名:________ 班级:________ 成绩:________一、单选题1 . 在平面直角坐标系中，直线（为常数）与抛物线交于，两点，且点在轴左侧，点坐标为，连结、，有以下说法：①；②当时，的值随的增大而增大；③当时，；④面积的最小值为．其中正确的是（）A．①B．②C．③D．④2 . 将一元二次方程配方后，原方程可化为（）A．B．C．D．3 . 下列成语中表示不确定事件的是（）A．水中捞月B．守株待兔C．刻舟求剑D．竹篮打水4 . 如图，已知点A在反比例函数y＝（x＞0）的图象上，作Rt△ABC，边BC在x轴上，点D为斜边AC的中点，连结DB并延长交y轴于点E，若△BCE的面积为4，则k的值是（）A．2B．4C．6D．85 . 下列图形中，是轴对称图形但不是中心对称图形的是（）A．B．C．D．6 . 杨树乡共有耕地公顷，该乡人均耕地面积与总人口之间的函数图象大致为（）A．B．C．D．7 . 下列属于正n边形的特征的有（）①各边相等；②各个内角相等；③各条对角线都相等；④从一个顶点可以引(n－2)条对角线；⑤从一个顶点引出的对角线将正n边形分成面积相等的(n－2)个三角形．A．2个B．3个C．4个D．5个8 . 如图，△AOB中，∠B=25°，将△AOB绕点O顺时针旋转60°，得到△A′OB′，边A′B′与边OB交于点C（A′不在OB上），则∠A′CO的度数为（）A．85°B．75°C．95°D．105°9 . 如图，是直径，是的切线，连接交于点，连接，，则的度数是（）.A．B．C．D．10 . 抛物线y=2x2+1向右平移1个单位，再向下平移1个单位，所得到的抛物线是（）A．y=2（x﹣1）2+3B．y=2（x+1）2﹣3C．y=2（x﹣1）2﹣1D．y=3（x﹣1）2+1二、填空题11 . 某体育公园的圆形喷水池的水柱如图①所示，如果曲线APB表示落点B离点O最远的一条水流(如图②)，其上的水珠的高度y(米)关于水平距离x(米)的函数解析式为y＝－x2＋4x＋，那么圆形水池的半径至少为_______米时，才能使喷出的水流不落在水池外．12 . 如图，在平行四边形ABCD中，∠B＝120°，AB与CD之间的距离是，AB＝28，在AB上取一点E（AE ＜BE），使得∠DEC＝120°，则AE＝_____．13 . 已知反比例函数的图象如图所示，则实数m的取值范围是___________．14 . 点P（a+2，b-1）关于原点的对称点Q的坐标是（-3，2），则ab=______15 . 一个不透明的盒子中装有15个黑球和若干个白球，它们除颜色不同外，其余均相同，从盒子中随机摸出一球记下其颜色，再把它放回盒子中摇匀，重复上述过程，共试验300次，其中有200次摸到白球，由此估计盒子中的白球大约有____个．16 . 用半径为8的半圆围成一个圆锥的侧面，则圆锥的底面半径等于_______．三、解答题17 . 如图，AB是⊙O的直径，D，E为⊙O上位于AB异侧的两点，连接BD并延长至点C，使得CD＝BD，连接AC交⊙O于点F，连接AE，DE，DF．（1）证明：∠E＝∠C；（2）若∠E＝55°，求∠BDF的度数．18 . 某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元，为了扩大销售减少库存，商场决定采取适当的降价措施．经调查发现，如果每件衬衫降价1元，商场平均每天可多售出2件．若设每件衬衫降价x元，解答下列问题：（1）当每件衬衫降价5元，则每件利润元，平均每天可售出件．（2）若平均每天获利为Q元，请求出Q与x的函数关系式．（3）若商场想平均每天盈利1200元，每件衬衫应降价多少元？19 . 解方程：（1）（x+2）2＝25（2）x2﹣2x﹣2＝0（3）x2﹣6x﹣16＝0（4）（x﹣2）2﹣（3x+8）2＝020 . （8分）如图，一次函数的图象与x轴交于点B，与反比例函数的图象的交点为A（﹣2，3）．（1）求反比例函数的解析式；（2）过点A作AC⊥x轴，垂足为C，若点P在反比例函数图象上，且△PBC的面积等于18，求P点的坐标．21 . 如图，AB为⊙O的直径，点C在AB的延长线上，CD、CE分别与⊙O相切于点D、E，若AD=2，∠DAC=∠DCA，求CE.22 . 为丰富学生的校园生活，某校举行“与爱同行”朗诵比赛，赛后整理参赛同学的成绩，绘制成如下不完整的统计图表，请根据图表中的信息解答下列问题．组别成绩x（分）频数（人数）A8.0≤x＜8.5aB8.5≤x＜9.08C9.0≤x＜9.515D9.5≤x＜103（1）图中a= ，这次比赛成绩的众数落在组；（2）请补全频数分布直方图；（3）学校决定选派本次比赛成绩最好的3人参加全市中学生朗诵比赛，并为参赛选手准备了2件白色、1件蓝色上衣和黑色、蓝色、白色的裤子各1条，小军先选，他从中随机选取一件上衣和一条裤子搭配成一套衣服，请用画树状图法或列表法求出上衣和裤子搭配成不同颜色的概率．23 . 如图，有一块矩形硬纸板，长50cm，宽30cm．在其四角各剪去一个同样的正方形，然后将四周突出部分折起，可制成一个无盖长方体盒子．当剪去正方形的边长取何值时，所得长方体盒子的侧面积为600cm2？24 . 在平面直角坐标系中，设二次函数y1=mx2﹣6mx+8m（m为常数）．（1）若函数y1经过点（1，3），求函数y1的表达式；（2）若m＜0，当x＜时，此二次函数y随x的增大而增大，求a的取值范围；（3）已知一次函数y2=x﹣2，当y1•y2＞0时，求x的取值范围．。

辽宁省2019-2020学年九年级上学期期末数学试题C卷姓名:________ 班级:________ 成绩:________一、单选题1 . 如图，能使△ACD∽△BCA相似的条件是（）A．B．C．D．2 . 绍兴市著名的桥乡，如图，石拱桥的桥顶到水面的距离CD为8m，桥拱半径OC为5m，则水面宽AB为（）A．4m B．5m C．6m D．8m3 . 点，，均在二次函数的图象上，则，，的大小关系是（）A．B．C．D．4 . 如图，在中，分别是边上的点，，若，则下列结论中正确的是（）A．B．C．D．5 . 如图，已知△ABC和△DEF均为等腰直角三角形，AB＝2，DE＝1，E、B、F、C在同一条直线上，开始时点B与点F重合，让△DEF沿直线BC向右移动，最后点C与点E重合，设两三角形重合面积为y，点F移动的距离为x，则y关于x的大致图象是（）A．B．C．D．6 . 用min{a，b}表示a，b两数中的最小数，若函数，则y的图象为（）A．B．C．D．7 . 已知线段 a=2，b=8，则 a，b 的比例中项线段为（）A．16B．±4C．4D．﹣48 . 在一个有 10 万人的小镇，随机调查了 1000 人，其中有 120 人周六早上观看中央电视台的“朝闻天下”节目，那么在该镇随便问一个人，他在周六早上观看中央电视台的“朝闻天下”节目的概率大约是（）A．B．C．D．9 . 如图，以O为圆心，任意长为半径画弧，与射线OM交于点A，再以A为圆心，AO长为半径画弧，两弧交于点B，画射线OB．则cos∠AOB的值等于（）A．B．C．B.10 . 以下命题：①直径相等的圆是等圆；②长度相等弧是等弧；③相等的弦所对的弧也相等；④圆的对称轴是直径；⑤相等的圆周角所对的弧相等；其中正确的个数是（）A．4B．3C．2D．1二、填空题11 . 将抛物线向右平移1个单位长度，再向下平移3个单位长度，平移后抛物线的解析式是．12 . 如图，AB是的一条弦，P是上一动点（不与点A，B重合），C，D分别是AB，BP的中点．若，，则CD长的最大值为________________．13 . 在一个不透明的盒子中装有a个除颜色外完全相同的球，其中只有6个白球．若每次将球充分搅匀后，任意摸出1个球记下颜色后再放回盒子，通过大量重复试验后，发现摸到白球的频率稳定在20%左右，则a的值约为_____．14 . 若半径为6cm的圆中，一段弧长为3πcm，则这段弧所对的圆心角度数为_______.15 . 已知点A（2,5），B（4,5）是抛物线上的两点，则这条抛物线的对称轴为直线__________.16 . 如图，在△ABC中，DE∥BC，BC=6,梯形DBCE面积是△ADE面积的3倍，则DE=________.三、解答题17 . （探索发现）如图①，将沿中位线折叠，使点的对称点落在边上，再将纸片分别沿等腰和等腰的底边上的高线，折叠，折叠后的三个三角形拼合形成一个新的图形.小刚在探索这个问题时发现四边形是矩形.小刚是这样想的：（1）请参考小刚的思路写出证明过程；（2）连接，当时，直接写出线段、、的数量关系：______；（理解运用）（3）如图②，在四边形中，，，，，，点为边的中点，把四边形折叠成如图②所示的正方形，顶点、落在点处，顶点、落在线段上的点处，求的长.18 . 计算：.19 . 二次函数的图象过，，，点在函数图象上，点，是二次函数图象上的一对对称点，一次函数图象过点，，求：一次函数和二次函数的解析式；写出使一次函数值大于二次函数值的的取值范围．20 . 小娜家购买了4个灯笼(外观完全一样)，灯笼上分别写有“欢”“度”“春”“节”．(1)小娜从四个灯笼中任取一个，取到“春”的概率是多少；(2)小娜从四个灯笼中先后取出两个灯笼，请用列表法或画树状图法求小娜恰好取到“春”“节”两个灯笼的概率．21 . 如图，在中，点在上，点在上，，，与交于点，试判断的形状，并说明理由.22 . 某商场要经营一种新上市的文具，进价为20元/件．试营销阶段发现：当销售单价为25元/件时，每天的销售量是150件；销售单价每上涨1元，每天的销售量就减少10件．（1）求商场销售这种文具每天所得的销售利润w（元）与销售单价x（元）之间的函数关系式；（2）求销售单价为多少元时，该文具每天的销售利润最大？（3）现商场规定该文具每天销售量不少于120件，为使该文具每天的销售利润最大，该文具定价多少元时，每天利润最大？23 . 如图，已知二次函数(b，c为常数)的图象经过点A(3，1)，点C(0，4)，顶点为点M，过点A作AB∥x轴，交y轴于点D，交该二次函数图象于点B，连结BA．（1）求该二次函数的解析式及点M的坐标；（2）若将该二次函数图象向下平移个单位，使平移后得到的二次函数图象的顶点与△ABC的外心重合，求的取值；（3）点P是坐标平面内的一点，使得△ACB与△MCP，且CM的对应边为AC，请写出所有点P的坐标(直接写出结果，不必写解答过程)．24 . 如图，某电视台大楼顶部安置了一电视发射铁塔CD，现有一位测试员分别在楼下相距16m的A，B两处测得D点和C点的仰角分别是45°和60°，已知A，B，E在一条直线上，C，D，E也在一条直线上，且BE＝30m.求电视发射铁塔的高度.（结果保留整数，参考数据：≈1.41，≈1.73）。

2019-2020学年辽宁省大连市普兰店区九年级上学期期末考试
数学试卷解析版
一、选择题（本题共10小题，每小题3分，共30分，在每个小题给出的四个选项中，只有一个选项正确）
1．（3分）下列图形中，既是轴对称图形又是中心对称图形的有（）
A．1个B．2个C．3个D．4个
【解答】解：第1个图形，是轴对称图形，也是中心对称图形，符合题意；
第2个图形，是轴对称图形，不是中心对称图形，不合题意；
第3个图形，是轴对称图形，也是中心对称图形，符合题意；
第4个图形，是轴对称图形，也是中心对称图形，符合题意．
故选：C．
2．（3分）方程x2＝2x的根是（）
A．x＝2B．x＝0C．x1＝0，x2＝2D．x1＝0，x2＝﹣2【解答】解：方程变形得：x2﹣2x＝0，
分解因式得：x（x﹣2）＝0，
可得：x＝0或x﹣2＝0，
解得：x1＝0，x2＝2．
故选：C．
3．（3分）抛物线y＝x2+2x+3的顶点坐标是（）
A．（﹣1，﹣2）B．（﹣1，2）C．（1，2）D．（1，﹣2）
【解答】解：∵原抛物线可化为：y＝x2+2x+3＝（x+1）2+2，
∴其顶点坐标为（﹣1，2）．
故选：B．
4．（3分）如图，点A、B、C在⊙O上，∠ABO＝22°，∠ACO＝42°，则∠BOC等于（）
第1 页共16 页。

辽宁省大连市九年级上册数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共20分)1. （2分） (2019九下·常熟月考) 在Rt△ABC中，∠C＝90°，如果∠A＝α，AB＝3，那么AC等于（）A . 3sinαB . 3cosαC .D .2. （2分）冬至时是一年中太阳相对于地球位置最低的时刻，只要此时能采到阳光，一年四季就均能受到阳光照射．此时竖一根a米长的竹杆，其影长为b米，某单位计划想建m米高的南北两幢宿舍楼（如图所示）．当两幢楼相距多少米时，后楼的采光一年四季不受影响？（）.A . 米B . 米C . 米D . abm米3. （2分） (2017九上·十堰期末) 某村耕地总面积为50公顷，且该村人均耕地面积y（单位：公顷/人）与总人口x（单位：人）的函数图象如图所示，则下列说法正确的是（）A . 该村人均耕地面积随总人口的增多而增多B . 该村人均耕地面积y与总人口x成正比例C . 若该村人均耕地面积为2公顷，则总人口有100人D . 当该村总人口为50人时，人均耕地面积为1公顷4. （2分）如图，四边形ABCD，M为BC边的中点．若∠B=∠AMD=∠C=45°，AB=8，CD=9，则AD的长为（）A . 3B . 4C . 5D . 65. （2分） (2018九上·武汉期中) 二次函数y＝2 ＋3的图象是一条抛物线，则下列说法错误的是（）A . 抛物线开口向上B . 抛物线的对称轴是直线x＝1C . 抛物线的顶点是(1，3)D . 当x＞1时，y随x的增大而减小6. （2分） (2019八上·兰州期末) 在△ABC中，∠C＝90°，c2＝2b2 ，则两直角边a，b的关系是（）A . a＜bB . a＞bC . a＝bD . 以上三种情况都有可能7. （2分） (2018七下·历城期中) 如图，△DAC和△E BC均是等边三角形，A E、BD分别与CD、CE交于点M、N，有如下结论：①△ACE≌△DCB；②CM=CN；③AC=DN；④∠DAE=∠DBC．其中正确的有（）A . ②④B . ①②③C . ①②④D . ①②③④8. （2分）(2020·宿州模拟) 如图，正方形OABC的边长为6，D为AB中点，OB交CD于点Q，Q是y＝上一点，k的值是（）A . 4B . 8C . 16D . 249. （2分） (2019九上·合肥月考) 中国贵州省内的射电望远镜（）是目前世界上口径最大，精度最高的望远镜，根据有关资料显示，该望远镜的轴截面呈现抛物线状，口径为500米，最低点到口径面的距离是100米，若按如图(2)建立平面直角坐标系，则抛物线的解析式是（）A .B .C .D .10. （2分） (2017九上·鞍山期末) 在平面直角坐标系中，将二次函数的图象向上平移2个单位，所得图象的表达式为（）A .B .C .D .二、填空题 (共8题；共8分)11. （1分） (2020九上·无锡月考) 若3x=5y，则 =________.12. （1分） (2019九上·句容期末) 已知 = ，则 =________.13. （1分） (2016九下·萧山开学考) 在△ABC中，∠A，∠B所对的边分别为a，b，∠C＝70°.若二次函数y＝(a＋b)x ²＋(a＋b)x－(a－b)的最小值为－，则∠A＝________.14. （1分）(2017·潍坊模拟) 计算﹣|2 ﹣2cos30°|+（）﹣1﹣（1﹣π）0的结果是________．15. （1分） (2019九上·海口期末) 如图，在平面直角坐标系中，已知点A（﹣2，4），B（﹣4，﹣2），以原点O为位似中心，相似比为，把△ABO缩小，则点A的对应点A'的坐标是________.16. （1分）如图，身高1.6米的某学生想测量一棵大树的高度，她沿着树影BA由B向A走去，当走到C点时，她的影子顶端正好与树的影子重合，测得BC=3米，CA=1米，则树的高度为________。

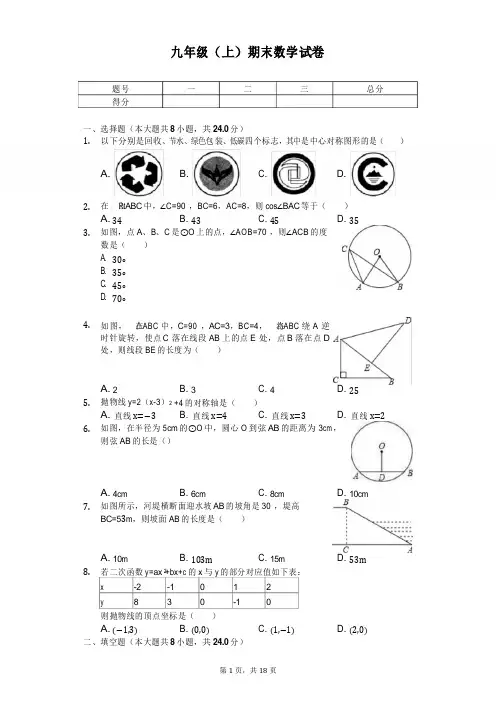
九年级（上）期末数学试卷题号一二三总分得分一、选择题（本大题共8小题，共24.0分）1. 以下分别是回收、节水、绿色包装、低碳四个标志，其中是中心对称图形的是（）A. B. C. D.2.在△R t ABC中，∠C=90°，BC=6，AC=8，则cos∠BAC等于（）A.34B.43C.45D.353.如图，点A、B、C是⊙O上的点，∠AOB=70°，则∠ACB的度数是（）A. B. C. D.30∘35∘45∘70∘4.如图，△在ABC中，C=90°，AC=3，BC=4，△将ABC绕A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，则线段BE的长度为（）A.2B.3C.4D.255.抛物线y=2（x-3）2+4的对称轴是（）A.直线x=−3B.直线x=4C.直线x=3D.直线x=26.如图，在半径为5cm的⊙O中，圆心O到弦AB的距离为3c m，则弦AB的长是（）A.4cmB.6cmC.8cmD.10cm7.如图所示，河堤横断面迎水坡AB的坡角是30°，堤高BC=53m，则坡面AB的长度是（）A.10mB.103mC.15mD.53m8.若二次函数y=ax+bx+c的x与y的部分对应值如下表：x y -28-131-12则抛物线的顶点坐标是（）A.(−1,3)B.(0,0)C.(1,−1)D.(2,0)二、填空题（本大题共8小题，共24.0分）29. 一个不透明的盒子里有 5 张完全相同的卡片，它们的标号分别为 1，2，3，4，5，随机抽取一张，抽中标号为奇数的卡片的概率是______． 10. 若关于 x 的一元二次方程-x +5x +c=0 的一个根为 3，则 c =______． 11. 抛物线 y =x +2x +m -1 与 x 轴有交点，则 m 的取值范围是______． 12. 如图， △在ABC 中，D 、E 分别是边 AB 、AC 的中点， △则ADE与△ABC 的面积比 ：S =______．13. 如图所示， △在ABC 中，∠B =40°，将△ABC 绕点 A 逆时针旋转 △至ADE 处，使点 B落在 BC 延长线上的 D 点处，则∠CAE =______度．14. 若一个圆锥的侧面展开图是一个半径为 6cm ，圆心角为 120°的扇形，则该圆锥的侧 面面积为______cm （结果保留 π）．15. 如图，线段 CD 两个端点的坐标分别为 C （1，2）、D （2，0），以原点为位似中心，将线段 CD 放大得 到线段 AB ，若点 B 的坐标为（5，0），则点 A 的坐 标为______．16. 如图，抛物线 y =ax +bx +c （a ≠0）与 x 轴的一个交点坐标为（3，0），与 y 轴交点坐标为（0，3），顶点坐标 为（2，-1），当 0＜x ＜3 时，二次函数 y 的取值范围 是______．三、解答题（本大题共 10 小题，共 102.0 分） 17. 解下列方程：（1）x +10x +16=0（2）x2−2x -14=0．2 2 △S ADE △ABC2218.平面直角坐标系中，点A（-2，-4）、B（0，-4）、C（-3，0）．（1）请在坐标系中画△出ABC绕原点O顺时针旋转90°后的△A△′B′C′，并直接写出A′、B′、C′的坐标；（2）点B旋转到点B′所经过的路径长为______．19.袋子装有2个黑球、1个白球，这些球的形状、大小、质地等完全相同，即除颜色外无其他差别，在看不到球的前提下，随机从袋子中摸出1个球，不放回去，再摸出一个球，求这两次摸出的球都是黑色的概率．20.如图，沿AD方向开山修路，为了加快施工进度，要在小山的另一边同时施工，已知∠A=40°，AB=500m，∠B=50°，求另一边开挖点C离B多远正好使A、C、D三点在一条直线上，（结果取整数，sin40°≈0.745，cos40°≈0.766）．21. 一面墙长 18m ，借助这面墙用长度为 32m 的篱笆围成面积为 120m 矩形的花园ABCD （墙的长度要大于花园的长 BC ），求矩形的宽 AB 的长．22. 平面直角坐标系中，点 A 坐标为（-1，0），直线 y =-x +31与 x 轴交于点 B ，与 y 轴交于点 C ，抛物线 y =ax +bx +c 2（a ≠0），经过 A 、B 、C 三点，直线 x =1.5 交抛物线 于点 D ，交 BC 于 E ，连接 CD 、BD ． （1）求二次函数解析式； （1） △求BCD 的面积．23. 如图，⊙O 的直径 AB 为 10cm ，弦 AC 为 6cm ，∠ACB 的平分线 CE 交 AB 于 D ，交 ⊙O 于 E ，EF 为⊙O 的切线，交 CB 的延长线于 F ．（1）求证：EF ∥AB ； （2）求 BF 的长．2224.△ABC中，AD⊥BC于D，tan∠B=12，tan∠C=1，AD=6，点E沿射线DC方向一直运动，将点E绕点D逆时针旋转90°得到点F（F在射线DA上），点G与点E关于点D成中心对称（点G在射线DB上），连接GE、EF、FG得△到GEF．（1）求BC的长；（2）在点E的运动过程中，设DE=x，△GEF △与ABC的重叠部分面积为S，求S 与x的函数关系式．25.【阅读理解】小白同学遇到这样一个问题：△ABC中，D 是BC的中点，E是AB上一点，延长DE、AC交于点F，DE=EF，AB=5，求AE的长．小白的想法是：过点E作EH∥B C交AC于H，再通过相似三角形的性质得到AE、BE的比，从而得出AE的长，请你按照小白的思路完成解答．【解决问题】请借助小白的解题经验，完成下面问题：△ABC中，AD平分∠BAC交BC于D，E为AB边上一点，AE=AD，H、Q为BC上两点，CQ=DH，DQ=mDH，G为AC上一点，连接EQ交HG、AD于F、P，∠EFG+∠EAD=180°，猜想并验证EP与GH的数量关系．26. 抛物线 y =ax +2ax +c （a ＞0，c ＜0），与 x 轴交于 A 、B 两点（A 在 B 左侧），与 y轴交于点 C ，A 点坐标为（-3，0），抛物线顶点为 D △，ACD 的面积为 3． （1）求二次函数解析式；（2）点 P （m ，n ）是抛物线第三象限内一点，P 关于原点的对称点 Q 在第一象限 内，当 QB 取最小值时，求 m 的值．2 2答案和解析1.【答案】C【解析】解：A、不是中心对称图形，故本选项错误；B、不是中心对称图形，故本选项错误；C、是中心对称图形，故本选项正确；D、不是中心对称图形，故本选项错误；故选：C．根据中心对称图形的定义，结合选项所给图形进行判断即可．此题主要考查了中心对称图形的概念，中心对称图形是要寻找对称中心，旋转180度后与原图重合．2.【答案】C【解析】解：由勾股定理，得AB==10．由余弦等于邻边比斜边，得cos∠BAC==，故选：C．根据勾股定理，可得AB的长，根据余弦等于邻边比斜边，可得答案．本题考查了锐角三角函数的定义，利用勾股定理得出AB的长是解题关键．3.【答案】B【解析】解：∵∠AOB=70°，∴∠ACB=∠AOB=35°．故选：B．根据圆周角定理得到∠ACB=∠AOB，即可计算出∠ACB．本题考查了圆周角定理：一条弧所对的圆周角是它所对的圆心角的一半．4.【答案】A【解析】解： △在ABC 中，∠C=90°，AC=3，BC=4， ∴AB=5，∵△ABC 绕点 A 逆时针旋转得到△AED ， ∴BE=AB-AE=2，故选：A ．由旋转的性质可求得 AE 、DE ，由勾股定理可求得 AB ，则可求得 BE ，连接 BD ， 在 Rt △BDE 中可求得 BD 的长．本题主要考查旋转的性质，掌握旋转前后对应线段相等、对应角相等是解题 的关键．5.【答案】C【解析】解：∵抛物线的解析式为：y =2（x-3） +4，∴此抛物线的对称轴是直线 x=3．故选：C ．根据二次函数的顶点式进行解答即可．本题考查的是二次函数的性质，用到的知识点：二次函数 y=a （x-h ） +k 的对称 轴是直线 x=h ．6.【答案】C【解析】解：连结 OA ，OD ⊥AB ，如图，∴AD=BD ，OD=3cm ，在 Rt △AOD 中，OA=5cm ，OD=3cm ， ∴AD==4cm ，∴AB=2AD=8cm ．故选：C ．连结 OA ，OD ⊥AB ，根据垂径定理得到 AD=BD ，且 OD=3cm ，在 Rt △AOD 中 根据勾股定理计算出 AD ，然后利用 AB=2AD 求解．本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧， 也考查了勾股定理．227.【答案】B【解析】解：∵河堤横断面迎水坡AB的坡角是30°，堤高BC=5m，∴sin30°=∴AB=，=10m．故选：B．直接利用坡角的度数结合锐角三角函数求出答案．本题考查了解直角三角形的应用-坡度坡角问题，属于基础题，掌握三角函数的定义是解答本题的关键．8.【答案】C【解析】解：∵当x=0或x=2时，y=0，当x=1时，y=-1，∴，解得，∴二次函数解析式为y=x -2x=（x-1）-1，∴抛物线的顶点坐标为（1，-1），故选：C．由表中所给数据，可求得二次函数解析式，则可求得其顶点坐标．本题主要考查二次函数的性质，利用条件求得二次函数的解析式是解题的关键．9.【答案】35【解析】【分析】此题考查了概率公式的应用．注意用到的知识点为：概率=所求情况数与总情况数之比．根据一个不透明的盒子里有5张完全相同的卡片，它们的标号分别为1，2，3，4，5，其中奇数有1，3，5，共3个，再根据概率公式即可得出答案．【解答】解：∵共有5个数字，奇数有3个，22∴随机抽取一张，抽中标号为奇数的卡片的概率是 ．故答案是 ．10.【答案】-6【解析】解：把 x=3 代入，得-3 +5×3+c=0，解得 c=-6．故答案是：-6．把 x=3 代入已知方程，列出关于 c 的新方程，通过解新方程可以求得 c 的值．本题考查了一元二次方程的解的定义．能使一元二次方程左右两边相等的未 知数的值是一元二次方程的解．11.【答案】m ≤2【解析】解：∵抛物线 y=x +2x+m-1 与 x 轴有交点，∴关于 x 的一元二次方程 x+2x+m-1=0 有解，∴△=22-4（m-1）=8-4m≥0，解得：m≤2．故答案为：m≤2．由抛物线与 x 轴有交点可得出方程 x +2x+m-1=0 有解，利用根的判别式△≥0△ ， 即可得出关于 m 的一元一次不等式，解之即可得出结论．本题考查了抛物线与 x 轴的交点以及根的判别式，利用根的判别式△≥0△ 找出 关于 m 的一元一次不等式是解题的关键．12.【答案】1：4【解析】解：∵D 、E 分别是边 AB 、AC 的中点，∴DE ∥B C ，DE= BC ，∴△ADE △∽ABC ，∴S△ADE△ABC） = ，故答案为：1：4．2 22 2：S =（ 2∽ABC，根据相根据三角形中位线定理得到DE∥BC，DE=BC，得到△ADE △似三角形的性质计算即可．本题考查的是相似三角形的性质、三角形中位线定理的应用，掌握相似三角形的面积比等于相似比的平方是解题的关键．13.【答案】100【解析】解∵△：ABC绕点A逆时针旋转至△ADE处，使点B落在BC延长线上的D点处，∴AB=AD，∠BAD等于旋转角，∴∠B=∠ADB=40°，∴∠BAD=180°-∠B-∠ADB=100°．故答案为100．根据旋转的性质得AB=AD，∠BAD等于旋转角，再根据等腰三角形的性质得∠B=∠ADB=40°，然后根据三角形内角和定理计算∠BAD的度数．本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．14.【答案】12π【解析】2解：该圆锥的侧面面积==12π（cm）．故答案为12π．由于圆锥的侧面展开图为扇形，所以根据扇形的面积公式计算即可，本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．15.【答案】（2.5，5）【解析】解：∵以原点O为位似中心，在第一象限内，将线段CD放大得到线段AB，∴B点与D点是对应点，又点D的坐标为（2，0），点B的坐标为（5，0），∴位似比为：5：2，∵C （1，2），∴点 A 的坐标为：（2.5，5）．故答案为：（2.5，5）．根据题意得到 B 点与 D 点是对应点，根据B 点与 D 点的坐标求出位似比，根 据位似变换的性质计算即可．本题主要考查了位似变换的概念和性质，正确把握位似比与对应点坐标的关 系是解题关键．16.【答案】-1≤y ＜3【解析】解：∵抛物线的开口向上，顶点坐标为（2，-1），∴a ＞0，对称轴为直线 x=2 ，∴当 x =0 时的 y 值大于 x=3 时的 y 值，且y 值最小值为-1，∴当 0＜x ＜3 时，-1≤y ＜3．故答案为：-1≤y ＜3．由抛物线的开口方向及顶点坐标，可得出a ＞0 且对称轴为直线 x=2 ，观察图象结合二次函数的性质，即可找出当0＜x ＜3 时二次函数 y 的取值范围．本题考查了抛物线与 x 轴的交点以及二次函数的性质，观察图形，利用数形 结合解决问题是解题的关键．17.【答案】解：（1）x +10x+16=0 ，（x+2 ）（x+8 ）=0，∴x+2=0 或 x+8=0 ，解得，x =-2，x =-8；1 2（2）x22 x-14 =0， ∵a=1 ，b=-2，c=-14 ， ∴△=(2)24×1×(14) =3＞0， ∴x=2±32×1= 2±32，∴x 1=232 ，x =2+32 ．2【解析】（1）先把方程左边进行因式分解，然后求解即可；2（2）先找出公式中的a，b，c的值，再代入求根公式即可得出答案．本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．18.【答案】2π【解析】解：（1）如图所示△，A′B′C′即为所求，A′的坐标为（-4，2）、B′的坐标为（-4，0）、C′的坐标为（0，3）；（2）∵OB=4、∠B OB′=90°，∴点B旋转到点B′所经过的路径长为=2π，故答案为：2π．（1）分别作出点A、B、C绕原点O顺时针旋转90°后得到的对应点，再顺次连接可得；（2）根据弧长公式即可得．本题主要考查作图-旋转变换，解题的关键是根据旋转变换的定义得出旋转后得到的对应点．19.【答案】解：画树状图得：∴一共有6种等可能的结果，其中两个球都是黑球的有2种情况，∴两个球都是黑球的概率为26=13．【解析】首先根据题意画出树状图，然后根据树状图求得所有等可能的结果与两个球都是黑球的情况，再利用概率公式求解即可．此题考查的是用树状图法求概率的知识．注意树状图法可以不重复不遗漏的列出所有可能的结果，适合两步或两步以上完成的事件；注意概率=所求情况数与总情况数之比．20.【答案】解：∵∠A=40°，∠D=50°，∴∠C=180°-40°-50°=90°，△R t ABC中，∠C=90°，∠A=40°，AB=500m，∴sin A=BCAB，∴BC=AB•cosB=500×sin40°=500×0.745=372.5≈373（米）．答：开挖点C到点B的距离约为373米．【解析】确定∠C=90°，然后在Rt△ABC中利用三角函数解答即可．本题考查了解直角三角形的应用，找到直角三角形，然后利用三角函数是解题的关键．21.【答案】解：设矩形的宽AB的长为xm，则BC的长为（32-2x）m，根据题意得：x（32-2x）=120，解得：x=6，x=10．12∵x＜32-2x，解得：x＜1023，∴x=6或10．答：矩形的宽AB的长为6m或10m．【解析】设矩形的宽AB的长为xm，则BC的长为（32-2x）m，根据矩形的面积公式，即可得出关于x的一元二次方程，解之即可得出结论．本题考查了一元二次方程的应用以及长方形的面积，找准等量关系，正确列出一元二次方程是解题的关键．22.【答案】解：（1）把y=0代入y=-x+3中，可得：x=3，1所以点B的坐标为（3，0），把x=0代入y=-x+3中，可得：y=3，1所以点C的坐标为（0，3）把A（-1，0）B（3，0）C（0，3）分别代入y=ax+bx+c（a≠0）中，可得：22a−b+c=09a+3b+c=0c=3解得：a=−1b=2c=3，所以二次函数解析式为 y =-x +2x +3， 2（2）把 x =1.5 代入 y =-x +2x +3 中，可得：y =154，所以点 D 的坐标为（1.5，154）， 所 △以BCD 的面积=3×154−12×3×3−12×1.5×154−12×1.5×34=278． 【解析】（1）根据一次函数解析式求出点 B ，C 的坐标，再代入抛物线 y =ax +bx+c （a ≠0）2中解答即可；（2）根据△BCD 的面积等于长方形面积减三个小三角形面积计算即可．本题主要考查的是待定系数法求二次函数的解析式、一次函数与坐标轴的交点 △，BCD 的面积等于长方形面积减三个小三角形面积是解题的关键． 23.【答案】（1）证明：连接 OE ．∵∠ACE =∠BCE ， ∴AE =BE ， ∴OE ⊥AB ， ∵EF 是切线， ∴OE ⊥EF ， ∴EF ∥AB ．（2）解：作 CH ⊥AB 于 H ． ∵AB 是直径， ∴∠ACB =90°，∴BC =AB2−AC2=102−62=8， ∵12•AC •BC =12•AB •CH ， ∴CH =245， ∵CH ∥OE ， ∴△CDH △∽EDO ，∴CDDE =CHOE =2425， ∵DB ∥EF ，∴BCBF =CDDE =2425， ∴BF=253． 【解析】（1）连接 OE ，只要证明 OE ⊥AB ，OE ⊥EF 即可；（2）利用面积法求出 CH ，由 CH ∥OE ，推出△CDH ∽△EDO ，可得= =，由 DB ∥EF ，可得= =，由此即可解决问题；本题考查切线的性质、圆周角定理、平行线的性质等知识，解题的关键是学2 2 2 2会添加常用辅助线，构造直角三角形以及相似三角形解决问题，属于中考常 考题型．24.【答案】解：（1）∵AD ⊥BC ，∴∠ADB =∠ADC =90°，∵tan ∠B =12，tan ∠C =1，AD =6， ∴CD =AD =6，BD =2AD =12， ∴BC =BD +CD =18．（2）①如图 1 中，当 0＜x ≤6 时，重叠部分 △是EFG ，S =12×2x ×x =x ．②如图 2 中，当 6＜x ＜12 时，重叠部分是五边形 ACGM ．作 BK ∥GF 交 DF 的延长线于 K ，作 MH ⊥BC 于 H ．易知：AB =65，DB =DK =12，∵FM ∥BK ，∴AFAK =AMAB ， ∴x−66=AM65， ∴AM=55（x -6）， ∵MH ∥AD ，∴MHAD =BMBA ，∴MH6=65−55(x −6)65， ∴MH =365-15x ，∴S =S -S =12×6×18-12×（12-x ）×（365-15x ）=-110x +245x +545． ③当 x ≥12 时，重叠部分 △是ABC ，S =54， 综上所述，S =x2(0＜x ≤6)−110x2+245x+545(6＜x ＜12)54(x ≥12)． 【解析】（1）解直角三角形求出 BD ，CD 即可解决问题；（2）分三种情形：①如图 1 中，当 0＜x≤6 时，重叠部分 △是EFG ．②如图 2 中，2 2 △ABC △BMG当6＜x＜12时，重叠部分是五边形ACGM．③当x≥12时，重叠部分是△ABC．分别求解即可解决问题；本题考查旋转变换，中心对称，解直角三角形，平行线的性质，多边形的面积等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．25.【答案】解：【阅读理解】如图1，过点E作EH∥BC交AC于H，∴∠FEH=∠FDC，∠FHE=∠C，∴△FEH △∽FDC，∴EHDC=FEFD，∵DE=EF，∴EHDC=12，∵BD=DC，∴EHBC=14，同理得△：AEH△∽ABC，∴AEAB=EHBC=14，∵AB=5，∴AE=54；【解决问题】猜想：EPGH=m+1m+2，理由是：如图2，过D作DM∥GH，交AC于M，∴∠CMD=∠CGH，∠CDM=∠CHG，∴△CDM△∽CHG，∴CDCH=DMGH，设DH=CQ=x，则DQ=mx，∴DMGH=mx+xmx+2x=m+1m+2，∵AD平分∠BAC，∴∠EAP=∠DAM，∵∠EFG+∠EAD=180°，∴∠AEP+∠ANF=180°，∵GH∥DM，∴∠ADM+∠DNG=∠ADM+∠ANF=180°，∴∠ADM=∠AFP，∵AE=AD，∴△AEP≌△ADM，∴EP=DM，∴EPGH=m+1m+2．【解析】【阅读理解】∽ABC，列比例式并根据DE=EF、作平行线，证明△FEH△∽FDC和△A EH△BD=DC ，可得结论；【解决问题】如图 2，作平行线，证明△CDM △∽CHG ，得 ，设 DH=CQ=x ，则DQ=mx ，再证明△AEP ≌△ADM ，得 EP=DM ，代入可得结论．本题考查了三角形综合题，涉及到了相似三角形的判定与性质，勾股定理等知识点，解题的关键是学会添加常用辅助线，构造相似三角形解决问题，属 于中考压轴题．26.【答案】解：（1）把A （-3，0）代入 y =ax +2ax +c 得到 c =-3a ，∴抛物线的解析式为 y =ax +2ax -3a =a （x +1）-4a ， ∴D （-1，-4a ），C （0，-3a ），∵S△ACD △AOD △OCD △AOC， ∴12×3×4a +12×3a ×1-12×3×3a =15， 解得 a =1，∴抛物线的解析式为 y =x +2x -3．（2）由题意 Q （-m ，-n ），B （1，0）， ∴QB =（m +1） +n ，∵n =（m +1） -4，∴（m +1） =n +4，∴QB =n +4+n =（n +12） +154， ∴n =-12 时，QB 2 有最小值，此时-12=（m +1） -4， 解得 m =-1-144 或-1+144（舍弃）． ∴当 QB 取最小值时，m 的值为-1-144． 【解析】（1）根据 S =S +S -S 构建方程即可解决问题；（2）构建二次函数，利用二次函数的性质即可解决问题；本题考查二次函数的性质、二次函数的最值问题、三角形的面积等知识，解题的关键是学会用分割法求三角形面积，学会构建二次函数解决在问题．2 2 2 =S +S -S 22 2 2 2222222△ACD △AOD △OCD △AOC。

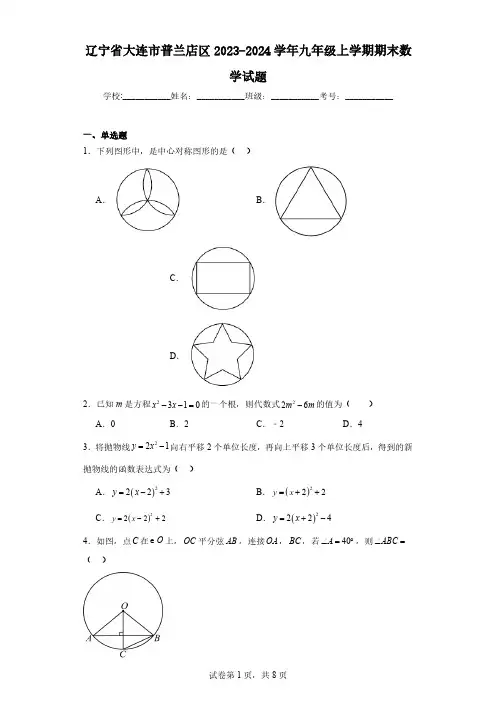
辽宁省大连市普兰店区2023-2024学年九年级上学期期末数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．下列图形中，是中心对称图形的是（ ）A ．B ．C ．D ．2．已知m 是方程的一个根，则代数式的值为（ ）A ．0B ．2C ．﹣2D ．43．将抛物线向右平移2个单位长度，再向上平移3个单位长度后，得到的新抛物线的函数表达式为（ ）A ．B ．C ．D ．4．如图，点在上，平分弦，连接，，若，则（ ）2310x x --=226m m -221y x =-()2223y x =-+()222y x =++()2222y x =-+()2224y x =+-C O e OC AB OA BC 40A ∠=︒ABC ∠=A ．B 6．如果将10个大小重量完全相同的乒乓球放入一个袋中，其中个红球，那么随机摸出一个红球概率为（A ．B 7．如图，直线A ．48．如图，将（ ）A ．5B ．9．圆锥的母线长为，底面半径长为A ．B ．10．二次函数50︒12a b ∥∥ABC V 9cm 227cm π2y ax bx =＋＋A ．B ．C ．当时，D ．函数的最大值为二、填空题三、解答题16．解下列方程：(1)；(2)．abc >240b ac -<31x -≤≤0y ≥a b c -+2340x x +-=22410x x --=根据以上信息，解答下列问题：(1) ， ；(2)根据以上数据分析，你认为哪个年级整体测试成绩更好，即可）；(3)已知初二年级组有名男生和名女生，从中随机抽取两名学生，用列表法或树状图法求出恰好抽到名男生和名女生的概率．a ＝b ＝B 2211的牺牲奉献，换来了我们国家的富强和人民的幸福，在抗美援朝期间“跳眼法”是炮兵常用的一种简易测距方法（图1）．如图2，点A 为左眼，点B 为右眼，点O 为右千大指，点C 为敌人的位置，点D 为敌人正左侧方的某一个参照物（，目测的长度后，然后利用相似三角形的知识来计算C 处敌人距离我方的大致距离．已知大多数人的眼距长约为厘米左右，手臂长约为厘米左右，若的估测长度为40米，那么的大致距离为多少米．21．如图．是的外接圆，且．连接交延长交于点D ．过点A 作，垂足为点E ．点F 在的延长线上，连接．使．(1)判断直线与的位置关系，并说明理由；(2)若，，求的半径．CD AB ∥CD AB 6.4OB 64CD CO O e ABC V AB AC =BO O e AE BD ⊥BD AF 2FAE ABD ∠=∠AF O e 1DE =4BC =O e23．小明同学在学习全等三角形的时候发现：当题目中存在“一边一角”的情况时，可以通过添加辅助线“造边”或“造角”构造全等三角形解决问题．(1)【问题初探】如图1，在中，，点在上，点在上，且，找出图中与相等的角，并证明；(2)【拓展探究】小明通过探究发现，图1中与之间存在固定的数量关系．证明小明发现的结论；(3)【类比迁移】如图2，将（1）中的条件“”改为“”，其他条件保持不变，当，时，求的值．ABC V AB AC =D BC E AD 2BED BAC CED ∠=∠=∠ABE ∠BE AE AB AC =AB AC >3BD CD =6BE =AE参考答案：1．C【分析】根据中心对称图形的概念判断．把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形．【详解】解：A 、不能找到这样的一个点，使图形绕某一点旋转180°后与原来的图形重合，所以不是中心对称图形，故此选项不符合题意；B 、不能找到这样的一个点，使图形绕某一点旋转180°后与原来的图形重合，所以不是中心对称图形，故此选项不符合题意；C 、能找到这样的一个点，使图形绕某一点旋转180°后与原来的图形重合，所以是中心对称图形，故此选项符合题意；D 、不能找到这样的一个点，使图形绕某一点旋转180°后与原来的图形重合，所以不是中心对称图形，故此选项不符合题意；故选：C ．【点睛】本题考查的是中心对称图形，中心对称图形是要寻找对称中心，旋转180度后与自身重合．2．B【分析】根据一元二次方程的解的定义得到，再把表示为，然后利用整体代入的方法计算．【详解】解：∵m 是方程的一个根，∴，∴，∴，故选：B ．【点睛】本题考查了代数式求值、一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．3．C【分析】根据二次函数图象平移的规律：左加右减，上加下减，进行解答即可．【详解】解：将抛物线向右平移2个单位长度，再向上平移3个单位长度后，得到的新抛物线的函数表达式为，231m m -=226m m -()223m m -2310x x --=2310m m --=231m m -=()2226=23=21=2m m m m --⨯221y x =-()2222y x =-+2，．选项A 正确，不合题意．抛物线与轴有两个不同交点，，选项B 不正确，符合题意．抛物线经过，对称轴为直线，抛物线经过，时，，选项C 正确，不合题意．抛物线开口向下，对称轴为直线，时，函数有最大值，选项D 正确，不合题意．故选：B ．11．【分析】根据二次函数的图像与性质，对于顶点式可以直接读出其顶点坐标，从而得到答案．【详解】解：抛物线的顶点坐标是，故答案为：．【点睛】本题考查二次函数图像与性质，熟记抛物线顶点式性质是解决问题的关键．12．【分析】平面直角坐标系中任意一点P （x ，y ），关于原点的对称点是（-x ，-y ），根据这一结论求得a ，b 的值，再进一步计算．【详解】解：∵点A （a ，5）与点B （－3，b ）关于原点对称，∴，∴a ＋b=3-5=-2；故答案为：.【点睛】本题主要考查了关于原点对称的点的坐标，掌握关于原点对称的点的坐标特征是解题的关键.13．1【分析】此题考查了二次函数图象与一元二次方程根的关系，根据二次函数图象与一元二次方程的关系“二次函数图象与x 轴的交点个数等于对应的一元二次方程根的个数，与x 轴横0c ∴>0abc ∴> x ∴240b ac ∆=-> (1,0)=1x -∴(3,0)-31x ∴-≤≤0y ≥ =1x -1x ∴=-y a b c =-+()1,2-()2212y x =++()1,2-()1,2-2-35a b =⎧⎨=-⎩2-由表格可知：有2名男生和2名女生，从中随机抽取两名学生共有抽到1名男生和1名女生的可能有恰好抽到1名男生和1名女生的概率为：19．(1)y 与x 之间的函数表达式为：(2)绿地面积增加时，矩形的长与宽都要增加∴272m∵，∴∴∵OA OB =OAB ABD∠=∠2AOF ABD∠=∠2FAE ABD∠=∠∴∵∴，∴，∴，∴，∴，∵是的半径，∴直线是的切线．（2）如图，连接，延长交于点M ，∵，，∴，，∴∵∴，∴，∵∴，∴，∵，∴，在中，，∵，∴FAE AOF∠=∠AE OD⊥90AEF ∠=︒90F FAE ∠+∠=︒90F AOF ∠+∠=︒90FAO ∠=︒AF OA ⊥OA O e AF O e OC AO BC OC OB =AC AB =AM BC ⊥BM CM =90OMB ∠=︒AE OD⊥90AEO ∠=︒OMB AEO ∠=∠AOE BOM∠=∠AOE BOM ≌V V BM AE =4BC =2BM AE ==Rt OAE △222OA OE AE =+1DE =()22212OA OA =-+当时，四边形是矩形，，，，四边形是矩形，24x ≤≤ ABCD 2AB CD ∴==A ADC ∠=∠=EF AB ⊥ 90AFG ∴∠=︒∴ADGF设，，，，即，，BC m =AE n =DE PM =MN BC ∥ AMN ABC ∴△∽△MN AD BC AE ∴=MN n y m n-=()m n y MN n -∴=m ⎛⎫则为的中位线时，矩形当在上方时，即，此时通风口的面积最大，面积为作于点S 交于点J ，，，MN EFG V PQNM ∴MN CD 2h b >ES FG ⊥CD CD FG ∥ EDC EFG ∴V V ∽，，AB AC = ABE ∠(ABE ACF SAS ∴V V ≌AE CF ∴=AEB Ð180AEB BED ∠+∠= BED CFD ∠∠∴=，，，，，P BED ∴∠=∠EBD ∠BDE CDP ∴V V ∽∴BD BE CD CP=6BE = 3BD CD =∴2BE CD CP BD⨯==。

大连市2020版九年级上学期期末数学试卷（I）卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）△ABC中，∠A，∠B均为锐角，且有，则△ABC是（）A . 直角（不等腰）三角形B . 等腰直角三角形C . 等腰（不等边）三角形D . 等边三角形2. （2分）(2014·深圳) 由几个大小相同的正方形组成的几何图形如图，则它的俯视图是（）A .B .C .D .3. （2分）(2019·义乌模拟) 已知不透明的袋中只装有黑、白两种球，这些球除颜色外都相同，其中白球有30个，黑球有n个．随机地从袋中摸出一个球，记录下颜色后，放回袋子中并摇匀，再从中摸出一个球，经过如此大量重复试验，发现摸出的黑球的频率稳定在0.4附近，则n的值约为（）A . 20B . 30C . 40D . 504. （2分）(2019·西安模拟) 如图，若△ABC和△DEF的面积分别为S1 ， S2 ，则（）A . S1＝ S2B . S1＝ S2C . S1＝ S2D . S1＝S25. （2分）已知一个直角三角形的面积为10，两直角边长的和为9，则两直角边长分别为（）A . 3，6B . 2，7C . 1，8D . 4，56. （2分） (2017九上·召陵期末) y= x+1是关于x的一次函数，则一元二次方程kx2+2x+1=0的根的情况为（）A . 没有实数根B . 有一个实数根C . 有两个不相等的实数根D . 有两个相等的实数根7. （2分） (2018九下·游仙模拟) 如图，将函数的图象沿y轴向上平移得到一条新函数的图象，其中点A（-4，m），B（-1，n）,平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9（图中的阴影部分），则新图象的函数表达式是（）A .B .C .D .8. （2分）如图，，，，、、、交于点P，则图中与相似的三角形的个数是（）个．A . 4B . 5C . 6D . 79. （2分）如图，在平面直角坐标系中，点A是x轴正半轴上的一个定点，点P是双曲线y=（x＞0）上的一个动点，PB⊥y轴于点B，当点P的横坐标逐渐增大时，四边形OAPB的面积将会（）A . 逐渐增大B . 不变C . 逐渐减小D . 先增大后减小10. （2分）如图，四边形ABCD中，∠BAD＝∠ACB＝90°，AB＝AD，AC＝4BC，设CD的长为x，四边形ABCD 的面积为y，则y与x之间的函数关系式是（）A .B .C .D .11. （2分）已知二次函数y=ax2+bx+c的图象如图所示，则下列结论正确的是（）A . a＞0B . b>0C . c＜0D . a+b+c＜012. （2分）如图，已知抛物线与x轴的一个交点A（1，0），对称轴是x=-1，则该抛物线与x轴的另一交点坐标是（）A . （-3，0）B . （-2，0）C . x=-3D . x=-2二、填空题 (共6题；共7分)13. （2分）已知方程的两根分别是、，则 ________， ________．14. （1分）如图，点A的坐标为（8，0），点B为y轴的负半轴上的一个动点，分别以OB，AB为直角边在第三、第四象限作等腰Rt△OBF、等腰Rt△ABE，连接EF交y轴于P点，当点B在y轴上移动时，PB的长度为________．15. （1分）(2020·内乡模拟) 如图，菱形OABC的顶点O在坐标原点，顶点A在x轴上，∠B＝120°，OA ＝1，将菱形OABC绕原点顺时针旋转105°至OA'B′C'的位置，则点B'的坐标为________.16. （1分）如图，AC为⊙O的直径，点B在圆上，OD⊥AC交⊙O于点D，连接BD，∠BDO=15°，则∠ACB=________．17. （1分） (2019九上·伊通期末) 一元二次方程的解是________．18. （1分）已知一个菱形的两条对角线长为8cm和6cm，则这个菱形的面积为________．三、解答题 (共7题；共78分)19. （5分）解方程：x2﹣6x﹣5=020. （13分）(2017·乐山) 为了了解我市中学生参加“科普知识”竞赛成绩的情况，随机抽查了部分参赛学生的成绩，整理并制作出如下的统计表和统计图，如图所示．请根据图表信息解答下列问题：组别分数段（分）频数频率A组60≤x＜70300.1B组70≤x＜8090nC组80≤x＜90m0.4D组90≤x＜100600.2（1）在表中：m=________，n=________；（2）补全频数分布直方图；（3）小明的成绩是所有被抽查学生成绩的中位数，据此推断他的成绩在________组；（4） 4个小组每组推荐1人，然后从4人中随机抽取2人参加颁奖典礼，恰好抽中A、C两组学生的概率是多少？并列表或画树状图说明．21. （10分）已知二次函数y=﹣ x2+bx+c的图象经过A（0，3），B（﹣4，﹣）两点．（1）求b，c的值．（2）二次函数y=﹣ x2+bx+c的图象与x轴是否有公共点，求公共点的坐标；若没有，请说明情况．22. （10分）小玲家在某24层楼的顶楼，对面新造了一幢28米高的图书馆，小玲在楼顶A处看图书馆楼顶B处和楼底C处的俯角分别是45°，60°．请问：（参考了数据：≈1.73，≈1.41）（1）两楼的间距是多少米？（精确到1m）（2）小玲家的这幢住宅楼的平均层高是多少米？（精确到0.1m）23. （10分）某地2015年为做好“精准扶贫”，投入资金 1280 万元用于异地安置，并规划投入资金逐年增加， 2017 年在 2015 年的基础上增加投入资金 1600 万元.（1）从 2015 年到 2017 年，该地投入异地安置资金的年平均增长率为多少？（2）在 2017 年异地安置的具体实施中，该地计划投入资金不低于 500 万元用于优先搬迁租房奖励，规定前 1000 户（含第 1000 户）每户每天奖励8元， 1000 户以后每户每天奖励5元，按租房 400 天计算，求 2017 年该地至少有多少户享受到优先搬迁租房奖励.24. （15分）(2016·海宁模拟) 如图，在平面直角坐标系中，四边形OABC是矩形，其中点A在x轴的正半轴上，点B的坐标为（4，2），点D为对角线OB上一个动点（不包括端点），∠BCD的平分线交OB于点E．（1）求线段OB所在直线的函数表达式，并写出CD的取值范围．（2）当∠BCD的平分线经过点A时，求点D的坐标．（3）点P是线段BC上的一个动点，求CD十DP的最小值．25. （15分）已知抛物线y=ax2+bx+c的顶点为（1，0），与y轴的交点坐标为（0，）．R（1，1）是抛物线对称轴l上的一点．（1）求抛物线y=ax2+bx+c的解析式.（2）若P是抛物线上的一个动点（如图一），求证：点P到R的距离与点P到直线y=﹣1的距离恒相等.（3）设直线PR与抛物线的另一交点为Q，E为线段PQ的中点，过点P、E、Q分别作直线y=﹣1的垂线．垂足分别为M、F、N（如图二）．求证：PF⊥QF．参考答案一、选择题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共6题；共7分)13-1、14-1、15-1、16-1、17-1、18-1、三、解答题 (共7题；共78分)19-1、20-1、20-2、20-3、20-4、21-1、21-2、22-1、22-2、23-1、23-2、24-1、24-2、24-3、25-1、25-2、25-3、。

辽宁省大连市2020版九年级上学期期末数学试卷（II）卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分） (2018九上·建平期末) 若反比例函数y= 图象经过点（5，-1），该函数图象在（）A . 第一、二象限B . 第一、三象限C . 第二、三象限D . 第二、四象限2. （2分） (2017七下·山西期末) 给出下列图形名称：（1）线段；（2）直角；（3）等腰三角形；（4）平行四边形；（5）长方形，在这五种图形中是轴对称图形的有（）A . 1个B . 2个C . 3个D . 4个3. （2分） (2018九上·三门期中) 如果2是方程x2﹣3x+k＝0的一个根，则常数k的值为（）A . 1B . 2C . ﹣1D . ﹣24. （2分） (2017九上·上城期中) 对于二次函数的图象与性质，下列说法正确的是（）A . 对称轴是直线，最小值是B . 对称轴是直线，最大值是C . 对称轴是直线，最小值是D . 对称轴是直线，最大值是5. （2分）如图，小明课间把老师的三角板的直角顶点放在黑板的两条平行线a、b上，已知∠1＝55°，则∠2的度数为（）A . 45°B . 35°6. （2分）(2018·岳阳模拟) 如下图，已知⊙O的直径为AB，AC⊥AB于点A, BC与⊙O相交于点D，在AC 上取一点E，使得ED=EA．下面四个结论：①ED是⊙O的切线；②BC=2OE③△BOD为等边三角形；④△EOD ∽ △CAD，正确的是（）A . ①②B . ②④C . ①②④D . ①②③④7. （2分）下列属于正多边形的特征的有（）①各边相等②各个内角相等③各个外角相等④各条对角线都相等⑤从一个顶点引出的对角线将正n边形分成面积相等的（n-2）个三角形A . 2个B . 3个C . 4个D . 5个8. （2分）(2016·十堰) 如图，从一张腰长为60cm，顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD，用此剪下的扇形铁皮围成一个圆锥的侧面（不计损耗），则该圆锥的高为（）A . 10cmB . 15cmC . 10 cmD . 20 cm9. （2分）在Rt△ABC中，∠C=90°，AB=5，BC=3，以AC所在的直线为轴旋转一周，所得圆锥的侧面积为（）A . 12πD . 30π10. （2分）若关于的方程没有实数根，则的取值范围是A .B .C .D .11. （2分）(2018·安顺模拟) 如图，边长为2的正方形ABCD中，AE平分∠DAC，AE交CD于点F，CE⊥AE，垂足为点E，EG⊥CD，垂足为点G，点H在边BC上，BH=DF，连接AH、FH，FH与AC交于点M，以下结论：①FH=2BH；②AC⊥FH；③S△ACF=1；④CE= AF；⑤ =FG•DG，其中正确结论的个数为（）A . 2B . 3C . 4D . 512. （2分）已知点A（x1 ， y1），B（x2 ， y2）是反比例函数y=﹣的图象上的两点，若x1＜0＜x2 ，则下列结论正确的是（）A . y1＜0＜y2B . y2＜0＜y1C . y1＜y2＜0D . y2＜y1＜0二、填空题 (共6题；共6分)13. （1分）(2020·西安模拟) 如图，在△ABC中，D、E、F分别为边AB、AC、BC上的点，连接DE、EF。

辽宁省大连市2020版九年级上学期数学期末考试试卷A卷姓名:________ 班级:________ 成绩:________一、单选题 (共8题；共16分)1. （2分）方程的根是（）A .B .C .D .2. （2分）(2017·启东模拟) 有9名同学参加歌咏比赛，他们的预赛成绩各不相同，现取其中前4名参加决赛，小红同学在知道自己成绩的情况下，要判断自己能否进入决赛，还需要知道这9名同学成绩的（）A . 众数B . 中位数C . 平均数D . 极差3. （2分）(2017·槐荫模拟) “a是实数，|a|＜0”这一事件是（）A . 必然事件B . 不确定事件C . 不可能事件D . 随机事件4. （2分）下列各函数中，y随x增大而增大的是（）①y=-x+1；②y=-（x＜0）；③y=x2+1；④y=2x-3．A . ①②B . ②③C . ②④D . ①③5. （2分）(2019·吉林模拟) 如图，四边形ABCD内接于圆O，AD∥BC，∠DAB＝48°，则∠AOC的度数是（）A . 48°B . 96°C . 114°D . 132°6. （2分）用一个5倍的放大镜去观察一个三角形，对此，四位同学有如下说法：甲说：三角形的每个内角都扩大到原来的5倍；乙说：三角形的每条边都扩大到原来的5倍；丙说：三角形的面积扩大到原来的5倍；丁说：三角形的周长都扩大到原来的5倍．上述说法中正确的是（）A . 甲和乙B . 乙和丙C . 丙和丁D . 乙和丁7. （2分）在下列三角形中，外心在它一条边上的三角形是（）A . 三角形的边长分别为2cm，2cm，3cmB . 三角形的边长都等于4cmC . 三角形的边长分别为5cm，12cm，13cmD . 三角形的边长分别为4cm，6cm，8cm8. （2分）(2019·宝鸡模拟) 二次函数y=ax2+bx+c（a≠0）的部分图象如图,图象过点（-1,0），对称轴为直线x=2,下列结论:①4a+b=0;②9a+c＞3b;③8a+7b+2c＞0;④当x＞-1时,y的值随x值的增大而增大.其中正确的结论有（）A . 1个B . 2个C . 3个D . 4个二、填空题 (共10题；共24分)9. （1分）已知，那么=________10. （1分） (2019九下·温州竞赛) 如图，在△ABC中，AB=AC，在∠ABC的内部作∠ABE=45°，EC⊥BC点D在AB上，DE、AC相交点F，若以DE为直径的⊙O与AB、BC都相切，切点分别为点D和G，则的值是________.11. （15分） (2020七下·恩施月考) 一辆货车从超市出发，向东走了3千米到达小彬家，继续走2.5米到达小颖家，然后向西走了10千米到达小明家，最后回到超市.（1）小明家距小彬家多远？（2）货车一共行驶了多少千米？（3）货车每千米耗油0.2升，这次共耗油多少升？12. （1分）从甲地到乙地有A，B，C三条不同的公交线路．为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况，在每条线路上随机选取了500个班次的公交车，收集了这些班次的公交车用时（单位：分钟）的数据，统计如下：30≤t≤3535＜t≤4040＜t≤4545＜t≤50合计公交车用时公交车用时的频数线路A59151166124500B5050122278500C4526516723500早高峰期间，乘坐________（填“A”，“B”或“C”）线路上的公交车，从甲地到乙地“用时不超过45分钟”的可能性最大．13. （1分）已知C、D是线段AB的两个黄金分割点，AB=2，则CD的长是________．（用含根号的式子表示）14. （1分）将抛物线y=x2的图象向上平移1个单位，则平移后的抛物线的解析式为________．15. （1分）若二次函数的图象经过点（-1,0），（1，-2），当随的增大而增大时，的取值范围是________。