五年级下圆的知识点加例题

第六单元：圆第1课时：圆的概念及特点班级：姓名: 等级:【基础训练】一、填空题1．从圆心到圆上任意一点的线段叫________．通过________并且________都在________的线段叫________．圆的位置由________确定，圆的大小决定于圆的________长短．2．圆中心的一点叫做（_____），用字母（_____）表示，它到圆上任意一点的距离都（_____）．3．一个圆有（________）条半径，经过圆心并且两端都在圆上的线段有（________）条。

4．用圆规画圆，圆规两脚间的距离是圆的．决定圆的大小，确定圆的位置．5．要用圆规画一个直径7cm的圆，圆规两脚间的距离应是（________）；要画一个周长6πcm的圆，圆规两脚间的距离应是（________）。

6．如果一个圆的直径是24厘米，那么这个圆的半径是厘米．7．在长10厘米，宽7厘米的长方形中画一个最大的圆，它的半径是厘米．二、选择题8．一张长13厘米，宽9厘米的长方形纸板，最多可以剪（）个半径2厘米的圆。

A．7 B．8 C．69．在一个周长是100厘米的正方形纸片内，要剪一个最大的圆，这个圆的半径是（）厘米。

A．100 B．25 C．12.510．在图中，（）线段最长．A．JK B．CD C．EF D．GH三、作图题11．在正方形内画一个最大的圆，并画出此组合图形的对称轴．四、判断题12．半径是线段，直径是射线。

（________）13．连接圆上任意两点的线段中，直径最长．（_______）14．圆的半径扩大2倍，直径就扩大4倍．_____．五、计算15．下图中大圆的直径是8厘米，小圆的直径是6厘米，线段AB的长是多少厘米？六、解答题16．画一画．（1）画出下面三角形的对称轴．（2）在下面长方形内画一个最大的圆，并用字母标出圆心和半径．17．用圆规画一个直径为4cm的圆，并标出圆心，半径和直径．【拓展运用】18．用一根绳子，在一棵大树干上绕一周的长度是1.57米．这棵大树的直径是多少厘米？参考答案1．半径圆心两端圆上直径圆心半径考点：圆的认识与圆周率．2．圆心 O 相等3．无数无数4．半径，半径，圆心5．3.5cm 3cm6．127．3.58．C9．C10．B11．如图12．×13．√14．×15．1厘米(8－6)÷2＝1(厘米)答：线段AB的长是1厘米．16．如图17．如图解：半径为：4÷2=2（厘米），如图所示：18．这棵大树的直径是50厘米解：1.57÷3.14=0.5（米）=50（厘米）；答：这棵大树的直径是50厘米．。

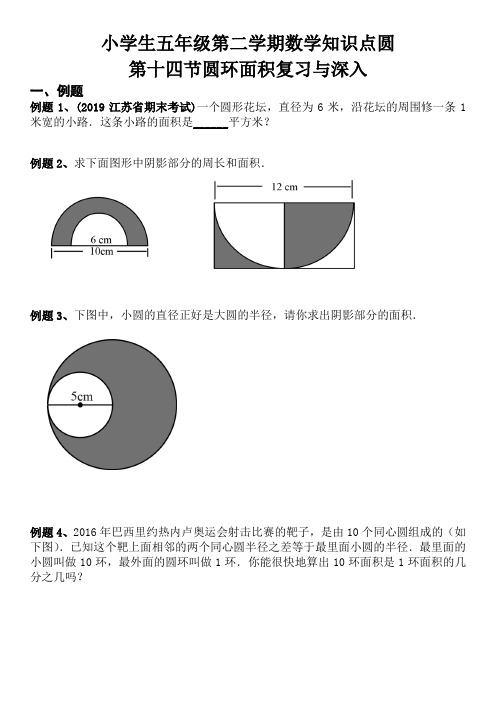
小学生五年级第二学期数学知识点圆第十四节圆环面积复习与深入一、例题例题1、(2019江苏省期末考试)一个圆形花坛，直径为6米，沿花坛的周围修一条1米宽的小路．这条小路的面积是______平方米？例题2、求下面图形中阴影部分的周长和面积．例题3、下图中，小圆的直径正好是大圆的半径，请你求出阴影部分的面积．例题4、2016年巴西里约热内卢奥运会射击比赛的靶子，是由10个同心圆组成的（如下图）．已知这个靶上面相邻的两个同心圆半径之差等于最里面小圆的半径．最里面的小圆叫做10环，最外面的圆环叫做1环．你能很快地算出10环面积是1环面积的几分之几吗？例题5、下图中阴影部分的面积是50cm 2，求环形的面积．例题6、(2017浙江省小升初真题)某运动场的200米跑道如图（1）所示，弯道为半圆形，跑道宽为1.22米，两名运动员沿各自跑道赛跑一周，为使二人距离相等，应让外跑道的运动员前移多少米？（得数保留两位小数）例题7、(2018江苏省小升初真题)已知图中阴影部分的面积是20cm 2，环形的面积是多少平方厘米？二、随练随练1、东方广场上有一个直径是8m 的大花坛，它的周围有一条2m 宽的环形水泥路面，路面的面积是多少？随练2、在一个半径是8m 的图形水池周围修一条3m 宽的小路，这条小路的面积是多少平方米？随练3、青年广场的东北角有一个圆形花坛，花坛的直径是20m ，花坛的周围有一条2m阴影部分的面积等于大正方形的面积减去小正方形的面积哟！宽的小路，小路的外边装有一圈铁栅栏．（1）这个花坛的面积是多少？（2）小路的面积是多少？（3）铁栅栏有多少米长？随练4、(2018江苏省小升初真题)图中阴影部分的面积是15平方厘米，求环形的面积。

五年级数学下册《圆》知识点与练习班级姓名课前热身7.6 + 0.1= 2.3 + 2.2=0.3 + 4.1= 5.5－1.2=5.8－5.7= 8.3－8.2=0.58－0.48= 0.72－0.22=0.92－0.52= 1.9 + 0.9=1.6 + 0.8= 1.7 + 0.6=7.4－1.4= 3.2 ÷ 4=0.21 ÷ 3= 2.1 × 0.2=3.2 × 0.3= 0.5 × 6=0.3 × 0.6= 0.6 × 7=0.6 × 0.8= 3.2 ÷ 0.8=5.4 ÷ 0.3= 4.9 ÷ 0.7=0.82÷0.41= 0.4 ÷ 0.1=模块一圆的周长知识点回顾1、任何一个圆的周长除以直径的商都是一个固定的数，我们把它叫做圆周率，用字母π表示，π是一个无限不循环小数。

2、π=3.141592653在计算时，一般保留两位小数，取它的近似值3.14.如果用C表示圆的周长，那么周长C 与直径d或半径r的关系是：C=πd或C=2πr经典例题1、有两个大小不同的圆，如果它们的半径都增加1cm，那么大圆的周长增加得（）。

A.多B.少C.与小圆同样多D.无法判断2、要画一个周长是15.7厘米的圆，圆规两脚尖的距离是厘米。

3、一个圆形池塘直径为30米，沿着池边每隔5米栽一棵树，最多能栽棵。

4、画出下列图形的所有对称轴。

5、一根13米长的绳子，绕一根圆柱形柱子4圈后还剩44厘米，求这根圆柱的半径。

6、自行车车轮的直径是0.6米，如果它每分钟转200圈，那么通过一座长1507.2米的桥，需要多少分钟？7、求下面各图形的周长：50厘米5cm120厘米8、一个座钟的分针长5厘米，它旋转一周，分针尖端所行的路程是多少厘米？9、有一捆绕成30圈的铁丝，每圈半径10分米，这捆铁丝长多少米？10、一辆金狮牌自行车,外轮胎半径是35厘米,如果每分转100周,要想通过一座659.4米长的大桥,需要骑多少分？11、在一个圆形水池的周围每隔0.628米放上一盆花，水池的半径是6米，至少需要多少盆花？模块二圆的面积知识点回顾圆的面积公式：S=2r⋅π经典例题1、一个圆形水池的周长是25.12米，这个水池的占地面积是多少。

青岛版五年级下册完美的图形——圆的知识点归纳一、圆的定义长方形、正方形、平行四边形、梯形、三角形等，都是由线段围成的平面图形，而圆是由曲线围成的一种平面图形。

二、圆的各部分名称1、圆心：画圆时，固定的点是圆心，圆心一般用字母O表示。

2、半径：连接圆心和圆上任意一点的线段叫作半径，一般用字母r 表示。

把圆规两脚分开，两脚之间的距离就是圆的半径。

3、直径：通过圆心并且两端都在圆上的线段叫作直径，一般用字母d 表示。

直径是一个圆内最长的线段。

4圆心角：顶点在圆心的角叫作圆心角。

图中∠1就是圆心角。

三、圆的主要特征1、在同一个圆里，有无数条半径，有无数条直径。

所有的半径都相等，所有的直径都相等。

1d。

2、直径是半径的2倍。

用字母表示为：d=2r或r=23、如果一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形是轴对称图形。

圆是轴对称图形，有无数条对称轴。

每条直径所在的直线都是圆的对称轴。

直径是圆的对称轴。

（×）因为对称轴是一条直线。

4、用圆规画圆的三要素：定点、定长、旋转。

5、圆的位置是由圆心确定的，大小是由半径决定的。

四、圆的周长（周长用字母C表示）1、围成圆的曲线的长叫作圆的周长。

(测圆周长的方法：绕绳法、滚动法等)2、圆的周长与圆的直径有关，圆的直径越长，圆的周长就越大。

3、推导圆的周长计算公式时，我们是用“化曲为直”的方法，得出：C =πd 或C =2πr。

4、知道圆的周长，求直径或半径公式:C=πd→d=C÷πC=2πr→r=C÷2π。

5、区分圆周长的一半和半圆的周长:(1)圆周长的一半：等于圆的周长÷2。

计算方法：2πr÷2=πr。

(2)半圆的周长：等于圆的周长的一半加直径。

计算方法：2πr÷2+2r=πr+2r。

五、圆周率1、圆周率：圆的周长和它的直径的比值是一个固定的数，这个比值就叫圆周率，用字母π表示。

例题：圆的周长与它的直径的比值是3.14。

小学生五年级第二学期数学知识点圆第十五节拓展练习拓展1、在纸上点一点，离这一点2cm 点上无数个点，这些点组成的图形是（ ）。

A.圆 B.平行四边形 C.正方形拓展2、井盖做成圆形的，这是因为（ ）。

A.圆形的井盖最美观B.利用“同圆内所有的直径都相等”防止井盖落入井里C.圆形的井盖最省材料拓展3、看一看，填一填．拓展4、根据表中有关数据完成下表．拓展5、甲圆的半径是4cm，乙圆的直径是8cm，那末，甲、乙两圆直径的比是（ ）．拓展6、在同一个圆内，所有的半径都（ ），所有的直径都（ ），直径是半径的（ ），半径是直径的（ ），半径与直径的比是（ ）． 圆的直径是（ ）， 正方形的边长是（ ）。

大圆的直径是（ ），小圆的半径是（ ）。

圆的直径是（ ），圆的半径是（ ）。

圆的直径是（ ），圆的半径是（ ）。

（1）（2）（3）（4）r ／m 4.2 2.5 ad ／m71.8b拓展7、下图中，点O 是圆的（ ），AB 是圆的（ ），OC 是圆的（ ）．拓展8、要在一张长16cm ，宽9cm 的长方形纸上剪出直径是3cm 的圆，最多可以剪出多少个？拓展9、（1）如图，圆上A 、B 两点之间的部份叫做（ ），读作（ ）；图中阴影部份是（ ）；像∠AOB 这样，顶点在圆心的角叫做（ ）．（2）在同一个圆中，扇形的大小与这个扇形的（ ）的大小有关． （3）以半圆为弧的扇形的圆心角是（ ），以14圆为弧的扇形的圆心角是（ ），以18圆为弧的扇形的圆心角是（ ）．拓展10、下面图形的阴影部份是扇形的在括号里画“√”．拓展11、(2022北京市期末测试卷)下面各图中，阴影部份是扇形的是图（ ）。

A.B.C.D.拓展12、一个扇形的圆心角是90°，半径是10分米，这个扇形的面积是（ ）平方分米．拓展13、求下面扇形的周长与面积．拓展14、把圆等分成32份相等的扇形，拼成一个宽为半径的近似长方形，已知长方形的周长是16.56厘米，那末圆的周长是多少厘米？面积是多少平方厘米？拓展15、如图，求阴影部份面积．（单位：cm）拓展16、下面三个圆的半径都为5cm，求阴影部份的面积和中间空白部份的周长． 拓展17、(2022山东省小升初真题)看图计算．求图中阴影部份的面积．（单位：cm）拓展18、填空。

第六单元圆【知识梳理】一、圆的认识1.圆的特征。

圆是由曲线围成的封闭图形,没有顶点。

2.圆和多边形的异同。

(1)相同点:圆和多边形都是平面图形。

(2)不同点:多边形由线段围成,有顶点;圆由曲线围成,没有顶点。

圆的画法:(1)把圆规的两脚分开,定好两脚间的距离。

(2)把有针尖的脚固定在一点上。

(3)把装有铅笔芯的脚旋转一周,就画成了一个圆。

旋转圆规时,两脚间的距离不能变。

3.圆的各部分的名称。

(1)圆心:用圆规画圆时,针尖固定的一点是圆心,通常用字母O表示,圆心决定圆的位置。

(2)半径:连接圆心和圆上任意一点的线段(如线段OA)是半径,通常用字母r 表示。

半径决定圆的大小,半径越长,圆越大;半径越短,圆越小。

(3)直径:通过圆心并且两端都在圆上的线段(如线段BC)是直径,通常用字母d表示。

如图:4.半径和直径的特征及圆的对称性。

(1)圆有无数条直径和半径。

在同圆或者等圆中,直径的长度是半径的2倍,。

(2)圆是轴对称图形,有无半径的长度是直径的一半,用字母表示是d=2r或r=d2数条对称轴。

二、扇形1.扇形。

一条弧和经过这条弧两端点的两条半径所围成的图形叫作扇形。

2.扇形各部分的名称。

弧的意义:圆上任意两点之间的曲线叫作弧。

3.圆心角的认识。

(1)圆心角的意义:顶点在圆心的角叫作圆心角。

(2)圆心角的大小:把量角器的0°刻度线和圆心角的一边重合,角的另一边对应的刻度是多少,这个圆心角就是多少度。

三、圆的周长1.圆的周长的意义。

围成圆的曲线的长叫作圆的周长。

2.圆周率的意义。

任何一个圆的周长除以直径的商都是一个固定的数,叫作圆周率,用字母π表示,π是一个无限不循环小数。

π=3.141592653…在计算时,一般保留两位小数,取它的近似值3.14。

3.圆的周长的公式。

如果用C表示圆的周长,那么周长C与直径d或半径r的关系:C=πd或C=2πr。

四、圆的面积1.圆的面积公式。

如果用S表示圆的面积,那么圆的面积公式用字母表示为S=πr2。

圆与椭圆例题和知识点总结一、圆的知识点圆是平面几何中一个非常重要的图形，具有许多独特的性质。

1、圆的定义平面内到定点的距离等于定长的点的集合叫做圆，定点称为圆心，定长称为半径。

2、圆的标准方程圆心为$（a,b)＄，半径为$r$的圆的标准方程为$（x a)＾2 ＋（y b)＾2 ＝ r^2$。

3、圆的一般方程＄x^2 ＋ y^2 ＋ Dx ＋ Ey ＋ F ＝ 0$（＄D^2 ＋ E^2 4F ＞ 0$），圆心坐标为$（＼frac{D}｛2}，＼frac{E}｛2}）＄，半径为$r ＝＼frac{1}｛2}＼sqrt{D^2 ＋ E^2 4F}＄。

4、圆的直径所对的圆周角为直角。

5、圆的弦心距、弦长与半径的关系设圆的半径为$r$，弦心距为$d$，弦长为$l$，则$l ＝ 2\sqrt{r^2d^2}＄。

6、圆的切线性质（1）圆心到切线的距离等于半径。

（2）切线垂直于经过切点的半径。

7、圆与圆的位置关系两圆的圆心距为$d$，两圆的半径分别为$r_1$，＄r_2$，则有：（1）外离：＄d ＞ r_1 ＋ r_2$（2）外切：＄d ＝ r_1 ＋ r_2$（3）相交：＄｜r_1 r_2| ＜ d ＜ r_1 ＋ r_2$（4）内切：＄d ＝｜r_1 r_2|＄（5）内含：＄d ＜｜r_1 r_2|＄二、椭圆的知识点椭圆是平面内到两个定点的距离之和等于常数（大于两定点间的距离）的点的轨迹。

1、椭圆的标准方程（1）焦点在$x$轴上：＄＼frac{x^2}｛a^2} ＋＼frac{y^2}｛b^2} ＝ 1$（＄a ＞ b ＞ 0$），其中$a$为长半轴长，＄b$为短半轴长，＄c$为半焦距，满足$c^2 ＝ a^2 b^2$，焦点坐标为$（＼pm c, 0)＄。

（2）焦点在$y$轴上：＄＼frac{y^2}｛a^2} ＋＼frac{x^2}｛b^2} ＝ 1$（＄a ＞ b ＞ 0$），焦点坐标为$（0, ＼pm c)＄。

苏教版数学五年级下册第6课时圆的面积（２）1.小丽用绕线的方法量出她的茶杯的圆形杯盖的周长是25.12厘米。

这个杯盖放在桌上占了多少平方厘米的面积?2.一根长62.8米的绳子正好绕一棵树的树干20圈。

这棵树绕绳处树干的横截面积大约是多少平方米?3.爷爷利用一面墙，用12.56米的篱笆围了一个半圆形羊圈。

这个羊圈的面积是多少平方米?4.图中每个圆的直径都是4厘米，且三角形的三个顶点分别位于三个圆的圆心。

求图中阴影部分的面积。

参考答案：1.50.24平方厘米2.0.785平方米3.12.56÷3.14=4（米）42×3.14÷2=25.12（平方米）4.4÷2=2（厘米）22×π÷2=2π（平方厘米）一、现代文阅读1．现代文阅读阅读下文，回答问题。

春季的气候变化无常。

在春季天气回暖过程中，常因冷空气的侵入，使气温明显降低，对作物造成危害，这种“前春暖，后春寒”的天气称为倒春寒。

倒春寒是南方早稻播种育秧期的主要灾害性天气，是造成早稻烂种烂秧的主要原因。

“倒春寒”发生时，可使正处于返青或拔节生长阶段的冬小麦遭受不同程度的冻害，可使已经播种尚未出土的棉花、水稻等农作物出现烂种，已经出土的幼苗大量被冻死。

春季天气转暖以后，人们身体的抗寒能力和抗病能力出现下降，会经受不住“倒春寒”时突然袭来的冷空气的刺激。

与此同时，天气变暖会使细菌迅速滋生。

如不注意预防，“倒春寒”对人体的健康会造成一定的危害。

尤其是抵抗能力较低的老人和儿童，更容易受冻感冒。

在“倒春寒”袭击时，怎样保健呢？一，注意收听收看天气预报，根据天气变化防寒保暖，适时、适度增减衣物。

要适当“春捂”，不要因为气温暂时升高就马上脱掉冬装。

早晚气温较低，要注意保暖。

在阳光充足的中午，便可适当减少衣物。

二，要适当进行户外活动，参加体育锻炼，呼吸新鲜空气，以改善心肺功能，使身体更好地进行调节，适应春季多变的气候。

小学生五年级第二学期数学知识点圆第十五节拓展练习拓展1、在纸上点一点，离这一点2cm 点上无数个点，这些点组成的图形是（ ）。

A.圆 B.平行四边形 C.正方形拓展2、井盖做成圆形的，这是因为（ ）。

A.圆形的井盖最美观B.利用“同圆内所有的直径都相等”防止井盖落入井里C.圆形的井盖最省材料拓展3、看一看，填一填．拓展4、根据表中有关数据完成下表．拓展5、甲圆的半径是4cm ，乙圆的直径是8cm ，那么，甲、乙两圆直径的比是（ ）．拓展6、在同一个圆内，所有的半径都（ ），所有的直径都（ ），直径是半径的（ ），半径是直径的（ ），半径与直径的比是（ ）． 圆的直径是（ ）， 正方形的边长是（ ）。

大圆的直径是（ ），小圆的半径是（ ）。

圆的直径是（ ），圆的半径是（ ）。

圆的直径是（ ），圆的半径是（ ）。

（1）（2）（3）（4）r ／m 4.2 2.5 a d ／m71.8b拓展7、下图中，点O是圆的（），AB是圆的（），OC是圆的（）．拓展8、要在一张长16cm，宽9cm的长方形纸上剪出直径是3cm的圆，最多可以剪出多少个？拓展9、（1）如图，圆上A、B两点之间的部分叫做（），读作（）；图中阴影部分是（）；像∠AOB这样，顶点在圆心的角叫做（）．（2）在同一个圆中，扇形的大小与这个扇形的（）的大小有关．圆为弧的扇形的圆心角是（3）以半圆为弧的扇形的圆心角是（），以14圆为弧的扇形的圆心角是（）．（），以18拓展10、下面图形的阴影部分是扇形的在括号里画“√”．拓展11、(2017北京市期末测试卷)下面各图中，阴影部分是扇形的是图（）。

A. B. C. D.拓展12、一个扇形的圆心角是90°，半径是10分米，这个扇形的面积是（）平方分米．拓展13、求下面扇形的周长与面积．拓展14、把圆等分成32份相等的扇形，拼成一个宽为半径的近似长方形，已知长方形的周长是16.56厘米，那么圆的周长是多少厘米？面积是多少平方厘米？拓展15、如图，求阴影部分面积．（单位：cm）拓展16、下面三个圆的半径都为5cm，求阴影部分的面积和中间空白部分的周长．拓展17、(2016山东省小升初真题)看图计算．求图中阴影部分的面积．（单位：cm）拓展18、填空。