激光医学第二章习题答案汇总

第二章开放式光腔与高斯光束1.证明如图所示傍轴光线进入平面介质界面的光线变换矩阵为1 21 0ηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。

证明：设入射光线坐标参数为11,rθ，出射光线坐标参数为22,rθ，根据几何关系可知211122,sin sinr rηθηθ==傍轴光线sinθθ则1122ηθηθ=，写成矩阵形式2121121 0r rθθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证2.证明光线通过图所示厚度为d的平行平面介质的光线变换矩阵为1210 1dηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。

证明：设入射光线坐标参数为11,rθ，出射光线坐标参数为22,rθ，入射光线首先经界面1折射，然后在介质2中自由传播横向距离d，最后经界面2折射后出射。

根据1题的结论和自由传播的光线变换矩阵可得212121121 0 1 010 00 1r rdθθηηηη⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦化简后21211210 1dr rθθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证。

、3．试利用往返矩阵证明共焦腔为稳定腔，即任意傍轴光线在其中可以往返无限多次，而且两次往返即自行闭合。

证：设光线在球面镜腔内的往返情况如下图所示：其往返矩阵为：由于是共焦腔，则有~12R R L ==将上式代入计算得往返矩阵()()()121010110101n nnn n n r L r L ⎡⎤⎡⎤⎡⎤===-=-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦A B C D T T T T T 可以看出，光线在腔内往返两次的变换矩阵为单位阵，所以光线两次往返即自行闭合。

于是光线在腔内往返任意多次均不会溢出腔外，所以共焦腔为稳定腔。

4.试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。

解：共轴球面腔稳定性条件1201g g <<其中121211,1L Lg g R R =--=- [对平凹共轴球面镜腔有12,0R R =∞>。

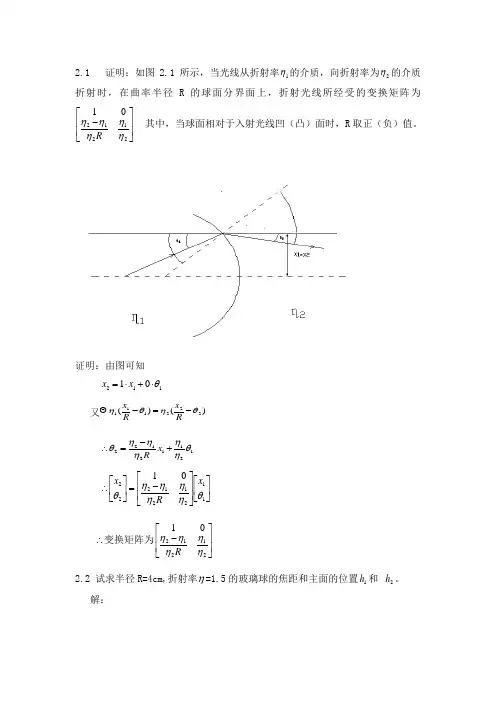
2.1 证明：如图2.1所示，当光线从折射率1η的介质，向折射率为2η的介质折射时，在曲率半径R 的球面分界面上，折射光线所经受的变换矩阵为⎥⎥⎦⎤⎢⎢⎣⎡-2121201ηηηηηR 其中，当球面相对于入射光线凹（凸）面时，R 取正（负）值。

证明：由图可知 11201θ⋅+⋅=x x 又)()(222111θηθη-=-RxR x 21121122x R ηηηθθηη-∴=+ ⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡∴11212122201θηηηηηθx Rx ∴变换矩阵为⎥⎥⎦⎤⎢⎢⎣⎡-2121201ηηηηηR 2.2 试求半径R=4cm,折射率η=1.5的玻璃球的焦距和主面的位置1h 和2h 。

解：变换矩阵⎥⎥⎦⎤⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=2112121221210110101n n R n n n l n n R n n n M 把11=n ，5.12=n ，cm R R 421=-=，cm l 8=代入，可得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡⨯-⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡--=3531316355.1145.115.10110815.145.1101M )(12f h A -=, f C 1-=, )(11f h D -= 求得 mm f 30-= mm h 201= mm h 202=2.3 焦距1f =5cm 和2f =-10c=m 的两个透镜相距5cm 。

第一个透镜前表面和第二个透镜后表面为参考平面的系统，其等效焦距为多少？焦点和主平面位置在何处？距1f 前表面20cm 处放置高为10cm 的物体，能在2f 后多远地方成像？像高为多少？ 解：（1）2110101010********1131101011110552A B L M CD f f ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥====⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-----⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦)(12f h A -=, f C 1-=, )(11f h D -=，求得cm f 5-= cm h 5.21= cm h 52-=第一个透镜前表面与前主面的距离为2.5cm ，第二个透镜后表面与后主面的距离为-5cm,前主面离焦点的距离为-5cm ，） （2）21201011===l x θ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡45252110235150235150111122θθθx x D C B A xcm l cm x 2,5.222-==（距2f 后表面-2cm ）2.4 一块折射率为η，厚度为d 的介质放在空气中，其两界面分别为曲率半径等于R 的凹球面和平面，光线入射到凹球面上。

第二章 开放式光腔与高斯光束1. 证明121 00 ηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。

证明：设入射光线坐标参数为11, r θ，出射光线坐标参数为22, r θ，根据几何关系可知211122, sin sin r r ηθηθ== 傍轴光线sin θθ则1122ηθηθ=，写成矩阵形式2121121 00 r r θθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证 2. 1210 1d ηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。

证明：设入射光线坐标参数为11, r θ，出射光线坐标参数为22, r θ，入射光线首先经界面1折射，然后在介质2中自由传播横向距离d ，最后经界面2折射后出射。

根据1题的结论和自由传播的光线变换矩阵可得212121121 0 1 01 0 0 0 1r r d θθηηηη⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦ 化简后2121121 0 1d r r θθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证。

3．试利用往返矩阵证明共焦腔为稳定腔，即任意傍轴光线在其中可以往返无限多次，而且两次往返即自行闭合。

证：设光线在球面镜腔内的往返情况如下列图所示：其往返矩阵为：由于是共焦腔，则有12R R L ==将上式代入计算得往返矩阵()()()121010110101n nnn n n r L r L ⎡⎤⎡⎤⎡⎤===-=-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦A B C D T T T T T 可以看出，光线在腔内往返两次的变换矩阵为单位阵，所以光线两次往返即自行闭合。

于是光线在腔内往返任意多次均不会溢出腔外，所以共焦腔为稳定腔。

4.试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。

解：共轴球面腔稳定性条件1201g g <<其中121211,1L Lg g R R =--=- 对平凹共轴球面镜腔有12,0R R =∞>。

则1221,1Lg g R ==-，再根据稳定性条件 1201g g <<可得22011LR R L <-<>⇒。

第二章 开放式光腔与高斯光束1. 证明121 00 ηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。

证明：设入射光线坐标参数为11, r θ，出射光线坐标参数为22, r θ，根据几何关系可知211122, sin sin r r ηθηθ== 傍轴光线sin θθ则1122ηθηθ=，写成矩阵形式2121121 00 r r θθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证 2. 1210 1d ηη⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦。

证明：设入射光线坐标参数为11, r θ，出射光线坐标参数为22, r θ，入射光线首先经界面1折射，然后在介质2中自由传播横向距离d ，最后经界面2折射后出射。

根据1题的结论和自由传播的光线变换矩阵可得212121121 0 1 01 0 0 0 1r r d θθηηηη⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦ 化简后2121121 0 1d r r θθηη⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦得证。

3．试利用往返矩阵证明共焦腔为稳定腔，即任意傍轴光线在其中可以往返无限多次，而且两次往返即自行闭合。

证：设光线在球面镜腔内的往返情况如下列图所示：其往返矩阵为：由于是共焦腔，则有12R R L ==将上式代入计算得往返矩阵()()()121010110101n nnn n n r L r L ⎡⎤⎡⎤⎡⎤===-=-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦A B C D T T T T T 可以看出，光线在腔内往返两次的变换矩阵为单位阵，所以光线两次往返即自行闭合。

于是光线在腔内往返任意多次均不会溢出腔外，所以共焦腔为稳定腔。

4.试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。

解：共轴球面腔稳定性条件1201g g <<其中121211,1L Lg g R R =--=- 对平凹共轴球面镜腔有12,0R R =∞>。

则1221,1Lg g R ==-，再根据稳定性条件 1201g g <<可得22011LR R L <-<>⇒。

第二章开放式光腔与XX光束1.证明如图2.1所示傍轴光线进入平面介质界面的光线变换矩阵为证明：设入射光线坐标参数为，出射光线坐标参数为，根据几何关系可知傍轴光线则，写成矩阵形式得证2.证明光线通过图2.2所示厚度为d的平行平面介质的光线变换矩阵为。

证明：设入射光线坐标参数为，出射光线坐标参数为，入射光线首先经界面1折射，然后在介质2xx自由传播横向距离d，最后经界面2折射后出射。

根据1题的结论和自由传播的光线变换矩阵可得化简后得证。

3.试利用往返矩阵证明共焦腔为稳定腔，即任意傍轴光线在其中可以往返无限多次，而且两次往返即自行闭合证：设光线在球面镜腔内的往返情况如下图所示:其往返矩阵为:由于是共焦腔，则有R i = R2 = L将上式代入计算得往返矩阵T m [A D1"101〔01 一可以看出，光线在腔内往返两次的变换矩阵为单位阵，所以光线两次往返即自行闭合。

于是光线在腔内往返任意多次均不会溢出腔外，所以共焦腔为稳定腔。

4.试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。

解：共轴球面腔稳定性条件其中对平凹共轴球面镜腔有则，再根据稳定性条件可得。

对双凹共轴球面腔有，则根据稳定性条件可得。

对凹凸共轴球面镜腔有，则根据稳定性条件可得。

5•激光器的谐振腔由一面曲率半径为的凸面镜和曲率半径为的凹面镜组成，工作物质长，其折射率为1.52，求腔长L在什么范围内是稳定腔。

解：设两腔镜和的曲率半径分别为和，工作物质长，折射率当腔内放入工作物质时，稳定性条件中的腔长应做等效，设工作物质长为,工作物质左右两边剩余的腔长分别为和，贝y。

设此时的等效腔长为，则光在腔先经历自由传播横向距离，然后在工作物质左侧面折射，接着在工作物质中自由传播横向距离，再在工作物质右侧面折射，最后再自由传播横向距离，则。

］「1 ql1 °=1 町n J(0dj o 冷0 1-所以等效腔长等于1 ■01.17m<L ：：2.17m6. 图2.3所示三镜环形腔，已知，试画出其等效透镜序列图，并求 球面镜的曲率半径R 在什么范围内该腔是稳定腔。

2.19某共焦腔氦氖激光器，波长λ＝0.6328μm ，若镜面上基模光斑尺寸为0.5mm ，试求共焦腔的腔长，若腔长保持不变，而波长λ＝3.39μm ，问：此时镜面上光斑尺寸多大？ 解：20/ 1.24s L m ωπλ=≈0/1.16mms L ωλπ==2.20考虑一台氩离子激光器，其对称稳定球面腔的腔长L=1m ，波长λ= 0.5145μm ，腔镜曲率半径R=4m ，试计算基模光斑尺寸和镜面上的光斑尺寸。

解：1/42021/42242()(2)(22)(2) 4.65104L R L R L R L RL L mλωπλπ-⎡⎤--=⎢⎥-⎣⎦⎡⎤-==⨯⎢⎥⎣⎦1/42121/4222422()()(2)4.9810(2)L R R L L R L R L R L mRL L λωωπλπ-⎡⎤-==⎢⎥--⎣⎦⎡⎤==⨯⎢⎥-⎣⎦2.21腔长L ＝75cm 的氦氖平凹腔激光器，波长λ＝0.6328μm ，腔镜曲率半径R ＝1m ，试求凹面镜上光斑尺寸，并计算该腔基模远场发散角θ。

解：1/41/4212211121121/41/422112212212()0.295mm()()(1)()0.591()()(1)s s R R L g L Lw L R L R R L g g g R R L g LL w mmL R L R R L g g g λλππλλππ⎡⎤⎡⎤-===⎢⎥⎢⎥-+--⎣⎦⎣⎦⎡⎤⎡⎤-===⎢⎥⎢⎥-+--⎣⎦⎣⎦1/41/42221212120212121212(2)(2)220.0014rad=0.0782()()()(1)L R R g g g g L R L R L R R L L g g g g λλθππ⎡⎤⎧⎫--+-===⎨⎬⎢⎥--+--⎣⎦⎩⎭2.22设稳定球面腔的腔长L ＝16cm ，两镜面曲率半径为1R ＝20cm ，2R ＝－32cm ，波长λ=410-cm ，试求：（1）最小光斑尺寸0ω和最小光斑位置；（2）镜面上光斑尺寸1s ω、2s ω；（3）0ω和1s ω、2s ω分别与共焦腔（1R ＝2R ＝L ）相应值之比。

激光医学测试题目及答案
一、选择题
1. 激光医学是研究什么的科学？
A. 激光物理学
B. 激光生物学
C. 激光工程学
D. 激光化学
答案：B
2. 下列哪项不是激光的特性？
A. 单色性
B. 相干性
C. 散射性
D. 定向性
答案：C
3. 激光在医学中的应用不包括以下哪项？
A. 诊断
B. 治疗
C. 手术
D. 通信
答案：D
二、填空题
4. 激光医学中，激光的_________特性使其在治疗上具有独特的优势。

答案：定向性
5. 激光医学的诊断方法包括但不限于_________和_________。

答案：激光光谱分析；激光成像技术
三、判断题
6. 激光手术是一种非侵入性手术。

（）
答案：错误
7. 激光可以用于治疗肿瘤，这是利用激光的热效应。

（）
答案：正确
四、简答题
8. 简述激光在医学诊断中的应用。

答案：激光在医学诊断中的应用包括利用激光的光谱特性进行血液
成分分析，利用激光的成像技术进行内窥镜检查等。

9. 描述激光手术相比传统手术的优势。

答案：激光手术相比传统手术具有创伤小、出血少、恢复快等优势，同时可以进行更精细的切割和凝固。

五、论述题
10. 论述激光医学在现代医疗中的重要性及其未来的发展趋势。

答案：激光医学在现代医疗中的重要性体现在其无创或微创的诊
断和治疗手段，提高了治疗的精确性和安全性。

未来发展趋势可能包
括激光技术的进一步创新，新型激光医疗设备的研制，以及激光技术
在个性化医疗中的应用等。

第二章 开放式光腔与高斯光束习题（缺2.18 2.19 2.20）1． 题略证明：设入射光()11,r θ，出射光()22,r θ，由折射定理1122sin sin ηθηθ=,根据近轴传输条件，则1122sin ,sin θθθθ≈≈1122ηθηθ∴=，联立21r r =，则所以变换矩阵为 2． 题略证明：由题目１知，光线进入平面介质时的变换矩阵为:经过距离ｄ的传播矩阵为： 光线出射平面介质时：故3. 试利用往返矩阵证明共焦腔为稳定腔，即任意傍轴光线在其中可以往返无限多次，而且两次往返即自行闭合。

证：设光线在球面镜腔内的往返情况如下图所示：其往返矩阵为：122212111210101122110101212(1) 222222[(1)][(1)(1)]A B L L T C D R R L L L R R L L L L R R R R R R ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭ ⎪ ⎪⎝⎭⎝⎭⎛⎫-- ⎪⎪= ⎪-+----- ⎪⎝⎭212211100r r θηηθ⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭21100T ηη⎛⎫= ⎪⎝⎭121100T ηη⎛⎫= ⎪⎝⎭2100d T ⎛⎫=⎪⎝⎭312100T ηη⎛⎫= ⎪⎝⎭3113213112211101010000r r r d T T T θθηηηηθ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭1232112211010*******0d d T T T T ηηηηηη⎛⎫⎛⎫⎛⎫⎛⎫∴=== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭由于是共焦腔，有 12R R L == 往返矩阵变为若光线在腔内往返两次，有可以看出，光线在腔内往返两次的变换矩阵为单位阵，所以光线两次往返即自行闭合。

于是光线在腔内往返任意多次均不会溢出腔外，所以共焦腔为稳定腔。

4. 试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。

第二章习题1、什么是激光？它与自然光有何区别？（1号）答：（1）激光是受激辐射光放大的简称，是指当一个光子hv射入一个粒子系统后，将产生两个或更多个特性完全相同的光子并离开该系统，从而实现光放大。

（2）激光来自于受激辐射，并非自发产生，必须有外来光子刺激才会产生，而且受激辐射光子与外来光子的频率、位相、传播方向振动态都完全相同，即激光是相干的。

自然光来自于自发辐射，其发出的光子的位相、振动态、频率（或波长）和传播方向都无确定方向，即自发辐射的光波是非相干的。

2、自发辐射与受激辐射的主要区别&特点（2号）自发辐射受激辐射不受外界辐射场影响在外来光作用下发生并发射一个与外来光子完全相同的光子自发辐射的光波是非相干的受激辐射光是相干光，会使光的强度增大不同原子产生的自发辐射光在频率、相位、偏振方向及传播方向都有一定的任意性。

受激辐射光子与外来光子的频率、相位、偏振方向都完全相同3.什么是粒子数反转？如何实现？（3号）设法使处于高能级上的粒子数多于低能级上的粒子数，即使粒子数处于正常分布的反转状态，这种分布称为粒子数反转（population inversion）。

实现：首先要具备必需要的能量输入系统，以便不断地从外界供给能量，使物质中有尽可能多的粒子吸收能量后从低能级不断激发到高能级上去，这一能量供应过程叫“激励”、“抽运”或“泵浦”。

用光激励能源的叫“光泵”，用化学能作为激励的叫“化学泵”，此外还有核泵、电泵等。

尽管激励方式不同，但目的都是要使物质尽可能多的粒子吸收能量后，从低能量不断发到高能级上去，有选择地使某个或某几个较高能级的粒子数大大地增加，且超过低能级上的粒子数，实现粒子数反转。

4.何谓激励过程? 有什么激励方式（4号）首先要具备必要的能量输入系统，以便不断地从外界供给能量，使物质中有尽可能多的粒子吸收能量后从低能量级不断激发到高能级上去，这一能量供应过程叫“激励”、“抽运”或“泵浦”。

第二章 开放式光腔与高斯光束习题（缺2.18 2.19 2.20）1． 题略证明：设入射光()11,r θ，出射光()22,r θ，由折射定理1122sin sin ηθηθ=,根据近轴传输条件，则1122sin ,sin θθθθ≈≈1122ηθηθ∴=，联立21r r =，则所以变换矩阵为 2． 题略证明：由题目１知，光线进入平面介质时的变换矩阵为:经过距离ｄ的传播矩阵为： 光线出射平面介质时： 故3. 试利用往返矩阵证明共焦腔为稳定腔，即任意傍轴光线在其中可以往返无限多次，而且两次往返即自行闭合。

证：设光线在球面镜腔内的往返情况如下图所示：其往返矩阵为：122212111210101122110101212(1) 222222[(1)][(1)(1)]A B L L T C D R R L L L R R L L L L R R R R R R ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭ ⎪ ⎪⎝⎭⎝⎭⎛⎫-- ⎪⎪= ⎪-+----- ⎪⎝⎭212211100r r θηηθ⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭21100T ηη⎛⎫= ⎪⎝⎭121100T ηη⎛⎫= ⎪⎝⎭2100d T ⎛⎫=⎪⎝⎭312100T ηη⎛⎫= ⎪⎝⎭3113213112211101010000r r r d T T T θθηηηηθ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭123211221101011000000d d T T T T ηηηηηη⎛⎫⎛⎫⎛⎫⎛⎫∴=== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭由于是共焦腔，有 12R R L == 往返矩阵变为若光线在腔内往返两次，有可以看出，光线在腔内往返两次的变换矩阵为单位阵，所以光线两次往返即自行闭合。

于是光线在腔内往返任意多次均不会溢出腔外，所以共焦腔为稳定腔。

4. 试求平凹、双凹、凹凸共轴球面镜腔的稳定性条件。

激光原理第二章习题答案1．估算2CO 气体在室温(300K)下的多普勒线宽D ν∆和碰撞线宽系数α。

并讨论在什么气压范围内从非均匀加宽过渡到均匀加宽。

解：2CO 气体在室温(300K)下的多普勒线宽D ν∆为11822770693103007.16107.161010.61044 0.05310HzD T M νν---⨯⎛⎫⎛⎫∆=⨯=⨯⨯⨯ ⎪ ⎪⨯⎝⎭⎝⎭=⨯ 2CO 气体的碰撞线宽系数α为实验测得，其值为49KHz/Pa α≈2CO 气体的碰撞线宽与气压p 的关系近似为L p να∆=当L D νν∆=∆时，其气压为930.053101081.6Pa 4910Dp να∆⨯===⨯所以，当气压小于1081.6Pa 的时候以多普勒加宽为主，当气压高于1081.6Pa 的时候，变为以均匀加宽为主。

2．考虑某二能级工作物质，2E 能级自发辐射寿命为s τ，无辐射跃迁寿命为τ。

假定在t=0时刻能级2E 上的原子数密度为2(0)n ，工作物质的体积为V ，自发辐射光的频率为ν，求：(1)自发辐射光功率随时间t 的变化规律；(2)能级2E 上的原子在其衰减过程中发出的自发辐射光子数；(3)自发辐射光子数与初始时刻能级2E 上的粒子数之比2η，2η称为量子产额。

解：(1) 在现在的情况下有可以解得：11()22()(0)s tn t n eττ-+=可以看出，t 时刻单位时间内由于自发辐射而减小的能级之上的粒子数密度为2/s n τ，这就是t 时刻自发辐射的光子数密度，所以t 时刻自发辐射的光功率为：222()()s dn t n ndt ττ=-+(2) 在t dt →时间内自发辐射的光子数为：所以(3) 量子产额为：3．根据红宝石的跃迁几率数据：7151332312121310.510,310,0.310,S sA sA s S S ---=⨯=⨯=⨯=估算13W 等于多少时红宝石对694.3nm λ=的光是透明的。