第12章《轴对称》常考题集(11)：12.3 等腰三角形

2.5等腰三角形的轴对称性【推本溯源】1.把等腰三角形纸片沿顶角平分线折叠，有什么发现？几何语言说明：由题意得AB=AC ，∠BAD=∠CAD ，在▲ABD 和▲ACD 中，⎪⎩⎪⎨⎧=AD AD CAD ∠=BAD ∠AC =AB ∴▲ABD ≌▲ACD （SAS ）所以三角形ABD 和三角形ACD 重合。

所以，∠B=∠C ，∠ADB=∠ADC=90°，BD=CD 。

由此可以发现，等腰三角形是轴对称图形，顶角平分线所在的直线是它的对称轴。

并且得到下面定理：（1）等腰三角形的两底角相等（简称“等边对等角”）几何语言：∵AB=AC ∴∠B=∠C（2）等腰三角形底边上的高线、中线及顶角平分线重合（三线合一）几何语言：（1）已知角平分线，用SAS 证高与中线。

几何语言：∵AB ＝AC ，∠BAD ＝∠CAD ∴AD ⊥BC ，BD ＝CD（2）已知中线，用SSS 证角平分线与高线。

几何语言：∵AB ＝AC ，BD ＝CD ∴∠BAD ＝∠CAD ，AD ⊥BC（3）已知高线，用HL 证角平分线与中线。

几何语言：∵AB ＝AC ，AD ⊥BC ∴∠BAD ＝∠CAD ，BD ＝CD2.按下列作法，用直尺和圆规作等腰三角形ABC ，使底边BC=a ，高AD=h 。

作法：（1）作线段BC=a ；（2）作线段BC 的垂直平分线，MN 交BC 与点D ；（3）在MN 上截取线段DA ，使DA=h ；（4）连接AB 、AC 。

▲ABC 就是所求作的等腰三角形。

3.已知如图，在△ABC 中，∠B ＝∠C ．求证：AB ＝AC ．方法1：作∠BAC 的平分线AD，交BC 于点D．由∠B＝∠C，∠BAD＝∠CAD，AD＝AD，可得△BAD≌△CAD，则AB＝AC．方法2：作BC 边上的高AD．由∠B＝∠C，∠BDA＝∠CDA＝90°，AD＝AD，可得△BAD≌△CAD，则AB＝AC．因此，可以得到有两个角相等的三角形是等腰三角形（简称“等角对等边”）几何语言：∵∠B ＝∠C ∴AB=AC4.（1）回想一下什么是等边三角形，也可以称为什么三角形？三边相等的三角形叫做等边三角形或正三角形。

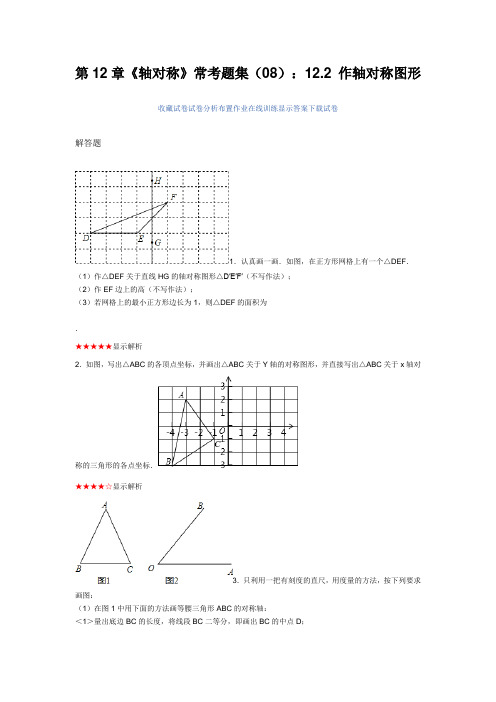
第12章《轴对称》常考题集（08）：12.2 作轴对称图形收藏试卷试卷分析布置作业在线训练显示答案下载试卷解答题1．认真画一画．如图，在正方形网格上有一个△DEF．（1）作△DEF关于直线HG的轴对称图形△D′E′F′（不写作法）；（2）作EF边上的高（不写作法）；（3）若网格上的最小正方形边长为1，则△DEF的面积为．★★★★★显示解析2．如图，写出△ABC的各顶点坐标，并画出△ABC关于Y轴的对称图形，并直接写出△ABC关于x轴对称的三角形的各点坐标．★★★★☆显示解析3．只利用一把有刻度的直尺，用度量的方法，按下列要求画图：（1）在图1中用下面的方法画等腰三角形ABC的对称轴：＜1＞量出底边BC的长度，将线段BC二等分，即画出BC的中点D；＜2＞画直线AD，即画出等腰三角形ABC的对称轴．（2）在图2中画∠AOB的对称轴，并写出画图的方法．★☆☆☆☆显示解析4．如图，已知△ABC的三个顶点分别为A（2，3）、B（3，1）、C（-2，-2）．（1）请在图中作出△ABC关于直线x=-1的轴对称图形△DEF（A、B、C的对应点分别是D、E、F），并直接写出D、E、F的坐标；（2）求四边形ABED的面积．★☆☆☆☆显示解析5．如图：（1）写出A、B、C三点的坐标；（2）若△ABC各顶点的横坐标不变，纵坐标都乘以-1，请你在同一坐标系中描出对应的点A′、B′、C′，并依次连接这三个点，所得的△A′B′C′与原△ABC有怎样的位置关系；（3）在②的基础上，纵坐标都不变，横坐标都乘以-1，在同一坐标系中描出对应的点A″、B″、C″，并依次连接这三个点，所得的△A″B″C″与原△ABC有怎样的位置关系．★☆☆☆☆显示解析6．如图，如下图均为2×2的正方形网格，每个小正方形的边长均为1．请分别在四个图中各画出一个与△ABC成轴对称、顶点在格点上，且位置不同的三角形．★☆☆☆☆显示解析7．如图，在正方形网格上有一个△ABC．（1）画出△ABC关于直线MN反射变换的像．（不写画法）；（2）画出△ABC边BC上的高；（3）若网格上的最小正方形边长为1，求△ABC的面积．★☆☆☆☆显示解析8．在一次学校组织的游艺活动中，某同学在玩“碰碰撞”时，想通过击球A，使撞击桌边MN后反弹回来击中彩球B，请在图上标明使主球撞击在MN上哪一点，才能达到目的（不写作法，保留作图痕迹）★☆☆☆☆显示解析9．如图，在所给的网格图（每小格边长均为1的正方形）中，完成下列各题：（1）将△ABC向右平移4个单位得到△A1B1C1；（2）以直线l1为对称轴作△ABC的轴对称图形△A2B2C2；（3）△A2B2C2可以看作是由△A1B1C1先向左平移4个单位，再以直线l1为对称轴作轴对称变换得到的．除此以外，△A2B2C2还可以看作是由△A1B1C1经怎样变换得到的？请选择一种方法，写出图形变换的步骤．★☆☆☆☆显示解析10．如图：（1）写出A、B、C关于y轴对称的点坐标；（2）作出与△ABC关于x轴对称的图形．★☆☆☆☆显示解析11．△ABC在平面直角坐标系中的位置如图所示．（1）作出与△ABC关于y轴对称的△A1B1C1；（2）将△ABC向下平移3个单位长度，画出平移后的△A2B2C2．★☆☆☆☆显示解析12．△ABC在平面直角坐标系中的位置如图所示．（1）作出△ABC关于y轴对称的△A1B1C1，并写出△A1B1C1各顶点的坐标；（2）将△ABC向右平移6个单位，作出平移后的△A2B2C2，并写出△A2B2C2各顶点的坐标；（3）观察△A1B1C1和△A2B2C2，它们是否关于某直线对称？若是，请在图上画出这条对称轴．★★★☆☆显示解析。

2.5等腰三角形的轴对称性一、单选题1．如图，l∥m ，等边∥ABC 的顶点A 在直线m 上，则∥α=（ ）A ．10°B ．20°C ．30°D ．40°【答案】B【解析】过B 点作BF∥l ，如图，∥BF∥l ，∥∥CBF=40°，∥l∥m ，∥BF∥m ，∥∥ABF=α，∥∥ABC 是等边三角形∥∥ABC=60°=∥CBF+∥ABF ，∥α=20°，故选：B ．2．如图，在ABC 中，AB AC =，AD 为BC 边上的中线，25B ∠=︒，则BAD ∠的度数为（）．A ．55°B ．65°C ．75°D ．45°【答案】B【解析】∥AB=AC ，AD 是BC 边上的中线，∥AD∥BC ，∥BAD=∥CAD ，∥∥B+∥BAD=90°，∥∥B=25°，∥∥BAD=65°，故选：B ．3．如图，∥ABC 中，AB 的垂直平分线交BC 边于点E ，AC 的垂直平分线交BC 边于点N ，若∥BAC ＝70°，则∥EAN 的度数为（ ）A ．35°B ．40°C ．50°D ．55° 【答案】B【解析】70BAC ∠=︒，18070110B C ∴∠+∠=︒-︒=︒， AB 的垂直平分线交BC 于点E ，AC 的垂直平分线交BC 于点N ，EA EB NA NC ∴==，，EAB B NAC C ∴∠=∠∠=∠，，BAC BAE NAC EAN B C EAN ∴∠=∠+∠-∠=∠+∠-∠，1107040EAN B C BAC ∴∠=∠+∠-∠=︒-︒=︒，故选：B ．4．如图，在∥ABC 中，AD∥BC ，垂足为D ，EF 垂直平分AC ，交AC 于点F ，交BC 于点E ，BD ＝DE ，若∥ABC 的周长为26cm ，AF ＝5cm ，则DC 的长为（ ）A ．8cmB ．7cmC ．10cmD ．9cm【答案】A 【解析】解：∥AD∥BC ，BD ＝DE ，EF 垂直平分AC ，∥AB ＝AE ＝EC ，∥∥ABC 周长26cm ，AF ＝5cm ，∥AC＝10（cm），∥AB+BC＝16（cm），∥AB+BE+EC＝16（cm），即2DE+2EC＝16（cm），∥DE+EC＝8（cm），∥DC＝DE+EC＝8（cm），故选：A．5．如图，∥ABC是等边三角形，D为AB的中点，DE∥AC于点E，EF//AB交BC于点F，已知AE=5，则∥EFC的周长为（）A．60B．45C．30D．15【答案】B【解析】解：∥∥ABC是等边三角形，∥∥A=60°，∥DE∥AC，∥∥ADE=30°，∥AD=2AE=2×5=10，∥D为AB的中点，∥AB=2AD=20，∥AC=AB=20，∥EC=AC﹣AE=15，∥EF∥AB，∥∥EFC=∥B=60°，∥FEC=∥A=60°，∥∥EFC是等边三角形，∥∥EFC的周长=3EC=3×15=45．故选：B．6．如图，是四张形状不同的纸片，用剪刀沿一条直线将它们分别剪开（只允许剪一次），不能够得到两个等腰三角形纸片的是（）A．B．C．D．【答案】B【解析】如图所示，∥ACD和∥BCD都是等腰三角形；如图所示，∥ABC不能够分成两个等腰三角形；如图所示，∥ACD和∥BCD都是等腰三角形；如图所示，∥ACD和∥BCD都是等腰三角形；故选B.7．如图，将两个全等的有一个角为30°的直角三角形拼成如下图形，其中两条长直角边在同一直线上，则图中等腰三角形的个数是（ ）A ．4B ．3C ．2D ．1【答案】B【解析】如图，∥将两个全等的有一个角为30°的直角三角形拼在一起，其中两条较长直角边在同一条直线上． ∥EF∥DG ，∥E=∥D=60°，∥∥ENM=∥D=60°，∥MGD=∥E=60°，∥EM=NM=EN ，DM=GM=DG ，∥∥MEN ，∥MDG 是等边三角形．∥∥A=∥B=30°，∥MA=MB ，∥∥ABM 是等腰三角形．∥图中等腰三角形有3个．故选：B ．8．如图，∥ABC 中，AB AC =，D 是BC 中点，下列结论，不一定正确的是（ ）A ．AD BC ⊥B ．AD 平分BAC ∠ C ．2AB BD = D ．B C ∠=∠【答案】C 【解析】解：∥AB=AC ，∥∥B=∥C ，∥AB=AC ，D 是BC 中点，∥AD 平分∥BAC ，AD∥BC ，所以，结论不一定正确的是AB=2BD ．故选：C ．二、填空题9．如图，在∥ABC 中，AB=AC ，BD∥AC ，CE∥AB ，D 、E 为垂足，BD 与CE 交于点O ，则图中全等三角形共有_________对．【答案】3【解析】解：有3对：理由是∥AB=AC ，∥∥ABC=∥ACB ，∥BD∥AC ，CE∥AB ，∥∥BDC=∥BEC=90°，∥BC=BC ，∥∥BEC∥∥BDC ，∥∥ADB=∥AEC ，∥A=∥A ，AB=AC ，∥∥ADB∥∥AEC ，∥AD=AE ，∥BE=DC ，∥∥EOB=∥DOC ，∥BEC=∥BDC ，∥∥BEO∥∥CDO ，故答案为3．10．如图，线段AB BC ，的垂直平分线12,l l 交于点O ．若35B ︒∠=，则AOC ∠=__________︒【答案】70【解析】解：连接BO 并延长，如图：线段AB BC ，的垂直平分线12,l l 交于点O∥AO=OB=OC∥A=∥ABO ，∥C=∥CBO∥∥A+∥C=∥ABC=35°∥70AOC AOD COD A ABO C CBO A C ABC ∠=∠+∠=∠+∠+∠+∠=∠+∠+∠=故答案为：7011．如图，在ABC 中，AB AC =，50A ∠=︒，AB 的垂直平分线MN 交AC 于D 点，连接BD ，则DBC ∠的度数是________．【答案】15°【解析】∥AB=AC ，∥A=50∥，∥ ∥ABC=12(180∥−∥A)=12(180∥−50∥)=65∥， ∥MN 垂直平分线AB ，∥AD=BD ，∥ ∥ABD=∥A=50∥，∥ ∥DBC=∥ABC−∥ABD=65∥−50∥=15∥.故答案为:15∥.12．如图，∥ABD ，∥ACE 都是等边三角形，BE 和CD 交于O 点，则∥BOC=__________度．【答案】120【解析】∥∥ABD 、∥ACE 都是正三角形，∥AD=AB ，AC=AE ，∥DAB=∥CAE=60°，∥∥DAC=∥BAE ，∥∥ADC∥∥ABE(SAS)，∥∥ADC=∥ABE ，∥∥DAB=∥BOD=60°，∥BOC=180-∥BOD=120°，故答案为：12013．已知：如图所示，点D 在BC 的延长线上，120ACD AB AC ︒∠==，，则ABC ∆的形状为___________【答案】等边三角形【解析】解：∥点D 在BC 的延长线上，120ACD ︒∠=，∥60ACB ︒∠=，∥AB AC =，∥∥ABC 的形状为等边三角形．故答案为：等边三角形．14．如图，在ABC 中，BO ，CO 分别是ABC ∠和ACB ∠的平分线，过O 点的直线分别交AB ､AC 于点D ､E ，且//DE BC ．若68==，AB cm AC cm ，则ADE 的周长为________．【答案】14cm【解析】DE BC ∥，DOB OBC ∴∠=∠，又BO 是ABC ∠的平分线，DBO OBC ∴∠=∠，DBO DOB ∴∠=∠，BD OD ∴=，同理：OE EC =，ADE ∴的周长14 AD OD OE AE AD BD AE EC AB AC cm ====＋＋＋＋＋＋＋．15．在Rt∥ABC 中，∥B=90°，AC=16，BC=8，那么∥C=______度．【答案】60°【解析】∥Rt∥ABC 中，∥B=90°，AC=16，BC=8， ∥BC=12AC ， ∥Rt∥ABC 中，∥B=90°，∥∥A=30°，∥∥C=90°-∥A=60°．故答案为：6016．如图，在ABC ∆中，AB AC =，D 是BC 的中点，DE AC ⊥，垂足为E ，50BAC ∠=︒，则ADE ∠的度数是______．【答案】65【解析】∥AB ＝AC ，D 为BC 的中点，∥∥BAD ＝∥CAD ，∥∥BAC ＝50°，∥∥DAC ＝25°，∥DE∥AC ，∥∥ADE ＝90°−25°＝65°，故答案为65°．17．等腰直角ABC 中，90ACB ∠=︒，AH HG ⊥，BG HG ⊥，12HG =，4AH =，则BG =________．【答案】8【解析】ABC 是等腰直角三角形，且90ACB ∠=︒，BC CA ∴=，90BCG ACH ∠+∠=︒，,A BG HG H HG ⊥⊥，90G H ∴∠=∠=︒，90BCG CBG ∠∴∠+=︒，CBG ACH ∴∠=∠，在BCG 和CAH 中，G H CBG ACH BC CA ∠=∠⎧⎪∠=∠⎨⎪=⎩，()BCG CAH AAS ∴≅，,CG AH BG CH ∴==，12,4H HG A ==，1248BG CH HG CG HG AH ∴==-=-=-=，故答案为：8．18．如图，在等边三角形ABC 中，BD=CE,AD,BE 交于点F,则AFE ∠=_________;【答案】60°【解析】解：在等边∥ABC 中，AB=BC ，∥ABC=∥C=60°，在∥ABD 和∥BCE 中，∥60AB BC ABC C BD CE =⎧⎪∠=∠=︒⎨⎪=⎩，∥∥ABD∥∥BCE （SAS ），∥∥BAD=∥CBE ，在∥ABF 中，∥AFE=∥BAD+∥ABF=∥CBE+∥ABF=∥ABC=60°，即∥AFE=60°．故答案为：60°．三、解答题19．如图，已知ABC 中，AB AC =．M 是BC 的中点，D 、E 分别是AB 、AC 边上的且AD AE =． 求证：MD ME =．【答案】见详解【解析】∥AB AC =，∥∥B=∥C ，∥M 是BC 的中点，∥BM=CM ，又∥AD AE =，∥AB -AD=AC -AE ，即BD=CE ，∥∆BDM∥∆CEM ，∥MD ME =．20．如图，点D ，E 在ABC 的边AB 上，,,8CA CB CD CE AE ===，求BD 的长．【答案】8BD =【解析】解：如图，过C 作CM AB ⊥，垂足为M ．∥AC BC =，CD CE =，且CM AB ⊥，∥,==AM BM DM EM ，∥+=+AM EM BM DM ，∥AE BD =．∥8AE =，∥8BD =．21．如图，在Rt ABC △和Rt BAD △中，AB 为斜边，AC BD =，BC 、AD 相交于点E ．（1）请说明AE BE =的理由；（2）若45=︒∠AEC ，1AC =，求CE 的长．【答案】（1）见解析；（2）CE=1.【解析】（1）证明：在Rt ACE 和Rt BDE △中，∥AEC ∠与BED ∠是对顶角，∥AEC BED ∠=∠．∥90C D ∠=∠=︒，AC BD =，∥Rt ACE ∥Rt BDE △（AAS ）．∥AE BE =．（2）∥45=︒∠AEC ，90C ∠=︒，∥45CAE ∠=︒，∥AEC CAE ∠=∠ ，∥1CE AC ==．22．如图，ABC ∆为等边三角形，BD 平分ABC ∠交AC 于点D ，//DE BC 交AB 于点E ． （1）求证：ADE ∆是等边三角形．（2）求证：12AE AB =．【答案】（1）见解析；（2）见解析【解析】(1)∥∥ABC 为等边三角形，∥∥A=∥ABC=∥C=60°．∥DE∥BC ，∥∥AED=∥ABC=60°，∥ADE=∥C=60°．∥∥ADE 是等边三角形(2)∥∥ABC 为等边三角形，∥AB=BC=AC ．∥BD 平分∥ABC ， ∥AD=12AC ∥∥ADE 是等边三角形，∥AE=AD ． ∥AE=12AB ． 23．已知ABC 中，90BAC ∠=︒，AB AC =，E 为BC 边上一点，过E 点的直线交AB 及AC 延长线于D 、F 两点，DE AE =．（1）求证DE EF =；（2）求证BD CF =；（3）若5BE =，3CE =，请直接写出CEF △的面积．【答案】（1）证明见解析；（2）证明见解析；（3）1.5.【解析】证明：（1）,ED EA =,EDA EAD ∴∠=∠90BAC ∠=︒，90,EAD EAC EDA F ∴∠+∠=︒=∠+∠,EAC F ∴∠=∠,EA EF ∴=.ED EF ∴=（2）如图，过D 作//DM AC 交BC 于M ，DMB ACB ∴∠=∠,EDM F ∠=∠，AB AC =,B ACB ∴∠=∠，B DMB ∴∠=∠，DB DM ∴=，在EDM △与EFC 中，EDM F DE FEDEM FEC ∠=∠⎧⎪=⎨⎪∠=∠⎩()EDM EFC ASA ∴≌,DM FC ∴=.BD CF ∴=（3）过D 作DP BC ⊥于P ，,90AB AC BAC =∠=︒，DB DM =，45B DMB ∴∠=∠=︒，45BDP MDP ∴∠=∠=︒，=BP MP DP ∴=，EDM EFC ≌，3EM EC ∴==，5BE =，2BM ∴=，1DP ，1131 1.522DME S ME DP ∴==⨯⨯=，1.5.CEF S ∴=24．如图，ABC ∆是等边三角形，BP 平分ABC ∠交AC 于点P ，延长BC 到点Q ，使得CP CQ =．（1）请用尺规作图的方法，过点P 作PM BQ ⊥，垂足为M ；（不写作法，保留作图痕迹）（2）求证：BM QM =．【答案】（1）答案见解析；（2）证明见解析．【解析】（1）解：如图，（2）证明：∥∥ABC是等边三角形，BP平分∥ABC，∥P是AC的中点（三线合一）∥∥ABC＝2∥PBC，∥CP＝CQ，∥∥Q＝∥CPQ．又∥∥ACB＝∥Q＋∥CPQ，∥∥ACB＝2∥Q，又∥∥ABC＝∥ACB，∥2∥PBC＝2∥Q，∥∥PBC＝∥Q，∥PB＝PQ．∆是等腰三角形，∥PBQ又∥PM∥BQ，∥BM＝QM．25．如图，∥ACB和∥DCE均为等腰三角形，∥ACB=∥DCE=90°，点A，D，E在同一条直线上，连接BE．（1）求证：AD=BE；（2）若∥CAE=15°，AD=4，求AB的长．【答案】（1）见解析；（2）8【解析】（1）∥ACB和∥DCE均为等腰三角形，∥ACB=∥DCE=90°，∴∠=∠,ADC BCE在ACD △与BCE 中，AC BC ACD BCE DC EC =⎧⎪∠=∠⎨⎪=⎩()ACD BCE SAS ∴≌，AD BE ∴=；（2）ABC 是等腰直角三角形，45ABC ∴∠=︒，由（1）可知，15CAE CBE ∠=∠=︒，4BE AD ==,451560ABE ABC CBE ∴∠=∠+∠=︒+︒=︒，90ABE ACB ∴∠=∠=︒，则在Rt AEB 中，30EAB ∠=︒，28AB BE ∴==．26．如图，已知∥ABC 是等边三角形，D 、E 分别是BC 、AC 边上的点，且BD CE =，AD 、BE 相交于点P .（1）求证：AD BE =；（2）求出APE ∠ 的度数．【答案】（1）见解析；（2）60°.【解析】（1）∥∥ABC 是等边三角形，∥AB=BC=AC ，∥ABC=∥BAC=∥C=60°，在∥ABD 和∥BCE ，AB BC ABD C BD CE ⎧⎪∠∠⎨⎪⎩＝＝＝ ，∥∥ABD∥∥BCE （SAS ），∥AD=BE．（2）∥∥ABD∥∥CBE，∥∥BAD=∥CBE，∥∥ABP+∥CBE=∥ABD=60°，∥∥ABP+∥BAD=60°，∥∥APB=180°-60°=120°．=180°-120°=60°．∥APE27．如图，∥ABC中，AB＝AC，∥A＝36°，AC的垂直平分线交AB于E，D为垂足，连接EC．（1）求∥ECD的度数；（2）若CE＝5，求BC长．【答案】（1）∥ECD=36°；（2）BC长是5．【解析】解：（1）∥DE垂直平分AC，∥CE＝AE，∥∥ECD＝∥A＝36°；（2）∥AB＝AC，∥A＝36°，∥∥B＝∥ACB＝72°，∥∥BEC＝∥A+∥ECD＝72°，∥∥BEC＝∥B，∥BC＝EC＝5．。

等腰三角形知识点+经典例题-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第一讲等腰三角形【要点梳理】要点一、等腰三角形的定义1.等腰三角形有两条边相等的三角形，叫做等腰三角形，其中相等的两条边叫做腰，另一边叫做底，两腰所夹的角叫做顶角，底边与腰的夹角叫做底角.如图所示，在△ABC中，AB＝AC，△ABC是等腰三角形，其中AB、AC为腰，BC为底边,∠A是顶角，∠B、∠C是底角．2.等腰三角形的作法已知线段a,b(如图).用直尺和圆规作等腰三角形ABC,使AB=AC=b,BC=a.作法：1.作线段BC=a；2.分别以B,C为圆心，以b为半径画弧，两弧相交于点A;3.连接AB,AC.△ABC为所求作的等腰三角形3.等腰三角形的对称性(1)等腰三角形是轴对称图形；(2)∠B＝∠C；(3)BD＝CD，AD为底边上的中线.(4)∠ADB＝∠ADC＝90°，AD为底边上的高线.结论：等腰三角形是轴对称图形，顶角平分线(底边上的高线或中线)所在的直线是它的对称轴.4.等边三角形三条边都相等的三角形叫做等边三角形.也称为正三角形.等边三角形是一类特殊的等腰三角形，有三条对称轴，每个角的平分线(底边上的高线或中线)所在的直线就是它的对称轴.要点诠释：（1）等腰三角形的底角只能为锐角，不能为钝角（或直角），但顶角可为钝角（或直角）.∠A＝180°－2∠B，∠B＝∠C＝1802A︒-∠ .（2）等边三角形与等腰三角形的关系：等边三角形是特殊的等腰三角形，等腰三角形不一定是等边三角形.要点二、等腰三角形的性质1.等腰三角形的性质性质1：等腰三角形的两个底角相等，简称“在同一个三角形中，等边对等角”．推论：等边三角形的三个内角都相等，并且每个内角都等于60°.性质2：等腰三角形的顶角平分线、底边上中线和高线互相重合.简称“等腰三角形三线合一”．2.等腰三角形中重要线段的性质等腰三角形的两底角的平分线（两腰上的高、两腰上的中线）相等.要点诠释：这条性质，还可以推广到一下结论：（1）等腰三角形底边上的高上任一点到两腰的距离相等。

专题12 轴对称30大高频考点一．生活中轴对称1．如图，桌球的桌面上有M，N两个球，若要将M球射向桌面的一边，反弹一次后击中N球，则A，B，C，D，4个点中，可以反弹击中N球的是点．2．数的运算中含有一些有趣的对称形式，如12×231＝132×21，按照此等式的形式填空：12×462＝×；×891＝×81．二．轴对称图形的辨析3．在“线段、角、直角三角形、等边三角形”这四个图形中，对称轴最多的图形是．4．如图，在3×3的正方形格纸中，有一个以格点为顶点的△ABC，请你找出格纸中所有与△ABC 成轴对称且也以格点为顶点的三角形，这样的三角形共有个．5．线段是轴对称图形，它的对称轴是；角是轴对称图形，它的对称轴是．三．镜面对称6．有两面可绕一立轴转动的立式镜，我站在这两面镜手前的一个点上，这个点位于镜面夹角的角平分面上．若两镜面的夹角为50°，我将可以看到自己的镜像数为（）A．10B．8C．6D．4四．剪纸类7．将一个正方形纸片对折后对折再对折，得到如图所示的图形，然后将阴影部分剪掉，把剩余部分展开后的平面图形是（）A．B．C．D．8．如图，从△ABC的纸片中剪去△CED，得到四边形ABDE．若∠1+∠2＝230°，则∠C＝（）A．230°B．130°C．50°D．110°五．设计轴对称图案9．如图是5个小正方形纸片拼成的图形，现将其中一个小正方形纸片平移，使它与原图中剩下的小正方形纸片有一条或两条边重合后拼成一个轴对称图形，在拼出的所有不同位置的轴对称图形中，全等的图形共有（）A．0对B．1对C．2对D．3对六．轴对称的性质10．如图，点P为∠AOB内部任意一点，点P与点P1关于OA对称，点P与点P2关于OB对称，OP＝4，∠AOB＝45°，则△OP1P2的面积为．11．如图，把一张长方形纸片ABCD的一角沿AE折叠，点D的对应点D′落在∠BAC的内部，若∠CAE＝2∠BAD′，且∠CAD′＝n，则∠DAE的度数为（用含n的式子表示）．七．：轴对称与最值12．如图，AD，BE在AB的同侧，AD＝4，BE＝4，AB＝8，点C为AB的中点，若∠DCE＝120°，则DE的最大值是．13．如图，点C，D在AB的同侧，AC＝5，AB＝10√2，BD＝10，点M为AB的中点，若∠CMD＝120°，则CD的最大值是．14．如图，△ABC中，∠B＝45°，∠C＝75°，AB＝4，D为BC上一动点，过D作DE⊥AC于点E，作DF⊥AB于点F，连接EF，则EF的最小值为．15．如图，在锐角△ABC中，∠A＝30°，BC＝3，S△ABC＝8，点P是边BC上的一动点，点P关于直线AB，AC的对称点分别是M，N，连接MN，则MN的最小值为．八．作图：轴对称的变换16．如图，在正方形网格中，△ABC的三个顶点分别在正方形网格的格点上，△A′B′C′和△ABC 关于直线l成轴对称，其中A′点的对应为A点．（1）请画出△A′B′C′，并标出相应的字母；（2）若网格中最小正方形的边长为1，求△A′B′C′的面积．17．如图，在平面直角坐标系的网格中，其最小正方形的边长为1个单位长度，△ABC的顶点都在格点上．（1）作出△ABC关于x轴对称的图形△A'B'C'，并写出△A'B'C'三个顶点的坐标；（2）判断△A'B'C'的形状，并简单加以说明．九．角平分线的性质18．如图，已知△ABC的周长是18，∠ABC和∠ACB的角平分线交于点O，OD⊥BC于点D，若OD＝3，则△ABC的面积是．19．如图，OP平分∠MON，P A⊥ON于点A，P A＝3，点Q是射线OM上一个动点，若PQ＝m，则m的取值范围是．20．如图，△ABC的三边AB、BC、CA长分别是30、40、50，∠ABC和∠ACB的角平分线交于O，则S△ABO：S△BCO：S△CAO等于（）A．1：1：1B．1：2：3C．2：3：4D．3：4：5十．角平分的性质与面积21．如图所示，点O是△ABC内一点，BO平分∠ABC，OD⊥BC于点D，连接OA，若OD＝5，AB ＝20，则△AOB的面积是．22．如图，已知△ABC的周长是18，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD＝3，△ABC的面积是．23．已知点O是△ABC的三个内角平分线的交点，若△ABC的周长为24cm，面积为36cm2，则点O 到AB的距离为cm．十一．角平分线的判定24．如图，O是△ABC内一点，且O到三边AB，BC，CA的距离相等（即OF＝OD＝OE），若∠BAC＝80°，则∠BOC（）A．110°B．120°C．130°D．140°25．东湖高新区为打造成“向往之城”，正建设一批精品口袋公园．如图所示，△ABC是一个正在修建的口袋公园．要在公园里修建一座凉亭H，使该凉亭到公路AB、AC的距离相等，且使得S△ABH ＝S△BCH，则凉亭H是（）A．∠BAC的角平分线与AC边上中线的交点B．∠BAC的角平分线与AB边上中线的交点C．∠ABC的角平分线与AC边上中线的交点D．∠ABC的角平分线与BC边上中线的交点十二．垂直平分线的性质26．如右图：AB比AC长3cm，BC的垂直平分线交AB于D，交BC于E，△ACD的周长是14cm，则AB＝cm．27．如图，在△ABC中，AB、AC的中垂线GF、DE分别交BC于点F、E，连接AE、AF，∠B+∠C＝50°，那么∠F AE的度数是（）A．80°B．70°C．60°D．50°十三．垂直平分线的判定28．如图，△ABC中，AD是高，E、F分别是AB、AC的中点．（1）若AB＝10，AC＝8，求四边形AEDF的周长；（2）求证：EF垂直平分AD．十四．角平分线与垂直平分线的融合29．如图，△ABC中，D为BC的中点，DE⊥BC交∠BAC的平分线于E，EF⊥AB，交AB于F，EG⊥AC，交AC的延长线于G，试问：BF与CG的大小如何？证明你的结论．十五．等腰三角形的性质30．如图，△ABC中，∠CAB＝∠CBA＝48°，点O为△ABC内一点，∠OAB＝12°，∠OBC＝18°，则∠ACO+∠AOB＝（）A．190°B．195°C．200°D．210°31．求证：等腰三角形两底角的平分线相等．32．如图，在△ABC中，AB＝AC，点D在AC上，且BD＝BC＝AD，求△ABC各角的度数．十六．等腰三角形的判定33．如图，已知△ABC，CD平分它的外角∠BCE，AB∥CD，证明：△ABC为等腰三角形．34．如图，在△ABC中，∠A＝60°．BE，CF交于点P，且分别平分∠ABC，∠ACB．（1）求∠BPC的度数；（2）连接EF，求证：△EFP是等腰三角形．十七．格点等腰三角形35．如图，在正方形网格中，网格线的交点称为格点；已知A，B是两格点，若C点也是图中的格点，且使得△ABC为等腰三角形，则符合条件的点C有个．36．如图，M，N是∠AOB的边OA上的两个点（OM＜ON），∠AOB＝30°，OM＝a，MN＝4．若边OB上有且只有1个点P，满足△PMN是等腰三角形，则a的取值范围是．十八．图形的存在性之等腰37．如图，在△ABC中，∠B＝25°，∠A＝100°，点P在△ABC的三边上运动，当△P AC成为等腰三角形时，其顶角的度数是．38．在△ABC中，∠A＝40°，当∠C＝时，△ABC为等腰三角形．39．如图，等边△ABC的边长为12cm，M，N两点分别从点A，B同时出发，沿△ABC的边顺时针运动，点M的速度为1cm/s，点N的速度为2cm/s，当点N第一次到达B点时，M，N两点同时停止运动，则当M，N运动时间t＝s时，△AMN为等腰三角形．十九．等腰三角形的性质与判定综合40．如图，点D在等边△ABC的外部，连接AD、CD，AD＝CD，过点D作DE∥AB交AC于点F，交BC于点E．（1）判断△CEF的形状，并说明理由；（2）连接BD，若BC＝10，CF＝4，求DE的长．41．在等边△ABC中，点E是AB上的动点，点E与点A、B不重合，点D在CB的延长线上，且EC＝ED．（1）如图1，若点E是AB的中点，求证：BD＝AE；（2）如图2，若点E不是AB的中点时，（1）中的结论“BD＝AE”能否成立？若不成立，请直接写出BD与AE数量关系，若成立，请给予证明．二十．等边三角形的性质42．如图，△ABC是等边三角形，BD是中线，延长BC至E，CE＝CD，（1）求证：DB＝DE．（2）在图中过D作DF⊥BE交BE于F，若CF＝4，求△ABC的周长．二十一．等边三角性的判定43．如图，AB＝AC，∠BAC＝120°，AD⊥AC，AE⊥AB．（1）求∠C的度数；（2）求证：△ADE是等边三角形．二十二．等边三角性的判定与性质的综合运用44．已知：如图，△ABC、△CDE都是等边三角形，AD、BE相交于点O，点M、N分别是线段AD、BE的中点．（1）求证：AD＝BE；（2）求∠DOE的度数；（3）求证：△MNC是等边三角形．45．如图，在△ABC中，∠ACB＝90°，∠A＝30°，AB的垂直平分线分别交AB和AC于点D，E．（1）求证：AE＝2CE；（2）连接CD，请判断△BCD的形状，并说明理由．二十三．含30°角的直角三角形46．如图，已知Rt△ABC中，∠ACB＝90°，∠B＝15°，边AB的垂直平分线交边BC于点E，垂足为点D，取线段BE的中点F，联结DF．求证：AC＝DF．（说明：此题的证明过程需要批注理由）二十四．直角三角形斜中线的运用47．【教材呈现】如图是华师版九年级上册数学教材第103﹣104页的部分内容．如图24.2.1，画Rt△ABC，并画出斜边AB上的中线CD，量一量，看看CD与AB有什么关系．相信你与你的同伴一定会发现，CD恰好是AB的一半．下面让我们用演绎推理证明这一猜想．已知：如图24.2.2，在Rt△ABC中，∠ACB＝90°，CD是斜边AB上的中线，求证：CD=12AB．定理证明：请根据教材图24.2.2的提示，结合图①完成直角三角形的性质：“直角三角形斜边上的中线等于斜边的一半”的证明．定理应用：（1）如图②，在△ABC中，AD⊥BC，垂足为点D（点D在BC上），CE是AB边上的中线，DG垂直平分CE．求证：∠B＝2∠BCE；（2）在（1）条件下，若BF⊥AC于点F，连接DE、EF、FD．当△DEF是等边三角形，且BD ＝3时，△DEF的周长为．48．如图，Rt△ABC中，∠CAB＝90°，∠ACB＝30°，D是AB上一点（不与A、B重合），DE⊥BC于E，若P是CD的中点，请判断△P AE的形状，并说明理由．二十五．新定义49．定义：若a，b，c是△ABC的三边，且a2+b2＝2c2，则称△ABC为“方倍三角形”．（1）对于①等边三角形②直角三角形，下列说法一定正确的是．A．①一定是“方倍三角形”B．②一定是“方倍三角形”C．①②都一定是“方倍三角形”D．①②都一定不是“方倍三角形”（2）若Rt△ABC是“方倍三角形”，且斜边AB=√3，则该三角形的面积为；（3）如图，△ABC中，∠ABC＝120°，∠ACB＝45°，P为AC边上一点，将△ABP沿直线BP 进行折叠，点A落在点D处，连接CD，AD．若△ABD为“方倍三角形”，且AP=√2，求△PDC 的面积．二十六．尺规作图50．如图，在△ABC中，∠C＝90°．（1）过点B作∠ABC的平分线交AC于点D（尺规作图，保留作图痕迹，标注有关字母，不用写作法和证明）；（2）若CD＝3，AB+BC＝16，求△ABC的面积．51．两个城镇A、B与两条公路ME，MF位置如图所示，其中ME是东西方向公路．现电信部门需在C处修建一座信号发射塔，要求发射塔到两个城镇A、B的距离必须相等，到两条公路ME，MF的距离也必须相等，且在∠FME的内部，请在图中，用尺规作图找出符合条件的点C．（不写已知、求作、作法，只保留作图痕迹）二十七．规律类52．如图，将一张正方形纸片剪成四个小正方形，得到4个小正方形，称为第一次操作；然后，将其中的一个正方形再剪成四个小正方形，共得到7个小正方形，称为第二次操作；再将其中的一个正方形再剪成四个小正方形，共得到10个小正方形，称为第三次操作；…，根据以上操作，若操作2022次，得到小正方形的个数是（）A．6065B．6066C．6067D．606853．如图，在第1个△A1BC中，∠B＝30°，A1B＝CB，在边A1B上任取一点D，延长CA1到A2，使A1A2＝A1D，得到第2个△A1A2D；在边A2D上任取一点E，延长A1A2到A3，使A2A3＝A2E，得到第3个△A2A3E；…按此做法继续下去，则第2022个三角形中以A2022为顶点的内角度数是（）A ．（12）2019•75°B ．（12）2020•75°C ．（12）2021•75°D ．（12）2022•75° 二十八．坐标中的轴对称54．已知点M （a ，﹣3），点N （﹣2，b ）关于y 轴对称，则（a +b ）2022的值（ ）A ．﹣3B ．﹣1C ．1D ．355．平面直角坐标系中，△ABC 的三个顶点坐标分别为A （1，4），B （3，4），C （3，﹣1）．（1）试在平面直角坐标系中，标出A 、B 、C 三点；（2）求△ABC 的面积．（3）若△A 1B 1C 1与△ABC 关于x 轴对称，写出A 1、B 1、C 1的坐标．二十九．三线合一的妙用56．如图，△ABC 中，AB ＝AC ，AD 是∠BAC 的角平分线交BC 于点D ，DE ⊥AC 于点E ，CF ⊥AB 于点F ，DE ＝3，则CF 的长为（ ）A ．4B ．6C ．9D ．1257．如图，在△ABC 中，AB ＝AC ，点D 是BC 的中点，点E 在AD 上．（1）求证：∠BAD＝∠CAD；（2）求证：BE＝CE．三十．角平分与平行、垂直的巧妙融合58．如图，在△ABC中，过点B作△ABC的角平分线AD的垂线，垂足为F，FG∥AB交AC于点G，若AB＝4，则线段FG的长为．59．如图，在△ABC中，ED∥BC，∠ABC和∠ACB的平分线分别交ED于点G、F，若FG＝5，ED＝9，求EB+DC＝．60．如图，已知S△ABC＝24m2，AD平分∠BAC，且AD⊥BD于点D，则S△ADC m2．。

2、下列图形中，轴对称图形的个数是()2 C .3D .4 教学主题 轴对称期中复习教学目标巩固轴对称易考题型重要知识点1.轴对称 2•线段、角的轴对称性 3•等腰三角形的轴对称性 教学过程知识点一、轴对称图形1、下列图案是几种名车的标志，请你从中判断哪些是轴对称图形，并画出其对称轴.丰也欧宅 A .11•下列图形中，不是轴对称图形的是A.两条相交直线C.有公共端点的两条相等线段2•到三角形的三个顶点距离相等的点是A.三条角平分线的交点C.三条高的交点 () B.线段D.有公其端点的两条不相等线段 () B.三条中线的交点 D.三条边的垂直平分线的交点A.a+bB.a —bC.2a+bD.a+2b 1•线段垂直平分线的性质定理：线段垂直平分线上的点2.线段垂直平分线的性质定理的逆定理：到线段两端距离相等的点例题:3..如图，在△ABC 中，AB=a,AC=b,BC 边上的垂直平分线DE 分别交BC 、BA 于点D 、已，则4 AEC 的周长等于()4. 如图，三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B 的直线折叠这个三角形，使顶点C落在AB 边上的点E 处，折痕为3。

，则4AED 的周长为cm ；连接CE ，则线段BD 、CE 的关系是•C角平分线上的点到角的两边距离.到角两边距离相等的点在.例题：1.如图，AD〃BC,DC丄AD,AE平分ZBAD,且E是DC的中点，EF丄AB于点F.问AD、BC与AB之间有何关系？为什么？2.如图，已知BD为ZABC的平分线，DE丄BC于E,且AB+BC=2BE(1)求证：ZBAD+ZBCD=180°；(2)若将条件“AB+BC=2BE”与结论“ZBAD+ZBCD=180°”互换，结论还成立吗？请说明理由知识点四、等腰三角形的轴对称性1、定理：等腰三角形的两底角相等(简称“等边对等角”).2、定理：等腰三角形底边上的高线、中线及角平分线重合.3•等边三角形的判定方法：(1)三角形是等边三角形；(2)定理：三角形是等边三角形；(3)定理：有一个角是。

专题13.13轴对称（精选精练）（全章常考知识点分类专题）【考点目录】【考点1】识别轴对称图形；【考点2】利用轴对称图形性质求解；【考点3】利用轴对称性质解决折叠问题；【考点4】利用线段垂直平分线性质与判定证明与求值；【考点5】利用轴对称性质求最值；【考点6】等腰三角形（等边对等角与等角对等边）；【考点7】等腰三角形（三线合一）；【考点8】利用等腰三角形求角或边长（分类讨论）；【考点9】等腰三角形性质与判定求值证明；【考点10】等边三角形的性质与判定求；【考点11】含30度的直角三角形；【考点12】课题学习（最短路径问题）.一、单选题【考点1】识别轴对称图形；1．（23-24八年级下·贵州黔西·期末）银行是现代金融业的主体，是国民经济运转的枢纽，下列银行标志图案是轴对称图形的是()A ．B ．C ．D ．2．（23-24七年级下·河南平顶山·期末）下列图形中，是轴对称图形，并且只有3条对称轴的是（）A ．圆B ．正方形C ．梯形D ．等边三角形【考点2】利用轴对称图形性质求解；3．（2024八年级上·浙江·专题练习）如图，ABC V 和AB C ''△关于直线l 对称，l 交CC '于点D ，若4,2,1AB B C CD ''===，则五边形ABCC B ''的周长为（）A ．14B ．13C ．12D ．114．（23-24九年级上·浙江温州·开学考试）如图，在平面直角坐标系中，点()5,6A -关于点()0,P m 对称的点A '在x 轴上，则m 的值为（）A ．3-B ．52-C ．52D ．3【考点3】利用轴对称性质解决折叠问题；5．（2024·浙江·模拟预测）如图，将一张长方形纸条折叠，如果2∠比1∠大90︒，则2∠的度数为（）A ．50︒B ．100︒C ．130︒D ．150︒6．（23-24八年级下·山东德州·开学考试）如图，把ABC V 纸片沿DE 折叠，当点A 落在四边形BCED 的外面时，此时测得1112∠=︒，40A ∠=︒，则2∠的度数为（）A ．32︒B ．33︒C ．34︒D ．36︒【考点4】利用线段垂直平分线性质与判定证明与求值；7．（24-25九年级上·吉林长春·开学考试）如图，用直尺和圆规作MAN ∠的角平分线，根据作图痕迹，下列结论不一定正确的是（）．A ．MAF NAF ∠=∠B ．EF DF =C ．DAF DFA ∠=∠D ．AF D E⊥8．（2024八年级上·浙江·专题练习）如图，在ABC V 中，AB 的垂直平分线DM 交BC 于点D ，边AC 的垂直平分线EN 交BC 于点E ．已知ADE V 的周长为8cm ，则BC 的长为（）A ．4cmB ．5cmC ．6cmD ．8cm【考点5】几何变换（利用轴对称性质求最值）；9．（15-16八年级上·重庆荣昌·期末）如图，四边形ABCD 中，130BAD ∠︒＝，90B D ∠∠︒＝＝，在BC ，CD 上分别找一点M ，N ，使AMN 的周长最小时，则ANM AMN ∠+∠的度数为（）A ．80︒B ．90︒C ．100︒D ．130︒10．（19-20九年级·安徽·阶段练习）如图，在Rt ABC △中，90,6,8ACB AC BC ∠=︒==，10,AB AD =是BAC ∠的平分线．若,P Q 分别是AD 和AC 上的动点，则PC PQ +的最小值是（）A ．2.4B ．4.8C ．4D ．5【考点6】等腰三角形（等边对等角与等角对等边）；11．（24-25八年级上·浙江宁波·开学考试）如图，在PAB 中，,,,PA PB M N K =分别是,,PA PB AB 上的点，且,AM AK BN BK ==，若44MKN ∠=︒，则P ∠=（）°A ．66B ．92C ．96D ．9812．（23-24七年级下·山东济南·期末）如图，在ABC V 中，BE ，CE 分别是ABC ∠和ACB ∠的平分线，ED AC ∥，交BC 于点D ，EF AB ⊥于点F ．若35BC =，5EF =，13DE =，则EBD △的面积为（）A ．50B ．55C ．60D ．65【考点7】等腰三角形（三线合一）；13．（2024·广西·模拟预测）如图，在ABC V 中，AB AC =，分别以点A 、B 为圆心，以适当的长为半径作弧，两弧分别交于E ，F ，作直线EF ，D 为BC 的中点，M 为直线EF 上任意一点．若ABC V 面积为40，且BM MD +长度的最小值为10，则BC 长为（）A ．5B ．6C ．8D ．1014．（23-24七年级下·福建福州·期末）如图，ABC V 中，90BAC ∠=︒，AD BC ⊥，ABC ∠的平分线BE 交AD 于点F ，AG 平分DAC ∠．下列结论：①AEF AFE ∠=∠；②EBC C ∠=∠；③AG EF ⊥；④FG AC ．其中正确的结论是（）A ．①②③④B ．①②③C ．①③④D ．①②【考点8】利用等腰三角形求角或边长（分类讨论）；15．（23-24八年级下·贵州毕节·阶段练习）已知a ，b 是等腰三角形的两腰，c 为底边，若22m a ac bc b =-+-，则下列说法正确的是（）A ． 0m >B ．0m =C ．0m <D ． 0m >或0m <16．（2024八年级上·江苏·专题练习）在ABC V 中，AB AC =，AB 的垂直平分线与AC 所在直线的夹角为50︒，则这个等腰三角形的顶角为（）A ．40︒B ．50︒C ．40︒或140︒D ．50︒或130︒【考点9】利用等腰三角形的性质与判定求值证明；17．（23-24八年级下·山东德州·开学考试）如图，B C ∠∠、的平分线相交于F ，过点F 作DE BC ∥，交AB于D ，交AC 于E ，那么下列结论正确的是①BDF CEF 、都是等腰三角形；②DE BD CE =+；③ADE V 的周长为+AB AC ；④BD CE =．（）A ．③④B ．①②C ．①②③D ．②③④18．（2024·四川泸州·二模）如图，在ABC V 中，AB AC =，按以下步骤作图：①以点A 为圆心，任意长为半径作弧，分别交AB AC ，于点D 和点E ；②以点B 为圆心，AD 长为半径作弧，交AB 于点F ；③以F 为圆心，DE 长为半径作弧，在ABC ∠内部交前面的弧于点G ；④过点G 作射线BG 交AC 于点H ．若62BC C A =∠=∠，，则AH 的长为（）A ．3B ．4C ．5D ．6【考点10】利用等边三角形的性质与判定求值证明;19．（2024八年级上·全国·专题练习）如图，在ABC V 中，60ABC ∠=︒，以AC 为边在ABC V 外作等边ACD ，过点D 作DE BC ⊥，垂足为E ，若5AB =，3CE =，则BC 的长为（）A ．4B ．92C ．5D ．20．（22-23八年级上·辽宁阜新·期末）如图，在ABC V 中，30A ACB ∠=∠=︒，分别以点B ，A 为圆心，BC ，AC 长为半径作弧，两弧交于点D ，连接CD ，交AB 的延长线于点E ．有下列结论：①60CBE ∠=︒；②ABC S BE CE =⋅△；③AC CD =；④AE 垂直平分线段CD ．其中，正确结论是（）A ．①④B ．①②④C ．①③④D ．①②③④【考点11】含30度的直角三角形；21．（2024·山东聊城·模拟预测）如图，在ABC V 中，90ABC ∠=︒，60BAC ∠=︒，以点A 为圆心，以AB 的长为半径画弧交AC 于点D ，连接BD ，再分别以点B ，D 为圆心，大于12BD 的长为半径画弧，两弧交于点P ，作射线AP 交BD 于点M ，交BC 于点E ，连接DE ，则:CDE ABC S S △△的值是（）A ．1:2B 3C ．2:5D ．1:322．（2024·内蒙古呼伦贝尔·中考真题）如图，在ABC V 中，90,30C B ∠=︒∠=︒，以点A 为圆心，适当长为半径画弧分别交,AB AC 于点M 和点N ，再分别以点,M N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，连接AP 并延长交BC 于点D ．若ACD 的面积为8，则ABD △的面积是（）A ．8B ．16C ．12D ．24【考点12】课题学习（最短路径问题）.23．（23-24八年级上·湖北武汉·阶段练习）如图，Rt ABC △中，90,345C AC BC AB D E F ∠︒===＝，，，、、分别是AB BC AC 、、边上的动点，则DEF 的周长的最小值是（）A ．2.5B ．3.5C ．4.8D ．624．（23-24八年级上·重庆合川·期末）如图，在五边形ABCDE 中，230AB BC AE DE AB BC AE DE BCD CDE ⊥⊥==∠+∠=︒，，，，，点P ，Q 分别在边BC ，D 上，连接AP ，AQ ，PQ ，当APQ △的周长最小时，PAQ ∠的度数为（）A ．50︒B ．80︒C ．100︒D ．130︒二、填空题【考点1】识别轴对称图形；25．（23-24七年级下·全国·假期作业）在线段、角、圆、等腰三角形、直角梯形和正方形中，不是轴对称图形的是．26．（23-24八年级上·全国·单元测试）如图，小张和小亮下棋，小张执圆形棋子，小亮执方形棋子，若棋盘中心的圆形棋子位置用()11-，表示，两人都将第4枚棋子放入棋盘后，所有棋子构成轴对称图形，则小亮放第4枚方形棋子的位置可能是．【考点2】利用轴对称图形性质求解；27．（22-23八年级上·江苏常州·阶段练习）如图，APT △与CPT △关于直线PT 对称，A APT ∠=∠，延长AT 交PC 于点F ，当A ∠=︒时，FTC C ∠=∠．28．（23-24八年级下·四川成都·期中）如图，在锐角ABC V 中，点O 为CAB ∠和ABC ∠的角平分线交点，过点O 作一条直线l ，交线段AB ，BC 分别于点N ，点M ．点B 关于直线l 的对称点为B '，连接B M '，B N '，分别交线段AC 于点E ，点F ．连接EO ，FO ．若ABC m ∠=︒，那么EOF ∠的度数为（用含有m 的代数式表示）．【考点3】利用轴对称性质解决折叠问题；29．（2024八年级上·浙江·专题练习）如图所示，数学拓展课上，小聪将直角三角形纸片ABC ()2565A B ∠=︒∠=︒，沿DE 向下折叠，点A 落在点A '处，当EA BC '∥时，1∠=度．30．（23-24七年级下·江苏苏州·开学考试）将一张长方形纸片ABCD 按如图所示方式折叠，AE 、AF 为折痕，点B 、D 折叠后的对应点分别为B '、D ¢，若8B AD ''∠=︒，则EAF ∠的度数为．【考点4】利用线段垂直平分线性质与判定证明与求值；31．（23-24九年级下·吉林·开学考试）如图，在ABC V 中，35A ∠=︒，ABC ∠的平分线BD 交AC 于点D ，分别以A 、B 为圆心，以大于12AB 的长为半径作弧，两弧交于点M 和N ，直线MN 刚好经过点D ，则C ∠的度数是．32．（23-24八年级下·四川成都·期末）如图，直线m n ∥，点A 是直线m 上一点，点B 是直线n 上一点，AB 与直线m ，n 均不垂直，点P 为线段AB 的中点，直线l 分别与m ，n 相交于点C ，D ，若90,CPD CD ∠=︒=，m ，n 之间的距离为2，则PC PD ⋅的值为．【考点5】几何变换（利用轴对称性质求最值）；33．（23-24七年级下·四川成都·期末）如图，在ABC V 中，AC 的垂直平分线FE 分别交AC ，AB 于点E ，F ，若点G 是直线EF 上一动点，H 是直线BC 上的一动点，7AB =，3CD =，5BC =，CD AB ⊥，则HG CG +的最小值为．34．（23-24八年级上·浙江宁波·期末）如图，20AOB ∠=︒，点M 、N 分别是边OA 、OB 上的定点，点P 、Q 分别是边OB 、OA 上的动点，记MPQ α∠=，PQN β∠=，当MP PQ QN ++最小时，则βα-的值为.【考点6】等腰三角形（等边对等角与等角对等边）；35．（23-24七年级下·广东深圳·期末）如图，在ABC V 中，45BAC ∠=︒，以BC 为边向外作等腰直角三角形BCD △，连接AD ，若4AC =，则ACD S = ．36．（2024八年级上·全国·专题练习）（23-24七年级下·山东烟台·期末）如图，A EGF ∠=∠，F 为BE ，CG 的中点，4DB =，8DE =，则AD 的长为．【考点7】等腰三角形（三线合一）；37．（24-25八年级上·上海·单元测试）如图，D 为ABC V 内一点，CD 平分ACB ∠，BE CD ⊥，垂足为D ，交AC 与点E ，A ABE ∠=∠．若7AC =，4BC =，则BD 的长为．38．（23-24八年级上·四川绵阳·期末）如图，在等腰ABC V 中，点D 是底边BC 的中点，过点D 分别作,DE AB DF AC ⊥⊥，垂足分别为点,E F ，若93,,22DF BE AF ===，则ABD △的面积为．【考点8】利用等腰三角形求角或边长（分类讨论）；39．（23-24八年级下·浙江金华·开学考试）等腰三角形一个外角是150︒，则该等腰三角形的顶角度数是．40．（23-24八年级上·河南郑州·期末）如图，120,AOC C ∠=︒是BO 延长线上的一点，10cm OC =，动点P 从点C 出发，沿CB 以2cm /s 的速度移动，动点Q 从点O 出发，沿OA 以1cm /s 的速度移动．如果点,P Q 同时出发，用s t 表示移动的时间，那么当t =时，POQ △是等腰三角形．【考点9】利用等腰三角形的性质与判定求值证明；41．（23-24九年级下·浙江台州·开学考试）如图，AB AC =，D 为AC 的垂直平分线上一点，且CD BC =，BD AB =，则A ∠=．42．（2024八年级上·全国·专题练习）如图，已知在Rt ABC △中，90ACB ∠=︒，8AC =，16BC =，D 是AC 上的一点，3CD =，点P 从B 点出发沿射线BC 方向以每秒2个单位的速度向右运动，设点P 的运动时间为t ．过点D 作DE AP ⊥于点E ．在点P 的运动过程中，当t 为时，能使DE CD =？【考点10】利用等边三角形的性质与判定求值证明.43．（22-23八年级上·广东湛江·期中）如图，ABC V 中，30,5A BC ∠=︒=，AB 的垂直平分线DE 交AB 于点D ，交边AC 于点E ，若CE CB =，则BCE 的周长为．44．（23-24七年级下·河南洛阳·期末）如图，将长方形纸片ABCD 对折，使AD 与BC 重合，展平纸片，得到折痕EF ；折叠纸片，使点B 落在EF 上，并使折痕经过点A ，得到折痕AM ，点B ，E 的对应点分别为G ，H ，展平纸片，连结BG ，BH ，则ABH ∠与GAM ∠的关系是．【考点11】含30度的直角三角形；45．（23-24九年级下·青海西宁·开学考试）如图，OP 平分AOB ∠，15AOP ∠=︒，PC OA ，PD OA ⊥于点D ，4PC =，则PD =．46．（23-24九年级下·广西南宁·开学考试）如图，ABC V 是等边三角形，4AB =．过点A 作AD BC ⊥于点D ，点P 是直线AD 上一点，以CP 为边，在CP 的下方作等边CPQ ，连接DQ ，则DQ 的最小值为．【考点12】课题学习（最短路径问题）.47．（23-24七年级下·四川宜宾·期末）在ABC V 中，80CAB ∠=︒，2AB =，3AC =，点E 是边AB 的中点，CAB ∠的角平分线交BC 于点D ．作直线AD ，在直线AD 上有一点P ，连结PC 、PE ，则PC PE -的最大值是．48．（2024·陕西西安·模拟预测）如图，在矩形ABCD 中，6,30AB DBC =∠=︒，点E 、F 分别是边AD 、BC 上的动点，且EF BD ⊥，当BE DF +取得最小值时，AE 的长为．参考答案：题号12345678910答案D D A A D A C D C B 题号11121314151617181920答案C B C C BCCDAD题号21222324答案DBCB1．D【分析】此题考查了轴对称图形的概念，根据概念逐一判断即可，如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴，这时，我们也可以说这个图形关于这条直线(成轴）对称，熟练掌握知识点是解题的关键．【详解】A 、不是轴对称图形，故本选项不符合题意；B 、不是轴对称图形，故本选项不符合题意；C 、不是轴对称图形，故本选项不符合题意；D 、是轴对称图形，故本选项符合题意；故选：D ．2．D【分析】此题考查了轴对称图形，根据轴对称图形的概念：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴；据此判断即可．【详解】解：A ．圆有无数条对称轴，故此选项不符合题意；B ．正方形有4条对称轴，故此选项不符合题意；C ．梯形中的等腰梯形是轴对称图形，只有1条对称轴，故此选项不符合题意；D ．等边三角形有3条对称轴，故此选项符合题意．故选：D ．3．A【分析】本题主要考查了轴对称图形的性质．根据轴对称图形的性质，得到每边的长度即可求出周长．【详解】解：∵ABC V 和AB C ''△关于直线l 对称，l 交CC '于点D ，∴,,AB AB BC B C DC DC ''''===，∵4,2,1AB B C CD ''===，∴4,2,1AB BC DC ''===，∴五边形ABCC B ''的周长为：42112414+++++=．故选：A ．4．A【分析】本题主要考查了坐标与图形，全等三角形的性质与判定，轴对称的性质，过A 作AH y ⊥轴于H ，则5AH =，6OH =，由轴对称的性质得到AP A P '=，证明()AAS APH A OP ' ≌，得到132OP PH OH ===，据此可得答案．【详解】解：过A 作AH y ⊥轴于H ，∵点()5,6A -，∴5AH =，6OH =，∵点A 与点A '关于点()0,P m 对称，∴AP A P '=，在APH V 与A PO '△中，90AHP A OP APH A POAP A P ∠=∠=︒⎧⎪∠=∠'='⎨'⎪⎩，∴()AAS APH A OP ' ≌，∴132OP PH OH ===，∴3m =-，故选：A．5．D【分析】本题考查了平行线性质及折叠的性质．根据平行线的性质、折叠的性质得到122BAD ADC ∠=∠=∠，进而求出1218012∠=︒-，结合“2∠比1∠大90︒”求解即可．【详解】解：如图，∵AB CD ∥，∴1,BAM BAD ADC ∠=∠∠=∠，∵长方形纸条折叠，∴BAD MAD ADC ∠=∠=∠，∴122BAD ADC ∠=∠=∠，∴112ADC ∠=∠，∴1218018012ADC ∠=︒-∠=︒-∠，∵2∠比1∠大90︒，∴2190∠=∠+︒，∴119018012∠+︒=︒-∠，∴160∠=︒，∴2150∠=︒，故选：D ．6．A【分析】本题主要考查了折叠的性质，三角形外角的性质等知识点，熟练掌握三角形外角的性质是解题的关键．根据折叠的性质得出40A A '∠=∠=︒，根据三角形外角的性质得出172DOA A ∠=∠-∠=︒，再次利用三角形外角的性质即可求出2∠的度数．【详解】解：如图，设A D '与AC 交于点O ，40A ∠=︒ ，∴根据折叠的性质，40A A '∠=∠=︒，1DOA A ∠=∠+∠ ，1112∠=︒，11124072DOA A ∴∠=∠-∠=︒-︒=︒，2DOA A '∠=∠+∠ ，2724032DOA A '∴∠=∠-∠=︒-︒=︒，故选：A ．7．C【分析】本题主要考查了角平分线的尺规作图，全等三角形的性质与判定，线段垂直平分线的判定，由作图方法可知AD AE DF EF ==，，则可证明DAF EAF △≌△得到DAF EAF DF EF ==∠∠，，进一步可证明AF 垂直平分DE ，据此可得答案．【详解】解：由作图方法可知AD AE DF EF ==，，又∵AF AF =，∴DAF EAF △≌△，∴DAF EAF DF EF ==∠∠，，∴AF 垂直平分DE ，∴MAF NAF ∠=∠，AF D E ⊥，根据现有条件无法得到DAF DFA ∠=∠，故选：C ．8．D【分析】本题考查了线段垂直平分线的性质，由线段垂直平分线的性质可得DA DB =，EA EC =，结合ADE V 的周长8cm ，得出8cm BD DE EC ++=，即可得解，熟练掌握线段垂直平分线的性质是解此题的关键．【详解】解：∵DM 是AB 的垂直平分线，∴DA DB =，∵EN 是AC 的垂直平分线，∴EA EC =，∵ADE V 的周长8cm ，∴8cm AD DE AE ++=，∴8cm BD DE EC ++=，∴8cm BC =，∴BC 的长为8cm ；故选：D ．9．C【分析】作A 点关于CD 的对称点F ，作A 点关于BC 的对称点E ，连接EF 交CD 于N ，交BC 于M ，连接AM 、AN 、此时AMN 的周长有最小值，由对称性求出50BAM DAN ∠+∠=︒，则有80MAN ∠=︒，即可求180100ANM AMN MAN ∠+∠=︒-∠=︒．【详解】解：如图，作A 点关于CD 的对称点F ，作A 点关于BC 的对称点E ，连接EF 交CD 于N ，交BC 于M ，连接AM 、AN ，∵==90B D ∠∠︒，∴=AN NF ，=AM EM ，∴AM N ∆的周长===AM AN MN NF MN EM EF ++++，此时AMN 的周长有最小值，∵=FAN F ∠∠，=E EAM ∠∠，∴=180E F BAD ∠+∠︒-∠，∵130BAD ∠=︒，∴=50E F ∠+∠︒，∴=50BAM FAN ∠+∠︒，∴()=13050=80MAN BAD BAM FAN ∠∠-∠+∠=︒-︒︒，∴=180=100ANM AMN MAN ∠+∠︒-∠︒，故选：C ．【点睛】本题考查轴对称求最短距离，熟练掌握轴对称求最短距离的方法，三角形内角和定理是解题的关键．10．B【分析】由题意可以把Q 关于B 对称到AB 的O 点，如此PC PQ +的最小值问题即变为C 与线段AB 上某一点O 的最短距离问题，最后根据“垂线段最短”的原理得解．【详解】解：如图，作Q 关于B 的对称点O ，则PQ PO =，连接PO ，过点C 作CM AB ⊥于点M ，所以O 、P 、C 三点共线时，CO PC PO PC PQ =+=+，此时PC PQ +有可能取得最小值，当CO 垂直于AB 即CO 移到CM 位置时，CO 的长度最小，∴PC PQ +的最小值即为CM 的长度， 1122ABC S AB CM AC CB =⨯=⨯V ，∴684.810CM ⨯==，即PC PQ +的最小值为4.8．故选：B ．【点睛】本题考查了轴对称最短路径问题，垂线段最短，通过轴对称把线段和最小的问题转化为线段外一点到线段某点连线段最短问题是解题关键．11．C【分析】根据等腰三角形的性质得出两个底角相等，即A B ∠=∠，同理得出12∠=∠，因为44MKN ∠=︒，运用平角性质算出()11218044682∠=∠=⨯︒-︒=︒，结合三角形内角和，列式计算，即可作答．本题考查等腰三角形的性质、三角形内角和定理及平角，熟练掌握相关判定定理及性质是解题关键．【详解】解：PA PB = ，A B ∴∠=∠，如图：∵,AM AK BN BK ==∴()()111180218022A B ∠=︒-∠∠=︒-∠，，∵A B ∠=∠∴12∠=∠∵44MKN ∠=︒∴()11218044682∠=∠=⨯︒-︒=︒∴44B A ∠=∠=︒在PAB 中，18092P A B ∠=︒-∠-∠=︒故选：B ．12．B【分析】本题考查了角平分线的性质、平行线的性质的综合应用以及等角对等边的应用；解题的关键是熟练掌握相关性质．过E 作EM BC ⊥于M ，根据角平分线上的点到角两边的距离相等可求得EM ，根据平行线和角平分线的性质易证DCE DEC ∠=∠，根据等角对等边求得CD ，从而求得BD ，最后根据三角形面积公式求解即可．【详解】解：过E 作EM BC ⊥于M ，BE 平分ABC ∠，EM BC ⊥，EF AB ⊥，5EF =，5EM EF ∴==，CE 平分ACB ∠，ACE DCE ∴∠=∠，ED AC ∥，ACE DEC ∴∠=∠，DCE DEC ∴∠=∠，13CD DE ∴==，35BC =Q ，351322BD BC CD ∴=-=-=，11·2255522EBD S BD EM ∴==⨯⨯=V ，故选：B ．13．C【分析】本题考查线段的垂直平分线的作图，线段的垂直平分线的性质，等腰三角形的三线合一的性质，垂线段最短等知识．如图，连接AM ，过点A 作AH BC ⊥于点H ．根据等腰三角形的三线合一的性质得出点H 与点D 重合，再根据垂线段最短，线段的垂直平分线的性质判断出10BM MD AM MD AH ∴+=+≥=最后利用三角形的面积公式求出BC 即可．【详解】解：如图，连接AM ，过点A 作AH BC ⊥于点H ．∵D 为BC 中点，AB AC =，∴点H 与点D 重合，EF 垂直平分线段AB ，MA MB =∴，10BM MD AM MD AH ∴+=+≥=，12ABC S BC AH ∆=⋅⋅ ，402810BC ⨯∴==，故选：C ．14．C【分析】本题主要考查了等腰三角形的判定与性质、平行线的判定、线段垂直平分线的性质等知识，熟练掌握等腰三角形的判定与性质是解题关键．根据直角三角形的性质可得90ABE AEF ∠+∠=︒，90CBE BFD ∠+∠=︒，再根据角平分线的定义可得ABE CBE ∠=∠，由此即可判断①正确；假设EBC C ∠=∠成立，可求出30C ∠=︒，根据已知条件即可判断②错误；先证出AB GB =，ABG 是等腰三角形，再根据等腰三角形的三线合一即可判断③正确；先根据等腰三角形的性质可得DAG AGF ∠=∠，从而可得CAG AGF ∠=∠，再根据平行线的判定即可判断④正确．【详解】解：∵90BAC ∠=︒，∴90ABE AEF ∠+∠=︒，∵AD BC ⊥，∴90CBE BFD ∠+∠=︒，∵BE 平分ABC ∠，∴ABE CBE ∠=∠，∴AEF BFD ∠=∠，又∵AFE BFD ∠=∠，∴AEF AFE ∠=∠，结论①正确；假设EBC C ∠=∠成立，∵90ABE CBE C ∠+∠+∠=︒，ABE CBE ∠=∠，∴30C ∠=︒，但已知条件不能得出这个结论，则假设不成立，结论②错误；∵90BAC ∠=︒，AD BC ⊥，∴90BAD ABC C ABC ∠+∠=︒=∠+∠，∴BAD C ∠=∠，∵AG 平分DAC ∠，∴DAG CAG ∠=∠，∴BAG BAD DAG C CAG BGA ∠=∠+∠=∠+∠=∠，∴AB GB =，ABG 是等腰三角形，∴AG EF ⊥，BE 垂直平分AG （等腰三角形的三线合一），结论③正确；∴AF FG =，∴DAG AGF ∠=∠，∴CAG AGF ∠=∠，∴FG AC ，结论④正确；综上，正确的结论是①③④，故选：C ．15．B【分析】该题主要考查了等腰三角形的定义以及整式加减运算，解题的关键是得出a b =．根据题意得出a b =，代入即可求解；【详解】解：∵a ，b 是等腰三角形的两腰，∴a b =，∴22220m a ac bc b a ac ac a ==-+-+-=-，故选：B ．16．C【分析】本题考查了等腰三角形的性质及三角形内角和定理，分类讨论是正确解答本题的关键．根据题意分两种情况，当ABC V 是锐角三角形时，当ABC V 是钝角三角形时，讨论求解即可；【详解】解：分两种情况：当ABC V 是锐角三角形时，如图：DE 是AB 的垂直平分线，90ADE ∴∠=︒，50AED ∠=︒ ，9040A AED ∴∠=︒-∠=︒；当ABC V 是钝角三角形时，如图：DE 是AB 的垂直平分线，90ADE ∴∠=︒，50AED ∠=︒ ，9040DAE AED ∴∠=︒-∠=︒，180140DAC DAE ∴∠=︒-∠=︒；综上所述：这个等腰三角形的顶角为40︒或140︒，故选：C ．17．C【分析】本题考查了等腰三角形的性质及角平分线的定义及平行线的性质；题目利用了两直线平行，内错角相等，及等角对等边来判定等腰三角形的；等量代换的利用是解答本题的关键．由平行线得到角相等，由角平分线得角相等，根据平行线的性质及等腰三角形的判定和性质，逐一进行判断即可．【详解】解：∵DE BC ∥，DFB FBC ∴∠=∠，EFC FCB ∠=∠，BF 是ABC ∠的平分线，CF 是ACB ∠的平分线，FBC DFB ∴∠=∠，FCE FCB ∠=∠，DBF DFB ∠=∠ ，EFC ECF ∠=∠，DFB ∴ ，FEC 都是等腰三角形．故①正确，DF DB ∴=，FE EC =，即有DE DF FE BD CE =+=+，故②正确，ADE ∴V 的周长AD AE DE AD AE DB EC AB AC ++=+++=+．故③正确，BD CE ，不一定相等，故④错误，故选：C ．18．D【分析】本题考查复杂作图，等腰三角形的判定和性质等知识，证明36A ABH ∠=∠=︒，72C BHC ∠=∠=︒，推出BC BH AH ==即可．【详解】解：∵AB AC =，∴ABC C ∠=∠，∵2C A ∠=∠，∴2ABC C A ∠=∠=∠，∵180A ABC C ∠+∠+∠=︒，∴22180A A A ∠+∠+∠=︒，∴36A ∠=︒，由作图可知，36ABH A ∠=∠=︒∴,AH BH =72ABC C ∠=∠=︒∴723636CBH ∠=︒-︒=︒，∴180367272CHB ∠=︒-︒-︒=︒∴C CHB ∠=∠，∴6BC BH AH ===．故选：D ．19．A【分析】根据等边ACD 可得AC CD =，再根据60ABC ∠=︒可以得出CAB DCE ∠=∠，过点C 作CP AB ⊥于点P ，进而证明全等三角形，将线段AB 一分为二，分别求出两段的长度，进而求出BC 的长度．【详解】解： 等边ACD ，AC CD ∴=，60ACD ∠=︒．120ACB DCE ∴∠+∠=︒．60ABC ∠=︒ ，120CAB ACB ∴∠+∠=︒．CAB DCE ∴∠=∠．过点C 作CP AB ⊥于点P，90APC ∴∠=︒．DE BC ⊥ ，90DEC ∴∠=︒．在DCE △和CAP 中，DEC CPA CAP DCE DC CA ∠=∠⎧⎪∠=∠⎨⎪=⎩(AAS)DCE CAP ∴△≌△．3CE AP ∴==．5AB = ，2BP ∴=．在Rt BPC △中，=60B ∠︒，∴9030BCP B ∠=︒-∠=︒，24BC BP ∴==．故选：A ．【点睛】本题考查的是等边三角形的性质，全等三角形的判定与性质，含30°的直角三角形的性质，利用已知条件构造全等三角形，灵活运用含有30°的直角三角形的性质求解，是解决本题的关键．20．D【分析】连接AD ，BD ，根据等角对等边可得BA BC =，再利用三角形的外角性质可得60CBE ∠=︒，然后根据题意可得：BC BD =，AD AC =，从而可得AE 是CD 的垂直平分线，进而可得90AEC ∠=︒，再利用直角三角形的两个锐角互余可得60ACE ∠=︒，30BCE ∠=︒，从而在Rt BCE 中，利用含30度角的直角三角形的性质可得2BC BE =，进而利用三角形的面积公式，进行计算可得ABC S BE CE =⋅△，最后再根据等边三角形的判定可得ACD 是等边三角形，从而可得AC CD =，即可解答．【详解】解：连接AD ，BD ，30CAB ACB ∠=∠=︒ ，BA BC ∴=，CBE ∠ 是ABC V 的一个外角，60CBE CAB ACB ∴∠=∠+∠=︒，由题意得：BC BD =，AD AC =，AE ∴是CD 的垂直平分线，90AEC ∴∠=︒，9060ACE CAB ∴∠=︒-∠=︒，9030BCE CBE ∠=︒-∠=︒，2BC BE ∴=，12ABC S AB CE ∴=⋅ 12BC CE =⋅122BE CE =⨯⋅BE CE =⋅，AC AD = ，60ACE ∠=︒，ACD ∴是等边三角形，AC CD ∴=，所以，上列结论，其中正确的是①②③④，故选：D ．【点睛】本题考查了含30度角的直角三角形，线段垂直平分线的性质，等腰三角形的判定，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．21．D【分析】先根据30︒角的直角三角形的性质得到12AB AC =，证明()SAS ABE ADE △≌△，再根据全等三角形的判定和性质定理即可得到结论．【详解】解：∵90ABC ∠=︒，60BAC ∠=︒，∴90906030C BAC Ð=°-Ð=°-°=°，∴12AB AC =，由题意得：AB AD =，AP 平分BAC ∠，∴BAE DAE ∠=∠，在ABE 与ADE V 中，AB AD BAE DAE AE AE =⎧⎪∠=∠⎨⎪=⎩，∴()SAS ABE ADE △≌△，∴ABE ADE S S =△△，∵12AD AB AC ==，∴AD CD =，∴ADE CDE S S = ，∴3ABC CDE S S =△△，∴:1:3CDE ABC S S =△△．故选：D ．【点睛】本题考查作图—基本作图，直角三角形两锐角互余，30︒角的直角三角形，全等三角形的判定和性质，角平分线的定义，等底同高的三角形面积相等．掌握基本作图及全等三角形的判定和性质是解题的关键．22．B【分析】本题考查了尺规作图，含30︒的直角三角形的性质，等腰三角形的判定等知识，由作图知AD 平分BAD ∠，则可求30CAD DAB ∠=∠=︒，利用含30︒的直角三角形的性质得出12CD AD =，利用等角对等边得出AD BD =，进而得出12CD BD =，然后利用面积公式即可求解．【详解】解：∵90,30C B ∠=︒∠=︒，∴60CAB ∠=︒，由作图知：AD 平分BAD ∠，∴30CAD DAB ∠=∠=︒，∴12CD AD =，B BAD ∠=∠，∴AD BD =，∴12CD BD =，∴112122ACD ABD CD AC S CD S BD BD AC ⋅===⋅ ，又ACD 的面积为8，∴ABD △的面积是2816⨯=，故选B ．23．C【分析】如图作D 关于直线AC 的对称点M ，作D 关于直线BC 的对称点N ，连接CM ，CN ，B ，EN ，FM ，DN ，DM ．由MCA DCA ∠∠=，BCN BCD ∠∠=，90ACD BCD ∠∠+=︒，推出180MCD NCD ∠∠+=︒，可得M 、B 、N 共线，由DF DE EF FM EN EF ++=++，FM EN EF MN ++≥，可知当M 、F 、E 、N 共线时，且CD AB ⊥时，DE EF FD ++的值最小，最小值2CD =，求出B 的值即可解决问题．【详解】解：如图，作D 关于直线AC 的对称点M ，作D 关于直线BC 的对称点N ，连接CM ，CN ，B ，EN ，FM ，DN ，DM．∴DF FM =，DE EN =，CD CM =，CD CN =，∴CD CM CN ==，∵MCA DCA ∠∠=，BCN BCD ∠∠=，90ACD BCD ∠∠+=︒，∴180MCD NCD ∠∠+=︒，∴M 、C 、N 共线，∵DF DE EF FM EN EF ++=++，∵FM EN EF MN ++≥，∴当M 、F 、E 、N 共线时，且CD AB ⊥时，DE EF FD ++的值最小，最小值为2MN CD =，∵CD AB ⊥，∴1··2AB CD =1··2BC AC ，∴CD =·BC AC AB =1252.4=，∴DE EF FD ++的最小值为4.8．故选：C ．【点睛】本题考查了轴对称-最短问题、两点之间线段最短、垂线段最短等知识，解题的关键是灵活运用轴对称以及垂线段最短解决最短问题，属于中考选择题中的压轴题．24．B【分析】本题考查轴对称图形的性质．延长A 到点G 使得BG AB =，延长AE 到点F 使得EF AE =，连接GF 交BC 、D 于点1P 、1Q ，则这时APQ △的周长最小，根据无变形的内角和求出BAE ∠的度数，根据轴对称的性质得到1P AG G ∠=∠，1Q AF F ∠=∠，然后计算解题即可．【详解】解：延长A 到点G 使得BG AB =，延长AE 到点F 使得EF AE =，∵AB BC AE DE ⊥⊥，，∴BC 、D 垂直平分AG 、AF ，连接GF 交BC 、D 于点1P 、1Q ，则11PG P A =，11Q F Q A =，∴11111111FG PG PQ Q F P A PQ Q A=++=++，这时APQ △的周长最小，∵AB BC AE DE ⊥⊥，，∴90ABC AED ∠=∠=︒，又∵230BCD CDE ∠+∠=︒，∴()5405409090230130BAE ABC AED BCD CDE ∠=︒-∠-∠-∠+∠=︒-︒-︒-︒=︒，∴180********G F BAE ∠+∠=︒-∠=︒-︒=︒，又∵11PG P A =，11Q F Q A =，∴1P AG G ∠=∠，1Q AF F ∠=∠，∴11111305080P AQ BAE P AG Q AF BAE G F ∠∠∠=∠--=∠-∠-∠=︒-︒=︒，故选：B ．25．直角梯形【分析】此题主要考查了轴对称图形，关键是掌握如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴；根据轴对称图形概念进行分析即可；【详解】解：线段、角、圆、等腰三角形和正方形都能找到一条(或多条)直线，使图形沿一条直线折叠直线两旁的部分能够互相重合，所以是轴对称图形；直角梯形不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；所以不是轴对称图形的是直角梯形，故答案为：直角梯形．26．(1,2)-【分析】根据题意建立平面直角坐标系，再根据轴对称图形的定义确定第4枚方形的位置，即可解答．此题主要考查了轴对称图形的性质以及点的坐标，正确得出原点位置是解题关键．【详解】解：如图：符合题意的点为(1,2)-．故答案为：(1,2)-．27．36【分析】本题考查轴对称的性质，三角形内角和定理，三角形的外角的性质等知识，证明2APF AFP A ∠∠∠==，利用三角形内角和定理构建方程求解即可．【详解】解：APT 与CPT △关于直线PT 对称，A C TA TC APT CPT ∠∠∠∠∴===，，，A APT ∠∠= ，A C APT CPT ∠∠∠∠∴===，FTC C ∠∠= ，22AFP C FTC C A ∠∠∠∠∠∴=+==，180A APF AFP ∠∠∠++=︒ ，5180A ∴∠=︒，36A ∴∠=︒，故答案为：36．28．1902m ︒-︒【分析】此题考查了角平分线的性质定理，全等三角形的性质和判定，轴对称性质等知识，过点O 作OH BC ⊥，OI AB ⊥，OJ B N '⊥，OK AC ⊥，OG B M '⊥，根据角平分线的性质定理得到OG OK =，然后证明出()Rt Rt HL GOF KOF ≌，得到GOF KOF ∠=∠，KOE JOE ∠=∠，然后求出12EOF GOJ ∠=∠，然后根据对称的性质得到A m B BC ∠=︒'∠=，进而求解即可．【详解】如图所示，过点O 作OH BC ⊥，OI AB ⊥，OJ B N '⊥，OK AC ⊥，OG B M '⊥∵点O 为CAB ∠和ABC ∠的角平分线交点，∴OH OI OK==∵点B 关于直线l 的对称点为B '，∴OM 平分B MB '∠，ON 平分B NB'∠∴OH OG =，OI OJ=∴OG OK=∵90OGF OKF ∠=∠=︒，OF OF=∴()Rt Rt HL GOF KOF ≌∴GOF KOF∠=∠同理可得，KOE JOE∠=∠∴111222EOF KOF KOE GOK JOK GOJ ∠=∠+∠=∠+∠=∠∵点B 关于直线l 的对称点为B '，∴A m B BC ∠=︒'∠=∵9090180B GO B JO ''∠+∠=︒+︒=︒∴180180GOJ B m '∠=︒-∠=︒-︒∴()11118090222EOF GOJ m m ∠=∠=︒-︒=︒-︒．故答案为：1902m ︒-︒．29．70【分析】本题主要考查了折叠的性质，平行线的性质以及三角形内角和定理．先根据已知条件求出ACB ∠的度数，然后根据折叠可知：∠AED ＝∠A ′ED ＝45°，再利用平行线的性质求出EFD ∠，最后利用三角形内角和求出1∠即可．【详解】解：由折叠可知：AED A ED ∠=∠'，∵2565A B ∠=︒∠=︒，，∴A B ∠∠=︒+90，∴90ACB ∠=︒，∵EA BC '∥，∴90AEA ACB ∠'=∠=︒，∴45AED A ED ∠=∠'=︒，∵'EA BC ∥，65B ∠=︒，∴65EFD B ∠=∠=︒，∵1180EFD A ED ∠+∠+∠'=︒，∴1180654570∠=︒-︒-︒=︒．故答案为：70．30．41︒/41度【分析】本题考查了折叠的性质，由长方形和折叠的性质结合题意可求出49EAB FAD ''∠+∠=︒．再根据EAF EAB FAD B AD ''''∠=∠+∠-∠，即可求出答案．掌握折叠的性质是解题的关键．【详解】解：由长方形的性质可知：90BAE EAD B AD B AF DAF ''''∠+∠+∠+∠+∠=︒，。

轴对称与等腰三角形知识点1、等腰三角形1、等腰三角形的定义：有两边相等的三角形叫做等腰三角形。

相等的两边叫做等腰三角形的腰，另一边叫做底边；两腰的夹角叫做顶角，腰和底边的夹角叫做底角。

注意：①等腰三角形的顶角不一定是锐角，但是底角一定是锐角；②钝角三角形也可以是等腰三角形2、等腰三角形的性质①等边对等角：等腰三角形的两底角相等；②三线合一：等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合；③等腰三角形两腰上的高、中线分别相等，两底角的平分线相等；④等腰三角形是轴对称图形，对称轴为顶角角平分线（三线合一）所在直线。

注意：①等腰三角形的性质是指在同一个等腰三角形而言的；②三线合一要注意位置，在等腰三角形中所有的中线、角平分线等并不是合一的。

3、等腰三角形的判定①有两个角相等的三角形是等腰三角形。

（等角对等边）②三线合一也能作为判定等腰三角形的依据③推论在直角三角形中，30°所对的直角边是斜边的一半1-9、如图，已知在等腰三角形ABC 中，AC AB =，BC AE //．求证：AE 平分∠DAC ．例2、等腰三角形的判定2-1、如图，OC 平分∠AOB ，OB CD //，若cm OD 3=，则CD 等于.2-2、已知：如图，在△ABC 中，∠ACB =90°，CD 是AB 上的高，AE 分别交CB 、CD 于E 、F ，且CF CE =，求证：AE 平分∠BAC .2-3、如图，△ABC 中，∠ACB =90º,CD ⊥BA 于D ，AE 平分∠BAC 交CD 于F ，交BC 于E ，求证△CEF 是等腰三角形。

DC AB 02-5、如图，在△ABC中，AB知识点2、等边三角形1、等边三角形的定义三边相等的三角形叫做等边三角形，也叫正三角形2、等边三角形性质：①每个角都是60°；②轴对称图形；③有3条对称轴。

3、等边三角形的判定定理①三边相等的三角形是等边三角形；②三个角都相等的三角形是等边三角形；③有一个角是60°的等腰三角形是等边三角形。

精品文档【知识点回顾】：一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就轴对称说这两个图形关于这条直线对称。

这条直线叫作对称轴，两个图形中的对应点叫做对称点。

、关于轴对称的图形全等。

轴对称的性质：1 那么对称轴是对称点连线的垂直平分线。

2、如果两个图形成轴对称，：线段的垂直平分线上的点到线段两端的距离相等线段垂直平分线的性质在这条线段的垂直平分线上。

线段垂直平分线的判定：到线段两端距离相等的点，等腰三角形的性质定理：等腰三角形有两边相等；。

定理：等腰三角形的两个底角相等（简写成“等边对等角”）：等腰三角形顶角的平分线平分底边并且垂直于底边，这就是说，等推论1 腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。

等腰三角形60°。

推论2：等边三角形的各角都相等，并且每一个角都等于是以底边的垂直平分线为对称轴的轴对称图形；等腰三角形的判定（简写如果一个三角形有两个角相等，那么这两个角所对的边也相等定理：）成“等角对等边”。

：三个角都相等的三角形是等边三角形。

推论160°的等腰三角形是等边三角形。

推论2：有一个角等于°，那么它所对的直角边等：在直角三角形中，如果一个锐角等于30推论3 于斜边的一半【典型例题】 100?，?AAB?AC平分。

，例1. 如图，中，BDABC?ABC?求证：。

CD?BAD?B A D 1 2 B FE C，上截取，只需证明分析：从要证明的结论出发，在BCAD?CFDBBF?，，易得，则有考虑到，想到在BC上截取，连结DEFDAD?1??2?ABE?B 只需证明，这就要从条件出发，通过角度计算可以得出。

CFDE?DE?CF?DFDF ，连结上截取DE、BC 证明：在DBE?BA，BBF?中，和在D?BDB2??BABE，1??，DEBD?AB?)SAS???ABD?EBD( 80??DEAD??，BED???100A?DEF?精品文档．精品文档 又100?AC，?A AB?1 40)100??C?(180????ABC21 20?40?????1?2 2 而F?BBD1180)?2)?(?180?(18020????BFD??BDF22 DFDE80????DEF??DFE? 40?，???DFE?80C40C?80??40??FDC??DFE??FC?DE?DFDF?FC?AD?C??FDC???AD?FC?BD?BC?B F?即CD?BAD?B 【随堂作业】）（1、下列图形中，不是轴对称图形的是°直角三角形有一个内角是45 B. A．有两个内角相等的三角形°的三角形°和120°的直角三角形D. 有两个角分别是30C. 有一个内角是30 ）（2、下列说法中正确的是角平分线上任意一点到角的两边的线段长相等①③线段不是轴对称图形②角是轴对称图形线段垂直平分线上的点到这条线段两个端点的距离相等④D.②③④①②③ C.②④ A.①②③④ B.3、小明从镜子里看到镜子对面电子钟的像如图所示）（实际时间是01D. 12：51 C. 10：A．21：10 B. 10：21 )( 4、下列推理中，错误的是 ABC是等边三角形C ，∴△BA．∵∠A＝∠＝∠是等边三角形，∴△ABC＝∠ B．∵AB＝AC，且∠BC 是等边三角形＝60°，∴△ABC C．∵∠A＝60°，∠B 是等边三角形60°，∴△ABC．∵AB＝AC，∠B＝ D) ( 5、等腰三角形两边的长分别为2cm和5cm，则这个三角形的周长是12cm 9cm B． A． 12cm之间12cm D．在9cm与 C．9cm和________ .°，则它的底角为、若等腰三角形的一个外角为6130 BC90?，BD?CBD?是等边三角形，则的度数是________ 如图，，7、ABC?1?CA 1 2 3 DB精品文档．精品文档上一个动点，中，，点是底边8、如图，在等腰三角形，则的最小值为2 分别是的周长的中点，若是（）D．C．．B．A，若于EDE∥BC交AC9、在等边三角形ABC中，CD是∠ACB的平分线，过D作)的周长为 ( 的边长为a，则△ADEABC △4a．5a DC．1． A．2a B．a 3在如图，点，，为的中点，中，10、）等于（ C 于点，则．C ．AD． B ．BC 在AC的垂直平分线，EABC△中，B为直角，DE是11、如图7—111，在Rt_________.＝5，则∠CBAE：∠BAC＝1：上，∠于交ACM作ME∥BA112—，∠BAC＝30°，AM是∠BAC的平分线，过12、如图7_________. ＝，则MD，ME＝10cm E，作MD⊥BA，垂足为DE、D为BC中点，120，等腰直角三角形ABC中，∠A＝90°，13、已知：如图7—．DE．求证：＝DF、AC上的点，且满足EA＝CFAB F分别为，且AE=BEBE是高，它们交于点H，AD、14已知：如图△ABC中，AB=AC，和．求证：AH=2BD AE HCD精品文档B．精品文档【课后作业】A，P，AD与BE相交于点1、如图：等边三角形ABC 中，BD＝CE 则E P）（∠APE的度数是CB DB ．55°A．45°75° D ．60°C．5cm，一腰上的中线把其周长分为两2、等腰三角形底边长为），则腰长为（部分的差为3cm 以上都不对8cm D. A. 2cm B. 8cm C. 2cm或ACB 与∠CE分别为∠ABC＝AC，∠A36°，BD、3、如图，△ABC中，AB＝）的角平分线，且相交于点F，则图中的等腰三角形有（ D. 9个 C.8个 A. 6个 B. 7个A °36 DE F C B_______度。