山东省滕州市第二中学2017-2018学年高三10月月考数学(理)试题 Word版含答案

滕州市第二中学2018-2019学年上学期高三数学10月月考试题 班级__________ 座号_____ 姓名__________ 分数__________一、选择题1． 设,,a b c 分别是ABC ∆中，,,A B C ∠∠∠所对边的边长，则直线sin 0A x ay c ++=与sin sin 0bx B y C -+=的位置关系是（ ）A ．平行B ． 重合C ． 垂直D ．相交但不垂直2． 复数z=（其中i 是虚数单位），则z 的共轭复数=（ ）A ．﹣iB ．﹣﹣iC ． +iD ．﹣ +i3． 在定义域内既是奇函数又是减函数的是（ ）A ．y=B ．y=﹣x+C ．y=﹣x|x|D ．y=4． 四棱锥的八条棱代表8种不同的化工产品，由公共点的两条棱代表的化工产品放在同一仓库是危险的，没有公共点的两条棱代表的化工产品放在同一仓库是安全的，现打算用编号为①、②、③、④的4个仓库存放这8种化工产品，那么安全存放的不同方法种数为（ ）A ．96B ．48C ．24D ．05． 实数x ，y 满足不等式组，则下列点中不能使u=2x+y 取得最大值的是（ ）A ．（1，1）B ．（0，3）C ．（，2）D ．（，0）6． sin 3sin1.5cos8.5，，的大小关系为（ ） A ．sin1.5sin 3cos8.5<< B ．cos8.5sin 3sin1.5<< C.sin1.5cos8.5sin 3<<D ．cos8.5sin1.5sin 3<<7． 函数f （x ）=sin ωx+acos ωx （a ＞0，ω＞0）在x=处取最小值﹣2，则ω的一个可能取值是（ ）A ．2B ．3C ．7D ．98． 已知f （x ），g （x ）都是R 上的奇函数，f （x ）＞0的解集为（a 2，b ），g （x ）＞0的解集为（，），且a 2＜，则f （x ）g （x ）＞0的解集为（ ）A ．（﹣，﹣a 2）∪（a 2，）B ．（﹣，a 2）∪（﹣a 2，）C ．（﹣，﹣a 2）∪（a 2，b ）D ．（﹣b ，﹣a 2）∪（a 2，）9． 命题“∀a ∈R ，函数y=π”是增函数的否定是（ ）A ．“∀a ∈R ，函数y=π”是减函数B ．“∀a ∈R ，函数y=π”不是增函数C ．“∃a ∈R ，函数y=π”不是增函数D ．“∃a ∈R ，函数y=π”是减函数10．某校新校区建设在市二环路主干道旁，因安全需要，挖掘建设了一条人行地下通道，地下通道设计三视图中的主（正）视力（其中上部分曲线近似为抛物）和侧（左）视图如图（单位：m ），则该工程需挖掘的总土方数为（ ）A ．560m 3B ．540m 3C ．520m 3D ．500m 311．已知a ＞b ＞0，那么下列不等式成立的是（ ）A ．﹣a ＞﹣bB ．a+c ＜b+cC ．（﹣a ）2＞（﹣b ）2D ．12．已知向量(1,2)a =，(1,0)b =，(3,4)c =，若λ为实数，()//a b c λ+，则λ=（ ） A ．14 B ．12C ．1D ．2 二、填空题13．不等式()2110ax a x +++≥恒成立，则实数的值是__________.14．已知f （x ），g （x ）都是定义在R 上的函数，g （x ）≠0，f ′（x ）g （x ）＞f （x ）g ′（x ），且f （x ）=a x g（x ）（a ＞0且a ≠1），+=．若数列{}的前n 项和大于62，则n 的最小值______.16．如图，函数f （x ）的图象为折线 AC B ，则不等式f （x ）≥log 2（x+1）的解集是 ．17．【南通中学2018届高三10月月考】定义在上的函数满足，为的导函数，且对恒成立，则的取值范围是__________________.三、解答题18．【盐城中学2018届高三上第一次阶段性考试】已知函数f （x ）=（2﹣a ）（x ﹣1）﹣2lnx ，g （x ）=1x xe -．（a ∈R ，e 为自然对数的底数）（Ⅰ）当a=1时，求f （x ）的单调区间； （Ⅱ）若函数f （x ）在10,2⎛⎫⎪⎝⎭上无零点，求a 的最小值； （Ⅲ）若对任意给定的x 0∈（0，e]，在（0，e]上总存在两个不同的x i （i=1，2），使得f （x i ）=g （x 0）成立，求a 的取值范围．19．（本小题满分12分）某超市销售一种蔬菜，根据以往情况，得到每天销售量的频率分布直方图如下：（Ⅰ）求频率分布直方图中的a 的值，并估计每天销售量的中位数；（Ⅱ）这种蔬菜每天进货当天必须销售，否则只能作为垃圾处理．每售出1千克蔬菜获利4元，未售出的蔬菜，每千克亏损2元．假设同一组中的每个数据可用该组区间的中点值代替，估计当超市每天的进货量为75千克时获利的平均值．0.0050.02频率组距O千克20．（本小题满分12分）某校为了解高一新生对文理科的选择，对1 000名高一新生发放文理科选择调查表，统计知，有600名学生选择理科，400名学生选择文科．分别从选择理科和文科的学生随机各抽取20名学生的数学成绩得如下累计表：（1率分布直方图．（2）根据你绘制的频率分布直方图，估计意向选择理科的学生的数学成绩的中位数与平均分．21．（本小题满分10分）选修4-4：坐标系与参数方程 已知椭圆C 的极坐标方程为222123cos 4sin ρθθ=+，点12,F F为其左、右焦点，直线的参数方程为222x t y ⎧=+⎪⎪⎨⎪=⎪⎩（为参数，t R ∈）. （1）求直线和曲线C 的普通方程；（2）求点12,F F 到直线的距离之和.22．（本小题满分10分）选修4-5：不等式选讲 已知函数()|21|f x x =-．（1）若不等式1()21(0)2f x m m +≤+>的解集为(][),22,-∞-+∞，求实数m 的值；（2）若不等式()2|23|2yy af x x ≤+++，对任意的实数,x y R ∈恒成立，求实数a 的最小值． 【命题意图】本题主要考查绝对值不等式的解法、三角不等式、基本不等式等基础知识，以及考查等价转化的能力、逻辑思维能力、运算能力．23．已知椭圆C：+=1（a＞b＞0）的左，右焦点分别为F1，F2，该椭圆的离心率为，以原点为圆心，椭圆的短半轴长为半径的圆与直线y=x+相切．（Ⅰ）求椭圆C的方程；（Ⅱ）如图，若斜率为k（k≠0）的直线l与x轴，椭圆C顺次交于P，Q，R（P点在椭圆左顶点的左侧）且∠RF1F2=∠PF1Q，求证：直线l过定点，并求出斜率k的取值范围．滕州市第二中学2018-2019学年上学期高三数学10月月考试题（参考答案）一、选择题1． 【答案】C 【解析】试题分析：由直线sin 0A x ay c ++=与sin sin 0bx B y C -+=，则sin (sin )2sin sin 2sin sin 0A b a B R A B R A B ⋅+⋅-=-=，所以两直线是垂直的，故选C. 1 考点：两条直线的位置关系. 2． 【答案】C【解析】解：∵z==，∴=．故选：C ．【点评】本题考查了复数代数形式的乘除运算，是基础题．3． 【答案】C 【解析】解：A.在定义域内没有单调性，∴该选项错误；B.时，y=，x=1时，y=0；∴该函数在定义域内不是减函数，∴该选项错误；C ．y=﹣x|x|的定义域为R ，且﹣（﹣x ）|﹣x|=x|x|=﹣（﹣x|x|）； ∴该函数为奇函数；；∴该函数在[0，+∞），（﹣∞，0）上都是减函数，且﹣02=02；∴该函数在定义域R 上为减函数，∴该选项正确；D.；∵﹣0+1＞﹣0﹣1；∴该函数在定义域R 上不是减函数，∴该选项错误． 故选：C ．【点评】考查反比例函数的单调性，奇函数的定义及判断方法，减函数的定义，以及分段函数单调性的判断，二次函数的单调性．4． 【答案】B【解析】排列、组合的实际应用；空间中直线与直线之间的位置关系．【专题】计算题；压轴题．【分析】首先分析题目已知由公共点的两条棱代表的化工产品放在同一仓库是危险的，没有公共点的两条棱代表的化工产品放在同一仓库是安全的，现打算用编号为①、②、③、④的4个仓库存放这8种化工产品，求安全存放的不同方法的种数．首先需要把四棱锥个顶点设出来，然后分析到四棱锥没有公共点的8条棱分4组，只有2种情况．然后求出即可得到答案．【解答】解：8种化工产品分4组，设四棱锥的顶点是P，底面四边形的个顶点为A、B、C、D．分析得到四棱锥没有公共点的8条棱分4组，只有2种情况，（PA、DC；PB、AD；PC、AB；PD、BC）或（PA、BC；PD、AB；PC、AD；PB、DC）那么安全存放的不同方法种数为2A44=48．故选B．【点评】此题主要考查排列组合在实际中的应用，其中涉及到空间直线与直线之间的位置关系的判断，把空间几何与概率问题联系在一起有一定的综合性且非常新颖．5．【答案】D【解析】解：由题意作出其平面区域，将u=2x+y化为y=﹣2x+u，u相当于直线y=﹣2x+u的纵截距，故由图象可知，使u=2x+y取得最大值的点在直线y=3﹣2x上且在阴影区域内，故（1，1），（0，3），（，2）成立，而点（，0）在直线y=3﹣2x上但不在阴影区域内，故不成立；故选D．【点评】本题考查了简单线性规划，作图要细致认真，注意点在阴影区域内；属于中档题．6． 【答案】B 【解析】试题分析：由于()cos8.5cos 8.52π=-，因为8.522πππ<-<，所以cos8.50<，又()sin3sin 3sin1.5π=-<，∴cos8.5sin 3sin1.5<<． 考点：实数的大小比较. 7． 【答案】C【解析】解：∵函数f（x）=sinωx+acosωx（a＞0，ω＞0）在x=处取最小值﹣2，∴sin+acos=﹣=﹣2，∴a=，∴f（x）=sinωx+cosωx=2sin（ωx+）．再根据f（）=2sin（+）=﹣2，可得+=2kπ+，k∈Z，∴ω=12k+7，∴k=0时，ω=7，则ω的可能值为7，故选：C．【点评】本题主要考查三角恒等变换，正弦函数的图象的对称性，属于基础题．8．【答案】A【解析】解：∵f（x），g（x）都是R上的奇函数，f（x）＞0的解集为（a2，b），g（x）＞0的解集为（，），且a2＜，∴f（x）＜0的解集为（﹣b，﹣a2），g（x）＜0的解集为（﹣，﹣），则不等式f（x）g（x）＞0等价为或，即a2＜x＜或﹣＜x＜﹣a2，故不等式的解集为（﹣，﹣a2）∪（a2，），故选：A．【点评】本题主要考查不等式的求解，根据函数奇偶性的对称性的性质求出f（x）＜0和g（x）＜0的解集是解决本题的关键．9．【答案】C【解析】解：因为全称命题的否定是特称命题，所以，命题“∀a∈R，函数y=π”是增函数的否定是：“∃a∈R，函数y=π”不是增函数．故选：C．【点评】本题考查命题的否定，特称命题与全称命题的否定关系，是基础题．10．【答案】A【解析】解：以顶部抛物线顶点为坐标原点，抛物线的对称轴为y轴建立直角坐标系，易得抛物线过点（3，﹣1），其方程为y=﹣，那么正（主）视图上部分抛物线与矩形围成的部分面积S1==2=4，下部分矩形面积S 2=24，故挖掘的总土方数为V=（S 1+S 2）h=28×20=560m 3．故选：A ．【点评】本题是对抛物线方程在实际生活中应用的考查，考查学生的计算能力，属于中档题．11．【答案】C【解析】解：∵a ＞b ＞0，∴﹣a ＜﹣b ＜0，∴（﹣a ）2＞（﹣b ）2，故选C ．【点评】本题主要考查不等式的基本性质的应用，属于基础题．12．【答案】B【解析】试题分析：因为(1,2)a =，(1,0)b =，所以()()1,2a b λλ+=+，又因为()//a b c λ+，所以()14160,2λλ+-==，故选B. 考点：1、向量的坐标运算；2、向量平行的性质.二、填空题13．【答案】1a = 【解析】试题分析：因为不等式()2110ax a x +++≥恒成立，所以当0a =时，不等式可化为10x +≥，不符合题意；当0a ≠时，应满足2(1)40a a a >⎧⎨∆=+-≤⎩，即20(1)0a a >⎧⎨-≤⎩，解得1a =.1考点：不等式的恒成立问题.14．【答案】 1 ．【解析】解：∵x 为实数，[x]表示不超过x 的最大整数， ∴如图，当x ∈[0，1）时，画出函数f （x ）=x ﹣[x]的图象，再左右扩展知f （x ）为周期函数． 结合图象得到函数f （x ）=x ﹣[x]的最小正周期是1．故答案为：1．【点评】本题考查函数的最小正周期的求法，是基础题，解题时要认真审题，注意数形结合思想的合理运用．15．【答案】{7，9}【解析】∵全集U={n∈N|1≤n≤10}，A={1，2，3，5，8}，B={1，3，5，7，9}，∴（∁U A）={4，6，7，9 }，∴（∁U A）∩B={7，9}，故答案为：{7，9}。

2015山东省滕州市第二中学第一学期高三期中考试数学（理）试题 第Ⅰ卷 （选择题 共50分）一、选择题：本大题共10个小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．在答题卷上的相应题目的答题区域作答．1． （2015•洛阳一模）集合 A={1，2，3，4，5}，B={1，2，3}C={z|z=xy ，x ∈A 且y ∈B}，则集合C 中的元素个数为（ ）A ．3,B ．11,C ．8,D ．12 2．（2014•温州模拟）直线x −y −1＝0的倾斜角α=（ ）A ．30°, B．60°, C．120°, D．150° 3．（2014•通州区二模）直线x=t （t ＞0）与函数f （x ）=x 2+1，g （x ）=lnx 的图象分别交于A 、B 两点，当|AB|最小时，t 值是（ ）A ．1B ．C ．D ．4．已知()()1,41,42x f x x f x x ⎧+<⎪=⎨⎛⎫≥⎪ ⎪⎝⎭⎩，则＝（ ）A ．B ．C ．D ．5．若方程在区间，，且上有一实根，则的值为（ ）A ．B ．C ．D ．6．函数),2||.0,0()sin(R x A B x A y ∈<>>++=πϕωϕω的部分图象如图所示，则函数表达式为（ ）A ．1)63sin(2+-=ππx y B ．1)36sin(2+-=ππx yC ．1)63sin(2++=ππx yD ．1)66sin(2++=ππx y7．用数学归纳法证明“)12(212)()2)(1(-⋅⋅⋅⋅=+++n n n n n n ”时，从“到”时，左边应添乘的式子是（ ）A ．B ．C ．D ．8．若正数，满足，且对任意，恒成立，则的取值范围是（ ）A ．，B ．，C ．，D ．，9．已知定义在上的函数满足：对任意，都有成立，且，设1(0),(),(3)2a fb fc f ===，则三者的大小关系是（ ）A ．B ．C ．D ．10．对于函数与和区间，如果存在，使，则称是函数与在区间上的“友好点”．现给出组函数： ①，； ②，；③，；④，；其中在区间，上存在“友好点”的有（ ） A ．①② B ．②③C．①④D ．③④第Ⅱ卷 （非选择题 共100分）二、填空题：本大题分必做题和选做题．（一）必做题：共4小题，每小题4分，满分16分．11．函数5123223+--=x x x y 在上的最小值分别是 ．12．若实数，满足220,4,5.x y x y +-≥⎧⎪≤⎨⎪≤⎩则的最大值为 ．13．在等差数列中，已知，则该数列前项和 ．14．已知函数的导函数为，与在同一直角坐标系下的部分图象如图所示，若方程在上有两解，则实数的取值范围是 ．（二）选做题：本题设有三个选考题，请考生任选2题作答，并在答题卡的相应位置填写答案，如果多做，则按所做的前两题计分，满分8分．15．（1）（选修4-2：矩阵与变换）设矩阵A ＝，B ＝，则＝ ．（2）（选修4-4：极坐标与参数方程）在平面直角坐标系中，以坐标原点为极点，轴的非负半轴为极轴建立极坐标系．已知直线的极坐标方程为，曲线的参数方程为（为参数）．若直线与曲线交于两点，则= ．（3）（选修4-5：不等式选讲）函数的最大值等于 ．三、解答题：本大题共6小题，共76分．解答应写出必要文字说明、证明过程或演算步骤．16．（本小题满分12分） 已知函数2()lg(23)f x x x =--的定义域为集合，函数的值域为集合 （1）求集合，；（2）若，求实数的取值范围．17．（本小题满分12分）在中，角、、所对的边分别是、、，则； （1）求；（2）若，，求的面积．18．（本小题满分12分）数列的前项和为，数列是首项为，公差为的等差数列，且，，成等比数列． （1）求数列与的通项公式；（2）若*2())(1)n nc n N n b =∈+，求数列的前项和．19．（本小题满分12分）已知向量33(cos ,sin ),(cos(),sin())444343x x x x a b ππ==+-+；令 （1）求解析式及单调递增区间；（2）若，求函数的最大值和最小值；（3）若=，求的值．20．（本小题满分12分）如图，某小区有一边长为（单位：百米）的正方形地块， 其中是一个游泳池，计划在地块内修一条与池边相切的直路（宽度不计），切点为，并把该地块分为两部分．现以点为坐标原点，以线段所在直线为轴，建立平面直角坐标系，若池边满足函数22(0y x x =-+≤≤的图象，且点到边距离为． （1）当时，求直路所在的直线方程；（2）当为何值时，地块在直路不含泳池那侧的面积取到最大，最大值是多少？21．（本小题满分14分）已知函数2()ln(1)f x a x ax x =+--． （1）若为函数的极值点，求的值； （2）讨论在定义域上的单调性；（3）证明：对任意正整数，222134232)1ln(nn n +++++<+ ． 2015山东省滕州市第二中学第一学期高三期中考试数学（理）试题参考答案一、选择题：（共10小题，每小题5分，满分50分） BCBAC ABDCD二、填空题：（共5小题，每小题４分，满分24分） 11．； 12．； 13．； 14． 15．（1） （2） （3）14．（解法一）设/2()()()2()x a g x f x f a e x e a =-=---令>0，则，所以在单调递增，在单调递减要使满足题意，则2220(1)()0(ln 2)022ln 20(2)ln 2ln 2(3)a a a e a e a g a g e a a a ⎧--+≥---≥⎧⎪⎪<⇒--+<--⎨⎨⎪⎪<<---------⎩⎩由（1），（3）可知设2()22ln 2a h a e a =--+，/()20a h a e a =-+<在恒成立 所以2()22ln 2a h a e a =--+在上单调递减，所以2()(2)62ln 20h a h e ≤=--< 所以（2）对任意的都成立 综上所述．（解法二）在上有两解函数/12()()y f x y f a ==与有两交点/1(),(,]y f x x a =∈-∞---表示右端点位置变化的函数--------表示与x 轴平行的一组直线，它的高低与的值有关 所以一定在/1(),(,]y f x x a =∈-∞的极值点右侧，同时三、解答题：本大题共6小题，共76分．解答应写出必要文字说明、证明过程或演算步骤．16．（本题满分12分） 解：（1）集合：， 解得：或集合B ：图象单调递增，，则{|4}B y a y a =-<≤- ．8分（2），由，结合数轴，或，解得或． 13分 17．（本题满分12分）解：由已知：（1），41)46(212s i n 21c os 22=⨯-=-=∴C C 又，415)41(1cos 1sin 22=-=-=∴C C ． ．． (5)（2），由正弦定理得，由余弦定理，得C ab b a c cos 2222-+=，得，从而．4154152121sin 21=⨯⨯⨯==∆C ab S ABC ．． (13)18．（本题满分13分）解：（1）当，时11222n n n n n n a S S +-=-=-= 又21112222a S ==-==，也满足上式，所以数列的通项公式为 ，设公差为，则由，，成等比数列， 得 2(22)2(28)d d +=⨯+ 解得（舍去）或所以数列的通项公式为 ．．…．7分 （2）解：21(1)(1)n n c n b n n ==++数列的前项和1111122334(1)n T n n =++++⨯⨯⨯⨯+11111111223111nn n n n =-+-++-=-=+++ ．．…．13分 19．解：22233()()212[cos cos()sin sin()]144344322cos()3x x x x f x a b a a b b x πππ=+=+⋅+=++-++=++ …2分 当，，即：422,33k k k Z πππππ-≤≤-∈时，单调递增， 增区间为：⎥⎦⎤⎢⎣⎡--32,342ππππk k ， …5分（Ⅱ）由得，当时当时， …9分（3）51()22cos()cos()3234f x x x ππ=++=∴+=，所以1sin()sin()cos()6634x x x πππ-=--=-+=-。

某某省枣庄市滕州二中2014-2015学年高一上学期10月月考数学试卷一、选择题（每小题5分，共60分）1．（5分）设集合A={0，1，2，3}，集合B={2，3，4}，则A∩B=（）A．{2，3} B．{0，1} C．{0，1，4} D．{0，1，2，3，4} 2．（5分）函数的定义域为（）A．{x|x＞﹣2，且x≠1}B．x≥﹣2，且x≠1C．7．（5分）已知函数则的值为（）A．B．4 C．2 D．8．（5分）已知a＞0，b＞0且ab=1，则函数f（x）=a x与函数g（x）=﹣log b x的图象可能是（）A．B． C．D．9．（5分）设函数f（x）=，则满足f（x）≤2的x的取值X围是（）A．B．C．上是增函数，设a=f（log47），b=f（log23），c=f（0.20.6），则a，b，c的大小关系是（）A．c＜b＜a B．b＜c＜a C．b＜a＜c D．a＜b＜c11．（5分）设函数，若f（x）的值域为R，则常数a的取值X围是（）A．（﹣∞，﹣1]∪C．（﹣∞，﹣2]∪12．（5分）若函数y=log a（x2﹣ax+1）有最小值，则a的取值X围是（）A．0＜a＜1 B．0＜a＜2，a≠1C．1＜a＜2 D．a≥2二、填空题（每小题4分，共16分）13．（4分）已知a=，函数f（x）=a x，若实数m，n满足f（m）＞f（n），则m，n 的大小关系为．14．（4分）若函数f（x）=的图象关于原点对称，则a=．15．（4分）函数f（x）=log（2x2﹣3x+1）的增区间是．16．（4分）已知函数f（x）是定义在R上的奇函数，且当x＞0时，，则f （﹣2+log35）=．三、解答题：（本大题共4小题，共44分）17．（10分）已知A={x|＜3x＜9}，B={x|log2x＞0}．（Ⅰ）求A∩B和A∪B；（Ⅱ）定义A﹣B={x|x∈A且x∉B}，求A﹣B和B﹣A．18．（10分）已知二次函数f（x）满足条件f（0）=1和f（x+1）﹣f（x）=2x．（1）求f（x）的解析式；（2）求f（x）在区间值域．19．（12分）已知a＞0且a≠1，函数f（x）=log a（x﹣1），g（x）=log（3﹣x）（1）若h（x）=f（x）﹣g（x），求函数h（x）的值域；（2）利用对数函数单调性讨论不等式f（x）+g（x）≥0中x的取值X围．20．（12分）已知函数f（x）=（）x，x∈，函数g（x）=f2（x）﹣2af（x）+3的最小值为h （a）．（1）求h（a）的解析式；（2）是否存在实数m，n同时满足下列两个条件：①m＞n＞3；②当h（a）的定义域为时，值域为？若存在，求出m，n的值；若不存在，请说明理由．某某省枣庄市滕州二中2014-2015学年高一上学期10月月考数学试卷参考答案与试题解析一、选择题（每小题5分，共60分）1．（5分）设集合A={0，1，2，3}，集合B={2，3，4}，则A∩B=（）A．{2，3} B．{0，1} C．{0，1，4} D．{0，1，2，3，4}考点：交集及其运算．专题：集合．分析：根据题意和交集的运算直接求出A∩B．解答：解：因为集合A={0，1，2，3}，集合B={2，3，4}，所以A∩B={2，3}，故选：A．点评：本题考查交集及其运算，属于基础题．2．（5分）函数的定义域为（）A． {x|x＞﹣2，且x≠1}B．x≥﹣2，且x≠1C．，解之得x≥﹣2且x≠1∴函数的定义域为{x|x≥﹣2且x≠1}故选C点评：本题给出含有根式且有分母的函数，求函数的定义域，着重考查了函数的定义域的概念及求函数定义域的方法等知识，属于基础题．3．（5分）设偶函数f（x）的定义域为R，当x∈∴集合M∩N=，∵b﹣a叫做集合x|a≤x≤b}的“长度”，∴集合M∩N的“长度”是故选A．点评：本题考查集合的含义，本题解题的关键是看清楚什么叫集合的长度，本题是一个基础题，注意简单数字的运算不要出错．5．（5分）下列函数中，满足“f（x+y）=f（x）f（y）”的单调递增函数是（）A．f（x）=x B．f（x）=x3C．f（x）=（）x D．f（x）=3x考点：抽象函数及其应用．专题：函数的性质及应用．分析：对选项一一加以判断，先判断是否满足f（x+y）=f（x）f（y），然后考虑函数的单调性，即可得到答案．解答：解：A．f（x）=，f（y）=，f（x+y）=，不满足f（x+y）=f（x）f （y），故A错；B．f（x）=x3，f（y）=y3，f（x+y）=（x+y）3，不满足f（x+y）=f（x）f（y），故B错；C．f（x）=，f（y）=，f（x+y）=，满足f（x+y）=f（x）f（y），但f（x）在R上是单调减函数，故C错．D．f（x）=3x，f（y）=3y，f（x+y）=3x+y，满足f（x+y）=f（x）f（y），且f（x）在R上是单调增函数，故D正确；故选D．点评：本题主要考查抽象函数的具体模型，同时考查幂函数和指数函数的单调性，是一道基础题．6．（5分）函数f（x）=是（）A．偶函数，在（0，+∞）是增函数B．奇函数，在（0，+∞）是增函数C．偶函数，在（0，+∞）是减函数D．奇函数，在（0，+∞）是减函数考点：函数奇偶性的判断；函数单调性的判断与证明．专题：函数的性质及应用．分析：判断函数的定义域为R，然后利用定义判断f（x）与f（﹣x）的关系，利用2x的单调性判断f（x）单调性．解答：解：f（x）的定义域为R，f（﹣x）==﹣f（x），则函数f（x）为奇函数；又y=2x为增函数，y=﹣2﹣x为增函数，∴f（x）为增函数；故选B．点评：本题考查了函数奇偶性的判定以及单调性的判定．7．（5分）已知函数则的值为（）A．B．4 C．2 D．考点：函数的值．专题：函数的性质及应用．分析：利用分段函数的性质求解．解答：解：∵函数，∴f（）==﹣3，=f（﹣3）=2﹣3=．故选：A．点评：本题考查函数值的求法，是基础题，解题时要认真审题．8．（5分）已知a＞0，b＞0且ab=1，则函数f（x）=a x与函数g（x）=﹣log b x的图象可能是（）A．B． C．D．考点：对数函数的图像与性质；指数函数的图像与性质．专题：常规题型；数形结合．分析：由条件ab=1化简g（x）的解析式，结合指数函数、对数函数的性质可得正确答案解答：解：∵ab=1，且a＞0，b＞0∴又所以f（x）与g（x）的底数相同，单调性相同故选B点评：本题考查指数函数与对数函数的图象，以及对数运算，属中档题9．（5分）设函数f（x）=，则满足f（x）≤2的x的取值X围是（）A．B．C．上是增函数，设a=f（log47），b=f（log23），c=f（0.20.6），则a，b，c的大小关系是（）A．c＜b＜a B．b＜c＜a C．b＜a＜c D．a＜b＜c考点：奇偶性与单调性的综合；对数值大小的比较．专题：综合题；函数的性质及应用．分析：由f（x）是定义在R上的偶函数，且在（﹣∞，0]上是增函数，可得出自变量的绝对值越小，函数值越大，由此问题转化为比较自变量的大小，问题即可解决．解答：解：f（x）是定义在R上的偶函数，且在（﹣∞，0]上是增函数，要得函数在（0，+∞）上是减函数，图象越靠近y轴，图象越靠上，即自变量的绝对值越小，函数值越大，由于0＜0.20.6＜1＜log47＜log49=log23，可得b＜a＜c，故选C．点评：本题解答的关键是根据函数的性质得出自变量的绝对值越小，函数值越大这一特征，由此转化为比较自变量的大小，使得问题容易解决．这也是本题解答的亮点．11．（5分）设函数，若f（x）的值域为R，则常数a的取值X围是（）A．（﹣∞，﹣1]∪C．（﹣∞，﹣2]∪考点：指数函数综合题．专题：计算题；函数的性质及应用．分析：由题意可知，y=2x+a＞4+a，y=x+a2≤2+a2，a2+2≥a+4，解不等式可求解答：解：当x＞2时，y=2x+a＞4+a当x≤2时，y=x+a2≤2+a2∵f（x）的值域为R，∴a2+2≥a+4解不等式可得，a≥2或a≤﹣1故选A点评：本题主要考查了指数函数的值域、一次函数的值域的求解，分段函数值域的应用是求解本题的关键12．（5分）若函数y=log a（x2﹣ax+1）有最小值，则a的取值X围是（）A．0＜a＜1 B．0＜a＜2，a≠1C．1＜a＜2 D．a≥2考点：对数函数的值域与最值．专题：计算题．分析：先根据复合函数的单调性确定函数g（x）=x2﹣ax+1的单调性，进而分a＞1和0＜a ＜1两种情况讨论：①当a＞1时，考虑地函数的图象与性质得到x2﹣ax+1的函数值恒为正；②当0＜a＜1时，x2﹣ax+1没有最大值，从而不能使得函数y=log a（x2﹣ax+1）有最小值．最后取这两种情形的并集即可．解答：解：令g（x）=x2﹣ax+1（a＞0，且a≠1），①当a＞1时，g（x）在R上单调递增，∴△＜0，∴1＜a＜2；②当0＜a＜1时，x2﹣ax+1没有最大值，从而不能使得函数y=log a（x2﹣ax+1）有最小值，不符合题意．综上所述：1＜a＜2；故选C．点评：本题考查对数的性质，函数最值，考查学生发现问题解决问题的能力，是中档题．二、填空题（每小题4分，共16分）13．（4分）已知a=，函数f（x）=a x，若实数m，n满足f（m）＞f（n），则m，n的大小关系为m＜n．考点：不等式比较大小．专题：不等式的解法及应用．分析：由题意可得：函数f（x）=a x在R上是单调减函数，又f（m）＞f（n），可得：m＜n．解答：解：因为a=a=∈（0，1），所以函数f（x）=a x在R上是单调减函数，因为f（m）＞f（n），所以根据减函数的定义可得：m＜n．故答案为：m＜n．点评：解决此类问题的关键是熟练掌握指数函数的单调性与定义，以及单调函数的定义，属于基础题．14．（4分）若函数f（x）=的图象关于原点对称，则a=﹣\frac{1}{2}．考点：函数的图象．专题：函数的性质及应用．分析：根据奇函数的图象的性质，可以函数f（x）图象关于原点对称，即f（x）为奇函数．解答：解：∵函数f（x）=的图象关于原点对称，∴函数f（x）为奇函数，∴f（﹣x）=﹣f（x），∴=﹣，∴（﹣2x+1）（﹣x+a）=（2x+1）（x+a）解得，a=﹣，故答案为：点评：本题主要考查了奇函数的图象和性质，属于基础题．15．（4分）函数f（x）=log（2x2﹣3x+1）的增区间是（﹣∞，）．考点：复合函数的单调性．专题：函数的性质及应用．分析：令t（x）=2x2﹣3x+1＞0，求得函数的定义域．根据复合函数的单调性，本题即求函数t（x）在定义域内的减区间．再利用二次函数的性质求得t（x）=2x2﹣3x+1在定义域内的减区间．解答：解：令t（x）=2x2﹣3x+1＞0，求得x＜或x＞1，故函数的定义域为{x|x＜或x＞1}，且 f（x）=log t（x），根据复合函数的单调性，本题即求函数t（x）在定义域内的减区间．∵二次函数y=2x2﹣3x+1在定义域内的减区间是（﹣∞，），∴f（x）的增区间是（﹣∞，）．故答案为：（﹣∞，）．点评：本题主要考查复合函数的单调性，二次函数的性质，体现了转化的数学思想，属于中档题．16．（4分）已知函数f（x）是定义在R上的奇函数，且当x＞0时，，则f （﹣2+log35）=．考点：奇函数；函数的值．专题：计算题；转化思想．分析：可利用奇函数的定义将f（﹣2+log35）的值的问题转化为求f（2﹣log35）的值问题，再根据函数的性质求出f（﹣2+log35）解答：解：由题意f（﹣2+log35）=﹣f（2﹣log35）由于当x＞0时，，故f（﹣2+log35）=﹣f（log3）==故答案为点评：本题考查函数的性质，求解的关键是根据奇函数的性质将求值的问题转化到x＞0时来求，这是奇函数性质的一个很重要的运用．三、解答题：（本大题共4小题，共44分）17．（10分）已知A={x|＜3x＜9}，B={x|log2x＞0}．（Ⅰ）求A∩B和A∪B；（Ⅱ）定义A﹣B={x|x∈A且x∉B}，求A﹣B和B﹣A．考点：交集及其运算．专题：集合．分析：（Ⅰ）求出A与B中其他不等式的解集确定出A与B，找出两集合的交集，并集即可；（Ⅱ）根据A﹣B的定义，求出A﹣B与B﹣A即可．解答：解：（Ⅰ）由A中的不等式变形得：3﹣1＜3x＜32，解得：﹣1＜x＜2，即A=（﹣1，2），由B中的不等式变形得：log2x＞0=log21，得到x＞1，∴B=（1，+∞），则A∩B=（1，2）；A∪B=（﹣1，+∞）；（Ⅱ）∵A=（﹣1，2），B=（1，+∞），A﹣B={x|x∈A且x∉B}，∴A﹣B=（﹣1，1]；B﹣A=值域．考点：函数解析式的求解及常用方法；函数的值域．专题：函数的性质及应用．分析：（1）f（x）=ax2+bx+1，代入求解f（x+1）﹣f（x）=2x，化简求解系数．（2）求对称轴，端点值，判断大小．解答：解：（1）二次函数f（x）满足条件f（0）=1设f（x）=ax2+bx+1，f（x+1）﹣f（x）=2x．∴a（x+1）2+b（x+1）+1﹣=2x展开化简得：2ax+a+b=2x，2a=2．a+b=0即a=1，b=﹣1，故f（x）=x2﹣x+1，（2）f（x）=x2﹣x+1，x∈∵=为对称轴，∈f（）=，f（﹣1）=3，f（1）=1，∴f（x）在区间值域为点评：本题考查了二次函数的性质，及待定系数法求解析式，利用等式恒成立解决．19．（12分）已知a＞0且a≠1，函数f（x）=log a（x﹣1），g（x）=log（3﹣x）（1）若h（x）=f（x）﹣g（x），求函数h（x）的值域；（2）利用对数函数单调性讨论不等式f（x）+g（x）≥0中x的取值X围．考点：其他不等式的解法；对数的运算性质．专题：函数的性质及应用；不等式的解法及应用．分析：（1）化简h（x）=f（x）﹣g（x），求出函数的定义域，然后通过a的X围讨论函数h（x）的值域；（2）利用对数函数单调性，讨论a的X围，列出不等式f（x）+g（x）≥0的不等式组，求出x的取值X围．解答：解：（1）由得1＜x＜3所以函数h（x）的定义域为（1，3）令t=（x﹣1）（3﹣x）而x∈（1，3）所以t∈（0，1]当0＜a＜1时log a t≥0即h（x）≥0当a＞1时log a t≤0即h（x）≤0所以当0＜a＜1时函数h（x）的值域为（2）由f（x）+g（x）≥0得f（x）≥﹣g（x）即log a（x﹣1）≥log a（3﹣x）①当0＜a＜1时要使不等式①成立则即1＜x≤2当时要使不等式①成立则即2≤x＜3综上所述当0＜a＜1时不等式f（x）+g（x）≥0中x的取值X围为（1，2]当a＞1时不等式f（x）+g（x）≥0中x的取值X围为，函数g（x）=f2（x）﹣2af（x）+3的最小值为h（a）．（1）求h（a）的解析式；（2）是否存在实数m，n同时满足下列两个条件：①m＞n＞3；②当h（a）的定义域为时，值域为？若存在，求出m，n的值；若不存在，请说明理由．考点：函数单调性的性质；函数最值的应用．分析：（1）g（x）为关于f（x）的二次函数，可用换元法，转化为二次函数在特定区间上的最值问题，定区间动轴；（2）由（1）可知a≥3时，h（a）为一次函数且为减函数，求值域，找关系即可．解答：解：（1）由，已知，令设f（x）=t，则g（x）=y=t2﹣2at+3，则g（x）的对称轴为t=a，故有：①当时，g（x）的最小值h（a）=②当a≥3时，g（x）的最小值h（a）=12﹣6a③当时，g（x）的最小值h（a）=3﹣a2综上所述，（2）当a≥3时，h（a）=﹣6a+12，故m＞n＞3时，h（a）在上为减函数，所以h（a）在上的值域为．由题意，则⇒，两式相减得6n﹣6m=n2﹣m2，又m≠n，所以m+n=6，这与m＞n＞3矛盾，故不存在满足题中条件的m，n的值．点评：本题主要考查一次二次函数的值域问题，二次函数在特定区间上的值域问题一般结合图象和单调性处理，“定轴动区间”、“定区间动轴”．。

阶段性质量检测数学试卷(理科)命题人：张修恒 审核人赵林 2016-10本试卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间120分钟。

第I 卷（选择题 共50分）一．选择题：本大题共10小题，每小题5分，共50分。

1.设集合A={x|-1≤x<2},B={x|x<a},若φ≠⋂B A ,则a 的取值范围是（ ）A.a<2B.a>2C.a>-1D.-1<a ≤2 2.⎩⎨⎧>>3321x x 是⎩⎨⎧>>+962121x x x x 成立的（ ）A.充分不必要条件B.必要不充分条件C.充要条件D. 既不充分也不必要条件3. 函数()3)2ln()1(---=x x x x f 的零点有（ ）A.0个B.1个C. 2个D.3个4. 设109log ,25lg,231.0===c b a ，则a ，b ，c 的大小关系是（ ） A.b>c>a B.a>c>b C.b>a>c D. a>b>c5．已知命题p ：存在x ∈R ，使3cos sin =-x x ，命题q ：集合{x|R x x x ∈=+-,0122}有2个子集，下列结论：①命题“p 且q ”是真命题；②命题“p 且q ⌝”是假命题③命题“q p ⌝⌝或”是真命题，其中正确的个数是（ ）A.0B.1C.2D.36. 已知函数f （x ）的导函数)(x f '，且满足f （x ）=2)1(f x '+lnx ，则)1(f '=（ ）A.-eB. -1C. 1D.e7. 函数)1,0(≠>-=aaaay x的定义域和值域都是[0,1]，则548log65logaa+=（）A.1B.2C. 3D. 48.函数αxxf=)(满足f（2）=4，那么函数g（x）=|)1(log+xa|的图像大致为（）9.设函数f（x）是定义在R上周期为3的奇函数，若f（1）<1，f（2）=112+-aa，则有（）A.21<a且a≠-1 B.a<-1或a>0 C.-1<a<0 D.-1<a<210. 已知⎪⎩⎪⎨⎧>+-≤<=3,83103130|,log|)(23xxxxxxf a，b，c，d是互不相同的正数，且f（a）=f（b）=f（c）=f（d），则abcd的取值范围是（）A.（18 ，28）B.（18 ，25 ）C.（20,25）D.（21,24）第II卷（非选择题共100分）注意事项：第II卷所有题目的答案考生需用黑色签字笔答在“数学”答题卡指定的位置。

2016—2017学年山东省枣庄市滕州二中高三(上）10月质检数学试卷（理科）一．选择题:本大题共10小题，每小题5分，共50分．1．设集合A={x｜﹣1≤x＜2}，B={x|x＞a｝，若A∩B≠∅，则a的取值范围是（）A．a＜2 B．a≤2 C．a＞﹣1 D．﹣1＜a≤22．是成立的（）A．充分而不必要条件 B．必要而不充分条件C．充要条件 D．既不充分也不必要条件3．函数f（x）=的零点有（)A．0 B．1 C．2 D．34．设a=20。

1，b=lg，c=log3，则a，b，c的大小关系是（）A．b＞c＞a B．a＞c＞b C．b＞a＞c D．a＞b＞c5．已知命题p：∃x∈R,使sinx﹣cosx=，命题q:集合{x|x2﹣2x+1=0,x∈R}有2个子集,下列结论：（1）命题“p∧q”是真命题；(2）命题“p∧(￢q）”是假命题；（3）命题“(￢p)∨(￢q）”是真命题．正确的个数是（)A．0 B．1 C．2 D．36．已知函数f（x）的导函数为f′（x）,且满足f（x)=2xf′（1）+lnx，则f′(1)=（）A．﹣e B．﹣1 C．1 D．e7．函数y=（a＞0,a≠1）的定义域和值域都是［0，1］，则log a+log a=（）A．1 B．2 C．3 D．48．函数f（x)=x a满足f（2）=4，那么函数g(x）=｜log a（x+1）｜的图象大致为（）A．B．C．D．9．设函数f（x）是定义在R上，周期为3的奇函数，若f（1）＜1，，则（）A．且a≠﹣1 B．﹣1＜a＜0 C．a＜﹣1或a＞0 D．﹣1＜a＜210．已知f（x）=，若a,b，c，d是互不相同的四个正数,且f（a)=f（b）=f(c)=f（d)，则abcd的取值范围是（）A．（21，25）B．（21，24）C．（20，24）D．(20，25）二．填空题（本大题共5个小题，每小题5分，共25分．）11．2lg+log25•lg2=．12．设函数f（x）=x2ln（﹣x+)+1，若f（a)=11，则f(﹣a）=．13．函数f(x)=log2（x2﹣ax+3a)在[2，+∞）上是增函数，则a的取值范围是．14．已知f（x）是定义在实数集上的函数，且f(x+2）=,f（1）=，则f＜”是真命题．其中正确命题的序号是．（把所有正确命题序号都填上）三．解答题：本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤．16．已知集合A=｛x｜log2x＜8}，B={x|＜0｝，C=｛x｜a＜x＜a+1}．（1）求集合A∩B；（2）若B∪C=B，求实数a的取值范围．17．设命题p:函数y=kx+1在R上是增函数，命题q：∃x∈R，x2+（2k﹣3）x+1=0，如果p ∧q是假命题，p∨q是真命题，求k的取值范围．18．已知函数f（x）=e x﹣x2﹣ax．(I）若函数f（x）的图象在x=0处的切线方程为y=2x+b,求a，b的值；（Ⅱ）若函数f（x）在R上是增函数，求实数a的最大值．19．已知函数f（x）=是定义在（﹣1,1）上的奇函数，且．（1）求函数f（x）的解析式；（2）证明f（x）在(﹣1，1）上是增函数；（3）解不等式f(t﹣1）+f（2t）＜0．20．已知函数f（x）=ax2﹣2x+1．（1)试讨论函数f（x）的单调性；（2）若，且f(x）在［1，3］上的最大值为M(a）,最小值为N（a),令g（a)=M(a）﹣N（a），求g（a）的表达式．21．设a∈R,函数f（x）=lnx﹣ax．（Ⅰ）求f（x)的单调递增区间;（Ⅱ)设F（x）=f(x）+ax2+ax,问F（x）是否存在极值，若存在，请求出极值；若不存在,请说明理由;(Ⅲ）设A(x1，y1），B（x2，y2）是函数g(x）=f（x）+ax图象上任意不同的两点，线段AB 的中点为C（x0，y0），直线AB的斜率为为k．证明：k＞g′（x0）．2016-2017学年山东省枣庄市滕州二中高三（上)10月质检数学试卷（理科）参考答案与试题解析一．选择题:本大题共10小题，每小题5分，共50分．1．设集合A={x|﹣1≤x＜2},B=｛x|x＞a},若A∩B≠∅，则a的取值范围是（）A．a＜2 B．a≤2 C．a＞﹣1 D．﹣1＜a≤2【考点】交集及其运算．【分析】由A,B，以及A与B的交集不为空集,确定出a的范围即可．【解答】解：∵A={x|﹣1≤x＜2},B={x｜x＞a},且A∩B≠∅，∴a＜2．故选:A．2．是成立的（）A．充分而不必要条件 B．必要而不充分条件C．充要条件 D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】分充分性和必要性两方面加以论证:根据不等式的性质，可证明出充分性成立；再通过举出反例说明必要性是不成立的．因此得出正确选项．【解答】解：①充分性，当x1＞3且x2＞3时，根据不等式的性质可得：x1x2＞9且x1+x2＞6∴充分性成立②必要性,当x1x2＞9且x1+x2＞6成立，x1＞3且x2＞3不一定成立‘比如：x1=2，x2=8满足“x1x2＞9且x1+x2＞6”,但“x1＞3且x2＞3”不成立∴必要性不成立所以是成立的充分不必要条件故选A3．函数f(x）=的零点有(）A．0 B．1 C．2 D．3【考点】函数的零点．【分析】先求定义域，然后令y=0,解出x的值,判断即可．【解答】解:函数的定义域是｛x|2＜x＜3或x＞3｝，令y=0，得x=3．显然无解．故选A．4．设a=20.1，b=lg，c=log3，则a,b，c的大小关系是(）A．b＞c＞a B．a＞c＞b C．b＞a＞c D．a＞b＞c【考点】对数值大小的比较．【分析】利用幂函数，指数函数,以及对数函数的性质判断即可．【解答】解：∵20。

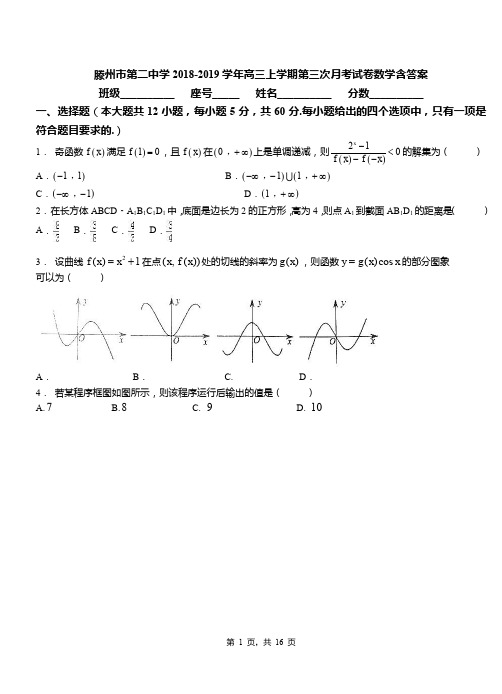
滕州市第二中学2018-2019学年高三上学期第三次月考试卷数学含答案 班级__________ 座号_____ 姓名__________ 分数__________一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的.）1． 奇函数()f x 满足()10f =，且()f x 在()0+∞，上是单调递减，则()()210x f x f x -<--的解集为（ ）A ．()11-，B ．()()11-∞-+∞，，C ．()1-∞-，D ．()1+∞，2． 在长方体ABCD ﹣A 1B 1C 1D 1中，底面是边长为2的正方形，高为4，则点A 1到截面AB 1D 1的距离是（ ）A ．B ．C ．D ．3． 设曲线2()1f x x =+在点(,())x f x 处的切线的斜率为()g x ，则函数()cos y g x x =的部分图象 可以为（ ）A ．B ． C. D ． 4． 若某程序框图如图所示，则该程序运行后输出的值是（ ） A.7B.8C. 9D. 10【命题意图】本题考查阅读程序框图，理解程序框图的功能，本质是循环语句循环终止的条件.5． 复数满足2＋2z1－i ＝i z ，则z 等于（ ）A ．1＋iB ．－1＋iC ．1－iD ．－1－i6． 一个正方体的顶点都在球面上，它的棱长为2cm ，则球的表面积是（ ）A ．8πcm 2B ．12πcm 2C ．16πcm 2D ．20πcm 27． 高考临近，学校为丰富学生生活，缓解高考压力，特举办一场高三学生队与学校校队的男子篮球比赛．由于爱好者众多，高三学生队队员指定由5班的6人、16班的8人、33班的10人按分层抽样构成一个12人的篮球队．首发要求每个班至少1人，至多2人，则首发方案数为（ ） A ．720 B ．270 C ．390 D ．3008． 设集合M={（x ，y ）|x 2+y 2=1，x ∈R ，y ∈R}，N={（x ，y ）|x 2﹣y=0，x ∈R ，y ∈R}，则集合M ∩N 中元素的个数为（ ） A ．1B ．2C ．3D ．49． 4213532,4,25a b c ===，则（ ）A ．b a c <<B ．a b c <<C ．b c a <<D ．c a b << 10．如图，1111D C B A ABCD -为正方体，下面结论：① //BD 平面11D CB ；② BD AC ⊥1；③ ⊥1AC 平面11D CB .其中正确结论的个数是（ ）A ．B ．C ．D ．11．一个几何体的三视图如图所示，则该几何体的体积是（ ）A ．64B ．72C ．80D ．112【命题意图】本题考查三视图与空间几何体的体积等基础知识，意在考查空间想象能力与运算求解能力. 12．若变量x ，y满足：，且满足（t+1）x+（t+2）y+t=0，则参数t 的取值范围为（ ）A ．﹣2＜t＜﹣ B ．﹣2＜t ≤﹣ C ．﹣2≤t ≤﹣ D ．﹣2≤t＜﹣二、填空题（本大题共4小题，每小题5分，共20分.把答案填写在横线上）13．曲线y ＝x 2＋3x 在点（－1，－2）处的切线与曲线y ＝ax ＋ln x 相切，则a ＝________．14．已知实数x ，y 满足2330220y x y x y ≤⎧⎪--≤⎨⎪+-≥⎩，目标函数3z x y a =++的最大值为4，则a =______．【命题意图】本题考查线性规划问题，意在考查作图与识图能力、逻辑思维能力、运算求解能力．15．（﹣2）7的展开式中，x 2的系数是 ．16．若函数()f x 的定义域为[]1,2-，则函数(32)f x -的定义域是 ．三、解答题（本大共6小题，共70分。

阶段性质量检测数学试卷(文科)本试卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间120分钟.第I 卷（选择题 共50分）命题人：颜文杰 审核人：马标一． 选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合A={x|-1≤x<2},B={x|x<a},若φ≠⋂B A ,则a 的取值范围是（ ）A.a<2B.a>2C.a>-1D.-1<a ≤2 2.⎩⎨⎧>>3321x x 是⎩⎨⎧>>+962121x x x x 成立的（ ）A.充分不必要条件B.必要不充分条件C.充要条件D. 既不充分也不必要条件3. 函数()3)2ln()1(---=x x x x f 的零点有（ ）A.0个B.1个C. 2个D.3个4. 设109log ,25lg,231.0===c b a ，则a ，b ，c 的大小关系是（ ） A.b>c>a B.a>c>b C.b>a>c D. a>b>c5．下列函数中，其在区间（-1,1）上为减函数的是（ ）A.xy -=11 B.y=cosx C.y=ln(1+x) D.xy -=26. 已知函数f （x ）的导函数)(x f '，且满足f （x ）=2)1(f x '+lnx ，则)1(f '=（ ）A.-eB. -1C. 1D.e7. 已知0x 是x x f x121)(+⎪⎭⎫ ⎝⎛=的一个零点，)0,(,,0201x x x x ∈∞-∈）（，则（ ）A.()1x f <0，()2x f <0B.()1x f >0，()2x f >0C.()1x f >0，()2x f <0D.()1x f <0，()2x f >08.函数αx x f =)( 满足f （2）=4，那么函数g （x ）=|)1(log +x a |的图像大致为（ ）9. 设函数f （x ）是定义在R 上周期为3的奇函数，若f （1）<1，f （2）=112+-a a ，则有（ ） A.21<a 且a ≠-1 B.a<-1或a>0 C.-1<a<0 D.-1<a<210. 已知命题p ：存在x ∈R ，使3cos sin =-x x ，命题q ：集合{x|R x x x ∈=+-,0122}有2个子集，下列结论：①命题“p 且q ”是真命题；②命题“p 且q ⌝”是假命题③命题“q p ⌝⌝或”是真命题，其中正确的个数是（ ）A.0B.1C.2D.3第II 卷（非选择题 共100分）注意事项：第II 卷所有题目的答案考生需用黑色签字笔答在“数学”答题卡指定的位置. 二．填空题（本大题共5个小题，每小题5分，共25分.） 11. =⋅+2lg 5log 2lg 2212. 已知()⎩⎨⎧≤+>=0,0,log 3x b a x x x f x ，且f （0）=2，f （-1）=3，则f （f （-3））=13.设函数1)1ln()(22+++-=x x x x f ，若f （a ）=11，则f （-a ） .14.若函数f （x ）=)3(log 22a ax x +-，在区间[2,+∞)上是增函数， 则实数a 的取值范围是 .15.已知函数f （x ）是定义在实数集上的函数，且)(1)(1)2(x f x f x f -+=+，f （1）=41，则f （2015）= .三．解答题：本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤. 16. （本小题满分12分） 已知集合A={x |3log 2<x },B={x|42-+x x <0}，C={x|a<x<a+1} （I ） 求集合B A ；（Ⅱ）若B C B = ，求实数a 的取值范围.17. （本小题满分12分）设命题p ：函数y=kx+1在R 上是增函数，命题q ：01)32(,2=+-+∈∃x k x R x ，如果qp ∧是假命题，q p ∨是真命题，求k 的取值范围.18. （本小题满分12分） 已知函数ax x e x f x--=2)(.（I ） 若函数f （x ）的图象在x=0处的切线方程为y=2x+b ，求a ，b 的值； （Ⅱ）若函数f （x ）在R 上是增函数，求实数a 的最大值.19.（本小题满分13分） 已知函数()f x =21ax b x ++是定义在（﹣1，1）上的奇函数，且12()25f =. (Ⅰ)求函数()f x 的解析式；（Ⅱ）证明()f x 在（－1，1）上是增函数； （Ⅲ）解不等式(1)()0f t f t -+<.20. （本小题满分13分）已知二次函数()x f 的二次项系数为a ，且不等式()x x f 2->的解集为()3,1， （I ）若方程()有两个相等的正根，求06=+ax f()的解析式x f（Ⅱ）若()的最大值为x f 正数，求a 的取值范围21．（本小题满分14分） 设R a ∈，函数ax x x f -=ln )(. （I ） 求f （x ）的单调增区间；（Ⅱ）设F （x ）=ax ax x f ++2)(，问F （x ）是否存在极值，若存在，请求出极值；若存在，请说明理由；高三数学（文科）答案与评分标准一、 选择题1.C 2.A 3A 4.D 5. D 6.B 7. C 8.C 9.B 10. C二填空题：本大题共5小题，每小题5分，共25分11．1； 12．-3 13．9-； 14(]4,4- 15 53-1617.19. (1)解：()f x 是（-1，1）上的奇函数(0)0f ∴= 0b ∴= （1分）又12()25f =2122151()2a ∴=+ 1a ∴= （2分） 2()1xf x x ∴=+ （4分） （2）证明：()()()()()()()()2222222221111()111,110,10x f x x x x x x x f x xx x x f x =+''+-+-'∴==++'∈-∴-∈∴>()f x ∴在（-1，1）上是增函数 （8分）（3）()f x 是奇函数 ∴不等式可化为(1)()()f t f t f t -<-=-即 (1)()f t f t -<- （9分） 又()f x 在（-1，1）上是增函数∴有111111t t t t-<-<⎧⎪-<<⎨⎪-<-⎩解之得102t << （12分）∴不等式的解集为1{|0}2t t << （13分）3-2a 或032（2）a 53x 56x 51（1）f(x)20.2+<<--<---=21.。

山东省滕州市第二中学2017届高三物理10月月考试题本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，满分100分，考试用时90分钟。

第Ⅰ卷（共48分）一、选择题（每小题的四个选项中，第1-8题只有一选项符合题目要求，第9-12题有有多项符合题目要求。

全部选对的得4分，选对但不全的得2分，有选错的得0分）1. 一只质量为m 的蚂蚁，在半径为R 的半球形碗内爬行，爬到距碗底高R )231(-的A 点停下来，再也爬不上去，设碗内每处的动摩擦因数相同，那么碗内的动摩擦因数为（ ）A ．21B ．23C ．231-D ．33 2．在如图所示的四幅图中，AB 、BC 均为轻质杆，各图中杆的A 、C 端都通过铰链与墙连接，两杆都在B 处由铰链相连接．下列关于杆受力的说法正确的是（ ）A.甲图中的AB 杆表现为支持力,BC 杆表现为拉力B.乙图中的AB 杆表现为拉力, BC 杆表现为支持力C.丙图中的AB 杆、BC 杆均表现为拉力D.丁图中的AB 杆、BC 杆均表现为支持力3、亚丁湾索马里海域六艘海盗快艇试图靠近中国海军护航编队保护的商船，中国特战队员发射爆震弹成功将其驱离。

假如其中一艘海盗快艇在海面上运动的v －t 图象如图所示，设运动过程中海盗快艇所受阻力不变．则下列说法正确的是 （ ）A ．海盗快艇在0～66 s 内从静止出发做加速度增大的加速直线运动B ．海盗快艇在66 s 末开始调头逃离C ．海盗快艇在96 s 末开始调头逃离D ．海盗快艇在96 s ～116 s 内做匀减速直线运动4、一质点做匀加速直线运动时，速度变化v 时发生位移x 1，紧接着速度变化同样的v 时发生位移x 2，则该质点的加速度为（ ）A ．(v)2⎪⎪⎭⎫⎝⎛+2111x xB ．122)(2x x v -∆ C ．(v)2⎪⎪⎭⎫⎝⎛-2111x xD ．122)(x x v -∆ 5.如图所示，一个半球形的碗放在桌面上，碗口水平，O 点为其球心，碗的内表面及碗口是光滑的一根细线跨在碗口上，线的两端分别系有质量为m 1和m 2的小球，当它们处于平衡状态时，质量为m 1的小球与O 点的连线与水平线夹角为= 600，两个球的质量比为（ ）A. B. C. D.6．A 、B 两物体按图中所示甲、乙两种形式叠放在一起沿斜面匀速下滑，A 、B 间保持相对静止，图甲中B 的上表面与斜面平行，图乙中B 的上表面与水平面平行，则关于A 、B 间的摩擦力，下列说法中正确的是（ ）A ．图甲、乙中均无摩擦力B ．图甲、乙中均有摩擦力C ．图甲中有摩擦，图乙中无摩擦D ．图乙中有摩擦，图甲中无摩擦7、如图所示，有一质量不计的杆AO ，长为R ，可绕A 自由转动．用绳在O 点悬挂一个重为G 的物体，另一根绳一端系在O 点，另一端系在以O 点为圆心的圆弧形墙壁上的C 点．当点C 由图示位置逐渐向上沿圆弧CB 移动过程中(保持OA 与地面夹角θ不变)，OC 绳所受拉力的大小变化情况是 （ ） A ．逐渐减小 B ．逐渐增大 C ．先减小后增大 D ．先增大后减小8．半径为R的球形物体固定在水平地面上，球心正上方有一光滑的小滑轮，滑轮到球面B的距离为h，轻绳的一端系一小球，靠放在半球上的A点，另一端绕过定滑轮后用力拉住，使小球静止，如图所示，现缓慢地拉绳，在使小球由A到B的过程中，半球对小球的支持力N和绳对小球的拉力T的大小变化的情况是（）A．N不变，T变小B．N不变，T先变大后变小C．N变小，T先变小后变大D．N变大，T变小9．如图所示，直线a和曲线b分别是在平直公路上行驶的汽车a和b的位置－时间(x－t)图线。

山东省滕州市第二中学2015-2016学年高二数学下学期第二次月考试题理（扫描版）高二下学期第二次质量检测数学（理）试卷 答案一 A B C D D B A D C A二 11 . i 232+- 12. 1- 13 20-. 14. 300 15. 0.516 1）由题意知：10=n (2)2）展开式通项 ：()32101013r r rr xC T -+-=令23210=-r，2=r 可得 23405x T = 所以系数为 405 (6)3）10333⎪⎪⎭⎫ ⎝⎛+x x 的展开式的通项：32101013rrr r x C T -+=102,1,0Λ=r令⎪⎩⎪⎨⎧≥≥--++1101101101103333r r r r r r r r C C C C8=∴r 所以二项式系数为45 ………12 17解：1）2-Θ是函数()3221ax e x x f x+=的一个极值点 ()02=-'∴f ，得0=a ……………4 令()0>'x f 得 20-<>x x 或令 ()0<'x f 得 02<<-x∴递增区间为()()∞+-∞-，及02,，递减区间为()0,2- ……………8 2）当[]2,2-∈x ，不等式()m x f >恒成立 等价于()m x f >min()[][]()()[]2,2,002,002-min -∈==∴x f x f x f 上递增，上递减，在，在Θ0<∴m (12)18：(I)由已知，有22222333486()35C C C C P A C +== 所以事件A 发生的概率为635. (4)(II)随机变量X 的所有可能取值为1,2,3,4()45348(1,2,3,4)k k C C P X k k C -=== (10)所以随机变量X 的分布列为X1 2 3 4P114 37 37 114 (12)19解：1）()()()()22211,0,1,121124111+===⎪⎪⎩⎪⎪⎨⎧=-+-=++x x f b a a b a b 于是，解得 (4)2）53,85,32,434321====x x x x (6)3）猜想 ()122++=n n x n (7)1）当1=n 时由计算可知成立 (8)2）假设当k n =时成立，()122++=k k x k 成立当1+=k n 时，()[]111+-=+k f x x k k=()()⎥⎦⎤⎢⎣⎡++-++21111122k k k()()()()()()[]11221212121222++++=+-+++•++=k k k k k k k所以当n=k+1时，猜想也成立。