湖北省各市中考数学圆专题
- 格式:doc
- 大小:217.06 KB
- 文档页数:9

武汉市中考数学专题——-隐圆问题生态课堂导学案:隐圆问题教与导学的过程:一、导疑――情境导入、提出疑问研究目标:了解圆的定义和隐圆的概念,能够利用隐圆解决几何问题。
在一个平面内,线段OA绕它的一个固定的端点O旋转一周,另一个端点A所形成的图形叫做圆。
从画圆的过程可以看出:(1)圆上各点到定点(圆心O)的距离都等于定长(半径r);(2)到定点的距离等于定长的点都在同一个圆上。
根据圆的定义,在解决几何问题中,只要观察出几个点到同一个定点的距离相等,这里常常隐藏了一个圆,我们就可以以这个定点为圆心,以这个距离为半径作出这个隐藏的圆,从而帮助我们解决问题。
因为这个圆没有画出,因此我们把它称为“隐圆”。
二、引探――自主研究、探究问题例1:如图,E、F是正方形ABCD的边AD上两个动点,满足AE=DF,连接CF交BD与点G,连接BE交AG与点H,若正方形的边长为2,则线段DH长度的最小值是多少?例2:如图,△ABC中,∠ABC=90°。
AB=6,BC=8,O为AC的中点,过O作OE⊥OF,OE,OF分别交射线AB,BC于E、F,则EF的最小值为多少?三、释疑――主动展示、阐释疑点例3:如图,∠xOy=45°,一把直角三角形△ABC的两个顶点A,B分别在Ox,Oy上移动,其中AB=10,点O到AB的距离的最大值为多少?例4:在平面直角坐标系中,点A的坐标为(3.0),点B为y轴正半轴上的一点,点C是第一象限内一点,且AC=2.设tan∠BOC=m,则m的取值范围是什么?例5:如图,已知A、B两点的坐标分别为(8,0)、(,-6),C的坐标为(,7),点P是坐标平面内一个动点,且PC=5,线段PB与x轴交于点D,则△ABD面积的最大值是多少?例6:如图,四边形ABCD中,∠ACD=∠ADB=90°,∠XXX°,则∠ABC等于多少度?例7:如图,⊙A与⊙B外切于点D,PC、PD、PE分别是圆的切线,C、D、E是切点,若∠CED=x0,∠ECD=y0,⊙B 的半径为R,则弧DE的长度是多少?1.在平面直角坐标系中,已知直线y = - x + 6与x轴、y 轴交于点A、B两点,点C在y轴的左边,且∠ACB = 90°,则点C的横坐标Xc的取值范围是__。

2019-2020年湖北省中考数学各地区模拟试题分类(武汉市专版)(三)——《圆》一.选择题1.(2020•武汉模拟)如图,AB为半圆⊙O的直径,AB=10,AC为⊙O的弦,AC=8,D 为的中点,DM⊥AC于M,则DM的长为()A.B.C.1D.2.(2020•武汉模拟)在平面直角坐标系中,圆心为坐标原点,⊙O的半径为10,则P(﹣10,1)与⊙O的位置关系为()A.点P在⊙O上B.点P在⊙O外C.点P在⊙O内D.无法确定3.(2020•武汉模拟)已知⊙O的半径等于8cm,圆心O到直线l上某点的距离为8cm,则直线l与⊙O的公共点的个数为()A.0B.1或0C.0或2D.1或2 4.(2020•武汉模拟)直角△ABC,∠BAC=90°,AB=8,AC=6,以A为圆心,4.8长度为半径的圆与直线BC的公共点的个数为()A.0B.1C.2D.不能确定5.(2020•武汉模拟)小名同学响应学习号召,在实际生活中发现问题,并利用所学的数学知识解决问题,他将汽车轮胎如图放置在地面台阶直角处,他测量了台阶高a为160mm,直角顶点到轮胎与底面接触点AB长为320mm,请帮小名计算轮胎的直径为()mm.A.350B.700C.800D.400 6.(2020•武汉模拟)如图,BC为⊙O直径,弦AC=2,弦AB=4,D为⊙O上一点,I 为AD上一点,且DC=DB=DI,AI长为()A.B.C.D.7.(2020•武汉模拟)如图是一个隧道的横截面,它的形状是以O为圆心的圆的一部分,CM=DM=2,MO交圆于E,EM=6,则圆的半径为()A.4B.2C.D.8.(2020•武汉模拟)已知⊙O的半径等于3,圆心O到点P的距离为5,那么点P与⊙O 的位置关系是()A.点P在⊙O内B.点P在⊙O外C.点P在⊙O上D.无法确定9.(2020•江岸区校级模拟)如图,AB为半圆O的直径,BC⊥AB且BC=AB,射线BD交半圆O的切线于点E,DF⊥CD交AB于F,若AE=2BF,DF=2,则⊙O的半径长为()A.B.4C.D.10.(2020•江夏区模拟)如图,BC是⊙O的直径,AB切⊙O于点B,AB=BC=8,点D 在⊙O上,DE⊥AD交BC于E,BE=3CE,则AD的长是()A.B.C.4D.3二.填空题11.(2020•武汉模拟)如图,在△ABC中,∠A=62°,⊙O截△ABC三边所得的弦长相等,则∠BOC的度数是.12.(2020•蔡甸区模拟)已知Rt△ABC中,AC=3,BC=4,以C为圆心,以r为半径作圆.若此圆与线段AB只有一个交点,则r的取值范围为.13.(2020•武汉模拟)如图,圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为.14.(2020•武汉模拟)如图,四边形ABCD是⊙O的内接四边形,∠BOD=100°,则∠BCD=°.15.(2019•武汉模拟)如图,正五边形ABCDE和正△AFG都是⊙O的内接多边形,则∠FOC=.16.(2019•武汉模拟)矩形ABCD的边AB=4,边AD上有一点M,连接BM,将MB绕M点逆时针旋转90°得MN,N恰好落在CD上,过M、D、N作⊙O,⊙O与BC相切,Q为⊙O上的动点,连BQ,P为BQ中点,连AP,则AP的最小值为.17.(2019•武汉模拟)圆心角为125°的扇形的弧长是12.5π.则扇形的面积为.18.(2019•江岸区校级模拟)已知圆锥的侧面积是其底面积的3倍,这个圆锥的侧面展开图的扇形角的度数为.19.(2019•江岸区校级模拟)如图,⊙O的半径为2,正八边形ABCDEFGH内接于⊙O,对角线CE、DF相交于点M,则△MEF的面积是.20.(2019•硚口区模拟)已知⊙O的直径AB为4cm,点C是⊙O上的动点,点D是BC 的中点,AD延长线交⊙O于点E,则BE的最大值为.21.(2019•江夏区校级模拟)如图,四边形ABCD内接于⊙O,连结AC,若∠BAC=35°,∠ACB=40°,则∠ADC=°.22.(2019•硚口区模拟)如图,⊙O是正△ABC的外接圆.若正△ABC的边心距为1,则⊙O的周长为.23.(2019•武昌区模拟)用48m长的篱笆在空地上围成一个正六边形的绿化场地,则其面积为m2三.解答题24.(2020•武汉模拟)如图1,在△ABC中,AB=CB且∠BAC=45°,以AB为直径作⊙O,线段AC交⊙O于点E,连接OC.(1)求证:AE=CE;(2)如图2,取CE的中点M,连接BM交OC于N,连接EN,求的值.25.(2020•武汉模拟)如图,⊙O过正方形ABCD的顶点A、D,且与BC相切于点M,⊙O 分别交AB、CD于E、F两点,连接MO并延长交AD于点N.(1)求证:AN=DN;(2)连接BF交⊙O于点G,连接EG.若AD=8,求EG的长.26.(2020•江岸区校级模拟)如图,AB为⊙O的直径,C为⊙O上的一点,AD⊥CD于点D,AC平分∠DAB.(1)求证:CD是⊙O的切线.(2)设AD交⊙O于E,=,△ACD的面积为6,求BD的长.27.(2020•武汉模拟)如图,在△ABC中,AB=AC,∠BAC=90°,点D在以AB为直径的⊙O上,且CD=CA.(1)求证:CD是⊙O切线.(2)求tan∠AEC的值.28.(2020•江岸区校级模拟)如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.(1)求证:△ABC是等边三角形.(2)若⊙O的半径为2,求等边△ABC的边心距.29.(2020•硚口区模拟)已知如图:在⊙O中,直径AB⊥弦CD于G,E为DC延长线上一点,BE交⊙O于点F.(1)求证:∠EFC=∠BFD;(2)若F为半圆弧AB的中点,且2BF=3EF,求tan∠EFC的值.30.(2020•武汉模拟)如图,A,B,C三点在⊙O上,=,AD⊥AB,DE∥AB交BC 于点E,在BC的延长线上取一点F,使得EF=ED.(1)求证:DF是⊙O的切线;(2)连接AF交DE于点M,若AD=4,BF=10,求tan∠AFD的值.参考答案一.选择题1.解:如图,连接OD交AC于H,连接BC.∵AB是直径,∴∠ACB=90°,∴BC==6,∵=,∴OD⊥AB,∵∠OAH=∠CAB,∠AOH=∠ACB=90°,∴△AOH∽△ACB,∴==∴==∴OH=,AH=,∵DH=OD﹣OH=5﹣=,∵DM⊥AC,∵∠DMH=∠AOH=90°,∠DHM=∠AHO,∴△DMH∽△AOH,∴=,∴=,∴DM=1,故选:C.2.解:∵圆心P的坐标为(﹣10,1),∴OP==.∵⊙O的半径为10,∴>10,∴点P在⊙O外.故选:B.3.解:∵⊙O的半径等于8cm,圆心O到直线l的距离为8cm,即圆心O到直线l的距离小于或等于圆的半径,∴直线l和⊙O相切或相交,∴直线l与⊙O公共点的个数为1或2.故选:D.4.解:∵∠BAC=90°,AB=8,AC=6,∴BC=10,∴斜边上的高为:=4.8,∴d=4.8cm=r=4.8cm,∴圆与该直线AB的位置关系是相切,交点个数为1,故选:B.5.解:如图,连接OB,OC,作CD⊥OB于D.设⊙O半径为xmm,在Rt△OCD中,由勾股定理得方程,(x﹣160)2+3202=x2,解得,x=400,∴2x=800,答:车轱辘的直径为800mm.故选:C.6.解:如图,连接IC,作IE⊥AC于E,IF⊥AB于F,IG⊥BC于G.∵DB=DC,∴=,∠DBC=∠DCB,∴∠BAD=∠CAD,∵DI=DC,∴∠DIC=∠DCI,∵∠DIC=∠DAC+∠ACI,∠DCI=∠DCB+∠ICB,∠DBC=∠DAC,∴∠ICA=∠ICB,∴点I为△ABC内心,∴IE=IF=IG,∵BC是直径,∴∠BAC=90°,∴BC===2,∵S=•AB•AC=•IE•(AB+AC+BC),△ABC∴IE=3﹣,∵∠IAE=∠AIE=45°,∴AI=IE=3﹣,故选:D.7.解:连接OC,∵M是⊙O弦CD的中点,根据垂径定理:EM⊥CD,设圆的半径是x,在Rt△COM中,有OC2=CM2+OM2,即:x2=22+(6﹣x)2,解得:x=,所以圆的半径长是.故选:D.8.解:∵r=3,d=5,∴d>r,∴点P在⊙O外.故选:B.9.解:连接AD,CF,作CH⊥BD于H,如图所示:∵AB是直径,∴∠ADB=90°,∴∠ADF+∠BDF=90°,∠DAB+∠DBA=90°,∵∠BDF+∠BDC=90°,∠CBD+∠DBA=90°,∴∠ADF=∠BDC,∠DAB=∠CBD,∴△ADF∽△BDC,∴==,∵∠DAE+∠DAB=90°,∠E+∠DAE=90°,∴∠E=∠DAB,∴△ADE∽△BDA,∴=,∴=,即=,∵AB=BC,∴AE=AF,∵AE=2BF,∴BC=AB=3BF,设BF=x,则AE=2x,AB=BC=3x,∴BE==x,CF==,由切割线定理得:AE2=ED×BE,∴ED===x,∴BD=BE﹣ED=,∵CH⊥BD,∴∠BHC=90°,∠CBH+∠BCH=∠CBH+∠ABE,∴∠CBH=∠ABE,∵∠BAE=90°=∠BHC,∴△BCH∽△EBA,∴==,即==,解得:BH=x,CH=x,∴DH=BD﹣BH=x,∴CD2=CH2+DH2=x2,∵DF⊥CD,∴CD2+DF2=CF2,即x2+(2)2=()2,解得:x=,∴AB=3,∴⊙O的半径长为;故选:A.10.解:连接AE、BD、DC,∵AB与⊙O相切于点B,∴∠ABC=90°,∵BC=8,BE=3CE,∴CE=2,BE=6,∵AB=8,∴由勾股定理得:AE===10,∵BC是直径,∴∠BDC=90°,∵∠ADE=90°,∴∠ABD+∠CBD=90°,∠DCE+∠CBD=90°,∴∠ABD=∠DCE,∵∠ADE=∠ABE=90°,∴∠DAB+∠DEB=360°﹣90°﹣90°=180°,∵∠DEC+∠DEB=180°,∴∠DEC=∠DAB,∴△DCE∽△DBA,∴===,∴AD=4DE,在Rt△ADE中,AE2=AD2+DE2,∴102=(4DE)2+DE2,∴DE=,∴AD=,故选:A.二.填空题(共13小题)11.解:∵△ABC中∠A=62°,⊙O截△ABC的三条边所得的弦长相等,∴O到三角形三条边的距离相等,即O是△ABC的内心,∴∠1=∠2,∠3=∠4,∠1+∠3=(180°﹣∠A)=(180°﹣62°)=59°,∴∠BOC=180°﹣(∠1+∠3)=180°﹣59°=121°.故答案是:121°.12.解:当以点C为圆心,r为半径的圆与斜边AB只有一个公共点时,过点C作CD⊥AB于点D,∵AC=3,BC=4.,∴AB=5,∴CD×AB=AC×BC,∴CD=r=,当直线与圆如图所示也可以有一个交点,∴3<r≤4,故答案为:3<r≤4或r=.13.解:∵h=8,r=6,可设圆锥母线长为l,由勾股定理,l==10,=×2×6π×10=60π,圆锥侧面展开图的面积为:S侧所以圆锥的侧面积为60πcm2.故答案为:60πcm2;14.解:∵∠BOD=100°,∴∠A=50°.∵四边形ABCD是圆内接四边形,∴∠BCD=180°﹣50°=130°.故答案为:130.15.解:连接OA,OB,∵五边形ABCDE是正五边形,∴∠AOB=∠BOC==72°,∵△AFG是正三角形,∴∠AOF==120°,∴∠BOF=∠AOF﹣∠AOB=48°,∴∠FOC=∠BOC﹣∠BOF=72°﹣48°=24°,故答案为:24°.16.解:设⊙O与BC的交点为F,连接OB、OF,如图1所示.∵△MDN为直角三角形,∴MN为⊙O的直径,∵BM与⊙O相切,∴MN⊥BM,∵将MB绕M点逆时针旋转90°得MN,∴MB=MN,∴△BMN为等腰直角三角形,∵∠AMB+∠NMD=180°﹣∠AMN=90°,∠MBA+∠AMB=90°,∴∠NMD=∠MBA,且BM=NP,∠A=∠NMD=90°,∴△ABM≌△DMN(AAS),∴DM=AB=4,DN=AM,设DN=2a,则AM=2a,OF=4﹣a,BM==2,∵BM=MP=2OF,∴2=2×(4﹣a),解得:a=,∴DN=2a=3,OF=4﹣=,∴⊙O半径为,如图2,延长BA,使AH=AB=4,连接HQ,OH,过O作OG⊥AB于G,∵AB=AH,BP=PQ,∴AP=HQ,HQ∥AP,∴当HQ取最小值时,AP有最小值,∴当点Q在HO时,HQ的值最小,∵HG=4+4﹣=,GO=3+4﹣2=5,∴OH===,∴HQ的最小值=﹣=,∴AP的最小值为,故答案为:.17.解:∵圆心角为125°的扇形的弧长是12.5π,∴12.5π=,解得:r=18,故扇形的面积为:×18×12.5π=112.5π.故答案为:112.5π.18.解:设底面圆的半径为r,侧面展开扇形的半径为R,扇形的圆心角为n度.由题意得S底面面积=πr2,l底面周长=2πr,S扇形=3S底面面积=3πr2,l扇形弧长=l底面周长=2πr.由S扇形=l扇形弧长×R得3πr2=×2πr×R,故R=3r.由l扇形弧长=得:2πr=,解得n=120°.故答案为:120°.19.解:设OE交DF于N,如图所示:∵正八边形ABCDEFGH内接于⊙O,∴DE=FE,∠EOF==45°,,∴∠OEF=∠OFE=∠OED,OE⊥DF,∴△ONF是等腰直角三角形,∴ON=FN=OF=,∠OFM=45°,∴EN=OE﹣OM=2﹣,∠OEF=∠OFE=∠OED=67.5°,∴∠CED=∠DFE=67.5°﹣45°=22.5°,∴∠MEN=45°,∴△EMN是等腰直角三角形,∴MN=EN,∴MF=MN+FN=ON+EN=OE=2,∴△MEF的面积=MF×EN=×2×(2﹣)=2﹣;故答案为:2﹣.20.解:如图,以OB为直径作⊙K,当直线AE切⊙K于D时,BE的值最大.∵AE是⊙K的切线,∴DK⊥AE,∴∠ADK=90°,∵AB是直径,∴∠AEB=90°,∴∠ADK=∠AEB,∴DK∥BE,∴=,∴=,∴BE=,故答案为.21.解:∠ABC=180°﹣∠BAC﹣∠ACB=105°,∵四边形ABCD内接于⊙O,∴∠ADC=180°﹣∠ABC=75°,故答案为:75.22.解:延长AO交BC于D,连接OB,如图,∵△ABC为等边三角形,∴∠ABC=60°,AB=AC,∵OB=OC,∴AO垂直平分BC,即OD⊥BC,∴OD=1,AD平分∠BAC,同理OB平分∠ABC,∴∠OBD=30°,在Rt△OBD中,OB=2OD=2,∴⊙O的周长=2π×2=4π.故答案为4π.23.解:由题意得:AB=48÷6=8m,过O作OC⊥AB,∵AB=BO=AO=8m,∴CO==4m,∴正六边形面积为:4×8××6=96m2,故答案为:96.三.解答题(共7小题)24.(1)证明:如图1中,∵AB是直径,∴∠AEB=90°,∴BE⊥AC,∵AB=CB,∴AE=EC.(2)解:如图2中,连接OE,BE,过点C作CT⊥EN交EN的延长线于T.∵BA=BC,∠ACB=45°,∴∠BAC=∠ACB=45°,∴∠ABC=90°,∵AE=EC,∴∠ABE=∠CBE=∠ABC=45°,∵BE⊥AC,∴EB=EC=EA,∵EM=MC,OA=OB,∴tan∠EBM==,tan∠OCB==,∴tan∠EBM=tan∠OCB,∴∠EBM=∠OCB,∵AO=OB.AE=EC,∴OE∥BC,∴∠EOC=∠OCB,∴∠EON=∠EBN,∴O,E,N,B四点共圆,∴∠EOB+∠ENB=180°,∵EA=EB,AO=OB,∴EO⊥AB,∴∠BOE=∠ENB=90°,∵∠BEN+∠EBN=90°,∠BEN+∠CET=90°,∴∠EBN=∠CET,∵EB=EC,∴△EBN≌△CET(AAS),∴EN=CT,∵∠ONE=∠CNT=∠EBO=45°,CT⊥NT,∴CT=TN,∴EN=NT,CN=NT,∴CN=EN,∴=.25.解:(1)证明:∵⊙O与BC相切于点M,∴∠BMN=90°,∵四边形ABCD是正方形,∴AD∥BC,∴∠ONA=90°,由垂径定理得,AN=DN;(2)如图,连接DE,EF,DG,∵∠DAE=90°,∴∠DFE=90°,∴DE是⊙O的直径,且四边形AEFD是矩形,由(1)知四边形ABMN是矩形,∴MN=AB=8,设OD=r,则ON=8﹣r,DN=4,在Rt△ODN中,根据勾股定理,得42+(8﹣r)2=r2,解得r=5,∴DE=10,∵AD=8,∴AE=6,∴BE=2,∵EF=AD=8,∴BF==2,∵∠BFE=∠EDG,∴sin∠BFE=sin∠EDG,∴=,即=,解得EG=.26.(1)证明:连接OC,∵OA=OC,∴∠OAC=∠OCA,∵AC平分∠DAB,∴∠OAC=∠DAC,∴∠DAC=∠OCA,∴OC∥AD,∴∠OCE=∠ADC=90°,∴CD是⊙O的切线;(2)解:∵=,∴设AC=5x,CD=3x,∴AD=4x,∵△ACD的面积为6,∴AD•CD==6,∴x=1(负值舍去),∴AD=4,CD=3,AC=5,连接BC,∵AB为⊙O的直径,∴∠ACB=90°,∴∠ACB=∠ADC,∵∠DAC=∠CAB,∴△ADC∽△ACB,∴=,∴=,∴AB=,∵∠DAC=∠CAB,∴=,连接BE交OC于F,∴OC⊥BE,BF=EF,∵AB为⊙O的直径,∴∠AEB=∠DEB=90°,∴四边形CDEF是矩形,∴EF=CD=3,∴BE=6,∴AE==,∴DE=4﹣=,∴BD==.27.(1)证明:连接OC,OD,∵OA=OD,AC=CD,OC=OC,∴△AOC≌△DOC(SSS),∴∠CDO=∠CAB=90°,∵OD为⊙O的半径,∴CD是⊙O切线;(2)解:过B作BH⊥AB交AD的延长线于H,∴∠BAC=∠ABH=90°,∵CD=AD,OD=OA,∴OC⊥AD于T,∴∠OTA=90°,∴∠1+∠2=∠2+∠3=90°,∴∠1=∠3,在△ACO和△BAH中,∴△ACO≌△BAH(ASA),∴BH=AO,设OA=OB=r,则AC=AB=2r,BH=r,在Rt△OAC中,OC===r,在Rt△ABC中,BC===2r,∵∠BAC+∠ABH=180°,∴BH∥AC,∴△BEH∽△CEA,∴,∴CE=BC=r,∴cos∠1==,∴CT=,在Rt△CET中,ET==r,∴tan∠AEC===3.28.(1)证明:在⊙O中,∵∠BAC与∠CPB是对的圆周角,∠ABC与∠APC是所对的圆周角,∴∠BAC=∠CPB,∠ABC=∠APC,又∵∠APC=∠CPB=60°,∴∠ABC=∠BAC=60°,∴△ABC为等边三角形;(2)过O作OD⊥BC于D,连接OB,则∠OBD=30°,∠ODB=90°,∵OB=2,∴OD=1,∴等边△ABC的边心距为1.29.(1)证明:如图,连接BD,∵AB⊥CD且AB为直径,∴=.∴∠BFD=∠CDB.又∵∠EFC+∠CFB=180°,而∠CFB+∠CDB=180°,∴∠EFC=∠CDB.∴∠EFC=∠BFD;(2)解:如图,连OF,OC,BC,可知∠EFC=∠BFD=∠BCG,又F为半圆AB的中点,∴∠FOB=∠FOA=90°,∴OF∥CD,∴OG:OB=EF:FB=2:3.设OG=2x,则0B=OC=3x,则CG=x.∴tan∠EFC=tan∠BCG==.30.(1)证明:连接BD,∵AD⊥AB,∴BD是⊙O的直径,∵=,∴BD平分∠ABC,∴∠ABD=∠CBD.∵DE∥AB,∴∠ABD=∠BDE.∴∠CBD=∠BDE.∵ED=EF,∴∠EDF=∠EFD.∵∠EDF+∠EFD+∠EDB+∠EBD=180°,∴∠BDF=∠BDE+∠EDF=90°.∴OD⊥DF.∵OD是半径,∴DF是⊙O的切线.(2)解:连接DC,∵BD是⊙O的直径,∴∠BAD=∠BCD=90°.∵∠ABD=∠CBD,BD=BD,∴△ABD≌△CBD(AAS).∴CD=AD=4,AB=BC.∵DE∥AB,∴∠ABD=∠BDE,∴∠DBE=∠BDE,∴DE=BE,∴DE=EF=EB=BF=5,∴EC===3,EF=DE=5.∴BC=BE+EC=8,∴BD===4,连接AC交BD于H,设BD与AF交于N,∵=,∴AC⊥BD,∴AH=CH===,∴DH==,∵∠DCF=∠BDF=90°,∴∠DBF+∠DFB=∠DFC+∠CDF=90°,∴∠DBC=∠CDF,∴△BDF∽△DCF,∴=,∴DF==2,∵DF⊥BD,AC⊥BD,∴AC∥DF,∴∠CAF=∠AFD,∴△AHN∽△FDN,∴=,∴=,∴DN=,∴tan∠AFD===.。

一」■上,将弧沿BCO中,点C折在优弧1. (2018年武汉第10题)如图,在.D. . AC. B2. (2018年武汉第21题)如图,PA是O O的切线,A是切点,是弦,连接PB PC, PC交AB于点E,且PA=PBPE'(1)求证:PB是O O的切线;AC是直径,AB,求BPC的值.)若/ APC=3/(3. (2018年黄石第8题)、如图,AB是O O的直径,点D为O O上一点,且/n n 2 C. A. D. B. ---------- 333BPABD= 30 °, BC BD(黄石第21题))叠后刚好经过(黄石第8题)BE 23,上五点,是O O O OECA214.(2018年黄石第题)如图,已知、B、、D、的直径BE的中点, 延长BA 到点P,使BA=AP似BCD=120,为,连接PE(1)求线段BD的长(5)求证:直线PE是O O的切线.5. (2018年襄阳第10题)如图,点A,B,C,D都在半径为2的O O上,若OA4丄BC,/ CDA=30°,则弦BC 的长为()€[:/ |;厂|3232D . . B. 2 C A . 46. (2018年襄阳第22题)如图,AB是O O的直径,AM和BN是O O的两条切线,E为O O 上一点,过点E作直线DC分别交AM,BN于点D,C,且CB=CE .⑴求证:DA=DE ;3,求图中阴影部分的面积. =4,CD⑵若AB=67. (2018年黄冈第11题)如图,ZABC内接于O O,AB为O O的直径,/ CAB=60 °,弦AD平分/CAB,若AD=6,(黄冈第11题)8. (2018年黄冈第18题)如图,AD 是O O 的直径,AB 为O O 的弦,0P 丄AD , OP 与AB 的延长线交于点P ,过B 点 的切线交0P 于点C .(1)求证:/ CBP=Z ADB .⑵若0A=2 , AB=1,求线段BP 的长.(2018?天门第22题)如图,在O 0中,AB 为直径,AC 为弦.过BC 延长线上 9一点G ,作GDI AO 于点D ,交AC 于点E,交O 0于点F , M 是GE 的中点,连 接 CF, CM.(1) 判断CM 与O 0的位置关系,并说明理由;(2) 若/ ECF=Z A , CM=6, CF=4 求 MF的(黄冈第18题) D贝 UAC=12. (2018年咸宁第7题)如图,已知O O 的半径为5,弦AB ,CD 所对的圆心角分别是/ AOB ,COD ,若/AOB 与/求半圆和菱形(2)若AD=7,DEBA(第21题) (2018?恩施州第23题)如图,AB 为。

2021年湖北省各地中考数学试题汇编--圆的综合运用1.(3分)(2020•随州)设边长为a 的等边三角形的高、内切圆的半径、外接圆的半径分别为h 、r 、R ,则下列结论不正确的是( )A .h =R +rB .R =2rC .r =√34aD .R =√33a2.(3分)(2020•荆州)如图,在6×6的正方形网格中,每个小正方形的边长都是1,点A ,B ,C 均在网格交点上,⊙O 是△ABC 的外接圆,则cos ∠BAC 的值为( )A .√55B .2√55C .12D .√323.(3分)(2020•武汉)如图,在半径为3的⊙O 中,AB 是直径,AC 是弦,D 是AĈ的中点,AC 与BD 交于点E .若E 是BD 的中点,则AC 的长是( )A .52√3B .3√3C .3√2D .4√24.(3分)(2020•恩施州)如图,已知半圆的直径AB =4,点C 在半圆上,以点A 为圆心,AC为半径画弧交AB于点D,连接BC.若∠ABC=60°,则图中阴影部分的面积为2√3−π.(结果不取近似值5.(3分)(2020•随州)如图,点A,B,C在⊙O上,AD是∠BAC的角平分线,若∠BOC =120°,则∠CAD的度数为.6.(10分)(2020•鄂州)如图所示:⊙O与△ABC的边BC相切于点C,与AC、AB分别交于点D、E,DE∥OB.DC是⊙O的直径.连接OE,过C作CG∥OE交⊙O于G,连接DG、EC,DG与EC交于点F.(1)求证:直线AB与⊙O相切;(2)求证:AE•ED=AC•EF;(3)若EF=3,tan∠ACE=12时,过A作AN∥CE交⊙O于M、N两点(M在线段AN上),求AN的长.7.(7分)(2020•黄冈)已知:如图,AB是⊙O的直径,点E为⊙O上一点,点D是AÊ上一点,连接AE并延长至点C,使∠CBE=∠BDE,BD与AE交于点F.(1)求证:BC是⊙O的切线;(2)若BD平分∠ABE,求证:AD2=DF•DB.8.(10分)(2020•恩施州)如图1,AB是⊙O的直径,直线AM与⊙O相切于点A,直线BN与⊙O相切于点B,点C(异于点A)在AM上,点D在⊙O上,且CD=CA,延长CD与BN相交于点E,连接AD并延长交BN于点F.(1)求证:CE是⊙O的切线;(2)求证:BE=EF;(3)如图2,连接EO并延长与⊙O分别相交于点G、H,连接BH.若AB=6,AC=4,求tan∠BHE.9.(8分)(2020•武汉)如图,在Rt △ABC 中,∠ABC =90°,以AB 为直径的⊙O 交AC 于点D ,AE 与过点D 的切线互相垂直,垂足为E .(1)求证:AD 平分∠BAE ;(2)若CD =DE ,求sin ∠BAC 的值.10.(10分)(2020•孝感)已知△ABC 内接于⊙O ,AB =AC ,∠ABC 的平分线与⊙O 交于点D ,与AC 交于点E ,连接CD 并延长与⊙O 过点A 的切线交于点F ,记∠BAC =α.(1)如图1,若α=60°,①直接写出DF DC 的值为 ;②当⊙O 的半径为2时,直接写出图中阴影部分的面积为 ;(2)如图2,若α<60°,且DF DC =23,DE =4,求BE 的长.11.(10分)(2020•荆门)如图,AC为⊙O的直径,AP为⊙O的切线,M是AP上一点,过点M的直线与⊙O交于点B,D两点,与AC交于点E,连接AB,AD,AB=BE.(1)求证:AB=BM;(2)若AB=3,AD=245,求⊙O的半径.12.(9分)(2020•咸宁)如图,在Rt△ABC中,∠C=90°,点O在AC上,以OA为半径的半圆O交AB于点D,交AC于点E,过点D作半圆O的切线DF,交BC于点F.(1)求证:BF=DF;(2)若AC=4,BC=3,CF=1,求半圆O的半径长.13.(9分)(2020•随州)如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,与BC交于点M,与AB的另一个交点为E,过M作MN⊥AB,垂足为N.(1)求证:MN是⊙O的切线;(2)若⊙O的直径为5,sin B=35,求ED的长.14.(8分)(2020•湖北)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D的直线EF交AC于点F,交AB的延长线于点E,且∠BAC=2∠BDE.(1)求证:DF是⊙O的切线;(2)当CF=2,BE=3时,求AF的长.15.(8分)(2019 武汉)已知AB是⊙O的直径,AM和BN是⊙O的两条切线,DC与⊙O 相切于点E,分别交AM、BN于D、C两点.(1)如图1,求证:AB2=4AD•BC;(2)如图2,连接OE并延长交AM于点F,连接CF.若∠ADE=2∠OFC,AD=1,求图中阴影部分的面积.。

武汉中考数学---圆考题汇总本文选编了2007—2012武汉中考、四月调考中圆相关内容的考题,如需可编辑版本请与作者联系:1.QQ邮箱:957468321@ 2.百度站内私信:用户名 ronnie_rocket2012 22.(本题满分8分)在锐角△ABC 中,BC =5,54sin =A . (1)如图1,求△ABC 的外接圆的直径; (2)如图2,点I 为△ABC 的内心,若BA =(四调)10.如图,E 为正方形ABCD 的边上任意一点.若正方形ABCD 的边长为4, D .21 O 相切于点E ,F ,G ,且AB ∥CD .OB 与EF 相交于点M ,OC 与FG 相交于点N ,连接MN . (1)求证:OB ⊥OC ;(2)若OB =6,OC =8,求MN 的长.第10题图PC第22题图CP2011. (本题满分8分)如图,PA 为⊙O 的切线,A 为切点,过A 作OP 的垂线AB ,垂足为点C,交⊙O 于点B,延长BO 与⊙O 交于点D ,与PA 的延长线交于点E,(1)求证:PB 为⊙O 的切线;(2)若tan ∠ABE=21,求sin ∠E.︒=30ABC ,AC 的延长线与过点B 的⊙O CD 的长为( ),弦CD 平分AC ,2010 22. (本题满分8分) 如图,点O 在∠APB 的平分在线,圆O 与PA 相切于点C ;(1) 求证:直线PB 与圆O 相切;(2) PO 的延长线与圆O 交于点E 。
若圆O 的半径为3,PC=4。
求弦CE 的长。
O 的直径22.如图,Rt ABC △中,90ABC ∠=°,以AB 为直径作O ⊙交AC 边于点D ,E 是边BC 的中点,连接DE .(1)求证:直线DE 是O ⊙的切线;(2)连接OC 交DE 于点F ,若OF CF =,求tan ACO ∠的值.EC EBA OFD(四调)10.如图,已知△ABC 的外接圆⊙O 的半径为1,D ,E 分别为AB ,AC 的中点,则sin ∠BAC 的值等于线段A .BC 的长.B .DE 的长.C .AD 的长. D .AE 的长22.(本题满分8分)如图,已知△ABC ,以边BC 为直径的圆与边AB 交于点D ,点E 为的中点,AF 为△ABC 的角平分线,且AF ⊥EC .AC 是弦,∠BAC 的平分线AD 交⊙O 于2007 22.(本题8分)如图,等腰三角形ABC 中,AC =BC =10,AB =12。
备战2021湖北省各市2019年中考数学圆真题汇编压轴题数学试题1.(2019•孝感)如图,点/是△/48C的内心,8/的延长线与△?!宓的外接圆。
0交于点。
,与4C交于点&延长CD、取相交于点R N4站的平分线交力7于点G.(1)求证:DG//CA-,(2)求证:AD= /P;(3)若。
£=4,8E=5,求夕的长.2.(2019•襄阳)如图,点£是4力宓的内心,的延长线和的外接圆。
0 相交于点。
,过。
作直线外〃8c.(1)求证:国是。
0的切线;(2)若DE=6, BC=#,求优弧氤的长.3.(2019•黄石)如图,>18是。
的直径,点。
在的延长线上,C、E是GO上的两点,CE=CB,4BCD=4CAE,延长交8c的延长线于点£(1)求证:勿是。
0的切线;(2)求证:CE= CF',(3)若劭=1, CD=正,求弦4C的长.4.(2019•荆门)已知锐角△?!宓的外接圆圆心为0,半径为兄(1)求证:¥[一 = 2求;S1ELD(2)若中/4=45° , N8=60° , 求8c的长及sinC的值.5.(2019•荆州)如图,是00的直径,点C为。
上一点,点P是半径08 上一动点(不与0, 8重合),过点?作射线4AB,分别交弦班BCTP, E两点、,在射线/上取点尸,卷.FC= FD.(1)求证:厂C是。
的切线;(2)当点E是标的中点时,①若N847=60° ,判断以0, B, E, C为顶点的四边形是什么特殊四边形, 并说明理由;②若tanN脑=* 且48=20,求的长.6.(2019 •咸宁)如图,在Rt^/l8C中,/ ACB=90。
,。
为四的中点,以CD 为直径的。
分别交4C, BC于点、E,尸两点,过点尸作尸G_L48于点G.(1)试判断尸G与。
0的位置关系,并说明理由.(2)若4G=3, CD=2.5,求fG的长.7.(2019•宜昌)已知:在矩形彳仇步中,E,尸分别是边四,朋上的点,过点尸作灰的垂线交勿于点H,以炉为直径作半圆0.(D填空:点4 (填“在”或“不在”)上;当菽=百时,tan N 〃■厂的值是;(2)如图1,在△&?/中,当生=/7/时,求证:AD=AE^DH](3)如图2,当△&?/的顶点尸是边4。
2020年湖北省中考数学各地区模拟试题分类(武汉市专版)(二)——《圆》一.选择题1.(2020•江岸区校级模拟)已知⊙O的半径为4,点O到直线m的距离为3,则直线m与⊙O的位置关系是()A.相离B.相交C.相切D.不确定2.(2020•武汉模拟)如图,AB是⊙O的直径,AB=a,点P在半径OA上,AP=b,过P 作PC⊥AB交⊙O于点C,在半径OB上取点Q,使得OQ=CP,DQ⊥AB交⊙O于点D,点C,D位于AB两侧,则弧AC与弧BD的弧长之和为()A.B.C.D.3.(2020•武汉模拟)在⊙O中内接四边形ABCD,其中A,C为定点,AC=8,B在⊙O 上运动,BD⊥AC,过O作AD的垂线,若⊙O的直径为10,则OE的最大值接近于()A.B.C.4 D.5 4.(2020•武昌区模拟)如图,正方形ABCD的边长为1,点E是AB边上的一点,将△BCE 沿着CE折叠得△FCE.若CF,CE恰好都与正方形ABCD的中心O为圆心的⊙O相切,则折痕CE的长为()A.2B.C.D.5.(2020•武汉模拟)如图,在等腰直角△ABC中,斜边AB的长度为8,以AC为直径作圆,点P为半圆上的动点,连接BP,取BP的中点M,则CM的最小值为()A.3B.2﹣C.﹣D.3﹣6.(2020•武汉模拟)如图,PA、PB为⊙O的切线,直线MN切⊙O且MN⊥PA.若PM =5,PN=4,则OM的长为()A.2 B.C.D.7.(2020•青山区模拟)如图,A,B,C,D为一直线上4个点,BC=3,△BCE为等边三角形,⊙O过A,D,E三点,且∠AOD=120°,设AB=x,CD=y,则y与x的函数关系式是()A.y=B.y=x C.y=3x+3 D.y=8.(2020•硚口区模拟)平面直角坐标系中,M点坐标为(﹣2,3),以2为半径画⊙M,则以下结论正确的是()A.⊙M与x轴相交,与y轴相切B.⊙M与x轴相切,与y轴相离C.⊙M与x轴相离,与y轴相交D.⊙M与x轴相离,与y轴相切9.(2020•武汉模拟)如图,在⊙O中,AB是直径,且AB=10,点D是⊙O上一点,点C 是的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,OP,CO.关于下列结论:①∠BAD=∠ABC;②GP =GD;③点P是△ACQ的外心;④点P是△AOC的内心;⑤若CB∥GD,则OP=.正确的个数有()A.2 B.3 C.4 D.0 10.(2020•武汉模拟)如图,BC为⊙O直径,弦AC=2,弦AB=4,D为⊙O上一点,I 为AD上一点,且DC=DB=DI,AI长为()A.B.C.D.二.填空题11.(2020•武汉模拟)如图,在⊙O中,弦AB=4,点C是上的动点(不为A,B),且∠ACB=120°,则CA+CB的最大值为.12.(2020•武汉模拟)如图,正方形的边长为8,剪去四个角后成为一个正八边形,则这个正八边形的面积为.13.(2020•武汉模拟)圆锥的侧面展开图是一个扇形,扇形的弧长为10πcm,扇形面积为65πcm2,则圆锥的高为.14.(2020•武汉模拟)正八边形半径为2,则正八边形的面积为.15.(2020•武汉模拟)如图,正方形ABCD中,AB=4,E,F分别是边AB,AD上的动点,AE=DF,连接DE,CF交于点P,过点P作PK∥BC,且PK=2,若∠CBK的度数最大时,则BK长为.16.(2020•武汉模拟)已知一个圆锥的高为6cm,半径为8cm,则这个圆锥的侧面积为.17.(2020•武汉模拟)正n边形内接于半径为R的圆,这个n边形的面积为3R2,则n等于.18.(2020•武汉模拟)如图,PA,PB分别与⊙O相切于A,B两点,∠P=70°,点C在劣弧AB上,则∠C=.19.(2020•武汉模拟)我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的周长,进而确定圆周率.某圆的半径为R,其内接正十二边形的周长为C.若R=,则C=,≈(结果精确到0.01,参考数据:≈2.449,≈1.414).三.解答题20.(2020•武汉模拟)如图,AB是⊙O的直径,CD与⊙O相切于D,作CH⊥AB于H,交⊙O于E,交AD于F,若AE∥CD.(1)求证:AE=EF;(2)若cos C=,AB=,求AF的长.21.(2020•青山区模拟)已知,⊙O过矩形ABCD的顶点D,且与AB相切于点E,⊙O 分别交BC,CD于H,F,G三点.(1)如图1,求证:BE﹣AE=CG;(2)如图2,连接DF,DE.若AE=3,AD=9,tan∠EDF=,求FC的值.22.(2020•武汉模拟)如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC、AB于点E.F.(1)试判断直线BC与⊙O的位置关系,并说明理由;(2)若BD=2,BF=2,求⊙O的半径.23.(2020•硚口区二模)如图,在Rt△ABC中,∠ACB=90°,以AB上的一点O为圆心,OA为半径作圆O,与BC相切于点D,交AB于点E,交AC于点F.(1)求证:DE=DF;(2)若CF:BE=4:5,求tan∠BDE的值.24.(2020•洛江区一模)如图①,AB为⊙O的直径,C为⊙O上一点,D为BC延长线一点,且BC=CD,直线CE与⊙O相切于点C,与AD相交于点E.(1)求证:CE⊥AD;(2)如图②,设BE与⊙O交于点F,AF的延长线与CE交于点P.①求证:∠PCF=∠CBF;②若PF=6,tan∠PEF=,求PC的长.参考答案一.选择题1.解:∵d=3<半径=4,∴直线与圆相交,故选:B.2.解:连接OC、OD,如图,∵CP⊥OA,DQ⊥OB,∴∠OPC=∠OQD=90°,在Rt△OPC和Rt△DQO中,∴Rt△OPC≌Rt△DQO(HL),∴∠POC=∠ODQ,而∠ODQ+∠DOQ=90°,∴∠POC+∠DOQ=90°,∴弧AC与弧BD的弧长之和==aπ.故选:B.3.解:如图,当点B与A重合时,连接CD.∵BD⊥AC,∴∠DAC=90°,∴CD是直径,∵OE⊥AD,∴AE=ED,∵OC=OD,∴OE=AC=4,此时OE的值最大,最大值为4∴OE的最大值为4,故选:C.4.解:连接OC,∵O为正方形ABCD的中心,∴∠DCO=∠BCO,∵CF与CE都为⊙O的切线,∴CO平分∠ECF,即∠FCO=∠ECO,∴∠DCO﹣∠FCO=∠BCO﹣∠ECO,即∠DCF=∠BCE,∵△BCE沿着CE折叠至△FCE,∴∠BCE=∠ECF,∴∠BCE=∠ECF=∠DCF=∠BCD=30°,在Rt△BEC中,cos∠ECB=,∴CE===,故选:B.5.解:如图,连接PA、PC,取AB、BC的中点E、F,连接EF、EM、FM,取EF的中点O,连接OM,OC,CM.∵AC是直径,∴∠APC=90°,∵BE=EA,BM=MP,∴EM∥PA,同理FM∥PC,∴∠BME=∠BPA,∠BMF=∠BPC,∴∠BME+∠BMF=∠BPA+∠BPC=90°,∴∠EMF=90°,∴点M的轨迹是,(EF为直径的半圆,图中红线部分)∵BC=AC,∠ACB=90°,AB=8,∴AC=BC=4,∵AE=EB,BF=CF=2,∴EF=AC=2,EF∥AC,∴∠EFB=∠EFC=∠ACB=90°,OE=OF=OM=,∴OC===,∵CM≥OC﹣OM,∴CM≥﹣故选:C.6.解:∵PA、PB为⊙O的切线,直线MN切⊙O于C,∴MB=MC,PA=PB,连接OC,OA,则四边形AOCN是正方形,设NC=OC=OA=AN=r,∵MN⊥PA,PM=5,PN=4,∴MN=3,∴CM=BM=3﹣r,∴5+3﹣r=4+r,解得:r=2,∴OC=2,CM=1,∴OM==,故选:D.7.解:连接AE,DE,∵∠AOD=120°,∴为240°,∴∠AED=120°,∵△BCE为等边三角形,∴∠BEC=60°;∴∠AEB+∠CED=60°;又∵∠EAB+∠AEB=∠EBC=60°,∴∠EAB=∠CED,∵∠ABE=∠ECD=120°;∴△ABE∽△ECD,∴=,即=,∴y=(0<x<6).8.解:∵M点坐标为(﹣2,3),∴点M到x轴的距离为3,到y轴的距离为2,∵⊙P的半径为2,∴圆心M到x轴的距离大于半径,到y轴的距离等于半径,故⊙M与x轴相离,与y轴相切,故选:D.9.解:不妨设∠BAD=∠ABC,则=,∵=,∴==,这个显然不符合题意,故①错误,连接OD,∵GD是⊙O的切线,∴OD⊥DG,∴∠ODG=90°,∴∠GDP+∠ODA=90°,∵GE⊥AB,∴∠AEP=90°,∴∠PAE+∠APE=90°,∵OA=OD,∴∠OAD=∠ODA,∵∠APE=∠GPD,∴∠GDP=∠GPD,∴GP=GD,故②正确,∵AB是直径,∴∠ACB=90°,∵∠ACP+∠BCE=90°,∠BCE+∠ABC=90°,∴∠ACE=∠ABC,∵=,∴∠CAP=∠ABC,∴∠PAC=∠PCA,∵∠AQC+∠CAP=90°,∠ACP+∠PCQ=90°,∴∠PCQ=∠PQC,∴PC=PQ,∴PA=PQ,∵∠ACQ=90°,∴点P是△ACQ的外接圆的圆心,故③正确,∵与不一定相等,∴∠CAP与∠DAB不一定相等,∴点P不一定是△AOC的内心,故④错误,∵DG∥BC,OD⊥DG,∴OD⊥BC,∴=,∵=,∴==,∴∠AOC=∠COD=∠DOB=60°,∠CAD=∠DAB=30°∵OA=OC,∴△OAC是等边三角形,∵CE⊥OA,∴∠ACE=∠OCE,∴点P是△AOC的外心,∴OP=AP=PC===,故⑤错误,故选:A.10.解:如图,连接IC,作IE⊥AC于E,IF⊥AB于F,IG⊥BC于G.∵DB=DC,∴=,∠DBC=∠DCB,∴∠BAD=∠CAD,∵DI=DC,∴∠DIC=∠DCI,∵∠DIC=∠DAC+∠ACI,∠DCI=∠DCB+∠ICB,∠DBC=∠DAC,∴∠ICA=∠ICB,∴点I为△ABC内心,∴IE=IF=IG,∵BC是直径,∴∠BAC=90°,∴BC===2,∵S△ABC=•AB•AC=•IE•(AB+AC+BC),∴IE=3﹣,∵∠IAE=∠AIE=45°,∴AI=IE=3﹣,故选:D.二.填空题(共9小题)11.解:取优弧AB中点P,连接PC,PA,PB,延长CA至M,使MA=CB,连接PM.∵=,∴PA=PB,∵∠APB+∠ACB=180°,∠ACB=120°,∴∠APB=60°,∴△APB是等边三角形,∴∠ACP=∠ABP=60°,∵∠PAM+∠PAC=180°,∠PAC+∠PBC=180°,∴∠PAM=∠PBC,∵AM=BC,AP=BP,∴△MAP≌△CBP(SAS),∴PM=PC,∵∠PCM=60°∴△MPC为等边三角形,∴PC=CM.∴CA+CB=PC,过点P作PD⊥AB连接OB,∵△PAB是等边三角形,∴PD过圆心O,∠BPD=30°,∴BD=AB=2,在Rt△BDP中,DP=6,在Rt△BDO中,根据勾股定理得,(6﹣OB)2+(2)2=OB2∴OB=4,当PC为圆的直径时,CA+CB的最大值为8.故答案为8.12.解:设剪掉的等腰直角三角形的直角边为x,则由2x+x=8,解得x=4(2﹣),∴S=64﹣2(8﹣4)2=128﹣128,故答案为:128﹣128.13.解:设母线长为R,由题意得:65π=×10π×R,解得R=13cm.设圆锥的底面半径为r,则10π=2πr,解得:r=5,故圆锥的高为:=12故答案为:12.14.解:连接OA,OB,作AC⊥BO于点C,∵⊙O的半径为2,则⊙O的内接正八边形的中心角为:=45°,∴AC=CO=2,∴S△ABO=OB•AC=×2×2=2,∴S正八边形=8S△ABO=16,故答案为:16.15.解:∵正方形ABCD中,AD=CD,∠A=∠CDA=90°,∵AE=DF,∴△ADE≌△DCF(SAS),∴∠ADE=∠DCF,∵∠ADE+∠CDE=90°,∴∠DCF+∠CDE=90°,∴∠CPD=90°,∴点P在以CD为直径的半圆上运动,取CD的中点O,过O作OM⊥CD,且点M在CD的右侧,MO=2,连接OP,KM,∵PK∥BC,BC⊥CD,∴PK⊥CD,∴PK∥OM,PK=OM=2,∴四边形POMK是平行四边形,∵CD=AB=4,∴OP=CD=2,∴OP=OM,∴四边形POMK是菱形,∴点K在以M为圆心,半径=2的半圆上运动,当BK与⊙M相切时,∠CBK最大,∴∠BKM=90°,∵BM==2,∴BK==6,故答案为:6.16.解:这个圆锥的母线长为=10,所以这个圆锥的侧面积=×2π×8×10=80π(cm2).故答案为80πcm2.17.解:根据正n边形内接于半径为R的圆,则可将其分割成n个全等的等腰三角形,其中等腰三角形的腰长为圆的半径R,顶角为,∵n边形的面积为3R2,∴n××R×R×sin=3R2n sin=6解得n=12.故答案为12.18.解:连结OA、OB,D为优弧AB上一点,∠ADB为弧AB所对的圆周角,如图,∵PA,PB分别与⊙O相切于A,B两点,∴OA⊥PA,OB⊥PB,∴∠OAP=∠OBP=90°,∴∠AOB+∠P=180°,∴∠AOB=180°﹣70°=110°,∴∠D=∠AOB=55°,∴∠ACB=180°﹣∠D=125°.故答案为:125°.19.解:如图,△AOB中,∠AOB=30°,OA=OB=+,作AH⊥OB于H.则AH=OA=,OH=AH=,∴BH=OB﹣OH=,∴AB===2,∴正十二边形的周长C=12×2=24,∴=≈3.11,故答案我为24,3.11.三.解答题(共5小题)20.(1)证明:连接OD,如图1,∵CD与⊙O相切于D,∴OD⊥DC,∴∠ODA+∠ADC=90°,∵OA=OD,∴∠ODA=∠OAD,∴∠OAD+∠ADC=90°,又∵CH⊥AB,∴∠AHC=90°,∴∠OAD+∠AFH=90°,∴∠ADC=∠AFH,∵AE∥CD,∴∠ADC=∠EAF,∴∠EAF=∠AFH,∴AE=EF;(2)解:∵AE∥CD,∴∠C=∠E,∴cos∠C=cos∠E=,设EH=4x,AE=5x,则AH=3x,连接OE,如图2,∵AB=,∴OA=OE=,∵EH2+OH2=OE2,∴,解得x=1,∴AE=EF=5,EH=4,AH=3,∴HF=1,∴AF==.21.解:(1)连接OE,延长EO与CD交于点M,∵⊙O与AB相切于点E,∴OE⊥AB,∵四边形ABCD是矩形,∴∠A=∠B=∠C=∠D=90°,AB∥CD,∴EM⊥CD,∴∠EMD=∠EMC=90°,DM=GM,∴四边形AEMD和四边形BEMC都是矩形,∴AE=DM,BE=CM,∵CM﹣CG=GM,∴BE﹣AE=CG;(2)连接EO,延长EO交⊙O于点N,交CD于点M,连接OD,EF,FN,过点N作NH⊥BC,与BC的延长线交于点H,如图2,由(1)知,四边形AEMD为矩形,∴AE=DM=MG=3,AD=EM=9,设⊙O的半径为r,则OD=r,OM=9﹣r,∵OD2﹣OM2=DM2,∴r2﹣(9﹣r)2=32,解得,r=5,∴BH=EN=2r=10,∴CH=BH﹣BC=BH﹣AD=1,∵EN为⊙O的直径,∴∠EFN=90°,∵∠ENF=∠EDF,tan∠EDF=,∴tan∠ENF=,设EF=4x,则FN=3x,∵EF2+FN2=EN2,∴16x2+9x2=100,解得,x=2,或x=﹣2(舍),∴EF=8,FN=6,设CF=y,BE=HN=z,则BF=9﹣y,FH=y+1,∵∠EFN=90°,∠B=∠H=90°,∴∠BFE+∠HFN=∠BFE+∠BEF=90°,∴∠BEF=∠HFN,∴△BEF∽△HFN,∴,即,解得,y=,即CF=.22.解:(1)线BC与⊙O的位置关系是相切,理由是:连接OD,∵OA=OD,∴∠OAD=∠ODA,∵AD平分∠CAB,∴∠OAD=∠CAD,∴∠ODA=∠CAD,∴OD∥AC,∵∠C=90°,∴∠ODB=90°,即OD⊥BC,∵OD为半径,∴线BC与⊙O的位置关系是相切;(2)设⊙O的半径为R,则OD=OF=R,在Rt△BDO中,由勾股定理得:OB2=BD2+OD2,即(R+2)2=(2)2+R2,解得:R=4,即⊙O的半径是4.23.(1)证明:连接OD、EF交于点M,∵AE是⊙O的直径,∴∠AFE=∠90°=∠ACB,∴EF∥BC,又∵BC切⊙O于D,∴∠ODB=90°,∴∠OME=∠ODB=90°,即OD⊥EF,∴=,∴DE=DF;(2)解:∵EF∥BC,∴=,∴可设AF=8k,AE=10k,∴OA=OE=OD=5k,∵∠AFE=90°,∴EF==6k,又∵OD⊥EF,∴EM=FM=3k,∵OD⊥EF,∴OM==4k,∴DM=OD﹣OM=k,∵EF∥BC,∴∠BDE=∠FED,∴tan∠BDE=tan∠FED===.24.(1)证明:如图①,连结OC.∵直线CE与⊙O相切于点C,∴OC⊥CE,即∠OCE=90°.∵OA=OB,BC=CD,∴OC是△BDA的中位线.∴OC∥AD.∴∠CED=∠OCE=90°,即OC⊥AD;(2)①证明:如图②,作直径CG,连结FG,连结CF,∵CG是直径,点F在圆上,∴∠CFG=90°.∴∠G+∠FCG=90°.由(1)可知∠OCE=∠PCF+∠FCG=90°,∴∠G=∠PCF.又∵∠G=∠CBF,∴∠PCF=∠CBF;②如图②,连结AC.∵AB是直径,点F在圆上,∴∠AFB=∠PFE=90°=∠CEA.又∵∠EPF=∠APE,∴△PEF∽△PAE.∴=,即PE2=PF•PA.在直角△PEF中,tan∠PEF==,又∵PF=6,∴EF=8,由勾股定理,可求得PE=10.∵∠FBC=∠PCF=∠CAF,∠CPF=∠APC ∴△PCF∽△PAC.∴=,即PC2=PF×PA.∴PC2=PE2,则PC=PE=10.。
备战2021湖北省各市2019年中考数学圆压轴题真题汇编数学试题1.(2019•孝感)如图,点I是△ABC的内心,BI的延长线与△ABC的外接圆⊙O 交于点D,与AC交于点E,延长CD、BA相交于点F,∠ADF的平分线交AF于点G.(1)求证:DG∥CA;(2)求证:AD=ID;(3)若DE=4,BE=5,求BI的长.2.(2019•襄阳)如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O 相交于点D,过D作直线DG∥BC.(1)求证:DG是⊙O的切线;(2)若DE=6,BC=6,求优弧的长.3.(2019•黄石)如图,AB是⊙O的直径,点D在AB的延长线上,C、E是⊙O 上的两点,CE=CB,∠BCD=∠CAE,延长AE交BC的延长线于点F.(1)求证:CD是⊙O的切线;(2)求证:CE=CF;(3)若BD=1,CD=,求弦AC的长.4.(2019•荆门)已知锐角△ABC的外接圆圆心为O,半径为R.(1)求证:=2R;(2)若△ABC中∠A=45°,∠B=60°,AC=,求BC的长及sin C的值.5.(2019•荆州)如图,AB是⊙O的直径,点C为⊙O上一点,点P是半径OB 上一动点(不与O,B重合),过点P作射线l⊥AB,分别交弦BC,于D,E两点,在射线l上取点F,使FC=FD.(1)求证:FC是⊙O的切线;(2)当点E是的中点时,①若∠BAC=60°,判断以O,B,E,C为顶点的四边形是什么特殊四边形,并说明理由;②若tan∠ABC=,且AB=20,求DE的长.6.(2019•咸宁)如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,以CD 为直径的⊙O分别交AC,BC于点E,F两点,过点F作FG⊥AB于点G.(1)试判断FG与⊙O的位置关系,并说明理由.(2)若AC=3,CD=2.5,求FG的长.7.(2019•宜昌)已知:在矩形ABCD中,E,F分别是边AB,AD上的点,过点F 作EF的垂线交DC于点H,以EF为直径作半圆O.(1)填空:点A(填“在”或“不在”)⊙O上;当=时,tan ∠AEF的值是;(2)如图1,在△EFH中,当FE=FH时,求证:AD=AE+DH;(3)如图2,当△EFH的顶点F是边AD的中点时,求证:EH=AE+DH;(4)如图3,点M在线段FH的延长线上,若FM=FE,连接EM交DC于点N,连接FN,当AE=AD时,FN=4,HN=3,求tan∠AEF的值.8.(2019•十堰)如图,△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,点E为AC延长线上一点,且∠CDE=∠BAC.(1)求证:DE是⊙O的切线;(2)若AB=3BD,CE=2,求⊙O的半径.9.(2019•随州)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC,BC于点D,E,点F在AC的延长线上,且∠BAC=2∠CBF.(1)求证:BF是⊙O的切线;(2)若⊙O的直径为3,sin∠CBF=,求BC和BF的长.10.(2019•湖北)已知△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,连接DB,DC.(1)如图①,当∠BAC=120°时,请直接写出线段AB,AC,AD之间满足的等量关系式:;(2)如图②,当∠BAC=90°时,试探究线段AB,AC,AD之间满足的等量关系,并证明你的结论;(3)如图③,若BC=5,BD=4,求的值.11.(2019•宜昌)如图,点O是线段AH上一点,AH=3,以点O为圆心,OA的长为半径作⊙O,过点H作AH的垂线交⊙O于C,N两点,点B在线段CN的延长线上,连接AB交⊙O于点M,以AB,BC为边作▱ABCD.(1)求证:AD是⊙O的切线;(2)若OH=AH,求四边形AHCD与⊙O重叠部分的面积;(3)若NH=AH,BN=,连接MN,求OH和MN的长.12.(2019•咸宁)定义:有一组邻边相等且对角互补的四边形叫做等补四边形.理解:(1)如图1,点A,B,C在⊙O上,∠ABC的平分线交⊙O于点D,连接AD,CD.求证:四边形ABCD是等补四边形;探究:(2)如图2,在等补四边形ABCD中,AB=AD,连接AC,AC是否平分∠BCD?请说明理由.运用:(3)如图3,在等补四边形ABCD中,AB=AD,其外角∠EAD的平分线交CD 的延长线于点F,CD=10,AF=5,求DF的长.13.(2019•鄂州)如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,连接OP交⊙O于E.过A点作AB⊥PO于点D,交⊙O于B,连接BC,PB.(1)求证:PB是⊙O的切线;(2)求证:E为△PAB的内心;(3)若cos∠PAB=,BC=1,求PO的长.参考答案1.(1)证明:∵点I是△ABC的内心,∴∠2=∠7,∵DG平分∠ADF,∴∠1=∠ADF,∵∠ADF=∠ABC,∴∠1=∠2,∵∠3=∠2,∴∠1=∠3,∴DG∥AC;(2)证明:∵点I是△ABC的内心,∴∠5=∠6,∵∠4=∠7+∠5=∠3+∠6,即∠4=∠DAI,∴DA=DI;(3)解:∵∠3=∠7,∠ADE=∠BDA,∴△DAE∽△DBA,∴AD:DB=DE:DA,即AD:9=4:AD,∴AD=6,∴DI=6,∴BI=BD﹣DI=9﹣6=3.2.(1)证明:连接OD交BC于H,连接OB、OC,如图,∵点E是△ABC的内心,∴AD平分∠BAC,∴∠BOD=∠COD,∴=,∴OD⊥BC,BH=CH,∵DG∥BC,∴OD⊥DG,∴DG是⊙O的切线;(2)解:连接BD、OB,如图,∵点E是△ABC的内心,∴∠ABE=∠CBE,∵∠DBC=∠BAD,∴∠DEB=∠BAD+∠ABE=∠DBC+∠CBE=∠DBE,∴DB=DE=6,∵BH=BC=3,在Rt△BDH中,sin∠BDH===,∴∠BDH=60°,而OB=OD,∴△OBD为等边三角形,∴∠BOD=60°,OB=BD=6,∴∠BOC=120°,∴优弧的长==8π.3.解:(1)连接OC,如右图所示,∵AB是⊙O的直径,∴∠CAD+∠ABC=90°,∵CE=CB,∴∠CAE=∠CAB,∵∠BCD=∠CAE,∴∠CAB=∠BCD,∵OB=OC,∴∠OBC=∠OCB,∴∠OCB+∠BCD=90°,∴∠OCD=90°,∴CD是⊙O的切线;(2)∵∠BAC=∠CAE,∠ACB=∠ACF=90°,AC=AC,∴△ABC≌△AFC(ASA),∴CB=CF,又∵CB=CE,∴CE=CF;(3)∵∠BCD=∠CAD,∠ADC=∠CDB,∴△DCB∽△DAC,∴,∴,∴DA=2,∴AB=AD﹣BD=2﹣1=1,设BC=a,AC=a,由勾股定理可得:,解得:a=,∴.4.解:(1)如图1,连接AO并延长交⊙O于D,连接CD,则∠ACD=90°,∠ABC=∠ADC,∵sin∠ABC=sin∠ADC=,∴=2R;(2)∵=2R,同理可得:==2R,∴2R==2,∴BC=2R•sin A=2sin45°=,如图2,过C作CE⊥AB于E,∴BE=BC•cos B=cos60°=,AE=AC•cos45°=,∴AB=AE+BE=,∵AB=2R•sin C,∴sin C==.5.解:(1)证明:连接OC,∵OB=OC,∴∠OBC=∠OCB,∵PF⊥AB,∴∠BPD=90°,∴∠OBC+∠BDP=90°,∵FC=FD∴∠FCD=∠FDC∵∠FDC=∠BDP∴∠OCB+∠FCD=90°∴OC⊥FC∴FC是⊙O的切线.(2)如图2,连接OC,OE,BE,CE,①以O,B,E,C为顶点的四边形是菱形.理由如下:∵AB是直径,∴∠ACB=90°,∵∠BAC=60°,∴∠BOC=120°,∵点E是的中点,∴∠BOE=∠COE=60°,∵OB=OE=OC∴△BOE,△OCE均为等边三角形,∴OB=BE=CE=OC∴四边形BOCE是菱形;②若tan∠ABC=,且AB=20,求DE的长.∵=tan∠ABC=,设AC=3k,BC=4k(k>0),由勾股定理得AC2+BC2=AB2,即(3k)2+(4k)2=202,解得k=4,∴AC=12,BC=16,∵点E是的中点,∴OE⊥BC,BH=CH=8,∴OE×BH=OB×PE,即10×8=10PE,解得:PE=8,由勾股定理得OP===6,∴BP=OB﹣OP=10﹣6=4,∵=tan∠ABC=,即DP=BP==3∴DE=PE﹣DP=8﹣3=5.6.解:(1)FG与⊙O相切,理由:如图,连接OF,∵∠ACB=90°,D为AB的中点,∴CD=BD,∴∠DBC=∠DCB,∵OF=OC,∴∠OFC=∠OCF,∴∠OFC=∠DBC,∴OF∥DB,∴∠OFG+∠DGF=180°,∵FG⊥AB,∴∠DGF=90°,∴∠OFG=90°,∴FG与⊙O相切;(2)连接DF,∵CD=2.5,∴AB=2CD=5,∴BC==4,∵CD为⊙O的直径,∴∠DFC=90°,∴FD⊥BC,∵DB=DC,∴BF=BC=2,∵sin∠ABC=,即=,∴FG=.7.解:(1)连接AO,∵∠EAF=90°,O为EF中点,∴AO=EF,∴点A在⊙O上,当=时,∠AEF=45°,∴tan∠AEF=tan45°=1,故答案为:在,1;(2)∵EF⊥FH,∴∠EFH=90°,在矩形ABCD中,∠A=∠D=90°,∴∠AEF+∠AFE=90°,∠AFE+∠DFH=90°,∴∠AEF=∠DFH,又FE=FH,∴△AEF≌△DFH(AAS),∴AF=DH,AE=DF,∴AD=AF+DF=AE+DH;(3)延长EF交HD的延长线于点G,∵F分别是边AD上的中点,∴AF=DF,∵∠A=∠FDG=90°,∠AFE=∠DFG,∴△AEF≌△DGF(ASA),∴AE=DG,EF=FG,∵EF⊥FH,∴EH=GH,∴GH=DH+DG=DH+AE,∴EH=AE+DH;(4)过点M作MQ⊥AD于点Q.设AF=x,AE=a,∵FM=FEEF⊥FH,∴△EFM为等腰直角三角形,∴∠FEM=∠FMN=45°,∵FM=FE,∠A=∠MQF=90°,∠AEF=∠MFQ,∴△AEF≌△QFM(ASA),∴AE=FQ=a,AF=QM,∵AE=AD,∴AF=DQ=QM=x,∵DC∥QM,∴,∵DC∥AB∥QM,∴,∴,∵FE=FM,∴,∠FEM=∠FMN=45°,∴△FEN~△HMN,∴,∴.8.解:(1)如图,连接OD,AD,∵AC是直径,∴∠ADC=90°,∴AD⊥BC,∵AB=AC,∴∠CAD=∠BAD=∠BAC,∵∠CDE=∠BAC.∴∠CDE=∠CAD,∵OA=OD,∴∠CAD=∠ADO,∵∠ADO+∠ODC=90°,∴∠ODC+∠CDE=90°∴∠ODE=90°又∵OD是⊙O的半径∴DE是⊙O的切线;(2)解:∵AB=AC,AD⊥BC,∴BD=CD,∵AB=3BD,∴AC=3DC,设DC=x,则AC=3x,∴AD==2x,∵∠CDE=∠CAD,∠DEC=∠AED,∴△CDE∽△DAE,∴=,即==∴DE=4,x=,∴AC=3x=14,∴⊙O的半径为7.9.(1)证明:连接AE,∵AB是⊙O的直径,∴∠AEB=90°,∴∠1+∠2=90°.∵AB=AC,∴2∠1=∠CAB.∵∠BAC=2∠CBF,∴∠1=∠CBF∴∠CBF+∠2=90°即∠ABF=90°∵AB是⊙O的直径,∴直线BF是⊙O的切线;(2)解:过点C作CH⊥BF于H.∵sin∠CBF=,∠1=∠CBF,∴sin∠1=,∵在Rt△AEB中,∠AEB=90°,AB=3,∴BE=AB•sin∠1=3×=,∵AB=AC,∠AEB=90°,∴BC=2BE=2,∵sin∠CBF==,∴CH=2,∵CH∥AB,∴=,即=,∴CF=6,∴AF=AC+CF=9,∴BF==6.10.解:(1)如图①在AD上截取AE=AB,连接BE,∵∠BAC=120°,∠BAC的平分线交⊙O于点D,∴∠DBC=∠DAC=60°,∠DCB=∠BAD=60°,∴△ABE和△BCD都是等边三角形,∴∠DBE=∠ABC,AB=BE,BC=BD,∴△BED≌△BAC(SAS),∴DE=AC,∴AD=AE+DE=AB+AC;故答案为:AB+AC=AD.(2)AB+AC=AD.理由如下:如图②,延长AB至点M,使BM=AC,连接DM,∵四边形ABDC内接于⊙O,∴∠MBD=∠ACD,∵∠BAD=∠CAD=45°,∴BD=CD,∴△MBD≌△ACD(SAS),∴MD=AD,∠M=∠CAD=45°,∴MD⊥AD.∴AM=,即AB+BM=,∴AB+AC=;(3)如图③,延长AB至点N,使BN=AC,连接DN,∵四边形ABDC内接于⊙O,∴∠NBD=∠ACD,∵∠BAD=∠CAD,∴BD=CD,∴△NBD≌△ACD(SAS),∴ND=AD,∠N=∠CAD,∴∠N=∠NAD=∠DBC=∠DCB,∴△NAD∽△CBD,∴,∴,又AN=AB+BN=AB+AC,BC=5,BD=4,∴=.11.解:(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,∵∠AHC=90°,∴∠HAD=90°,即OA⊥AD,又∵OA为半径,∴AD是⊙O的切线;(2)解:如右图,连接OC,∵OH=OA,AH=3,∴OH=1,OA=2,∵在Rt△OHC中,∠OHC=90°,OH=OC,∴∠OCH=30°,∴∠AOC=∠OHC+∠OCH=120°,∴S扇形OAC==,∵CH==,∴S△OHC=×1×=,∴四边形ABCD与⊙O重叠部分的面积=S扇形OAC+S△OHC=+;(3)设⊙O半径OA=r=OC,OH=3﹣r,在Rt△OHC中,OH2+HC2=OC2,∴(3﹣r)2+12=r2,∴r=,则OH=,在Rt△ABH中,AH=3,BH=+1=,则AB=,在Rt△ACH中,AH=3,CH=NH=1,得AC=,在△BMN和△BCA中,∠B=∠B,∠BMN=∠BCA,∴△BMN∽△BCA,∴=即==,∴MN=,∴OH=,MN=.12.解:(1)证明:∵四边形ABCD为圆内接四边形,∴∠A+∠C=180°,∠ABC+∠ADC=180°,∵BD平分∠ABC,∴∠ABD=∠CBD,∴,∴AD=CD,∴四边形ABCD是等补四边形;(2)AC平分∠BCD,理由如下:如图2,过点A分别作AE⊥BC于点E,AF垂直CD的延长线于点F,则∠AEB=∠AFD=90°,∵四边形ABCD是等补四边形,∴∠B+∠ADC=180°,又∠ADC+∠ADF=180°,∴∠B=∠ADF,∵AB=AD,∴△ABE≌△ADF(AAS),∴AE=AF,∴AC是∠BCF的平分线,即AC平分∠BCD;(3)如图3,连接AC,∵四边形ABCD是等补四边形,∴∠BAD+∠BCD=180°,又∠BAD+∠EAD=180°,∴∠EAD=∠BCD,∵AF平分∠EAD,∴∠FAD=∠EAD,由(2)知,AC平分∠BCD,∴∠FCA=∠BCD,∴∠FCA=∠FAD,又∠AFC=∠DFA,∴△ACF∽△DAF,∴,即,∴DF=5﹣5.13.(1)证明:连结OB,∵AC为⊙O的直径,∴∠ABC=90°,∵AB⊥PO,∴PO∥BC∴∠AOP=∠C,∠POB=∠OBC,OB=OC,∴∠OBC=∠C,∴∠AOP=∠POB,在△AOP和△BOP中,,∴△AOP≌△BOP(SAS),∴∠OBP=∠OAP,∵PA为⊙O的切线,∴∠OAP=90°,∴∠OBP=90°,∴PB是⊙O的切线;(2)证明:连结AE,∵PA为⊙O的切线,∴∠PAE+∠OAE=90°,∵AD⊥ED,∴∠EAD+∠AED=90°,∵OE=OA,∴∠OAE=∠AED,∴∠PAE=∠DAE,即EA平分∠PAD,∵PA、PB为⊙O的切线,∴PD平分∠APB∴E为△PAB的内心;(3)解:∵∠PAB+∠BAC=90°,∠C+∠BAC=90°,∴∠PAB=∠C,∴cos∠C=cos∠PAB=,在Rt△ABC中,cos∠C===,∴AC=,AO=,∵△PAO∽△ABC,∴,∴PO===5.。
2021年湖北省各市中考数学真题汇编压轴题:《圆》1.(2021•孝感)如图,点I是△ABC的内心,BI的延长线与△ABC的外接圆⊙O交于点D,与AC交于点E,延长CD、BA相交于点F,∠ADF的平分线交AF于点G.(1)求证:DG∥CA;(2)求证:AD=ID;(3)若DE=4,BE=5,求BI的长.2.(2021•襄阳)如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D,过D作直线DG∥BC.(1)求证:DG是⊙O的切线;(2)若DE=6,BC=6,求优弧的长.3.(2021•黄石)如图,AB是⊙O的直径,点D在AB的延长线上,C、E是⊙O上的两点,CE=CB,∠BCD=∠CAE,延长AE交BC的延长线于点F.(1)求证:CD是⊙O的切线;(2)求证:CE=CF;(3)若BD=1,CD=,求弦AC的长.4.(2021•荆门)已知锐角△ABC的外接圆圆心为O,半径为R.(1)求证:=2R;(2)若△ABC中∠A=45°,∠B=60°,AC=,求BC的长及sin C的值.5.(2021•荆州)如图,AB是⊙O的直径,点C为⊙O上一点,点P是半径OB上一动点(不与O,B重合),过点P作射线l⊥AB,分别交弦BC,于D,E两点,在射线l 上取点F,使FC=FD.(1)求证:FC是⊙O的切线;(2)当点E是的中点时,①若∠BAC=60°,判断以O,B,E,C为顶点的四边形是什么特殊四边形,并说明理由;②若tan∠ABC=,且AB=20,求DE的长.6.(2021•咸宁)如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,以CD为直径的⊙O分别交AC,BC于点E,F两点,过点F作FG⊥AB于点G.(1)试判断FG与⊙O的位置关系,并说明理由.(2)若AC=3,CD=2.5,求FG的长.7.(2021•宜昌)已知:在矩形ABCD中,E,F分别是边AB,AD上的点,过点F作EF 的垂线交DC于点H,以EF为直径作半圆O.(1)填空:点A(填“在”或“不在”)⊙O上;当=时,tan∠AEF的值是;(2)如图1,在△EFH中,当FE=FH时,求证:AD=AE+DH;(3)如图2,当△EFH的顶点F是边AD的中点时,求证:EH=AE+DH;(4)如图3,点M在线段FH的延长线上,若FM=FE,连接EM交DC于点N,连接FN,当AE=AD时,FN=4,HN=3,求tan∠AEF的值.8.(2021•十堰)如图,△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,点E为AC延长线上一点,且∠CDE=∠BAC.(1)求证:DE是⊙O的切线;(2)若AB=3BD,CE=2,求⊙O的半径.9.(2021•随州)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC,BC于点D,E,点F在AC的延长线上,且∠BAC=2∠CBF.(1)求证:BF是⊙O的切线;(2)若⊙O的直径为3,sin∠CBF=,求BC和BF的长.10.(2021•湖北)已知△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,连接DB,DC.(1)如图①,当∠BAC=120°时,请直接写出线段AB,AC,AD之间满足的等量关系式:;(2)如图②,当∠BAC=90°时,试探究线段AB,AC,AD之间满足的等量关系,并证明你的结论;(3)如图③,若BC=5,BD=4,求的值.11.(2021•宜昌)如图,点O是线段AH上一点,AH=3,以点O为圆心,OA的长为半径作⊙O,过点H作AH的垂线交⊙O于C,N两点,点B在线段CN的延长线上,连接AB交⊙O于点M,以AB,BC为边作▱ABCD.(1)求证:AD是⊙O的切线;(2)若OH=AH,求四边形AHCD与⊙O重叠部分的面积;(3)若NH=AH,BN=,连接MN,求OH和MN的长.12.(2021•咸宁)定义:有一组邻边相等且对角互补的四边形叫做等补四边形.理解:(1)如图1,点A,B,C在⊙O上,∠ABC的平分线交⊙O于点D,连接AD,CD.求证:四边形ABCD是等补四边形;探究:(2)如图2,在等补四边形ABCD中,AB=AD,连接AC,AC是否平分∠BCD?请说明理由.运用:(3)如图3,在等补四边形ABCD中,AB=AD,其外角∠EAD的平分线交CD的延长线于点F,CD=10,AF=5,求DF的长.13.(2021•鄂州)如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,连接OP交⊙O 于E.过A点作AB⊥PO于点D,交⊙O于B,连接BC,PB.(1)求证:PB是⊙O的切线;(2)求证:E为△PAB的内心;(3)若cos∠PAB=,BC=1,求PO的长.参考答案1.(1)证明:∵点I是△ABC的内心,∴∠2=∠7,∵DG平分∠ADF,∴∠1=∠ADF,∵∠ADF=∠ABC,∴∠1=∠2,∵∠3=∠2,∴∠1=∠3,∴DG∥AC;(2)证明:∵点I是△ABC的内心,∴∠5=∠6,∵∠4=∠7+∠5=∠3+∠6,即∠4=∠DAI,∴DA=DI;(3)解:∵∠3=∠7,∠ADE=∠BDA,∴△DAE∽△DBA,∴AD:DB=DE:DA,即AD:9=4:AD,∴AD=6,∴DI=6,∴BI=BD﹣DI=9﹣6=3.2.(1)证明:连接OD交BC于H,连接OB、OC,如图,∵点E是△ABC的内心,即∠BAD=∠CAD,∴∠BOD=∠COD,∴=,∴OD⊥BC,BH=CH,∵DG∥BC,∴OD⊥DG,∴DG是⊙O的切线;(2)解:连接BD、OB,如图,∵点E是△ABC的内心,∴∠ABE=∠CBE,∵∠DBC=∠BAD,∴∠DEB=∠BAD+∠ABE=∠DBC+∠CBE=∠DBE,∴DB=DE=6,∵BH=BC=3,在Rt△BDH中,sin∠BDH===,∴∠BDH=60°,而OB=OD,∴△OBD为等边三角形,∴∠BOD=60°,OB=BD=6,∴∠BOC=120°,∴优弧的长==8π.3.解:(1)连接OC,如右图所示,∵AB是⊙O的直径,∴∠CAD+∠ABC=90°,∵CE=CB,∴∠CAE=∠CAB,∵∠BCD=∠CAE,∴∠CAB=∠BCD,∵OB=OC,∴∠OBC=∠OCB,∴∠OCB+∠BCD=90°,∴∠OCD=90°,∴CD是⊙O的切线;(2)∵∠BAC=∠CAE,∠ACB=∠ACF=90°,AC=AC,∴△ABC≌△AFC(ASA),∴CB=CF,又∵CB=CE,∴CE=CF;(3)∵∠BCD=∠CAD,∠ADC=∠CDB,∴△DCB∽△DAC,∴,∴,∴DA=2,∴AB=AD﹣BD=2﹣1=1,设BC=a,AC=a,由勾股定理可得:,解得:a=,∴.4.解:(1)如图1,连接AO并延长交⊙O于D,连接CD,则∠ACD=90°,∠ABC=∠ADC,∵sin∠ABC=sin∠ADC=,∴=2R;(2)∵=2R,同理可得:==2R,∴2R==2,∴BC=2R•sin A=2sin45°=,如图2,过C作CE⊥AB于E,∴BE=BC•cos B=cos60°=,AE=AC•cos45°=,∴AB=AE+BE=,∵AB=2R•sin C,∴sin C==.5.解:(1)证明:连接OC,∵OB=OC,∴∠OBC=∠OCB,∵PF⊥AB,∴∠BPD=90°,∴∠OBC+∠BDP=90°,∵FC=FD∴∠FCD=∠FDC∵∠FDC=∠BDP∴∠OCB+∠FCD=90°∴OC⊥FC∴FC是⊙O的切线.(2)如图2,连接OC,OE,BE,CE,①以O,B,E,C为顶点的四边形是菱形.理由如下:∵AB是直径,∴∠ACB=90°,∵∠BAC=60°,∴∠BOC=120°,∵点E是的中点,∴∠BOE=∠COE=60°,∵OB=OE=OC∴△BOE,△OCE均为等边三角形,∴OB=BE=CE=OC∴四边形BOCE是菱形;②若tan∠ABC=,且AB=20,求DE的长.∵=tan∠ABC=,设AC=3k,BC=4k(k>0),由勾股定理得AC2+BC2=AB2,即(3k)2+(4k)2=202,解得k=4,∴AC=12,BC=16,∵点E是的中点,∴OE⊥BC,BH=CH=8,∴OE×BH=OB×PE,即10×8=10PE,解得:PE=8,由勾股定理得OP===6,∴BP=OB﹣OP=10﹣6=4,∵=tan∠ABC=,即DP=BP==3∴DE=PE﹣DP=8﹣3=5.6.解:(1)FG与⊙O相切,理由:如图,连接OF,∵∠ACB=90°,D为AB的中点,∴CD=BD,∴∠DBC=∠DCB,∵OF=OC,∴∠OFC=∠OCF,∴∠OFC=∠DBC,∴OF∥DB,∴∠OFG+∠DGF=180°,∵FG⊥AB,∴∠DGF=90°,∴∠OFG=90°,∴FG与⊙O相切;(2)连接DF,∵CD=2.5,∴AB=2CD=5,∴BC==4,∵CD为⊙O的直径,∴∠DFC=90°,∴FD⊥BC,∵DB=DC,∴BF=BC=2,∵sin∠ABC=,即=,∴FG=.7.解:(1)连接AO,∵∠EAF=90°,O为EF中点,∴AO=EF,∴点A在⊙O上,当=时,∠AEF=45°,∴tan∠AEF=tan45°=1,故答案为:在,1;(2)∵EF⊥FH,∴∠EFH=90°,在矩形ABCD中,∠A=∠D=90°,∴∠AEF+∠AFE=90°,∠AFE+∠DFH=90°,∴∠AEF=∠DFH,又FE=FH,∴△AEF≌△DFH(AAS),∴AF=DH,AE=DF,∴AD=AF+DF=AE+DH;(3)延长EF交HD的延长线于点G,∵F分别是边AD上的中点,∴AF=DF,∵∠A=∠FDG=90°,∠AFE=∠DFG,∴△AEF≌△DGF(ASA),∴AE=DG,EF=FG,∵EF⊥FH,∴EH=GH,∴GH=DH+DG=DH+AE,∴EH=AE+DH;(4)过点M作MQ⊥AD于点Q.设AF=x,AE=a,∵FM=FEEF⊥FH,∴△EFM为等腰直角三角形,∴∠FEM=∠FMN=45°,∵FM=FE,∠A=∠MQF=90°,∠AEF=∠MFQ,∴△AEF≌△QFM(ASA),∴AE=FQ=a,AF=QM,∵AE=AD,∴AF=DQ=QM=x,∵DC∥QM,∴,∵DC∥AB∥QM,∴,∴,∵FE=FM,∴,∠FEM=∠FMN=45°,∴△FEN~△HMN,∴,∴.8.解:(1)如图,连接OD,AD,∵AC是直径,∴∠ADC=90°,∴AD⊥BC,∵AB=AC,∴∠CAD=∠BAD=∠BAC,∵∠CDE=∠BAC.∴∠CDE=∠CAD,∵OA=OD,∴∠CAD=∠ADO,∵∠ADO+∠ODC=90°,∴∠ODC+∠CDE=90°∴∠ODE=90°又∵OD是⊙O的半径∴DE是⊙O的切线;(2)解:∵AB=AC,AD⊥BC,∴BD=CD,∵AB=3BD,∴AC=3DC,设DC=x,则AC=3x,∴AD==2x,∵∠CDE=∠CAD,∠DEC=∠AED,∴△CDE∽△DAE,∴=,即==∴DE=4,x=,∴AC=3x=14,∴⊙O的半径为7.9.(1)证明:连接AE,∵AB是⊙O的直径,∴∠AEB=90°,∴∠1+∠2=90°.∵AB=AC,∴2∠1=∠CAB.∵∠BAC=2∠CBF,∴∠1=∠CBF∴∠CBF+∠2=90°即∠ABF=90°∵AB是⊙O的直径,∴直线BF是⊙O的切线;(2)解:过点C作CH⊥BF于H.∵sin∠CBF=,∠1=∠CBF,∴sin∠1=,∵在Rt△AEB中,∠AEB=90°,AB=3,∴BE=AB•sin∠1=3×=,∵AB=AC,∠AEB=90°,∴BC=2BE=2,∵sin∠CBF==,∴CH=2,∵CH∥AB,∴=,即=,∴CF=6,∴AF=AC+CF=9,∴BF==6.10.解:(1)如图①在AD上截取AE=AB,连接BE,∵∠BAC=120°,∠BAC的平分线交⊙O于点D,∴∠DBC=∠DAC=60°,∠DCB=∠BAD=60°,∴△ABE和△BCD都是等边三角形,∴∠DBE=∠ABC,AB=BE,BC=BD,∴△BED≌△BAC(SAS),∴DE=AC,∴AD=AE+DE=AB+AC;故答案为:AB+AC=AD.(2)AB+AC=AD.理由如下:如图②,延长AB至点M,使BM=AC,连接DM,∵四边形ABDC内接于⊙O,∴∠MBD=∠ACD,∵∠BAD=∠CAD=45°,∴BD=CD,∴△MBD≌△ACD(SAS),∴MD=AD,∠M=∠CAD=45°,∴MD⊥AD.∴AM=,即AB+BM=,∴AB+AC=;(3)如图③,延长AB至点N,使BN=AC,连接DN,∵四边形ABDC内接于⊙O,∴∠NBD=∠ACD,∵∠BAD=∠CAD,∴BD=CD,∴△NBD≌△ACD(SAS),∴ND=AD,∠N=∠CAD,∴∠N=∠NAD=∠DBC=∠DCB,∴△NAD∽△CBD,∴,∴,又AN=AB+BN=AB+AC,BC=5,BD=4,∴=.11.解:(1)证明:∵四边形ABCD 是平行四边形, ∴AD ∥BC ,∵∠AHC =90°,∴∠HAD =90°,即OA ⊥AD ,又∵OA 为半径,∴AD 是⊙O 的切线;(2)解:如右图,连接OC ,∵OH =OA ,AH =3,∴OH =1,OA =2,∵在Rt △OHC 中,∠OHC =90°,OH =OC , ∴∠OCH =30°,∴∠AOC =∠OHC +∠OCH =120°,∴S 扇形OAC ==, ∵CH ==, ∴S △OHC =×1×=,∴四边形ABCD 与⊙O 重叠部分的面积=S 扇形OAC +S △OHC =+;(3)设⊙O 半径OA =r =OC ,OH =3﹣r , 在Rt △OHC 中,OH 2+HC 2=OC 2,∴(3﹣r )2+12=r 2,∴r =,则OH =,在Rt △ABH 中,AH =3,BH =+1=,则AB =, 在Rt △ACH 中,AH =3,CH =NH =1,得AC =, 在△BMN 和△BCA 中,∠B =∠B ,∠BMN =∠BCA ,∴△BMN∽△BCA,∴=即==,∴MN=,∴OH=,MN=.12.解:(1)证明:∵四边形ABCD为圆内接四边形,∴∠A+∠C=180°,∠ABC+∠ADC=180°,∵BD平分∠ABC,∴∠ABD=∠CBD,∴,∴AD=CD,∴四边形ABCD是等补四边形;(2)AC平分∠BCD,理由如下:如图2,过点A分别作AE⊥BC于点E,AF垂直CD的延长线于点F,则∠AEB=∠AFD=90°,∵四边形ABCD是等补四边形,∴∠B+∠ADC=180°,又∠ADC+∠ADF=180°,∴∠B=∠ADF,∵AB=AD,∴△ABE≌△ADF(AAS),∴AE=AF,∴AC是∠BCF的平分线,即AC平分∠BCD;(3)如图3,连接AC,∵四边形ABCD是等补四边形,∴∠BAD+∠BCD=180°,又∠BAD+∠EAD=180°,∴∠EAD=∠BCD,∵AF平分∠EAD,∴∠FAD=∠EAD,由(2)知,AC平分∠BCD,∴∠FCA=∠BCD,∴∠FCA=∠FAD,又∠AFC=∠DFA,∴△ACF∽△DAF,∴,即,∴DF=5﹣5.13.(1)证明:连结OB,∵AC为⊙O的直径,∴∠ABC=90°,∵AB⊥PO,∴PO∥BC∴∠AOP=∠C,∠POB=∠OBC,OB=OC,∴∠OBC=∠C,∴∠AOP=∠POB,在△AOP和△BOP中,,∴△AOP≌△BOP(SAS),∴∠OBP=∠OAP,∵PA为⊙O的切线,∴∠OAP=90°,∴∠OBP=90°,∴PB是⊙O的切线;(2)证明:连结AE,∵PA为⊙O的切线,∴∠PAE+∠OAE=90°,∵AD⊥ED,∴∠EAD+∠AED=90°,∵OE=OA,∴∠OAE=∠AED,∴∠PAE=∠DAE,即EA平分∠PAD,∵PA、PB为⊙O的切线,∴PD平分∠APB∴E为△PAB的内心;(3)解:∵∠PAB+∠BAC=90°,∠C+∠BAC=90°,∴∠PAB=∠C,∴cos∠C=cos∠PAB=,在Rt△ABC中,cos∠C===,∴AC=,AO=,∵△PAO∽△ABC,∴,∴PO===5.。
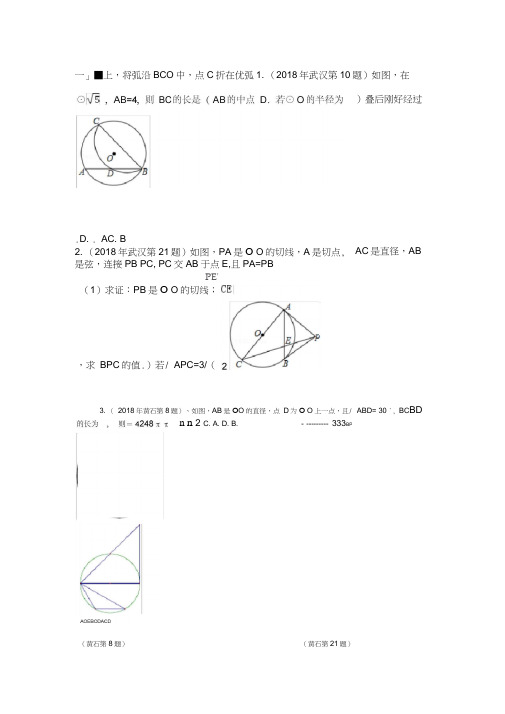
上,将弧沿BCO中,点C折在优弧1.(2018年武汉第10题)如图,在
⊙,AB=4,则BC的长是(AB的中点D.若⊙O的半径为)叠后刚好经过
.D..AC. B
2.(2018年武汉第21题)如图,PA是⊙O的切线,A是切点,AC是直径,AB 是弦,连接PB、PC,PC交AB于点E,且PA=PB.
(1)求证:PB是⊙O的切线;
,求BPC的值.)若∠APC=3∠(2
3.(2018年黄石第8题)、如图,AB是⊙O的直径,点D为⊙O上一点,且∠ABD=30°,BO BD 的长为,则=4248ππππ2 C. A. D. B. 333BP
AOEBODACD
(黄石第8题)(黄石第21题)
BE 23,上五点,是⊙O⊙OECA214.(2018年黄石第题)如图,已知、B、、D、的直径BE的中点,延长BA到点P,使BA=APA∠BCD=120°,为,连接PE
(1)求线段BD的长
(5)求证:直线PE是⊙O的切线.
5.(2018年襄阳第10题)如图,点A,B,C,D都在半径为2的⊙O上,若OA4⊥BC,
∠CDA=30°,则弦BC的长为( )
3232D..B.2 C A.4
6.(2018年襄阳第22题)如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,E为⊙O 上一点,过点E作直线DC分别交AM,BN于点D,C,且CB=CE.
(1)求证:DA=DE;
3,求图中阴影部分的面积.=4,CD (2)若AB=6
7.(2018年黄冈第11题)如图,△ABC内接于⊙O,AB为⊙O的直径,∠CAB=60°,弦AD平分∠CAB,若AD=6,
则AC=.
(黄冈第18题)(黄冈第11题)
8.(2018年黄冈第18题)如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P,过B点的切线交OP于点C.
(1)求证:∠CBP=∠ADB.
(2)若OA=2,AB=1,求线段BP的长.
(2018?天门第22题)如图,在⊙O中,AB为直径,AC为弦.过BC延长线上9.一点G,作GD⊥AO于点D,交AC于点E,交⊙O于点F,M是GE的中点,连接CF,CM.
(1)判断CM与⊙O的位置关系,并说明理由;
(2)若∠ECF=2∠A,CM=6,CF=4,求MF的
长.
10.(2018年宜昌第21题)如图,在△ABC中,AB=AC,以AB为直径的半圆交AC于点D,
交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;CF的面积.ABFC BE=2,求半圆和菱形(2)若AD=7,DE
BA
(第21题)
(2018?恩施州第23题)如图,AB为⊙O直径,P点为半径OA上异于O点和11.A 点的一个点,过P点作与直径AB垂直的弦CD,连接AD,作BE⊥AB,OE∥AD
交BE于E点,连接AE、DE、AE交CD于F点.
(1)求证:DE为⊙O切线;
(2)若⊙O的半径为3,sin∠ADP=,求AD;
(3)请猜想PF与FD的数量关系,并加以证明.
12. (2018年咸宁第7题)如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,COD,若∠AOB与∠
COD互补,弦CD=6,则弦AB的长为()
5.C.D5A.6 B.8
13.(2018年咸宁第21题)如图,以△ABC的边AC为直径的⊙O恰为△ABC的外接圆,∠ABC的平分线交⊙O于点D,过点D作DE∥AC交BC的延长线于点E.
(1)求证:DE是⊙O的切线;
=,求DE,BC的长.(2)若AB=2
14. (2018年鄂州第8题).如图,PA、PB是⊙O的切线,切点为A、B. AC是⊙O的直径,OP与AB交于点D,连接BC. 下列结论:
2 = 4ODOP ④AC③若tanC =
3 ,则OP = 5BC ①∠APB= 2∠BAC ②OP∥BC ?其中正确结论的个数为()
A.4 个B.3个C.2个D.1个
15.(2018年鄂州第22题)如图,四边形ABCD内接于⊙O,BC为⊙O的直径,AC与BD交于点E,P为CB延长线上一点,连接PA,且∠PAB = ∠ADB .
(1)求证:PA为⊙O的切线;
3 (2)若AB= 6 , tan∠ADB = , 求PB长;
4 (3)在(2)的条件下,若AD = CD ,求△CDE的面积.
16.交于⊥OBC是OB的中点,CD题)如图,扇形OAB中,∠AOB=100°,OA=12,9 (2018年十堰第)(OA 于点E,则图中阴影部分的面积是点D,以OC为半径的交
6D.6 B.12π+36C.A.12π+18
17.(2018年十堰第23题)如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作FG ⊥AC于点F,交AB的延长线于点G.
(1)求证:FG是⊙O的切线;
,求=2的值.(2)若tanC
(2018?随州第8题)正方形ABCD的边长为2,以各边为直径在正方形内画18.半圆,得到如图所示阴影部分,若随机向正方形ABCD内投一粒米,则米粒落在
阴影部分的概率为()
.B.A.C.D
(2018?随州第12题)如图,点A,B,C在⊙O上,∠A=40度,∠C=20度,19则∠B=度.
(2018?随州第21题)如图,AB是⊙O的直径,点C为⊙O上一点,CN为⊙20.O 的切线,OM⊥AB于点O,分别交AC、CN于D、M两点.
(1)求证:MD=MC;
AC=4,求MC的长.)若⊙O的半径为5,(2
(2018?孝感第23题)如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于21.点D,交AC于点E,过点D作DF⊥AC于点F,交AB的延长线于点G.
(1)求证:DF是⊙O的切线;
BD=2,CF=2,求AE和BG2()已知的长.
22.(2018年荆州第10题)如图,平面直角坐标系中,⊙P经过三点A(8,0),O(0,0),B(0,6),点D是⊙P上的一动
点.当点D到弦OB的距离最大时,tan∠BOD的值是()
A.2 B.3 C.4 D.5
23.β=,求α+β的度数.β均为锐角,tan,α=tan:已知年荆州第(201823题)α、
探究:(1)用6个小正方形构造如图所示的网格图(每个小正方形的边长均为1),请借助这个网格图求出α+β的度数;延伸:(2)设经过图中M、P、H三点的圆弧与AH交于R,求的弧长.。