2015年小学数学试题

小学五年级（上）数学期末试题（人教）（20分）1、0.62公顷＝（）平方米 2时45分＝（）时2.03公顷＝（）公顷（）平方米 0.6分＝（）秒2、14.1÷11的商是（）循环小数，商可以简写作（），得数保留三位小数约是（）。

3、把2.54、2.54·、2.545和2.55……用“＞”按顺序排列起来（）。

4、在○填上“＜”、“＞”或“＝”号。

（1）0.18÷0.09〇0.18×0.09 （2） 0.7×0.7〇0.7+0.7（3）3.07×0.605〇0.307×6.05 （4） 4.35×10〇0.8×43.55、一桶豆油重100千克，每天用去x千克，6天后还剩下79千克，用方程表示是（）＝79；x＝（）。

6、一个直角三角形，直角所对的边长是10厘米，其余两边分别是8厘米和6厘米，直角所对边上的高是（）厘米。

7、小明今年a岁，爸爸的年龄比他的3倍大b岁，爸爸今年（）岁。

8、100千克花生可榨油39千克，照这样计算，每千克花生可榨油（）千克。

9、两个因数的积是3.6，如果一个因数扩大2倍，另一个因数扩大10倍，积是（）。

10、686.8÷0.68的商的最高位在（）位上。

，错的打“×”）。

（5分）1、0.05乘一个小数，所得的积一定比0.05小。

（）2、小数除法的商都小于被除数。

（）3、两个面积相等的三角形可以拼成一个平行四边形。

（）4、当长方形和平行四边形的周长相等时，面积也相等。

（）5、含有未知数的等式叫做方程。

（）三、选一选。

（把正确答案的字母填在括号里）（5分）1、下列算式中与99÷0.03结果相等的式子是（）。

A、9.9÷0.003B、990÷0.003C、9900÷302、把一个平行四边形拉成一个长方形（边长不变），它的面积（）。

A、比原来大B、比原来小C、与原来一样大3、因为38×235=8930，所以0.38×2.35+100＝（）。

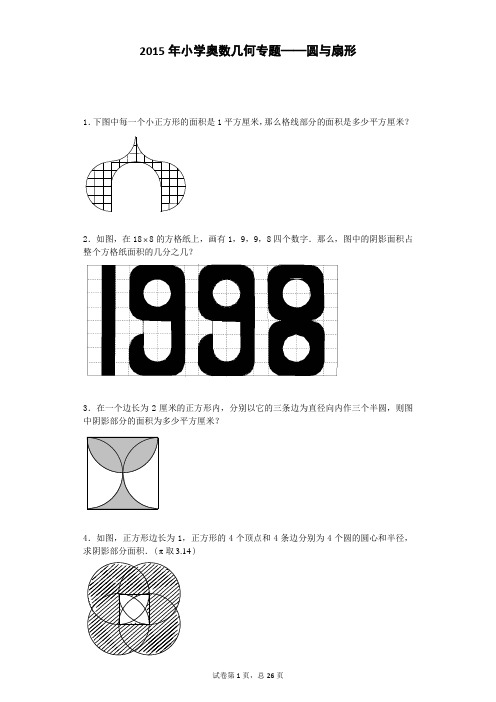
2015年小学奥数几何专题——圆与扇形1．下图中每一个小正方形的面积是1平方厘米，那么格线部分的面积是多少平方厘米？2．如图，在18 8的方格纸上，画有1，9，9，8四个数字．那么，图中的阴影面积占整个方格纸面积的几分之几？3．在一个边长为2厘米的正方形内，分别以它的三条边为直径向内作三个半圆，则图中阴影部分的面积为多少平方厘米？4．如图，正方形边长为1，正方形的4个顶点和4条边分别为4个圆的圆心和半径，求阴影部分面积．(π取3.14)5．图中的4个圆的圆心是正方形的4个顶点，它们的公共点是该正方形的中心．如果每个圆的半径都是1厘米，那么阴影部分的总面积是多少平方厘米？6．如右图，有8个半径为1厘米的小圆，用它们的圆周的一部分连成一个花瓣图形，图中的黑点是这些圆的圆心．则花瓣图形的面积是多少平方厘米？ (π取3)7．如图中三个圆的半径都是5cm，三个圆两两相交于圆心．求阴影部分的面积和．(圆周率取3.14)8．计算图中阴影部分的面积(单位：分米)。

A9．请计算图中阴影部分的面积．10．求图中阴影部分的面积．11．求如图中阴影部分的面积．(圆周率取3.14)12．求下列各图中阴影部分的面积．(1)1010(2)ba13．如图，ABCD 是正方形，且1FA AD DE ===，求阴影部分的面积．(取π3=)14．如图，长方形ABCD 的长是8cm ，则阴影部分的面积是多少2cm ．(π 3.14=)15．如图所示，在半径为4cm 的图中有两条互相垂直的线段，阴影部分面积A 与其它部分面积B 之差(大减小)是多少2cm ．16．求右图中阴影部分的面积．(π取3)17．如图，边长为3的两个正方形BDKE 、正方形DCFK 并排放置，以BC 为边向内侧作等边三角形，分别以B 、C 为圆心，BK 、CK 为半径画弧．求阴影部分面积．(π 3.14=)E18．如图，已知扇形BAC 的面积是半圆ADB 面积的34倍，则角CAB 的度数是多少？ DCBA19．如下图，直角三角形ABC 的两条直角边分别长6和7，分别以,B C 为圆心，2为半径画圆，已知图中阴影部分的面积是17，那么角A 是多少度(π3=)67CBA20．如图，大小两圆的相交部分(即阴影区域)的面积是大圆面积的415，是小圆面积的35．如果量得小圆的半径是5厘米，那么大圆半径是多少厘米？21．有七根直径5厘米的塑料管，用一根橡皮筋把它们勒紧成一捆(如图)，此时橡皮筋的长度是多少厘米？(π取3)22．如图，边长为12厘米的正五边形，分别以正五边形的5个顶点为圆心，12厘米为半径作圆弧，请问：中间阴影部分的周长是多少？(π 3.14)23．如图是一个对称图形．比较黑色部分面积与灰色部分面积的大小，得：黑色部分面积________灰色部分面积．24．如图，大圆半径为小圆的直径，已知图中阴影部分面积为1S ，空白部分面积为2S ，那么这两个部分的面积之比是多少？(圆周率取3.14)25．用一块面积为36平方厘米的圆形铝板下料，从中裁出了7个同样大小的圆铝板．问：所余下的边角料的总面积是多少平方厘米？26．如图，若图中的圆和半圆都两两相切，两个小圆和三个半圆的半径都是1．求阴影部分的面积．27．如图所示，求阴影面积，图中是一个正六边形，面积为1040平方厘米，空白部分是6个半径为10厘米的小扇形．(圆周率取3.14)28．如下图所示，AB是半圆的直径，O是圆心，AC CD DB==，M是CD的中点，H 是弦CD的中点．若N是OB上一点，半圆的面积等于12平方厘米，则图中阴影部分的面积是多少平方厘米．29．如图，两个半径为1的半圆垂直相交，横放的半圆直径通过竖放半圆的圆心，求图中两块阴影部分的面积之差．(π取3)30．如图，两个正方形摆放在一起，其中大正方形边长为12，那么阴影部分面积是多少？(圆周率取3.14)EAF31．如图，ABC是等腰直角三角形，D是半圆周的中点，BC是半圆的直径．已知==，那么阴影部分的面积是多少？(圆周率取3.14)AB BC10DBPCA32．图中给出了两个对齐摆放的正方形，并以小正方形中右上顶点为圆心，边长为半径作一个扇形，按图中所给长度阴影部分面积为多少？(π 3.14=)6433．如图，图形中的曲线是用半径长度的比为2:1.5:0.5的6条半圆曲线连成的．问：涂有阴影的部分的面积与未涂有阴影的部分的面积的比是多少？34．奥运会的会徽是五环图，一个五环图是由内圆直径为6厘米，外圆直径为8厘米的五个环组成，其中两两相交的小曲边四边形(阴影部分)的面积都相等，已知五个圆环盖住的面积是77.1平方厘米，求每个小曲边四边形的面积．(π 3.14=)35．已知正方形ABCD 的边长为10厘米，过它的四个顶点作一个大圆，过它的各边中点作一个小圆，再将对边中点用直线连擎起来得右图．那么，图中阴影部分的总面积等于多少平方厘米．(π 3.14=)36．如图，ABCD 是边长为a 的正方形，以AB 、BC 、CD 、DA 分别为直径画半圆，求这四个半圆弧所围成的阴影部分的面积．(π取3)37．在桌面上放置3个两两重叠、形状相同的圆形纸片.它们的面积都是100平方厘米，盖住桌面的总面积是144平方厘米，3张纸片共同重叠的面积是42平方厘米.那么图中3个阴影部分的面积的和多少是平方厘米？38．如图所示，ABCD 是一边长为4cm 的正方形，E 是AD 的中点，而F 是BC 的中点．以C 为圆心、半径为4cm 的四分之一圆的圆弧交EF 于G ，以F 为圆心、半径为2cm 的四分之一圆的圆弧交EF 于H 点，若图中1S 和2S 两块面积之差为2π(cm )m n -(其中m 、n 为正整数)，请问m n +之值为何？S 2S 1G HFE DCB AS图1S 2S 1G HF E DCBA39．如图，矩形ABCD 中，AB =6厘米，BC =4厘米，扇形ABE 半径AE =6厘米，扇形CBF 的半径CB =4厘米，求阴影部分的面积．(π取3)CB A40．如图所示，阴影部分的面积为多少？(圆周率取3)41．已知右图中正方形的边长为20厘米，中间的三段圆弧分别以1O 、2O 、3O 为圆心，求阴影部分的面积．(π3=) O342．一个长方形的长为9，宽为6，一个半径为l 的圆在这个长方形内任意运动，在长方形内这圆无法运动到的部分，面积的和是多少．(π取3)43．已知半圆所在的圆的面积为62.8平方厘米，求阴影部分的面积．(π 3.14=)B44．如图，等腰直角三角形ABC的腰为10；以A为圆心，EF为圆弧，组成扇形AEF；两个阴影部分的面积相等．求扇形所在的圆面积．45．如图，直角三角形ABC中，AB是圆的直径，且20AB=，阴影甲的面积比阴影乙的面积大7，求BC长．(π 3.14=)46．图中的长方形的长与宽的比为8:3，求阴影部分的面积．47．如图，求阴影部分的面积．(π取3)48．如图，直角三角形的三条边长度为6,8,10，它的内部放了一个半圆，图中阴影部分的面积为多少？6849．大圆半径为R，小圆半径为r，两个同心圆构成一个环形．以圆心O为顶点，半径R为边长作一个正方形：再以O为顶点，以r为边长作一个小正方形．图中阴影部分的面积为50平方厘米，求环形面积．(圆周率取3.14)50．已知图中正方形的面积是20平方厘米，则图中里外两个圆的面积之和是多少．(π取3.14)51．图中大正方形边长为6，将其每条边进行三等分，连出四条虚线，再将虚线的中点连出一个正方形(如图)，在这个正方形中画出一个最大的圆，则圆的面积是多少？(π 3.14)52．如下图所示，两个相同的正方形，左图中阴影部分是9个圆，右图中阴影部分是16个圆．哪个图中阴影部分的面积大？为什么？53．如图，在33⨯方格表中，分别以A 、E 、F 为圆心，半径为3、2、1，圆心角都是90°的三段圆弧与正方形ABCD 的边界围成了两个带形，那么这两个带形的面积之比12:?S S =CD 1D 212C54．如图中，正方形的边长是5cm ，两个顶点正好在圆心上，求图形的总面积是多少？(圆周率取3.14)55．如下图，AB 与CD 是两条垂直的直径，圆O 的半径为15厘米，AEB 是以C 为圆心，AC 为半径的圆弧，求阴影部分面积．EOD CBA56．如图，AB 与CD 是两条垂直的直径，圆O 的半径为15，是以C 为圆心，AC 为半径的圆弧．求阴影部分面积．57．如下图所示，曲线PRSQ 和ROS 是两个半圆．RS 平行于PQ ．如果大半圆的半径是1米，那么阴影部分是多少平方米？(π取3.14)P58．在右图所示的正方形ABCD 中，对角线AC 长2厘米．扇形ADC 是以D 为圆心，以AD 为半径的圆的一部分． 求阴影部分的面积．D A321AB CD59．某仿古钱币直径为4厘米，钱币内孔边缘恰好是圆心在钱币外缘均匀分布的等弧(如图)．求钱币在桌面上能覆盖的面积为多少？60．传说古老的天竺国有一座钟楼，钟楼上有一座大钟，这座大钟的钟面有10平方米．每当太阳西下，钟面就会出现奇妙的阴影(如右图)．那么，阴影部分的面积是多少平方米．96312123699631261．如下图，两个半径相等的圆相交，两圆的圆心相距正好等于半径，AB 弦约等于17厘米，半径为10厘米，求阴影部分的面积．O 2O 1BA62．下图中，3AB ，阴影部分的面积是DA63．如图，ABCD是平行四边形，8cmAD=，10cmAB=，30DAB∠=︒，高4cmCH=，弧BE、DF分别以AB、CD为半径，弧DM、BN分别以AD、CB为半径，则阴影部分的面积为多少？(精确到0.01)FA64．如图所示，两条线段相互垂直，全长为30厘米．圆紧贴直线从一端滚动到另一端(没有离开也没有滑动)．在圆周上设一个定点P，点P从圆开始滚动时是接触直线的，当圆停止滚动时也接触到直线，而在圆滚动的全部过程中点P是不接触直线的．那么，圆的半径是多少厘米？(设圆周率为3．14，除不尽时，请四舍五入保留小数点后两位．如有多种答案请全部写出)P65．将一块边长为12厘米的有缺损的正方形铁皮(如图)剪成一块无缺损的正方形铁皮，求剪成的正方形铁皮的面积的最大值.B′CCC图1 图2 图366．正三角形ABC的边长是6厘米，在一条直线上将它翻滚几次，使A点再次落在这条直线上，那么A点在翻滚过程中经过的路线总长度是多少厘米？如果三角形面积是15平方厘米，那么三角形在滚动过程中扫过的面积是多少平方厘米？(结果保留π)67．草场上有一个长20米、宽10米的关闭着的羊圈，在羊圈的一角用长30米的绳子拴着一只羊(见如图)．问：这只羊能够活动的范围有多大？(圆周率取3.14)68．如图是一个直径为3cm的半圆，让这个半圆以A点为轴沿逆时针方向旋转60︒，此时B点移动到'B点，求阴影部分的面积．(图中长度单位为cm，圆周率按3计算)．69．如图所示，直角三角形ABC的斜边AB长为10厘米，60∠=︒，此时BC长5ABC厘米．以点B为中心，将ABC∆顺时针旋转120︒，点A、C分别到达点E、D的位置．求AC边扫过的图形即图中阴影部分的面积．(π取3)E70．如图，ABCD是一个长为4，宽为3，对角线长为5的正方形，它绕C点按顺时针方向旋转90︒，分别求出四边扫过图形的面积．71．半径为25厘米的小铁环沿着半径为50厘米的大铁环的内侧作无滑动的滚动，当小铁环沿大铁环滚动一周回到原位时，问小铁环自身转了几圈？72．如图，15枚相同的硬币排成一个长方形，一个同样大小的硬币沿着外圈滚动一周，回到起始位置．问：这枚硬币自身转动了多少圈？73．一枚半径为1cm 的圆形硬币相互紧靠着平放在桌面上，让一枚硬币沿着它们的外轮廓滚过后回到原来的位置，那么与原A 点重合的点是______．硬币自己转动______，硬币圆心的运动轨迹周长为_______．74．先做一个边长为2cm 的等边三角形，再以三个顶点为圆心，2cm 为半径作弧，形成曲边三角形(如左图)．再准备两个这样的图形，把一个固定住(右图中的阴影)，另一个围绕着它滚动，如右图那样，从顶点相接的状态下开始滚动．请问此图形滚动时经过的面积是多少平方厘米？(π 3.14=)CBA 22275．下图中每一个小正方形的面积是1平方厘米，那么格线部分的面积是多少平方厘米？76．在4×7的方格纸板上面有如阴影所示的”6”字，阴影边缘是线段或圆弧．问阴影面积占纸板面积的几分之几？77．如图，在一个边长为4的正方形内，以正方形的三条边为直径向内作三个半圆．求阴影部分的面积．78．如图所示，四个全等的圆每个半径均为2m ，阴影部分的面积是 ．2m79．如图，大圆半径为小圆的直径，已知图中阴影部分面积为1S ，空白部分面积为2S ，那么这两个部分的面积之比是多少？(圆周率取3.14)80．如图，阴影部分的面积是多少？222481．如图，四分之一大圆的半径为7，求阴影部分的面积，其中圆周率π取近似值227．82．求图中阴影部分的面积(单位：cm )．43283．一块圆形稀有金属板平分给甲、乙二人．但此金属板事先已被两条互相垂直的弦切割成如图所示尺寸的四块．现甲取②、③两块，乙取①、④两块．如果这种金属板每平方厘米价值1000元，问：甲应偿付给乙多少元？84．如图，C 、D 是以AB 为直径的半圆的三等分点，O 是圆心，且半径为6．求图中阴影部分的面积．85．如右图，两个正方形边长分别是10和6，求阴影部分的面积．(π取3)86．如图，正方形ABCD的边长为4厘米，分别以B、D为圆心以4厘米为半径在正方形内画圆．求阴影部分面积．(π取3)DBA87．在图中，两个四分之一圆弧的半径分别是2和4，求两个阴影部分的面积差．(圆周率取3.14)88．求图中阴影部分的面积．89．如右图，正方形的边长为5厘米，则图中阴影部分的面积是多少平方厘米，(π 3.14)FE DCBA90．图中阴影部分的面积是多少．(π取3.14)3391．三角形ABC 是直角三角形，阴影I 的面积比阴影II 的面积小225cm ，8cm AB ，求BC 的长度． I IABCI92．如图，三角形ABC 是直角三角形，阴影部分①比阴影部分②的面积小28平方厘米，AB 长40厘米．求BC 的长度？(π取3.14)93．图中阴影部分的面积是225cm ，求圆环的面积．94．图中小圆的面积是30平方厘米，则大圆的面积是多少平方厘米．(π取3.14)95．一些正方形内接于一些同心圆，如图所示．已知最小圆的半径为1cm，请问阴影部分的面积为多少平方厘米？(取22π7 =)96．图中是一个钟表的圆面，图中阴影部分甲与阴影部分乙的面积之比是多少？9397．传说古老的天竺国有一座钟楼，钟楼上有一座大钟，这座大钟的钟面有10平方米．每当太阳西下，钟面就会出现奇妙的阴影(如左下图)．那么，阴影部分的面积是多少平方米？398．如图，已知三角形GHI是边长为26厘米的正三角形，圆O的半径为15厘米．90AOB COD EOF∠=∠=∠=︒．求阴影部分的面积．GG99．直角三角形ABC 放在一条直线上，斜边AC 长20厘米，直角边BC 长10厘米．如下图所示，三角形由位置Ⅰ绕A 点转动，到达位置Ⅱ，此时B ，C 点分别到达1B ，1C 点；再绕1B 点转动，到达位置Ⅲ，此时A ，1C 点分别到达2A ，2C 点．求C 点经1C 到2C 走过的路径的长．100．如图，一条直线上放着一个长和宽分别为4cm 和3cm 的长方形Ⅰ．它的对角线长恰好是5cm ．让这个长方形绕顶点B 顺时针旋转90°后到达长方形Ⅱ的位置，这样连续做三次，点A 到达点E 的位置．求点A 走过的路程的长．ⅣⅢⅡⅠEDCBA101．一只狗被拴在底座为边长3m 的等边三角形建筑物的墙角上(如图)，绳长是4m ，求狗所能到的地方的总面积．(圆周率按3.14计算)102．如右图，以OA 为斜边的直角三角形的面积是24平方厘米，斜边长10厘米，将它以O 点为中心旋转90︒，问：三角形扫过的面积是多少？(π取3)103．如图，直角三角形ABC中，B∠为直角，且2∆BC=厘米，4AC=厘米，则在将ABC 绕C点顺时针旋转120︒的过程中，AB边扫过图形的面积为多少．(π 3.14=)AB104．如果半径为25厘米的小铁环沿着半径为50厘米的大铁环的外侧作无滑动的滚动，当小铁环沿大铁环滚动一周回到原位时，问小铁环自身转了几圈？105．如图所示，大圆周长是小圆周长的n(1n>)倍，当小圆在大圆内侧(外侧)作无滑动的滚动一圈后又回到原来的位置，小圆绕自己的圆心转动了几周？106．12个相同的硬币可以排成下面的4种正多边形(圆心的连线)．用一个同样大小的硬币，分别沿着四个正多边形的外圈无滑动地滚动一周．问：在哪个图中这枚硬币自身转动的圈数最多，最多转动了多少圈？参考答案1．36【解析】割补法．如右图，格线部分的面积是36平方厘米．2．37 72【解析】我们数出阴影部分中完整的小正方形有8+15+15+16=54个，其中部分有6+6+8=20个，部分有6+6+8=20(个)，而1个和1个正好组成一个完整的小正方形，所以阴影部分共包含54+20=74(个)完整小正方形，而整个方格纸包含8⨯18=144(个)完整小正方形．所以图中阴影面积占整个方格纸面积的74144，即3772．3．2【解析】采用割补法．如果将阴影半圆中的2个弓形移到下面的等腰直角三角形中，那么就形成两个相同的等腰直角三角形，所以阴影部分的面积等于两个等腰直角三角形的面积和，即正方形面积的一半，所以阴影部分的面积等于21222⨯=平方厘米．4．7.14【解析】把中间正方形里面的4个小阴影向外平移，得到如右图所示的图形，可见，阴影部分的面积等于四个正方形面积与四个90︒的扇形的面积之和，所以，221444441π14π7.14S S S S S =⨯+⨯=⨯+=⨯+⨯=+=圆阴影圆．5．8【解析】如下图所示：可以将每个圆内的阴影部分拼成一个正方形，每个正方形的面积为11240.542⨯÷⨯=⨯=（）（平方厘米），所以阴影部分的总面积为248⨯=（平方厘米）． 6．19 【解析】本题直接计算不方便，可以利用分割移动凑成规则图形来求解． 如右上图，连接顶角上的4个圆心，可得到一个边长为4的正方形．可以看出，与原图相比，正方形的每一条边上都多了一个半圆，所以可以把原花瓣图形的每个角上分割出一个半圆来补在这些地方，这样得到一个正方形，还剩下4个14圆，合起来恰好是一个圆，所以花瓣图形的面积为224π119+⨯=(平方厘米)．在求不规则图形的面积时，我们一般要对原图进行切割、移动、补齐，使原图变成一个规则的图形，从而利用面积公式进行求解．这个切割、移动、补齐的过程实际上是整个解题过程的关键，我们需要多多练习，这样才能快速找到切割拼补的方法。

人教版小学数学三年级上册第二单元测试题一、算一算，要细心。

1、把算式和相应的得数连起来。

2、请你接着算，并验算。

308 验算625 验算+ 594 －337二、你认为下面的计算正确吗？（对的画√，错的改过来）339 257 7 6+ 471 －180 －5 8800 ( ) 7 7 ( ) 185 ( )三、选一选。

1、340与153的和是（）。

A、393 B、493 C、1872、现在这台VCD比原来的价格便宜（）钱。

A、131元B、149元C、49元3、冷饮店上午卖出雪糕82只，下午卖出雪糕101只，下午比上午多卖出（）只。

A、193 B、82 C、19四、解决问题。

1、暑假里小强一家要从北京到济南旅游。

左下图是“北京——济南”火车里程表，你知道从北京到济南有多少千米吗？2、养鸡场有公鸡168只，公鸡比母鸡少382只。

母鸡有多少只？3、（1）买1辆自行车和1个电饭锅，能获奖吗？（2）买一台抽油烟机和一块手表，能获奖吗？（3）你想怎样买？能获奖吗？五、调查了解自己家第三季度（7、8、9月）的用电情况，完成下表（单位：千瓦时）（1）分别算出自己家7月、8月、9月的用电数。

（2）你家第三季度的用电数量是多少？其他同学呢？（3）和同学交流一下，说说怎样才能节约用电？人教版小学三年级上册数学第二单元测试班级：姓名：一、直接写得数。

75+35= 28+38= 142+58= 364+636=200—101= 486—196= 345—99= 82—28=300+600= 523—212= 420+300= 653—210=二、笔算下面各题，并进行验算。

507—348= 376+284=549+867= 500—185=三、检验下面各题，把错改过来。

6 3 4 4 0 4— 1 8 2 改正：— 1 8 6 改正：5 5 2 3 1 86 6 3 2 3 9+ 2 8 2 改正：+ 5 7 1 改正：8 4 5 8 0 0四、脱式计算。

五年级第二学期期末试卷一、填空题（每空1分，共25分）1、如果小红向北走50米，记作+50米，那么小明走了—60米，表示他向（ ）走了（ ）米。

2、一篮香蕉共6千克，平均分给8名同学，每人分得香蕉总数的()()，每人分得()()千克香蕉。

3、用直线上的点表示25 、710 、112 和125 。

4、有一个最简真分数，它的分子与分母的乘积是24。

如果这个真分数不是124 ，那么它就一定是( )。

5、右图是一位同学卧室一面墙上贴的瓷砖，中间（ ）块组成了一个图案。

在保持组合图案不变的情况下，有（ ）种不同贴法。

6、在括号里填上适当的最简分数或者整数。

200平方米=（ ）公顷 90平方厘米=（ ）平方分米80克=（ ）千克 15分=（ ）小时 7、6和9的最小公倍数是（ ）；24和36的最大公因数是（ ）。

8、从一个长5分米，宽4分米的长方形木板上锯下一个最大的圆，圆的面积是（ ）平方分米，剩下的木板是（ ）平方分米。

9、3÷4＝（ ）12 ＝12（ ）＝18÷（ ）＝（ ）（填小数）10、有两根木棒，一根长18分米，另一根长27分米。

现在要把它们锯成同样长的小段且没有剩余。

每段木棒最长（ ）分米，一共能锯成（ ）段。

二、选择题（共5分） 1、在49、515、219、257、6517中，最简分数有（ ）个。

A. 2 B. 3 C. 4 D. 52、甲、乙两人举行百米赛跑，甲用了0.3分钟，乙用了51分钟，谁跑得快一些。

（ ） A. 甲 B. 乙 C. 一样快 D. 不确定 3、△□△⊙△□△⊙△□△⊙……照这样排下去，第26个图形是（ ）。

A. □B. △C. ⊙D. …… 4、大于0.7而小于0.8的小数有（ ）A.1个B.9个C.无数个D. 没有5、用一张长是7分米，宽3分米的长方形剪出一个最大的圆，像这样的圆最多可以剪（ ）个。

A. 2B. 1C. 0D. 无数个 三、判断题（共5分）1、等式两边同时加、减、乘或除以相同的数，结果仍然是等式。

2015小学数学奥林匹克试题预赛(A)卷1. 计算: 12-22+32-42+52-62+…-1002+1012=________。

2. 一个两位数等于其个位数字的平方与十位数字之和，这个两位数是________。

3. 五个连续自然数，每个数都是合数，这五个连续自然数的和最小是________。

4. 有红、白球若干个。

若每次拿出一个红球和一个白球，拿到没有红球时，还剩下50个白球；若每次拿走一个红球和3个白球，则拿到没有白球时，红球还剩下50个。

那么这堆红球、白球共有________个。

5. 一个年轻人今年（2000年）的岁数正好等于出生年份数字之和，这位年轻人今年_ __岁。

6. 如下图, ABCD是平行四边形，面积为72平方厘米，E，F分别为AB，BC的中点，则图中阴影部分的面积为_____平方厘米。

7. a是由2000个9组成的2000位整数，b是由2000个8组成的2000位整数，则a×b的各位数字之和为________。

8. 四个连续自然数，它们从小到大顺次是3的倍数、5的倍数、7的倍数、9的倍数，这四个连续自然数的和最小是____。

9. 某区对用电的收费标准规定如下：每月每户用电不超过10度的部分，按每度0.45元收费；超过10度而不超过20度的部分，按每度0.80元收费；超过20度的部分，按每度1.50元收费。

某月甲用户比乙用户多交电费7.10元，乙用户比丙用户多交3.75元，那么甲、乙、丙三用户共交电费________元（用电都按整度数收费）。

10. 一辆小汽车与一辆大卡车在一段9千米长的狭路上相遇，必须倒车，才能继续通行。

已知小汽车的速度是大卡车的速度的3倍，两车倒车的速度是各自速度的；小汽车需倒车的路程是大卡车需倒车的路程的4倍。

如果小汽车的速度是50千米/时，那么要通过这段狭路最少用________小时。

11. 某学校五年级共有110人，参加语文、数学、英语三科活动小组，每人至少参加一组。

2015年下半年小学五年级数学单元测试卷（1）小数的乘法班级姓名成绩一.精卫填海。

（每空1分，共21分）(1) 3.72+3.72+3.72+3.72+3.72改写成乘法算式是（）；(2)看竖式，在（）填上合适的数。

①扩大到它的( )倍②扩大到它的( )倍(3)根据32×12=384，很快得出下面各小题的积：320×120=( ) 320×0.12=( ) 3.2×0.12=( )(4) 用数对表示位置，一般先表示第几（），后表示第几（）。

(5)在下面的○里填上“>”、“<”或“=”。

348×0.9○348 (0.5×0.4) ×0.3○0.5×(0.4×0.3) 4.35×1.03○4.35(6) 6.9537保留整数约是（）；精确到百分位约是（）。

(7) 2.35×0.5的积是（）位小数，如果2.35扩大10倍，要使积不变，必须把0.5改为（）。

（8）两个因数的积是8.45。

如果两个因数同时扩大10倍，则积是（）。

（9）取积的近似值时，如果要保留一位小数，就要根据积的（）上的数决定是“四舍”还是“五入”。

（10）一个数的2.4倍是12，这个数的1.8倍是（）。

二.明镜高悬。

（对的打“√”，错的打“×”）（5分）(1)一个数（0除外）的0.916倍比这个数大。

（）(2) 1.25×(0.8＋1) = 1.25×0.8＋1 （）(3)整数乘法的运算定律对于小数乘法也适用。

（）(4)一个数乘小数，积一定比这个数小。

（）(5) 一个数乘0.01,等于将这个数缩小到它的百分之一。

（）三.火眼金睛。

（将正确答案的序号填在括号里）（5分）(1)0.76×0.25×0.4与76×25×4的运算顺序（）①一样②不一样③无法判断(2) 一个两位小数“四舍五入”保留一位小数是10.0，这个数最大是（）。

2015五年级上册数学期末试卷（卷面满分100分答卷时间60分钟）20分每空1分）1、8.51平方分米＝（）平方米 0.8小时＝（）分2.45公顷＝（）公顷（）平方米 0.5分＝（）秒2、一台拖拉机上午耕地m公顷，下午耕地n公顷，这台拖拉机一天工作5小时，平均每小时耕地（）公顷。

3、把 2.54、2.54·、2.545和 2.55用“＞”按顺序排列起来（）。

4、在○填上“＜”、“＞”或“＝”号。

（1）0.18÷0.09〇0.18×0.09 （2） 0.7×0.7〇0.7+0.7（3）3.07×0.605〇0.307×6.05 （4） 4.35×10〇0.8×43.55、一个平行四边形的面积是41平方分米，与它等底等高的三角形的面积是（）平方分米。

6、一个平行四边形的面积是24平方厘米，与它等底等高的三角形的面积是（）平方厘米。

7、100千克花生可榨油39千克，每千克花生可榨油（）千克。

8、4.9565656……是（）小数，可以简写成（）。

保留一位小数约是（），保留两位小数约是（）。

10分1、0.5乘一个小数，所得的积一定比0.5小。

（）2、小数除法的商都小于被除数。

（）3、两个面积相等的三角形可以拼成一个平行四边形。

（）4、2a=a²。

（）5、方程都是等式，但等式不都是方程。

（）（把正确答案的字母填在括号里）10分1、下列算式中与99÷0.03结果相等的式子是（）。

A、9.9÷0.003B、990÷0.003C、9900÷302、一个三角形面积是S平方厘米，高是2厘米，那么底是（）。

A、S÷2 B、2S÷2 C、2S3、两个数相乘，一个因数扩大3倍，另一个因数扩大5倍，积扩大（）。

A、8倍B、5倍C、15倍4、3除a与b的和，商是多少？列式为（）A、3÷a+bB、3÷(a+b)C、(a+b)÷35、一个三角形中，其中两个角的平均度数是45度，这个三角形是（）三角形。

2015-2016小学数学六年级毕业考试试题及答案学校：__________年级：2015-2016小学数学六年级毕业考试试题班级：__________姓名：__________。

学号：__________。

总分：__________一、填空题。

（每空1分，共23分）1、一个数的亿位上是5、万级和个级的最高位上也是5，其余数位上都是0，这个数写作__________。

2、一个笼子里关着鸡和兔，共10个头，26条腿，那么笼子里鸡和兔分别有（）只。

A、4，6.B、3，7.C、7，3.D、5，53、在一幅地图上，用2厘米表示实际距离90千米，这幅地图的比例尺是（）。

A、1:45.B、1:4500.C、1:.D、1:xxxxxxxx4、一个长方体，长6厘米，宽3厘米，高2厘米，它的最小面的面积与表面积的比是（）。

A、1:3.B、1:6.C、1:12.D、1:245、庄浪气象台绘制统计图，公布一周平均每天气温的高低和变化情况，应选用(。

)统计图。

二、计算题。

（共77分）1、把(1.23×10^8)省略万位后面的尾数是__________，改写成用亿作单位的数是__________。

2、0.375的计数单位是__________，它有__________个这样的单位，它的倒数是__________。

3、6.……是__________循环小数，用简便方法记作__________，把它保留两位小数封装是__________。

4、1/6＜(_____)＜5/2，(_____)里可以填写的最大整数是__________。

5、按规律填数：2、1/4、4/9、(_____)、16/25、32/36、(_____)。

6、A=2×3×5，B=2×3×3，A和B的最大公因数是__________。

最小公倍数是__________。

7、被减数、减数、差相加得1，差是减数的3倍，这个被减数是__________。

2015年第十三届小学“希望杯”全国数学邀请赛试卷（五年级第2试）一、填空题（每小题5分，满分60分）1．（5分）用3、4、7、8、这四个数组成两个两位数（每个数字只能用一次，且必须使用），它们的乘积最大是．2．（5分）有三个自然数，它们的和是2015，两两相加的和分别是m+1，m+2011和m+2012，则m= ．3．（5分）用1、2、3、5、6、7、8、9这8个数字最多可以组成个质数（每个数字只能使用一次，且必须使用）．4．（5分）一次数学竞赛中，某小组10个人的平均分是84分，其中小明得93分，则其他9个人的平均分是分．5．（5分）同时掷4个相同的小正方体（小正方体的六个面上分别写有数字1、2、3、4、5、6，则朝上一面的4个数字的和有种．6．（5分）某长方体的长、宽、高（长、宽、高均大于1）是三个彼此互质的自然数，若这个长方体的体积是665，则它的表面积是．（5分）大于0的自然数n是3的倍数，3n是5的倍数，则n的最小值是．7．8．（5分）从1、2、3、4、5中任取3个组成一个三位数，其中不能被3整除的三位数有个．9．（5分）观察下表中的数的规律，可知第8行中，从左向右第5个数是．10．（5分）如果2头牛可以换42只羊，3只羊可以换26只兔，2只兔可以换3只鸡，则3头牛可以换多少只鸡？11．（5分）用一根34米长的绳子围成一个矩形，且矩形边长都是整数米，共有种不同的围法（边长相同的矩形算同一种围法）．12．（5分）将五位数“12345”重复写403次组成一个2015位数“123451234512345…”，从左往右，先删去这个数中所有位于奇数位上的数字，得到一个新数，再删去新数中所有位于奇数位上的数字；按上述规则已知删下去，直到剩下一个数字为止，则最后剩下的数字是．二、解答题（每个小题15分，共60分），每题都要写出推算过程13．（15分）甲、乙两船顺流每小时行8千米，逆流每小时行4千米，若甲船顺流而下，然后返回；乙船逆流而上，然后返回，两船同时出发，经过3小时同时回到各自的出发点，在这3小时中有多长时间甲、乙两船同向航行？14．（15分）图中有多少个三角形？15．（15分）如图，在一个平行四边形纸片上剪去甲、乙两个直角三角形．甲直角三角形的两条直角边边分别为8cm和5cm．乙直角三角形的两条直角边边分别为6cm和2cm．求图中阴影部分的面积．16．（15分）有158个小朋友排成一排，从左边第一个人起（第一个人发一个苹果），每隔1人发一个苹果，又从右边第一个人起（第一个人发一个香蕉），每隔2人发一个香蕉，求没有得到水果的小朋友的人数．2015年第十三届小学“希望杯”全国数学邀请赛试卷（五年级第2试）参考答案与试题解析一、填空题（每小题5分，满分60分）1．（5分）用3、4、7、8、这四个数组成两个两位数（每个数字只能用一次，且必须使用），它们的乘积最大是6142 ．【分析】根据乘法的计算法则及乘法算式的性质可知，乘法算式中的因数越大，积就越大；根据数位知识可知，一个数的高位上数字越大，其值就越大．又因为现在各个数的和一定的情况下，两个因数越接近，它们的乘积就越大，由此可知，用3、4、7、8这四个数字组成可组成的两位数，乘积最大可为74×83=6142．【解答】解：根据乘法的性质及数位知识可知，3、4、7、8这四个数字组成可组成的两位数，乘积最大可为：74×83=6142．故答案为：6142．【点评】了解乘法算式的性质及数位知识是完成本题的关键．2．（5分）有三个自然数，它们的和是2015，两两相加的和分别是m+1，m+2011和m+2012，则m= 2 ．【分析】两两相加的和分别是m+1，m+2011和m+2012，把这三个和相加就是三个自然数和的2倍，也就是2015的2倍，由此可以列出方程求出m的值．【解答】解：由题意可知：m+1+m+2011+m+2012=2015×23m+4024=40303m=6m=2故答案为：2．【点评】解决本题关键是理解两两相加和的和就是三个数相加和的2倍，再由此列出方程求解．3．（5分）用1、2、3、5、6、7、8、9这8个数字最多可以组成 6 个质数（每个数字只能使用一次，且必须使用）．【分析】首先从已有的质数考虑，有2、3、5、7，剩下1、6、8、9两两结合，个位只能为奇数，恰好能组成61、89，由此得出结论．【解答】解：可以组成下列质数：2、3、5、7、61、89，一共有6个．答：用1、2、3、5、6、7、8、9这8个数字最多可以组成 6个质数．故答案为：6．【点评】此题主要利用质数的定义进行组合．4．（5分）一次数学竞赛中，某小组10个人的平均分是84分，其中小明得93分，则其他9个人的平均分是83 分．【分析】用10个人的平均分乘总人数计算出10个人的总份数，减去小明的得分即可得出剩下9人的总分，再除以9即可计算出9人的平均分．【解答】解：（84×10﹣93）÷（10﹣1）=747÷9=83（分）答：其他9个人的平均分是83分．故答案为：83．【点评】此题主要考查平均数计算公式的灵活运用：总分=平均分×总人数，平均分=总分÷总人数．5．（5分）同时掷4个相同的小正方体（小正方体的六个面上分别写有数字1、2、3、4、5、6，则朝上一面的4个数字的和有21 种．【分析】同时掷4个相同的小正方体，则朝上一面的4个数字的和最小是：1×4=4，最大是6×4=24，有1、2、3、4、5、6公差是1，所以朝上一面的4个数字的和有：24﹣4+1=21种．【解答】解：根据分析可得，朝上一面的4个数字的和最小是：1×4=4，最大是6×4=24，24﹣4+1=21（种）答：朝上一面的4个数字的和有 21种．故答案为：21．【点评】本题考查了数字的极值问题，关键是确定和的取值范围．6．（5分）某长方体的长、宽、高（长、宽、高均大于1）是三个彼此互质的自然数，若这个长方体的体积是665，则它的表面积是526 ．【分析】首先把665分解质因数，求出长、宽、高，再根据长方体的表面积公式：S=（ab+ah+bh）×2，把数据代入公式解答即可．【解答】解：665=19×7×5，因为长、宽、高（长、宽、高均大于1）是三个彼此互质的自然数，所以长、宽、高分别是19、7、5，（19×7+19×5+7×5）×2=（133+95+35）×2=263×2=526，答：它的表面积是526．故答案为：526．【点评】此题主要考查长方体的体积公式、表面积公式的灵活运用，关键是利用分解质因数的方法求出长、宽、高．（5分）大于0的自然数n是3的倍数，3n是5的倍数，则n的最小值是15 ．7．【分析】大于0的自然数n是3的倍数，3n是5的倍数，3n的个位数一定是0或5，即3n=15，逐个分析可知：当3n=45时，n=15，这时n是3的倍数，3n 是5的倍数，据此解答即可．【解答】解：3n是5的倍数，3n的个数一定是0或5又因为大于0的自然数n是3的倍数，所以3n最小是453n=45n=15所以n最小取15时，n是3的倍数，3n是5的倍数．答：n的最小值是15．故答案为：15．【点评】解答本题的关键是3n的个位数一定是0或5．8．（5分）从1、2、3、4、5中任取3个组成一个三位数，其中不能被3整除的三位数有18 个．【分析】根据能被3整除的数的特征：各位上数字之和能被3整除，这个数就能被3整除，所以1，2，3，4，5可把这五个数字三个三个相加，相加的和不能被3整除的三个数，组成的三位数也不会被3整除，据此解答即可．【解答】解：1+2+3=6，1+2+4=7，1+2+5=8，2+3+4=9，2+3+5=10，3+4+5=12，其中不能被3整除的数的和是7、8、10，即有三组（1、2、4），（1、2、5）（2、3、5），每一组可以组成3×2×1=6个，三组共可以组成6×3=18个，即不能被3整除的数共有18个．故答案为：18．【点评】此题主要考查的是排列组合与数字分组，以及能被3整除数的特征的应用．9．（5分）观察下表中的数的规律，可知第8行中，从左向右第5个数是54 ．【分析】由图形中数字的排列得出第n行的最后一个数为n×n，从而知第7行最后一个数为7×7、第8行中，从左向右第5个数为7×7+5．【解答】解：由图可知，第1行的数为1，第2行的最后一个数为2×2=4，第3行的最后一个数为3×3=9，…所以第7行最后一个数为7×7=49，则第8行第1个数为49+1=50，第5个数为50+4=54，故答案为：54．【点评】本题主要考查数阵图中找规律，根据数字排列规律得出第n行的最后一个数为n×n是解题的关键．10．（5分）如果2头牛可以换42只羊，3只羊可以换26只兔，2只兔可以换3只鸡，则3头牛可以换多少只鸡？【分析】根据2头牛可以换42只羊，得出1头牛换21只羊；根据3只羊可以换26只兔，得出1头牛也就是21只羊可以换26×7=182只兔子；又因为2只兔子可以换3只鸡，所以1头牛换182÷2×3=273只鸡，再乘3即得3头牛可以换多少只鸡．【解答】解：42÷2=21（只）21÷3×26=7×26=182（只）182÷2×3=91×3=273（只）273×3=819（只）答：3头牛可以换819只鸡．【点评】解决此题的关键是根据2头牛可以换42只羊，3只羊可以换26只兔，2只兔可以换3只鸡，得出1头牛换的鸡只数，进而求出3头牛换的鸡只数．11．（5分）用一根34米长的绳子围成一个矩形，且矩形边长都是整数米，共有8 种不同的围法（边长相同的矩形算同一种围法）．【分析】设矩形的长为am，宽为bm，且a≥b，根据题意，a+b=17，由于a，b 均为整数，可得（a，b）的取值情况．【解答】解：设矩形的长为am，宽为bm，且a≥b，根据题意，a+b=17，由于a，b均为整数，因此（a，b）的取值有以下8种：（16，1），（15，2），（14，3），（13，4），（12，5），（11，6），（10，7），（9，8），故答案为8．【点评】本题考查列举法解决实际问题，考查学生分析解决问题的能力，正确列举是关键．12．（5分）将五位数“12345”重复写403次组成一个2015位数“123451234512345…”，从左往右，先删去这个数中所有位于奇数位上的数字，得到一个新数，再删去新数中所有位于奇数位上的数字；按上述规则已知删下去，直到剩下一个数字为止，则最后剩下的数字是 4 ．【分析】将五位数“12345”重复写403次组成一个2015位数“123451234512345…”，对2015位数从左向右进行编号，从到2015第1轮操作，依此可以求得删去的数，和剩下的数是几的倍数，不难求得结果．【解答】解：根据分析，对2015位数从左向右进行编号，从1到2015第1轮操作，删去的数=（2015+1）÷2=1008，剩下=2015﹣1008=1007，留下的是编号为偶数的数字；第2轮操作，删去的数字数=（1007+1）÷2=504，剩下=1007﹣504=503，留下的是编号是4的倍数的数字；第3轮操作，删去的数字数=（503+1）÷2=252，剩下=503﹣252=251，留下的是编号是8的倍数的数字；第4轮操作，删去的数字数=（251+1）÷2=126，剩下=251﹣126=125，留下的是编号为16的倍数的数字；第5轮操作，删去的数字数=（125+1）÷2=63，剩下=125﹣63=62，留下的是编号为32的倍数的数字；第6轮操作，删去的数字数=（63+1）÷2=63，剩下=63﹣32=31，留下的是编号为64的倍数的数字；第7轮操作，删去的数字数=（31+1）÷2=16，剩下=31﹣16=15，留下的是编号为128的倍数的数字；第8轮操作，删去的数字数=（15+1）÷2=8，剩下=15﹣8=7，留下的是编号为256的倍数的数字；第9轮操作，删去的数字数=（7+1）÷2=4，剩下=7﹣4=3，留下的是编号为512的倍数的数字；第10轮操作，删去的数字数=（3+1）÷2=2，剩下=3﹣2=1，留下的是编号为1024的倍数的数字；一共要进行10轮操作，而原来的2015位数是按照1234512345…5个1组的规律进行排列的1024÷5=204…4，多出来的这4个数字依此是1234，∴编号为1024的数字=4，故答案是：4．【点评】本题考查了数字问题，突破点是：对2015位数从左向右进行编号，从到2015第1轮操作，依此求得删去的数和剩下的数．二、解答题（每个小题15分，共60分），每题都要写出推算过程13．（15分）甲、乙两船顺流每小时行8千米，逆流每小时行4千米，若甲船顺流而下，然后返回；乙船逆流而上，然后返回，两船同时出发，经过3小时同时回到各自的出发点，在这3小时中有多长时间甲、乙两船同向航行？【分析】根据题意可知往返路程相等，此题可以设未知数求解，设3小时顺流行驶单趟用的时间为x小时，则逆流行驶单趟用的时间为（3﹣x）小时，由于路程一定，行驶时间与速度成反比例，故x：（3﹣x）=4：8解出即可得到顺流和逆流各自所需时间，当两条船同时从同一地方出发，一条顺流开始返回（逆流行走），这时另一条还在逆流前进，求出时间差就是两船同时向上游前进的时间．【解答】解：设3小时顺流行驶单趟用时间为x小时，则逆流行驶单趟用的时间为（3﹣x）小时，故：x：（3﹣x）=4：88x=4×（3﹣x）8x=12﹣4x12x=12x=1逆流行驶单趟用的时间：3﹣1=2（小时），两船航行方向相同的时间为：2﹣1=1（小时），答：在3个小时中，有1小时两船同向都在逆向航行．【点评】根据往返路程相等得到等量关系是解决本题的关键．14．（15分）图中有多少个三角形？【分析】按照一定规律来找：先计数最内部的正方形中三角形的个数有：8+4+4=16个；同理，中间的正方形中三角形的个数，除了和内部的正方形中三角形的个数同样有16个外，又增加了红色部分的三角形：3×4=12个，共有16+12=28个；那么最外部的正方形中三角形的个数也有28个，然后相加即可求解．【解答】解：最内部的正方形中三角形的个数有：8+4+4=16（个），中间的正方形中三角形的个数有：8+4+4+4×3=28（个），外边的正方形中三角形的个数有：8+4+4+4×3=28（个），共有：16+28+28=72（个）答：图中有72个三角形．【点评】本题考查了组合图形的计数．注意分类数三角形的个数时，不能忽略了组合的三角形．15．（15分）如图，在一个平行四边形纸片上剪去甲、乙两个直角三角形．甲直角三角形的两条直角边边分别为8cm和5cm．乙直角三角形的两条直角边边分别为6cm和2cm．求图中阴影部分的面积．【分析】可以将图形进行扩展，甲乙可以平移，扩展后变成一个长方形，阴影部分的面积可以通过大长方形的面积减去几个直角三角形的面积即可求得．【解答】解：根据分析，如图，将图进行扩展，△AEB、△ABH、△CDM的面积相等，△BCN、△BCP、△AFD的面积相等，由图可知，阴影部分的面积=长方形ENMF的面积﹣△AEB﹣△ABH﹣△CDM﹣△BCN﹣△BCP﹣△AFD=长方形ENMF的面积﹣3×（S甲+S乙）；由图可知，长方形ENMF的长=6+8=14cm，宽=5+2=7cm，故长方形ENMF的面积=14×7=98cm2，阴影部分的面积=98﹣3××（5×8+6×2）=20cm2．故答案是：20．【点评】本题考查了三角形面积，突破点是：利用等积变形，不难求得阴影部分的面积．16．（15分）有158个小朋友排成一排，从左边第一个人起（第一个人发一个苹果），每隔1人发一个苹果，又从右边第一个人起（第一个人发一个香蕉），每隔2人发一个香蕉，求没有得到水果的小朋友的人数．【分析】首先分析把从右边看的过程转换成从左边看．找到2次的大周期．枚举即可解决．【解答】解：依题意可知：把从右边第一个人起（第一个人发一个香蕉），每隔2人发一个香蕉，周期为3．158÷3=52…2，那么从左边看就是第一个人不给，从第二个开始每3个人给第一个．那么去掉第一个和最后一个共156人，周期为2×3=6．枚举一个周期为：苹果不给给不给给不给给香蕉给不给不给给不给不给一个周期中共有2个人没有水果．156÷6=26周期．共没有水果人数为26×2=52人．答：没有得到水果的小朋友的人数有52人．【点评】本题考查对周期性的理解和运用，关键问题是找到两次周期枚举法问题解决．。

二年级数学第一单元姓名班级一、判断题，对的在括号里打“√”，错的打“×”。

1、一棵大树高6厘米。

…………………………………………（）2、小明比小红高3米。

………………………………………（）3、一枝铅笔长16厘米。

……………………………………（）4、教室的宽是60厘米。

……………………………………（）二、填空题。

1、在下面的括号里填上“厘米”或“米”。

⑴语文课本的宽是14（）⑵一根跳绳长3（）⑶教室的黑板长是4（）⑷课桌高是70（）⑸教室里的门高是2（）⑹妈妈的一个手指长7（）2、在○里填上“〉”“〈”或“=”。

15厘米○12厘米 4米○5厘米 98厘米○1米20米○15米 1米○100厘米 3厘米○3米3、把30厘米、25厘米、1米、90厘米按从小到大顺序排列。

（）< （）<（）< （）4、在直尺上从0刻度到8刻度是（）厘米5、数一数下面的图形是由几条线段组成的。

（）条（）条（）条（）条三、按要求画线段。

（1）画一条6厘米长的线段。

（2）画一条比3厘米短1厘米的线段。

（3）画一条比6厘米长3厘米的线段。

（4）画一条线段，比下面的中条线段短2厘米四、列式计算。

1、一块布长20米，用去6米，还剩下多少米？2、一棵大树高10米，另一棵大树高8米，两棵大度相差多少米？3、一条线段长40厘米，另一条线段长8厘米。

两条线段连接在一起后是多少厘米？4、一根绳子对折后是4米，这根绳子长多少米？这根绳子剪去2米后，还剩多少米？二年级数学上册第一单元练习题一、填一填。

（34分）1、量较长物体的长度，可以用（）作单位。

量较短物体的长度可以用（）作单位。

2、量物体的长度时，要把尺子的（）刻度对准物体的一端，再看物体的另一端对着几。

3、1米=（）厘米400厘米=（）米15厘米+8厘米＝（）厘米30米+6米＝（）米 16厘米－9厘米＝（）厘米6米－5米＝（）厘米4、看一看，填一填。

这支回形针长( )厘米这支铅笔长( )厘米。