定积分的近似运算

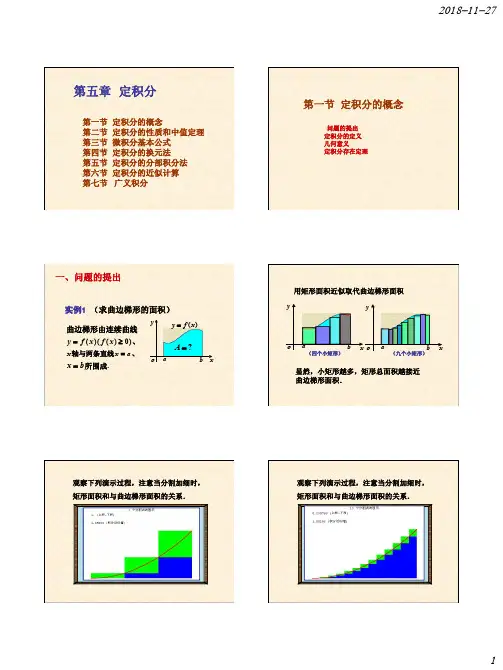
第五章 定积分第一节 定积分的概念第二节 定积分的性质和中值定理第三节 微积分基本公式第四节 定积分的换元法第五节 定积分的分部积分法第六节 定积分的近似计算第七节 广义积分问题的提出定积分的定义 几何意义定积分存在定理第一节 定积分的概念abxyo?=A 曲边梯形由连续曲线实例1 （求曲边梯形的面积）)(x f y =)0)((≥x f 、x 轴与两条直线a x =、b x =所围成.一、问题的提出)(x f y =ab xyoab x yo用矩形面积近似取代曲边梯形面积显然，小矩形越多，矩形总面积越接近曲边梯形面积．（四个小矩形）（九个小矩形）观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．曲边梯形如图所示，,],[1210b x x x x x a b a n n =<<<<<=- 个分点，内插入若干在区间a bxyoi ξi x 1x 1-i x 1-n x ;],[],[11---=∆i i i i i x x x x x n b a 长度为，个小区间分成把区间形面积，曲边梯形面积用小矩上任取一点在每个小区间i i i x x ξ-],[1ii i x f A ∆ξ≈)(:))(],[(1近似为高为底，以i i i f x x ξ-（1）分割（2）近似ini i x f A ∆≈∑=)(1ξ曲边梯形面积的近似值为ini i x f A ∆=∑=→)(lim 10ξλ时，趋近于零即小区间的最大长度当分割无限加细)0(},,max{,21→∆∆∆=λλn x x x 曲边梯形面积为（3）求和（4）取极限实例2 （求变速直线运动的路程）设某物体作直线运动，已知速度)(t v v =是时间间隔],[21T T 上t 的一个连续函数，且0)(≥t v ，求物体在这段时间内所经过的路程.思路：把整段时间分割成若干小段，每小段上速度看作不变，求出各小段的路程再相加，便得到路程的近似值，最后通过对时间的无限细分过程求得路程的精确值．（1）分割212101T t t t t t T n n =<<<<<=- 1--=∆i i i t t t ii i t v s ∆≈∆)(τ部分路程值某时刻的速度（3）求和ii ni t v s ∆≈∑=)(1τ（4）取极限},,,max{21n t t t ∆∆∆= λini i t v s ∆=∑=→)(lim 10τλ路程的精确值（2）近似设函数)(x f 在],[b a 上有界，记},,,max{21n x x x ∆∆∆= λ，如果不论对],[b a 在],[b a 中任意插入若干个分点bx xx x x a nn =<<<<<=-121把区间],[b a 分成n 个小区间，各小区间的长度依次为1--=∆i i i x x x ，),2,1( =i ，在各小区间上任取一点i ξ（i i x ∆∈ξ），作乘积i i x f ∆)(ξ ),2,1( =i 并作和i i ni x f S∆=∑=)(1ξ，二、定积分的定义定义怎样的分法，⎰==ba I dx x f )(ii ni x f ∆∑=→)(lim 10ξλ被积函数被积表达式积分变量积分区间],[b a 也不论在小区间],[1i i x x -上点i ξ怎样的取法，只要当0→λ时，和S 总趋于确定的极限I ，我们称这个极限I 为函数)(x f 在区间],[b a 上的定积分，记为积分上限积分下限积分和几点说明：（1） 定积分是一个数值，它仅与被积函数及积分区间有关，⎰b a dx x f )(⎰=b a dt t f )(⎰=ba duu f )(而与积分变量的字母无关.)( ,)()( 2⎰⎰⎰=-=aaabbadx x f dx x f dx x f 规定：）（.],[)(],[)( 3的取法无关的分法及的和式的极限与所表示上可积，则在区间若）（i bab a dx x f b a x f ξ⎰,0)(≥x f ⎰=ba Adx x f )(曲边梯形的面积,0)(≤x f ⎰-=ba Adx x f )(曲边梯形的面积的负值a b xyo)(x f y =AxyoabA -)(x f y =三、定积分的几何意义1A 2A 3A 4A 4321)(A A A A dx x f ba ⎰=-+-,],[)(变号时在区间b a x f 三、定积分的几何意义.)(是面积的代数和⎰badx x f几何意义：积取负号．轴下方的面在轴上方的面积取正号；在数和．之间的各部分面积的代直线的图形及两条轴、函数它是介于x x b x a x x f x ==,)(++--当函数)(x f 在区间],[b a 上连续时，定理1定理2 设函数)(x f 在区间],[b a 上有界，且只有有限个间断点，则)(x f 在四、定积分的存在定理区间],[b a 上可积.例1 利用定义计算定积分.12dx x ⎰解将]1,0[n 等分，分点为nix i =，(n i ,,2,1 =)小区间],[1i i x x -的长度nx i 1=∆，(n i ,,2,1 =)取i i x =ξ，(n i ,,2,1 =)i i n i x f ∆∑=)(1ξi i ni x ∆=∑=21ξ,12i ni ix x ∆=∑=.,102的选取无关及法故和式极限与区间的分可积因为i dx x ξ⎰n n i ni 121⋅⎪⎭⎫ ⎝⎛=∑=∑==n i i n 12316)12)(1(13++⋅=n n n n ,121161⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=n n ∞→⇒→n 0λdx x ⎰102i i ni x ∆=∑=→210lim ξλ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=∞→n n n 121161lim .31= 几何上是曲线y=x 2,直线x=1及x 轴围成的曲边三角形面积.例2 利用定义计算定积分.121dx x⎰解在]2,1[中插入分点 12,,,-n q q q ,典型小区间为],[1ii q q -，（n i ,,2,1 =）小区间的长度)1(11-=-=∆--q qq q x i i i i ,取1-=i i qξ，（n i ,,2,1 =）i i ni x f ∆∑=)(1ξi ni ix ∆=∑=11ξ)1(1111-=-=-∑q q q i ni i ∑=-=ni q 1)1()1(-=q n 取2=nq即nq 12=),12(1-=n n )12(lim 1-+∞→xx x x xx 112lim1-=+∞→,2ln =)12(lim 1-∴∞→nn n ,2ln =dx x ⎰211i ni ix ∆=∑=→101lim ξλ)12(lim 1-=∞→n n n .2ln =i i ni x f ∆∑=)(1ξ原式⎥⎦⎤⎢⎣⎡π+π-++π+π=∞→n n n n n n n nsin )1(sin 2sin sin 1lim π=∑=∞→n i n n i n 1sin 1lim n n i ni n π⋅⎪⎭⎫ ⎝⎛ππ=∑=∞→1sin lim 1.sin 10⎰ππ=xdx ix ∆i ξ例3：将下列和式极限表示成定积分.⎥⎦⎤⎢⎣⎡-+++∞→n n n n n n πππ)(sin sin sin lim121 ：五、小结１．定积分的实质：特殊和式的极限．２．定积分的思想和方法：分割化整为零求和积零为整取极限精确值——定积分求近似以直（不变）代曲（变）取极限Z .思考n n n n f n f n f ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛∞→ 21lim 试证.1)(ln ⎰=dxx f e 2：将和式极限，表示成定积分.⎥⎦⎤⎢⎣⎡-++-+-∞→2222241241141lim n n n n n 证明n n n n f n f n f ⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫⎝⎛∞→ 21lim ⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛∞→=n n n n f n f n f e21lim ln n n n n f n f n f ⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛∞→ 21lim 试证.1)(ln ⎰=dx x f e 利用对数的性质得⎪⎭⎫⎝⎛∑==∞→n i f n ni n e1ln 1lim n n i f ni n e1ln lim 1⋅⎪⎭⎫ ⎝⎛∑==∞→ 指数上可理解为：)(ln x f 在]1,0[区间上的一个积分和．分割是将]1,0[n 等分分点为nix i =，（n i ,,2,1 =）⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛∞→=n n n n f n f n f e21ln lim 极限运算与对数运算换序得nn i f n i n 1ln lim 1⋅⎪⎭⎫ ⎝⎛∑=∞→⎰=10)(ln dx x f 故nn n n f n f n f ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛∞→ 21lim.10)(ln ⎰=dxx f e 因为)(x f 在区间]1,0[上连续，且0)(>x f 所以)(ln x f 在]1,0[上有意义且可积 ,2：将和式极限，表示成定积分.⎥⎦⎤⎢⎣⎡-++-+-∞→2222241241141lim n n n n n ⎰∑-=-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-++-+-=⎥⎦⎤⎢⎣⎡-++-+-=∞→∞→∞→1021222222222411)(41lim )(41)2(41)1(411lim 41241141lim dxx n ni n n n n n n n n n n i n n n 解第二节 定积分的性质、中值定理1.定积分性质2.中值定理对定积分的补充规定:（1）当b a =时，0)(=⎰ba dx x f ；（2）当b a >时，⎰⎰-=abb adx x f dx x f )()(.说明 在下面的性质中，假定定积分都存在，且不考虑积分上下限的大小．一、定积分性质和中值定理证⎰±ba dxx g x f )]()([i i i ni x g f ∆±=∑=→)]()([lim 10ξξλi i ni x f ∆=∑=→)(lim 10ξλii ni x g ∆±∑=→)(lim 10ξλ⎰=ba dx x f )(.)(⎰±ba dx x g ⎰±b a dx x g x f )]()([⎰=b a dx x f )(⎰±ba dx x g )(.（此性质可以推广到有限多个函数作和的情况）性质1⎰⎰=ba b a dx x f k dx x kf )()( (k 为常数).证⎰ba dx x kf )(ii ni x kf ∆=∑=→)(lim 10ξλi i n i x f k ∆=∑=→)(lim 1ξλii ni x f k ∆=∑=→)(lim 10ξλ.)(⎰=ba dx x f k 性质2⎰ba dx x f )(⎰⎰+=bcca dx x f dx x f )()(.补充：不论 的相对位置如何, 上式总成立.c b a ,,例 若,c b a <<⎰c a dx x f )(⎰⎰+=cb b a dx x f dx x f )()(⎰b a dx x f )(⎰⎰-=cb c a dxx f dx x f )()(.)()(⎰⎰+=bc ca dx x f dx x f （定积分对于积分区间具有可加性）假设bc a <<性质3dx b a ⋅⎰1dx ba⎰=a b -=.则0)(≥⎰dx x f ba. )(b a <证,0)(≥x f ,0)(≥ξ∴i f ),,2,1(n i =,0≥∆i x ,0)(1≥∆ξ∴∑=i i ni x f },,,max{21n x x x ∆∆∆= λi i ni x f ∆∴∑=→)(lim 1ξλ.0)(⎰≥=ba dx x f 性质4性质5如果在区间],[b a 上0)(≥x f ，例1 比较积分值dx e x⎰-20和dx x ⎰-20的大小.解令,)(x e x f x -=]0,2[-∈x ,0)(>x f ,0)(02>-∴⎰-dx x exdx ex⎰-∴2,02dx x ⎰->于是dx e x ⎰-2.20dx x ⎰-<性质5的推论：证),()(x g x f ≤ ,0)()(≥-∴x f x g ,0)]()([≥-∴⎰dx x f x g ba ,0)()(≥-⎰⎰ba ba dx x f dx x g 于是 dx x f ba ⎰)( dx x g ba ⎰≤)(.则dx x f ba ⎰)( dx x g ba ⎰≤)(. )(b a <如果在区间],[b a 上)()(x g x f ≤，（1）dx x f b a ⎰)(dx x f ba⎰≤)(.)(b a <证,)()()(x f x f x f ≤≤- ,)()()(dx x f dx x f dx x f ba ba ba ⎰⎰⎰≤≤-∴即dx x f ba ⎰)(dx x f ba⎰≤)(.说明： 可积性是显然的.|)(x f |在区间],[b a 上的性质5的推论：（2）设M 及m 分别是函数证,)(M x f m ≤≤ ,)(⎰⎰⎰≤≤∴ba ba b a Mdx dx x f dx m ).()()(a b M dx x f a b m ba -≤≤-⎰（此性质可用于估计积分值的大致范围）则 )()()(a b M dx x f a b m ba -≤≤-⎰.)(x f 在区间],[b a 上的最大值及最小值，性质6例2 估计积分dx x⎰π+03sin 31值的范围.解,sin 31)(3xx f +=],,0[π∈∀x ,1sin 03≤≤x ,31sin 31413≤+≤x ,31sin 31410030dx dx x dx ⎰⎰⎰πππ≤+≤.3sin 31403π≤+≤π∴⎰πdx x例3 估计积分dx xx⎰ππ24sin 值的范围.解,sin )(xx x f =2sin cos )(x x x x x f -='2)tan (cos x x x x -=⎥⎦⎤⎢⎣⎡∈2,4ππx ,0<)(x f 在]2,4[ππ上单调下降,,22)4(π=π=f M ,2)2(π=π=f m ,442π=π-π=-a b ,422sin 4224π⋅π≤≤π⋅π∴⎰ππdx x x .22sin 2124≤≤∴⎰ππdx x x 如果函数)(x f 在闭区间],[b a 上连续，上的平均值在],[)()(1b a x f dxx f a b ba⎰-则在积分区间],[b a 上至少存在一个点 ξ，使dx x f b a ⎰)())((a b f -=ξ. )(b a ≤≤ξ性质7（定积分中值定理）积分中值公式证Mdx x f a b m ba≤-≤∴⎰)(1)()()(a b M dx x f a b m ba -≤≤-⎰ 由闭区间上连续函数的介值定理知在区间],[b a 上至少存在一个点 ξ,)(1)(⎰-=ξbadx x f a b f dx x f ba ⎰)())((ab f -=ξ.)(b a ≤≤ξ即在区间],[b a 上至少存在一个点ξ，1. 积分中值公式的几何解释：xyoa b ξ)(ξf 使得以区间],[b a 为以曲线)(x f y =底边，为曲边的曲边梯形的面积等于同一底边而高为)(ξf 的一个矩形的面积。

定积分的近似计算方法定积分近似计算方法指的是利用数值计算方法来估算给定函数在一定区间上的积分值。

这些方法常常用于当函数在该区间内无法求得解析式时，或者解析式难以求得的情况下。

下面将介绍常用的数值积分近似计算方法。

一、矩形法矩形法即将积分区间等分为若干小区间，然后在每个小区间中选择一个代表点，将函数在该点的函数值作为近似积分的值。

具体可以分为左矩形法、右矩形法和中矩形法。

1.左矩形法左矩形法即取每个小区间的左端点作为代表点，近似积分的值为：∫[a, b]f(x)dx ≈ Δx * [f(a) +f(a+Δx) + … + f(a+(n-1)Δx)]其中，Δx=(b-a)/n，n为区间的等分数。

2.右矩形法右矩形法即取每个小区间的右端点作为代表点，近似积分的值为：∫[a, b]f(x)dx ≈ Δx * [f(a+Δx) + f(a+2Δx) + … +f(a+nΔx)]其中，Δx=(b-a)/n，n为区间的等分数。

3.中矩形法中矩形法即取每个小区间的中点作为代表点，近似积分的值为：∫[a, b]f(x)dx ≈ Δx * [f(a+Δx/2) + f(a+3Δx/2) + … +f(a+(2n-1)Δx/2)]其中，Δx=(b-a)/n，n为区间的等分数。

二、梯形法梯形法是通过将积分区间上的曲线拟合为多个梯形来近似计算定积分的方法。

将积分区间[a,b]等分为n个小区间，然后在每个小区间上用两个端点处的函数值拟合成一个梯形，然后将这些梯形的面积加起来即可得到近似的定积分的值。

具体计算公式为：∫[a, b]f(x)dx ≈ Δx/2 * [f(a) + 2f(a+Δx) + 2f(a+2Δx)+ … + 2f(a+(n-1)Δx) + f(b)]其中，Δx=(b-a)/n，n为区间的等分数。

三、辛普森法辛普森法是通过将积分区间上的曲线拟合为多个二次多项式的方法。

将积分区间[a,b]等分为n个小区间，每两个相邻区间拟合成一个二次多项式。

定积分算法定积分算法定积分是微积分中的一个重要概念，它可以用来求解曲线下方的面积、体积等问题。

在实际应用中，定积分也被广泛应用于物理、经济、工程等领域。

本文将介绍定积分的定义及其算法。

一、定积分的定义定积分是一个数学概念，它描述了一个函数在一段区间上的面积大小。

具体来说，设函数f(x)在区间[a,b]上连续，则[a,b]上f(x)与x轴所围成的曲边梯形面积为：其中a和b是曲边梯形底边两端点的x坐标，f(x)是曲边梯形边界上每个点的纵坐标。

当n趋向于无穷大时，Δx趋向于0，则上式右侧称为函数f(x)在区间[a,b]上的定积分，记作：二、定积分算法1. 矩形法矩形法是最简单易懂的一种求解定积分的方法。

其基本思想是将区间[a,b]等分成n个小区间，并在每个小区间中取一个代表点xi（i=1,2,...,n），然后用xi代替f(xi)计算出每个小区间的面积，最后将这些面积相加即可得到定积分的近似值。

具体来说，设函数f(x)在区间[a,b]上连续，则将区间[a,b]等分成n个小区间，每个小区间的长度为Δx=(b-a)/n。

然后，在每个小区间中取一个代表点xi（i=1,2,...,n），用xi代替f(xi)计算出每个小区间的面积：最终，将这些面积相加即可得到定积分的近似值：其中，Rn表示用矩形法求解定积分时所得到的近似值。

2. 梯形法梯形法是比矩形法更精确的一种求解定积分的方法。

其基本思想是将区间[a,b]等分成n个小区间，并在每个小区间中取两个代表点xi和xi+1（i=0,1,...,n-1），然后用这两个点对应的函数值f(xi)和f(xi+1)计算出每个小梯形的面积，最后将这些面积相加即可得到定积分的近似值。

具体来说，设函数f(x)在区间[a,b]上连续，则将区间[a,b]等分成n个小区间，每个小区间的长度为Δx=(b-a)/n。

然后，在每个小区间中取两个代表点xi和xi+1（i=0,1,...,n-1），用这两个点对应的函数值f(xi)和f(xi+1)计算出每个小梯形的面积：最终，将这些面积相加即可得到定积分的近似值：其中，Tn表示用梯形法求解定积分时所得到的近似值。

定积分定义的四要素分割近似求和积分是数学中的一种重要的操作。

它的基本概念是“定积分”，即把一段区间分割为若干小段，逐个处理每一小段，最后将每一小段的处理结果累加，从而得到全局结果。

定积分通常有四个要素，即函数f(x)、上下限a、b、以及分割数n，因此它也可以简称为“四要素定积分”，即f(x)、a、b、n。

定积分的基本思想是，把一段区间[a,b]分割为n个相近的小段，即将区间[a,b]分割为n个相等的子区间[x0,x1,…,xn-1]。

然后用区间[x0,x1]来计算函数f(x)在[x0,x1]上的积分值，再用区间[x1,x2]来求解f(x)在[x1,x2]上的积分值，以此类推，最后将各区间上的积分值累加起来，就可以得到函数f(x)在区间[a,b]上的积分值。

由于定积分是一种细长的计算，为了更有效地求解，科学家们开发出了“近似求和”的方法，即利用以某种适当的算法，分割区间[a,b]，使得每一小段上的函数f(x)的大小值都比较接近，然后将每一小段上的函数f(x)值累加，从而得到函数f(x)在区间[a,b]的近似积分值。

近似求和方法与四要素定积分有着很大的不同，四要素定积分完全依赖于n，也就是区间[a,b]分割多少段，只有当n足够大时，才能最精确地求解函数f(x)在区间[a,b]上的积分值，而近似求和方法却不受n的限制，可以快速有效地求解函数f(x)在区间[a,b]上的积分值。

目前对近似求和方法的研究越来越深入，已有许多在实践中得到验证的算法，核心思想是把一个区间分割成若干小的区间，利用一定的方法来求解每一段的积分值，使得每一段的积分值都比较接近。

比如，改进的梯形法是一种常见的近似求和方法，它利用梯形计算函数f(x)在每一段区间上的积分值，然后将每段区间上的积分值累加，就可以得到函数f(x)在整个区间上的积分值。

除此之外，还可以使用其它的改进方法，例如Simpson规则、Lagrange插值法等。

最后，四要素定积分和近似求和方法各有特点，定积分的优势在于可以求出很精确的积分值，但是其计算量较大，而近似求和方法则可以求出大致的积分值，节省计算量。

定积分的近似计算方法摘要 本文主要讨论了一元函数常见的数值积分方法,例如插值型求积公式、龙贝格求积公式、高斯求积公式等近似计算方法,在用这些方法计算定积分时,会产生一些误差,为了减少误差, 可以利用复化求积公式、复化高斯公式等.本文围绕这些方法,系统介绍它们的计算公式以及截断误差,并用例题分析它们产生误差的大小、计算量等.关键词 插值型积分 龙贝格积分 高斯积分 误差分析 近似计算1引言在计算定积分的值()b aI f x dx =⎰时,常常根据微积分学基本定理求出)(x f 的一个原函数)(x F ,再用牛顿-莱布尼茨公式求的积分,()()()baI f x dx F b F a ==-⎰.但在实际应用中,这种方法只限于解决一小部分定积分的求值问题.当函数没有具体表达式,只是一些实验测得数据形成的表格或图形或者是()F x 无法用初等函数表示,例如,2bx ae dx ⎰,2sin ba x dx ⎰等等,这就需要我们用一些近似方法求的积分值.与数值积分一样,把积分区间细分,在每个小区间上,找到简单函数)(x ϕ来近似代替()f x ,且()b a x dx ϕ⎰的值容易求的.这样就把计算复杂的()ba f x dx ⎰转化为求简单的积分值()bax dx ϕ⎰.因此,定积分的近似计算实质上是就是被积函数的近似计算问题.2常见数值方法 2.1牛顿-科茨数值方法牛顿-科茨求积公式是求积节点等距离分布的插值型求积公式.利用插值多项式来构造数值积分公式是最常用、最基本的方法,具体做法是：给定区间[,]a b 上一组节点01...n a x x x b =<<<=,以及节点处函数()(0,1,2,i f x i n =,作()f x 的n 次拉格朗日多项式()()()nn i i i x f x l x ϕ==∑,其中 011011()()()()()()()()()i i n i i i i i i i n x x L x x x x L x x l x x x L x x x x L x x -+-+----=----,将插值公式(1)1()()()()(1)!n n n f f x x x n ξϕω++=++.其中1012()()()()()n n x x x x x x x L x x ω+=----,[,]a b ξ∈,依赖于变量x , 上式积分得(1)1()()()()(1)!n bb bn n aa af f x dx x dx x dx n ξϕω++=++⎰⎰⎰(1)(1)0()()()()(1)!n nb biiin aai f f x l x dx x dx n ξω++==++∑⎰⎰(1)(1)0()()()()(1)!n nbbi i n aai f f x b l x dx x dxn ξω++==++∑⎰⎰若记 (),(0,1,2,bi ia A l x dx i ==⎰….. )n (1)(1)1()[]()(1)!n bn af R f x dxn ξω++=+⎰, (2)则有()()[]nbi i ai f x dx A f x R f ==+∑⎰(3)称式(3)为插值求型公式,其中(0,1,2,i A i =…. )n 与()f x 无关,叫求积系数, i x 为求积节点,[]R f 为求积公式余项,其中求积系数由(1)决定.2.1.1梯形求积公式1梯形公式当插值节点01,x x 分别选取区间端点,a b 时,由式(3)分别求出求积系数10012bb aa x x xb b aA dx dx x x a b ---===--⎰⎰,01102bb aa x x x ab a A dx dx x x b a ---===--⎰⎰.从而的求积公式()[()()]2bab a f x dx f a f b -≈+⎰. (4) 称求积公式(4)为梯形求积公式,简称梯形公式.2梯形公式截断误差: 3*()[](),12b a R f f ξ-''=- *[,]a b ξ∈. (5) 3梯形求积公式的代数精度:1 当()1f x =时,式(5)中 1(1)2bab adx b a x b a -=-=+=-⎰. 精确成立.2.1.2 辛普森求积公式1辛普森求积公式当选取节点为012,,2a bx a x x b +===时,由式(1)求下列求积系数 1200102()()()()2()()6()()2b b a a a b x x b x x x x b a A dx dx a b x x x x a a b +-----===+----⎰⎰,0211002()()()()2()()()3()()22bb aa x x x x x a xb b a A dx dx a b a b x x x x a b -----===++----⎰⎰.0122021()()()()2()()6()()22b b a a a bx a x x x x x b a A dx dx a b a b x x x x a b +-----===++----⎰⎰ .从而求积公式()[()4()()]62bab a a bf x dx f a f f b -+≈++⎰. （6）称式(6)为抛物线积分公式或辛普森积分公式.2抛物线求积公式误差估计定理1.若()f x 在[,]a b 上有四阶连续导数,则抛物线公式(6)的余项为:5(4)**()[](),[,]2880b a R f f a b ξξ--=∈. (7) 3抛物线公式的代数精度为3.易验证,当23()1,,,f x x x x =时,式(6)精确成立,而当4()f x x =时,式(6)不能精确成立.2.1.3 牛顿-科茨公式1牛顿-科茨公式在等距离节点i x a ih =+下,其中(0,1,2b ah i n-==…. )n .作为变量替换x a th =+,那么由求积公式(1),得系数:10(1)(1)(1)()!(1)(1)!ni n t t t i t i t n A h dt i n ---+---==--⎰10(1)(1)...(1)(1)...()(0,1,2,...)!(1)!n nb a t t t i t i t n dt i n n i n -----+---=-⎰ (8)则 ()()n i i A b a C =- (9) 于是差值求积公式为:()0()()()[]nbn i i ai f x dx b a C f x R f ==-+∑⎰(10)称公式(10)为牛顿-科茨求积公式,其中()n iC 称为科茨系数.显然,科茨系数与被积函数()f x 及积分区间[,]a b 无关,它指依赖于n ,且为多项式积分.因此,只要给出n ,就能看出i A ,并写出相应地牛顿-科茨公式.2牛顿-科茨公式的截断误差与代数精度.当1n =与2n =情况分析牛顿-科茨公式的截断误差为(1)()[]()()()(1)!n b b bn aaaf R f f x dx x dx x dxn ξϕω+=-=+⎰⎰⎰牛顿-科茨公式的截断误差还可以写成(2)*1()[]()((2)!n bn a f R f x dx n n ξω++=+⎰为偶数）(1)*1()[]()(1)!n bn a f R f x dx n ξω++=+⎰ (n 为奇数） (11) 其中*[,]a b ξ∈,且不依赖于x ,101()()()...()n n x x x x x x x ω+=---,对()f x 为任何并不超过n 次多项式,均有(1)()0n fx +≡,因而[]0R f ≡,即0()()nbi i ai f x dx A f x ==∑⎰精确成立,也就是说,牛顿-科茨公式的代数精度至少为n ,牛顿-科茨公式在n 为偶数时,至少具有1n +次代数精度,在n 为奇数情况时,至少具有n 次代数精度.2.1.4复化梯形求积公式将区间[,]a b 等分,节点为i x a ih =+ (步长b ah n-=),0,1,2...,i n =)在每个小区间1[,]i i x x -上采用梯形公式(4)得11111()()[(()()]2ii nnbx i i i i ax i i x x f x dx f x dx f x f x ---==-=≈+=∑∑⎰⎰11[()()]2ni i i hf x f x +=+=∑11[()2()()]2n i n i hf a f x f b T -=++=∑ (12)称式(12)为复化梯形公式. 复化梯形公式余项为()2()()()12i n b a R f h f η-''=-(13) 2.1.5复化辛普森求积公式在每个小区间],[1+i i x x 上,辛普森公式(6)得11102()[()4()()]6n bi i ai i hf x dx f x f x f x -++==++∑⎰（14）111012[()4()2((6)]6n n i i i i hf a f x f x f --+===+++∑∑记 )]()(2)(4)([6111021b f x f x f a f hS n i i n i i n +++=∑∑-=-=+ (15)式中,21+i x为],[1+i i x x 的中点,即h x x i i 2121+=+.式(15)称为复化辛普森公式,其余项为∑-=-=-=10)4(4)()2(180)()(n i i n n f h h S f I f R η, 1(,).i i i x x η+∈故 ),(),()2(180)(R )4(4b a f h a b f n ∈--=ηη (16) 为复化辛普森的截断误差. 2.1.6复化科茨求积公式将区间[,]a b n 等分, 4n m =,m 为正整数,在每个子区间444[,]k k x x -上用科茨求积公式得到复化求积公式:412()[7()7()32()45mbk ak hf x dx f a f b f x -≈++∑⎰14241411112()32()14()mmm k k k N k k k f xf x f x C ---===+++=∑∑∑ (17)其中 4b a b a h n m--==, k x a kh =+ 其截断误差为6(6)2()[,](),()945n b a R f C h f a b ηη-=-<. 2.1.7 变步长复化求积方法复化求积公式虽然计算简单,也达到了提高精度的目的,但为了满足精度要求必须顾及误差,利用误差公式往往很困难,因为误差表达式中含有未知函数的导数,而估计各阶导数的最大值不太容易.我们可以采取把积分的区间[,]a b 细分的办法,在计算积分时将步长逐步折半,利用前后两次结果进行误差估计,如此继续,直到相邻两次结果相差不大,取最小的步长算出的结果为积分值,这种方法称为变步长积分法.以复化梯形公式为例,把区间[,]a b 分成n 等分,设复化梯形公式的近似值为n T ,原积分值为I ,由复化梯形公式误差公式(14)知:2"11()()()n b a b a I T f a b N N ηη--=-<<再把区间[,]a b 分成2n 等分,得近似值2n T ,则2222()()()122k b a b a I T f a b nηη--''=-<< 假定()f x ''在[,]a b 上变化不大,既有12()()f f ηη''''≈. 由上式得 .24kkI T I T -≈-于是 222211()()341n n n n n n I T T T T T T ≈+-=+-- (18) 式(18)表明若用2n T 作为I 的近似值,其截断误差约为2()3n n T T - (19)2.2 龙贝格求积公式龙贝格积分法的基本思想是采用复化梯形求积方法不断折半步长过程中,在积分结果中加入时候误差估计值进行补偿,使积分计算的收敛性加速,就可以加工出,,,...n n n S C R 精度较高的积分结果.由式(19), 2n T 的误差大致为23n nT T -,因此,可用这个误差值作为2n T 的一种补偿,加到2n T 上,则可得到积分准确值I ,比2n T 的更好近似值~T .222141()333n n n n nT T T T T T =+-=- 2221(2)21n n T T =-- (20)式(20)左端1n =时 记122121141()333S T T T T T =+-=- 112()()332a b T b a f +=+- [()4()()]62b a a b f a f f b -+=++恰好为[,]a b 上应用辛普生公式(16)的结果.在每个小区间应用辛普生公式:11[()2()()]2n n k k hT f a f x f b -==++∑121()112[()2()()2()]4n n n k k k k hT f a f x f b f x --===+++∑∑代入式(20)的左端得11111[()2()()2()32n nk k k k h f a f x f b f x -==+++--∑∑ 11[()2()()]2n k k h f a f x f b -++∑11111[()4()2()()]62n n k k k k f a f x f x f b -===+-++∑∑n S =从而复化辛普森公式与复化梯形公式公式有以下关系式2441n nn T T S -=- (21)类似也可以推证,在辛普森序列基础上,利用以下关系式22242161151541n n n n n S S C S S -=-=- (22)可以造出收敛速度更快的科茨序列12,...,...n C C C 将此推行下去,在科茨序列基础上,通过243431n nn C C R -=- (23)构造出收敛速度比科茨序列更快的龙贝格序列12,,......n R R R .以上这种通过逐步构造龙贝格序列的积分近似值法就称为龙贝格积分法.2.3高斯求积公式由定理()()()baf x F b F a =-⎰知,插值型求积公式的代数精度与求积节点的个数有关,具有1n +个节点的插值型求积公式至少具有n 次代数精度.不仅如此,代数精度与节点的选取有关,在构造牛顿-科茨求积公式时,为了简化处理过程,限定用等分节点作为求积节点,这样做,虽然公式确实得到简化,但同时也限制了公式的代数精度. 设积分,1,1=-=b a 本段讨论如下求积公式11()()ni i i f x A f x -==∑⎰(24)对任意积分区间[,]a b ,通过变 22ba t ab x ++-= 可以转换到区间]1,1[-上,这时11()()222bab a b a a bf x dx f t dt ---+=+⎰⎰ 此时,求积公式写为0()()222n bii ai b a a b b af x dx A f t =-+-=+∑⎰若一组节点]1,1[.....,10-∈n x x x 使插值型求积公式(24)具有21n +次代数精度,则称此组节点为高斯点,并称相应求积公式(24)为高斯求积公式.2.3.1 高斯求积公式的余项(2)2()[]()()()(22)!n nbb k k aa k f R f f x dx A f x x dx n ηω+==-=+∑⎰⎰ 其中01()()()...(),[,]n x x x x x x x a b ωη=---∈,且不依赖于x .2.3.2 复化高斯求积公式复化高斯求积公式的基本思想是:将积分区间[,]a b 分成n 个等长小区间1[,](1,...)i i t t i m -=,然后在低阶(2n =)高斯求积公式算出近似值,最后将他们相加的积分()baf t dt ⎰的近似值m G ,即11111111()()[]222ii mmbt i i i i i i at i i t t t t t t f t dt f t dt dt -----==-+-==+∑∑⎰⎰⎰1111[()]222m i h ha i h x dx-==+-+∑⎰101[()]222m n j j mi j h hA f a i h x G ==≈+-+≈∑∑ (25)其中mab h -=,j A 与(0,1,2,...,)j t j n =可由书中表中查出. 3 应用3.1插值型积分的应用例1 用牛顿-科茨公式(1,2,4n =)计算积分12211I x =+⎰. 解 1n =时2210112[]0.4512101()2I -≈+=++2n =时22211112[4]0.463725116101()1()42I -≈++=+++4n =时2222111112[7321232]0.46363311390101()1()1()848I =++++≈++++例2 利用复化梯形求积公式计算积分 12211I dx x =+⎰解 设211)(xx f +=,分点个数为n =1,2,4,5时,求出相应积分n T , 111[(()())],21,2(),.n n i i i i i T f a f b f h b a h n n f x f x a ih ih -=⎧=++⎪⎪-⎪==⎨⎪=⎪⎪=+=⎩∑列表如下:n =1的计算结果见表1-1所列 n h0x 1x 0f1f1T10.50.00.51.00.80.45n =2的表格如下 n h0x1x2x0f1f 2f 2T20.250.000.250.501.000.941765 0.800.460294n =4时计算结果如下表 n h 0x1x2x3x4x40.1250.000.1250.250.3750.500f1f2f3f4f4T1.000.98461540.94117650.8767120.800.462813n = 5时计算结果如下 n h0x1x2x3x4x5x50.10.00.10.20.30.40.50f1f2f3f4f5f5T1.00.9900990.96153850.917430.8620690.80.463114例3 利用复化求积公式120x e dx ⎰,问积分区间为多少等分才能得证有5位有效数字？解 由式（14）知322()[],()()1212n b a b a R f h f n f n n--''''=-=- 有1(),(),2x xf x e f x e b a ''==-=,当]21,0[∈x 时,在12|()|f x e ''≤,所以122|[]|96n eR f n≤ 由于120x e dx ⎰的准确值具有一位整数,所以要使近似值具有5位有效数字,n 必须满足4242211048,102196⨯≥⨯≤-e n n e 或 取对数有 19=n .即将区间]21,0[19等分可满足给定的精度要求.例4 利用复化抛物线求积公式计算 120211I dx x =+⎰. 解 设11)(2+=x x f ,取m =1,2, 3时,公式()⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧++=+=====-=+++=+---=-=+∑∑.)12(,2),(),(),(,,242[31221212221111,1222h i a x ih a x x f f x f f b f f a f f m a b n f f f f h S i i i i i i b a m i m i i b a m当m =1,2,3时结果如下表所示 当m =1时m h(0.0)f )25.0(f )5.0(f2S1 0.25 1.0 0.9411765 0.80 0.463725当m =2时mh(0.0)f(0.125)f (0.025)f (0.35)f )5.0(f4S20.125 1.0 0.9846154 0.9411765 0.8767123 0.80 0.463653当m =3时mh(0.0)f(0.08333)f (0.16667)f (0.35)f(0.33333)f (0.14166667)f )5.0(f4S30.83331.00.99310340.9729730.9411760.90.852070.80.4636例5 用复化梯形公式,辛普森公式和科茨公式计算积分10sin xdx x ⎰的近似值.解按精度要求确定]1,0[分多少等分,即确定步长,要使6441021)1(28801|],[|-⨯≤≤M m S f R n ,只需.4642880102M m ⨯≥令10sin ()cos xf x txdt x==⎰, 则1()0sin ()()(cos )k kk k k d xd fx tx dt dx xdx ==⎰1cos().2k t tx kdt π=+⎰dt ktx t x f k k |)2cos(|max )(|max 10)(π+≤⎰11.1k t d t t≤=+⎰)10(≤≤x (4)1max |()| 5.f x ≤所以只要,9.13831288010264=⨯⨯≥-m 取m =4即可, 当4n =时,在每个子区间上用式(25）,或(14),或(17),结果.9460829.0,9460833.0,9456911.0888===C S T3.2 龙贝格积分公式应用例6 用龙贝格算法计算积分1241I dx x=+⎰的近似值,要求误差小于510-. 解 .3,0,14)(2==+=b a x x f 步骤如下:2)1(,4)0()1(==f f 得.3)]1()0([211=+=f f T )2(计算,1.3)]21([21,516)21(12=+==f T T f 由此得 301333334121=-=T T S . (3)算出），（43),41(f f 从而,3013118)]43()41([412124=++=f f T T,14157.334242=-=T T S.30142121516121=-=S S C (4)计算),87(),85(),83(),81(f f f f 从而得到:13899.3)]87()85()83()81([812148=++++=f f f f T T ,,14159.334482=-=T T S,14059.31516242=-=S S C .1458.36364121=-=C C R(5)再计算),1615(),1613(),1611(),169(),167(),165(),163(),161(f f f f f f f f从而得到: 14094.316=T30141598=S ,,14159.3,14159.324==R C 51210||-≤-R R , 所以12043.14159.1dx x ≈+⎰3.3高斯求积公式的应用例7 用两点复化高斯求积公式计算10,x I e dx =⎰要求允许误差.106-=ε解 在本算法中取21=+n 时,,110==A A 其中;,)(mab h e x f x -== =++--=∑=)22(2201j jj b a x a b f A a b G.87189637800.1][21)32121()32121(=++-eem =2时, h =21, ]4121)21([4120202j i j j x i f A G +⨯-=∑∑==.57182571650.1)(41341333413341333413=+++=++--eeee m =3时, h =31. .37182769352.1]631)21([6130203=+⨯-=∑∑==j i j j x i f A G .101027.71||||56323--<⨯≈+-G G G3.4 几种方法的比较分析例8 计算积分211ln 2dx x =⎰，精确到0.001.(1)利用矩形公式计算, 因为对于x x f 1)(=,有320()2f x x''<=<(如果1<x <2),所以按照公式0)2(S =+-dx b a x ba . 0<n R <2112n . 如果取n =10,则我们公式的余项的余数得31010.84101200R -<<⨯,我们还必须加进由于在计算函数值实行四舍五入所产生的误差的界限相差于0.16⨯310-,为了这个目的只要计算1x的值到四位小数精确到0.00005就够了.我们有1232527292132152172192 1.051.151.251.351.551.651.751.851.95x x x x x x x x x =========5128.05405.05714.06061.06897.07407.08.08696.09524.02192172152132927252321=========y y y y y y y y y 和6.928469284.0109284.6=(2) 按照梯形公式作同样的计算,在这种情况下,作公式 210,||6n n R R n<<在这儿也试一试取n =10,虽然此时仅可以证3107.16001||-⨯<<n R ,纵坐标是9.18.17.16.15.14.13.12.11.1987654321=========x x x x x x x x x 5263.05556.05882.06250.06667.07143.07692.08333.09091.0987654321=========y y y y y y y y y和1877.669377.01877.621500101=+）（ (3) 用辛普森公式做同样的计算作公式 .0))(()2(180)()4(45<≤≤⨯--=n n R b a f n a b R ξξ 并且n =5时有55104.1||-⨯<R .实行计算到五位数字,精确到0.0000058.16.14.12.14321====x x x x 45636.555556.062500.071429.083333.04321和====y y y y 9.17.15.13.11.12927252321=====x x x x x83820.1352632.058824.066667.076923.090909.029********和=====y y y y y.20.150==x x 50000.150000.060000.150和==y y6931525.083820.345636.550000.1301=++）（. 由此可见，用辛普森公式计算得到的值误差最小，计算量相对一般；而用矩形公式计算得到的值误差较大，计算量也比较大；用梯形公式计算的值误差比用矩形公式得到的值要误差小，计算量也是如此.所以我们计算定积分时用辛普森公式往往得到的值误差小，而对没有要求误差大小的，则可以选择辛普森或者是梯形公式，因为这两种方法计算量相对较小.结 束 语本文只讨论了一些一维数值积分方法及其它们的应用,误差分析等有关内容.其中最常用的方法是插值型积分以及复化方法、龙贝格积分方法和高斯积分方法,并讨论了相关求积方法的代数精度和误差分析,并给出了一些例题,分析各种方法的近似值,得出误差分析最小的近似方法.由于篇幅有限,对于高维数值积分方法本文便不再讨论.参考文献[1] 华东师范大学数学系，数学分析（第一版）[M]，北京:高等教育出版社,2001. [2] 李庆阳,关治,白峰杉，数值计算原理（第二版）[M]，北京: 清华大学出版社, 2008. [3] 肖筱南，现代数值计算方法（第一版）[M]，北京: 北京大学出版社, 1999.[4] 菲赫金格尔茨，微积分学教程（第三版）[M]，北京: 高等教育出版社, 2005. [5] 裴礼文，数学分析中的典型问题与方法（第一版）[M] ，北京: 北京大学出版社,2004. [6] 李桂成，计算方法（第三版）[M]，北京: 高等教育出版社,2010.[7] Yin Y uezhu ,Yang Zhonglian.Calculating Skillfully the Curve Integral and Surface Integral Type 2 bySymmetry, SCIENCE & TECHNOLOGY INFORMATION ,2008(30)The Approximate Numerical Method of the Definite IntegralAbstract This paper mainly discusses common numerical methods of unary function, such as approximate calculation method of interpolation integral, Lebesgue integral and Gauss integration. With these methods in calculating the integral, it will produce some error. In order to reduce the error, we can use after the formula for product and after the Gauss formula. This paper focus on these methods introducing formula of introduction and truncation errors .In addition they can provide examples to analysis size of the error and computation.Keywords interpolation integral Lebesgue integral Gauss integral error analysis approximate computation。

高等数学定积分的计算方法
定积分是高等数学中的一个重要概念，它是求解某种函数在某一区间上的积分，可以用来计算曲线下某一区域的面积或体积。

计算定积分的方法有很多，其中最常用的是求和法和分段法。

求和法是指将定积分的区间分割成若干小区间，然后将每个小区间上的函数值加起来，从而求出定积分的近似值。

具体的计算方法是：首先，将定积分的区间[a,b]分割成n个小区间，即
a=x_0<x_1<x_2<…<x_n=b，其中x_i=a+i*h，h=(b-a)/n；然后，将每个小区间上的函数值加起来，即
∫_a^bf(x)dx≈h*[f(x_0)+f(x_1)+f(x_2)+…+f(x_n)]，其中h=(b-
a)/n。

分段法是指将定积分的区间分割成若干段，然后分别求出每段上的积分，最后将每段上的积分加起来，从而求出定积分的近似值。

具体的计算方法是：首先，将定积分的区间[a,b]分割成
n段，即a=x_0<x_1<x_2<…<x_n=b，其中x_i=a+i*h，h=(b-
a)/n；然后，分别求出每段上的积分，即
∫_a^bf(x)dx≈∑_(i=1)^n▒f(x_i)*h，其中h=(b-a)/n；最后，将每
段上的积分加起来，即∫_a^bf(x)dx≈∑_(i=1)^n▒f(x_i)*h。

以上就是计算定积分的两种常用方法，它们都是基于求和原理的，只是求和的方式不同而已。

在实际应用中，我们可以根据实际情况选择合适的方法，以达到最优的计算效果。

定积分的近似计算方法定积分是数学中重要的概念之一，用于计算曲线下面积、体积、质量等问题。

然而，很多情况下，定积分的精确计算是困难的，因此需要使用近似计算的方法来求解。

下面将介绍一些常用的定积分近似计算方法。

1.矩形法：矩形法是最基本的一种近似计算方法，它将定积分区间划分为若干个小区间，并在每个小区间上选择一个代表点，然后计算这些小区间的矩形面积之和。

通常有三种矩形法：左矩形法（取每个小区间左端点的函数值）、右矩形法（取每个小区间右端点的函数值）和中矩形法（取每个小区间中点的函数值）。

它们的近似公式分别为：左矩形法：$\int_{a}^{b}f(x)dx \approx \sum_{k=0}^{n-1}f(x_k)(x_{k+1}-x_k)$右矩形法：$\int_{a}^{b}f(x)dx \approx\sum_{k=1}^{n}f(x_k)(x_k-x_{k-1})$中矩形法：$\int_{a}^{b}f(x)dx \approx \sum_{k=0}^{n-1}f(\frac{x_k+x_{k+1}}{2})(x_{k+1}-x_k)$2.梯形法：梯形法是一种比矩形法更精确的近似计算方法。

它的基本思想是将定积分区间划分为若干个小区间，在每个小区间上选择两个端点，然后计算这些小区间内的梯形面积之和。

近似公式为：$\int_{a}^{b}f(x)dx \approx \sum_{k=1}^{n}\frac{f(x_{k-1})+f(x_k)}{2}(x_k-x_{k-1})$3.辛普森法：辛普森法是一种更加精确的近似计算方法，它将定积分区间划分为若干个小区间，并在每个小区间上选择三个点，通过连接这三个点构造一个二次插值多项式，然后计算这些二次插值多项式下的曲线面积之和。

近似公式为：$\int_{a}^{b}f(x)dx \approx\frac{h}{3}\sum_{k=0}^{\frac{n}{2}-1}(f(x_{2k})+4f(x_{2k+1})+f(x_{2k+2}))$其中，$h=\frac{b-a}{n}$，$n$为划分小区间的个数。

定积分的近似计算方法定积分是微积分中的重要概念，它代表了曲线与坐标轴之间的有限面积。

在实际问题中，有时候我们需要计算一些函数在一定范围内的定积分，以获得其中一种物理量或求解其中一种问题的解析解。

然而，有些函数的原函数较复杂甚至难以找到，这时候我们就需要使用定积分的近似计算方法。

下面将介绍几种常用的定积分近似计算方法：1.矩形法：矩形法是最简单的一种近似计算方法。

它的思想是将积分区间等分成若干个小区间，然后在每个小区间上选择一个代表点，通过函数在这些代表点处的函数值与小区间长度的乘积来近似计算定积分。

具体计算公式为：∫[a,b]f(x)dx ≈ Δx * (f(x₁) + f(x₂) + ... + f(xₙ))其中，Δx=(b-a)/n，n为小区间个数，x₁、x₂等为代表点。

当n越大时，近似结果越接近真实结果。

2.梯形法：梯形法是将积分区间分成若干个小区间，然后在每个小区间上构造一个梯形，通过计算梯形的面积来近似计算定积分。

具体计算公式为：∫[a,b]f(x)dx ≈ Δx * (f(x₁) + f(x₂))/2 + Δx * (f(x₂) +f(x₃))/2 + ... + Δx * (f(xₙ-1) + f(xₙ))/2其中，Δx=(b-a)/n，n为小区间个数，x₁、x₂等为小区间的端点。

3.辛普森法：辛普森法是一种比矩形法和梯形法更精确的近似计算方法。

它的思想是将积分区间分成若干个小区间，然后在每个小区间上构造一个二次多项式，通过计算这些二次多项式的面积来近似计算定积分。

具体计算公式为：∫[a,b]f(x)dx ≈ Δx * (f(x₀)+4f(x₁)+f(x₂))/3 + Δx *(f(x₂)+4f(x₃)+f(x₄))/3 + ... + Δx * (f(xₙ-2)+4f(xₙ-1)+f(xₙ))/3其中，Δx=(b-a)/n，n为小区间个数，x₀、x₁、x₂等为小区间的端点。

4.蒙特卡洛法：蒙特卡洛法是通过随机抽取点的方法来近似计算定积分。

定积分的近似计算方法摘要 本文主要讨论了一元函数常见的数值积分方法,例如插值型求积公式、龙贝格求积公式、高斯求积公式等近似计算方法,在用这些方法计算定积分时,会产生一些误差,为了减少误差, 可以利用复化求积公式、复化高斯公式等.本文围绕这些方法,系统介绍它们的计算公式以及截断误差,并用例题分析它们产生误差的大小、计算量等.关键词 插值型积分 龙贝格积分 高斯积分 误差分析 近似计算1引言在计算定积分的值()b aI f x dx =⎰时,常常根据微积分学基本定理求出)(x f 的一个原函数)(x F ,再用牛顿-莱布尼茨公式求的积分,()()()baI f x dx F b F a ==-⎰.但在实际应用中,这种方法只限于解决一小部分定积分的求值问题.当函数没有具体表达式,只是一些实验测得数据形成的表格或图形或者是()F x 无法用初等函数表示,例如,2bx ae dx ⎰,2sin ba x dx ⎰等等,这就需要我们用一些近似方法求的积分值.与数值积分一样,把积分区间细分,在每个小区间上,找到简单函数)(x ϕ来近似代替()f x ,且()bax dx ϕ⎰的值容易求的.这样就把计算复杂的()baf x dx ⎰转化为求简单的积分值()bax dx ϕ⎰.因此,定积分的近似计算实质上是就是被积函数的近似计算问题.2常见数值方法 2.1牛顿-科茨数值方法牛顿-科茨求积公式是求积节点等距离分布的插值型求积公式.利用插值多项式来构造数值积分公式是最常用、最基本的方法,具体做法是：给定区间[,]a b 上一组节点01...n a x x x b =<<<=,以及节点处函数()(0,1,2,i f x i n =,作()f x 的n 次拉格朗日多项式()()()nn i i i x f x l x ϕ==∑,其中 011011()()()()()()()()()i i n i i i i i i i n x x L x x x x L x x l x x x L x x x x L x x -+-+----=----,将插值公式(1)1()()()()(1)!n n n f f x x x n ξϕω++=++. 其中 1012()()()()()n n x xx x xx x L x x ω+=----,[,]a b ξ∈,依赖于变量x , 上式积分得(1)1()()()()(1)!n bb bn n aa af f x dx x dx x dx n ξϕω++=++⎰⎰⎰(1)(1)0()()()()(1)!n nb biiin aai f f x l x dx x dx n ξω++==++∑⎰⎰(1)(1)0()()()()(1)!n nb bi i n aai f f x b l x dx x dxn ξω++==++∑⎰⎰若记 (),(0,1,2,bi ia A l x dx i ==⎰….. )n (1)(1)1()[]()(1)!n bn af R f x dxn ξω++=+⎰, (2)则有()()[]nbi i ai f x dx A f x R f ==+∑⎰(3)称式(3)为插值求型公式,其中(0,1,2,i A i =…. )n 与()f x 无关,叫求积系数, i x 为求积节点,[]R f 为求积公式余项,其中求积系数由(1)决定.2.1.1梯形求积公式1梯形公式当插值节点01,x x 分别选取区间端点,a b 时,由式(3)分别求出求积系数10012bb aa x x xb b aA dx dx x x a b ---===--⎰⎰,01102bb aa x x x ab a A dx dx x x b a ---===--⎰⎰.从而的求积公式()[()()]2bab af x dx f a f b -≈+⎰. (4) 称求积公式(4)为梯形求积公式,简称梯形公式.2梯形公式截断误差: 3*()[](),12b a R f f ξ-''=- *[,]a b ξ∈. (5) 3梯形求积公式的代数精度:1 当()1f x =时,式(5)中 1(1)2bab adx b a x b a -=-=+=-⎰. 精确成立.2.1.2 辛普森求积公式1辛普森求积公式当选取节点为012,,2a bx a x x b +===时,由式(1)求下列求积系数 1200102()()()()2()()6()()2b b a a a b x x b x x x x b a A dx dx a b x x x x a a b +-----===+----⎰⎰,0211002()()()()2()()()3()()22bb aa x x x x x a xb b a A dx dx a b a b x x x x a b -----===++----⎰⎰.0122021()()()()2()()6()()22b b a a a bx a x x x x x b a A dx dx a b a b x x x x a b +-----===++----⎰⎰ .从而求积公式()[()4()()]62bab a a bf x dx f a f f b -+≈++⎰. （6）称式(6)为抛物线积分公式或辛普森积分公式.2抛物线求积公式误差估计定理1.若()f x 在[,]a b 上有四阶连续导数,则抛物线公式(6)的余项为:5(4)**()[](),[,]2880b a R f f a b ξξ--=∈. (7) 3抛物线公式的代数精度为3.易验证,当23()1,,,f x x x x =时,式(6)精确成立,而当4()f x x =时,式(6)不能精确成立.2.1.3 牛顿-科茨公式1牛顿-科茨公式在等距离节点i x a ih =+下,其中(0,1,2b ah i n-==…. )n .作为变量替换x a th =+,那么由求积公式(1),得系数:10(1)(1)(1)()!(1)(1)!ni n t t t i t i t n A h dt i n ---+---==--⎰10(1)(1)...(1)(1)...()(0,1,2,...)!(1)!n nb a t t t i t i t n dt i n n i n -----+---=-⎰ (8)则 ()()n i iA b a C =- (9)于是差值求积公式为:()0()()()[]nbn i i ai f x dx b a C f x R f ==-+∑⎰(10)称公式(10)为牛顿-科茨求积公式,其中()n iC 称为科茨系数.显然,科茨系数与被积函数()f x 及积分区间[,]a b 无关,它指依赖于n ,且为多项式积分.因此,只要给出n ,就能看出i A ,并写出相应地牛顿-科茨公式.2牛顿-科茨公式的截断误差与代数精度.当1n =与2n =情况分析牛顿-科茨公式的截断误差为(1)()[]()()()(1)!n b b bn aaaf R f f x dx x dx x dxn ξϕω+=-=+⎰⎰⎰牛顿-科茨公式的截断误差还可以写成(2)*1()[]()((2)!n bn a f R f x dx n n ξω++=+⎰为偶数）(1)*1()[]()(1)!n bn af R f x dx n ξω++=+⎰ (n 为奇数） (11) 其中*[,]a b ξ∈,且不依赖于x ,101()()()...()n n x x x x x x x ω+=---,对()f x 为任何并不超过n 次多项式,均有(1)()0n fx +≡,因而[]0R f ≡,即0()()nbi i ai f x dx A f x ==∑⎰精确成立,也就是说,牛顿-科茨公式的代数精度至少为n ,牛顿-科茨公式在n 为偶数时,至少具有1n +次代数精度,在n 为奇数情况时,至少具有n 次代数精度.2.1.4复化梯形求积公式将区间[,]a b 等分,节点为i x a ih =+ (步长b ah n-=),0,1,2...,i n =)在每个小区间1[,]i i x x -上采用梯形公式(4)得11111()()[(()()]2ii nnbx i i i i ax i i x x f x dx f x dx f x f x ---==-=≈+=∑∑⎰⎰11[()()]2ni i i hf x f x +=+=∑11[()2()()]2n i n i hf a f x f b T -=++=∑ (12)称式(12)为复化梯形公式. 复化梯形公式余项为()2()()()12i n b a R f h f η-''=-(13) 2.1.5复化辛普森求积公式在每个小区间],[1+i i x x 上,辛普森公式(6)得11102()[()4()()]6n bi i ai i hf x dx f x f x f x -++==++∑⎰（14）111012[()4()2((6)]6n n i i i i hf a f x f x f --+===+++∑∑记 )]()(2)(4)([6111021b f x f x f a f hS n i i n i i n +++=∑∑-=-=+ (15)式中,21+i x为],[1+i i x x 的中点,即h x x i i 2121+=+.式(15)称为复化辛普森公式,其余项为∑-=-=-=10)4(4)()2(180)()(n i i n n f h h S f I f R η, 1(,).i i i x x η+∈ 故 ),(),()2(180)(R )4(4b a f h a b f n ∈--=ηη (16) 为复化辛普森的截断误差. 2.1.6复化科茨求积公式将区间[,]a b n 等分, 4n m =,m 为正整数,在每个子区间444[,]k k x x -上用科茨求积公式得到复化求积公式:412()[7()7()32()45mbk ak hf x dx f a f b f x -≈++∑⎰14241411112()32()14()mmm k k k N k k k f xf x f x C ---===+++=∑∑∑ (17)其中 4b a b ah n m--==, k x a kh =+ 其截断误差为6(6)2()[,](),()945n b a R f C h f a b ηη-=-<. 2.1.7 变步长复化求积方法复化求积公式虽然计算简单,也达到了提高精度的目的,但为了满足精度要求必须顾及误差,利用误差公式往往很困难,因为误差表达式中含有未知函数的导数,而估计各阶导数的最大值不太容易.我们可以采取把积分的区间[,]a b 细分的办法,在计算积分时将步长逐步折半,利用前后两次结果进行误差估计,如此继续,直到相邻两次结果相差不大,取最小的步长算出的结果为积分值,这种方法称为变步长积分法.以复化梯形公式为例,把区间[,]a b 分成n 等分,设复化梯形公式的近似值为n T ,原积分值为I ,由复化梯形公式误差公式(14)知:2"11()()()n b a b a I T f a b N N ηη--=-<<再把区间[,]a b 分成2n 等分,得近似值2n T ,则2222()()()122k b a b a I T f a b nηη--''=-<< 假定()f x ''在[,]a b 上变化不大,既有12()()f f ηη''''≈. 由上式得 .24kkI T I T -≈-于是 222211()()341n n n n n n I T T T T T T ≈+-=+-- (18) 式(18)表明若用2n T 作为I 的近似值,其截断误差约为2()3n n T T - (19)2.2 龙贝格求积公式龙贝格积分法的基本思想是采用复化梯形求积方法不断折半步长过程中,在积分结果中加入时候误差估计值进行补偿,使积分计算的收敛性加速,就可以加工出,,,...n n n S C R 精度较高的积分结果.由式(19), 2n T 的误差大致为23n nT T -,因此,可用这个误差值作为2n T 的一种补偿,加到2n T 上,则可得到积分准确值I ,比2n T 的更好近似值~T .222141()333n n n n nT T T T T T =+-=-2221(2)21n n T T =-- (20)式(20)左端1n =时 记122121141()333S T T T T T =+-=- 112()()332a b T b a f +=+- [()4()()]62b a a b f a f f b -+=++恰好为[,]a b 上应用辛普生公式(16)的结果.在每个小区间应用辛普生公式:11[()2()()]2n n k k hT f a f x f b -==++∑121()112[()2()()2()]4n n n k k k k hT f a f x f b f x --===+++∑∑代入式(20)的左端得11111[()2()()2()32n nk k k k h f a f x f b f x -==+++--∑∑ 11[()2()()]2n k k h f a f x f b -++∑11111[()4()2()()]62n n k k k k f a f x f x f b -===+-++∑∑nS =从而复化辛普森公式与复化梯形公式公式有以下关系式2441n nn T T S -=- (21)类似也可以推证,在辛普森序列基础上,利用以下关系式22242161151541n n n n n S S C S S -=-=- (22)可以造出收敛速度更快的科茨序列12,...,...n C C C 将此推行下去,在科茨序列基础上,通过243431n nn C C R -=- (23)构造出收敛速度比科茨序列更快的龙贝格序列12,,......n R R R .以上这种通过逐步构造龙贝格序列的积分近似值法就称为龙贝格积分法.2.3高斯求积公式由定理()()()baf x F b F a =-⎰知,插值型求积公式的代数精度与求积节点的个数有关,具有1n +个节点的插值型求积公式至少具有n 次代数精度.不仅如此,代数精度与节点的选取有关,在构造牛顿-科茨求积公式时,为了简化处理过程,限定用等分节点作为求积节点,这样做,虽然公式确实得到简化,但同时也限制了公式的代数精度. 设积分,1,1=-=b a 本段讨论如下求积公式11()()ni i i f x A f x -==∑⎰(24)对任意积分区间[,]a b ,通过变 22ba t ab x ++-= 可以转换到区间]1,1[-上,这时11()()222bab a b a a bf x dx f t dt ---+=+⎰⎰ 此时,求积公式写为0()()222n bii ai b a a b b af x dx A f t =-+-=+∑⎰若一组节点]1,1[.....,10-∈n x x x 使插值型求积公式(24)具有21n +次代数精度,则称此组节点为高斯点,并称相应求积公式(24)为高斯求积公式.2.3.1 高斯求积公式的余项(2)2()[]()()()(22)!n nbb k k aa k f R f f x dx A f x x dx n ηω+==-=+∑⎰⎰ 其中 01()()()...(),[,]n x x x x x x x ab ωη=---∈,且不依赖于x .2.3.2 复化高斯求积公式复化高斯求积公式的基本思想是:将积分区间[,]a b 分成n个等长小区间1[,](1,...)i i t t i m -=,然后在低阶(2n =)高斯求积公式算出近似值,最后将他们相加的积分()baf t dt ⎰的近似值m G ,即11111111()()[]222ii mmbt i i i i i i at i i t t t t t t f t dt f t dt dt -----==-+-==+∑∑⎰⎰⎰1111[()]222m i h ha i h x dx-==+-+∑⎰101[()]222m n j j mi j h hA f a i h x G ==≈+-+≈∑∑ (25)其中mab h -=,j A 与(0,1,2,...,)j t j n =可由书中表中查出. 3 应用3.1插值型积分的应用例1 用牛顿-科茨公式(1,2,4n =)计算积分12211I x =+⎰. 解 1n =时2210112[]0.4512101()2I -≈+=++2n =时22211112[4]0.463725116101()1()42I -≈++=+++4n =时2222111112[7321232]0.46363311390101()1()1()848I =++++≈++++例2 利用复化梯形求积公式计算积分 12211I dx x =+⎰解 设211)(xx f +=,分点个数为n =1,2,4,5时,求出相应积分n T , 111[(()())],21,2(),.n n i i i i i T f a f b f h b a h n n f x f x a ih ih -=⎧=++⎪⎪-⎪==⎨⎪=⎪⎪=+=⎩∑列表如下:n =1的计算结果见表1-1所列 n h0x 1x 0f1f1T10.50.00.51.0 0.8 0.45n =2的表格如下 n hx1x2xf1f2f2T20.250.00 0.25 0.50 1.00 0.941765 0.80 0.460294n =4时计算结果如下表 n h 0x1x2x3x4x40.1250.00 0.125 0.25 0.375 0.50f1f2f3f4f4T1.00 0.9846154 0.9411765 0.876712 0.80 0.462813n = 5时计算结果如下 n hx1x2x3x4x5x50.10.0 0.1 0.2 0.3 0.40.5f1f2f3f4f5f5T1.0 0.990099 0.9615385 0.91743 0.862069 0.80.463114例3 利用复化求积公式120x e dx ⎰,问积分区间为多少等分才能得证有5位有效数字？解 由式（14）知322()[],()()1212n b a b a R f h f n f n n--''''=-=- 有1(),(),2x x f x e f x e b a ''==-=,当]21,0[∈x 时,在12|()|f x e ''≤,所以122|[]|96n eR f n≤ 由于120x e dx ⎰的准确值具有一位整数,所以要使近似值具有5位有效数字,n 必须满足4242211048,102196⨯≥⨯≤-e n n e 或 取对数有 19=n .即将区间]21,0[19等分可满足给定的精度要求.例4 利用复化抛物线求积公式计算 120211I dx x =+⎰. 解 设11)(2+=x x f ,取m =1,2, 3时,公式()⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧++=+=====-=+++=+---=-=+∑∑.)12(,2),(),(),(,,242[31221212221111,1222h i a x ih a x x f f x f f b f f a f f m a b n f f f f h S i i i i i i b a m i m i i b a m当m =1,2,3时结果如下表所示 当m =1时m h(0.0)f )25.0(f )5.0(f2S1 0.25 1.0 0.9411765 0.80 0.463725当m =2时mh(0.0)f(0.125)f (0.025)f (0.35)f )5.0(f4S20.125 1.0 0.9846154 0.9411765 0.8767123 0.80 0.463653当m =3时mh(0.0)f(0.08333)f (0.16667)f (0.35)f(0.33333)f (0.14166667)f )5.0(f4S30.83331.00.99310340.9729730.9411760.90.852070.80.4636例5 用复化梯形公式,辛普森公式和科茨公式计算积分10sin xdx x ⎰的近似值.解按精度要求确定]1,0[分多少等分,即确定步长,要使6441021)1(28801|],[|-⨯≤≤M m S f R n ,只需.4642880102M m ⨯≥令10sin ()cos xf x txdt x==⎰,则1()0sin ()()(cos )k kk k k d xd fx tx dt dx x dx==⎰ 1cos().2k t tx kdt π=+⎰dt ktx t x f k k |)2cos(|max )(|max 10)(π+≤⎰11.1k t d t t≤=+⎰)10(≤≤x (4)1max |()| 5.f x ≤所以只要,9.13831288010264=⨯⨯≥-m 取m =4即可, 当4n =时,在每个子区间上用式(25）,或(14),或(17),结果.9460829.0,9460833.0,9456911.0888===C S T3.2 龙贝格积分公式应用例6 用龙贝格算法计算积分1241I dx x=+⎰的近似值,要求误差小于510-. 解 .3,0,14)(2==+=b a x x f 步骤如下:2)1(,4)0()1(==f f 得.3)]1()0([211=+=f f T )2(计算,1.3)]21([21,516)21(12=+==f T T f 由此得301333334121=-=T T S . (3)算出），（43),41(f f 从而,3013118)]43()41([412124=++=f f T T,14157.334242=-=T T S .30142121516121=-=S S C(4)计算),87(),85(),83(),81(f f f f 从而得到:13899.3)]87()85()83()81([812148=++++=f f f f T T ,,14159.334482=-=T T S ,14059.31516242=-=S S C.1458.36364121=-=C C R (5)再计算),1615(),1613(),1611(),169(),167(),165(),163(),161(f f f f f f f f 从而得到: 14094.316=T30141598=S ,,14159.3,14159.324==R C 51210||-≤-R R , 所以12043.14159.1dx x ≈+⎰3.3高斯求积公式的应用例7 用两点复化高斯求积公式计算10,x I e dx =⎰要求允许误差.106-=ε解 在本算法中取21=+n 时,,110==A A 其中;,)(mab h e x f x-== =++--=∑=)22(2201j jj b a x a b f A a b G.87189637800.1][21)32121()32121(=++-eem =2时, h =21, ]4121)21([4120202j i j j x i f A G +⨯-=∑∑==.57182571650.1)(41341333413341333413=+++=++--eeee m =3时, h =31. .37182769352.1]631)21([6130203=+⨯-=∑∑==j i j j x i f A G.101027.71||||56323--<⨯≈+-G G G3.4 几种方法的比较分析例8 计算积分211ln 2dx x =⎰，精确到0.001.(1)利用矩形公式计算, 因为对于x x f 1)(=,有320()2f x x''<=<(如果1<x <2),所以按照公式0)2(S =+-dx ba xb a . 0<n R <2112n . 如果取n =10,则我们公式的余项的余数得31010.84101200R -<<⨯,我们还必须加进由于在计算函数值实行四舍五入所产生的误差的界限相差于0.16⨯310-,为了这个目的只要计算1x的值到四位小数精确到0.00005就够了.我们有1232527292132152172192 1.051.151.251.351.551.651.751.851.95x x x x x x x x x =========5128.05405.05714.06061.06897.07407.08.08696.09524.02192172152132927252321=========y y y y y y y y y和6.928469284.0109284.6= (2) 按照梯形公式作同样的计算,在这种情况下,作公式 210,||6n n R R n<<在这儿也试一试取n =10,虽然此时仅可以证3107.16001||-⨯<<n R ,纵坐标是9.18.17.16.15.14.13.12.11.1987654321=========x x x x x x x x x 5263.05556.05882.06250.06667.07143.07692.08333.09091.0987654321=========y y y y y y y y y和1877.669377.01877.621500101=+）（ (3) 用辛普森公式做同样的计算作公式 .0))(()2(180)()4(45<≤≤⨯--=n n R b a f n a b R ξξ 并且n =5时有55104.1||-⨯<R .实行计算到五位数字,精确到0.0000058.16.14.12.14321====x x x x 45636.555556.062500.071429.083333.04321和====y y y y 9.17.15.13.11.12927252321=====x x x x x83820.1352632.058824.066667.076923.090909.029********和=====y y y y y.20.150==x x 50000.150000.060000.150和==y y6931525.083820.345636.550000.1301=++）（. 由此可见，用辛普森公式计算得到的值误差最小，计算量相对一般；而用矩形公式计算得到的值误差较大，计算量也比较大；用梯形公式计算的值误差比用矩形公式得到的值要误差小，计算量也是如此.所以我们计算定积分时用辛普森公式往往得到的值误差小，而对没有要求误差大小的，则可以选择辛普森或者是梯形公式，因为这两种方法计算量相对较小.结 束 语本文只讨论了一些一维数值积分方法及其它们的应用,误差分析等有关内容.其中最常用的方法是插值型积分以及复化方法、龙贝格积分方法和高斯积分方法,并讨论了相关求积方法的代数精度和误差分析,并给出了一些例题,分析各种方法的近似值,得出误差分析最小的近似方法.由于篇幅有限,对于高维数值积分方法本文便不再讨论.参考文献[1] 华东师范大学数学系，数学分析（第一版）[M]，北京:高等教育出版社,2001. [2] 李庆阳,关治,白峰杉，数值计算原理（第二版）[M]，北京: 清华大学出版社, 2008. [3] 肖筱南，现代数值计算方法（第一版）[M]，北京: 北京大学出版社, 1999.[4] 菲赫金格尔茨，微积分学教程（第三版）[M]，北京: 高等教育出版社, 2005. [5] 裴礼文，数学分析中的典型问题与方法（第一版）[M] ，北京: 北京大学出版社,2004. [6] 李桂成，计算方法（第三版）[M]，北京: 高等教育出版社,2010.[7] Yin Y uezhu ,Yang Zhonglian.Calculating Skillfully the Curve Integral and Surface Integral Type 2 bySymmetry, SCIENCE & TECHNOLOGY INFORMATION ,2008(30)The Approximate Numerical Method of the Definite IntegralAbstract This paper mainly discusses common numerical methods of unary function, such as approximate calculation method of interpolation integral, Lebesgue integral and Gauss integration. With these methods in calculating the integral, it will produce some error. In order to reduce the error, we can use after the formula for product and after the Gauss formula. This paper focus on these methods introducing formula of introduction and truncation errors .In addition they can provide examples to analysis size of the error and computation.Keywords interpolation integral Lebesgue integral Gauss integral error analysis approximate computation。

定积分的近似计算方法一、矩形法（Rectangle Method）矩形法是将定积分区间划分成若干个子区间，并在每个子区间上选取一个点作为代表，然后利用函数在这些点上的取值乘以子区间的长度来近似计算定积分。

1.1. 零点矩形法（Midpoint Rectangle Method）零点矩形法是将每个子区间的中点作为代表点，然后计算每个子区间的长度乘以函数在代表点上的取值，并将所有子区间的结果相加，即可得到定积分的近似值。

1.2. 左点矩形法（Left Rectangle Method）左点矩形法是将每个子区间的左端点作为代表点，然后计算每个子区间的长度乘以函数在代表点上的取值，并将所有子区间的结果相加，即可得到定积分的近似值。

1.3. 右点矩形法（Right Rectangle Method）右点矩形法是将每个子区间的右端点作为代表点，然后计算每个子区间的长度乘以函数在代表点上的取值，并将所有子区间的结果相加，即可得到定积分的近似值。

二、梯形法（Trapezoidal Rule）梯形法将定积分区间划分成若干个子区间，然后在每个子区间上用一个梯形来近似表示函数的曲线部分。

梯形的面积等于底边长度的一半乘以两个高的和。

2.1. 边均值梯形法（Midpoint Trapezoidal Rule）边均值梯形法是将每个子区间的左右端点的函数值相加除以2，然后计算每个子区间的长度乘以边均值的结果，并将所有子区间的结果相加，即可得到定积分的近似值。

三、辛普森法（Simpson's Rule）辛普森法将定积分区间划分成若干个子区间，然后利用多项式函数在这些子区间上的插值来计算定积分的近似值。

具体而言，辛普森法在每个子区间上构造一个二次多项式，使其与原函数在子区间端点处以及中点处的函数值相等，然后计算每个子区间上的插值多项式的积分，并将所有子区间的结果相加，即可得到定积分的近似值。

总结起来，定积分的近似计算方法有矩形法、梯形法和辛普森法三种。

辛普森法则求积分
辛普森法则是一种数值积分方法，用于近似计算函数的定积分。

这种方法将定积分区间分成若干个等宽子区间，并在每个子区间内用一个二次函数逼近被积函数。

然后通过对这些二次函数进行积分，得到整个定积分的近似值。

具体而言，设被积函数为$f(x)$，积分区间为$[a,b]$，将积分区间等距地分成$2n$个子区间，每个子区间的长度为$h=\frac{b-a}{2n}$。

则辛普森法则的近似公式为：
$$
\int_a^bf(x)dx\approx\frac{h}{3}\left[f(a)+2\sum_{i=1}^{n-1}f(a+2ih)+4\s um_{i=1}^nf(a+(2i-1)h)+f(b)\right]
$$
其中$f(a)$和$f(b)$是被积函数在积分区间端点处的函数值，$f(a+2ih)$和$f(a+(2i-1)h)$是偶数项和奇数项的子区间中心点处的函数值。

这个公式可以通过简单的代数运算和积分计算得到，它的精度随着子区间数的增加而增加，当子区间数增加至一定程度时，可以得到较高的精度。

定积分的近似计算定积分的近似计算是数学中一种常用的方法，它可以帮助我们计算具体函数在一定区间上的面积或曲线长度。

在实际应用中，定积分的近似计算有多种方法，包括矩形法、梯形法、辛普森法等。

本文将侧重介绍这些方法的原理和应用。

1. 矩形法（Reimann和法）：矩形法是定积分近似计算的最简单方法之一、其基本思想是将给定区间等分为若干个小区间，然后在每个小区间内选择一个代表点，以该点处函数值与小区间长度的乘积作为该小区间的面积近似值，然后对所有小区间的面积近似值求和得到最终的近似计算结果。

具体而言，设函数f(x)在区间[a,b]上连续，将该区间分为n个小区间：x0=a, x1=a+h, x2=a+2h, ..., xn=a+nh=b其中h=(b-a)/n，xi为每个小区间的代表点。

此时，对于每个小区间，我们可以将其面积近似为S_i=h*f(xi)，然后对所有小区间的面积进行求和，即：S=a*h*f(x0)+a*h*f(x1)+...+a*h*f(xn-1)对于当n趋向于无穷大时，通过这一方法可以得到函数f(x)在区间[a,b]上的定积分值。

2.梯形法：梯形法是定积分近似计算的另一种常用方法。

与矩形法类似，梯形法也是将给定区间等分为若干个小区间，然后在每个小区间内用该区间两个端点处的函数值构造出一个梯形，以该梯形的面积作为小区间面积的近似值，最终对所有小区间的面积进行求和得到近似计算结果。

设函数f(x)在区间[a,b]上连续，将该区间分为n个小区间，并选取区间端点[a,b]分别作为梯形的上底和下底，连线得到梯形。

此时，对于每个小区间，梯形的面积可以近似表示为：S_i=(h/2)*(f(xi)+f(xi+1))其中h=(b-a)/n，xi为每个小区间的起点。

最后，对于所有小区间的面积近似值进行求和，即：S=(h/2)*[f(a)+2f(a+h)+2f(a+2h)+...+2f(b-h)+f(b)]对于当n趋向于无穷大时，通过这一方法也可以得到函数f(x)在区间[a,b]上的定积分值。