第十七章-----在无界区域上定义的函数PPT课件

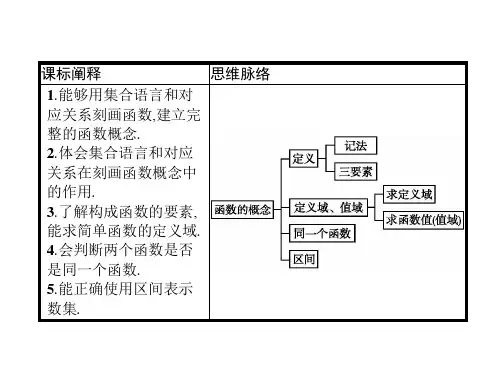
函数的概念课件在数学中，函数是一个核心的概念。

它描述了变量之间的依赖关系，用函数的观点去看待问题，是数学学习中一个极为重要的思想方法。

因此，大家要认真理解函数的概念，掌握函数的基本性质，为后续学习做好准备。

函数是数学中的一种关系，它把一个数集中的元素与另一个数集中的元素对应起来，其中对应的规则称为对应关系。

我们可以用解析式、图象、表格等多种形式来表示函数。

例如，如果y是x的函数，那么可以用y=x^2表示一个二次函数。

（1）函数的单调性：在区间(a,b)上，如果对于任意x1<x2，都有f(x1)<f(x2)，则称f(x)在(a,b)上单调递增；如果对于任意x1<x2，都有f(x1)>f(x2)，则称f(x)在(a,b)上单调递减。

（2）函数的奇偶性：如果对于函数f(x)的定义域内的任意x，都有f(-x)=f(x)，则称f(x)为偶函数；如果对于函数f(x)的定义域内的任意x，都有f(-x)=-f(x)，则称f(x)为奇函数。

（3）函数的值域：函数值的取值范围称为函数的值域。

（2）定义域为[0,∞)，值域为[1,∞)解：（1）在区间(-∞,0)上单调递减，在区间(0,∞)上单调递增。

本节课我们学习了函数的概念和基本性质，掌握了函数的表示方法，了解了函数的单调性、奇偶性和值域等概念。

希望大家能够认真领会函数的思想方法，为后续学习做好准备。

函数是高中数学的核心概念，是数学学习中不可或缺的一部分。

函数的概念是理解函数的基础，也是进一步学习函数性质和应用的前提。

本课件旨在帮助学生理解函数的基本概念，掌握函数的定义和性质，为后续的学习奠定坚实的基础。

通过本课件的学习，学生应能理解函数的基本概念，掌握函数的定义和性质，能够判断一个映射是否为函数，并能够根据函数的定义和性质解决一些基本问题。

函数的定义：我们将介绍函数的定义，包括自变量、因变量和对应关系。

通过举例和反例，帮助学生理解函数的定义。

函数的概念课件(公开课)一、引言在数学领域中，函数是一个基本且重要的概念，它描述了两个量之间的依赖关系。

函数的概念起源于17世纪，经过几百年的发展，已经成为数学、自然科学和工程技术等领域不可或缺的工具。

本课件旨在阐述函数的基本概念、性质和应用，帮助大家深入理解函数的本质，为后续学习打下坚实基础。

二、函数的定义与表示1.函数的定义函数是一种特殊的关系，它将一个集合（称为定义域）中的每个元素对应到另一个集合（称为值域）中唯一的元素。

用数学符号表示为：f:X→Y，其中X表示定义域，Y表示值域。

函数通常用f(x)表示，x为自变量，f(x)为因变量。

2.函数的表示方法（1）解析法：直接给出函数的解析式，如f(x)=x²。

（2）表格法：列出定义域中部分元素的值和对应的函数值，如：x-f(x)-1-12-43-9（3）图象法：绘制函数的图象，展示函数的变化趋势。

三、函数的性质1.基本性质（1）单调性：函数在定义域内的某个区间上，随着自变量的增加（或减少），函数值单调增加（或减少）。

（2）奇偶性：若对于任意的x，都有f(-x)=f(x)，则称函数为偶函数；若对于任意的x，都有f(-x)=-f(x)，则称函数为奇函数。

（3）周期性：若存在非零常数T，使得对于任意的x，都有f(x+T)=f(x)，则称函数具有周期性，T为函数的周期。

2.极值与最值（1）极值：在函数的定义域内，若存在某个点x₀，使得在x₀的某邻域内，f(x₀)为最大值或最小值，则称f(x₀)为函数的极大值或极小值。

（2）最值：在函数的定义域内，若存在某个点x₀，使得对于任意的x，都有f(x₀)≥f(x)（或f(x₀)≤f(x)），则称f(x₀)为函数的最大值（或最小值）。

四、函数的应用1.数学分析函数是数学分析的基础，微积分中的导数、积分等概念都是建立在函数的基础上。

通过对函数的求导、积分等运算，可以研究函数的性质、解决实际问题。

2.应用数学函数在物理学、生物学、经济学等领域的模型建立中具有重要意义。