武汉理工大学《结构动力学》2013年期末试卷及标准答案

结构动力学问答题答案-武汉理工-研究生结构动力学问答题答案-武汉理工-研究生《结构动力学》思考题第1章1、对于任一振动系统，可划分为由激励、系统和响应三部分组成。

试结合生活或工程分别举例说明：何为响应求解、环境识别和系统识别？响应求解：结构系统和荷载已知，求响应。

又称响应预估问题，是工程正问题的一种，通常在工程中是指结构系统已知，具体指结构的形状构件及离散元件等，环境识别：主要是荷载的识别，结构和响应已知，求荷载。

属于工程反问题的一种。

在工程中，如已知桥梁的结构和响应，根据这些来反推出桥梁所受到的荷载。

系统识别：荷载和响应已知，求结构的参数或数学模型。

又称为参数识别，是工程反问题的一种，在土木工程领域，房屋、桥梁和大坝等工程结构被视为“系统”，而“识别”意味着由振动实验数据求得结构的动力特性（如频率、阻尼比和振型）。

如模态分析和模态试验技术等基本成型并得到广泛应用。

2、如何从物理意义上理解线性振动系统解的可叠加性。

求补充3、正确理解等效刚度的概念，并求解单自由度系统的固有频率。

复杂系统中存在多个弹性元件时，用等效弹性元件来代替原来所有的弹性元件，等效原则是等效元件刚度等于组合元件刚度，则等效元件的刚度称为等效刚度。

4、正确理解固有频率f 和圆频率ω的物理意义。

固有频率f ：物体做自由振动时，振动的频率与初始条件无关，而仅与系统的本身的参数有关(如质量、形状、材质等)，它是自由振动周期的倒数，表示单位时间内振动的次数。

圆频率ω：ω=2π/T=2πf 。

即为单位时间内位移矢量在复平面内转动的弧度，又叫做角频率。

它只与系统本身的参数m ，k 有关，而与初始条件无关5、正确理解过阻尼、临界阻尼、欠阻尼的概念。

一个系统受初扰动后不再受外界激励，因为受到阻力造成能量损失而位移峰值渐减的振动称为阻尼振动。

系统的状态按照阻尼比ζ来划分。

把ζ=0的情况称为无阻尼，即周期运动;把0<ζ<1的情况称为欠阻尼，即系统所受的阻尼力较小，振幅在逐渐减小，最后才达到平衡位置;把ζ>1的情况称为过阻尼，如果阻尼再增大，系统需要较长的时间才能达到平衡;把ζ=1的情况称为临界阻尼，即阻尼的大小刚好使系统作非"周期"运动。

武汉理工大学《结构动力学》2013年期末试卷及标准答案案场各岗位服务流程销售大厅服务岗：1、销售大厅服务岗岗位职责：1)为来访客户提供全程的休息区域及饮品;2)保持销售区域台面整洁;3)及时补足销售大厅物资,如糖果或杂志等;4)收集客户意见、建议及现场问题点；2、销售大厅服务岗工作及服务流程阶段工作及服务流程班前阶段1）自检仪容仪表以饱满的精神面貌进入工作区域2）检查使用工具及销售大厅物资情况，异常情况及时登记并报告上级。

班中工作程序服务流程行为规范迎接指引递阅资料上饮品（糕点）添加茶水工作要求1）眼神关注客人，当客人距3米距离时，应主动跨出自己的位置迎宾，然后侯客迎询问客户送客户注意事项15度鞠躬微笑问候：“您好！欢迎光临！”2）在客人前方1-2米距离领位，指引请客人向休息区，在客人入座后问客人对座位是否满意：“您好！请问坐这儿可以吗？”得到同意后为客人拉椅入座“好的，请入座！”3）若客人无置业顾问陪同，可询问：请问您有专属的置业顾问吗？，为客人取阅项目资料，并礼貌的告知请客人稍等，置业顾问会很快过来介绍，同时请置业顾问关注该客人；4）问候的起始语应为“先生-小姐-女士早上好，这里是XX销售中心，这边请”5）问候时间段为8:30-11:30 早上好11:30-14:30 中午好 14:30-18:00下午好6）关注客人物品，如物品较多，则主动询问是否需要帮助（如拾到物品须两名人员在场方能打开，提示客人注意贵重物品）；7）在满座位的情况下，须先向客人致歉，在请其到沙盘区进行观摩稍作等待；阶段工作及服务流程班中工作程序工作要求注意事项饮料（糕点服务）1）在所有饮料（糕点）服务中必须使用托盘；2）所有饮料服务均已“对不起，打扰一下，请问您需要什么饮品”为起始；3）服务方向：从客人的右面服务；4）当客人的饮料杯中只剩三分之一时，必须询问客人是否需要再添一杯，在二次服务中特别注意瓶口绝对不可以与客人使用的杯子接触；5）在客人再次需要饮料时必须更换杯子；下班程序1）检查使用的工具及销售案场物资情况，异常情况及时记录并报告上级领导；2）填写物资领用申请表并整理客户意见；3）参加班后总结会；4）积极配合销售人员的接待工作，如果下班时间已经到，必须待客人离开后下班；1.3.3.3吧台服务岗1.3.3.3.1吧台服务岗岗位职责1）为来访的客人提供全程的休息及饮品服务；2）保持吧台区域的整洁；3)饮品使用的器皿必须消毒；4）及时补充吧台物资；5）收集客户意见、建议及问题点；1.3.3.3.2吧台服务岗工作及流程阶段工作及服务流程班前阶段1）自检仪容仪表以饱满的精神面貌进入工作区域2）检查使用工具及销售大厅物资情况，异常情况及时登记并报告上级。

一、多选(共计35分,每题2.5分,每题答案完全一样得满分,少选、多选、错选均不得分。

)1、焊缝连接计算方法分为两类，它们是（）。

A. 手工焊缝和自动焊缝B. 仰焊缝和俯焊缝C. 对接焊缝和角焊缝D. 连接焊缝和断续焊缝错误:【C】2、混凝土材料的基本特点是混凝土的（）。

A. 抗压强度≥抗拉强度B. 抗压强度=抗拉强度C. 抗压强度≤抗拉强度D. 抗压强度抗拉强度错误:【A】3、工字形梁受压翼缘宽厚比限值为：≤15，式中b1为（）。

A. 受压翼缘板外伸宽度B. 受压翼缘板全部宽度C. 受压翼缘板全部宽度的1/3D. 受压翼缘板的有效宽度错误:【A】4、确定梁的经济高度的原则是（）。

A. 制造时间性最短B. 用钢量最省C. 最便于施工D. 免于变截面的麻烦错误:【B】5、钢在构件发生断裂破坏前，有明显先兆的情况是（）的典型特征（）。

A. 强度提高B. 塑性提高C. 冷弯性能提高D. 可焊性提高错误:【A】6、计算工字形梁的抗弯强度，用公式Mx/yxWnx≤f,取yx=1.05梁的翼缘外伸肢宽厚比不小于（）。

A.B.C.D.错误:【B】7、焊接梁的腹板局部稳定采用配置加劲肋的方法来解决，当＞170时，（）。

A. 可能发生剪切失稳，应配置横向加劲肋B. 可能发生弯曲失稳，应配置横向和纵向加劲肋C. 可能会发生弯曲失稳，应配置横向加劲肋D. 可能发生剪切失稳和弯曲失稳，应配置横向和纵向加劲肋错误:【D】8、工字形梁受压翼缘宽厚比限值为：≤15 ，式中b1为（）。

A. 受压翼缘板外伸宽度B. 受压翼缘板全部宽度C. 受压翼缘板全部宽度的1/3D. 受压翼缘板的有效宽度错误:【A】9、第二类T形截面的判别条件是（）。

A. x≤h′fB. x>h′fC. x≤xbD. x≥2α′s错误:【B】10、钢材经历了应变硬化（应变强化）之后（）。

A. 强度提高B. 塑性提高C. 冷弯性能提高D. 可焊性提高错误:【A】11、《规范》规定x≤xb是为了防止梁发生（）。

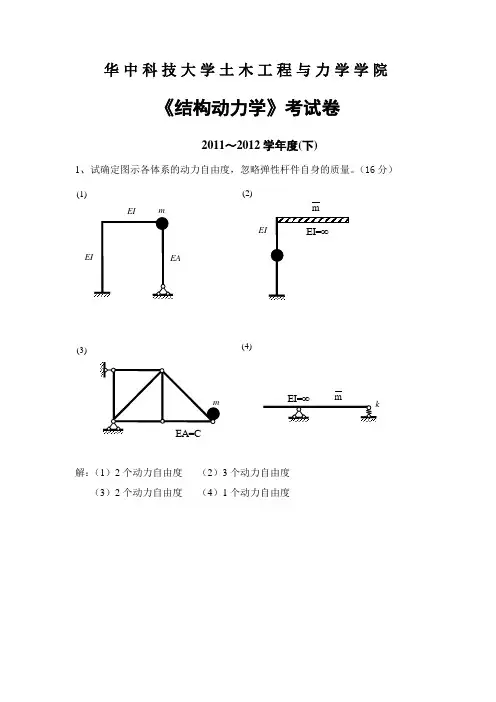
华中科技大学土木工程与力学学院《结构动力学》考试卷2011～2012学年度(下)1、试确定图示各体系的动力自由度，忽略弹性杆件自身的质量。

（16分）解：（1）2个动力自由度 （2）3个动力自由度 （3）2个动力自由度 （4）1个动力自由度(1)(2)m(3)(4)m2、试求图示结构的自振频率ω（15分）解：图示结构为单自由度体系，以横梁转角ϕ为自由度。

由0A M =∑ 有： 22200lm x dx ml kl ϕϕϕ⋅⋅⋅⋅++=⎰化简得：()303klm m ϕϕ⋅⋅+=+∴自振频率ω=3、如图所示体系，各杆长为l ，EI=常数，1处有集中质量m ，2处受动力偶()M t =Msin tθ；θ（14分）解：结构体系的1M 、p M 如下图所示：tm m B3111122=2EI 233l l l l EIδ⎛⎫∴⨯⨯⨯⨯= ⎪⎝⎭21111sin sin 236MMl l l M t t EI EI θθ⎛⎫∆=⨯⨯⨯= ⎪⎝⎭ ∴体系微分方程为:()321112sin 36M t lMl y m y m y t EI EI δθ⋅⋅⋅⋅⎛⎫⎛⎫=-+∆=-⋅+⋅ ⎪ ⎪⎝⎭⎝⎭33sin 24EI My y t ml mlθ⋅⋅⇒+⋅=⋅ 2max23331133344622M M Ml y EI EI EI ml ml EIml ml ml θ∴=⋅=⋅=--- ∴惯性力幅值22max3362EI Ml MI m y m ml EI lθ==⋅⋅=M M MMMl1t θ4、图示（a ）所示梁的跨中有一台电动机，实测得此梁自由振动时跨中点位移时程曲线如图所示（b ），周期T=0.06s ，若忽略梁的分布质量。

（20分）试求：（1）阻尼比ξ；（2）共振时的动力系数β；（3）共振时电动机每分钟的转数 n ；（4）若电动机转数为600r/min ，由于其离心力引起梁中点稳态的振幅为2mm ，求共振时的振幅A 。

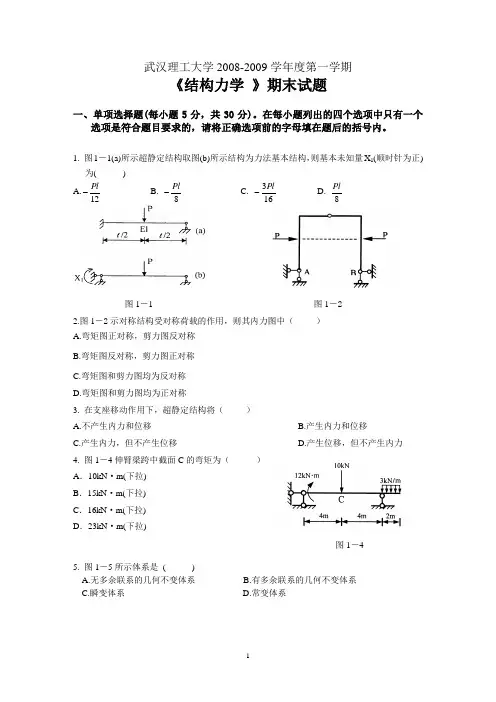
武汉理工大学2008-2009学年度第一学期《结构力学 》期末试题一、单项选择题(每小题5分，共30分)。

在每小题列出的四个选项中只有一个选项是符合题目要求的，请将正确选项前的字母填在题后的括号内。

1. 图1－1(a)所示超静定结构取图(b)所示结构为力法基本结构，则基本未知量X 1(顺时针为正)为( ) A.12Pl - B. 8Pl - C. 163Pl - D. 8Pl1－2图1－22.图1－2示对称结构受对称荷载的作用，则其内力图中（ ）A.弯矩图正对称，剪力图反对称B.弯矩图反对称，剪力图正对称C.弯矩图和剪力图均为反对称D.弯矩图和剪力图均为正对称3. 在支座移动作用下，超静定结构将（ ）A.不产生内力和位移B.产生内力和位移C.产生内力，但不产生位移D.产生位移，但不产生内力4. 图1－4伸臂梁跨中截面C 的弯矩为（ ）A ．10kN ·m(下拉)B ．15kN ·m(下拉)C ．16kN ·m(下拉)D ．23kN ·m(下拉)5. 图1－5所示体系是 ( )A.无多余联系的几何不变体系B.有多余联系的几何不变体系C.瞬变体系D.常变体系图1－1 图1－4图1—56. 图1－6三铰拱，已知三个铰的位置，左半跨受均布荷载，其合理拱轴的形状为 ( )A.全跨圆弧B.全跨抛物线C.AC 段为园弧，CB 段为直线D.AC 段为抛物线，CB 段为直线二、填空题 (每小题5分，共25分)。

1. 位移互等定理的表达式是______________________。

2. 图2－2对称结构，截面K 弯矩的绝对值为________。

3. 图2－3示对称结构受反对称荷载作用，则结构上与对称轴相交截面C 的内力之一______________不为零。

图2－3 4. 如图2－4所示结构的计算简图及弯矩图，则AB 杆跨中截面弯矩为________。

5. 图2－5示结构的超静定次数为______________。

某大学《结构动力学》课程考试试卷适用专业： 考试日期:考试时间:120分钟 考试形式:闭卷 试卷总分:100分1、求解单自由振动位移方程0y 2=+y ω，设初始时刻t =0质点有初始位移y 0和初始速度v 0？(10)2、如图所示为一等截面竖直悬臂杆，长度为l ，截面面积为A ，惯性矩为I ， 弹性模量为E ，杆顶有重物，其重量为W 。

设杆件本身质量可忽略不计，试分别求水平振动和竖向振动时的自振周期？（15分）3、如下为简谐荷载作用下单自由度体系的强迫振动位移公式，试分析进入平稳阶段后动力系数随ωθ变化特性？(15))sin (sin 11)(y t t y t stωωθθωθ--= 4、突加荷载作用下求t>0时位移如何计算？（15分）⎭⎬⎫⎩⎨⎧><=000)(0t F t t F p p ，当，当5、有阻尼振动的动力系数β随ωθ变化的公式如下，其中ξ为阻尼系数，求共振动力系数和最大动力系数？分析其之间的关系？（15分） /2122222241-⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎪⎭⎫⎝⎛-=ωθξωθβ6、6、某结构自由振动经过10个周期后，振幅降为原来的10%。

试求结构的阻尼比ξ和在简谐荷载作用下共振时的动力系数？（15分）7、如图所示为两层钢架，其横梁为无限刚性，设质量集中在楼层上，一二层质量分别为m 1和m 2，层间侧移刚度等别为k 1和k 2，试求刚架水平振动时的自振频率和主振型？（15分）（其中m 1= m 2，k 1= k 2）某大学《结构动力学》课程考试试卷答案适用专业： 考试日期:考试时间:120分钟 考试形式:闭卷 试卷总分:100分1、求解单自由振动位移方程0y 2=+y ω，设初始时刻t =0质点有初始位移y 0和初始速度v 0？(10)答：02=+y y ωmk=ω t C t C t y ωωcos sin )(21+= 0)0(y y =，0)0(yν= C 1=ων0,C 2=y(0) t t y t y ωωνωsin cos )(00+=2、如图所示为一等截面竖直悬臂杆，长度为l ，截面面积为A ，惯性矩为I ， 弹性模量为E ，杆顶有重物，其重量为W 。

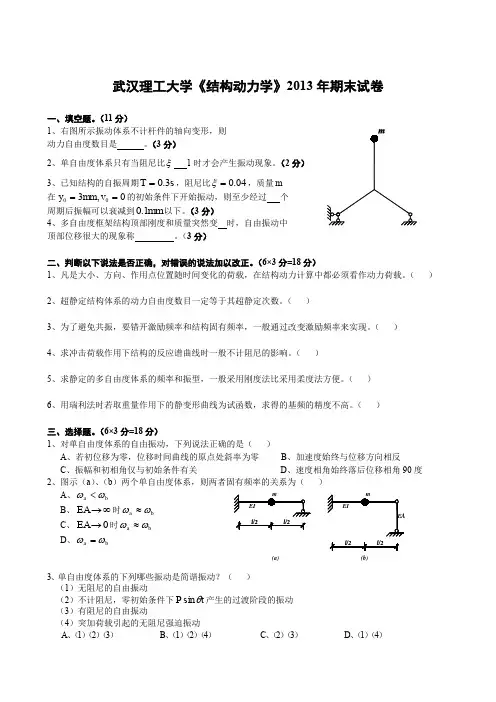
武汉理工大学《结构动力学》2013年期末试卷一、填空题。

（11分）1、右图所示振动体系不计杆件的轴向变形，则 动力自由度数目是 。

（3分）2、单自由度体系只有当阻尼比ξ 1时才会产生振动现象。

（3、已知结构的自振周期s T 3.0=，阻尼比04.0=ξ，质量m 在0,300==v mm y 的初始条件下开始振动，则至少经过 个周期后振幅可以衰减到mm 1.0以下。

（3分）4、多自由度框架结构顶部刚度和质量突然变 时，自由振动中顶部位移很大的现象称 。

（3分）二、判断以下说法是否正确，对错误的说法加以改正。

（6×3分=18分）1、凡是大小、方向、作用点位置随时间变化的荷载，在结构动力计算中都必须看作动力荷载。

（ ）2、超静定结构体系的动力自由度数目一定等于其超静定次数。

（ ）3、为了避免共振，要错开激励频率和结构固有频率，一般通过改变激励频率来实现。

（ ）4、求冲击荷载作用下结构的反应谱曲线时一般不计阻尼的影响。

（ ）5、求静定的多自由度体系的频率和振型，一般采用刚度法比采用柔度法方便。

（ ）6、用瑞利法时若取重量作用下的静变形曲线为试函数，求得的基频的精度不高。

（ ）三、选择题。

（6×3分=18分）1、对单自由度体系的自由振动，下列说法正确的是（ ）A C 、振幅和初相角仅与初始条件有关 2、图示（a ）、（b A 、b a ωω<B 、∞→EA 时b a ωω≈C 、0→EA 时b a ωω≈D 、b a ωω=3、（1）无阻尼的自由振动（2）不计阻尼，零初始条件下t P θsin 产生的过渡阶段的振动 （3）有阻尼的自由振动（4）突加荷载引起的无阻尼强迫振动 A 、（1）（2）（3） B 、（1）（2）（4） C 、（2）（3） D 、（1）（4）五、下图所示剪切型刚架的质量已集中在横梁上，t m t m 140,25021==，横梁抗弯刚度为无穷大，各柱m MN ⋅。

考生请注意：1．本试题共6 题，共2 页，考生请认真检查；2．答题时，直接将答题内容写在我校提供的答题纸上；答在试卷上一律无效；3．本试题不得拆开，拆开后遗失后果自负。

一、简述题（本题共20分，每小题5分）1．自由振动、强迫振动自由振动：系统受到初始激励作用后，仅靠其本身的弹性恢复力“自由地”振动，其振动特性仅取决于系统本身的物理特性（质量和刚度）。

强迫振动：系统受到外界持续的激励作用而“被动地”进行振动，其振动特性除取决于系统本身的特性外，还取决于激励的特性。

2．广义坐标、振型函数广义坐标：是一种坐标形式，它是有几组互相正交的模态组成，任何变量都可由这几组模态的唯一线性组合而成。

振型函数：是一种函数形式，描述振型在几维空间中的振幅值的表现。

3．稳态响应、瞬态响应稳态响应：当系统在外力作用下，经过一段时间后，系统振动趋于稳定时的响应。

瞬态响应：当系统在外力作用下，在系统振动趋于稳定之前的响应。

瞬态响应发生在稳态响应之前，他们组合构成完整的外力作用时的振动响应。

4．哈密顿原理具有完整约束的动力学系统，在满足协调性条件、约束条件或边界条件，同时满足起始t1时刻与结束t2时刻条件的可能的位移随时间变化的形式中，真实解对应的那种变化形式使Lagrange泛函L取最小值，即2 1(T V W)0t t dt式中：T为系统的动能，V为系统的势能，W为外力所作虚功。

二．质量均为m 的两个球，系于具有很大张力T 的弦上，如图所示，求系统的固有频率。

（本题10分）解：由于弦的张力T 很大，两个球只能在竖向发生微幅振动。

（1分）如下图所示，两个球在外力1()F t 和2()F t 作用下发生竖向微幅振动，位移分别为1x 和2x 。

对两个球，分别作受力分析：外荷载；惯性力； 张力分力。

（3分）运用达朗贝尔原理，分别列出 两个球的竖向运动方程：12111()x x x mx T T F t L L-+⋅-⋅=22122()x x xmx T T F t L L-+⋅+⋅= （5分）写成矩阵形式：1112222()002()TT x x F t m L L m x T T x F t L L ⎡⎤-⎢⎥⎧⎫⎧⎫⎧⎫⎡⎤+=⎢⎥⎨⎬⎨⎬⎨⎬⎢⎥⎣⎦⎩⎭⎩⎭⎩⎭⎢⎥-⎢⎥⎣⎦得频率方程：[][]222202T Tm LLK M T T m L Lωωω---==-- （7分） 解得： 1ω=2ω= （10分）ll l F 2(t)三．图示简支梁，梁长为4l ，在四等分处有3个质量m 1=m 2=m 3=m ，梁的抗弯刚度为EI ，忽略梁自身的质量，要求：（1）写出系统振动方程；（2）求系统的各阶固有频率； （3）画出相应的主振型。

《结构力学》教学大纲一、本课程的性质与任务本课程为土木工程专业本科生的一门主要技术基础课。

通过本课程的教学，使学生了解杆件体系的组成规律，了解各类结构的受力性能，撑握杆件结构的计算原理和方法，培养分析与解决工程实际中杆系结构力学问题的能力，为学习后续有关专业课程以及将来进行结构设计和科学研究打下力学基础。

二、本课程的教学内容、基本要求及学时分配1．绪论（4学时）（1）教学内容1.1结构力学的学科内容和教学要求。

1.2结构力学计算简图及简化要点。

1.3杆件结构的分类。

1.4荷载的分类。

（2）教学要求了解结构力学的任务以及与其它课程的关系，正确理解结构计算简图的概念、简化要点和条件，了解荷载的分类。

2.几何构造分析（6学时）（1）教学内容2.1几何构造分析中的几个基本概念。

2.2平面几何不变体系的组成规律。

2.3平面杆件体系的计算自由度。

（2）教学要求理解几何不变体系、几何可变体系、几何瞬变体系、自由度（静力自由度）约束及其类型等基本概念。

正确理解和应用几何不变体系的组成规则（两刚片法则、三刚片法则、二元体法则），会计算平面杆件体系的计算自由度。

3.静定结构的内力计算（14学时）（1）教学内容3.1梁的内力计算的回顾。

3.2静定多跨梁的组成、计算和内力图的绘制。

3.3静定平面刚架的内力计算和内力图的绘制。

3.4三铰拱的特点和内力计算。

三铰拱的合理拱轴曲线。

3.5静定平面桁架的特点、组成及分类。

用结点及截面法计算桁架的内力，结点法和截面法的联合应用。

3.6静定组合结构的特点、计算和内力图的绘制。

3.7静定结构的一般性质。

（2）教学要求巩固在材料力学中已经建立的截面法的概念与方法，并把它推广应用在结构计算上。

熟练掌握杆件上的荷载与内力的微分关系、增量关系，并用以定性分析内力图的形状。

熟练掌握分段叠加法作弯矩图的方法。

正确、灵活选取和画出隔离体图，熟练掌握应用隔离体图和平衡条件计算结构支反力、内力的方法；熟练掌握静定梁、静定刚架内力计算和内力图的绘制以及静定平面桁架内力的求解方法；掌握静定组合结构、三铰拱的内力计算和内力图的绘制方法；了解静定结构的力学特征。