武汉理工大学2013-2014学年第一学期概率论与数理统计期末考试试题及答案

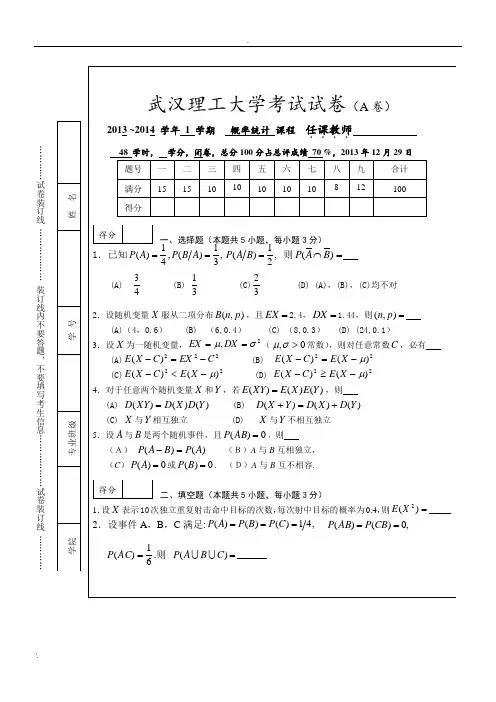
…………试卷装订线………………装订线内不要答题，不要填写考生信息………………试卷装订线……………………试卷装订线………………装订线内不要答题，不要填写考生信息………………试卷装订线…………武汉理工大学考试试题答案（A 卷）2013 ~2014 学年 1 学期 概率统计 课程一、C B D B A二、（1）18.4 （2）127（3） 2.0 （4） .1-X （5）（4.412，5.588） 三、1、解：)()()()()(7.0B P A P B P A P B A P -+== ⇒ 73=α。

……5分2、解：)(1)()()(B A P B A P B A P AB P ⋃-=⋃==)]()()([1AB P B P A P -+-=α-=1)(B P ……5分四．解：设A 为产品合格事件，则A A ,是产品的一个划分。

又设B 为产品检查合格事件， 则9.0)(=A P ，98.0)|(=A B P ，05.0)|(=A B P 。

（1） 由全概率公式，一个产品被认为合格的概率)|()()|()()(A B P A P A B P A P B P +=887.005.01.098.09.0=⨯+⨯=。

……6分（2）由贝叶斯定理，“合格品”确实合格的概率)(/)|()()|(B P A B P A P B A P =994.0887.0/98.09.0=⨯= …… 10分五．解：（1）联合密度为,01,0(,)0,其他ye x yf x y -⎧<<>⎪=⎨⎪⎩………..3分(1) 112200(2)21xyP X Y dx e dy e -->==-⎰⎰ ……………6分(3) ()()(,)z x y zF Z P X Y z f x y d σ-≤=-≤=⎰⎰ 当0z <时，110()(1)y z z x zF Z dx e dy e e +∞---==-⎰⎰当01z ≤<时，110()11x z y z z zF Z dx e dy z e ---=-=+-⎰⎰当1z ≥时，()1z F Z = ………………8分1'1(1),0()()1,010,1z z z z e e z f Z F Z e z z --⎧-<⎪==-≤<⎨⎪≥⎩…………………10分六．解：（1）由(,)1f x y dxdy +∞+∞-∞-∞=⎰⎰，得A ＝1 ……2分（2）1()0xxDE XY xydxdy dx xydy -===⎰⎰⎰⎰ 2()3DE X xdxdy ==⎰⎰ ……6分 ()0DE Y ydxdy ==⎰⎰ cov ,)()()()0X Y E XY E X E Y (＝－＝ ……8分（3）0XY ρ= X 与Y 不相关 ……10分七解：（1）32+-=θEX ，59523121=++++=X ，θ的矩估计值为：53ˆ=θ ……5分 （2）224)1()]1(2[)(θθθθθ--=L ，=θθd L d )(ln 0146=--θθ，⇒θ的最大似然估计值为53ˆ=θ。

2012年概率论与数理统计期末考试试卷一. 填空题(每题5分, 共30分)1. 设随机变量X 服从正态分布(1,4)N , 已知(1)a Φ=, 其中()x Φ表示标准正态分布的分布函数, 则{13}P X -≤≤=21a -.解: 111311{13}11(1)(1)2222(1)(1(1))2(1)12 1.X X P X P P a -----⎧⎫⎧⎫-≤≤=≤≤=-≤≤=Φ-Φ-=⎨⎬⎨⎬⎩⎭⎩⎭Φ--Φ=Φ-=- 2. 设概率()0.3,()0.5,()0.6P A P B P A B ==+=, 则()P AB = 0.1 . 解: ()()()()0.2P AB P A P B P A B =+-+=,()()()0.30.20.1P AB P A P AB =-=-=.3. 设随机变量,X Y 的数学期望分布是-2, 1, 方差分别是1, 4, 两者相关系数是—0.5, 则由契比雪夫不等式估计(|2|6)P X Y +≥≤ 13/36 . 解: 由已知条件得, (2)2220E X Y EX EY +=+=-+=,(2)4()2(,2)4()4(,)D X Y DX D Y Cov X Y DX D Y Cov X Y +=++=++4()41164(1/2)213DX D Y ρ=++=++⋅-⋅=, 所以, 13(|2|6)36P X Y +≥≤. 4. 已知,X Y 是具有相同分布的两个独立随机变量, 且1(1)(1)2P X P Y =-==-=, 1(0)(0)2P X P Y ====, 则()P X Y == 1/2 . 解:()(0,0)(1,1)1(0)(0)(1)(1).2P X Y P X Y P X Y P X P Y P X P Y ====+=-=-===+=-=-=5. 设1216,,,X X X 是来自2(0,)N σ的样本, S 是样本均方差, 则1614ii XS=∑服从t (15).解: 由定理3(15)t ,161611(15)4i ii X X X t S ===∑∑.6. 设1281,,,(,9)X X X N μ, 要检验假设0:0H μ=, 则当0H 为真时, 用于检验的统计量3X 服从的分布是(0,1)N . 解: 由定理1(0,1)X N , 3(0,1)X N .二. 解答下列各题:7. (10分)已知男人中色盲人数所占比例是5%, 女人中色盲人数所占比例是0.25%. 现从男女人数各占一半的人群中随机选取一人, 求该人恰是色盲者的概率.解: 设A =“该人是色盲”, 1A =“该人是男人”, 2A =“该人是女人”.由全概率公式知, 2111()()()0.050.0025 2.625%22i i i P A P A P A A ===⨯+⨯=∑.8. (10分) 从只含3红, 4白两种颜色的球袋中逐次取一球, 令1,,0,i X ⎧=⎨⎩第次取出球第次取出白球，i 红i 1,2i =. 实在不放回模式下求12,X X 的联合分布律,4/7 3/7 j P因为1212{0,0}{0}{0}P X X P X P X ==≠==, 所以12,X X 不独立. 9. (10分)设随机向量(,)X Y 的联合概率密度函数为3,01,,(,)20,xx x y x f x y ⎧<<-<<⎪=⎨⎪⎩其他，求,X Y 的边缘概率密度函数. 解: 当01x <<时, 23()(,)32xX x xf x f x y dy dy x +∞-∞-===⎰⎰.所以,23,01,()0,.其他X x x f x ⎧<<=⎨⎩当10y -<<时, 1233()(1)24Y y x f y dx y -==-⎰;当01y ≤<时, 1233()(1)24Y y x f y dx y ==-⎰; 所以,23(1),11,()40,.其他Y y y f y ⎧--<<⎪=⎨⎪⎩10. (10分) 设,X Y 相互独立, 且(1)(1)0P X P Y p ====>, (0)(0)10P X P Y p ====->,令1,0,X Y Z X Y +⎧=⎨+⎩当为偶数,当为奇数,求Z 的分布律.解:{0}{0,1}{1,0}{0}{1}{1}{0}2(1)P Z P X Y P X Y P X P Y P X P Y p p ====+=====+===- 22{1}{0,0}{1,1}{0}{0}{1}{1}(1).P Z P X Y P X Y P X P Y P X P Y p p ====+=====+===+- 所以, Z11. (10分12,,X 是来自具有分布的总体的随机样本,试用中心极限定理计算()5P X >.(已知(2)0.508Φ=.)解: 由题知1()3i E X =,2()1i E X =,故()228()9i i i D X EX EX =-=. 由中心极限定理知,20012001600(,)39ii X N =∑. 所以, 11111()4014052005n i n n i i i i i X P X P P X P X ===⎛⎫ ⎪⎛⎫⎛⎫ ⎪>=>=>=-≤ ⎪ ⎪ ⎪⎝⎭⎝⎭⎪⎝⎭∑∑∑1200200403311(2)(2)0.508404033n i i X P =⎛⎫-- ⎪ ⎪=-≤≈-Φ-=Φ= ⎪ ⎪⎝⎭∑. 12. (10分)设总体X 的密度函数为36(),0,(;)0,其他,xx x f x θθθθ⎧-<<⎪=⎨⎪⎩求θ的矩估计ˆθ并计算ˆD θ.解: 依题意,306()()2xE X xx dx X θθθθ=-==⎰,得参数θ的矩估计量为ˆ2X θ=. 4ˆ4D DX DX n θ==. 而2223063()()10x E X x x dx θθθθ=-=⎰,故22244ˆ()5D DX EX E X n n n θθ==-=.13. (10分) 某电器零件平均电阻一直保持在2.64Ω,使用新工艺后,测得100个零件平均电阻在2.62Ω,如改变工艺前后电阻均方差保持在0.06Ω,问新工艺对零件电阻有无显著影响?(取0.01α=)(1.96)0.975,Φ=(1.64)0.95,Φ=(2.58)0.995Φ=. 解: 设X 为零件的平均电阻, 则2~(,0.06)X N μ. (1)假设0: 2.64H μ=; (2)取统计量~(0,1)X U N=;(3)由0.01α=, 确定临界值22.58u α=, , 使得2{||}0.01P U u α>=;(4)由样本值 2.62x =, 得统计量U 的观察值3.33x u ==≈-.(5)因为 2.58u >,所以拒绝原假设0H ,认为新工艺对零件电阻有显著影响.2013年概率论与数理统计期末考试试卷一. 填空题(每题4分, 共20分)1. 设随机变量,X Y 相互独立, 且同分布, {1}{1}0.5P X P X =-===,{1}{1}0.5P Y P Y =-===, 则{}P X Y == 1/2 .解: 1{}{1,1}{1,1}{1}{1}{1}{1}.2P X Y P X Y P X Y P X P Y P X P Y ===-=-+====-=-+===2.22x edx +∞-=⎰2. 解:因为221x +∞--∞=⎰,所以22xe +∞--∞=⎰即2202x e +∞-=⎰. 3. 设连续型随机变量X的密度函数22()2()x f x μσ--=, x -∞<<+∞, 则EX =μ, DX =2σ. 解:因为22()2()x X f x μσ--=, 所以2(,)X N μσ.4. 设总体(3,10)XN , 12100,,,X X X 为来自总体X 的简单随机样本, 则10011100i i X X ==∑1~(3,)10X N . 解: 由定理1知, 1~(3,)10X N . 5. 设袋中有8个红球, 2个黑球, 每次从袋中摸取一个球并且不放回, 那么第一次与第三次都摸到红球的概率是 28/45 . 解: 记i A =“第i 次摸到红球”, 1,2,3i =.13131223123123()()(())()P A A P A A P A A A A P A A A A A A =Ω=+=+123123121312121312()()()()()()()()P A A A P A A A P A P A A P A A A P A P A A P A A A =+=+876827281098109845=⨯⨯+⨯⨯=. 二. 解答题6. (12分) 某矿内有甲乙两个报警系统, 单独使用时甲的有效性为0.92, 乙为0.93, 且在甲失灵的条件下乙有效的概率为0.85, 求意外发生时, 甲乙至少有一个有效的概率, 以及乙失灵时甲有效的概率. 参考练习册反12第4题. 解: 设A =“甲有效”, B =“乙有效”.题目转为: 已知()0.92,()0.93P A P B ==, {}0.85P B A =, 求()P A B +和{}P A B . 因为()()()(){}0.851()1()()P BA P B A P B P AB P B A P A P A P A --====--, 所以, ()0.862P AB =.所以, ()()()()0.988P A B P A P B P AB +=+-=;()()()()0.920.862{}0.831()1()10.93()P AB P A B P A P AB P A B P B P B P B ---====≈---. 7. (12分)设连续型随机变量X 的分布函数为()arctan ()F x a b x x =+-∞<<+∞, 求常数,a b 以及随机变量X 的密度函数. 解: 根据分布函数的性质得()1,2()0,2b F a b F a ππ⎧+∞=+=⎪⎪⎨⎪-∞=-=⎪⎩ 所以1,21.a b π⎧=⎪⎪⎨⎪=⎪⎩X 的密度函数为21()(1)f x x π=+.8. (14分) 设某种类型人造卫星的寿命X (单位: 年)的密度函数为21,0,()20,0.xe xf x x -⎧>⎪=⎨⎪≤⎩若2颗这样的卫星同时升空投入使用, 试求:(1) 3年后这2颗卫星都正常运行的概率;(2) 3年后至少有1颗卫星正常运行的概率. 参考教材P37例3 解: 1颗卫星3年内正常运行的概率为32231{3}2x P X e dx e +∞--≥==⎰. 记Y 表示2颗卫星在3年内正常运行的颗数, 则32(2,)Y B e -.(1) 3年后这2颗卫星都正常运行的概率2332{2}P Y e e --⎛⎫=== ⎪⎝⎭;(2) 3年后至少有1颗卫星正常运行的概率232{1}1{0}11P Y P Y e -⎛⎫≥=-≥=-- ⎪⎝⎭.9. (14分) 设某高校英语考试成绩近似服从均值为72的正态分布, 96分以上的考生占总数的2.3%(已知满分为100, 合格线为60), 试求: (1) 考生成绩在60-84之间的概率;(2) 该校考生的合格率.((2)0.977,(1)0.8413)Φ=Φ= 解: 设某高校英语考试成绩为X , 则2(72,)XN σ.由题意知{96}0.023P X ≥=, 即7296720.023X P σσ--⎧⎫≥=⎨⎬⎩⎭, 所以241()0.023σ-Φ=, 即24()0.977(2)σΦ==Φ.因此, 12σ=.(1) 考生成绩在60-84之间的概率6072728472{6084}(1)(1)2(1)10.6826;121212X P X P ---⎧⎫≤≤=≤≤=Φ-Φ-=Φ-=⎨⎬⎩⎭(2) 合格率726072{60}1(1)(1)0.8413.1212X P X P --⎧⎫≥=≥=-Φ-=Φ=⎨⎬⎩⎭10. (14分) 一工厂生产的某种电池的寿命服从正态分布(25,100)N , 现在从这种电池中随机抽取16个, 测得平均寿命为23.8小时, 由此能否断定: 在显著性水平为0.05α=时, 该种电池的平均寿命小于25小时. ((1.96)0.975,(1.64)0.95)Φ=Φ= 解: 设X 为电池寿命, 则~(,100)X N μ.(1)假设00:25H μμ≥=; (2)取统计量~(0,1)X U N=;(3) 由0.05α=, 确定临界值 1.64u α-=-, 使得{}0.05P U u α<-=; (4)由样本均值23.8x =, 得统计量U 的观察值00.48u ===-.(5)因为00.48 1.64u =->-,此时没有充分理由说明小概率事件{ 1.64}u <-一定发生. 所以接受原假设0H , 认为这种电池的平均寿命不小于25小时. 注: 原假设不能设为00:25H μμ<=,此时μ取不到0μ,统计量X U =就没有意义了!11. (14分)设总体X 是离散型随机变量, 其所有可能的取值为0, 1, 2, 已知2(1)EX θ=-, 2{2}(1)P X θ==-, θ为参数. 对X 取容量为10的样本如下 1, 1, 0, 2, 2, 1, 1, 1, 0, 2.求参数θ的矩估计和极大似然估计.解:(1) 由2(1)X θ=-, 得θ的矩估计量为12Xθ=-; 结合 1.1x =, θ的矩估计值为10.452x θ=-=.(2) 构造似然函数为11912101210(){1,1,,2}{1}{1}{2}32(1)L P X X X P X P X P X θθθ=========-,取对数ln ()ln3211ln(1)9ln L θθθ=+-+,求导数(ln ())11901d L d θθθθ=-+=-, 得θ的极大似然估计值为920θ=.2014年概率论与数理统计期末考试试卷一. 填空题(共40分, 每空5分)1. 设~(,)X B n p , ~(,)Y B m p , 且X 与Y 独立, 则X Y +~(),(p m n B +)分布;2. 设2~(,)X N μσ, 则X 的密度函数()f x =(222)(21σμσπ--x e);3. 设总体X 的方差为2σ, 12,,,n X X X 为样本, X 为样本均值, 则期望211()n i i E X X n =⎛⎫-= ⎪⎝⎭∑(21σn n -); 4. 设12,,,n X X X 为样本, 则统计量211n i i X n =∑的名称为(样本2阶原点矩);5. 设总体~(,1)X N μ, 12,,,n X X X 为来自该总体的样本, 则21()ni i X μ=-∑服从()(2n χ)分布;6. 一批产品中有5个正品, 3个次品, 从中任取2个, 恰有1个次品, 1个正品的概率为(2815281315=C C C );7. 样本的特性是(独立、同分布且与总体分布相同);8. 在假设检验中, 可能犯两类错误. 其中第一类错误也称为弃真, 弃真的确切含义为(当原假设是真的时，拒绝了它). 二. 计算题(60分, 每题10分)1. 假设某贪官收受一次贿赂而被曝光的概率为0.05, 到目前为止共收受80次贿赂, 假设案发前每次收受贿赂是否曝光相互独立. 试用概率说明 “多行不义必自毙”. (取20190.3520⎛⎫≈ ⎪⎝⎭)解：记i A 为事件“第i 次收受贿赂而被曝光”（1,2,,80i），---------------------2 于是案发的概率为 )(801∑=i i A P ------------- ------------- -----------------4 )(1)(1801801∏∏==-=-=i i i i A P A P----------------------6985.035.01)2019(195.0148080=-=-=-=。

《概率论与数理统计》试卷A一、单项选择题（本大题共20小题,每小题2分，共40分） 1、A,B 为二事件，则AB =()A 、AB B 、A BC 、A BD 、A B2、设A ，B ，C 表示三个事件，则A B C 表示()A 、A ，B ，C 中有一个发生 B 、A ，B,C 中恰有两个发生C 、A,B,C 中不多于一个发生D 、A,B ，C 都不发生 3、A 、B 为两事件，若()0.8P AB =,()0.2P A =，()0.4P B =，则()成立A 、()0.32P AB = B 、()0.2P A B =C 、()0.4P B A -=D 、()0.48P B A = 4、设A ，B 为任二事件,则()A 、()()()P AB P A P B -=- B 、()()()P AB P A P B =+C 、()()()P AB P A P B =D 、()()()P A P AB P AB =+ 5、设事件A 与B 相互独立,则下列说法错误的是()A 、A 与B 独立 B 、A 与B 独立C 、()()()P AB P A P B =D 、A 与B 一定互斥 6、设离散型随机变量X 的分布列为其分布函数为()F x ，则(3)F =()A 、0B 、0.3C 、0。

8D 、17、设离散型随机变量X 的密度函数为4,[0,1]()0,cx x f x ⎧∈=⎨⎩其它 ，则常数c =()A 、15 B 、14C 、4D 、5 8、设X ～)1,0(N ,密度函数22()x x ϕ-=，则()x ϕ的最大值是()A 、0B 、1 C、9、设随机变量X 可取无穷多个值0，1,2，…,其概率分布为33(;3),0,1,2,!k p k e k k -==,则下式成立的是()A 、3EX DX ==B 、13EX DX == C 、13,3EX DX == D 、1,93EX DX ==10、设X 服从二项分布B(n ，p ），则有()A 、(21)2E X np -=B 、(21)4(1)1D X np p +=-+C 、(21)41E X np +=+D 、(21)4(1)D X np p -=-11、独立随机变量,X Y ，若X~N(1,4），Y~N （3,16）,下式中不成立的是()A 、()4E X Y +=B 、()3E XY =C 、()12D X Y -= D 、()216E Y += 12、设随机变量X 的分布列为:则常数c=()A 、0B 、1C 、14 D 、14- 13、设X ~)1,0(N ，又常数c 满足{}{}P X c P X c ≥=<，则c 等于()A 、1B 、0C 、12D 、—1 14、已知1,3EX DX =-=，则()232E X ⎡⎤-⎣⎦=()A 、9B 、6C 、30D 、36 15、当X 服从（ )分布时,EX DX =.A 、指数B 、泊松C 、正态D 、均匀 16、下列结论中,()不是随机变量X 与Y 不相关的充要条件。

概率论与数理统计期末考试试题库及答案概率论与数理统计概率论试题一、填空题1.设 A、B、C是三个随机事件。

试用 A、B、C分别表示事件1)A、B、C 至少有一个发生 2)A、B、C 中恰有一个发生3)A、B、C不多于一个发生2.设 A、B为随机事件, ,,。

则=3.若事件A和事件B相互独立, ,则4. 将C,C,E,E,I,N,S等7个字母随机的排成一行,那末恰好排成英文单词SCIENCE的概率为5. 甲、乙两人独立的对同一目标射击一次,其命中率分别为0.6和0.5,现已知目标被命中,则它是甲射中的概率为6.设离散型随机变量分布律为则A______________7. 已知随机变量X的密度为,且,则________________8. 设~,且,则 _________9. 一射手对同一目标独立地进行四次射击,若至少命中一次的概率为,则该射手的命中率为_________10.若随机变量在(1,6)上服从均匀分布,则方程x2+x+10有实根的概率是11.设,,则12.用()的联合分布函数F(x,y)表示13.用()的联合分布函数F(x,y)表示14.设平面区域D由y x , y 0 和 x 2 所围成,二维随机变量x,y在区域D上服从均匀分布,则(x,y)关于X的边缘概率密度在x 1 处的值为。

15.已知,则=16.设,且与相互独立,则17.设的概率密度为,则=18.设随机变量X1,X2,X3相互独立,其中X1在[0,6]上服从均匀分布,X2服从正态分布N(0,22),X3服从参数为3的泊松分布,记YX1-2X2+3X3,则D(Y)19.设,则20.设是独立同分布的随机变量序列,且均值为,方差为,那么当充分大时,近似有~ 或 ~ 。

特别是,当同为正态分布时,对于任意的,都精确有~ 或~.21.设是独立同分布的随机变量序列,且,那么依概率收敛于22.设是来自正态总体的样本,令则当时~。

23.设容量n 10 的样本的观察值为(8,7,6,9,8,7,5,9,6),则样本均值,样本方差24.设X1,X2,…Xn为来自正态总体的一个简单随机样本,则样本均值服从二、选择题1. 设A,B为两随机事件,且,则下列式子正确的是(A)P A+B P A; (B)(C) (D)2. 以A表示事件“甲种产品畅销,乙种产品滞销”,则其对立事件为 (A)“甲种产品滞销,乙种产品畅销”; (B)“甲、乙两种产品均畅销”(C)“甲种产品滞销”;(D)“甲种产品滞销或乙种产品畅销”。

《概率论与数理统计》期末考试试题及解答一、填空题（每小题3分，共15分）1．设事件A,B仅发生一个的概率为0.3，且P(A)?P(B)?0.5，则A,B至少有一个不发生的概率为__________.答案：0.3解：P(A?B)?0.3即0.3?P(A)?P(B)?P(A)?P(AB)?P(B)?P(AB)?0.5?2P(AB)所以P(AB)?0.1P(?)?P(AB)?1?P(AB)?0.9.2．设随机变量X服从泊松分布，且P(X?1)?4P(X?2)，则P(X?3)?______.答案：1?1e6解答：P(X?1)?P(X?0)?P(X?1)?e????e,??P(X?2)??22e??????2?? 由P(X?1)?4P(X?2) 知e??e?2?e2 即2????1?0 解得??1，故P(X?3)?1?1e 623．设随机变量X在区间(0,2)上服从均匀分布，则随机变量Y?X在区间(0,4)内的概率密度为fY(y)?_________.答案：0?y?4,fY(y)?FY?(y)?fX? 0,其它.?解答：设Y的分布函数为FY(y),X的分布函数为FX(x)，密度为fX(x)则FY(y)?P(Y?y)?P(X?2y)?y?)yX)Xy? ?)y 因为X~U(0,2)，所以FX(?0，即FY(y)?FX故10?y?4,fY(y)?FY?(y)?fX? 0,其它.?另解在(0,2)上函数y?x2严格单调，反函数为h(y)?所以0?y?4,fY(y)?fX? ?0,其它.?24．设随机变量X,Y相互独立，且均服从参数为?的指数分布，P(X?1)?e，则??_________，P{min(X,Y)?1}=_________.答案：??2，P{min(X,Y)?1}?1?e-4解答：P(X?1)?1?P(X?1)?e???e?2，故??2P{min(X,Y)?1}?1?P{min(X,Y)?1}?1?P(X?1)P(Y?1)?1?e?4.5．设总体X的概率密度为???(??1)x,0?x?1, f(x)?? ???1. ?其它?0,X1,X2,?,Xn是来自X的样本，则未知参数?的极大似然估计量为_________.答案：???11nlnxi?ni?1?1解答：似然函数为L(x1,?,xn;?)??(??1)xi??(??1)n(x1,?,xn)?i?1nlnL?nln(??1)??n?lnxi?1ni解似然方程得?的极大似然估计为dlnLn???lnxi?0 d???1i?12?? ?11n?lnxini?1?1.二、单项选择题（每小题3分，共15分）1．设A,B,C为三个事件，且A,B相互独立，则以下结论中不正确的是（A）若P(C)?1，则AC与BC也独立.（B）若P(C)?1，则A?C与B也独立.（C）若P(C)?0，则A?C与B也独立.（D）若C?B，则A与C也独立. （）答案：（D）.解答：因为概率为1的事件和概率为0的事件与任何事件独立，所以（A），（B），（C）都是正确的，只能选（D）.事实上由图可见A与C不独立.2．设随机变量X~N(0,1),X的分布函数为?(x)，则P(|X|?2)的值为（A）2[1??(2)]. （B）2?(2)?1.（C）2??(2). （D）1?2?(2). （）答案：（A）解答：X~N(0,1)所以P(|X|?2)?1?P(|X|?2)?1?P(?2?X?2)(2)??(?2)?1?[2?(2?) ?1??1]?2?[1 ? 应选（A）.3．设随机变量X和Y不相关，则下列结论中正确的是（A）X与Y独立. （B）D(X?Y)?DX?DY.（C）D(X?Y)?DX?DY. （D）D(XY)?DXDY. （） 3答案：（B）解答：由不相关的等价条件知，?xy?0?cov（x，y）?0 D(X?Y)?DX?DY+2cov （x，y）应选（B）.4．设离散型随机变量X和Y的联合概率分布为(X,Y)(1,1)(1,2)(1,3)(2,1)(2,2)(2,3) P111169183??若X,Y独立，则?,?的值为（A）??29,??19. （A）??129,??9.（C）??16,??16 （D）??518,??118.4 ）（答案：（A）解答：若X,Y独立则有??P(X?2,Y?2)?P(X?2)P(Y?2) 1121 ?(????)(??)?(??) 393921 ???，??99 故应选（A）.5．设总体X的数学期望为?,X1,X2,?,Xn为来自X的样本，则下列结论中正确的是（A）X1是?的无偏估计量. （B）X1是?的极大似然估计量.（C）X1是?的相合（一致）估计量. （D）X1不是?的估计量. （）答案：（A）解答：EX1??，所以X1是?的无偏估计，应选（A）.三、（7分）已知一批产品中90%是合格品，检查时，一个合格品被误认为是次品的概率为0.05，一个次品被误认为是合格品的概率为0.02，求（1）一个产品经检查后被认为是合格品的概率；（2）一个经检查后被认为是合格品的产品确是合格品的概率.解：设A?‘任取一产品，经检验认为是合格品’B?‘任取一产品确是合格品’则（1）P(A)?P(B)P(A|B)?P()P(A|)?0.9?0.95?0.1?0.02?0.857.（2）P(B|A)?四、（12分）从学校乘汽车到火车站的途中有3个交通岗，假设在各个交通岗遇到红灯的事件是相互独立的，并且概率都是2/5. 设X为途中遇到红灯的次数，求X的分布列、分布函数、数学期望和方差.5 P(AB)0.9?0.95??0.9977. P(A)0.857解：X的概率分布为P(X?k)?C3()()k25k353?kk?0,1,2,3.X即X的分布函数为P02712515412523612538 125x?0,?0,?27?,0?x?1,?125??81,1?x?2, F(x)???125?117 2?x?3,?125,?x?3.?1,?26EX?3??,552318DX?3???.5525五、（10分）设二维随机变量(X,Y)在区域D?{(x,y)|x?0,y?0,x?y?1} 上服从均匀分布. 求（1）(X,Y)关于X的边缘概率密度；（2）Z?X?Y的分布函数与概率密度.（1）(X,Y)的概率密度为?2,(x,y)?Df(x,y)??0,其它.?fX(x)?（2）利用公式fZ(z)? 其中f(x,z?x)????????????2?2x,0?x?1f(x,y)dy??0,其它??f(x,z?x)dx?2,0?x?1,0?z?x?1?x?2,0?x?1,x?z?1.??0,其它??0,其它.当z?0或z?1时fZ(z)?0 0?z?1时fZ(z)?2?z0dx?2x0?2zz6故Z的概率密度为??2z,0?z?1,fZ(z)????0,其它.Z的分布函数为fZ(z)??z??z?0?0,?0,z?0,?z??fZ(y)dy???2ydy,0?z?1??z2,0?z?1, 0??1,z?1.?z?1??1,或利用分布函数法?z?0,?0,?FZ(z)?P(Z?z z1,)?P(X?Y?)z,y0??????2dxd?D1?1,z?1.??0,?2, ??z?1,?z?0,0?z?1, z?1.?2z,?0,0?z?1,其它.fZ(z)?FZ?(z)??六、（10分）向一目标射击，目标中心为坐标原点，已知命中点的横坐标X和纵坐标Y相互独立，且均服从N(0,2)分布. 求（1）命中环形区域D?{(x,y)|1?x?y?2}的概率；（2）命中点到目标中心距离Z?1）P{X,Y)?D}?222.??f(x,y)dxdyD???2??4D?x2?y28dxdy? 18?r282??2?21e?r28rdrd??（2）EZ?E? ?21e?r28d(?)??e 82??e?e；1?18?12 ?? ??r28 ????1e?04 ???1e8??x2?y28dxdy?18???2???0re?rdrd??r28r2dr7??rer2?8????0??0e?r28dr??????r28dr?.七、（11分）设某机器生产的零件长度（单位：cm）X~N(?,?2)，今抽取容量为16的样本，测得样本均值?10，样本方差s2?0.16. （1）求?的置信度为0.95的置信区间；（2）检验假设H0:?2?0.1（显著性水平为0.05）.（附注）t0.05(16)?1.746,t0.05(15)?1.753,t0.025(15)?2.132,解：（1）?的置信度为1??下的置信区间为(?t?/2(n?222?0.05(16)?26.296,?0.05(15)?24.996,?0.025(15)?27.488. ?t?/2(n??10,s?0.4,n?16,??0.05,t0.025(15)?2.132所以?的置信度为0.95的置信区间为（9.7868，10.2132）2 （2）H0:?2?0.1的拒绝域为?2???(n?1).15S22?15?1.6?24，?0.05 ??(15)?24.996 0.12 因为?2?24?24.996??0.05(15)，所以接受H0.2《概率论与数理统计》期末考试试题（A）专业、班级：姓名：学号：一、单项选择题(每题3分共18分)891011121314151617《概率论与数理统计》课程期末考试试题（B）专业、班级：姓名：学号：181920212223242526272829共8页30。

全国2013年1月高等教育自学考试概率论与数理统计(经管类)试题一、单项选择题(本大题共10小题，每小题2分，共20分)二、填空题(本大题共15小题，每小题2分，共30分)三、计算题(本大题共2小题，每小题8分，共16分)四、综合题(本大题共2小题，每小题12分，共24分)五、应用题(10分)全国2013年1月高等教育自学考试 概率论与数理统计(经管类)答案1、本题考查的是和事件的概率公式，答案为C.2、解：()()(|)1()()P B AB P AB P B AB P AB P AB ⋂===()()()0.50.15(|)0.5()()1()0.7P BA P B P AB P B A P B P A P A --=====- ()()0.15(|)0.3()()()0.5P B AB P AB P AB B P A P B P B ⋂=====()()(|)1()()P A AB P AB P A AB P AB P AB ⋂=== ，故选B.3、解：本题考查的是分布函数的性质。

由()1F +∞=可知，A 、B 不能作为分布函数。

再由分布函数的单调不减性，可知D 不是分布函数。

所以答案为C 。

4、解：选A 。

{||2}{2}{2}1{2}{2}1(2)(2)1(2)1(2)22(2)P X P X P X P X P X >=>+<-=-≤+<-=-Φ+Φ-=-Φ+-Φ=-Φ 5、解：因为(2)0.20.16P Y c ===+，所以0.04c =又(2)10.80.20.02P X c d ==-==++，所以10.020.040.14d =--= ，故选D 。

6、解：若~()X P λ，则()()E X D X λ==，故 D 。

7、解：由方差的性质和二项分布的期望和方差：1512(1)()()3695276633D X Y D X D Y -+=+=⨯⨯+⨯⨯=+= ，选A8、解：由切比雪夫不等式2(){|()|}1D X P X E X εε-<>-，可得21600{78008200}{|8000|200}10.96200P X P X <<=-<>-= ，选C 。

武汉理工大学教务处试题标准答案及评分标准用纸课程名称—概率论与数理统计——（B 卷）一. 选择题（每小题3分，共15分）1.C2.D3.B4.D5.A 二. 填空题（每小题3分，共15分）1.157 2. 41 3.20 4. 0.3 5.221σ+-n n三．解：（1）3.004.07.0)()()()(=+-=+-=AB P A P B A P B P ……5分（2）)()()()()(B P A P A P B A P B P +-= ，5.06.03.0)(1)()()(==--=A P A PB A P B P ……10分四．（1）),(Y X 的联合密度函数⎪⎩⎪⎨⎧∈--=,,0),(,))((1),(其他D y x c d a b y x f … 5分 （2）⎰∞+∞-⎪⎩⎪⎨⎧≤≤-==,,0,,1),()(其他b x a a b dy y x f x f X⎰∞+∞-⎪⎩⎪⎨⎧≤≤-==,,0,,1),()(其他d y c cd dx y x f y f Y … 7分 （3）)()(),(y f x f y x f Y X = ，Y X 与∴ 独立。

……10分五、设A 为产品合格事件，则A A ,是产品的一个划分。

又设B 为产品检查合格事件。

则9.0)(=A P ，98.0)|(=A B P ，05.0)|(=A B P …… 4分 （1）由全概率公式，一个产品被认为合格的概率)|()()|()()(A B P A P A B P A P B P +=887.005.01.098.09.0=⨯+⨯=。

…… 8分（2）由贝叶斯定理，“合格品”确实合格的概率)(/)|()()|(B P A B P A P B A P =994.0887.0/98.09.0=⨯=。

…… 10分六．12411218381=+++++B A (1) ……3分若x 与y 独立, 应有:()()()212,1=⋅====y P x P y x P⎪⎭⎫⎝⎛+⋅⎪⎭⎫ ⎝⎛++=⇒A 12124112181121 (2) ……6分综合(1)(2)有:41=A 81=B ……10分 七．0>y 时，dx x f y F yyX Y ⎰-=)()( ……4分 221)()(yY Y e y y F y f -='=π ……6分0≤y 时，0)(=y F Y ⎪⎩⎪⎨⎧≥>=-0021)(2y y e yy f y Y π …… 10分八、（1）1)()(+==⎰+∞--θθθdx xe X E x X =+1θ ， θ的矩估计为：.1-X ……… 5分 （2）∑-=⋅=ni ix n n e e x x x L 1),,,(21θθ0ln >θd L d ， L 为θ的单调增函数，故 }{min 1i n i x ≤≤=θ … 10分九(0,1)X N ………3分{1.4 5.4}}2(163P X P <<=<=Φ- ………7分解2(10.953Φ-≥ 得34.6n ≥ n 至少取35 (10)()1{0,1}()()()8P AB P X Y P AB P AB P A B ====-= ………………8分|1115{0,0}18888P X Y ===---= ………………10分| 五. （10分）（1）由(,)1f x yd x d y +∞+∞-∞-∞=⎰⎰，得A ＝1 ………………2分 |（2）10()0xxDE XY xydxdy dx xydy -===⎰⎰⎰⎰2()3DE X xdxdy ==⎰⎰ …………6分 ()0DE Y ydxdy ==⎰⎰ cov ,)()()()0X Y E XY E X E Y (＝－＝ (9)分（3）0XY ρ= X 与Y 不相关 ………………10分六.（10分）设同时开着的灯数为X ，(10000,0.7)X b ………………2分(0,1)N （近似） (5)分{69007100}210.971P X ≤≤=Φ-= ………………10分七.（10分）1101()(2E X dx θθθθ++==+⎰+1)x ………………3分 解12X θθ+=+，得θ的矩估计量为211X X-- ………………5分1()1()ni i L x θθθ=+∏n＝（） 1ln ln 1ln nii L n xθθ==+∑（）+ (7)分令1ln ln 01ni i d L nx d θθ==+=+∑ 得θ的极大似然估计量为11ln nii nX=--∑ …………10分八.（10(0,1)X N ………………3分{1.4 5.4}21P X P <<=<=Φ- ………………7分解2(10.953Φ-≥ 得34.6n ≥ n 至少取35 ………………10分九.（10分）T =(1)X t n - 0.005{(1)}0.99P T t n <-= ……………4分0.0050.005{(1)(1)}0.99P X n X X n -<<-= ..................8分 所求为（1485.61，1514.39） (10)分。

一、单选( 每题参考分值2.5分)1、设总体服从泊松分布：，其中为未知参数，为样本，记，则下面几种说法错误的是（）A. 是的无偏估计B. 是的矩估计C. 是的矩估计D. 是的矩估计错误:【D】2、设随机变量的分布函数为，则（）A.B.C.D.错误:【B】3、A.-1B. 1C.D.错误:【B】4、在下列结果中，构成概率分布的是（）A.B.C.D.错误:【B】5、A.B.C.D.错误:【D】6、设是的特征值且，则是（）特征值A.B.C.D.错误:【D】7、已知，则为（）A.B.C.D.错误:【C】8、设三阶方阵的特征值为，对应的特征向量为，若，则A.B.C.D.错误:【D】9、已知向量，若可由线性表出那么（）A. ，B. ，C. ，D. ，错误:【A】10、实二次型，则负惯性指数为（）A.B.C.D.错误:【B】11、与的相关系数，表示与（）A. 相互独立B. 不线性相关C. 存在常数使D. 满足错误:【B】12、设总体为参数的动态分布，今测得的样本观测值为0.1,0.2,0.3,0.4，则参数的矩估计值为（）A. 0.2B. 0.25C. 1D. 4错误:【B】13、设是来自正态总体的样本，则服从的分布为（）A.B.C.D.错误:【A】14、若是矩阵，是的导出组，则（）A. 若有无穷多个解，则仅有零解B. 仅有零解，则有唯一解C. 若有无穷多个解，则有非零解D. 有非零解，则有无穷多个解错误:【C】15、以下结论中不正确的是（）A. 若存在可逆矩阵，使，则是正定矩阵B. 二次型是正定二次型C. 元实二次型正定的充分必要条件是的正惯性指数为D. 阶实对称矩阵正定的充分必要条件是的特征值全为正数错误:【B】16、设随机事件A与B相互独立，A发生B不发生的概率与B发生A不发生的概率相等，且，则（）B.C.D.错误:【B】17、对于正态分布，抽取容量为10的样本，算得样本均值，样本方差，给定显著水平，检验假设.则正确的方法和结论是（）A. 用检验法，查临界值表知，拒绝B. 用检验法，查临界值表知，拒绝C. 用检验法，查临界值表知，拒绝D. 用检验法，查临界值表知，拒绝错误:【C】18、设随机变量和的密度函数分别为若与相互独立，则（）B.C.D.错误:【D】19、设二维随机变量，则（）A.B. 3C. 18D. 36错误:【B】20、A.B.C.D.错误:【B】21、已知为阶方阵，以下说法错误的是（）A.B. 的全部特征向量为的全部解C. 若有个互不相同的特征值，则必有个线性无关的特征向量D. 若可逆，而矩阵的属于特征值的特征向量也是矩阵属于特征值的特征向量错误:【B】22、设离散的随机变量X的分布为则（）A.B. 任意正实数C.D.错误:【C】23、称是来自总体的一个简单随机样本（简称样本），即满足（）A. 相互独立，不一定同分布B. 相互独立同分布，但与总体分布不一定相同C. 相互独立且均与总体同分布D. 与总体同分布，但不一定相互独立错误:【C】24、设是次重复试验中事件出现的次数，是事件在每次试验中出现的概率，则对任意均有（）A. =0B. =1C. >0D. 不存在错误:【A】25、设随机变量为独立同分布序列，且服从参数为的指数分布，则下面式子中正确的是（）A.B.C.D.错误:【A】26、设4个3维列向量组成的矩阵经初等行变换后变为，则可表示为（）A.B.C.D.错误:【A】27、A.B.C.D.错误:【C】28、设是二阶矩阵的两个特征，那么它的特征方程是（）A.B.C.D.错误:【D】29、已知线性无关则（）A. 必线性无关B. 若为奇数，则必有线性无关C. 若为偶数，则线性无关D. 以上都不对错误:【C】30、设是一非齐次线性方程组，是其任意2个解，则下列结论错误的是（）A. 是的一个解B. 是的一个解C. 是的一个解D. 是的一个解错误:【A】31、设总体的分布函数为,则总体均值和方差的矩估计分别为（）A.B.C.D.错误:【B】32、设一批产品有1000件，其中有50件次品，从中随机地、有放回地抽取500件产品，表示抽到次品的件数，则（）A.B.C.D.错误:【C】33、两个独立事件A和B发生的概率分别为和，则其中之一发生的概率为（）A.B.C.D.错误:【D】34、设A、B、C是三个事件，且，，，则A、B、C至少有1个发生的概率为（）A.B.C.D.错误:【C】35、A.B.C.D.错误:【D】36、设二维随机变量，且与相互独立，则（）A.B.C.D.错误:【D】37、下列结论正确的是（）A.正交向量组一定线性无关B.线性无关向量组一定是正交向量组C.正交向量组不含零向量D.线性无关向量组不含零向量错误:【D】38、向量空间的维数等于（）A. 0B. 1C. 2D. 3错误:【C】39、下列说法正确的是（）A.B.C.D.错误:【D】40、若阶可逆矩阵与相似，且则（）A.B.C.D.错误:【C】41、设总体的分布中带有未知参数，为样本，和是参数的两个无偏估计，若对任意的样本容量，若为比有效的估计量，则必有（）A.B.C.D.错误:【B 】42、若二次型 为正定二次型，则的取值范围为（ ）A.B.C.D.错误:【C 】43、已知方阵相似于对角阵，则常数（ ）A.B.C.D.错误:【A】44、实二次型为正定的充要条件是（）A.的秩为B.的正惯性指数为C.的正惯性指数等于的秩D.的负惯性指数为错误:【B】45、A.B.C.D.错误:【C】46、A.B.C.D.以上都不对错误:【C】47、二次型的标准型为（）A.B.C.D.错误:【D】48、若，则的特征值为（）A.或B.或C.D.错误:【B】49、设与都是来自于总体的两独立样本，，与分别是两样本的均值和方差，，则有（）A.对于任意的常数是的无偏估计，且，，达到最小B.对于任意的常数是的无偏估计，且，，达到最小C.对于任意常数，都是的无偏估计，并且当时，达到最小D.对于任意常数，都是的无偏估计错误:【D】50、已知是正定矩阵，则（）A.B.C.D.错误:【B】。