新人教版七年级数学上册专题训练：角的计算

人教版七年级上册数学期末复习：角的计算综合练习题汇编1．如图所示，∠AOB是平角，OM、ON分别是∠AOC、∠BOD的平分线．（1）当∠BOC＝140°时，求∠AOM的度数；（2）当∠AOC＝30°，∠BOD＝60°时，求∠MON的度数；（3）当∠COD＝x度时，则∠MON＝度．（请直接写出答案）2．如图所示，OC是∠AOD的平分线，OE是∠BOD的平分线，∠EOC＝65°，∠DOC＝25°，求∠AOB的度数．3．如图，已知射线OC在∠AOB内，OM和ON分别平分∠AOC和∠BOC．（1）若∠AOC＝50°，∠BOC＝30°，求∠MON的度数．（2）探究∠MON与∠AOB的数量关系．4．如图，已知A、O、B三点在一条直线上，OC平分∠AOD，∠AOC+∠EOB＝90°．（1）求∠COE的度数；（2）判断∠DOE和∠EOB之间有怎样的关系，并说明理由．5．填空，完成下列说理过程．如图，点A、O、B在同一条直线上，OD，OE分别平分∠AOC和∠BOC．（1）求∠DOE的度数；（2）如果∠COD＝65°，求∠AOE的度数．解：（1）如图，因为OD是∠AOC的平分线，所以∠COD＝∠AOC因为OE是∠BOC的平分线，所以∠COE＝所以∠DOE＝∠COD+ ＝（∠AOC+∠BOC）＝∠AOB＝°（2）由（1）可知∠DOE＝90°因为∠COD＝65°所以＝∠COD＝65°则：∠AOE＝∠AOD+ ＝°6．如图，O为直线AB上一点，∠BOE＝80°，直线CD经过点O．。

新人教版七年级数学上册专题训练：角的计算(含答案)专题训练角的计算类型1 利用角度的和、差关系要求求解的角与已知角之间有和、差关系，可以利用角度和、差来计算。

1.如图，已知 $\angle AOC=\angle BOD=75°$，$\angle BOC=30°$，求 $\angle AOD$ 的度数。

解：因为 $\angle AOC=75°$，$\angle BOC=30°$，所以$\angle AOB=\angle AOC-\angle BOC=75°-30°=45°$。

又因为$\angle BOD=75°$，所以 $\angle AOD=\angle AOB+\angle BOD=45°+75°=120°$。

2.将一副三角板的两个顶点重叠放在一起（两个三角板中的锐角分别为45°、45°和30°、60°）。

1) 如图1所示，在此种情形下，当 $\angle DAC=4\angle BAD$ 时，求 $\angle CAE$ 的度数。

2) 如图2所示，在此种情形下，当 $\angle ACE=3\angle BCD$ 时，求 $\angle ACD$ 的度数。

解：(1) 因为 $\angle BAD+\angle DAC=90°$，$\angle DAC=4\angle BAD$，所以 $5\angle BAD=90°$，即 $\angle BAD=18°$。

所以 $\angle DAC=4\times18°=72°$。

因为 $\angle DAE=90°$，所以 $\angle CAE=\angle DAE-\angle DAC=18°$。

2) 因为 $\angle BCE=\angle DCE-\angle BCD=60°-\angle BCD$，$\angle ACE=3\angle BCD$，所以 $\angle ACB=\angle ACE+\angle BCE=3\angle BCD+60°-\angle BCD=90°$。

专题6 角一、单选题1．（新人教版数学七年级上册第四章几何图形初步4.3.2《角的比较与运算》课时练习）如图所示，从点O出发的5条射线，可以组成的角的个数是（）．A. 4B. 6C. 8D. 10【答案】D2．北京时间上午8：30时，时钟上时针和分针之间的夹角(小于平角)是（）A. 85°B. 75°C. 70°D. 60°【答案】B【解析】在钟面上，被12小时划分为12大格，每1大格对应的度数是30度，上午8:30的时候，时针指向8时和9时的中间位置，分针指向6时，两针之间刚好间隔2.5格，∴8:30时，时针和分针之间的夹角为：30° 2.5=75°.3．如图，下列说法错误的是（）A. OA的方向是北偏东40°B. OB的方向是北偏西75°C. OC的方向是西南方向D. OD的方向是南偏东40°【答案】A【解析】A选项中，由图可知“OA的方向是北偏东50°”，所以本选项说法错误；B选项中，由图可知：“OB的方向是北偏西75°”是正确的；C选项中，由图可知；“OC的方向是西南方向”是正确的；D选项中，由图可知：“OD的方向是南偏东40°”是正确的；故选A.4．下列说法正确的是（）A. A在B的南偏东30°的方向上，则B也在A的南偏东30°的方向上；B. A在B的南偏东30°的方向上，则B在A的南偏东60°的方向上；C. A在B的南偏东30°的方向上，则B在A的北偏西30°的方向上；D. A在B的南偏东30°的方向上，则B在A的北偏西60°的方向上【答案】C5．（北师大版数学七年级上册第四章基本平面图形4.3角同步测试题）一个角是70°18′，则这个角等于（）A. 70.18° B. 70.3° C. 70.018° D. 70.03°【答案】B【解析】70°18′=70°+18′ 60=70°+0.3°=70.3°.故选B.6．如图，射线OC，OD分别在∠AOB的内部、外部，下列结论错误的是()A. ∠AOB<∠AODB. ∠BOC<∠AOBC. ∠COD>∠AODD. ∠AOB>∠AOC【答案】C【解析】观察图形可知：A.∠AOB＜∠AOD正确；B.∠BOC＜∠AOB正确；C.∠COD＞∠AOD错误；D.∠AOB＞∠AOC正确.故选C.7．（新人教版数学七年级上册第四章几何图形初步4.3.2《角的比较与运算》课时练）下列语句中，正确的是（）．A. 比直角大的角钝角; B. 比平角小的角是钝角C. 钝角的平分线把钝角分为两个锐角;D. 钝角与锐角的差是锐角【答案】C8．（新人教版数学七年级上册第四章几何图形初步4.3.1《角》课时练习）已知α 、β都是钝角，甲、乙、丙、丁四个同学的计算16（α +β）的结果依次为28°、48°、60°、88°，其中只有一个同学计算结果是正确的，则得到正确结果的同学是（）A. 甲B. 乙C. 丙D. 丁【答案】B【解析】甲、乙、丙、丁四个同学的计算16（α +β）的结果依次为28°、48°、60°、88°，那么这四个同学计算α+β的结果依次为168°、288°、360°、528°，又因为两个钝角的和应大于180°且小于360°，所以只有乙同学的计算正确，故选B.9．（山东省东昌府区梁水镇中心中学2016-2017学年七年级下学期期中考试数学试题）如图，如果∠AOC=∠BOD，则∠AOB与∠DOC的大小关系是（）A. ∠AOB>∠DOCB. ∠AOB<∠DOCC. ∠AOB=∠DOCD. 无法比较【答案】C【解析】∵∠AOC=∠BOD，∴∠AOC-∠BOC=∠BOD-∠BOC，∴∠AOB=∠DOC.故选C.10．如图，OB、OC是∠AOD的任意两条射线，OM平分∠AOB，ON平分∠COD，若∠MON=α，∠BOC=β，则表示∠AOD的代数式为( )。

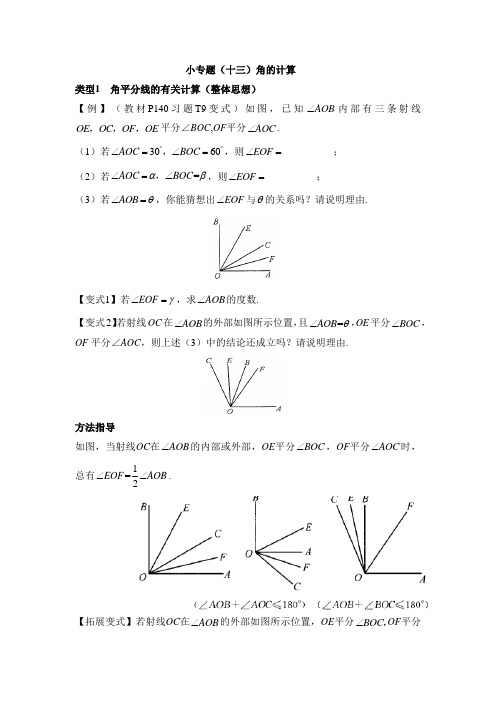
小专题（十三）角的计算类型1 角平分线的有关计算（整体思想）【例】（教材P140习题T9变式）如图，已知AOB ∠内部有三条射线OE OC OF OE ，，，平分∠BOC ,OF 平分AOC ∠.（1）若3060AOC BOC ︒︒∠=∠=，，则EOF ∠=__________；（2）若=AOC BOC αβ∠=∠，，则EOF ∠=__________；（3）若AOB θ∠=，你能猜想出EOF ∠与θ的关系吗？请说明理由.【变式1】若EOF γ∠=，求AOB ∠的度数.【变式2】若射线OC 在AOB ∠的外部如图所示位置，且=AOB θ∠，OE 平分BOC ∠，OF 平分∠AOC ，则上述（3）中的结论还成立吗？请说明理由.方法指导如图，当射线OC 在AOB ∠的内部或外部，OE 平分BOC ∠，OF 平分AOC ∠时，总有1=2EOF AOB ∠∠.【拓展变式】若射线OC 在AOB ∠的外部如图所示位置，OE 平分BOC ∠，OF 平分AOC ∠，则EOF AOB ∠∠与的数量关系是__________.变式训练1.如图，已知AOB ∠内部有顺次的四条射线： OE OC OD OF OE ，，，平分AOC ∠，OF 平分BOD ∠.（1）若16040AOB COD ︒︒∠=∠=，，则EOF ∠的度数为______；（2）若AOB COD αβ∠=∠=，，求EOF ∠的度数；（3）从（1）、（2）的结果，你能看出什么规律吗？类型2 直接计算2.如图，点A O E ，，在同一直线上，40AOB ︒∠=,2846BOD ︒'∠=，OD 平分COE ∠，求∠COB 的度数.3.已知40AOB ︒∠=，OD 是BOC ∠的平分线.（1）如图1，当AOB BOC ∠∠与互补时，求COD ∠的度数；（2）如图2，当AOB BOC ∠∠与互余时，求COD ∠的度数.类型3 方程思想4.一个角的补角加上10︒后等于这个角的余角的3倍，求这个角.5.如图，AOB COB COD ∠∠∠，，的度数之比是2：1：3，且140AOC DOB ︒∠+∠=，求AOD ∠的度数.6.如图，已知12AOB BOC ∠=∠，3COD AOD AOB ∠=∠=∠,求AOB COD ∠∠和的度数.类型4 分类讨论思想7.已知：如图，OC 是AOB ∠的平分线.（1）当60AOB ︒∠=时，求AOC ∠的度数；（2）在（1）的条件下，90EOC ︒∠=，请在图中补全图形，并求AOE ∠的度数；（3）当AOB α∠=时，90EOC ︒∠=，直接写出AOE ∠的度数.（用含α的式子表示）类型5 角的运动问题8.已知，点O 是直线AB 上的一点，COD ∠是直角，OE 平分BOC ∠.（1）如图1.①若60AOC ︒∠=，则DOE ∠的度数为__________；②若AOC α∠=，则DOE ∠的度数为_____________（用含α的式子表示）；（2）将图1中的DOC ∠绕点O 顺时针旋转至图2的位置，试探究DOE ∠和AOC ∠的度数之间的关系，写出你的结论，并说明理由.参考答案【例】解：（1）45︒（2）2αβ+（3）12EOF θ∠=,理由；因为OE 平分BOC ∠，OF 平分AOC ∠，所以11,22EOC BOC COF AOC ∠=∠∠=∠.所以11111()22222EOF EOC COF BOC AOC BOC AOC AOB θ∠=∠+∠=∠+∠=∠+∠=∠=.【变式1】解：因为OE 平分BOC ∠，OF 平分AOC ∠，所以12EOC BOC ∠=∠，12COF AOC ∠=∠.所以1122EOF EOC COF BOC AOC ∠=∠+∠=∠+∠11()22BOC AOC AOB =∠+∠=∠.因为EOF γ∠=，所以2AOB γ∠=. 【变式2】解：12EOF θ∠=成立.理由：因为OE 平分BOC ∠，OF 平分∠AOC ，所以1122EOC BOC COF AOC ∠=∠∠=∠，.所以EOF COF EOC ∠=∠-∠1122AOC BOC =∠-∠1()2AOC BOC =∠-∠11.22AOB θ=∠= 【拓展变式】11802EOF AOB ︒∠=-∠ 变式训练1.解：（1）100︒（2）因为OE 平分AOC ∠，OF 平分BOD ∠，所以12COE AOC ∠=∠，12DOF BOD ∠=∠.所以12EOF COE COD DOF AOC COD ∠=∠+∠+∠=∠+∠1111111()2222222BOD AOC COD BOD COD AOB COD αβ+∠=∠+∠+∠+∠=∠+∠=+1()2αβ=+.（3）若AOB ∠内部有顺次的四条射线：,,,,OE OC OD OF OE 平分AOC ∠，OF 平分BOD ∠，则1()2EOF AOB COD ∠=∠+∠.2.解：因为2846EOD ︒'∠=，OD 平分COE ∠，所以2=228465732COE EOD ︒'︒'∠=∠⨯=.又因为40AOB ︒∠=，所以1801804057328228COB AOB COE ︒︒︒︒'︒'∠=∠-∠=-=--.3.解：（1）因为AOB BOC ∠∠与互补，所以180AOB BOC ︒∠+∠=.因为40AOB ︒∠=，所以18040140BOC ︒︒︒∠=-=.因为OD 是BOC ∠的平分线，所以1702COD BOC ︒∠=∠=.（2）因为AOB BOC ∠∠与互余，所以90AOB BOC ︒∠+∠=.因为=40AOB ︒∠，所以=904050BOC ︒︒︒∠-=.因为OD 是BOC ∠的平分线，所以1252COD BOC ︒∠=∠=. 4.解：这个角为40︒.5.解：设COB x ︒∠=，则2,3AOB x COD x ︒︒∠=∠=.根据题意,得23140x x x x +++=.解得20x =.所以236620120AOD x x x x ︒︒︒︒︒︒∠=++==⨯=.6.解：设AOB x ︒∠=，则33COD AOD AOB x ︒∠=∠=∠=.因为12AOB BOC =∠，所以2BOC x ︒∠=.因为360BOC COD AOD AOB ︒∠+∠+∠+∠=，所以233360x x x x +++=.解得40x =.所以40120AOB COD ︒︒∠=∠=，.7.解：（1）因为OC 是AOB ∠的平分线，所以12AOC AOB ∠=∠.因为60AOB ︒∠=，所以30AOC ︒∠=，（2）如图1，9030120AOE EOC AOC ︒︒︒∠=∠+∠=+=；如图2，903060.AOE EOC AOC ︒︒︒∠=∠-∠=-=（3）902α︒+或902α︒-.8.解：（1）①30︒②12α（2）12DOE AOC ∠=∠，理由如下：因为180BOC AOC ︒∠=-∠.OE 平分BOC ∠，所以1118022COE BOC AOC ︒∠=∠=-∠（）1902AOC ︒=-∠.所以1190909022DOE COE AOC AOC ︒︒︒∠==--∠=∠∠-（）.。

2022-2023学年人教版七年级数学上册《4.3.2角的比较与运算》题型分类练习题（附答案）一．角平分线的定义1．如图，两个直角∠AOB，∠COD有相同的顶点O，下列结论：①∠AOC＝∠BOD；②∠AOC+∠BOD＝90°；③若OC平分∠AOB，则OB平分∠COD；④∠AOD的平分线与∠COB的平分线是同一条射线．其中正确的个数有（）A．1个B．2个C．3个D．4个2．如图，OE为∠AOD的平分线，∠COD＝∠EOC，∠COD＝15°，求：①∠EOC的大小；②∠AOD的大小．3．如图，已知O为直线AB上一点，过点O向直线AB上方引三条射线OC、OD、OE，且OC平分∠AOD，∠2＝3∠1，∠COE＝70°，求∠2的度数．4．如图，OB是∠AOC的平分线，OD是∠COE的平分线．（1）若∠AOB＝50°，∠DOE＝30°，那么∠BOD是多少度？（2）若∠AOE＝160°，∠AOB＝50°，那么∠COD是多少度？5．已知：如图，OC是∠AOB的角平分线，∠AOD＝2∠BOD，∠COD＝18°．请你求出∠BOD的度数．6．如图，O为直线AB上一点，∠AOC＝58°，OD平分∠AOC，∠DOE＝90°．（1）求出∠BOD的度数；（2）请通过计算说明：OE是否平分∠BOC．二．角的计算7．把两块三角板按如图所示那样拼在一起，则∠ABC等于（）A．70°B．90°C．105°D．120°8．如图，已知∠AOB：∠BOC＝2：3，∠AOC＝75°，那么∠AOB＝（）A．20°B．30°C．35°D．45°9．如图，已知∠COB＝2∠AOC，OD平分∠AOB，且∠COD＝20°，则∠AOB的度数为．10．如图，射线OB和OD分别为∠AOC和∠COE的角平分线，∠AOB＝45°，∠DOE＝20°，则∠AOE＝（）A．110°B．120°C．130°D．140°11．如图所示，OB，OC是∠AOD的任意两条射线，OM平分∠AOB，ON平分∠COD，若∠MON＝α，∠BOC＝β，则表示∠AOD的代数式是（）A．2α﹣βB．α﹣βC．α+βD．以上都不正确12．如图所示，将一张长方形纸片斜折过去，使顶点A落在A′处，BC为折痕，然后再把BE折过去，使之与BA′重合，折痕为BD，若∠ABC＝58°，则求∠E′BD的度数（）A．29°B．32°C．58°D．64°13．如图，将两块三角尺AOB与COD的直角顶点O重合在一起，若∠AOD＝4∠BOC，OE为∠BOC的平分线，则∠DOE的度数为（）A．36°B．45°C．60°D．72°14．如图，将三个同样的正方形的一个顶点重合放置，那么∠1的度数为．15．如图，将一张纸折叠，若∠1＝65°，则∠2的度数为．16．如图，OB、OC是∠AOD内部的两条射线，OM平分∠AOB，ON平分∠COD，∠MON ＝80°．（1）若∠BOC＝40°，求∠AOD的度数；（2）若∠AOD＝x°，求∠BOC的度数（用含x的代数式表示）．17．已知：如图，∠AOB是直角，∠AOC＝40°，ON是∠AOC的平分线，OM是∠BOC 的平分线．（1）求∠MON的大小；（2）当锐角∠AOC的大小发生改变时，∠MON的大小是否发生改变？为什么？18．如图，点O是直线AB上一点，OD平分∠BOC，∠COE＝90°．（1）若∠AOC＝48°，求∠DOE的度数．（2）若∠AOC＝α，则∠DOE＝（用含α的代数式表示）．19．如图，将两块直角三角尺的直角顶点C叠放在一起，（1）若∠DCE＝35°，求∠ACB的度数；（2）若∠ACB＝140°，求∠DCE的度数；（3）猜想∠ACB与∠DCE的大小关系，并说明理由．20．如图，已知同一平面内∠AOB＝90°，∠AOC＝60°，（1）填空∠BOC＝；（2）如OD平分∠BOC，OE平分∠AOC，直接写出∠DOE的度数为°；（3）试问在（2）的条件下，如果将题目中∠AOC＝60°改成∠AOC＝2α（α＜45°），其他条件不变，你能求出∠DOE的度数吗？若能，请你写出求解过程；若不能，请说明理由．三．角的大小比较21．比较：28°15′28.15°（填“＞”、“＜”或“＝”）．22．下列说法正确的个数是（）（1）连接两点之间的线段叫两点间的距离；（2）木匠师傅锯木料时，一般先在模板上画出两个点，然后过这两点弹出一条墨线，这样做的原理是：两点之间，线段最短；（3）若AB＝2CB，则点C是AB的中点；（4）若∠A＝20°18′．∠B＝20°28″，∠C＝20.25°，则有∠A＞∠C＞∠B．A．1个B．2个C．3个D．4个参考答案一．角平分线的定义1．解：①∵∠AOB＝∠COD＝90°，∴∠AOC＝90°﹣∠BOC，∠BOD＝90°﹣∠BOC，∴∠AOC＝∠BOD，∴①正确；②∵只有当OC，OB分别为∠AOB和∠COD的平分线时，∠AOC+∠BOD＝90°，∴②错误；③∵∠AOB＝∠COD＝90°，OC平分∠AOB，∴∠AOC＝∠COB＝45°，则∠BOD＝90°﹣45°＝45°∴OB平分∠COD，∴③正确；④∵∠AOB＝∠COD＝90°，∠AOC＝∠BOD（已证）；∴∠AOD的平分线与∠COB的平分线是同一条射线，∴④正确；故选：C．2．解：①由∠COD＝∠EOC，得∠EOC＝4∠COD＝4×15°＝60°；②由角的和差，得∠EOD＝∠EOC﹣∠COD＝60°﹣15°＝45°．由角平分线的性质，得∠AOD＝2∠EOD＝2×45°＝90°．3．解：设∠1＝x，则∠2＝3∠1＝3x，（1分）∵∠COE＝∠1+∠3＝70°∴∠3＝（70﹣x）（2分）∵OC平分∠AOD，∴∠4＝∠3＝（70﹣x）（3分）∵∠1+∠2+∠3+∠4＝180°∴x+3x+（70﹣x）+（70﹣x）＝180°（4分）解得：x＝20（5分）∴∠2＝3x＝60°（6分）答：∠2的度数为60°．（7分）4．解：（1）OB是∠AOC的平分线，∴∠BOC＝∠AOB＝50°；∵OD是∠COE的平分线，∴∠COD＝∠DOE＝30°，∴∠BOD＝∠BOC+∠COD＝50°+30°＝80°；（2）OB是∠AOC的平分线，∴∠AOC＝2∠AOB＝100°，∴∠COE＝∠AOE﹣∠AOC＝160°﹣100°＝60°，∵OD是∠COE的平分线，∴∠COD＝∠COE＝30°．5．解：∵OC是∠AOB的角平分线∴∠BOC＝∠AOB，∵∠AOD＝2∠BOD，∴∠AOB＝3∠BOD，即∠BOD＝∠AOB；∴∠COD＝∠AOB﹣∠AOB＝∠AOB，∴∠BOD＝2∠COD，∵∠COD＝18°，∴∠BOD＝36°．6．解：（1）∵∠AOC＝58°，OD平分∠AOC，∴∠AOD＝29°，∴∠BOD＝180°﹣29°＝151°；（2）OE是∠BOC的平分线．理由如下：∵∠AOC＝58°，∴∠BOC＝122°．∵OD平分∠AOC，∴∠DOC＝×58°＝29°．∵∠DOE＝90°，∴∠COE＝90°﹣29°＝61°，∴∠COE＝∠BOC，即OE是∠BOC的平分线．二．角的计算7．解：∠ABC＝30°+90°＝120°．故选：D．8．解：∵∠AOB：∠BOC＝2：3，∠AOC＝75°，∴∠AOB＝∠AOC＝×75°＝30°，故选：B．9．解：∵∠COB＝2∠AOC，OD平分∠AOB，且∠COD＝20°，∴设∠COB＝2∠AOC＝2x，∠AOD＝∠BOD＝1.5x，∴∠COD＝0.5x＝20°，∴x＝40°，∴∠AOB的度数为：3×40°＝120°．故答案为：120°．10．解：∵OB是∠AOC的角平分线，∠AOB＝45°，∴∠COB＝∠AOB＝45°∵OD是∠COE的角平分线，∠DOE＝20°，∴∠DOC＝∠DOE＝20°，∴∠AOE＝∠AOB+∠COB+∠DOC+∠DOE＝45°×2+20°×2＝130°．故选：C．11．解：∵∠MON＝α，∠BOC＝β∴∠MON﹣∠BOC＝∠CON+∠BOM＝α﹣β又∵OM平分∠AOB，ON平分∠COD∴∠CON＝∠DON，∠AOM＝∠BOM由题意得∠AOD＝∠MON+∠DON+∠AOM＝∠MON+∠CON+∠BOM＝α+（α﹣β）＝2α﹣β．故选：A．12．解：∵根据折叠得出∠ABC＝∠A′BC，∠EBD＝∠E′BD，又∵∠ABC+∠A′BC+∠EBD+∠E′BD＝180°，∴∠ABC+∠E′BD＝90°，∵∠ABC＝58°，∴∠E′BD＝32°．故选：B．13．解：∵∠AOB＝90°，∠COD＝90°，∴∠AOB+∠COD＝180°，∵∠AOB＝∠AOC+∠BOC，∠COD＝∠BOC+∠BOD，∴∠AOC+∠BOC+∠BOC+∠BOD＝180°，∴∠AOD+∠BOC＝180°，∵∠AOD＝4∠BOC，∴4∠BOC+∠BOC＝180°，∴∠BOC＝36°，∵OE为∠BOC的平分线，∴∠COE＝∠BOC＝18°，∴∠DOE＝∠COD﹣∠COE＝90°﹣18°＝72°，故选：D．14．解：∵∠BOD＝90°﹣∠AOB＝90°﹣30°＝60°∠EOC＝90°﹣∠EOF＝90°﹣40°＝50°又∵∠1＝∠BOD+∠EOC﹣∠BOE∴∠1＝60°+50°﹣90°＝20°故答案是：20°．15．解：∵将一张纸条折叠，∠1＝65°，∴∠1+∠2＝180°﹣∠1即65°+∠2＝180°﹣65°，得∠2＝50°．故答案为：50°．16．解：（1）∵∠MON﹣∠BOC＝∠BOM+∠CON，∠BOC＝40°，∠MON＝80°，∴∠BOM+∠CON＝80°﹣40°＝40°，∵OM平分∠AOB，ON平分∠COD，∴∠AOM＝∠BOM，∠DON＝∠CON，∴∠AOM+∠DON＝40°，∴∠AOD＝∠MON+∠AOM+∠DON＝80°+40°＝120°；（2）∵∠AOD＝x°，∠MON＝80°，∴∠AOM+∠DON＝∠AOD﹣∠MON＝（x﹣80）°，∵∠BOM+∠CON＝∠AOM+∠DON＝（x﹣80）°，∴∠BOC＝∠MON﹣（∠BOM+∠CON）＝80°﹣（x﹣80）°＝（160﹣x）°．17．解：（1）∵∠AOB是直角，∠AOC＝40°，∴∠AOB+∠AOC＝90°+40°＝130°，∵OM是∠BOC的平分线，ON是∠AOC的平分线，∴，．∴∠MON＝∠MOC﹣∠NOC＝65°﹣20°＝45°，（2）当锐角∠AOC的大小发生改变时，∠MON的大小不发生改变．∵＝，又∠AOB是直角，不改变，∴．18．解：（1）∵O是直线AB上一点，∴∠AOC+∠BOC＝180°，∵∠AOC＝48°，∴∠BOC＝132°，∵OD平分∠BOC，∴∠COD＝∠BOC＝66°，∵∠DOE＝∠COE﹣∠COD，∠COE＝90°，∴∠DOE＝90°﹣66°＝24°；（2）∵O是直线AB上一点，∴∠AOC+∠BOC＝180°，∵∠AOC＝α，∴∠BOC＝180°﹣α，∵OD平分∠BOC，∴∠COD＝∠BOC＝（180°﹣α）＝90°﹣α，∵∠DOE＝∠COE﹣∠COD，∠COE＝90°，∴∠DOE＝90°﹣（90°﹣α）＝α．故答案为：α．19．解：（1）∵∠ECB＝90°，∠DCE＝35°∴∠DCB＝90°﹣35°＝55°∵∠ACD＝90°∴∠ACB＝∠ACD+∠DCB＝145°．（2）∵∠ACB＝140°，∠ACD＝90°∴∠DCB＝140°﹣90°＝50°∵∠ECB＝90°∴∠DCE＝90°﹣50°＝40°．（3）猜想得∠ACB+∠DCE＝180°（或∠ACB与∠DCE互补）理由：∵∠ECB＝90°，∠ACD＝90°∴∠ACB＝∠ACD+∠DCB＝90°+∠DCB∠DCE＝∠ECB﹣∠DCB＝90°﹣∠DCB∴∠ACB+∠DCE＝180°．20．解：（1）∵∠AOB＝90°，∠AOC＝60°，∴∠BOC＝∠AOB+∠AOC＝90°+60°＝150°，故答案为：150°；（2）∵OD平分∠BOC，OE平分∠AOC，∴∠COD＝∠BOC＝75°，∠COE＝∠AOC＝30°，∴∠DOE的度数为：∠COD﹣∠COE＝45°；故答案为：45；（3）∵∠AOB＝90°，∠AOC＝2α，∴∠BOC＝90°+2α，∵OD、OE平分∠BOC，∠AOC，∴∠DOC＝∠BOC＝45°+α，∠COE＝∠AOC＝α，∴∠DOE＝∠DOC﹣∠COE＝45°．三．角的大小比较21．解：∵28°15′＝28°+（15÷60）°＝28.25°，∴28°15′＞28.15°．故答案为：＞．22．解：（1）连接两点之间的线段的长度叫两点间的距离，错误；（2）木匠师傅锯木料时，一般先在模板上画出两个点，然后过这两点弹出一条墨线，这样做的原理是：两点确定一条直线，错误；（3）当C在线段AB上，且AB＝2CB时，点C是AB的中点，当C不在线段AB上时，则不是中点，故命题错误；（4）若∠A＝20°18′．∠B＝20°28″，∠C＝20.25°，则有∠A＞∠C＞∠B，正确；故选：A．。

人教版七年级数学上册《6.3.2角的比较与运算》同步测试题带答案一、单选题1．把2.36︒用度、分、秒表示，正确的是（ ）A ．221'36"︒B ．218'36''︒C ．230'60"︒D ．23'6"︒2．若383A '∠=︒，38.3B ∠=︒则（ ）A ．AB ∠<∠ B ．A B ∠>∠C ．A B ∠=∠D ．无法确定3．用一副三角尺的两个角不能拼成（ ）度的角．A ．15B ．105C ．110D ．1204．若1290∠+∠=︒，15825'∠=︒那么∠2的度数是（ ）A ．3175'︒B ． 3135'︒C ．4175'︒D ．4125︒'5．如图，已知:2:3AOB BOC ∠∠=，30AOB ∠=︒那么AOC ∠=（ ）A ．45︒B ．50︒C ．60︒D ．75︒6．如下图2BOC AOB ∠=∠，OP 平分AOB ∠，已知12AOP ∠=︒，则POC ∠=（ ）A ．60︒B ．72︒C ．78︒D ．84︒7．入射光线和平面镜的夹角为40°，转动平面镜，使入射角减小20°，反射光线与入射光线的夹角和原来相比较将（ ）A ．减小40°B ．增大40°C ．减小20°D ．不变8．如图，设锐角AOB ∠的度数为α，若一条射线平分AOB ∠，则图中所有锐角的和为2α．若四条射线五等分AOB ∠，则图中所有锐角的和为( )A ．7αB ．6αC ．5αD ．4a二、填空题9．若130.45︒∠=，23028︒'∠=则1∠ 2∠（用“＞”“=”“＜”填空）．10．将一副直角三角尺如图放置，若22AOD ∠=︒，则BOC ∠的大小为 ．11．如图，已知()585AOB BOC x ∠=︒∠=+︒，， ()27AOC x ∠=-︒那么AOC ∠= 度．12．小明从O 点出发向北偏西40︒走了500米到达A 点，小丽从O 点出发向南偏东40︒走了300米到达B 点，这时A 、B 两点之间的距离是 米．13．如图，已知点O 是直线AB 上一点，OC OD OM ON 、、、为从点O 引出的四条射线，若30BOD ∠=︒87COD AOC ∠=∠ 90MON ∠=︒ 则AON ∠与COM ∠之间的数量关系是 ；三、解答题14．计算：(1)89352020''︒+︒（结果用度、分、秒表示）．(2)123246036''︒-︒（结果用度表示）．15．如图，直线CD ，EF 交于点O ，OA ，OB 分别平分COE ∠和DOE ∠，且3OGB ∠=∠．(1)求证：1290∠+∠=︒；(2)若332∠=∠，求1∠的度数．16．已知直线AB 与CD 相交于点O ，且OM 平分AOC ∠．(1)如图1，若ON 平分BOC ∠，求MON ∠的大小；(2)如图2，若MON α∠=，13CON BON ∠=∠求BON ∠的大小．（用含α的式子表示） 参考答案 题号1 2 3 4 5 6 7 8 答案 A A C B DA A A1．【答案】A【分析】根据大单位化小单位除以进率，可得答案．【详解】解：2.36°＝2°＋0.36×60′＝2°21′＋0.6×60″＝2°21′36″故选：A ．【点睛】此题主要考查度、分、秒的转化运算，进行度、分、秒的转化运算，注意以60为进制． 2．【答案】A【分析】将∠A 或∠B 的大小统一成用度或用度分秒表示的形式，即可得出结论．【详解】解：∠∠A =38°3′，∠B =38.3°=38°18′故选：A ．【点睛】本题主要考查了角的大小比较，统一角的大小单位是解决问题的关键．3．【答案】C【分析】本题考查了角的计算．用三角板拼特殊角其实质是角的和差运算，理解题意是关键．用三角板画出角，无非是用角度加减法．根据选项一一分析，排除错误答案．【详解】解：A ．15︒的角453015︒-︒=︒；故本选项不符合题意；B ．105︒的角4560105︒+︒=︒；故本选项不符合题意；C ．110︒的角，无法用三角板中角的度数拼出；故本选项符合题意；D ．120︒的角9030120︒+︒=︒；故本选项不符合题意．故选C ．4．【答案】B【分析】本题考查角度的加减计算．根据角度的加减法计算即可，注意进率为60．【详解】解：根据题意2901896058253135'''∠=︒-∠=︒-︒=︒．故选：B ．5．【答案】D【分析】本题考查角的有关计算，按比例分配求出45BOC ∠=︒是解答的关键．根据:2:3AOB BOC ∠∠=求出45BOC ∠=︒，然后利用AOC AOB BOC ∠=∠+∠求解即可．【详解】解：∠:2:3AOB BOC ∠∠= 30AOB ∠=︒∠45BOC ∠=︒∠75AOCAOB BOC ．故选：D ．6．【答案】A【分析】本题主要考查了几何图形中角度的计算，角平分线的定义，先由角平分线的定义得到12224BOP AOP AOB AOP =∠=︒==︒∠，∠∠，再由已知条件得到248BOC AOB ∠=∠=︒，则60POC BOC BOP =+=︒∠∠∠． 【详解】解：∠OP 平分AOB ∠ 12AOP ∠=︒∠12224BOP AOP AOB AOP =∠=︒==︒∠，∠∠∠248BOC AOB ∠=∠=︒∠60POC BOC BOP =+=︒∠∠∠7．【答案】A【分析】分别求出平面镜转动前后反射光线与入射光线的夹角，再对两者进行比较即可得到解答．【详解】解：入射光线与平面镜的夹角是40°，所以入射角为90°−40°=50°．根据光的反射定律，反射角等于入射角，反射角也为50°所以入射光线与反射光线的夹角是100° ．入射角减小20°，变为50°−20°=30°，所以反射角也变为30°此时入射光线与反射光线的夹角为60°．则反射光线与入射光线间的夹角和原来比较将减小40°．故选：A ．【点睛】本题考查角度与光反射的综合应用，熟练掌握光的反射规律及角度的计算方法是解题关键． 8．【答案】A 【分析】本题考查了角度的计算，角的数量问题，根据题意可得每一个小角的度数为15α，进而将所有角的度数相加即可求解．【详解】∠四条射线五等分AOB ∠∠每个小角的度数为15α．如图图中所有锐角的和为()()AOC COD DOE EOF BOF AOD COE DOF BOE ∠+∠+∠+∠+∠+∠+∠+∠+∠+()()AOE COF BOD AOF BOC AOB ∠+∠+∠+∠+∠+∠=123454325555ααααα⨯+⨯+⨯+⨯+ 7α=故选：A ．9．【答案】＜【分析】将∠1进行换算，再和∠2比较即可判断大小．【详解】解：∠0.45°=27′∠∠1=30.45°=30°+0.45°=30°27′∠∠2=30°28′∠∠1＜∠2．故答案为：＜．【点睛】本题主要考查度分秒的换算，换成形式一样的即可比较大小．10．【答案】158︒【分析】根据角的和差关系求解即可；【详解】由题意得：90COD ∠=︒ 90AOB ∠=︒∠22AOD ∠=︒∠902268AOC COD AOD ∠=∠-∠=︒-︒=︒∠6890158BOC AOC AOB ∠=∠+∠=︒+︒=︒故答案为：158︒【点睛】本题主要考查角的和差关系，熟练掌握角的和差关系是解此类题的关键．11．【答案】133【分析】本题考查了几何图形中角度计算问题，结合图形得出AOC AOB BOC ∠=∠+∠，代数进行计算，得出x 的值，然后把x 的值代入()27AOC x ∠=-︒进行计算，即可作答．【详解】解：∠()585AOB BOC x ∠=︒∠=+︒， ()27AOC x ∠=-︒ 且AOC AOB BOC ∠=∠+∠∠()()27585x x -︒=︒++︒∠70x =则把70x =代入()27AOC x ∠=-︒∠133AOC ︒∠=故答案为：133．12．【答案】800【分析】本题考查了方位角，线段的和差，角的和差，由方位角的定义得40AOD BOC ∠=∠=︒，由角的和差得 180AOD DOE BOE ∠+∠+∠=︒，可得A 、O 、B 三点在同一条直线上，由线段的和差即可求解；理解方位角，会判断三点共线时是解题的关键．【详解】解：如图由题意得：40AOD BOC ∠=∠=︒90DOE ∠=︒500OA =300OB =9040BOE ∴∠=︒-︒50=︒AOD DOE BOE ∴∠+∠+∠409050=︒+︒+︒180=︒∴A 、O 、B 三点在同一条直线上AB OA OB ∴=+500300=+800=(米)故答案：800．13．【答案】20AON COM ∠+︒=∠ 【分析】本意考查了角的计算，根据87COD AOC ∠=∠，设78AOC x COD x ∠=∠=，，由180AOC COD BOD ∠︒+∠+∠=可求出x 的值，再由AON MON AOC COM ∠+∠=∠+∠即可得出答案．【详解】解：设78AOC x COD x ∠=∠=，由180AOC COD BOD ∠︒+∠+∠=7830180x x ∴++︒=︒10x ∴=︒即7080AOC COD ∠=︒∠=︒，AON MON AOC COM ∠+∠=∠+∠9070AON COM ∴∠+︒=︒+∠即20AON COM ∠+︒=∠故答案为：20AON COM ∠+︒=∠．14．【答案】(1)10955'︒(2)62.8︒【分析】本题考查了度分秒的换算，熟练掌握度分秒的进制是解题的关键．（1）根据度分秒的进制进行计算，即可解答；（2）根据度分秒的进制进行计算，即可解答．【详解】（1）89352020''︒+︒10955'=︒；（2）123246036''︒-︒123.460.6=︒-︒62.8=︒．15．【答案】(1)1290∠+∠=︒(2)54︒【分析】本题主要考查了角平分线的有关计算，平行线的判定以及性质，平角的定义，掌握这些定义以及性质是解题的关键．（1）由角平分线的定义得出11,22AOC COE BOD DOE ∠=∠∠=∠，由平角的定义得出180COE DOE ∠+∠=°，进而得出90AOC BOD ∠+∠=︒，再证明AB CD ∥，由平行线的性质可得出12AOC BOD ∠=∠∠=∠，，等量代换可得出1290∠+∠=︒．（2）由角平分线的定义和平行线的性质得出122BOD BOG DOG ∠=∠=∠=∠，设2x ∠=，则3323x ∠=∠=．根据平角的定义得出3180DOG ∠+∠=︒，代入计算得出2∠的度数，再根据（1）可求出1∠的度数．【详解】（1）证明OA ，OB 分别平分COE ∠和DOE ∠11,22AOC COE BOD DOE ∴∠=∠∠=∠． 180COE DOE ∠+∠=︒．()1111180902222AOC BOD COE DOE COE DOE ∴∠+∠=∠+∠=∠+∠=⨯︒=︒． 3OGB ∠=∠AB CD ∴∥．12AOC BOD ∴∠=∠∠=∠，．2190∴∠+∠=︒（2）OB 平分DOE ∠ AB CD ∥122BOD BOG DOG ∴∠=∠=∠=∠． 设2x ∠=，则3323x ∠=∠=．3180DOG ∠+∠=︒即32180x x +=︒解得36x =︒236∴∠=︒．1903654∴∠=︒-︒=︒16．【答案】(1)90︒ (2)2703BON α∠=-【分析】本题主要考查了角平分线的相关计算和角的和差倍分、解一元一次方程； （1）根据平角的定义，角的平分线的意义计算即可；（2）设设BON x ∠=︒，则13COM x α∠=-︒，由OM 平分AOC ∠得到1223AOC MOC x α⎛⎫∠=∠=-︒ ⎪⎝⎭，根据180AOC BON CON ∠+∠+∠=︒列方程解方程即可得到答案．【详解】（1）解：∠OM 平分AOC ∠，ON 平分BOC ∠ ∠12MOC AOC ∠=∠ 12CON BOC ∠=∠ ∠1()2MOC CON AOC BOC ∠+∠=∠+∠ ∠111809022MON AOB ∠=∠=⨯︒=︒． （2）设BON x ∠=︒ ∠1133CON BON x ∠=∠=︒ MON α∠= ∠13COM x α∠=-︒ ∠OM 平分AOC ∠ ∠1223AOC MOC x α⎛⎫∠=∠=-︒ ⎪⎝⎭ ∠180AOC BON CON ∠+∠+∠=︒ ∠11218033x x x α⎛⎫-++= ⎪⎝⎭ ∠2703x α=-∠2703BON α∠=-．。