下载文档原格式
齿轮机构(Gears)是现代机械中应用最广泛的一种传动机构，与其它传动机构相比，齿轮机构的优点是：结构紧凑，工作可靠，效率高，寿命长，能保证恒定的传动比，适用的范围广。
齿轮机构可以分为定传动比齿轮机构和变传动比齿轮机构。
本章仅讨论定传动比的齿轮机构。
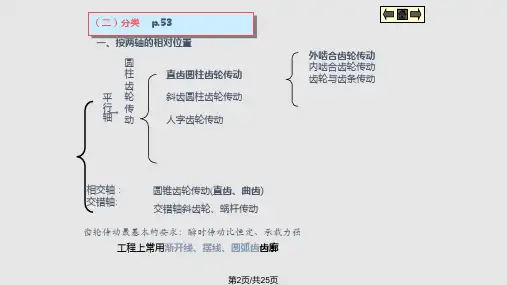
齿轮机构的类型很多，根据其传动轴线的相对位置，它可分为三类：1、平行轴齿轮机构(Gears with Parallel Axes)两齿轮的传动轴线平行，这是一种平面齿轮机构，如表5-1所示。
它可分为：外啮合齿轮机构（有直齿轮、斜齿轮和人字齿轮传动三类）内啮合齿轮机构（有直齿轮和斜齿轮传动两类）齿轮齿条机构（有直齿条和斜齿条传动两类）点击表中图形，观察各类齿轮传动的运动特点和齿形。
表5-1 平行轴齿轮机构2、相交轴齿轮机构(Gears with Intersecting Axes)两齿轮的传动轴线相交于一点，这是一种空间齿轮机构，如表5-2所示。
它有直齿圆锥齿轮传动、斜齿圆锥齿轮传动和曲线齿圆锥齿轮传动。
表5-2 相交轴齿轮机构ff3、交错轴齿轮机构(Gears with Skew Axes)两齿轮的传动轴线为空间任意交错位置，它也是空间齿轮机构，如表5-3所示。
表5-3 交错轴齿轮机构此外，还有实现变传动比运动的非圆齿轮机构(Non-circular Gear)，如下图所示。
图5-2一、斜齿圆柱齿轮齿廓曲面的形成渐开线直齿齿廓曲面的生成原理如图5-33a 所示，发生面S在基圆柱上作纯滚动时，其上与基圆柱母线平行的直线KK所展成的渐开面即为直齿轮的齿面。
(a) (b) (c)图5-33斜齿轮的齿面形成原理如图5-34a所示，发生面S 沿基圆柱纯滚动时，其上一条与基圆柱母线呈βb角的直线KK所展成的渐开螺旋面就是斜齿轮的齿廓曲面。
(a) (b) (c)图5-34一对直齿轮啮合时，齿面的接触线与齿轮的轴线平行（图5-33b），而一对斜齿轮啮合时，齿面接触线是斜直线（图5-34b），接触线先由短变长，而后又由长变短，直至脱离啮合。
齿轮机构及其设计齿轮机构是现代机械中应用最广泛的一种传动机构。
与其它传动机构相比，齿轮机构的优点是结构紧凑，工作可靠，效率高，寿命长，能保证恒定的传动比，而且其传动的功率与适用的速度范围达。
但是，其制造安装费用较高，及精度齿轮传动的振动噪声较大。
齿轮机构根据实现传动比的情况，分为定传动比和变传动比齿轮机构。
定传动比的圆形齿轮机构根据两传动轴线的相对位置，可分三类：平行轴齿轮机构（两齿轮的传动轴线平行）、相交轴齿轮机构（两齿轮的传动轴线相较于一点）、交错轴齿轮机构（两齿轮的传动轴线为空间任意交错位置）。
1.瞬时传动比两齿轮的传动比总等于齿数的反比，即n1/n2=z2/z1，但其瞬时传动比却与齿廓的形状有关。
按三心定理，公法线n-n与二齿轮连心线的交点C为二齿轮的相对速度瞬心，即二齿轮在C点的线速度应相等：ω1 O1C=ω2 O2C，由此得瞬时传动比і12：і12= ω1/ω2= O2C/ O1C=r2/r1该式说明，具有任意齿廓的二齿轮啮合时，其瞬时角速度的比值等于齿廓接触点公法线将其中心距分成两段长度的反比。
这就是齿廓啮合基本定律。
满足齿廓啮合基本定律的传动比为常数或按一定规律变化的一对齿廓称为共轭齿廓。
在齿轮机构中，相对速度瞬心C称为啮合节点，简称节点。
为实现定传动比传动，要求两齿廓在任何位置啮合时，其节点C都为中心线上的一个固定点，分别以O1、O2为圆心、以O1C 和O2C为半径的圆C1和C2，称为齿轮的节圆（注意非分度圆）。
故节圆是齿轮的相对瞬心线，齿轮的啮合传动相当于其两节圆作无滑动的纯滚动。
2.渐开线圆柱齿轮及其基本齿廓1）齿轮的各部分名称•齿顶圆（直径d a）•齿根圆（直径d f）•齿厚（分度圆处s，任意圆周处sі）•齿槽宽（分度圆处e，任意圆周处eі）•齿距（分度圆处p，任意圆周处pі=sі+eі）•分度圆（直径d，规定标准齿轮分度圆上的齿厚s与齿槽宽e相等，即s=e=1/2 p）•齿顶高（齿顶部分的径向高度h a）•齿根高（齿根部分的径向高度h f）•全齿高（齿顶圆与齿根圆之间的径向距离，h=h a+h f）。
齿轮机构的工作原理特点
齿轮机构是一种常见的传动机构，它通过齿轮之间的啮合传递动力和运动。
其工作原理和特点如下：
工作原理：
1. 齿轮之间通过齿间啮合产生传动关系，其中一个齿轮称为驱动齿轮，另一个齿轮称为从动齿轮。
2. 当驱动齿轮转动时，齿轮的齿将从动齿轮的齿牙推动，使从动齿轮一起转动。
3. 齿轮大小不同会产生不同的转动速度和转矩比例。
特点：
1. 高传动效率：齿轮机构由于齿间啮合的特性，传动效率较高，通常可以达到95%以上。
2. 稳定的传动比：齿轮机构具有固定的传动比，可以准确地传递动力和运动。
3. 半径间隙传动：齿轮机构是通过齿间啮合进行传动，相对于其他摩擦传动方式，如皮带传动或链条传动，其传动性能更为稳定可靠。
4. 不可逆转性：常见的齿轮机构是通过大齿轮驱动小齿轮，所以在实际应用中很难出现从动齿轮推动驱动齿轮转动的情况，具有一定的不可逆性。
5. 较大的体积和重量：齿轮机构由于齿轮本身的特点，需要一定的空间和材料来实现传动，所以相对来说有一定的体积和重量。
总的来说，齿轮机构具有高效率、稳定的传动比和靠谱的传动性能，在机械传动
领域中得到广泛应用。
了解齿轮机构的类型及应用齿轮机构是一种由齿轮组成的传动装置，广泛应用于各个行业中，它的类型和应用也非常多样。
下面我将详细介绍齿轮机构的几种主要类型和常见的应用。
一、齿轮机构的类型1. 平行轴齿轮机构：平行轴齿轮机构是指齿轮的轴线平行排列的一种传动形式。
常见的平行轴齿轮机构有直齿轮、斜齿轮、锥齿轮等。
其中，直齿轮是最常见的，适用于传递轴上速比不变或接近1的场合；斜齿轮适用于不平行的轴系，可以实现轴线间的交角传动；锥齿轮适用于轴线交叉或交叉变位的场合。
2. 交叉轴齿轮机构：交叉轴齿轮机构是指齿轮轴线相交或交叉的传动形式。
常见的交叉轴齿轮机构有交叉齿轮、曲柄齿轮机构等。
其中，交叉齿轮机构是一种常见的齿轮传动形式，适用于平行齿轮轴和能够传递大扭矩的场合；曲柄齿轮机构适用于输出轴速度或转矩要求变化的场合。
3. 锁定齿轮机构：锁定齿轮机构是指通过锁止装置将齿轮固定不动的传动形式。
常见的锁定齿轮机构有钩齿轮机构、棘轮机构等。
其中，钩齿轮机构适用于以连续运动为主且随时可以切换的场合；棘轮机构适用于需要间歇工作的场合。
4. 齿条齿轮机构：齿条齿轮机构是一种由齿条和齿轮组成的传动形式，齿条的传输方式为直线传输，齿轮则将旋转运动转换为直线运动。
齿条齿轮机构适用于需要直线运动的场合，如升降设备、翻盖机构等。
二、齿轮机构的应用1. 汽车行业：齿轮机构在汽车行业中有着广泛的应用，常见的应用场景包括变速器、差速器、传动轴等。
通过不同类型的齿轮组合，实现不同速比和扭矩的变化，从而实现车辆行驶过程中的高、低速变换和转向控制。
2. 机械设备：齿轮机构在机械设备中起到传动力、速度和转矩变换的作用。
比如，工厂中的机床设备、输送机、提升设备等都广泛使用齿轮机构来实现驱动和传动。
3. 电力传动：齿轮机构在发电厂、输电线路等电力传动领域中也有着重要的应用。
例如，发电机组中的主动齿轮与发动机相连，通过齿轮传动转化为电能。
4. 航空航天：在航空航天领域，由于其重量轻、强度高和可靠性好的特点，齿轮机构被广泛应用于飞行器的起落架、引擎传动等关键部件中。
第五章齿轮机构案例导入：通过机床、汽车、摩托车、手表等仪器设备中广泛应用的齿轮传动，引入齿轮传动的类型、特点及基本要求、齿轮传动啮合的特点。
在所有众多的齿轮机构中，直齿圆柱齿轮机构是最基本、也是最常用的一种，本章以直齿圆柱齿轮为研究的重点。
第一节齿轮机构的齿廓啮合基本规律、特点和类型一、齿轮机构的特点和类型齿轮传动是近代机械传动中用得最多的传动形式之一。
它不仅可用于传递运动，如各种仪表机构；而且可用于传递动力，如常见的各种减速装置、机床传动系统等。
同其他传动形式比较，它具有下列优点：①能保证传动比恒定不变；②适用的载荷与速度范围很广，传递的功率可由很小到几万千瓦，圆周速度可达150m/s；③结构紧凑；④效率高，一般效率η＝～；⑤工作可靠且寿命长。
其主要缺点是：①对制造及安装精度要求较高；②当两轴间距离较远时,采用齿轮传动较笨重。
齿轮的分类方法很多，按照两轴线的相对位置，可分为两类：平面齿轮传动和空间齿轮传动。
a) b) c)d) e)图5-1 平面齿轮传动1.平面齿轮传动该传动的两轮轴线相互平行，常见的有直齿圆柱齿轮传动（图5-1a）,斜齿圆柱齿轮传动（图5-1d），人字齿轮传动（图5-1e）。
此外，按啮合方式区分，前两种齿轮传动又可分为外啮合传动（图5-1a、d）,内啮合传动（图5-1b）和齿轮齿条传动（图5-1c）。
2.空间齿轮传动两轴线不平行的齿轮传动称为空间齿轮传动，如直齿圆锥齿轮传动（图5-2a ）、交错轴斜齿轮传动（图5-2b ）和蜗杆传动(图5-2c ）。
另外，齿轮传动按照齿轮的圆周速度可分为：①低速传动 v < 3m/s ；②中速传动 v =3～15m/s ，(3)高速传动v >15m/s 。
按齿轮的工作情况可以分为：①开式齿轮传动；②闭式齿轮传动。
二、齿轮啮合的基本规律齿轮传动最基本的要求是其瞬时传动比必须恒定不变。
否则当主动轮以等速度回转时，从动轮的角速度为变数，因而产生惯性力，影响齿轮的寿命，同时也引起振动，影响其工作精度。
要满足这一基本要求，则齿轮的齿廓曲线必须符合一定的条件。
图5-3所示为两啮合齿轮的齿廓C 1和C 2在K 点接触的情况，设两轮的角速度分别为ω1和ω2，则齿廓C 1上K 点的速度k o v K 111ω=；齿廓C 2上K 点的速度k o v K 222ω=。
过K 点作两齿廓的公法线NN 与两轮中心连线21o o 交于C 点，为保证两轮连续和平稳的运动，v k 1与v k 2在公法线上得分速度应相等，否则两齿廓将互相嵌入或分离，即2211cos cos K K K K v v αα=过2o 作z o 2平行于NN ，与k o 1的延长线交于Z 点，因kab ∆∽z ko 2∆，于是有a) b) c)图5-2 空间齿轮传动图5-3 齿廓啮合基本定律k o k o v v ka kb k o kz K K 2211212ωω=== 经整理有 211ωω=k o kz 又因为NN ∥O 2Z ，故△O 1O 2Z ∽△O 1CK ，得c o c o k o kz 121= 故传动比可写为 co c o i 122112==ωω （5-1） 上式表明：两轮的角速度之比与连心线被齿廓接触点的公法线分得的两线段成反比。
由此可见，要使两轮的角速度比恒定不变，则应使c o c o 12恒为常数。
但因两轮的轴心为定点，即21o o 为定长，故欲使齿轮传动得到定传动比，必须使C 点成为连心线上的一个固定点。
此固定点称为节点。
因此，齿廓的形状必须符合下述条件：不论轮齿齿廓在哪个位置接触，过接触点所作齿廓公法线均须通过节点C,这就是齿廓啮合的基本定律。
理论上，符合上述条件的齿廓曲线有无穷多，但齿廓曲线的选择应考虑制造、安装和强度等要求。
目前，工程上通常用的曲线为渐开线、摆线和圆弧。
由于渐开线齿廓易于制造，故大多数的齿轮都是用渐开线作为齿廓曲线。
本章只讨论渐开线齿轮传动。
如图5-3所示分别以1o 和2o 为圆心，过节点C 所作的圆称为齿轮的节圆，其半径c o 1和c o 2称为节圆半径，分别用'1r 和'2r 表示。
由式（5-1）有c o c o 2211ωω=即通过节点的两节圆具有相同的圆周速度，它们之间作纯滚动。
第二节 渐开线齿廓一、渐开线的形成和性质当一条直线L 沿一圆周作纯滚动时，此直线上任一点K 的轨迹即称为该圆的渐开线,如图5-4所示。
该圆称为渐开线的基圆，基圆半径以br 表示，该直线 L 称为渐开线的发生线。
根据渐开线形成过程可知它具有下列特性：(1)因发生线在基圆上作无滑动的纯滚动，故发生线所滚过的一段长度必等于基圆上被滚过的圆弧的长度。
(2)当发生线沿基圆作纯滚动时，N 点为速度瞬心，K 点的速度垂直于NK ，且与渐开线K 点的切线方向一致，所以发生线即渐开线在K 点的法线。
又因NK 线切于基圆，所以渐开线上任一点的法线必与基圆相切。
图5-4 渐开线的形成此外，N 点为渐开线上K 点的曲率中心，线段NK 为渐开线上K 点的曲率半径。
显然，渐开线愈接近基圆部分，其曲率半径愈小，即曲率愈大。
(3)渐开线的形状完全决定于基圆的大小。
基圆大小相同时，所形成的渐开线相同。
基圆愈大渐开线愈平直，当基圆半径为无穷大时，渐开线就变成一条与发生线垂直的直线(齿条的齿廓)。
(4)基圆以内无渐开线。
齿轮啮合传动时，渐开线上任一点法线压力的方向线F n (即渐开线在该点的法线)和该点速度方向K v 之间所夹锐角称为该点的压力角K α。
由图可知：K b K r r OK ON ==αcos （5-2）上式表明渐开线上各点的压力角K α的大小随K 点的位置而异，K 点距圆心愈远，其压力角愈大；反之，压力角愈小；基圆上的压力角为零。
二、 渐开线齿廓啮合特点1.中心距可分性图5-5所示两渐开线齿轮的外啮合情况，节点为C ，两齿轮的基圆半径分别为1b r 和2b r ，与两基圆的内公切线N 1N 2构成一对相似三角形△O 1N 1C 和△O 2N 2C ，由相似三角形的性质和式（5-1）知两齿轮的传动比为12122112b b r r c o c o i ===ωω （5-3） 可见渐开线齿轮的传动比取决于两齿轮基圆半径的大小，当一对渐开线齿轮制成后，两齿轮的基圆半径就确定了，即使安装后两齿轮中心距稍有变化，由于两齿轮基圆半径不变，所以传动比仍保持不变。
渐开线齿轮这种不因中心距变化而改变传动比的特性称为中心距可分性。
这一特性可补偿齿轮制造和安装方面的误差，是渐开线齿轮传动的一个重要优点。
2.啮合线为直线两齿轮啮合时，其接触点的轨迹称为啮合线，由渐开线特性可知，两渐开线齿廓在任何位置接触时，过接触点所作两齿廓的公法线即为两基圆的内公切线N 1N 2，故接触点的轨迹必然在这内公切线上。
所以，其啮合线是唯一直线。
过节点C 作两节圆的公切线t t ，它与啮合线所夹的锐角称为啮合角。
通常用α'来表示。
第三节 渐开线标准齿轮各部分名称、参数和几何尺寸一、齿轮各部分名称图5-6所示为一直齿圆柱齿轮的一部分，相邻两齿的空间称为齿间。
齿间底部连成的圆称为齿根圆，直径用d f 表示。
连接齿轮各齿顶的圆称为齿顶圆，直径用d a 表示。
图5-5 渐开线齿轮的啮合在任意直径为d K 的圆周上，一个轮齿左右两侧齿廓的弧长称为该圆上的齿厚，用s k 表示；而一齿间的弧长称为该圆上的齿槽宽，用e k 表示；相邻两齿对应点之间的弧线长称为该圆上的齿距，用p k 表示，p k = e k + s k 。
二、主要参数设K d 为任意圆的直径，z 为齿数，根据齿距的定义可得 z d p K K π= 或 z p d K K π= ( 5-4 ) 上式中含有无理数“π”，为了便于设计、制造及互换使用，在齿轮上取一基准圆，使该圆周上的πp K比值等于一些较简单的数值，并使该圆上的压力角等于规定的某一数值，该圆称为分度圆，其直径用d 表示，分度圆上的压力角以α表示之，我国采用ο20为标准值。
显然有分度圆直径z pd π=，我们把比值π/p 规定为标准值，用m 来表示，称为模数，单位为mm 。
于是分度圆上的齿距p 和直径d 分别为m p π=(mm) (5-5) mz d =(mm) (5-6)模数是齿轮尺寸计算中的一个基本参数，模数愈大，则齿距愈大，轮齿也就愈大，轮齿的抗弯能力愈强。
齿轮模数已标准化，我国常用的标准模数见表5-1。
表5-1 常用的标准模数m （摘自GB/T1357-87）第一系列 1 2 3 4 5 68 10 12 16 20 25 32 40 50第二系列79 (11) 14 18 22 28 36 45 注：①本表适用于渐开线圆柱齿轮。
对斜齿轮是指法向模数。
优先采用第一系列，括号内的数尽量不用。
②圆锥齿轮大端模数除了可在上表中选取外，还可选、等。
对于任一轮齿，其齿顶圆与分度圆间的部份称为齿顶，它沿半径方向的高度称为齿顶高，用h a 表示；而齿根圆与分度圆间的部分称为齿根，它沿半径方向的高度称为齿根高，用h f 表示；齿顶圆与齿根圆间沿半径方向的高度称为全齿高，用h 表示，因此，h = h a + h f （5-7）设计中，将模数m 作为齿轮各部分几何尺寸的计算基础，因此，齿顶高可表示为h a =h a *m ，齿根高可表示为h f =(h a *+c *)m ，其中，h a *称为齿顶高系数，c * 称为顶隙系数。
它们有两种标准数值正常齿 h a *= 1, c *=短齿 h a *= , c *=图5-6 齿轮的几何尺寸凡模数、压力角、齿顶高系数与顶隙系数等于标准数值，且分度圆上齿厚与齿槽宽 相等的齿轮称为标准齿轮。
因此，对于标准齿轮s = e =22m p π= (5-8) 对于一对模数、压力角相等的标准齿轮，由于其分度圆上的齿厚与齿槽宽相等，因此，正确安装时分度圆与节圆重合，可看成两轮的分度圆相切作纯滚动。
标准齿轮的这种安装称为标准安装，其中心距称为标准中心距。
对于单个齿轮而言，节圆、啮合角都是不存在的，只有当一对齿轮互相啮合时，节圆和啮合角才有意义。
这时，节圆可能和分度圆重合，也可能不重合，须视两齿轮的安装是否正确而定。
对于正确安装的一对齿轮，其啮合角'α等于分度圆上的压力角α。
三、标准直齿圆柱齿轮的几何尺寸标准直齿圆柱齿轮的几何尺寸按表5-2进行计算。
表5-2 标准直齿圆柱齿轮各部分尺寸的几何关系例5-1 已知一正常齿制的标准直齿圆柱齿轮，齿数z 1=20，模数m = 2mm ，拟将该齿轮作某外啮合传动的主动齿轮，现须配一从动齿轮，要求传动比i =，试计算从动齿轮的几何尺寸及两轮的中心距。
解：根据给定的传动比i ，可计算从动轮的齿数z 2 = i z 1 =× 20 = 70已知齿轮的齿数z 2及模数m ，由表5-2所列公式可以计算从动轮各部分尺寸。
