牛顿后插公式

数值计算实验二姓名:方小开学号:20060810202 班级:计科0602一. 实验目的：1、差分的matlab实现；2、Newton插值的matlab实现；二. 实验原理：MATLAB在线性代数，矩阵分析，数值及优化，数理统计和随机信号分析，电路系统，系统动力学，信号与图像处理，控制理论分析和系统设计，过程控制，建模和仿真，通信系统，等有广泛的应用。

它具有功能强大，界面友好，语言自然即开放性等特点。

三．试验环境MATLAB7.0四. 试验过程及现象：1、牛顿插值公式：把下面的matlab程序在matlab中建立M-file文件并保存；function [d,v1]=newtonjz(x,y,v) %d 插商表 v是要插入x v1是插入的y值n=length(x);d=zeros(n,n);d(:,1)=y';for j=2:nfor i=j:nd(i,j)=(d(i,j-1)-d(i-1,j-1))/(x(i)-x(i-j+1));endendw=1;v1=d(1,1);for i=2:nw=w*(v-x(i-1));v1=v1+d(i,i)*w;end分别给x,y赋初值，并调用Newton插值函数得到结果如下：x=[0.40,0.55,0.65,0.80,0.90,1.05];y=[0.41075,0.57815,0.69675,0.88811,1.02652,1.25382];[z,xy]=newtonjz(x,y,0.596);z =0.4108 0 0 0 0 00.5782 1.1160 0 0 0 00.6967 1.1860 0.2800 0 0 00.8881 1.2757 0.3589 0.1973 0 01.0265 1.3841 0.4335 0.2130 0.0312 01.2538 1.5153 0.5249 0.2287 0.0314 0.0003xy =0.63192Newton前插公式：把Newton前插公式的matlab程序写在matlab中建立M-file文件并保存；function [d,v1]=newtonBefore(x,y,t)n=length(x);d=zeros(n,n);d(:,1)=y';for j=2:nfor i=1:n-j+1d(i,j)=(d(i+1,j-1)-d(i,j-1));endendw=1;m=1;v1=d(1,1);for i=2:nw=w*(t-i+2);m=m*(i-1);v1=v1+d(1,i)*(w/m);end分别给x,y赋初值，并调用Newton前插函数得到结果如下；x=[1 1.05 1.10 1.15 1.20 1.25 1.30];y=[1 1.0247 1.04881 1.07238 1.09544 1.11803 1.14017];>> [z,qc]=newtonBefore(x,y,0.2);qc =1.004992263808003、Newton后插公式：把Newton后插公式的matlab程序写在matlab中建立M-file文件并保存；function [d,v1]=newtonAfter(x,y,t)n=length(x);d=zeros(n,n);d(:,1)=y';for j=2:nfor i=j:nd(i,j)=(d(i,j-1)-d(i-1,j-1));endendw=1;m=1;v1=d(1,1);for i=2:nw=w*(t+i-2);m=m*(i-1);v1=v1+d(n,i)*(w/m);end分别给x,y赋初值，并调用Newton后插函数得到结果如下；x=[1 1.05 1.10 1.15 1.20 1.25 1.30];y=[1 1.0247 1.04881 1.07238 1.09544 1.11803 1.14017];>> [z,hc]=newtonAfter(x,y,-0.4);hc=1.13136982835200五．遇到的问题在调试的过程中也遇到了一些小小的问题，如输出的结果只显示4位有效数字，结果的精度太低了，不能满足要求，因此在matlab中把数据的格式从short型改成了long型，这样就大大的提高了结果的精确度，减少了误差。

牛顿法代数插值ndash 差商表的求法原文地址：牛顿法代数插值–差商表的求法作者：大关牛顿法代数插值–差商表的求法下面的求插商的方法并不是好的求插商的方式，因为他的效率并不是很高，不论是从空间效率还是时间效率，但是下面主要探讨的是一种将塔形的数据转换成一位数组的方式。

实际上求插商仅通过一个n个元素的一位数组就能解决，但本文强调的是一种思路，希望对大家有所借鉴。

牛顿插商公式：f[xi,xj]=(f(xj)– f(xi))/(xj– xi)f[xi,xj,xk]=(f[xj,xk]– f[xi,xj])/(xk– xi)….f[x0,x1,x2…,xn]=(f[x1,x2,…,xn]– f[x0,x1,…,xn-1])/(xn– x0)转换成均插表(或称差商表)形式如下：定义1：f[xi,xi+1,…xj]简记为f(i,j)其中i=0&&i=n&&j=0&&j=n&&i j；记f(xi)为f[xi,xi]即f(i,i)根据定义1可以推出：f[x0,x1]=f(0,1),f[x0,x1…xn]=f(0,n)….根据定义1：可以将插商表转换为如下形式。

根据上图，可以给出实际一维数组存储时的序列关系，如下图所示：此时f(0,0)位置是数组下标0，f(1,1)是数组下标为1….这样，我们从中找出相应的规律。

推论1：已知f(i,j)，n为变量的数目，令k=j– i。

当k不等于0时，f(i,j)在数组中的下标通过计算得：Index=k*n–((k-1)*k)/2+i当k等于0时Index=i。

推论1很容易证明(实际就是一个等差数列求和问题)这里证明略。

推论2：n为变量的数目，则一维数组的长度可以计算得((1+n)*n)/2推论2可以通过等差数列求和得以证明。

证明略。

推论3：各阶插商就是f(0,k)k=1,2….n.推论3：根据插商的定义和定义1可以直接推出。

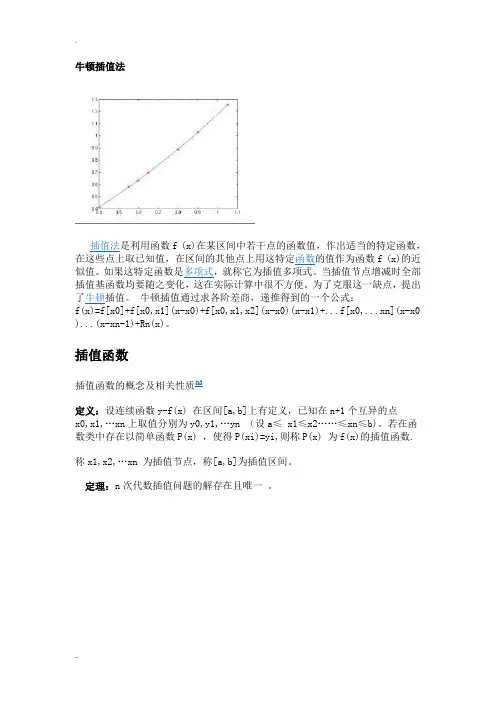
牛顿插值法插值法是利用函数f (x)在某区间中若干点的函数值，作出适当的特定函数，在这些点上取已知值，在区间的其他点上用这特定函数的值作为函数f (x)的近似值。

如果这特定函数是多项式，就称它为插值多项式。

当插值节点增减时全部插值基函数均要随之变化，这在实际计算中很不方便。

为了克服这一缺点，提出了牛顿插值。

牛顿插值通过求各阶差商，递推得到的一个公式：f(x)=f[x0]+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x-x1)+...f[x0,...xn](x-x0 )...(x-xn-1)+Rn(x)。

插值函数插值函数的概念及相关性质[1]定义：设连续函数y-f(x) 在区间[a,b]上有定义，已知在n+1个互异的点x0,x1,…xn上取值分别为y0,y1,…yn （设a≤ x1≤x2……≤xn≤b)。

若在函数类中存在以简单函数P(x) ，使得P(xi)=yi,则称P(x) 为f(x)的插值函数.称x1,x2,…xn 为插值节点，称[a,b]为插值区间。

定理：n次代数插值问题的解存在且唯一。

牛顿插值法C程序程序框图#include<stdio.h>void main(){float x[11],y[11][11],xx,temp,newton;int i,j,n;printf("Newton插值:\n请输入要运算的值:x=");scanf("%f",&xx);printf("请输入插值的次数(n<11):n=");scanf("%d",&n);printf("请输入%d组值:\n",n+1);for(i=0;i<n+1;i++){ printf("x%d=",i);scanf("%f",&x[i]);printf("y%d=",i);scanf("%f",&y[0][i]);}for(i=1;i<n+1;i++)for(j=i;j<n+1;j++){ if(i>1)y[i][j]=(y[i-1][j]-y[i-1][j-1])/(x[j]-x[j-i]);elsey[i][j]=(y[i-1][j]-y[i-1][j-1])/(x[j]-x[j-1]);printf("%f\n",y[i][i]);}temp=1;newton=y[0][0];for(i=1;i<n+1;i++){ temp=temp*(xx-x[i-1]);newton=newton+y[i][i]*temp;}printf("求得的结果为:N(%.4f)=%9f\n",xx,newton);牛顿插值法Matlab程序function f = Newton(x,y,x0)syms t;if(length(x) == length(y))n = length(x);c(1:n) = 0.0;elsedisp(&apos;x和y的维数不相等！&apos;);return;endf = y(1);y1 = 0;l = 1;for(i=1:n-1)for(j=i+1:n)y1(j) = (y(j)-y(i))/(x(j)-x(i));endc(i) = y1(i+1);l = l*(t-x(i));f = f + c(i)*l;simplify(f);y = y1;if(i==n-1)if(nargin == 3)f = subs(f,&apos;t&apos;,x0);elsef = collect(f); %将插值多项式展开f = vpa(f, 6);endend牛顿插值法摘要：值法利用函数f (x)在某区间中若干点的函数值，作出适当的特定函数，在这些点上取已知值，在区间的其他点上用这特定函数的值作为函数f (x)的近似值。

2012-2013（1）专业课程实践论文牛顿后插公式王瑜，0818180218，R数学08-2班一、算法理论由牛顿前插公式)()!1())...(1()()1(1ξ+++--=n a n n f h n n t t t x R ，),(0n x x ∈ξ如果要求表示函数在n x 附近的值)(x f ，此时应用Newton 插值公式，插值点应按的次序排列，有)()](,,,[))(](,,[)](,[)()(1011211x x x x x x x f x x x x x x x f x x x x f x f x N n n n n n n n n n n n n n --++--+-+=----- 作变换)01(≤≤-+=t th x x n 错误！未找到引用源。

，并利用公式代入上式带入得n n n n n n n f n n t t t f t t f t f th x N ∇-++++∇++∇+=+!)1()1(!2)1()(2称为Newton 后插公式，其余项。

。

),(,)!1()()()1()()()(0)1(1n n n n n n x x n f h n t t t th x N x f x R ∈+++=+-=++ξξ 若用Newton 后插公式求)(x f 的值，因x 在n x 附近，则其系数)(x f 在点n x 的各阶向后差分。

二、算法框图结束判断是否继续输入提示是否继续输入输出结果判断输入区间合法性Input x 提示正确的X 区间信息开始是否是否三、算法程序class Interpolation{public:Interpolation(int num, double x1, double x2, double func[]);double ComputeBackwardValue(double x); // compute backward interpolation value ~Interpolation();private:// Check(); // checking the inputsvoid GetBackwardTable(); // get the backward differential tableprivate:int m_num; // the number of interpolation pointsdouble m_x1, m_x2; // the first point m_x1 and last point m_x2double m_step; // the interpolation stepdouble* m_func; // the function value of interpolation pointsdouble* m_btable; // the backward differential table};#include <iostream>#include <limits>using namespace std;#define NUM 15//样本个数#define MIN 4000//上面输入区间下限#define MAX 11000//上面输入区间上限int main(){double func[NUM]={1.38, 1.48, 1.58, 1.69, 1.81,1.94,2.10, 2.28, 2.50, 2.76,3.06, 3.41, 3.83,4.33, 4.93};//输入对应的函数值double x1=MIN, x2=MAX, x;int num=NUM;char flag='Y';Interpolation test(num, x1, x2, func);while(flag=='Y'){cout<<"Input x: ";cin>>x;if (!cin){cin.clear();cin.ignore(numeric_limits<int>::max(), '\n'); // clear input buffercontinue;}if(x<x1 || x>x2){cout<<"---Invalid input: "<<x<<"---"<<endl;cout<<"Only the number between "<<x1<<" and "<<x2<<" is valid..."<<endl; }else{cout<<"Backward interpolation value:"<<puteBackwardValue(x)<<endl;}cout<<endl<<"Do you want to process? please input(Y/N):"<<endl;cin>>flag;}return 0;}Interpolation::Interpolation(int num, double x1, double x2, double func[]) {m_num = num;m_x1 = x1;m_x2 = x2;m_step = (m_x2-m_x1)/(num-1);m_func = new double[m_num];m_btable = new double[m_num];for (int i=0; i<m_num; ++i){m_func[i] = func[i];m_btable[i] = func[i];}GetBackwardTable();}Interpolation::~Interpolation(){delete m_func;delete m_btable;}void Interpolation::GetBackwardTable(){// get the backward differential tableint i, j;double tmp;for (i=1; i<m_num; ++i) {tmp = m_btable[m_num-1];for (j=m_num-1; j>=i; --j) {m_btable[j] = m_btable[j]-m_btable[j-1];}m_btable[i-1] = tmp;}}double Interpolation::ComputeBackwardValue(double x){// compute backward interpolation valuedouble* coef; //coefficient talbedouble result, t;int i;coef = new double[m_num];t = (x-m_x2)/m_step;for (i=1, coef[0]=1; i<m_num; ++i) //compute the coefficient table {coef[i] = coef[i-1]*(t+i-1)/i;}for (i=0, result=0; i<m_num; ++i){result += m_btable[i]*coef[i];}delete coef;return result;}四、算法实现例1．在微电机设计计算中需要查磁化曲线表，通常给出的表如图是磁密B每间隔100高斯磁路每厘米长所需安匝数at的值，下面要解决B从4000到11000区间的查表问题书上给出的可以用后插公式的区间为10500＜B≤11000解：在此谨以10500以上的数为例，首先输入样本个数和所在区间然后逐一输入对应的函数值。