下载文档原格式
解一元三次方程专题---一元三次方程是指次数最高为三次的方程，通常的形式为：$$ax^3+bx^2+cx+d=0$$解一元三次方程的方法有多种，下面将介绍其中的几种常用方法。
---方法一：分离变量法分离变量法是一种常用的解一元三次方程的方法。
它的基本思想是将方程中的$x$和常数项用不同的符号表示，然后将方程化为两个关于不同变量的方程，进而求得解。
具体步骤如下：1. 将方程变形，使得方程右边为0。
2. 令$x=y-\frac{b}{3a}$，将原方程转化为以$y$为变量的形式。
3. 将变量分离，得到两个方程。
4. 解两个方程，得到$y$的值。
5. 将$y$的值代入$x=y-\frac{b}{3a}$，求得$x$的值。
注意：分离变量法只能得到方程的实数根。
---方法二：高斯消元法高斯消元法是解一元三次方程的另一种常用方法。
它的基本思想是通过变量替换和高斯消元的操作，将方程化为一个二次方程和一个一次方程，从而求得解。
具体步骤如下：1. 将方程变形，使得方程右边为0。
2. 令$u=x-\frac{b}{3a}$，将原方程转化为以$u$为变量的形式。
3. 减去方程两边的$d$，得到$u^3+pu+q=0$的形式。
4. 利用高斯消元法求解$u^3+pu+q=0$，得到$u$的值。
5. 将$u$的值代入$x=u-\frac{b}{3a}$，求得$x$的值。
注意：高斯消元法可以得到方程的实数根和复数根。
---方法三：牛顿迭代法牛顿迭代法是一种数值解法，可以用来解一元三次方程。
它的基本思想是通过迭代逼近的方式，不断改进初始值，从而求得解。
具体步骤如下：1. 将方程变形，使得方程右边为0。
2. 选取一个初始值$x_0$。
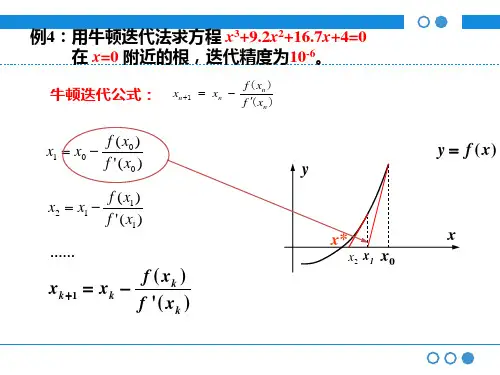
3. 根据牛顿迭代公式 $x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$，不断迭代，直到满足精确度要求或达到迭代次数。
4. 得到近似解。
注意：牛顿迭代法可以得到方程的实数根和复数根，但要求初始值选择得当。
《算法统宗》的三次方程三次方程是代数中重要的一类方程，其形式为ax^3 + bx^2 + cx +d = 0，其中a、b、c、d是已知的实数系数且a ≠ 0。
求解三次方程的过程较为复杂，需要运用多种方法和技巧。
本文将介绍几种经典的解三次方程的方法。
一、卡尔达诺公式16世纪意大利数学家卡尔达诺首次研究了三次方程的求解方法，他给出了一种可以将三次方程转化为两个二次方程的方法。
设三次方程为x^3 + ax^2 + bx + c = 0，通过将x = y - a/3进行代换，化简方程为y^3 + py + q = 0，其中p = b - a^2/3，q = c - ab/3 + 2a^3/27、然后利用卡尔达诺公式求解二次方程y^3 + py + q = 0，得到y的三个实数解y1、y2、y3、最后通过反代得到x的三个实数解（x = y - a/3）。
二、牛顿迭代法牛顿迭代法是一种数值计算方法，可以用来求解三次方程的近似解。
设f(x)为三次方程的函数，若x0是方程的一个近似解，那么x0的迭代公式为x1=x0-f(x0)/f'(x0)，其中f'(x0)是f(x)在x0处的导数。
通过不断迭代，满足一个精度要求时的近似解即为三次方程的近似解。
三、三项式解法对于特定的三次方程形式，可以利用特殊的方法求解。
常见的三项式形式有齐次三项式和非齐次三项式。
对于齐次三项式形式，可以通过观察系数的特点，通过代换将其转化为一个简单的二次方程，再进行求解。
对于非齐次三项式形式，可以利用求根公式来求解。
但需要注意的是，求解齐次三项式时的特殊情况，即当方程有一个根为0时，需要额外进行讨论。
四、图像法利用三次方程的图像性质，可以近似地求解三次方程的解。
通过绘制y = ax^3 + bx^2 + cx + d 的函数图像，找到方程与x轴的交点来确定近似解的范围，然后通过x的数值逐渐逼近解的准确值。
虽然这种方法不够严谨，但对于一些无法使用其他方法求解的特殊三次方程，可以提供一种可行的求解途径。
3次方程求解方法三次方程，即含有三次项的方程，可一般表示为：ax^3 + bx^2 + cx + d = 0其中a、b、c、d为已知系数，且a≠0。
解三次方程一般有四种方法：代入法、化为二次方程法、牛顿迭代法和Cardano公式法。
下面将逐一介绍这四种方法。
一、代入法代入法是一种直观的解方程的方法。
步骤如下：1.假设已知解为x=r，将r代入原方程得到一个二次方程；2.求解二次方程，得到解r；3.将r代入原方程，检验是否满足。
当然，这种方法的前提是我们能够猜测到一个解r，且这个解确实存在。
二、化为二次方程法化为二次方程法又称Vieta定理法。
其思想是通过变量代换将三次方程转化为二次方程，再用求解二次方程的方法求解。
步骤如下：1.设x=t-b/3a，其中t是未知数，代入原方程化简；2.移项整理后得到一个以t为未知数的二次方程；3.求解二次方程，得到解t；4.通过t求解原方程。
三、牛顿迭代法牛顿迭代法是一种数值计算方法，可以用来求方程的近似解。
步骤如下：1.假设已知解x0；2.假设x0附近存在解，通过牛顿迭代公式x=x0-f(x0)/f'(x0)求解近似解；3.重复步骤2，直至近似解达到所需精度。
四、Cardano公式法Cardano公式法适用于一般的立方方程。
步骤如下：1. 将原方程形式化为x^3 + px + q = 0；2. 令y = x + p/3x，将方程化为y^3 + ry + s = 0；3.引入一个新的变量z，使得y和z的线性项抵消，得到一个关于z 的二次方程；4.求解这个二次方程，得到根z；5.通过z回代求解y；6.通过y回代求解x。
四种方法中，代入法和化为二次方程法相对简单，适用于能够猜测到解的情况。
而牛顿迭代法和Cardano公式法更加复杂，适用于无法直接得到解的情况。
综上所述，解三次方程有多种方法，我们可以根据具体问题的特点选择合适的方法进行求解。
在实践中，通过结合多种方法，可以更加高效地求解三次方程。
牛顿迭代法求根例题牛顿迭代法是一种常用的数值计算方法，用于求解方程的根。
它基于函数在某一点附近的局部线性逼近，并通过不断迭代逼近方程的根。
下面我将以求解方程 f(x) = 0 的根为例，详细介绍牛顿迭代法的步骤和原理。
假设我们要求解方程 f(x) = 0 的根，首先需要选择一个初始近似解 x0。
然后，我们可以利用函数 f(x) 在 x0 附近的切线来逼近方程的根。
切线的斜率等于函数在 x0 处的导数 f'(x0)，切线与x 轴的交点即为新的近似解 x1。
通过不断迭代这个过程，我们可以逐渐接近方程的根。
具体的迭代公式如下：x_(n+1) = x_n f(x_n) / f'(x_n)。
其中，x_n 表示第 n 次迭代得到的近似解，x_(n+1) 表示第n+1 次迭代得到的近似解。
下面以求解方程 f(x) = x^2 a = 0 的正根为例，来演示牛顿迭代法的步骤。
1. 选择初始近似解 x0。
2. 计算函数 f(x) 在 x0 处的导数 f'(x0)。
3. 根据迭代公式计算新的近似解 x1 = x0 f(x0) / f'(x0)。
4. 判断 x1 与 x0 的差值是否满足要求，如果满足则停止迭代，x1 即为方程的近似根；如果不满足，则将 x1 作为新的 x0，重复步骤 2 和步骤 3，直到满足要求。
通过不断迭代，我们可以逐渐逼近方程的根。
需要注意的是，牛顿迭代法的收敛性和迭代次数与初始近似解的选择有关，不同的初始近似解可能会得到不同的结果。
总结起来，牛顿迭代法是一种通过不断逼近函数根的数值计算方法。
它的步骤包括选择初始近似解、计算函数的导数、利用迭代公式计算新的近似解，直到满足要求为止。
该方法在实际应用中具有广泛的应用领域，如求解非线性方程、优化问题等。
牛顿迭代法的基本原理知识点牛顿迭代法是一种求解方程近似解的数值计算方法，通过不断逼近方程的根，以获得方程的解。
它基于牛顿法则和泰勒级数展开，被广泛应用于科学和工程领域。
本文将介绍牛顿迭代法的基本原理和相关知识点。
一、牛顿迭代法的基本原理牛顿迭代法的基本原理可以总结为以下几个步骤：1. 假设要求解的方程为 f(x) = 0，给定一个初始近似解 x0。
2. 利用泰勒级数展开，将方程 f(x) = 0 在 x0 处进行二阶近似，得到近似方程：f(x) ≈ f(x0) + f'(x0)(x - x0) + 1/2 f''(x0)(x - x0)^23. 忽略近似方程中的高阶无穷小，并令f(x) ≈ 0，得到近似解 x1：0 ≈ f(x0) + f'(x0)(x1 - x0) + 1/2 f''(x0)(x1 - x0)^2求解上述方程，得到近似解 x1 = x0 - f(x0)/f'(x0)。
4. 通过反复迭代的方式，不断更新近似解，直到满足精度要求或收敛于方程的解。
二、牛顿迭代法的收敛性与收敛速度牛顿迭代法的收敛性与收敛速度与初始近似解 x0 的选择和方程本身的性质有关。
1. 收敛性：对于某些方程，牛顿迭代法可能无法收敛或者收敛到错误的解。
当方程的导数为零或者初始近似解离根太远时，迭代可能会发散。
因此，在应用牛顿迭代法时，需要对方程和初始近似解进行合理的选择和判断。
2. 收敛速度：牛顿迭代法的收敛速度通常较快，二阶收敛的特点使其在数值计算中得到广泛应用。
在满足收敛条件的情况下，经过每一次迭代，近似解的有效数字将至少加倍，迭代次数的增加会大幅提高精度。
三、牛顿迭代法的优点与局限性1. 优点：1) 收敛速度快：牛顿迭代法的二阶收敛特性决定了它在求解方程时的高效性和快速性。
2) 广泛适用：牛顿迭代法可以用于求解非线性方程、方程组和最优化问题等，具有广泛的应用领域。
(){}21()(11),5,10,20:12521()1,(0,1,2,,)()2,(0,1,2,,)()()235,20:1100(i i ii n n k k k Newton f x x n x f x x i i n f x nxy i n Newton N x S x n x k y f x =-≤≤=+=-+====-+= 题目：插值多项式和三次样条插值多项式。
已知对作、计算函数在点处的值；、求插值数据点的插值多项式和三次样条插值多项式；、对计算和相应的函数值),()() (1,2,,99)4:()max ()()max()n k n k n k n k n k n k kkN x S x k E N y N x E S y S x ==-=- 和；、计算，；解释你所得到的结果。
算法组织:本题在算法上需要解决的问题主要是：求出第二问中的Newton 插值多项式)(x N n 和三次样条插值多项式()n S x 。
如此，则第三、四问则迎刃而解。
计算两种插值多项式的算法如下：一、求Newton 插值多项式)(x N n ，算法组织如下：Newton 插值多项式的表达式如下：)())(()()(110010--⋅⋅⋅--+⋅⋅⋅+-+=n n n x x x x x x c x x c c x N其中每一项的系数c i 的表达式如下：1102110),,,(),,,(),,,(x x x x x f x x x f x x x f c i i i i i -⋅⋅⋅-⋅⋅⋅=⋅⋅⋅=-根据i c 以上公式，计算的步骤如下：⎪⎪⎪⎩⎪⎪⎪⎨⎧⋅⋅⋅+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅----),,,,(1),,,(),,,,(),(,),,(2)(,),(),(11101111011010n n n n n n n n x x x x f n x x x f x x x f n x x f x x f x f x f x f 、计算、计算、计算、计算 二、求三次样条插值多项式)(x S n ，算法组织如下：所谓三次样条插值多项式)(x S n 是一种分段函数，它在节点i x 011()n n a x x x x b -=<<⋅⋅⋅<<=分成的每个小区间1[,]i i x x -上是3次多项式，其在此区间上的表达式如下：22331111111()[()()]()()666[,]1,2,,.i i i i i i i i i i i i i i i i i h x x h x x S x x x M x x M y M y M h h h x x x i n --------=-+-+-+-∈=⋅⋅⋅，，因此，只要确定了i M 的值，就确定了整个表达式，i M 的计算方法如下： 令：11111111116()6(,,)i i i i i i i i i i i i i ii i i i i i i h h h h h h y y y y d f x x x h h h h μλμ++++--+++⎧===-⎪++⎪⎨--⎪=-=⎪+⎩， 则i M 满足如下n-1个方程：1121,2,,1i i i i i i M M M d i n μλ-+++==⋅⋅⋅-，方程中有n+1个未知量，则令0M 和n M 分别为零，则由上面的方程组可得到(11)i M i n ≤≤-的值，可得到整个区间上的三次样条插值多项式)(x S n 。
牛顿迭代法例题牛顿迭代法是一种求函数零点的近似解的方法，其基本思想是通过函数的切线来逐步逼近零点。
下面是一个使用牛顿迭代法求解方程 x^2 - 2 = 0 的例题：设函数 f(x) = x^2 - 2，要求求解方程 f(x) = 0，即求出函数 f(x) 的根。
首先，选择一个初始近似解 x0，通常选择一个离目标解较近的值作为初始解。
假设初始解为 x0 = 1。
接下来，利用牛顿迭代公式来不断更新近似解，直到满足精度要求。
牛顿迭代公式为：xn+1 = xn - f(xn) / f'(xn)，其中 f'(xn) 表示函数 f(x) 在点 xn 处的导数。
对于函数 f(x) = x^2 - 2，求导得到 f'(x) = 2x。
代入初始近似解 x0 = 1，得到 f'(x0) = 2。
根据牛顿迭代公式，更新近似解：x1 = x0 - f(x0) / f'(x0)= 1 - (1^2 - 2) / 2= 1 - (-1) / 2= 1 + 1/2= 1.5再继续进行迭代：x2 = x1 - f(x1) / f'(x1)= 1.5 - (1.5^2 - 2) / 2= 1.5 - (2.25 - 2) / 2= 1.5 - 0.25 / 2= 1.5 - 0.125= 1.375经过一定次数的迭代后，我们可以得到一个接近方程解的近似解 x2 = 1.375。
可以继续进行迭代，直到满足精度要求或者达到迭代次数限制。
通过以上步骤，可以使用牛顿迭代法求得方程 x^2 - 2 = 0 的近似解x ≈ 1.375。
