牛顿法最优潮流
- 格式:ppt
- 大小:1.21 MB
- 文档页数:24

电力系统最优潮流分析电力系统是现代社会中最重要的系统工程之一,为社会生产和人民生活提供了绝大部分能量。
电能的生产需要耗费大量的燃料,而目前电能在输送、分配和消费过程中存在着大量的损耗。
因此如何采取适当措施节约能源,提高整个电力系统的运行效率,优化系统的运行方式,是国内外许多学者一直关注与研究的热点。
电力系统的最优化运行是指在确保电力系统安全运行、满足用户用电需求的前提下,如何通过调度系统中各发电机组或发电厂的运行,从而使系统发电所需的总费用或所消耗的总燃料达到最小的运筹决策问题。
数学上可将此问题描述为非线性规划或混合非线性规划问题。
最优潮流问题是指在满足必须的系统运行和安全约束条件下,通过调整系统中可利用控制手段实现预定目标最优的系统稳定运行状态。
同经典的经济调度法相比,最优潮流具有全面规划、统筹考虑等优点,它可将安全运行和最优经济运行等问题进行综合考虑,通过统一的数学模型来描述,从而将电力系统对经济性、安全性以及电能质量等方面的要求统一起来。
最优潮流问题的提出把电力系统的最优运行理论提高到一个新的高度,受到了国内外学者高度重视。
最优潮流已在电力系统中的安全运行、电网规划、经济调度、阻塞管理、可靠性分析以及能量管理系统等方面得到了广泛应用,成为了电力系统网络运行分析和优化中不可或缺的工具。
一、最优潮流问题研究的意义最优潮流可将电力系统可靠性与电能质量量化成相应的经济指标,并最终达到优化资源配置、降低成本、提高服务质量的目的。
因此最优潮流研究具有传统潮流计算无法比拟的意义,主要体现在以下两个方面。
一方面,通过最优潮流计算可指导系统调度员的操作,保证系统在经济、安全、可靠的状态下运行。
具体表现为:第一,当所求问题以目标函数、控制变量和约束条件的形式固定下来后,就一定可以求出唯一最优解,并且该结果不受人为因素的影响。
第二,最优潮流的寻优过程可以自动识别界约束,在解逐渐趋于最优的过程中可得到网络传输瓶颈信息,从而可以指导电网扩容与规划。


牛顿法牛顿法作为求解非线性方程的一种经典的迭代方法,它的收敛速度快,有内在函数可以直接使用。
结合着matlab 可以对其进行应用,求解方程。
牛顿迭代法(Newton ’s method )又称为牛顿-拉夫逊方法(Newton-Raphson method ),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法,其基本思想是利用目标函数的二次Taylor 展开,并将其极小化。
牛顿法使用函数()f x 的泰勒级数的前面几项来寻找方程()0f x =的根。
牛顿法是求方程根的重要方法之一,其最大优点是在方程()0f x =的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根,此时非线性收敛,但是可通过一些方法变成线性收敛。
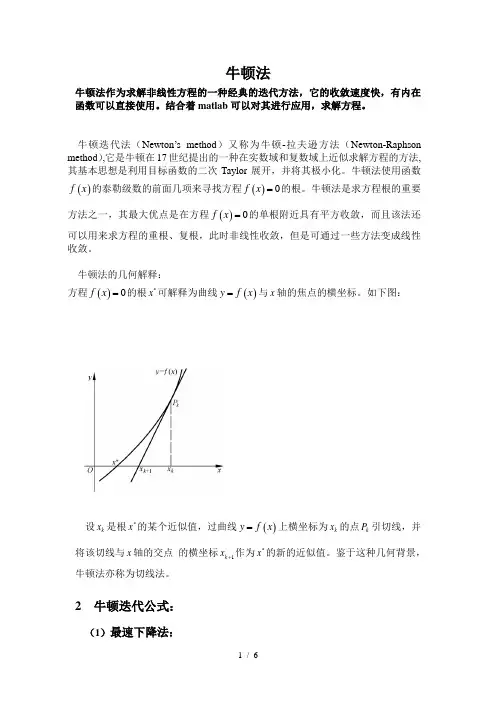
牛顿法的几何解释:方程()0f x =的根*x 可解释为曲线()y f x =与x 轴的焦点的横坐标。
如下图:设k x 是根*x 的某个近似值,过曲线()y f x =上横坐标为k x 的点k P 引切线,并将该切线与x 轴的交点 的横坐标1k x +作为*x 的新的近似值。
鉴于这种几何背景,牛顿法亦称为切线法。
2 牛顿迭代公式:(1)最速下降法:以负梯度方向作为极小化算法的下降方向,也称为梯度法。
设函数()f x 在k x 附近连续可微,且()0k k g f x =∇≠。
由泰勒展开式: ()()()()()Tk k k k fx f x x x f x x x ο=+-∇+- (*)可知,若记为k k x x d α-=,则满足0Tk k d g <的方向k d 是下降方向。
当α取定后,Tk k d g 的值越小,即T kk d g -的值越大,函数下降的越快。
由Cauchy-Schwartz 不等式:T k k kk d g d g ≤,故当且仅当k k d g =-时,Tk k d g 最小,从而称k g -是最速下降方向。
最速下降法的迭代格式为: 1k k k k x x g α+=-。

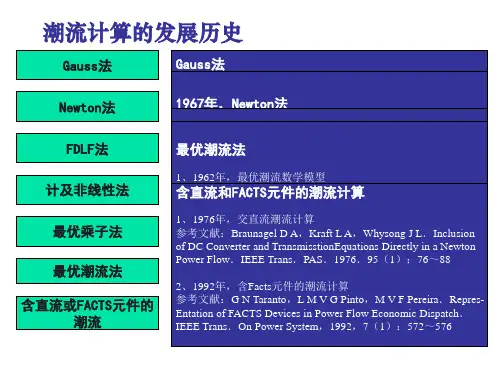
0 引言潮流是配电网络分析的基础,用于电网调度、运行分析、操作模拟和设计规划,同时也是电压优化和网络接线变化所要参考的内容.潮流计算通过数值仿真的方法把电力系统的详细运行情况呈现给工作人员,从而便于研究系统在给定条件下的稳态运行特点。
随着市场经济的发展,经济利益是企业十分看重的,而线损却是现阶段阻碍企业提高效益的一大因素.及时、准确的潮流计算结果,可以给出配电网的潮流分布、理论线损及其在网络中的分布,从而为配电网的安全经济运行提供参考.从数学的角度来看,牛顿—拉夫逊法能有效进行非线性代数方程组的计算且具有二次收敛的特点,具有收敛快、精度高的特点,在输电网中得到广泛应用.随着现代计算机技术的发展,利用编程和相关软件,可以更好、更快地实现配电网功能,本文就是结合牛顿—拉夫逊法的基本原理,利用C++程序进行潮流计算,计算结果表明该方法具有良好的收敛性、可靠性及正确性。
1 牛顿-拉夫逊法基本介绍1。
1 潮流方程对于N个节点的电力网络(地作为参考节点不包括在内),如果网络结构和元件参数已知,则网络方程可表示为:YV I (1—1)=式中,Y为N*N阶节点导纳矩阵;V为N*1维节点电压列向量;I为N*1维节点注入电流列向量。
如果不计网络元件的非线性,也不考虑移相变压器,则Y为对称矩阵。
电力系统计算中,给定的运行变量是节点注入功率,而不是节点注入电流,这两者之间有如下关系:ˆˆ=EI S(1—2)式中,S为节点的注入复功率,是N*1维列矢量;ˆS为S的共轭;ˆˆi diag ⎡⎤=⎢⎥⎣⎦E V 是由节点电压的共轭组成的N*N 阶对角线矩阵。
由(1-1)和(1-2),可得:ˆˆ=S EYV上式就是潮流方程的复数形式,是N 维的非线性复数代数方程组.将其展开,有:ˆi i iij j j iP jQ V Y V ∈-=∑ j=1,2,….,N (1—3)式中, j i ∈表示所有和i 相连的节点j ,包括j i =。

牛顿-拉夫逊法在潮流计算中的应用简介牛顿迭代法又称为牛顿-拉夫逊方法,它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。
多数方程不存在求根公式,因此求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要。
方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x) = 0的根。
牛顿迭代法是求方程根的重要方法之一,其最大优点是在方程f(x) = 0的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根。
由于便于编写程序用计算机求解,应用较广。
下面以一元非线性代数方程的求解为例,来说明牛顿-拉夫逊法的基本思想。
设欲求解的非线性代数方程为f(x)=o设方程的真实解为x*,则必有f(x*)=0。
用牛顿-拉夫逊法求方程真实解x*的步骤如下:首先选取余割合适的初始估值x°作为方程f(x)=0的解,若恰巧有f(x°)=0,则方程的真实解即为x*= x°若f(x°)≠0,则做下一步。
取x¹=x°+Δx°为第一次的修正估值,则f(x¹)=f(x°+Δx°)其中Δx°为初始估值的增量,即Δx°=x¹-x°。
设函数f(x)具有任意阶导数,即可将上式在x°的邻域展开为泰勒级数,即:f(x¹)=f(x°+Δx°)=f(x°)+f'(x°)Δx°+[f''(x°)(Δx°)2]/2+…若所取的|Δx°|足够小,则含(Δx°)²的项及其余的一切高阶项均可略去,并使其等于零,即:f(x¹)≈f(x°)+f'(x°)Δx°=0Δx°=-f(x°)/f'(x°)x¹= x°-f(x°)/f'(x°)可见,只要f'(x°)≠0,即可根据上式求出第一次的修正估值x¹,若恰巧有f(x¹)=0,则方程的真实解即为x*=x¹。


目录摘要11.设计意义与要求2 1.1设计意义21.2设计要求32.牛顿—拉夫逊算法3 2.1牛顿算法数学原理:32.2 直角坐标系下牛顿法潮流计算的原理43 详细设计过程10 3.1节点类型103.2待求量103.3导纳矩阵103.4潮流方程113.5修正方程124.程序设计15 4.1 节点导纳矩阵的形成154.2 计算各节点不平衡量164.3 雅克比矩阵计算- 19 -4.4 LU分解法求修正方程- 22 -4.5 计算网络中功率分布- 25 -5.结果分析- 25 -6.小结- 29 -参考文献- 30 -附录:- 31 -摘要潮流计算是电力网络设计及运行中最基本的计算,对电力网络的各种设计方案及各种运行方式进行潮流计算,可以得到各种电网各节点的电压,并求得网络的潮流及网络中各元件的电力损耗,进而求得电能损耗。
在数学上是多元非线性方程组的求解问题,求解的方法有很多种。
牛顿—拉夫逊法是数学上解非线性方程式的有效方法,有较好的收敛性。
将牛顿法用于潮流计算是以导纳矩阵为基础的,由于利用了导纳矩阵的对称性、稀疏性及节点编号顺序优化等技巧,使牛顿法在收敛性、占用存、计算速度等方面都达到了一定的要求。
本文以一个具体例子分析潮流计算的具体方法,并运用牛顿—拉夫逊算法求解线性方程关键词:电力系统潮流计算牛顿—拉夫逊算法1.设计意义与要求1.1设计意义潮流计算是电力系统分析中的一种最基本的计算,他的任务是对给定运行条件确定系统运行状态,如各母线上的电压(幅值及相角)、网络中的功率分布及功率损耗等。
潮流计算的结果是电力系统稳定计算和故障分析的基础。
具体表现在以下方面:(1)在电网规划阶段,通过潮流计算,合理规划电源容量及接入点,合理规划网架,选择无功补偿方案,满足规划水平的大、小方式下潮流交换控制、调峰、调相、调压的要求。
(2)在编制年运行方式时,在预计负荷增长及新设备投运基础上,选择典型方式进行潮流计算,发现电网中薄弱环节,供调度员日常调度控制参考,并对规划、基建部门提出改进网架结构,加快基建进度的建议。
牛顿法牛顿法作为求解非线性方程的一种经典的迭代方法,它的收敛速度快,有内在函数可以直接使用。
结合着matlab 可以对其进行使用,求解方程。
牛顿迭代法(Newton ’s method )又称为牛顿-拉夫逊方法(Newton-Raphson method ),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法,其基本思想是利用目标函数的二次Taylor 展开,并将其极小化。
牛顿法使用函数()f x 的泰勒级数的前面几项来寻找方程()0f x =的根。
牛顿法是求方程根的重要方法之一,其最大优点是在方程()0f x =的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根,此时非线性收敛,但是可通过一些方法变成线性收敛。
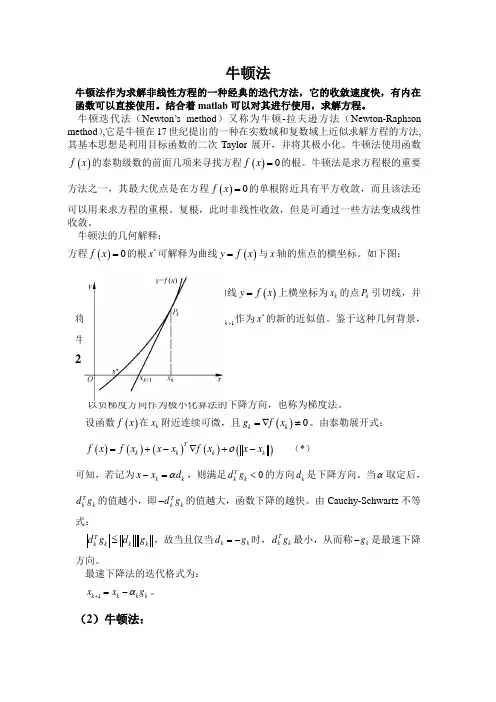
牛顿法的几何解释:方程()0f x =的根*x 可解释为曲线()y f x =与x 轴的焦点的横坐标。
如下图:设k x 是根*x 的某个近似值,过曲线()y f x =上横坐标为k x 的点k P 引切线,并将该切线与x 轴的交点 的横坐标1k x +作为*x 的新的近似值。
鉴于这种几何背景,牛顿法亦称为切线法。
2 牛顿迭代公式:(1)最速下降法:以负梯度方向作为极小化算法的下降方向,也称为梯度法。
设函数()f x 在k x 附近连续可微,且()0k k g f x =∇≠。
由泰勒展开式: ()()()()()T k k k k fx f x x x f xx x ο=+-∇+- (*)可知,若记为k k x x d α-=,则满足0T k k d g <的方向k d 是下降方向。
当α取定后,T k k d g 的值越小,即T k k d g -的值越大,函数下降的越快。
由Cauchy-Schwartz 不等式:Tk k kk d g d g ≤,故当且仅当k k d g =-时,T k k d g 最小,从而称k g -是最速下降方向。
最速下降法的迭代格式为: 1k k k k x x g α+=-。

高电分简总结潮流计算1、牛顿法的计算流程:a) 初始化,形成节点导纳矩阵,给出初值x (0);b) 令k=0,进入迭代循环;c) 计算函数值f (x (k )),判断是否收敛‖f(x (k))‖≤εd) 计算雅克比矩阵∇f(x (k));e) 计算修正量∆x (k)=−(∇f(x (k )))−1f(x (k))f) 对变量进行修正x (k+1)=x (k )+∆x (k ),k =k +1返回 g) 输出计算结果高斯赛德尔法流程初始化,形成节点导纳矩阵;迭代计算各节点电压Ui ;计算功率2、牛拉法、高斯、PQ (快速解耦)法的优缺点比较;潮流计算中G-S (高斯-赛德尔)\N-R (牛顿-拉夫逊法)\FDLF (快速分解法)的优缺点i. 高斯法:原理简单,存储量小,但具有一阶敛速,收敛速度慢,迭代次数过多,在系统病态的情况下,收敛困难,每次迭代速度快,但节点间相互影响太小,收敛缓慢,编程简单灵活(阻抗矩阵法的收敛性要比导纳矩阵法的收敛性好);ii. 牛顿-拉夫逊法:具有二阶收敛性,开始时收敛慢,在几次迭代后收敛速度非常快,对初值很敏感,对函数的平滑性敏感,处理的函数越接近线性,收敛性越好,对以节点导纳矩阵为基础的G-S 法呈病态的系统,N-L 法一般可以可靠收敛,但需要在每次迭代过程中重新生成雅克比矩阵,计算量大;iii. PQ 法:迭代矩阵为常数阵,只需形成求解一次,大大缩短了迭代时间,迭代矩阵对称,可上(下)三角储存,减少内存量和计算量,初始计算线性收敛度迭代次数多于牛拉法,但每次迭代时间短,因此整体计算速度比牛拉法有很大地提高。
PQ 分解法派生于极坐标表示下的牛拉法修正方程:N-L (∆P ∆Q)=(H N J L )(∆δ∆U/U ) PQ (∆P ∆Q )=(H 00L )(∆δ∆U/U) 3、直流潮流的前提是什么?可用在那些地方?● 应用条件:正常运行电力系统,节点电压运行于额定值附近;之路两端相角差很小; 高压电网中,要求R ≪X .● 应用范围:专门研究电网中有功潮流分布;对计算精度要求不高,如电网规划;对计算速度要求较高,如在线实时应用。
在配电网中基于牛顿-拉夫逊法解最优潮流的应用赵君;于泓;赵华松【摘要】Power flow calculation is an important solution of determining the basic data of electric system. Optimal power flow is the condition of maintaining low cost for the entire power system. The article expounds how to achieve the minimum value of cost function by adjusting the output of generators on the basis of Newton-Laphson. It has significant meaning for judging the optimum operation and development of present system.%潮流计算是用来确定电力系统基本数据的重要解决方案,最优潮流是整个电力系统成本最低的条件。
基于牛顿—拉夫逊法,通过调节发电机的输出口来实现成本函数的最小值,对于判定现有系统的最佳运行和发展具有重要意义。
【期刊名称】《农业科技与装备》【年(卷),期】2014(000)010【总页数】3页(P34-36)【关键词】电力系统;潮流计算;牛顿-拉夫逊法;最优潮流;目标函数【作者】赵君;于泓;赵华松【作者单位】沈阳农业大学信息与电气工程学院,沈阳 110866;沈阳农业大学信息与电气工程学院,沈阳 110866;沈阳农业大学信息与电气工程学院,沈阳110866【正文语种】中文【中图分类】TP273电力系统潮流中的牛顿—拉夫逊法首次应用于20世纪60年代,该方法解决了早期阿尔瓦拉多和托马斯研究方法的收敛性较差的问题。