试验设计与分析复习题.doc

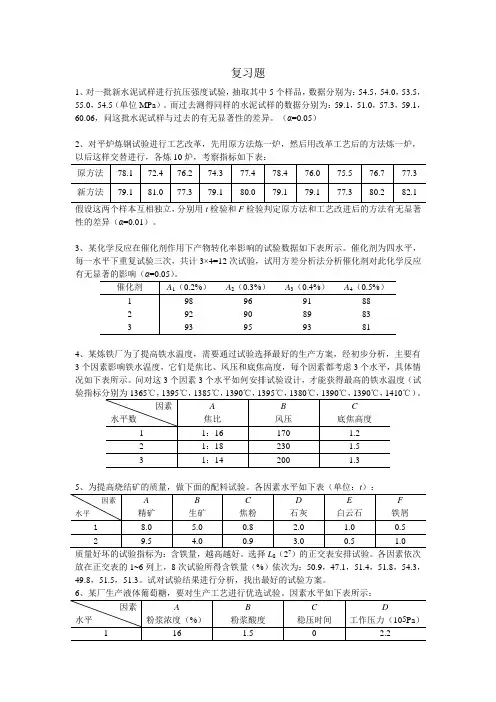
复习题1、对一批新水泥试样进行抗压强度试验，抽取其中5个样品，数据分别为：54.5，54.0，53.5，55.0，54.5（单位MPa）。

而过去测得同样的水泥试样的数据分别为：59.1，51.0，57.3，59.1，60.06，问这批水泥试样与过去的有无显著性的差异。

（α=0.05）2、对平炉炼钢试验进行工艺改革，先用原方法炼一炉，然后用改革工艺后的方法炼一炉，以后这样交替进行，各炼10炉，考察指标如下表：假设这两个样本互相独立，分别用t检验和F检验判定原方法和工艺改进后的方法有无显著性的差异（α=0.01）。

3、某化学反应在催化剂作用下产物转化率影响的试验数据如下表所示。

催化剂为四水平，每一水平下重复试验三次，共计3×4=12次试验，试用方差分析法分析催化剂对此化学反应4、某炼铁厂为了提高铁水温度，需要通过试验选择最好的生产方案，经初步分析，主要有3个因素影响铁水温度，它们是焦比、风压和底焦高度，每个因素都考虑3个水平，具体情况如下表所示。

问对这3个因素3个水平如何安排试验设计，才能获得最高的铁水温度（试验指标分别为1365℃，1395℃，1385℃，1390℃，1395℃，1380℃，1390℃，1390℃，1410℃）。

质量好坏的试验指标为：含铁量，越高越好。

选择L8（2）的正交表安排试验。

各因素依次放在正交表的1~6列上，8次试验所得含铁量（%）依次为：50.9，47.1，51.4，51.8，54.3，49.8，51.5，51.3。

试对试验结果进行分析，找出最好的试验方案。

试验指标有两个：（1）产量，越高越好；（2）总还原糖，在32~40%之间。

用正交表L9（34）安排试验，9次试验所得结果如下：产量（kg）：498，568，568，577，512，540，501，550，510；还原糖（%）：41.6，39.4，31.0，42.4，37.2，30.2，42.2，40.4，30.0。

【西北农林科技大学试验设计与分析复习题】员海燕版一、名词解释(15分)1．重复：一个条件值的每一个实现。

或因素某水平值的多次实现。

2．因素：试验中要考虑的可能会对试验结果产生影响的条件。

常用大写字母表示。

3．水平：因素所处的不同状态或数值。

4．处理：试验中各个因素的每一水平所形成的组合 5．响应：试验的结果称为响应；响应函数：试验指标与因素之间的定量关系用模型ε+=),,(1n x x f y 表示，其中),,(1n x x f y =是因素的值n x x ,,1 的函数，称为响应函数。

678912．试验设计的基本流程是什么？ 1明确试验目的2选择试验的指标，因素，水平 3设计试验方案 4实施试验5对获得的数据进行分析和推断。

3．试验设计的相关分析有哪几种？一是相关系数，即用数理统计中的两个量之间的相关程度来分析的一种方法。

二是等级相关，是把数量标志和品质标志的具体体现用等级次序排序，再测定标志等级和标志等级相关程度的一种方法。

有斯皮尔曼等级差相关系数和肯德尔一致相关系数） 4．为什么要进行方差分析？方差分析可检验有关因素对指标的影响是否显著，从而可确定要进行试验的因素；另外，方差分析的观点认为，只需对显著因素选水平就行了，不显著的因素原则上可在试验范围内取任一水平，或由其它指标确定。

5．均匀设计表与正交表，拉丁方设计的关系6．产品的三次设计是什么？产品的三次设计是系统设计，参数设计，容差设计。

三、(15分)1．写出所有3阶拉丁方格，并指出其中的标准拉丁方格和正交拉丁方格123再将这六个的第一行不动，分别交换第二，三行又得到六个，共12个。

用的试验3．说明均匀设计表)6(6*6U是如何构造的？略五、分析题(30分)1由张护士和实习生刘某记录的七个病人的收缩压数据如下：病人：1234567张护士：105，149，133，160，141，120，152 刘某：110，140，138，150，130，147，158 计算斯皮尔曼等级差相关系数。

一、理论题1.根据研究目的确定的研究对象的全体称为总体(population)，其中的一个研究单位称为个体(individual)；总体的一部分称为样本(sample)。

通常把n≤30的样本叫小样本，n>30的样本叫大样本。

2.由总体计算的特征数叫参数(parameter), ；由样本计算的特征数叫统计量(statistic)。

常用希腊字母表示参数，例如用μ表示总体平均数，用σ表示总体标准差；常用拉丁字母表示统计量，例如用x表示样本平均数，用S表示样本标准差。

3. 准确性(accuracy)指在调查或试验中某一试验指标或性状的观测值与其真值接近的程度，精确性(precision)指调查或试验中同一试验指标或性状的重复观测值彼此接近的程度。

4. 高斯对数理统计和试验设计学科的主要贡献包括：1.建立了回归分析的最小二乘法；2.运用极大似然法及其他数学知识，推导出测量误差的概率分布公式,发现误差的高斯分布曲线，即今天的正态分布。

5.方差分析由R. 费雪于1918年首创, “方差分析法是一种在若干能相互比较的资料组中，把产生变异的原因加以区分开来的方法与技术”。

6.20世纪50年代，日本田口玄一将试验设计中应用最广的正交设计表格化；同一时期，我国著名数学家华罗庚积极倡导和普及“优选法”；在1978年我国数学家王元和方开泰首先提出了均匀设计。

7.两组精度不同的同一试验结果在计算加权平均数时权重通常由绝对误差平方倒数的比值来确定，即认为测量结果的可靠程度与测量次数成正比。

8.样本标准误差的无偏计算公式中分母的n-1来自于自由度的概念。

9. 实验最重要的因素是混杂问题。

所谓混杂是指，由于实验处理，针对你的假说所作的处理，导致的差异与其他因素可能导致的差异无法区分开来。

10. 重复是指在符合实验条件的空间和时间范围内，各组要有足够数量的例数。

重复非常必要，因为变异（差异）是生物体遗传固有的本质。

11. 生物数据中比正态分布更常见的是正偏斜，偏斜数据通常必须进行数据转换（例如对数和幂转换），以改善它们的正态性。

试验设计与数据分析试题AIMB standardization office【IMB 5AB- IMBK 08- IMB 2C】试验设计与数据分析试题（A）一、选择题：1、已知某样品质量的称量结果为：2.010±g，则其相对误差，为：A、2.0，B、2.0±， C、%2 D、%2.02、用法寻找某实验的最优加入量时，若当前存优范围是[628,774]，好点是718，则此时要做试验的加入点值是 ()A、.628＋7742 B、628＋×(774－628)C、628＋774－718D、2×718－7743、经过平面上的6个点，一定可以找到一个次数不高于（）的多项式。

A、4B、5C、6D、74．有一条1 000 m长的输电线路出现了故障，在线路的开始端A处有电，在末端B 处没有电，现在用对分法检查故障所在位置，则第二次检查点在 () A．500 m处 B．250 m处C．750 m处 D．250 m或750 m处5、 L8（27）中的7代表（）A. 最多允许安排因素的个数B. 因素水平数C. 正交表的横行数D. 总的实验次数6、. 在L9（34）表中，有A，B，C三个因素需要安排。

则它们应该安排在（）列A. 1，2，3B. 2，3，4C. 3，4，5D. 任意3列★7、某实验因素对应的目标函数是单峰函数，若用分数法需要从[0，21]个试验点中找最佳点，则需要做试验的次数是 ()A．6次 B．7次 C．10次 D．20次★8、. 用L 8（27）进行正交实验设计，若因素A 和B 安排在第1、2列，则A×B ，应排在第（ ）列。

A. 3B. 4C. 5D. 6★9、正方体的边长为2.010±，则体积的绝对误差限为： A 、32.0 B 、32.0⨯ C 、2.0 D 、60★10、有一双因素优选试验，20≤x ≤40,10≤y ≤20.使用纵横对折法进行优选．分别对因素x 和y 进行了一次优选后其新的存优范围的面积为（ ）A 、200B 、100C 、150D 、50二、填空题1．已知某样品质量的称量结果为：2.07.58±g ，则其绝对误差限为 ；相对误差为 。

一、填空题（共25分）1．根据误差产生的原因，误差可分为 随机 误差、 系统 误差和 过失 误差三大类。

其中 过失 误差是一种显然与事实不符的误差2．秩和检验法是用来检验A 、B 两组数据是否存在显著性差异的一种方法。

假设A 组数据无系统误差，如果A 与B 有显著性差异，则认为B 有 系统误差；如果A 与B 无显著性差异，则认为B 无 系统误差。

3．列出三种常用的数据图： 线图 、 条形图 、 圆形图 。

4．在回归分析中，设i y 、y 、i y 分别为试验值、算术平均值和回归值，则21()ni i i y y =-∑称为 残差 平方和，21()ni i y y =-∑称为 回归 平方和。

5．在试验设计中，黄金分割法是在试验区间内取两个试验点，这两个试验点分别是该试验区间的 0.618 倍和 0.382 倍。

6．L 8(41×24)是一个 正交设计（或混合水平正交设计） 试验表，其中8是 试验次数 （或横行数） ，它可以安排4水平的因素 1 个， 2 水平的因素 4 个，共 5 个因素的试验。

二、简答题（共20分）1．回归分析的用途是什么？写出用Excel 软件进行回归分析时的操作步骤。

（10分） 答：（1）回归分析是一种变量之间相关关系最常用的统计方法，用它可以寻找隐藏在随机性后面的统计规律。

通过回归分析可以确定回归方程，检验回归方程的可靠性等。

（2）用Excel 软件进行回归分析时的操作步骤是：① 从工具菜单中选择数据分析，则会弹出数据分析对话框，然后在分析工具库中选择回归选项，单击确定之后，弹出回归对话框。

② 填写回归对话框。

③ 填好回归对话框后，点击确定，即可得到回归分析的结果。

2．正交试验设计的基本步骤有哪些？ （10分）答：（1）明确试验目的，确定评价指标； （2）挑选因素，确定水平（3）选正交表，进行表头设计； （4）明确试验方案，进行试验，得到结果； （5）对试验结果进行统计分析； （6）进行验证试验，作进一步分析。

DOE Training Test1. 一个32的实验设计意味着我们会有A 两个水平, 三个因子B 两个水平, 三个因子, 两个中心点C 三个水平, 三个因子D 三个水平, 两个因子D2．以下哪个不是DOE的目的?A，筛选输入变量B，筛选输出变量C，优化输出变量D，确定输入变量的设定范围B3．某个2水平全因子DOE设计包括4个因子(其中之一乃离散属性的)加3个中心点, 6 个复制, 请问如果你执行Minitab 里的Stat > DOE > Factorial > Create Factorial Design .. 你会总共得到多少个运行次数?A，99B，100C，98D，102D4．根据以下试验结果,计算AB interaction 的效果(Effect) 为 B Run A B Response1 50 10% 122 100 10% 133 50 20% 94 100 20% 20A，5B，10C，-5D，0解答：50,20（9）100,20 (20)50,10(12) 100,10(13)AB交互效果=(（12+20）-（9+13）)/2=5左对角线之和减去右对角线之和。

5．根据下图,以下哪一个描述正确?A, 温度的main effect为1.6B, 时间的main effect为1.8C, Interaction为0.7D, 时间肯定是统计上算显著A解析：算某个因子的main effect时，利用它的高水平时的响应值之和减去低水平响应值之和，最后平均。

本例中，temp高水平950时的响应值为9.9和10.1，低水平850时的响应值为8和12，那么=(（9.9+10.1）-（8+12）)/2=1.6。

6.与两水平的因子试验相比, 以下哪一个是三水平试验的优点?A.可以评估交互作用B.可以识别曲率C.试验设计可以被扩展(两水平同样可以扩展)D.试验效果的绩效最大B7.以下的哪一种试验设计不能分析交互作用A.部分因子试验设计B.有复制的部分因子试验设计C.有复制的全因子试验设计D.有复制的饱和筛选设计D8. 一个用于优化电子控制模块可靠性的2水平5 因子试验，只复制全因子试验设计次数的一半。

1.正交表的基本性质是什么？三者之间的关系是怎样的？答：正交表的三个基本性质是正交性，代表性和综合可比性。

其中，正交表是核心，是基础，代表性和综合可比性是正交性的必然结果。

2.什么是统计假设检验？为什么统计推断的结论可能发生错误？有哪两个错误？答：统计假设检验又叫显著性检验，是一种由样本的差异去推断样本所在总体是否存在差异的统计方法。

显著性检验是根据小概率事件实际不可能性原理来否定或接受无效假设，所以不论是接受还是否定无效假说，都没有100％的把握，也就是说，在检验无效假说H0时可能犯两种错误，其中当无效假说本身正确，但是通过假设检验后却否定了它，也就是将非真实差异错判为真实差异，这样的错误统计上称为第一错误，反之，当无效假设本身错误时，通过假设检验后接受了它，也即把真实差异错判为非真实差异，这样的错误叫做第二类错误。

3.直线回归与相关分析是对两个变量间的关系进行描述，所以回归预测不受自变量x的取值区间的限制，这种说法对吗？为什么？答：不对，直线回归与相关分析一般是在一定取值区间内对两个变量间的关系进行描述，超出这个区间，变量间关系类型可能会发生改变，所以回归预测必须限制在自变量x的取值区间以内，外推要谨慎，否则会得出错误的结果。

4.对一元线性回归方程的显著性检验有哪些方法？这些方法的检验效果是否等价？答：对一元线性回归方程的显著性检验，通常采用3种方法，即相关系数检验法，F-检验法和t检验法，三种方法检验效果相同，是等价的。

5.试验设计的基本原则是什么？答：试验设计的基本原则是重复化原则，随机化原则，局部控制原则。

1.用最小二乘法确定直线回归方程的原则是各观察点与直线的纵向距离的平方和最小。

（√）2.试验数据的精密度高意味着正确度也高（×）3.各观察值均加（或减）同一数后，均数和标准差均改变（×）4.正态分布有两个参数μ和δ，δ越大相应的正态曲线的形态约扁平。

（√）5.比较身高和体重两组数据变异度大小宜采用变异系数。

《实验设计与分析》习题与解答P41 习题一1。

设用三种方法测定某溶液浓度时，得到三组数据，其平均值如下：1x (1.540.01)mol /L =± 2x (1.70.2)/mol L =± 3x (1.5370.005)mol /L =±试求它们的加权平均值。

解：①计算权重：211100000.01w ==212250.2w == 213400000.005w ==1:2:310000:25:40000400:1:1600w w w ==②计算平均值1.54400 1.71 1.5371600 1.538 1.5/40011600x mol L ⨯+⨯+⨯==≈++5.今欲测量大约8kPa （表压）的空气压力，试验仪表用①1.5级，量程0.2MPa 的弹簧管式压力表;②标尺分度为1mm 的U 形管水银柱压差计；③标尺分度为1mm 的U 形管水柱压差计。

求最大绝对误差和相对误差解：①max 0.21000 1.5%3x kPa ∆=⨯⨯=R E =3100%37.5%8R E =⨯=②33max 1109.8113.610133.4160.133x Pa kPa -∆=⨯⨯⨯⨯==0.133100% 1.66%8R E =⨯= ③33max1109.81109.810.00981x Pa kPa -∆=⨯⨯⨯== 0.00981100%0.12%8R E =⨯=6。

在用发酵法生产赖氨酸的过程中,对产酸率（％）作6次测定.样本测定值为:3。

48, 3.37， 3。

47, 3.38， 3.40, 3.43，求该组数据的算术平均值、几何平均值、调和平均值、标准差s 、总体标准差σ、样本方差s 2、总体方差σ2、算术平均误差Δ和极差R 。

解：①算术平均值: 3.48 3.37 3.47 3.38 3.40 3.433.426x +++++==②几何平均值: 3.42G x = ③调和平均值：63.421111113.48 3.37 3.47 3.38 3.40 3.43H ==+++++④标准差：0.0463s =⑤总体标准差:0.0422σ⑥样本方差:()()()()()()22222223.48 3.42 3.37 3.42 3.47 3.42 3.38 3.42 3.40 3.42 3.43 3.420.0021261s-+-+-+-+-+-==-⑦总体方差：()()()()()()22222223.48 3.42 3.37 3.42 3.47 3.42 3.38 3.42 3.40 3.42 3.43 3.420.001766σ-+-+-+-+-+-==⑧算术平均误差:3.48 3.42 3.37 3.42 3.47 3.42 3.38 3.42 3.40 3.42 3.43 3.420.03836-+-+-+-+-+-∆==⑨极差：R=3.48-3。