数字信号处理实验——信号系统及系统响应

实验一 信号、系统及系统响应一、实验目的1、熟悉理想采样的性质，了解信号采样前后的频谱变化，加深对时域采样定理的理解。

2、熟悉离散信号和系统的时域特性。

3、熟悉线性卷积的计算编程方法：利用卷积的方法，观察、分析系统响应的时域特性。

4、掌握序列傅里叶变换的计算机实现方法，利用序列的傅里叶变换对离散信号、系统及其系统响应进行频域分析。

二、 实验原理1.理想采样序列：对信号x a (t)=A e −αt sin(Ω0t )u(t)进行理想采样，可以得到一个理想的采样信号序列x a (t)=A e −αt sin(Ω0nT ),0≤n ≤50，其中A 为幅度因子，α是衰减因子，Ω0是频率，T 是采样周期。

2.对一个连续时间信号x a (t)进行理想采样可以表示为该信号与一个周期冲激脉冲的乘积，即x ̂a (t)= x a (t)M(t),其中x ̂a (t)是连续信号x a (t)的理想采样；M(t)是周期冲激M(t)=∑δ+∞−∞(t-nT)=1T ∑e jm Ωs t +∞−∞,其中T 为采样周期，Ωs =2π/T 是采样角频率。

信号理想采样的傅里叶变换为X ̂a (j Ω)=1T ∑X a +∞−∞[j(Ω−k Ωs )],由此式可知：信号理想采样后的频谱是原信号频谱的周期延拓，其延拓周期为Ωs =2π/T 。

根据时域采样定理，如果原信号是带限信号，且采样频率高于原信号最高频率分量的2倍，则采样以后不会发生频率混叠现象。

三、简明步骤产生理想采样信号序列x a (n),使A=444.128，α=50√2π，Ω0=50√2π。

（1） 首先选用采样频率为1000HZ ，T=1/1000，观察所得理想采样信号的幅频特性，在折叠频率以内和给定的理想幅频特性无明显差异，并做记录；（2） 改变采样频率为300HZ ，T=1/300，观察所得到的频谱特性曲线的变化，并做记录；（3） 进一步减小采样频率为200HZ ，T=1/200，观察频谱混淆现象是否明显存在，说明原因，并记录这时候的幅频特性曲线。

数字信号处理实验实验一信号、系统及系统响应1、实验目的认真复习采样理论、离散信号与系统、线性卷积、序列的z 变换及性质等有关内容；掌握离散时间序列的产生与基本运算，理解离散时间系统的时域特性与差分方程的求解方法，掌握离散信号的绘图方法；熟悉序列的z 变换及性质，理解理想采样前后信号频谱的变化。

2、实验内容a. 产生长度为500 的在[0,1]之间均匀分布的随机序列，产生长度为500 的均值为0 单位方差的高斯分布序列。

b. 线性时不变系统单位脉冲响应为h(n)=(0.9)nu(n)，当系统输入为x(n)=R10(n)时，求系统的零状态响应，并绘制波形图。

c. 描述系统的差分方程为：y(n)-y(n-1)+0.9y(n-2)=x(n)，其中x(n)为激励，y(n)为响应。

计算并绘制n=20,30,40,50,60,70,80,90,100 时的系统单位脉冲响应h(n)；计算并绘制n=20,30,40,50,60,70,80,90,100 时的系统单位阶跃响应s(n)；由h(n)表征的这个系统是稳定系统吗？d. 序列x(n)=(0.8)nu(n)，求DTFT[x(n)]，并画出它幅度、相位，实部、虚部的波形图。

观察它是否具有周期性？e. 线性时不变系统的差分方程为y(n)=0.7y(n-1)+x(n)，求系统的频率响应H(ejω)，如果系统输入为x(n)=cos(0.05πn)u(n)，求系统的稳态响应并绘图。

f. 设连续时间信号x(t)=e-1000|t|，计算并绘制它的傅立叶变换；如果用采样频率为每秒5000 样本对x(t)进行采样得到x1(n)，计算并绘制X1(ejω)，用x1(n)重建连续信号x(t)，并对结果进行讨论；如果用采样频率为每秒1000 样本对x(t)进行采样得到x2(n)，计算并绘制X2(ejω)，用x2(n)重建连续信号x(t)，并对结果进行讨论。

加深对采样定理的理解。

g. 设X1(z)=z+2+3z-1，X2(z)=2z2+4z+3+5z-1，用卷积方法计算X1(z)X2(z)。

实验报告2012年04月26 日课程名称：数字信号处理实验名称：系统及系统响应班级：学号：姓名：实验二系统及系统响应一、实验目的（1）观察离散系统的频率响应；（2）熟悉连续信号经理想采样前后的频谱变化关系，加深对时域采样定理的理解；（3）利用序列的FT对连续信号、离散信号及系统响应进行频域分析；（4）利用卷积方法观察分析系统的时域特性。

二、实验内容（1）给定一因果系统H(z)= ，求出并绘制H(z)的幅频响应与相频响应；（2）对信号x a(t)=Au(n) 0n50 其中A=444.128，a=50，=50，实现下列实验内容：a、取采样频率fs=10KHZ，观察所得采样x a(n)的幅频特性|X()|和图中的|Xa(j)|在折叠频率附近有无明显差别。

b、改变采样频率fs=1KHZ，观察|X()|的变化，并作记录：进一步降低采样频率，fs=300HZ，观察频谱混叠是否明显存在，说明原因，并记录这时的|X()|曲线。

（3）给定系统的单位抽样响应为h1(n)=R10(n)a、利用线性卷积求信号x1(n)=(n)，通过该系统的响应y1(n)。

比较所求响应y1(n)和h1(n)之间有无差别，绘图说明，并用所学理论解释所得结果。

b、利用线性卷积求信号x2(n)=R10(n)，通过该系统的响应y2(n)，并判断y2(n)图形及其非0值序列长度是否与理论结果一致，改变x2(n)的长度，取N=5，重复该试验。

注意参数变化的影响，说明变化前后的差异，并解释所得结果。

（4）求x(n)=11(n+2)+7(n+1)-(n-1)+4(n-2)+2(n-3)通过系统h(n)=2(n+1)+3(n)-5(n-2)+2(n-3)+(n-4)的响应y(n)。

三、实验程序及解析（1）1、程序clear; close all;b=[1,sqrt(2),1];a=[1,-0.67,0.9];[h,w]=freqz(b,a);am=20*log10(abs(h));% am=20*log10(abs(h))为幅频响应取dBsubplot(2,1,1);%将窗口划分为2*1的小窗口并选择第一个显示plot(w,abs(h));xlabel('w');ylabel('幅频响应');title('系统响应')ph=angle(h);subplot(2,1,2); %选择第二个窗口显示plot(w,ph);xlabel('w');ylabel('相频响应');2、系统响应结果图1 因果系统的H(z)的系统响应3、结果分析分析z域系统的特性主要是由系统的零点和极点的分布得出结论的。

实验一: 系统响应及系统稳定性： 班级： 学号： 一、实验目的（1）学习并掌握求系统响应的方法。

（2）掌握时域离散系统的时域特性。

（3）分析、观察及检验系统的稳定性。

二、实验原理与方法在时域中，描写系统特性的方法是差分方程和单位脉冲响应，在频域可以用系统函数描述系统特性。

已知输入信号可以由差分方程、单位脉冲响应或系统函数求出系统对于该输入信号的响应。

最简单的方法是采用MATLAB 语言的工具箱函数filter 函数。

也可以用MATLAB 语言的工具箱函数conv 函数计算输入信号和系统的单位脉冲响应的线性卷积，求出系统的响应。

系统的时域特性指的是系统的线性时不变性质、因果性和稳定性。

重点分析实验系统的稳定性，包括观察系统的暂态响应和稳定响应。

系统的稳定性是指对任意有界的输入信号，系统都能得到有界的系统响应。

或者系统的单位脉冲响应满足绝对可和的条件。

系统的稳定性由其差分方程的系数决定。

实际中检查系统是否稳定，不可能检查系统对所有有界的输入信号，输出是否都是有界输出，或者检查系统的单位脉冲响应满足绝对可和的条件。

可行的方法是在系统的输入端加入单位阶跃序列，如果系统的输出趋近一个常数（包括零），就可以断定系统是稳定的[19]。

系统的稳态输出是指当∞→n 时，系统的输出。

如果系统稳定，信号加入系统后，系统输出的开始一段称为暂态效应，随n的加大，幅度趋于稳定，达到稳态输出。

判断系统的稳定性，还可以根据系统函数的极点是否在单位圆来判断系统是否稳定。

当系统函数的极点都在单位圆时，系统函数的时域的傅里叶变换存在，即满足傅里叶变换的条件，那么系统稳定，反之，当系统函数的极点不在单位圆时，那么系统就不稳定。

三、实验容及步骤（1）给定一个低通滤波器的差分方程为)1(9.0)1(05.0)(05.0)(-+-+=n y n x n x n y 输入信号 )()(81n R n x = )()(2n u n x =a) 分别求出系统对)()(81n R n x =和)()(2n u n x =的响应序列，并画出其波形。

实验一：信号、系统及系统响应1. 实验目的① 熟悉连续信号经过理想抽样前后的频谱变化关系，加深对时域抽样定理的理解。

② 熟悉时域离散系统的时域特性。

③ 利用卷积方法观察分析系统的时域特性。

④ 掌握序列傅里叶变换的计算机实验方法，利用序列的傅里叶变换对连续信号、离散信号及系统响应进行频域分析。

2. 实验原理与方法(1)对一个连续信号x a (t)进行理想抽样的过程可用（1.1）式表示。

)(ˆt x a = )(t x a δT (t) ,其中)(ˆt xa 为x a (t)的理想抽样，δT (t)为周期冲激脉冲，即∑∞-∞=-=n T nT t t )()(δδ)(ˆt x a 的傅里叶变换)(ˆΩj X a 为)(ˆΩj X a= ∑∞-∞=Ω-Ωk s a k j X T )]([1 下面导出用序列的傅里叶变换来计算)(ˆΩj X a 的公式。

)(ˆΩj X a = ⎰∞∞-Ω-dt et x tj a )(ˆ = dt e nT t nT x t j n a Ω-∞∞-∞-∞=⎰∑⎥⎦⎤⎢⎣⎡-)()(δ=∑⎰∞-∞=∞∞-Ω-⎥⎦⎤⎢⎣⎡-n nTj adt nT t enT x)()(δ = ∑∞-∞=Ω-n nTj a enT x )( 式中的x a (nT)就是采样后得到的序列x(n)，即x(n) = x a (nT) x(n)的序列傅里叶变换为X(e j ω) =∑∞-∞=-n nj en x ω)(为了在数字计算机上观察分析各种序列的频域特性，通常对X(e j ω)在[0，2π]上进行M 点采样来观察分析。

对长度为N 的有限长序列x(n)，有∑-=-=1)()(N n n j j k ke n x eX ωω其中k Mk πω2=, k = 0,1, …, M-1,通常M 应取得大一些，以便观察谱的细节变化。

取模|)(k j e X ω|可绘出幅频待性曲线。

(2) 一个时域离散线性非移变系统的输入/输出关系为y(n) = x(n) * h(n) =∑∞-∞=-m m n h m x )()(上述卷积运算也可以在频域实现(即卷积定理：时域卷积，频域相乘。

实验一系统响应及系统稳定性一、实验目的1．掌握求系统响应的方法。

2. 掌握时域离散系统的时域特性。

3. 分析、观察及检验系统的稳定性。

二、实验原理与方法在时域中，描写系统特性的方法是差分方程和单位脉冲响应，在频域中可以用系统函数描述系统特性。

已知差分方程、单位脉冲响应或者系统函数求出系统对于该输入信号的响应。

本实验采用matlab语言工具箱中的filter函数和conv 函数计算输入信号和系统的单位脉冲响应的线性卷积，即求出系统的响应。

三、实验内容1．编程，包括产生输入信号，单位脉冲响应序列的子序列，用filter函数和conv 函数求解系统输出响应的子程序。

程序中要有绘制信号波形的功能。

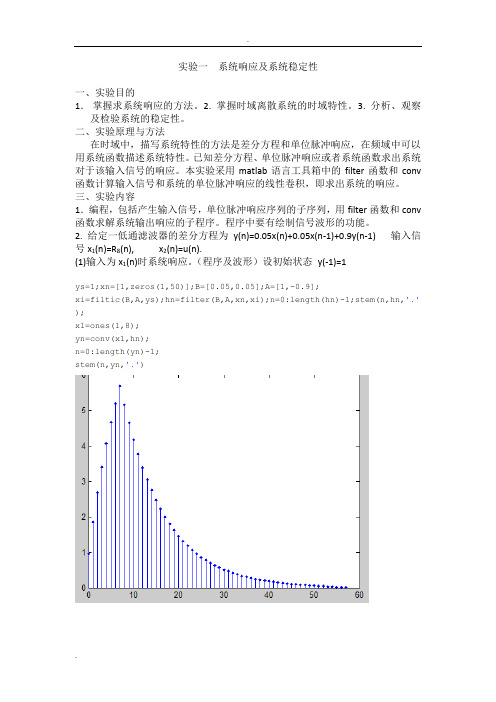
2. 给定一低通滤波器的差分方程为y(n)=0.05x(n)+0.05x(n-1)+0.9y(n-1) 输入信号x1(n)=R8(n), x2(n)=u(n).(1)输入为x1(n)时系统响应。

（程序及波形）设初始状态y(-1)=1ys=1;xn=[1,zeros(1,50)];B=[0.05,0.05];A=[1,-0.9];xi=filtic(B,A,ys);hn=filter(B,A,xn,xi);n=0:length(hn)-1;stem(n,hn,'.' );x1=ones(1,8);yn=conv(x1,hn);n=0:length(yn)-1;stem(n,yn,'.')输入为u(n)时的系统响应：ys=1;xn=[1,zeros(1,50)];B=[0.05,0.05];A=[1,-0.9];xi=filtic(B,A,ys);hn=filter(B,A,xn,xi);n=0:length(hn)-1;stem(n,hn,'.' );x2=ones(1,50);yn=conv(x2,hn);n=0:length(yn)-1;stem(n,yn,'.')(2)求出系统的单位脉冲响应：ys=1;xn=[1,zeros(1,50)];B=[0.05,0.05];A=[1,-0.9];xi=filtic(B,A,ys);hn=filter(B,A,xn,xi);n=0:length(hn)-1;stem(n,hn,'.');3.给定系统的单位脉冲响应为h1(n)=R10(n), h2(n)=δ(n)+2.5δ(n-1)+2.5δ(n-2)+δ(n-3).用线性卷积求出x1(n)=R8(n)分别对于两系统的输出响应，并画出波形。

实验报告思考题要点提示数字信号处理实验一：信号、系统及系统响应1、简述线性卷积结果y (n)的非零区间与x (n )、h (n )非零区间的关系？激励x (n )延时时输出如何变化？由线性移不变系统特性可知，当激励x (n )延时n 0时，输出y (n )也延时n 0。

2、 简述系统函数零极点分布与系统幅频特性间的对应关系。

（1） 位于原点处的零、极点对幅频特性没有影响，只影响相频特性。

（2） 极点位置主要影响幅频特性峰值的位置及尖锐程度，极点越靠近单位圆，所对应的峰值越尖锐。

（3） 零点位置主要影响幅频特性谷值的位置及形状，零点越靠近单位圆，谷值越小。

3、 y (n )=x (n )*h (n )，当输入x (n )有一时移时y (n )与)e (Y j ω有无变化，并说明为什么？由线性移不变系统特性可知，当激励x (n )延时n 0时，输出y (n )也延时n 0。

所以当输入x (n )有一时移时，y(n )也有同样的时移。

)()]([)()]([00ωωωj j e Y e n n y DTFT DTFT e Y n y DTFT n j -=-=的时移特性可知，由设,即时域位移，频域相移，所以幅频特性)e(Y j ω无变化。

数字信号处理实验二：信号的谱分析1、 描述随着DFT 变换点数N 的增加，X (k )的幅度谱的变化并解释原因。

随着DFT 变换点数N 的增加，X (k )的幅度谱序列间隔越来越密，其包络逐渐逼近x (n )的幅度谱)(ωj e X 。

这是因为M 点有限长序列x (n )的N 点DFT 是对有限长序列x (n )的频谱)(ωj e X 在频域0~2π区间内的N 点等间隔抽样。

即： k Nj e X n x DFT k X πωω2)()]([)(=== 因此变换点数越多，抽样间隔越小。

2、 用DFT 对连续非周期信号进行谱分析，试分析（1）采样点数足够多（即数据截断长度足够长）的情况下，采样频率对谱分析的影响；（2）采样频率足够高（即无明显的频域混叠现象）时，采样点数N (相应地时窗截断长度NT s )对谱分析的影响。

数字信号处理实验报告一-系统响应及系统稳定性实验一: 系统响应及系统稳定性姓名：班级：学号：一、实验目的（1）学习并掌握求系统响应的方法。

（2）掌握时域离散系统的时域特性。

（3）分析、观察及检验系统的稳定性。

二、实验原理与方法在时域中，描写系统特性的方法是差分方程和单位脉冲响应，在频域可以用系统函数描述系统特性。

已知输入信号可以由差分方程、单位脉冲响应或系统函数求出系统对于该输入信号的响应。

最简单的方法是采用MATLAB语言的工具箱函数filter函数。

也可以用MATLAB语言的工具箱函数conv函数计算输入信号和系统的单位脉冲响应的线性卷积，求出系统的响应。

系统的时域特性指的是系统的线性时不变性质、因果性和稳定性。

重点分析实验系统的稳定性，包括观察系统的暂态响应和稳定响应。

系统的稳定性是指对任意有界的输入信号，系统都能得到有界的系统响应。

或者系统的单位脉冲响应满足绝对可和的条件。

系统的稳定性由其差分方程的系数决定。

实际中检查系统是否稳定，不可能检查系统对所有有界的输入信号，输出是否都是有界输出，或者检查系统的单位脉冲响应满足绝对可和的条件。

可行的方法是在系统的输入端加入单位阶跃序列，如果系统的输出趋近一个常数（包括零），就可以断定系统是稳定的[19]。

系统的稳态输出是指当∞n时，系统的→输出。

如果系统稳定，信号加入系统后，系统输出的开始一段称为暂态效应，随n的加大，幅度趋于稳定，达到稳态输出。

判断系统的稳定性，还可以根据系统函数的极点是否在单位圆内来判断系统是否稳定。

当系统函数的极点都在单位圆内时，系统函数的时域的傅里叶变换存在，即满足傅里叶变换的条件，那么系统稳定，反之，当系统函数的极点不在单位圆内时，那么系统就不稳定。

三、实验内容及步骤（1）给定一个低通滤波器的差分方程为)1(9.0)1(05.0)(05.0)(-+-+=n y n x n x n y 输入信号 )()(81n R n x = )()(2n u n x =a) 分别求出系统对)()(81n R n x =和)()(2n u n x =的响应序列，并画出其波形。

北华大学数字信号实验实验项目：信号、系统及系统响应班级：信息10-1姓名：张慧学号：36实验一 信号、系统及系统响应一．实验目的1．熟悉理想采样的性质，了解信号采用前后的频谱变化，加深对采样定理的理解。

2．熟悉离散信号和系统的时域特性。

3．熟悉线性卷积的计算编程方法：利用卷积的方法，观察、分析系统响应的时域特性。

4．掌握序列傅氏变换的计算机实现方法，利用序列的傅氏变换对离散信号、系统及系统响应进行频域分析。

二．实验原理1．连续时间信号的采样)()()(ˆt M t x t xa a = 其中)(ˆt xa 是连续信号)(t x a 的理想采样，)(t M 是周期冲激脉冲 ∑+∞-∞=-=n nT t t M )()(δ它也可以用傅立叶级数表示为：∑+∞-∞=Ω=n tjm s e T t M 1)(其中T 为采样周期，T s /2π=Ω是采样角频率。

设)(s X a 是连续时间信号)(t x a 的双边拉氏变换，即有：⎰+∞∞--=dt e t x s X sta a )()( 此时理想采样信号)(ˆt x a 的拉氏变换为 ∑⎰+∞-∞=+∞∞--Ω-===m s a sta ajm s X T dt e t x s X )(1)(ˆ)(ˆ作为拉氏变换的一种特例，信号理想采样的傅立叶变换[]∑+∞-∞=Ω-Ω=Ωm s a a m j X T j X )(1)(ˆ∑+∞-∞=-=n nzn x z X )()(以ωj e 代替上式中的z ，就可以得到序列)(n x 的傅立叶变换 ∑+∞-∞=-=n nj j en x e X ωω)()(具有如下关系：Tj a e X j X Ω==Ωωω)()(ˆ信号卷积∑+∞-∞=-=*=m m n h m x n h n x n y )()()()()()()()(z H z X z Y =)()()(ωωωj j j e H e X e Y =三．实验内容及步骤1， 分析理想采样的特性。

西安郵電學院数字信号处理课内实验报告书系部名称：计算机系学生姓名：常成娟专业名称：电子信息科学与技术班级：电科0603学号：04062095（22号）时间： 2008-11-23实验一： 信号、 系统及系统响应一. 实验目的(1) 熟悉连续信号经理想采样前后的频谱变化关系， 加深对时域采样定理的理解。

(2) 熟悉时域离散系统的时域特性。

(3) 利用卷积方法观察分析系统的时域特性。

(4) 掌握序列傅里叶变换的计算机实现方法， 利用序列的傅里叶变换对连续信号、 离散信号及系统响应进行频域分析。

二. 实验原理与方法采样是连续信号数字处理的第一个关键环节。

对一个连续信号xa(t)进行理想采样的过程可用(10.3.1)式表示。

(10.3.1)其中 (t)为xa(t)的理想采样， p(t)为周期冲激脉冲， 即(10.3.2)(t)的傅里叶变换 (j Ω)为 (10.3.3)将(10.3.2)式代入(10.3.1)式并进行傅里叶变换，(10.3.4)式中的xa(nT)就是采样后得到的序列x(n)， 即x(n)的傅里叶变换为 (10.3.5)比较(10.3.5)和(10.3.4)可知^()()()a a x t x t p t =^x ()()n p t t nT δ∞=-∞=-∑^x ^a X 1()[()]a a s m X j X j m T ∞⋅=-∞Ω=Ω-Ω∑^()[()()]()()()j t a a n j t a n j t a n X j x t t nT e dtx t t nT e dtx nT e dt δδ∞∞-Ω-∞=-∞∞∞-Ω-∞=-∞∞-Ω=-∞Ω=-=-=∑⎰∑⎰∑()()a x n x nT =()()j j nn X e x n e ωω∞-=-∞=∑（10.3.6)在数字计算机上观察分析各种序列的频域特性，通常对X(ej ω)在［0, 2π］上进行M 点采样来观察分析。