遗传算法优化BP神经网络权值和阈值(完整版)

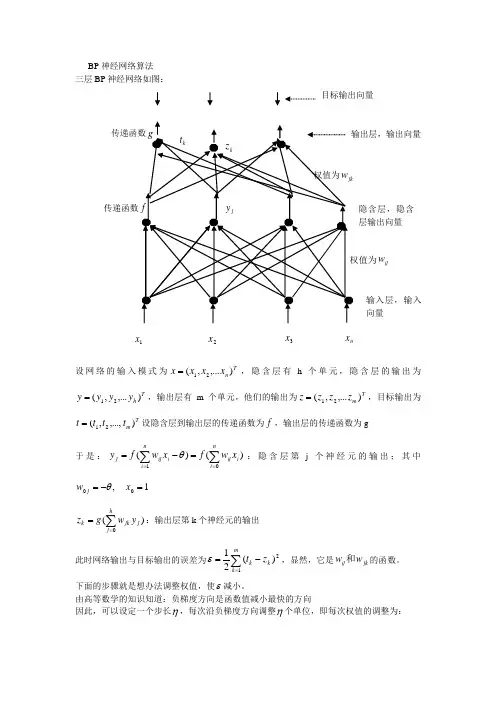
BP 神经网络算法 三层BP 神经网络如图：设网络的输入模式为Tn x x x x ),...,(21=，隐含层有h 个单元，隐含层的输出为T h y y y y ),...,(21=，输出层有m 个单元，他们的输出为T m z z z z ),...,(21=，目标输出为T m t t t t ),...,,(21=设隐含层到输出层的传递函数为f ，输出层的传递函数为g于是：)()(1∑∑===-=ni i ij ni iij j x w f xw f y θ：隐含层第j 个神经元的输出；其中1,00=-=x w j θ)(0∑==hj j jk k y w g z ：输出层第k 个神经元的输出此时网络输出与目标输出的误差为∑=-=m k k k z t 12)(21ε，显然，它是jk ij w w 和的函数。

下面的步骤就是想办法调整权值，使ε减小。

由高等数学的知识知道：负梯度方向是函数值减小最快的方向因此，可以设定一个步长η，每次沿负梯度方向调整η个单位，即每次权值的调整为：1x 3x 2x n x隐含层，隐含层输出向量ij w传递函数输入层，输入向量目标输出向量pqpq w w ∂∂-=∆εη，η在神经网络中称为学习速率 可以证明：按这个方法调整，误差会逐渐减小。

BP 神经网络（反向传播）的调整顺序为： 1）先调整隐含层到输出层的权值 设k v 为输出层第k 个神经元的输入∑==hj j jkk y wv 0j k k k jkk k k k m k k k jk m k k k jk y v g z t w v v z z z t w z t w )(')()(21)(211212--=∂∂∂∂∂-=∂-=∂∂∑∑==ε -------复合函数偏导公式若取x e x f x g -+==11)()(，则)1()111(11)1()('2k k v v v v k z z ee e e u g kk k k -=+-+=+=---- 于是隐含层到输出层的权值调整迭代公式为：j k k jk jk y z z t w t w )1()()1(-+=+η2）从输入层到隐含层的权值调整迭代公式为：其中j u 为隐含层第j 个神经元的输入：∑==ni iij j xw u 0注意：隐含层第j 个神经元与输出层的各个神经元都有连接，即jy ∂∂ε涉及所有的权值ij w ，因此∑∑==--=∂∂∂∂∂-∂=∂∂m k jk k k k j k k k m k k k k j w u f z t y u u z z z t y 002)(')()(ε于是：因此从输入层到隐含层的权值调整迭代为公式为：i j ij ij x t w t w ηδ+=+)()1(ijj j j j m k k k ij m k k k ij w u u y y z t w z t w ∂∂∂∂∂-=∂-=∂∂∑∑==1212)(21)(21εi j i j m k jk k k k ij mk k k ij x x u f w u f z t w z t w δε-=--=∂-=∂∂∆==∑∑)('})('){()(21012例：下表给出了某地区公路运力的历史统计数据，请建立相应的预测模型，并对给出的2010和73.3900 3.9635 0.98802011 75.5500 4.0975 1.0268function main()clc % 清屏clear all; %清除内存以便加快运算速度close all; %关闭当前所有figure图像SamNum=20; %输入样本数量为20TestSamNum=20; %测试样本数量也是20ForcastSamNum=2; %预测样本数量为2HiddenUnitNum=8; %中间层隐节点数量取8,比工具箱程序多了1个InDim=3; %网络输入维度为3OutDim=2; %网络输出维度为2%原始数据%人数(单位：万人)sqrs=[20.55 22.44 25.37 27.13 29.45 30.10 30.96 34.06 36.42 38.09 39.13 39.99 ...41.93 44.59 47.30 52.89 55.73 56.76 59.17 60.63];%机动车数(单位：万辆)sqjdcs=[0.6 0.75 0.85 0.9 1.05 1.35 1.45 1.6 1.7 1.85 2.15 2.2 2.25 2.35 2.5 2.6...2.7 2.85 2.953.1];%公路面积(单位：万平方公里)sqglmj=[0.09 0.11 0.11 0.14 0.20 0.23 0.23 0.32 0.32 0.34 0.36 0.36 0.38 0.49 ...0.56 0.59 0.59 0.67 0.69 0.79];%公路客运量(单位：万人)glkyl=[5126 6217 7730 9145 10460 11387 12353 15750 18304 19836 21024 19490 20433 ...22598 25107 33442 36836 40548 42927 43462];%公路货运量(单位：万吨)glhyl=[1237 1379 1385 1399 1663 1714 1834 4322 8132 8936 11099 11203 10524 11115 ...13320 16762 18673 20724 20803 21804];p=[sqrs;sqjdcs;sqglmj]; %输入数据矩阵t=[glkyl;glhyl]; %目标数据矩阵[SamIn,minp,maxp,tn,mint,maxt]=premnmx(p,t); %原始样本对（输入和输出）初始化rand('state',sum(100*clock)) %依据系统时钟种子产生随机数rand是产生0到1的均匀分布，randn是产生均值为0，方差为1的正态分布rand(n)或randn(n)产生n*n阶矩阵，rand(m,n)或randn(n)产生m*n的随机数矩阵NoiseVar=0.01; %噪声强度为0.01（添加噪声的目的是为了防止网络过度拟合）Noise=NoiseVar*randn(2,SamNum); %生成噪声SamOut=tn + Noise; %将噪声添加到输出样本上TestSamIn=SamIn; %这里取输入样本与测试样本相同因为样本容量偏少TestSamOut=SamOut; %也取输出样本与测试样本相同MaxEpochs=50000; %最多训练次数为50000lr=0.035; %学习速率为0.035E0=0.65*10^(-3); %目标误差为0.65*10^(-3)W1=0.5*rand(HiddenUnitNum,InDim)-0.1; %初始化输入层与隐含层之间的权值B1=0.5*rand(HiddenUnitNum,1)-0.1; %初始化输入层与隐含层之间的阈值W2=0.5*rand(OutDim,HiddenUnitNum)-0.1; %初始化输出层与隐含层之间的权值B2=0.5*rand(OutDim,1)-0.1; %初始化输出层与隐含层之间的阈值ErrHistory=[]; %给中间变量预先占据内存for i=1:MaxEpochsHiddenOut=logsig(W1*SamIn+repmat(B1,1,SamNum)); % 隐含层网络输出NetworkOut=W2*HiddenOut+repmat(B2,1,SamNum); % 输出层网络输出Error=SamOut-NetworkOut; % 实际输出与网络输出之差SSE=sumsqr(Error) %能量函数（误差平方和）ErrHistory=[ErrHistory SSE];if SSE<E0,break, end %如果达到误差要求则跳出学习循环% 以下六行是BP网络最核心的程序% 他们是权值（阈值）依据能量函数负梯度下降原理所作的每一步动态调整量Delta2=Error;Delta1=W2'*Delta2.*HiddenOut.*(1-HiddenOut);dW2=Delta2*HiddenOut';dB2=Delta2*ones(SamNum,1);dW1=Delta1*SamIn';dB1=Delta1*ones(SamNum,1);%对输出层与隐含层之间的权值和阈值进行修正W2=W2+lr*dW2;B2=B2+lr*dB2;%对输入层与隐含层之间的权值和阈值进行修正W1=W1+lr*dW1;B1=B1+lr*dB1;endHiddenOut=logsig(W1*SamIn+repmat(B1,1,TestSamNum)); % 隐含层输出最终结果NetworkOut=W2*HiddenOut+repmat(B2,1,TestSamNum); % 输出层输出最终结果a=postmnmx(NetworkOut,mint,maxt); % 还原网络输出层的结果x=1990:2009; % 时间轴刻度newk=a(1,:); % 网络输出客运量newh=a(2,:); % 网络输出货运量figure ;subplot(2,1,1);plot(x,newk,'r-o',x,glkyl,'b--+') %绘值公路客运量对比图；legend('网络输出客运量','实际客运量');xlabel('年份');ylabel('客运量/万人');subplot(2,1,2);plot(x,newh,'r-o',x,glhyl,'b--+') %绘制公路货运量对比图；legend('网络输出货运量','实际货运量');xlabel('年份');ylabel('货运量/万吨');% 利用训练好的网络进行预测% 当用训练好的网络对新数据pnew进行预测时，也应作相应的处理pnew=[73.39 75.553.96354.09750.9880 1.0268]; %2010年和2011年的相关数据；pnewn=tramnmx(pnew,minp,maxp); %利用原始输入数据的归一化参数对新数据进行归一化；HiddenOut=logsig(W1*pnewn+repmat(B1,1,ForcastSamNum)); % 隐含层输出预测结果anewn=W2*HiddenOut+repmat(B2,1,ForcastSamNum); % 输出层输出预测结果%把网络预测得到的数据还原为原始的数量级；anew=postmnmx(anewn,mint,maxt)。

基于遗传算法的BP神经网络算法人工神经网络（Artificial Neural Network，ANN）是一种模拟人脑中神经元运作原理的数学模型。

反向传播神经网络（Back Propagation Neural Network，BPNN）是一种常用的人工神经网络模型，其训练方法是通过计算输出与期望输出之间的误差，并将误差反向传播进行网络参数的调整。

遗传算法（Genetic Algorithm，GA）是一种基于生物进化理论的优化方法，通过模拟基因遗传和进化的过程来最优解。

BP神经网络算法结合遗传算法能够提高网络的训练效果，并进一步提升算法的性能。

1.随机初始化BP神经网络的权重和阈值。

BP神经网络的训练需要初始化网络的权重和阈值，遗传算法可以随机生成初始值作为种群的个体。

2.选择适应度函数。

适应度函数用于评估每个个体的适应度程度，即个体在解决问题中的优劣程度。

对于BP神经网络，适应度函数可以选择网络的误差函数，如均方误差。

3.选择遗传算子。

遗传算子包括选择、交叉和变异操作。

选择操作根据个体的适应度确定被选中参与下一代个体的概率。

交叉操作模拟基因交换，通过交叉操作可以产生新的个体。

变异操作则模拟基因突变，通过变异操作可以增加种群的多样性。

4.根据选择的适应度函数计算种群的适应度值。

对于BP神经网络，可以使用遗传算法对初始种群进行迭代并通过BP算法进行训练，根据训练结果计算个体的适应度值。

5.根据选择的适应度值进行选择操作。

根据适应度值选择种群中的个体，并根据选择的概率生成新的种群。

6.进行交叉操作。

通过交叉操作将选定的个体进行基因交换，并生成新的个体。

7.进行变异操作。

对选定的个体进行基因突变，增加种群的多样性。

8.根据选择的适应度函数计算新种群的适应度值。

对新生成的个体进行适应度评估。

9.判断终止条件。

终止条件可以根据算法的需求进行设置，如达到指定的迭代次数或达到指定的适应度阈值。

10.重复进行步骤5至步骤9，直到满足终止条件。

利用云模型和遗传算法优化BP神经网络权值摘要：标准BP算法主要根据训练样本确定神经网络的权值，由于BP算法采用沿梯度下降的搜索算法，因而其结果对初始权值非常敏感，收敛速度慢，易陷入局部极小。

结合正态云模型云滴的随机性和稳定倾向性，以及遗传算法的全局搜索能力，收敛速度快等特性优化神经网络的权值和阈值。

分类实验结果表明，该算法比标准BP算法收敛速度快，分类正确率高。

关键词：云模型；遗传算法；标准BP算法；神经网络0 引言BP算法(Back Propogation Algorithm)是目前应用最为广泛的神经网络学习算法，但由于BP算法采用沿梯度下降的搜索算法，因而其结果对初始权值非常敏感，不同的初始权值可能导致不同的结果以及易陷入局部极小等问题。

本文结合遗传算法的高度并行、随机、自适应的全局性概率搜索以及正态云模型云滴的随机性和稳定倾向性特点优化神经网络的权值和阈值。

该算法中的交叉概率、变异概率由X条件云发生器产生。

1 优化原理先利用神经网络试探出最好的网络隐层结点数，再利用本文提出的算法调整网络的权值以及阈值，然后再用调整好的权值和阈值进行分类。

编码：对于包含一层隐藏层模式为m-n-l多层神经网络共有q=m*n+n*l+n+l个权值和阈值需要优化，其中m为输入层结点数，n 为隐藏层结点数，l为输出层结点数。

将这q个权值和阈值记为W=(W 1,W2,…,W q)，采用实数编码，将行向量W看作是一条染色体，而其中每个实数W i(i=1,2,…,q)是染色体的一个基因位。

选择算子：采用轮盘赌和精英保留选择策略。

每个染色体产生后代的数目正比于它的适应度值的大小，并且每一代中染色体的总数保持不变，这种方法也称为轮盘赌选择。

假设群体的大小为n，个体A i的适应度值为f(A i)，则个体A i被选择的概率P(A i)为：P(A i)=f(A i)∑ni=1f(A i)交叉算子：随机产生二串长度为q的二进制串，设有两个父代，P=(P1,P2,…,P q)以及M=(M1,M2,…,M q)，采用下面的方式得到两个子代：C=(C1,C2,…,C q) 和D=(D1,D 2,…,D q)，用其中的一个二进制串产生子代C，用另一个二进制串产生子代D。

基于遗传算法改进的BP神经网络加热炉控制系统参数优化摘要以加热炉控制系统为研究对象，提出了一种基于遗传算法改进的BP网络优化PID控制参数方法，并与经典的临界比例度―Ziegler-Nichols方法进行比较。

仿真结果表明该算法具有较好的控制效果。

关键词 PID控制；BP神经网络；遗传算法；参数优化1 引言由于常规PID控制具有鲁棒性好，结构简单等优点，在工业控制中得到了广泛的应用。

PID控制的基本思想是将P（偏差的比例），I（偏差的积分）和 D （偏差的微分）进线性组合构成控制器，对被控对象进行控制。

所以系统控制的优劣取决于这三个参数。

但是常规PID控制参数往往不能进行在线调整，难以适应对象的变化，另外对高阶或者多变量的强耦合过程，由于整定条件的限制，以及对象的动态特性随着环境等的变化而变化，PID参数也很难达到最优的状态。

神经网络具有自组织、自学习等优点，提出了利用BP神经网络的学习方法，对控制器参数进行在线调整，以满足控制要求。

由于BP神经网络学习过程较慢，可能导致局部极小点[2]。

本文提出了改进的BP算法，将遗传算法和BP算法结合对网络阈值和权值进行优化，避免权值和阈值陷入局部极小点。

2 加热炉的PID控制加热炉控制系统如图1所示，控制规律常采用PID控制规律。

图1 加热炉控制系统简图若加热炉具有的数学模型为：则PID控制过程箭图可以用图2表示。

其中，采用经典参数整定方法――临界比例度对上述闭环系统进行参数整定，确定PID控制器中 K p=2.259， K i=0.869， K d=0.276。

参考输入为单位阶跃信号，仿真曲线如图3所示。

图2 PID控制系统图3 Z―N整定的控制曲线仿真曲线表明，通过Z―N方法整定的参数控制效果不佳，加上PID参数不易实现在线调整，所以该方法不宜用于加热炉的在线控制。

3 基于遗传算法改进的BP神经网络PID控制器参数优化整定对于加热炉控制系统设计的神经网络自整定PID控制，它不依赖对象的模型知识，在网络结构确定之后，其控制功能能否达到要求完全取决于学习算法。

遗传算法优化神经网络-更好拟合函数1.案例背景BP神经网络是一种反向传递并且能够修正误差的多层映射函数，它通过对未知系统的输入输出参数进行学习之后，便可以联想记忆表达该系统。

但是由于BP网络是在梯度法基础上推导出来的，要求目标函数连续可导，在进化学习的过程中熟练速度慢，容易陷入局部最优，找不到全局最优值。

并且由于BP网络的权值和阀值在选择上是随机值，每次的初始值都不一样，造成每次训练学习预测的结果都有所差别。

遗传算法是一种全局搜索算法，把BP神经网络和遗传算法有机融合，充分发挥遗传算法的全局搜索能力和BP神经网络的局部搜索能力，利用遗传算法来弥补权值和阀值选择上的随机性缺陷，得到更好的预测结果。

本案例用遗传算法来优化神经网络用于标准函数预测，通过仿真实验表明该算法的有效性。

2.模型建立2.1预测函数2.2 模型建立遗传算法优化BP网络的基本原理就是用遗传算法来优化BP网络的初始权值和阀值，使优化后的BP网络能够更好的预测系统输出。

遗传算法优化BP网络主要包括种群初始化，适应度函数，交叉算子，选择算子和变异算子等。

2.3 算法模型3.编程实现3.1代码分析用matlabr2009编程实现神经网络遗传算法寻找系统极值，采用cell工具把遗传算法主函数分为以下几个部分：Contents•清空环境变量•网络结构确定•遗传算法参数初始化•迭代求解最佳初始阀值和权值•遗传算法结果分析•把最优初始阀值权值赋予网络预测•BP网络训练•BP网络预测主要的代码段分析如下：3.2结果分析采用遗传算法优化神经网络，并且用优化好的神经网络进行系统极值预测，根据测试函数是2输入1输出，所以构建的BP网络结构是2-5-1，一共去2000组函数的输入输出，用其中的1900组做训练，100组做预测。

遗传算法的基本参数为个体采用浮点数编码法，个体长度为21，交叉概率为0.4，变异概率为0.2，种群规模是20，总进化次数是50次，最后得到的遗传算法优化过程中最优个体适应度值变化如下所示：4 案例扩展4.1 网络优化方法的选择4.2 算法的局限性清空环境变量clcclear网络结构建立%读取数据load data input output%节点个数inputnum=2;hiddennum=5;outputnum=1;%训练数据和预测数据input_train=input(1:1900,:)';input_test=input(1901:2000,:)';output_train=output(1:1900)';output_test=output(1901:2000)';%选连样本输入输出数据归一化[inputn,inputps]=mapminmax(input_train);[outputn,outputps]=mapminmax(output_train);%构建网络net=newff(inputn,outputn,hiddennum);遗传算法参数初始化maxgen=50; %进化代数，即迭代次数sizepop=20; %种群规模pcross=[0.4]; %交叉概率选择，0和1之间pmutation=[0.2]; %变异概率选择，0和1之间%节点总数numsum=inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum;lenchrom=ones(1,numsum);bound=[-3*ones(numsum,1) 3*ones(numsum,1)]; %数据围%------------------------------------------------------种群初始化--------------------------------------------------------individuals=struct('fitness',zeros(1,sizepop), 'chrom',[]); %将种群信息定义为一个结构体avgfitness=[]; %每一代种群的平均适应度bestfitness=[]; %每一代种群的最佳适应度bestchrom=[]; %适应度最好的染色体%初始化种群for i=1:sizepop%随机产生一个种群individuals.chrom(i,:)=Code(lenchrom,bound); %编码（binary和grey的编码结果为一个实数，float的编码结果为一个实数向量）x=individuals.chrom(i,:);%计算适应度individuals.fitness(i)=fun(x,inputnum,hiddennum,outputnum,net,inputn, outputn); %染色体的适应度end%找最好的染色体[bestfitness bestindex]=min(individuals.fitness);bestchrom=individuals.chrom(bestindex,:); %最好的染色体avgfitness=sum(individuals.fitness)/sizepop; %染色体的平均适应度% 记录每一代进化中最好的适应度和平均适应度trace=[avgfitness bestfitness];迭代求解最佳初始阀值和权值进化开始for i=1:maxgeni% 选择individuals=Select(individuals,sizepop);avgfitness=sum(individuals.fitness)/sizepop;%交叉individuals.chrom=Cross(pcross,lenchrom,individuals.chrom,sizepop,bou nd);% 变异individuals.chrom=Mutation(pmutation,lenchrom,individuals.chrom,sizep op,i,maxgen,bound);% 计算适应度for j=1:sizepopx=individuals.chrom(j,:); %解码individuals.fitness(j)=fun(x,inputnum,hiddennum,outputnum,net,inputn, outputn);end%找到最小和最大适应度的染色体及它们在种群中的位置[newbestfitness,newbestindex]=min(individuals.fitness);[worestfitness,worestindex]=max(individuals.fitness);% 代替上一次进化中最好的染色体if bestfitness>newbestfitnessbestfitness=newbestfitness;bestchrom=individuals.chrom(newbestindex,:);endindividuals.chrom(worestindex,:)=bestchrom;individuals.fitness(worestindex)=bestfitness;avgfitness=sum(individuals.fitness)/sizepop;trace=[trace;avgfitness bestfitness]; %记录每一代进化中最好的适应度和平均适应度endi =1i =2i =3i =4i =5i =6i =7i =8i =9i =10i =11i =12i =13i =14i =15i =16i =17i =18i =19i =20i =21i =22i =23i =24i =25i =26i =27i =28i =29i =30i =31i =32i =33i =34i =35i =36i =37i =38i =39i =40i =41i =42i =43i =44i =45i =46i =47i =48i =49i =50遗传算法结果分析figure(1)[r c]=size(trace);plot([1:r]',trace(:,2),'b--');title(['适应度曲线 ''终止代数＝' num2str(maxgen)]); xlabel('进化代数');ylabel('适应度');legend('平均适应度','最佳适应度');disp('适应度变量');x=bestchrom;Warning: Ignoring extra legend entries.适应度变量把最优初始阀值权值赋予网络预测%用遗传算法优化的BP网络进行值预测w1=x(1:inputnum*hiddennum);B1=x(inputnum*hiddennum+1:inputnum*hiddennum+hiddennum);w2=x(inputnum*hiddennum+hiddennum+1:inputnum*hiddennum+hiddennum+hidd ennum*outputnum);B2=x(inputnum*hiddennum+hiddennum+hiddennum*outputnum+1:inputnum*hidd ennum+hiddennum+hiddennum*outputnum+outputnum);net.iw{1,1}=reshape(w1,hiddennum,inputnum);net.lw{2,1}=reshape(w2,outputnum,hiddennum);net.b{1}=reshape(B1,hiddennum,1);net.b{2}=B2;BP网络训练%网络进化参数net.trainParam.epochs=100;net.trainParam.lr=0.1;%net.trainParam.goal=0.00001;%网络训练net=train(net,inputn,outputn);BP网络预测%数据归一化inputn_test=mapminmax('apply',input_test,inputps);an=sim(net,inputn_test);test_simu=mapminmax('reverse',an,outputps);error=test_simu-output_test;figure(2)plot(error)k=error./output_testk =Columns 1 through 9-0.0003 0.0010 0.0003 0.0001 0.0002 -0.0005 0.0003 0.0003 0.0109Columns 10 through 18-0.0007 -0.0003 0.0002 -0.0008 -0.0015 -0.0002 0.0011 0.0002 0.0004Columns 19 through 270.0002 0.0003 -0.0000 0.0000 -0.0004 -0.0004 0.0005 0.0001 0.0023Columns 28 through 36-0.0000 -0.0003 0.0000 -0.0005 -0.0002 0.0003 -0.0002 -0.0002 0.0001Columns 37 through 450.0001 0.0002 0.0002 0.0011 -0.0004 -0.0006 0.0002 0.0000 0.0000Columns 46 through 540.0001 0.0001 0.0000 -0.0001 0.0016 0.0002 -0.0003 -0.0000 -0.0000Columns 55 through 630.0000 0.0003 -0.0004 0.0001 0.0002 0.0002 0.0002 0.0000 0.0002Columns 64 through 720.0002 -0.0001 0.0003 0.0005 0.0002 -0.0003 -0.0001 -0.0000 0.0002Columns 73 through 810.0000 -0.0002 -0.0002 0.0002 -0.0000 -0.0003 0.0001 -0.0001 0.0006Columns 82 through 90-0.0006 0.0003 0.0068 -0.0005 0.0001 -0.0001 -0.0001 -0.0010 -0.0002Columns 91 through 990.0001 0.0002 -0.0000 0.0003 0.0000 0.0000 -0.0003 -0.0001 0.0003Column 100-0.0004。