传热学思考题答案(第六章)

传热学第六章答案解析第六章复习题1、什么叫做两个现象相似，它们有什么共性？答：指那些用相同形式并具有相同内容的微分方程式所描述的现象，如果在相应的时刻与相应的地点上与现象有关的物理量一一对于成比例，则称为两个现象相似。

凡相似的现象，都有一个十分重要的特性，即描述该现象的同名特征数（准则）对应相等。

（1）初始条件。

指非稳态问题中初始时刻的物理量分布。

（2）边界条件。

所研究系统边界上的温度（或热六密度）、速度分布等条件。

（3）几何条件。

换热表面的几何形状、位置、以及表面的粗糙度等。

（4）物理条件。

物体的种类与物性。

2．试举出工程技术中应用相似原理的两个例子．3．当一个由若干个物理量所组成的试验数据转换成数目较少的无量纲以后，这个试验数据的性质起了什么变化？4．外掠单管与管内流动这两个流动现象在本质上有什么不同？5、对于外接管束的换热，整个管束的平均表面传热系数只有在流动方向管排数大于一定值后才与排数无关，试分析原因。

答：因后排管受到前排管尾流的影响（扰动）作用对平均表面传热系数的影响直到10排管子以上的管子才能消失。

6、试简述充分发展的管内流动与换热这一概念的含义。

答：由于流体由大空间进入管内时，管内形成的边界层由零开始发展直到管子的中心线位置，这种影响才不发生变法，同样在此时对流换热系数才不受局部对流换热系数的影响。

7、什么叫大空间自然对流换热？什么叫有限自然对流换热？这与强制对流中的外部流动和内部流动有什么异同？答：大空间作自然对流时，流体的冷却过程与加热过程互不影响，当其流动时形成的边界层相互干扰时，称为有限空间自然对流。

这与外部流动和内部流动的划分有类似的地方，但流动的动因不同，一个由外在因素引起的流动，一个是由流体的温度不同而引起的流动。

8．简述射流冲击传热时被冲击表面上局部表面传热系数的分布规律．9．简述数数，数，Gr Nu Pr 的物理意义．Bi Nu 数与数有什么区别？ 10．对于新遇到的一种对流传热现象，在从参考资料中寻找换热的特征数方程时要注意什么？相似原理与量纲分析6－1 、在一台缩小成为实物1/8的模型中，用200C 的空气来模拟实物中平均温度为2000C 空气的加热过程。

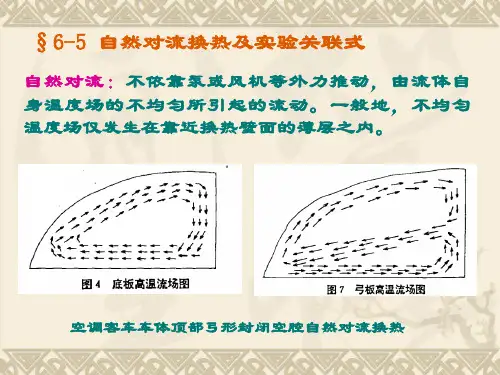
绪论思考题与习题（89P -）答案：1．冰雹落体后溶化所需热量主要是由以下途径得到： Q λ—— 与地面的导热量 f Q ——与空气的对流换热热量注：若直接暴露于阳光下可考虑辐射换热，否则可忽略不计。

2．略 3．略 4．略 5．略6．夏季：在维持20℃的室内，人体通过与空气的对流换热失去热量，但同时又与外界和内墙面通过辐射换热得到热量，最终的总失热量减少。

（T T 〉外内）冬季：在与夏季相似的条件下，一方面人体通过对流换热失去部分热量，另一方面又与外界和内墙通过辐射换热失去部分热量，最终的总失热量增加。

（T T 〈外内）挂上窗帘布阻断了与外界的辐射换热，减少了人体的失热量。

7．热对流不等于对流换热，对流换热 = 热对流 + 热传导 热对流为基本传热方式，对流换热为非基本传热方式 8．门窗、墙壁、楼板等等。

以热传导和热对流的方式。

9．因内、外两间为真空，故其间无导热和对流传热，热量仅能通过胆壁传到外界，但夹层两侧均镀锌，其间的系统辐射系数降低，故能较长时间地保持热水的温度。

当真空被破坏掉后，1、2两侧将存在对流换热，使其保温性能变得很差。

10．t R R A λλ=⇒ 1t R R A λλ==2218.331012m --=⨯11．q t λσ=∆ const λ=→直线 const λ≠ 而为λλ=（t ）时→曲线 12、略13．解：1211t q h h σλ∆=++＝18(10)45.9210.361870.61124--=++2W m111()f w q h t t =-⇒ 11137.541817.5787w f q t t h =-=-=℃ 222()w f q h t t =-⇒ 22237.54109.7124w f q t t h =+=-+=-℃ 45.92 2.83385.73q A W φ=⨯=⨯⨯= 14. 解：40.27.407104532t K R W A HL λσσλλ-====⨯⨯⨯30.24.4441045t R λσλ-===⨯2m K W • 3232851501030.44.44410t KW q m R λ--∆-==⨯=⨯ 3428515010182.37.40710t t KW R λφ--∆-==⨯=⨯ 15．()i w f q h t h t t =∆=-⇒i w f qt t h=+51108515573=+=℃0.05 2.551102006.7i Aq d lq W φππ===⨯⨯=16.解：12441.2 1.2()()100100w w t t q c ⎡⎤=-⎢⎥⎣⎦44227350273203.96()()139.2100100W m ++⎡⎤=⨯-=⎢⎥⎣⎦12''441.21.2()()100100w w t t qc ⎡⎤=-⎢⎥⎢⎥⎣⎦442273200273203.96()()1690.3100100W m ++⎡⎤=⨯-=⎢⎥⎣⎦'21.2 1.2 1.21690.3139.21551.1Wq q q m ∆=-=-=17．已知：224A m =、215000()Wh m K =•、2285()Wh m K =•、145t =℃2500t =℃、'2285()Wk h m K ==•、1mm σ=、398λ=()W m K •求：k 、φ、∆解：由于管壁相对直径而言较小，故可将此圆管壁近似为平壁 即：12111k h h σλ=++＝3183.5611101500039085-=⨯++2()W m k • 383.5624(50045)10912.5kA t KW φ-=∆=⨯⨯-⨯= 若k ≈2h'100k k k -∆=⨯％8583.561.7283.56-==％ 因为：1211h h ，21h σλ 即：水侧对流换热热阻及管壁导热热阻远小于燃气侧对流换热热阻，此时前两个热阻均可以忽略不记。

第六章传热习题热传导6-1. 如图所示，某工业炉的炉壁由耐火砖λ1= 1.3W/(m ·K)、绝热层λ2 = 0.18W/(m ·K)及普通砖λ3= 0.93W/(m ·K)三层组成。

炉膛壁内壁温度1100℃，普通砖层厚12cm, 其外表面温度为50℃。

通过炉壁的热损失为1200W/m 2, 绝热材料的耐热温度为900℃。

求耐火砖层的最小厚度及此时绝热层厚度。

设各层间接触良好，接触热阻可以忽略。

解：()()()433332222111t t t t t t q -=-=-=δλδλδλ ()5012.093.012003-=t 1553=t ℃ 6-2. 如图所示，为测量炉壁内壁的温度，在炉外壁及距外壁 1/3 厚度处设置热电偶，测得 t 2=300℃, t 3 =50℃。

求内壁温度 t 1 。

设炉壁由单层均质材料组成。

解：()()322211t t t t q -=-=δλδλ8001=t ℃6-3. 某火炉通过金属平壁传热使另一侧的液体蒸发，单位面积的蒸发速率为0.048kg/（m 2·s ），与液体交界的金属壁的温度为110℃。

时间久后，液体一侧的壁面上形成一层2mm 厚的污垢，污垢导热系数λ=0.65W/(m ·K)。

设垢层与液面交界处的温度仍为110℃，且蒸发速率需维持不变，求与垢层交界处的金属壁面的温度。

液体的汽化热r =2000kJ/kg 。

解：2kW/m 962000048.0=⨯=q38.4051=t ℃6-4. 为减少热损失，在外径Φ150mm 的饱和蒸汽管道外复盖保温层。

已知保温材料的导热系数λ=0.103+0.000198t (式中t 为℃)，蒸汽管外壁温度为 180℃，要求保温层外壁温度不超过 50℃,每米管道由于热损失而造成蒸汽冷凝的量控制在 1×10-4kg/(m ·s)以下，问保温层厚度应为多少？解：查180℃水蒸汽kJ/kg 3.2019=r126.0250180000198.0103.0=⎪⎭⎫⎝⎛+⨯+=λW/(m ﹒℃) *6-5. 如图所示，用定态平壁导热以测定材料的导热系数。

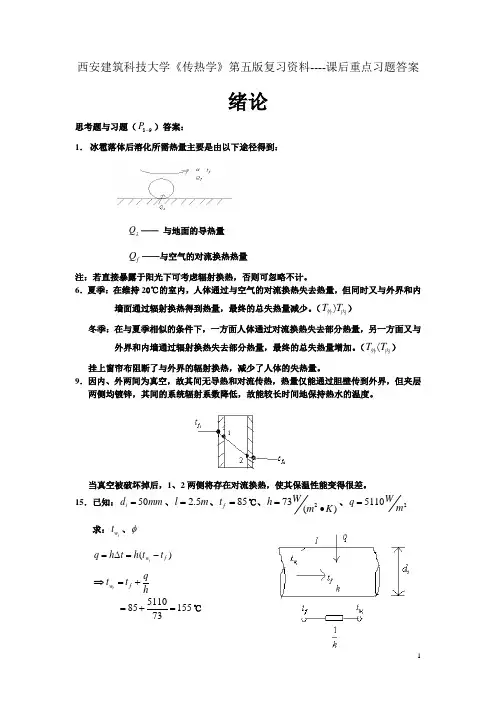
西安建筑科技大学《传热学》第五版复习资料----课后重点习题答案绪论思考题与习题（89P -）答案：1． 冰雹落体后溶化所需热量主要是由以下途径得到：Q λ—— 与地面的导热量 f Q ——与空气的对流换热热量注：若直接暴露于阳光下可考虑辐射换热，否则可忽略不计。

6．夏季：在维持20℃的室内，人体通过与空气的对流换热失去热量，但同时又与外界和内墙面通过辐射换热得到热量，最终的总失热量减少。

（T T 〉外内） 冬季：在与夏季相似的条件下，一方面人体通过对流换热失去部分热量，另一方面又与外界和内墙通过辐射换热失去部分热量，最终的总失热量增加。

（T T 〈外内） 挂上窗帘布阻断了与外界的辐射换热，减少了人体的失热量。

9．因内、外两间为真空，故其间无导热和对流传热，热量仅能通过胆壁传到外界，但夹层 两侧均镀锌，其间的系统辐射系数降低，故能较长时间地保持热水的温度。

当真空被破坏掉后，1、2两侧将存在对流换热，使其保温性能变得很差。

15．已知：50i d mm =、 2.5l m =、85f t =℃、273()Wh m K =•、25110Wq m =求：i w t 、φ()i w f q h t h t t =∆=-⇒i w f qt t h =+51108515573=+=℃0.05 2.551102006.7i Aq d lq W φππ===⨯⨯=17．已知：224A m =、215000()Wh m K =•、2285()Wh m K =•、145t =℃2500t =℃、'2285()Wk h m K ==•、1mm σ=、398λ=()Wm K •求：k 、φ、∆解：由于管壁相对直径而言较小，故可将此圆管壁近似为平壁 即：12111k h h σλ=++＝3183.5611101500039085-=⨯++2()W m k • 383.5624(50045)10912.5kA t KW φ-=∆=⨯⨯-⨯=若k ≈2h'100k k k -∆=⨯％8583.561.7283.56-==％ 因为：1211h h ，21h σλ 即：水侧对流换热热阻及管壁导热热阻远小于燃气侧对流换热热阻，此时前两个热阻均可以忽略不记。

第六章复习题1、什么叫做两个现象相似，它们有什么共性？答：指那些用相同形式并具有相同内容的微分方程式所描述的现象，如果在相应的时刻与相应的地点上与现象有关的物理量一一对于成比例，则称为两个现象相似。

凡相似的现象，都有一个十分重要的特性，即描述该现象的同名特征数（准则）对应相等。

（1） 初始条件。

指非稳态问题中初始时刻的物理量分布。

（2） 边界条件。

所研究系统边界上的温度（或热六密度）、速度分布等条件。

（3） 几何条件。

换热表面的几何形状、位置、以及表面的粗糙度等。

（4） 物理条件。

物体的种类与物性。

2．试举出工程技术中应用相似原理的两个例子．3．当一个由若干个物理量所组成的试验数据转换成数目较少的无量纲以后，这个试验数据的性质起了什么变化？4．外掠单管与管内流动这两个流动现象在本质上有什么不同？5、对于外接管束的换热，整个管束的平均表面传热系数只有在流动方向管排数大于一定值后才与排数无关，试分析原因。

答：因后排管受到前排管尾流的影响（扰动）作用对平均表面传热系数的影响直到10排管子以上的管子才能消失。

6、试简述充分发展的管内流动与换热这一概念的含义。

答：由于流体由大空间进入管内时，管内形成的边界层由零开始发展直到管子的中心线位置，这种影响才不发生变法，同样在此时对流换热系数才不受局部对流换热系数的影响。

7、什么叫大空间自然对流换热？什么叫有限自然对流换热？这与强制对流中的外部流动和内部流动有什么异同？答：大空间作自然对流时，流体的冷却过程与加热过程互不影响，当其流动时形成的边界层相互干扰时，称为有限空间自然对流。

这与外部流动和内部流动的划分有类似的地方，但流动的动因不同，一个由外在因素引起的流动，一个是由流体的温度不同而引起的流动。

8．简述射流冲击传热时被冲击表面上局部表面传热系数的分布规律．9．简述数数，数，Gr Nu Pr 的物理意义．Bi Nu 数与数有什么区别？ 10．对于新遇到的一种对流传热现象，在从参考资料中寻找换热的特征数方程时要注意什么？ 相似原理与量纲分析6－1 、在一台缩小成为实物1/8的模型中，用200C 的空气来模拟实物中平均温度为2000C 空气的加热过程。

绪论思考题与习题（89P -）答案：1．冰雹落体后溶化所需热量主要是由以下途径得到： Q λ—— 与地面的导热量 f Q ——与空气的对流换热热量注：若直接暴露于阳光下可考虑辐射换热，否则可忽略不计。

2．略 3．略 4．略 5．略6．夏季：在维持20℃的室内，人体通过与空气的对流换热失去热量，但同时又与外界和内墙面通过辐射换热得到热量，最终的总失热量减少。

（T T 〉外内）冬季：在与夏季相似的条件下，一方面人体通过对流换热失去部分热量，另一方面又与外界和内墙通过辐射换热失去部分热量，最终的总失热量增加。

（T T 〈外内）挂上窗帘布阻断了与外界的辐射换热，减少了人体的失热量。

7．热对流不等于对流换热，对流换热 = 热对流 + 热传导 热对流为基本传热方式，对流换热为非基本传热方式 8．门窗、墙壁、楼板等等。

以热传导和热对流的方式。

9．因内、外两间为真空，故其间无导热和对流传热，热量仅能通过胆壁传到外界，但夹层两侧均镀锌，其间的系统辐射系数降低，故能较长时间地保持热水的温度。

当真空被破坏掉后，1、2两侧将存在对流换热，使其保温性能变得很差。

10．t R R A λλ= ⇒ 1t R R A λλ== 2218.331012m --=⨯11．q t λσ=∆ const λ=→直线 const λ≠ 而为λλ=（t ）时→曲线12、略13．解：1211t q h h σλ∆=++＝18(10)45.9210.361870.61124--=++2W m111()f w q h t t =-⇒ 11137.541817.5787w f q t t h =-=-=℃222()w f q h t t =-⇒ 22237.54109.7124w f q t t h =+=-+=-℃ 45.92 2.83385.73q A W φ=⨯=⨯⨯= 14. 解：40.27.407104532t K R W A HL λσσλλ-====⨯⨯⨯30.2 4.4441045t R λσλ-===⨯2m K W • 3232851501030.44.44410t KW q m R λ--∆-==⨯=⨯ 3428515010182.37.40710t t KW R λφ--∆-==⨯=⨯ 15．()i w f q h t h t t =∆=-⇒i w f qt t h=+51108515573=+=℃0.05 2.551102006.7i Aq d lq W φππ===⨯⨯=16.解：12441.2 1.2()()100100w w t t q c ⎡⎤=-⎢⎥⎣⎦ 44227350273203.96()()139.2100100W m ++⎡⎤=⨯-=⎢⎥⎣⎦12''441.21.2()()100100w w t t qc ⎡⎤=-⎢⎥⎢⎥⎣⎦442273200273203.96()()1690.3100100W m ++⎡⎤=⨯-=⎢⎥⎣⎦'21.2 1.2 1.21690.3139.21551.1Wq q q m ∆=-=-=17．已知：224A m =、215000()Wh m K =•、2285()Wh m K =•、145t =℃2500t =℃、'2285()Wk h m K ==•、1mm σ=、398λ=()W m K •求：k 、φ、∆解：由于管壁相对直径而言较小，故可将此圆管壁近似为平壁即：12111k h h σλ=++＝3183.5611101500039085-=⨯++2()W m k • 383.5624(50045)10912.5kA t KW φ-=∆=⨯⨯-⨯= 若k ≈2h'100k k k -∆=⨯％8583.561.7283.56-==％ 因为：1211h h =，21h σλ= 即：水侧对流换热热阻及管壁导热热阻远小于燃气侧对流换热热阻，此时前两个热阻均可以忽略不记。

传热学思考题参考答案第一章：1、用铝制水壶烧开水时，尽管炉火很旺，但水壶仍安然无恙。

而一旦壶内的水烧干后水壶很快就被烧坏。

试从传热学的观点分析这一现象。

答：当壶内有水时，可以对壶底进展很好的冷却〔水对壶底的对流换热系数大〕，壶底的热量被很快传走而不至于温度升得很高；当没有水时，和壶底发生对流换热的是气体，因为气体发生对流换热的外表换热系数小，壶底的热量不能很快被传走，故此壶底升温很快，容易被烧坏。

2、什么是串联热阻叠加原那么，它在什么前提下成立？以固体中的导热为例，试讨论有哪些情况可能使热量传递方向上不同截面的热流量不相等。

答：在一个串联的热量传递过程中，如果通过每个环节的热流量都一样，那么各串联环节的总热阻等于各串联环节热阻的和。

例如：三块无限大平板叠加构成的平壁。

例如通过圆筒壁，对于各个传热环节的传热面积不相等，可能造成热量传递方向上不同截面的热流量不相等。

第二章：1、扩展外表中的导热问题可以按一维问题处理的条件是什么有人认为,只要扩展外表细长,就可按一维问题处理,你同意这种观点吗答：条件：〔1〕材料的导热系数，外表传热系数以及沿肋高方向的横截面积均各自为常数〔2〕肋片温度在垂直纸面方向〔即长度方向〕不发生变化，因此可取一个截面〔即单位长度〕来分析〔3〕外表上的换热热阻远远大于肋片中的导热热阻，因而在任一截面上肋片温度可认为是均匀的〔4〕肋片顶端可视为绝热。

并不是扩展外表细长就可以按一维问题处理，必须满足上述四个假设才可视为一维问题。

2、肋片高度增加引起两种效果:肋效率下降及散热外表积增加。

因而有人认为随着肋片高度的增加会出现一个临界高度，超过这个高度后，肋片导热热流量会下降，试分析该观点的正确性。

答：确实肋片高度增加会导致肋效率下降及散热外表积增加，但是总的导热量是增加的，只是增加的局部的效率有所减低，所以我们要选择经济的肋片高度。

第三章：1、由导热微分方程可知，非稳态导热只与热扩散率有关,而与导热系数无关。

第五章复习题1、试用简明的语言说明热边界层的概念。

答：在壁面附近的一个薄层内，流体温度在壁面的法线方向上发生剧烈变化，而在此薄层之外，流体的温度梯度几乎为零，固体表面附近流体温度发生剧烈变化的这一薄层称为温度边界层或热边界层。

2、与完全的能量方程相比，边界层能量方程最重要的特点是什么？答：与完全的能量方程相比，它忽略了主流方向温度的次变化率σα22x A，因此仅适用于边界层内，不适用整个流体。

3、式（5—4）与导热问题的第三类边界条件式（2—17）有什么区别？答：=∂∆∂-=yyt th λ（5—4）)()(f w t t h h t-=∂∂-λ （2—11）式（5—4）中的h 是未知量，而式（2—17）中的h 是作为已知的边界条件给出，此外（2—17）中的λ为固体导热系数而此式为流体导热系数，式（5—4）将用来导出一个包括h 的无量纲数，只是局部表面传热系数，而整个换热表面的表面系数应该把牛顿冷却公式应用到整个表面而得出。

4、式（5—4）表面，在边界上垂直壁面的热量传递完全依靠导热，那么在对流换热中，流体的流动起什么作用？答：固体表面所形成的边界层的厚度除了与流体的粘性有关外还与主流区的速度有关，流动速度越大，边界层越薄，因此导热的热阻也就越小，因此起到影响传热大小5、对流换热问题完整的数字描述应包括什么内容？既然对大多数实际对流传热问题尚无法求得其精确解，那么建立对流换热问题的数字描述有什么意义？答：对流换热问题完整的数字描述应包括：对流换热微分方程组及定解条件，定解条件包括，（1）初始条件 （2）边界条件 （速度、压力及温度）建立对流换热问题的数字描述目的在于找出影响对流换热中各物理量之间的相互制约关系，每一种关系都必须满足动量，能量和质量守恒关系，避免在研究遗漏某种物理因素。

基本概念与定性分析5-1 、对于流体外标平板的流动，试用数量级分析的方法，从动量方程引出边界层厚度的如下变化关系式：x xRe 1~δ解：对于流体外标平板的流动，其动量方程为：221xy u v dx d y u v xy u ∂+-=∂∂+∂∂ρρ 根据数量级的关系，主流方的数量级为1，y 方线的数量级为δ则有2211111111δρδδv +⨯-=⨯+⨯ 从上式可以看出等式左侧的数量级为1级，那么，等式右侧也是数量级为1级， 为使等式是数量级为1，则v 必须是2δ量级。

绪论1． 冰雹落体后溶化所需热量主要是由以下途径得到：Q λ—— 与地面的导热量 f Q ——与空气的对流换热热量注：若直接暴露于阳光下可考虑辐射换热，否则可忽略不计。

6．夏季：在维持20℃的室内，人体通过与空气的对流换热失去热量，但同时又与外界和内墙面通过辐射换热得到热量，最终的总失热量减少。

（T T 〉外内）冬季：在与夏季相似的条件下，一方面人体通过对流换热失去部分热量，另一方面又与外界和内墙通过辐射换热失去部分热量，最终的总失热量增加。

（T T 〈外内）挂上窗帘布阻断了与外界的辐射换热，减少了人体的失热量。

7．热对流不等于对流换热，对流换热 = 热对流 + 热传导 热对流为基本传热方式，对流换热为非基本传热方式 8．门窗、墙壁、楼板等等。

以热传导和热对流的方式。

9．因内、外两间为真空，故其间无导热和对流传热，热量仅能通过胆壁传到外界，但夹层两侧均镀锌，其间的系统辐射系数降低，故能较长时间地保持热水的温度。

当真空被破坏掉后，1、2两侧将存在对流换热，使其保温性能变得很差。

10．t R R A λλ= ⇒ 1t R R A λλ== 2218.331012m --=⨯11．q t λσ=∆ const λ=→直线 const λ≠ 而为λλ=（t ）时→曲线 12. i R α 1R λ 3R λ 0R α 1f t −−→ q首先通过对流换热使炉子内壁温度升高，炉子内壁通过热传导，使内壁温度生高，内壁与空气夹层通过对流换热继续传递热量，空气夹层与外壁间再通过热传导，这样使热量通过空气夹层。

（空气夹层的厚度对壁炉的保温性能有影响，影响a α的大小。

）13．已知：360mm σ=、0.61()W m K λ=• 118f t =℃2187()Wh m K =•210f t =-℃ 22124()Wh m K =• 墙高2.8m ，宽3m求：q 、1w t 、2w t 、φ 解：1211t q h h σλ∆=++＝18(10)45.9210.361870.61124--=++2W m111()f w q h t t =-⇒ 11137.541817.5787w f q t t h =-=-=℃ 222()w f q h t t =-⇒ 22237.54109.7124w f q t t h =+=-+=-℃ 45.92 2.83385.73q A W φ=⨯=⨯⨯=14.已知：3H m =、0.2m σ=、2L m =、45λ=()W m K • 1150w t =℃、2285w t =℃ 求：t R λ、R λ、q 、φ解：40.27.407104532t K R W A HL λσσλλ-====⨯⨯⨯30.2 4.4441045t R λσλ-===⨯2m K W • 3232851501030.44.44410t KW q m R λ--∆-==⨯=⨯ 3428515010182.37.40710t t KW R λφ--∆-==⨯=⨯ 15．已知：50i d mm =、 2.5l m =、85f t =℃、273()Wh m K =•、25110Wq m =求：i w t 、φ()i w f q h t h t t =∆=-⇒i w f qt t h=+51108515573=+=℃0.05 2.551102006.7i Aq d lq W φππ===⨯⨯=16.已知:150w t =℃、220w t =℃、241.2 3.96()W c m K =•、1'200w t =℃求： 1.2q 、'1.2q 、 1.2q ∆解：12441.2 1.2()()100100w w t t q c ⎡⎤=-⎢⎥⎣⎦44227350273203.96()()139.2100100W m ++⎡⎤=⨯-=⎢⎥⎣⎦12''441.21.2()()100100w w t t qc ⎡⎤=-⎢⎥⎢⎥⎣⎦442273200273203.96()()1690.3100100W m ++⎡⎤=⨯-=⎢⎥⎣⎦'21.2 1.2 1.21690.3139.21551.1Wq q q m ∆=-=-=17．已知：224A m =、215000()Wh m K =•、2285()Wh m K =•、145t =℃2500t =℃、'2285()Wk h m K ==•、1mm σ=、398λ=()W m K •求：k 、φ、∆解：由于管壁相对直径而言较小，故可将此圆管壁近似为平壁 即：12111k h h σλ=++＝3183.5611101500039085-=⨯++2()W m k • 383.5624(50045)10912.5kA t KW φ-=∆=⨯⨯-⨯= 若k ≈2h'100k k k -∆=⨯％8583.561.7283.56-==％ 因为：1211h h ，21h σλ 即：水侧对流换热热阻及管壁导热热阻远小于燃气侧对流换热热阻，此时前两个热阻均可以忽略不记。

传热学思考题答案（第六章）1、热辐射与导热和对流换热相比有何本质区别？答：1、辐射换热不依靠物质的接触进行热传递，而导热和对流换热都必须由冷、热物体直接接触或通过中间介质接触才能进行。

2、辐射换热过程伴有能量的两次转化，首先是发射物体的内能转化为电磁波向外发射，到达吸收物体时电磁波能又转化为内能。

3、一切物体只要温度高于绝对零度，即T>O K时，都在不断地发射热射线。

对有a 差的两物体，高温物体辐射给低温物体的能量大于低温物体辐射给高温物体的能量;相同温度的物体间仍在进行辐射换热，只是悔物体辐射出去的能量等于吸收的能量。

2、什么叫黑体？在热辐射理论中为什么引入这一概念？答：吸收比a=1的物体叫做黑体，黑体是一个理想化的物体，黑体辐射的特征反映了物体辐射在波长、温度和方向上的变化规律，这位研究实际物体的辐射提供了理论依据和简化分析基础。

3、一个物体，只要温度T>0K就会不断向外界辐射能量，试问它的温度为什么不会因热辐射而降至0K？4、温度均匀的空腔壁面上的小孔具有黑体辐射的特性，那么空腔内部的辐射是否也是黑体辐射？答：空间内壁壁面不一定是黑体辐射，之所以小孔呈现出黑体特性，是因为辐射在空腔内经历了很多次吸收和反射过程，使离开小孔的能量微乎其微。

5、黑体的辐射能按空间方向是怎样分布？定向辐射强度与空间方向无关是否意味着黑体的辐射能在半球空间各方向上是均匀分布的？答：黑体辐射能按空间方向分布服从兰贝特定律。

定向辐射强度与空间方向无关并不意味着黑体辐射能在半球空间各方向上是均匀分布的，因为辐射强度是指单位可见面积的辐射能，在不同方向，可见面积是不同的，即定向辐射力是不同的。

6、为什么要引入灰体这样的理想物体？说明引入灰体的简化对工程辐射换热计算的意义。

答：光谱吸收比与波长无关的物体叫做灰体，灰体的吸收比恒等于同温度下的发射率，把实际物体当做灰体如理，可以不必考虑投入辐射的特性，将大大简化辐射换热的计算。

绪论思考题与习题（89P -）答案：1． 冰雹落体后溶化所需热量主要是由以下途径得到：Q λ—— 与地面的导热量 f Q ——与空气的对流换热热量注：若直接暴露于阳光下可考虑辐射换热，否则可忽略不计。

6．夏季：在维持20℃的室内，人体通过与空气的对流换热失去热量，但同时又与外界和内墙面通过辐射换热得到热量，最终的总失热量减少。

（T T 〉外内）冬季：在与夏季相似的条件下，一方面人体通过对流换热失去部分热量，另一方面又与外界和内墙通过辐射换热失去部分热量，最终的总失热量增加。

（T T 〈外内）挂上窗帘布阻断了与外界的辐射换热，减少了人体的失热量。

7．热对流不等于对流换热，对流换热 = 热对流 + 热传导 热对流为基本传热方式，对流换热为非基本传热方式 8．门窗、墙壁、楼板等等。

以热传导和热对流的方式。

9．因内、外两间为真空，故其间无导热和爱上大声地大得多411231啊实打实大对流传热，热量仅能通过胆壁传到外界，但夹层两侧均镀锌，其间的系统辐长时间地保持热水的温度。

当真空被破坏掉后，1、2两侧将存在对流换热，使其保温性能变得很差。

10．t R R A λλ= ⇒ 1t R R A λλ== 2218.331012m --=⨯11．q t λσ=∆ c o n s t λ=→直线 c o n s t λ≠ 而为λλ=（t ）时→曲线12. R R R R t −−→ q首先通过对故其间无导热和爱上大声地大得多411231啊实打实大对，空气夹层与外壁间再通过热传导，这样使热量通过空气夹层。

（空气夹层的厚度对壁炉的保温性能有影响，影响a α的大小。

）13．已知：360mm σ=、0.61()Wm K λ=∙ 118f t =℃ 2187()Wh m K =∙210f t =-℃ 22124()Wh m K =∙ 墙高2.8m ，宽3m求：q 、1w t 、2w t 、φ 解：12t q h h σλ∆=++＝18(10)45.9210.361870.61124--=++2W m111()f w q h t t =-⇒ 11137.541817.5787w f q t t h =-=-=℃222()w f q h t t =-⇒ 22237.54109.7124w f q t t h =+=-+=-℃ 45.92 2.83385.73q A W φ=⨯=⨯⨯=14.已知：3H m =、0.2m σ=、2L m =、45λ=()W m K ∙ 1150w t =℃、2285w t =℃求：t R λ、R λ、q 、φ解：40.27.407104532t K R W A HL λσσλλ-====⨯⨯⨯30.24.4441045t R λσλ-===⨯2m K W ∙3232851501030.44.44410t KW q m R λ--∆-==⨯=⨯ 3428515010182.37.40710t t KW R λφ--∆-==⨯=⨯ 15．已知：50i d mm =、 2.5l m =、85f t =℃、273()Wh m K =∙、25110Wq m =求：i w t 、φ()i w f q h t h t t =∆=-⇒i w f qt t h =+51108515573=+=℃0.05 2.551102006.7i Aq d lq Wφππ===⨯⨯=16.已知:150w t =℃、220w t =℃、241.2 3.96()W c m K =∙、1'200w t =℃求： 1.2q 、'1.2q 、 1.2q ∆ 解：12441.21.2()()100100w w t t q c ⎡⎤=-⎢⎥⎣⎦44227350273203.96()()139.2100100W m ++⎡⎤=⨯-=⎢⎥⎣⎦12''441.21.2()()100100w w t t qc ⎡⎤=-⎢⎥⎢⎥⎣⎦442273200273203.96()()1690.3100100W m ++⎡⎤=⨯-=⎢⎥⎣⎦'21.2 1.2 1.21690.3139.21551.1Wq q q m ∆=-=-=17．已知：224A m =、215000()Wh m K =∙、2285()Wh m K =∙、145t =℃2500t =℃、'2285()Wk h m K ==∙、1mm σ=、398λ=()Wm K ∙求：k 、φ、∆解：故其间无导热和爱上大声地大得多411231啊实打实大对即：12111k h h σλ=++＝3183.5611101500039085-=⨯++2()W m k ∙ 383.5624(50045)10912.5kA t KW φ-=∆=⨯⨯-⨯=若k ≈2h'100k k k -∆=⨯％8583.561.7283.56-==％ 因为：1211h h ，21h σλ 即：水故其间无导热和爱上大声地大得多411231啊实打实大对18．略第一章导热理论基础 思考题与习题（24P ）答案： 1． 略2． 已知：10.62()W m K λ=∙、20.65()W m K λ=∙、30.024()W m K λ=∙、40.016()W m K λ=∙求：'R λ、''R λ解：故其间无导热和爱上大声地大得多411231啊实打实大对 4．略 5．6．已知：50mm σ=、2t a bx =+、200a =℃、2000b =-℃/m 2、45()Wm K λ=∙求：（1）0x q=、6x q= （2）v q解：（1）00020x x x dtq bx dxλλ====-=-=3322452(2000)5010910x x x dt Wq bx m dxσσσλλ-====-=-=-⨯⨯-⨯⨯=⨯（2）由220vq d t dx λ+=2332245(2000)218010v d t W q b m dxλλ=-=-=-⨯-⨯=⨯7．略8．略9．取如图所示球坐标，其为无内热源一维非稳态导热 故有：22t a t r r r r τ∂∂∂⎛⎫= ⎪∂∂∂⎝⎭00,t t τ==0,0tr r∂==∂ ,()f tr R h t t rλ∂=-=-∂10．解：建立如图坐标，在x=x 位置取dx 长度微元体，根据能量守恒有：x dx x Q Q Q ε++= （1）x dt Q dx λ=-+()x dx d dt Q t dx dx dxλ+=-++∙ 4()b b Q EA E A T Udx εεεσ===代入式（1），合并整理得：2420b fU d t T dx εσλ-= 该问题数学描写为：2420b fU d t T dx εσλ-= 00,x t T == ,0()x ldtx l dx===假设的4()b e x ldt fT f dxλεσ=-=真实的第二章稳态导热思考题与习题（P 51-53）答案 1.略 2.略3.解：（1）温度分布为 121w w w t t t t x δ-=-(设12w w t t >)其与平壁的材料无关的根本原因在c o u s tλ=（即常物性假设），否则t 与平壁的材料有关 （2）由 dtq dxλ=- 知，q 与平壁的材料即物性有关 4.略5.解： 2111222()0,(),w w w w d dt r dr drr r t t t t r r t t ===>==设有： 12124()11w w Q t t r r πλ=-- 21214F r r R r r λπλ-=6.略7.已知：4,3,0.25l m h m δ=== 115w t =℃, 25w t =-℃, 0.7/()W m k λ=⋅ 求：Q解： ,l h δ ，可认为该墙为无限大平壁 15(5)0.7(43)6720.25tQ FW λδ∆--∴==⨯⨯⨯= 8.已知：2220,0.14,15w F m m t δ===-℃，31.28/(), 5.510W m k Q W λ=⋅=⨯ 求：1w t解： 由 tQ Fλδ∆= 得一无限平壁的稳态导热312 5.510150.141520 1.28w w Q t t F δλ⨯=+=-+⨯=⨯℃ 9.已知：12240,20mm mmδδ==，120.7/(),0.58/()W m k W m k λλ=⋅=⋅3210.06/(),0.2Wm k q q λ=⋅= 求：3δ解： 设两种情况下的内外面墙壁温度12w w t t 和保持不变，且12w w t t >由题意知：1211212w w t t q δδλλ-=+221313212tw tw 1λ12λ23λ3122312123w w t t q δδδλλλ-=++再由： 210.2q q =，有121231212121230.2w w w wt t t t δδδδδλλλλλ--=+++得： 123312240204()40.06()90.60.70.58mm δδδλλλ=+=⨯⨯+= 10.已知：1450w t =℃，20.0940.000125,50w t t λ=+=℃，2340/q W m ≤ 求：δ 解： 412,0.094 1.25102w w t t tq m m λλδ+∆==+⨯⨯41212[0.094 1.2510]2w w w w t t t t t mq qδλ+-∆==+⨯⋅ 44505045050[0.0941.2510]0.14742340m +-=+⨯⨯⨯= 即有 2340/147.4q W m m mδ≤≥时有 11.已知：11120,0.8/()mm W m k δλ==⋅，2250,0.12/()mm W m k δλ==⋅33250,0.6/()mm W m k δλ==⋅求：'3?δ= 解： '2121'3123112313,w w w wt t t t q q δδδδδλλλλλ--==+++ 由题意知：'q q = 即有：2121'3123112313w w w wt t t t δδδδδλλλλλ--=+++ '33322λδδδλ=+220.6250505000.12mm =+⨯=12.已知：1600w t =℃，2480w t =℃，3200w t =℃，460w t =℃ 求：123,,R R R R R R λλλλλλ解：由题意知其为多层平壁的稳态导热 故有： 14122334123w w w w w w w w t t t t t t t t q R R R R λλλλ----====∴112146004800.2260060w w w w R t t R t t λλ--===-- 223144802000.5260060w w w w R t t R t t λλ--===-- 33414200600.2660060w w w w R t t R t t λλ--===-- 13.略14.已知：1）11012,40/(),3,250f mm W m k mm t δλδ==⋅==℃，60f t =℃ 220112,75/(),50/()h W m k h W m k λλ==⋅=⋅ 2）223,320/()mm W m k δλ==⋅ 3）2'23030,,70/()h W m k δδλλ===⋅求：12312,,,,,q q q k k k ∆∆∆ 解：未变前的122030102250605687.2/1113101754050f f t t q W m h h δλ---===⨯++++ 1）21311121129.96/()12101754050k W m k h h δλ-===⋅⨯++++ 21129.96(25060)5692.4/q k t W m =∆=⨯-=25692.45687.2 5.2/q q q W m ∆=-=-=tw 1tw 4tw 2tw 3R 1R2R3R =R 1+R 2R3+t αt f222）22321221129.99/()11131017532050k W m k h h δλ-===⋅⨯++++ 22229.99(25060)5698.4/q k t W m =∆=⨯-=22205698.45687.211.2/q q q W m ∆=-=-=3) 22330'101136.11/()11131********k W m k h h δλ-===⋅⨯++++ 23336.11(25060)6860.7/q k t W m =∆=⨯-=23306860.75687.21173.5/q q q W m ∆=-=-= 321q q q ∴∆∆>∆ ，第三种方案的强化换热效果最好 15.已知：35,130A C B mm mm δδδ===，其余尺寸如下图所示，1.53/(),0.742/(A CB Wm k W m k λλλ==⋅=⋅ 求：R λ解：该空斗墙由对称性可取虚线部分，成为三个并联的部分11113222,A B C A B C R R R R RR R R R =++==++ 3321111311135101301020.1307()/1.53 1.53C A B A B C R R m k W δδδλλλ--⨯⨯∴=++=⨯+==⋅ 332322235101301020.221()/1.530.742C A B R m k W δδδλλλ--⨯⨯=++=⨯+=⋅R 1R 1R 1R2R3R 2R 2R3R32212115.0410()/1111220.13070.221R m k W R R λ-∴===⨯⋅⨯+⨯+16.已知：121160,170,58/()d mm d mm W m k λ===⋅，2230,0.093/()mm W m k δλ==⋅33140,0.17/(),300w m m W m k t δλ==⋅=℃，450w t =℃ 求：1）123,,R R R λλλ; 2) l q : 3) 23,w w t t . 解：1）4211111170lnln 1.66410()/2258160d R m k W d λπλπ-===⨯⋅⨯2222221117060lnln 0.517()/220.093170d R m k W d λδπλπ++===⋅⨯ 223332222111706080lnln 0.279()/2220.1717060d R m k W d λδδπλδπ++++===⋅+⨯+132R R R λλλ∴< 2) 2330050314.1/0.5170.279l i t t q W m R R R λλλ∆∆-====++∑3）由 121w w l t t q R λ-=得 tw 1112323tw 44211300314.1 1.66410299.95w w l t t q R λ-=-=-⨯⨯=℃同理：34350314.10.279137.63w w l t t q R λ=+=+⨯=℃17.已知：1221211,,22m m d d δδλλ=== 求：'ll q q 解：忽略管壁热阻010*******22211ln ln 222d d R d d λδδδπλπλδ+++=++'010*******22211ln ln 222d d R d d λδδδπλπλδ+++=++'',l l t tq q R R λλ∆∆== （管内外壁温13,w w t t 不变）01012'20101'010121020122211lnln 222ln ln 222l l d d q R d d q R d d λλδδδπλπλδδδδπλπλδ+++++∴==++01010010101001241lnln 22ln ln 22d d d d d d δδδδδδ++++=++由题意知： 1001011[(2)]2m d d d d δδ=++=+ 2112011[(2)]32mm m d d d d δδ=++=+ 即：2101010232()m m d d d d d δδδ=⇒+=+⇒= （代入上式） ''15ln 3ln23 1.277ln 3ln 23l l q R q R λλ+∴===+ 即： '0.783l l q q =3'21.7%l llq q q -∆==即热损失比原来减小21.7%。