多采样率信号处理

多采样率数字信号处理在数字语音系统中的
应用
随着数字信号处理技术的快速发展，多采样率数字信号处理在数字语音系统中发挥着重要作用。

它通过在数字语音处理过程中使用不同的采样率，提供了更高的灵活性和更好的性能。

首先，多采样率数字信号处理在数字语音编解码中提供了更高的质量和效率。

在语音编码过程中，为了减小数据量和节省传输带宽，采样率通常会降低。

然而，在一些要求高质量语音的应用中，如语音通信和语音识别，需要更高的采样率来保证声音的清晰度和真实性。

通过多采样率数字信号处理技术，可以在编码过程中灵活地提高采样率，从而提供更高质量的语音信号。

其次，多采样率数字信号处理在音频变速和音高转换中发挥重要作用。

在一些音频应用中，如音乐制作和语音合成，需要对音频进行变速和音高转换，以满足不同的需求。

通过多采样率数字信号处理技术，可以按照不同的速度和音高要求，灵活地改变采样率，从而实现音频的变速和音高转换。

此外，多采样率数字信号处理还在降噪和回声消除等音频处理算法中起到重要作用。

在一些嘈杂环境下，语音信号可能会受到环境噪声和回声的干扰。

通过多采样率数字信号处理技术，可以对输入信号进行不同采样率的处理，从而提取出噪声和回声的特征，并通过合适的算法进行降噪和回声消除，提高语音信号的清晰度和可懂性。

总之，多采样率数字信号处理在数字语音系统中具有广泛的应用。

它通过灵活调整采样率，提供了更高质量和更好性能的音频处理和编
解码功能。

因此，在设计和实现数字语音系统时，我们应充分利用多
采样率数字信号处理技术，以提升语音系统的性能。

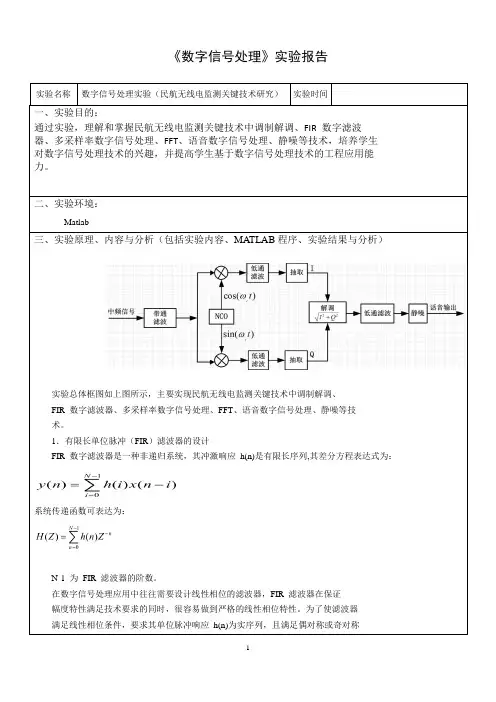
《数字信号处理》实验报告实验名称数字信号处理实验（民航无线电监测关键技术研究）实验时间一、实验目的：通过实验，理解和掌握民航无线电监测关键技术中调制解调、FIR 数字滤波器、多采样率数字信号处理、FFT、语音数字信号处理、静噪等技术，培养学生对数字信号处理技术的兴趣，并提高学生基于数字信号处理技术的工程应用能力。

二、实验环境：Matlab三、实验原理、内容与分析（包括实验内容、MATLAB程序、实验结果与分析）实验总体框图如上图所示，主要实现民航无线电监测关键技术中调制解调、FIR 数字滤波器、多采样率数字信号处理、FFT、语音数字信号处理、静噪等技术。

1．有限长单位脉冲（FIR）滤波器的设计FIR 数字滤波器是一种非递归系统，其冲激响应h(n)是有限长序列,其差分方程表达式为：系统传递函数可表达为：N-1 为FIR 滤波器的阶数。

在数字信号处理应用中往往需要设计线性相位的滤波器，FIR 滤波器在保证幅度特性满足技术要求的同时，很容易做到严格的线性相位特性。

为了使滤波器满足线性相位条件，要求其单位脉冲响应h(n)为实序列，且满足偶对称或奇对称条件，即h(n)=h(N-1-n)或h(n)=-h(N-1-n)。

这样，当N 为偶数时，偶对称线性相位FIR 滤波器的差分方程表达式为：由上可见FIR 滤波器不断地对输入样本x(n)延时后，再做乘法累加算法，将滤波器结果y(n)输出，因此，FIR 实际上是一种乘法累加运算。

而对于线性相位FIR 而言，利用线性相位FIR 滤波器系数的对称特性，可以采用结构精简的FIR 结构将乘法器数目减少一半。

2．AM 调制解调AM 调制解调过程如下：3．多采样率数字信号处理一般认为，在满足采样定理的前提下，首先将以采样率F1 采集的数字信号进行D/A 转换, 变成模拟信号，再按采样率F2 进行A/D 变换，从而实现从F1 到F2 的采样率转换。

但这样较麻烦，且易使信号受到损伤，所以实际上改变采样率是在数字域实现的。

数字信号处理教案目录第1章 概 论................................................................................................................................... 1 第2章 离散时间信号与系统 ......................................................................................................... 1 第3章Z 变换及其性质 .................................................................................................................. 3 第4章 连续时间信号采样与量化误差 ......................................................................................... 4 第5章变换域分析 ........................................................................................................................... 4 第6章 离散傅立叶变换 ................................................................................................................. 5 第7章 快速傅立叶变换 ................................................................................................................. 6 第8章 离散时间系统的实现 ......................................................................................................... 6 第9章 FIR 数字滤波器的设计 ..................................................................................................... 7 第10 章 IIR 数字滤波器的设计 ................................................................................................... 8 第11 章多采样率信号处理 ............................................................................................................ 8 第12 章多采样率信号处理 ............................................................................................................ 9 第13 章 其它信号变换法 (10)第1章 概 论习题1、将)5cos()cos( t t ωω+展成Fourier 复指数形式。

多采样率信号处理的发展作者：万伟程李艳华周三文来源：《现代电子技术》2014年第13期摘要：数字通信系统中，为适应传输、降低资源消耗、适于处理操作，常需要变换信号的采样率。

多采样率信号处理理论从语音信号处理中发展起来，在应用中不断丰富。

随着软件无线电的应用，多采样率变换在数字信号领域占据越来越重要的地位。

多采样率信号处理技术与小波分析、分数阶傅里叶变换等其他信号处理技术相结合是未来发展的方向。

关键词：多采样率；信号处理；数字滤波器；傅里叶变换中图分类号： TN911.72⁃34 文献标识码： A 文章编号： 1004⁃373X（2014）13⁃0057⁃03Development of signal processing at multi⁃sampling ratesWAN Wei⁃cheng， LI Yan⁃hua， ZHOU San⁃wen（Beijing Research Institute of Telemetry， Beijing 100076， China）Abstract： The sampling rate of signal often needs to be changed for fitting transmission，reducing resource consumption and suiting process handling in digital communication system. Multirate signal processing theory arose from speech signal processing and was enriched in application. Multirate signal processing plays an important role in digital signal processing with the application of software radio. It′s a tendency of combining the multirate signal processing with wavelet analysis and fractional Fourier transform.Keywords： multirate sample； signal processing； digital filter； Fourier transform0 引言20世纪60年代以来，数字信号由于处理灵活、精度高、稳定性好等优点得到广泛应用[1]。

[离散时间信号处理学习笔记]14.多采样率信号处理多采样率信号处理⼀般是指利⽤增采样、减采样、压缩器和扩展器等⽅式来提⾼信号处理系统效率的技术（These multirate techniques refer in general to utilizing upsampling, downsampling, compressors, and expanders in a variety of ways to increase the efficiency of signal-processing systems. ）本⽂章主要讨论多采样率技术中的两个研究成果：滤波与压缩器/扩展器的互换；多相分解。

尽管上⼀篇⽂章中已经讨论过这部分内容，不过由于这部分是理解本⽂所必须的关键知识点，这⾥将在时域与频域展开更详细的分析。

压缩器假设压缩器的压缩率为M，那么压缩器在时域上的表⽰为x_d[n] = x[nM]x[n]的采样频率为T，那么x_d[n]的采样频率为T_d = MT，按照，有\begin{align*} X(e^{j\omega}) &= \frac{1}{T}\sum_{k=-\infty}^{\infty}X_c\left[ j\left(\frac{\omega}{T}-\frac{2\pi k}{T}\right)\right ]\\ X_d(e^{j\omega}) &= \frac{1}{MT}\sum_{r=-\infty}^{\infty}X_c\left[ j\left(\frac{\omega}{MT}-\frac{2\pi r}{MT}\right)\right ] \end{align*}压缩前的序列频谱X(e^{j\omega})与压缩后的序列频谱X_d(e^{j\omega})之间有如下关系\begin{align*} X_d(e^{j\omega}) &= \frac{1}{MT}\sum_{r=-\infty}^{\infty}X_c\left[ j\left(\frac{\omega}{MT}-\frac{2\pi r}{MT}\right)\right ] \\ & = \frac{1}{MT}\left\{\cdot\cdot\cdot+X_c\left[j\left(\frac{\omega}{MT}-\frac{-2\pi}{MT} \right ) \right ] +X_c\left[ j\left(\frac{\omega}{MT}-\frac{0} {MT}\right)\right ] + X_c\left[j\left(\frac{\omega}{MT}-\frac{2\pi}{MT} \right ) \right ]+\cdot\cdot\cdot \right \}\\ & = \frac{1}{MT}\left\{\cdot\cdot\cdot+X_c\left[j\left(\frac{\omega}{MT}-\frac{0}{MT} \right ) \right ]+\cdot\cdot\cdot +X_c\left[ j\left(\frac{\omega}{MT}-\frac{2(M-1)\pi} {MT}\right)\right ]\right.\\ &\quad\qquad\qquad\left.+ X_c\left[j\left(\frac{\omega}{MT}-\frac{2M\pi}{MT} \right ) \right ]+\cdot\cdot\cdot+X_c\left[j\left(\frac{\omega}{MT}-\frac{2M\pi}{MT} -\frac{2(M-1)\pi}{MT}\right ) \right ]+\cdot\cdot\cdot \right \}\\ \end{align*} \begin{align*} \qquad\quad\ &= \frac{1}{MT}\left\{\cdot\cdot\cdot+\sum_{i=0}^{M-1}X_c\left[j\left(\frac{\omega}{MT}-\frac{2i\pi}{MT} \right ) \right ]+\sum_{i=0}^{M-1}X_c\left[j\left(\frac{\omega}{MT}-\frac{2i\pi}{MT}-\frac{2\pi}{T} \right ) \right ]+\cdot\cdot\cdot\right\}\\ &= \frac{1} {MT}\sum_{k=-\infty}^{\infty} \sum_{i=0}^{M-1}X_c\left[j\left(\frac{\omega}{MT}-\frac{2\pi i}{MT}-\frac{2\pi k}{T} \right ) \right ] \\ &=\frac{1} {M}\sum_{i=0}^{M-1}\left\{\frac{1}{T}\sum_{k=-\infty}^{\infty}X_c\left[j\left(\frac{\omega-2\pi i}{MT}-\frac{2\pi k}{T} \right ) \right ]\right\}\\&=\frac{1}{M}\sum_{i=0}^{M-1}X(e^{j(\omega-2\pi i)/M}) \end{align*}如下图所⽰扩展器假设扩展器的扩展率为L，那么扩展器在时域上的表⽰为x_e[n] = \left\{\begin{matrix} x[n/L], &n=0,\pm L,\pm 2L,\cdot\cdot\cdot \\ 0, &else \end{matrix}\right.扩展前的序列频谱X(e^{j\omega})与扩展后的序列频谱X_e(e^{j\omega})之间有如下关系\begin{align*} X_e(e^{j\omega}) &= \sum_{n=-\infty}^{\infty}x_e[n]e^{-j\omega n}\\ &=\sum_{n=-\infty}^{\infty}x[n/L]e^{-j\omega n}\quad n=0,\pm L,\pm 2L,\cdot\cdot\cdot\\ &=\sum_{k=-\infty}^{\infty}x[k]e^{-j\omega kL}\quad letting\ n=kL\\ &=X(e^{j\omega L}) \end{align*}如下图所⽰滤波器与压缩器互换如上⼀篇⽂章所描述的减采样就是⼀个滤波器与压缩器的级联系统。

万方数据多采样率数字信号处理及其MATLAB仿真作者：黄硕， 魏亚楠， 安永丽作者单位：唐山钢铁股份有限公司,唐山,063016刊名：科技资讯英文刊名：SCIENCE & TECHNOLOGY INFORMATION年，卷(期)：2009，(23)引用次数：0次1.杨小牛.楼才义.徐建良软件无线电原理与应用 20052.李忠琦.凌翔.胡剑浩软件无线电架构研究[期刊论文]-电信科学 2007(7)3.尹健华试论软件无线电技术及其应用[期刊论文]-企业技术开发(学术版) 2007(8)1.学位论文赵启敏中频采样技术的分析与研究2004该课题结合数字软件化雷达的研制,研究了数字软件化雷达中频采样技术的实现以及对雷达主要技术指标的影响.该论文针对传统模拟相参正交采样技术存在的不足,论述了基于A/D变换和数字下变频的中频采样方法,并在此基础上设计了中频采样数据采集卡,并对该硬件进行了调试和试验,试验结果证明,中频采样技术比传统模拟相参正交采样技术更具优势,较好的解决了传统模拟相参正交采样中存在的幅相误差问题,以及该采集卡具有小的孔径抖动,可以满足中频采样的要求.该论文在中频采样技术中首先研究了数据采集技术对雷达性能的影响,接着根据目前数字下变频器件自身的限制不能适应高速数据流的问题,详细研究了利用欠采样技术的镜频加数字下变频实现解调的方法,以及一种利用多速率信号处理技术将抽取和滤波提前的数字下变频的高效结构,通过仿真证明此两种方法都能较好的解决硬件本身限制与高速数据流不匹配的问题,并通过分析得出此数字下变频的高效结构的运算量大大低于传统数字下变频的运算量.此外该论文还着重讨论了孔径抖动对雷达各项性能的影响.2.期刊论文张明珊.孟利民.ZHANG Ming-shan.MENG Li-min基于频域采样技术的软件无线电接收机-浙江工业大学学报2005,33(1)目前软件无线电面临的一个难题是如何对高工作频带内的射频信号进行直接模/数转换.利用频域采样技术提出了一种接收信号进行处理的方法,并用数学理论证明了它的可行性,最后还给出了软件无线电接收机模型.其关键思想是提取接收信号的频域成份,然后在频域中对信号进行处理.这种方法大大降低了A/D转换器的要求,从而使得实现软件无线电接收机成为可能,对当前微电子工艺下的软件无线电系统设计带来很大的理论意义和实用价值,而且克服了传统Rake接收机的一些缺点,特别适合于多径丰富的无线环境.3.学位论文杨清海软件无线电的功能实现20011992年，JeoMitola提出了软件无线电的概念，很快引起了国际通信界的关注。

多采样率数字信号处理在数字语音系统中的应用多采样率数字信号处理在数字语音系统中的应用随着计算机技术的发展和进步，数字化语音系统得到了广泛应用和发展，为人们的生活带来了诸多便利。

其中，多采样率数字信号处理在数字语音系统中的应用尤为重要。

多采样率数字信号处理是指通过在不同的时间间隔内对信号进行采样，以获得更加准确和丰富的信息。

在数字语音系统中，多采样率数字信号处理可以用于多个方面。

首先，多采样率数字信号处理在语音编解码中起到了重要作用。

在数字通信中，语音信号是以数字信号的形式进行传输的。

在编码过程中，语音信号需要被采样，并经过一系列处理，如量化和编码压缩等，以减小数据量并保留重要信息。

多采样率数字信号处理可以提高编码的准确性和质量，从而提高语音信号的传输效果。

其次，多采样率数字信号处理在语音合成中也有广泛的应用。

语音合成是指通过计算机生成逼真的语音信号。

在语音合成过程中，需要对数字信号进行采样和处理，以模拟人声的特征和音调。

多采样率数字信号处理可以提高语音合成的自然度和逼真度，使得生成的语音信号更加接近真实的人声，提高用户体验。

此外，多采样率数字信号处理还可以在语音识别和语音增强中发挥重要作用。

在语音识别中，需要对输入的语音信号进行特征提取和模式匹配，以识别出语音中的文字内容。

多采样率数字信号处理可以提高特征的准确性和区分度，从而提高识别的准确率。

在语音增强中，可以通过多采样率数字信号处理的技术，如降噪和增益调整等，对语音信号进行优化和改善，使得信号更加清晰可辨，提高语音增强的效果。

总结起来，多采样率数字信号处理在数字语音系统中有着广泛的应用。

它可以在语音编解码、语音合成、语音识别和语音增强等方面发挥重要作用。

通过提高采样率和对信号进行处理，可以提高数字语音系统的性能和效果，为用户提供更好的语音体验。

9.3　名校考研真题详解1．以20kHz 的采样率对最高频率为l0kHz 的带限信号采样，然后计算x（n ）的N ＝1000个采样点的DFT ，即：（1）求k ＝150对应的模拟频率是多少？k ＝800呢？（2）求频谱采样点之间的间隔为多少？[华南理工大学2007研]解：（1）根据数字频率与模拟频率的关系得：N 点的离散傅里叶变换DFT 是对离散信号的傅里叶变换DFT 在N 个频率点上的采样，即：所以，X （k ）对应的模拟频率为：所以，当N ＝1000时，序号k ＝150对应的模拟频率是f ＝3kHz 。

当k ＝800时，当N ＝1000时，，此时对应的模拟频率为：（2）由N 可得频谱采样点之间的间隔为：2．用DFT 对模拟信号进行谱分析，设模拟信号的最高频率为200Hz ，其频谱如图所示。

现以奈奎斯特频率采样得到时域离散序列，要求频率分辨率为10Hz 。

（1）求离散序列x （n ）的傅里叶变换，并画出其幅度频谱示意图；（2）求，并画出其谱线示意图；（3）求每个k值所对应的数字频率和模拟频率的取值，并在图中标出。

[中南大学2007研]解：（1）由题意知，最高频率，频率分辨率，所以采样频率为：所以：记录时间为：则采样点数为：对采样得：x （n）的傅里叶变换为：其幅度频谱示意图：（2）由（1）得：谱线示意图为：（3）的图示如下；由上分析可得：当时，对应的，由于得当时，对应的数字频率，与的对应关系为，其中。

3．已知连续时间信号为对该信号进行抽样，抽样频率为4kHz ，得到抽样序列x[n]，求x[nJ 的表达式。

[北京大学2005研]解：已知连续时间信号为：抽样频率后，直接令t ＝n ，代入x a （t ）得x （n ），即：s T4．利用数字系统处理模拟信号的框图如图所示，其中X （jw ）为连续信号x （t ）的频谱，是离散系统h[k]的频率响应。

当抽样间隔时，试画出信号x[k]、)(Ωj e H s T 401=y[k]、y （t ）的频谱。

数字信号处理课程设计题⽬_12级数字信号处理课程设计选题本次课程设计共有六组选题，每组选题每班可有4-5⼈选择，组内同学独⽴完成课程设计选题⼀：⼀、⼀个连续信号含两个频率分量，经采样得()=sin(2*0.125*n)+cos(2*(0.125+f)*n),0,1,,1x n n N ππ?=-当N=16，Δf 分别为1/16和1/64时，观察其频谱；当N=128时，Δf 不变，其结果有何不同，为什么？绘出相应的时域与频域特性曲线，分析说明如何选择DFT 参数才能在频谱分析中分辨出两个不同的频率分量。

⼆、对周期⽅波信号进⾏滤波1）⽣成⼀个基频为10Hz 的周期⽅波信号。

2）选择适当的DFT 参数，对其进⾏DFT ，分析其频谱特性，并绘出相应曲线。

3）设计⼀个滤波器，滤除该周期信号中40Hz 以后的频率分量，观察滤波前后信号的时域和频域波形变化4）如果该信号淹没在噪声中，试滤除噪声信号。

三、⾳乐信号处理：1）获取⼀段⾳乐或语⾳信号，设计单回声滤波器，实现信号的单回声产⽣。

给出单回声滤波器的单位脉冲响应及幅频特性，给出加⼊单回声前后的信号频谱。

2）设计多重回声滤波器，实现多重回声效果。

给出多回声滤波器的单位脉冲响应及幅频特性，给出加⼊多重回声后的信号频谱。

3）设计全通混响器，实现⾃然声⾳混响效果。

给出混响器的单位脉冲响应及幅频特性，给出混响后的信号频谱。

4）设计均衡器，使得不同频率的混合⾳频信号，通过⼀个均衡器后，增强或削减某些频率分量**。

（**可选做）课程设计选题⼆：⼀、已知序列1）为了克服频谱泄露现象，试确定DFT 计算所需要的信号数据长度N 。

2）求()x n 的N 点DFT ，画出信号的幅频特性。

3）改变信号数据长度，使其⼤于或⼩于计算出的N 值，观察此时幅频特性的变化。

分析说明变化原因。

791()=cos()0.5cos()0.75cos()16162x n n n n πππ++⼆、多采样率语⾳信号处理 1）读取⼀段语⾳信号2）按抽取因⼦D=2进⾏抽取，降低信号采样率，使得数据量减少。

采样定理在数字信号处理中的应用
采样定理是指在数字信号处理中，为了将模拟信号转换为数字信号，需要对模拟信号进行采样。

采样定理指出，在采样过程中，采样频率必须大于信号带宽的 2 倍，以确保信号的完整性。

采样定理也称为斯姆特 - 霍夫定律。

采样过程是指将模拟信号转换为数字信号的过程。

在采样过程中，需要将模拟信号进行量化，即将模拟信号的值映射到数字信号的二进制表示中。

采样频率是指每秒采样的次数，即采样率。

采样率越高，所采集的信号数据就越多，信号的精度就越高。

在实际应用中，采样定理对于数字信号处理非常重要。

如果采样频率不足，会导致信号的失真和丢失，甚至出现崩溃现象。

如果采样频率过高，会导致数字信号的存储空间过大，计算量过大，从而影响系统的性能和效率。

因此，在采样过程中，需要根据具体情况选择合适的采样频率。

除了采样定理，数字信号处理中还存在其他重要的定理和准则，如香农 - 哈特利定理、傅里叶变换和拉普拉斯变换等。

这些定理和准则对于数字信号处理的理论和应用都有着重要的意义。