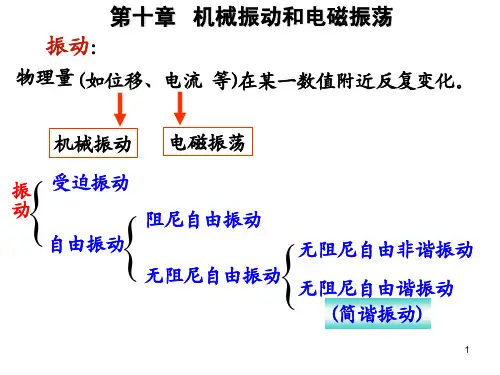
机械振动和电磁振荡
- 格式:ppt
- 大小:2.56 MB
- 文档页数:61

oscillation 用法(一)Oscillation(振荡)的用法介绍什么是振荡?振荡(Oscillation)是指物体在固定时间内在两个或多个状态之间来回变化的过程。
在不同领域中,振荡都有不同的涵义和应用。
物理领域中的振荡1.机械振荡:机械振荡是指由于物体的弹性形变或势能的变化而产生的周期性运动。
例如,钟摆的摆动、弹簧的拉伸和压缩等都是机械振荡的例子。
2.电磁振荡:电磁振荡是指电荷或电磁场的能量在电路中周期性地来回转化的过程。
例如,交流电的频率就是电磁振荡的频率。
3.光学振荡:光学振荡是指光波在介质中传播时的周期性变化。
例如,激光器中的光波就是通过光学振荡来产生和放大的。
数学领域中的振荡1.正弦振荡:正弦振荡是指以正弦函数为基础的周期性变化。
在数学中,正弦函数是最基本的一类周期函数,描述了很多自然界中的变化规律。
2.傅里叶级数:傅里叶级数是把一个周期函数分解为多个正弦函数的和的方法。
利用傅里叶级数理论,我们可以分析和预测振荡的性质和特征。
3.振荡方程:振荡方程是描述振荡系统行为的方程。
例如,单摆的运动可以用简谐振动方程描述,而电路中的振荡行为可以用LCR电路的振荡方程表示。
其他领域中的振荡1.经济领域:在经济学中,振荡可以用于描述市场的周期性波动。
经济振荡往往与经济周期和商业周期有关,对于经济预测和政策制定有一定的指导意义。
2.生物领域:在生物学中,振荡现象广泛存在于生物体内。
例如,生物钟调控着生物体的昼夜节律,心脏的搏动也是一种生物振荡现象。
3.信息领域:在信息科学中,振荡可以用于描述信号的周期性变化。
例如,音频和视频信号中的波形振动就是一种经典的振荡现象。
以上只是振荡在不同领域中的一些常见应用和用法,振荡作为一个重要的概念和现象,还有许多其他领域中的应用和深入研究。
物理领域中的振荡的用法1. 机械振荡•弹簧振荡:当给弹簧施加力或变形后,会产生弹性形变,从而使弹簧发生周期性的振动。
•摆锤振荡:摆锤是一个具有一定质量的物体,在重力作用下能够以固定点为中心进行摆动。



010203定义稳态受迫振动和非稳态受迫振动。
类型应用振荡频率电感线圈振荡的频率与电感量、电阻和电容有关,通过调节这些参数可以改变振荡频率。
振荡原理电感线圈中,当电流发生变化时,会产生感应电动势来阻碍电流的变化,从而产生振荡。
应用振荡电路是许多电子设备中的重要组成部分,如信号发生器、无线电等。
电感线圈振荡电磁场振荡电磁波传播电磁波传播原理电磁波的特性应用单摆模型描述物体在平衡位置附近往复运动的模型,可以用于描述机械振动和某些电磁振荡。
单摆的周期公式是 T =2π√(L/g),其中L是悬摆的长度,g是重力加速度。
在不同的星球或不同的重力场中,单摆的周期会发生变化,因此可以用来测量重力场的变化。
弹簧质量模型弹簧质量模型的振动方程是 m(d^2x/dt^2) = -kx,其中m 是质量块的质量,k是弹簧的弹性系数。
解这个方程可以得到振动的频率和振幅,从而可以描述物体的振动特性。
描述一个质量块在弹性力作用下运动的模型,可以用于描述机械振动和某些电磁振荡。
电感线圈模型描述电感线圈在电磁场中运动的模型,可以用于描述某些电磁振荡。
电感线圈的动态方程是d^2i/dt^2 + R(di/dt) + (1/L) *(Li) = 0,其中i是电流,R是电阻,L是电感。
解这个方程可以得到电流的时间变化,从而可以描述电磁振荡的特性。
简谐振动的数学公式简谐振动的数学公式简谐振动的特点简谐振动的描述阻尼振动的数学公式阻尼振动的描述阻尼振动的数学公式阻尼振动的特点03受迫振动的特点受迫振动的数学公式01受迫振动的描述02受迫振动的数学公式1电感线圈振荡的数学公式23电感线圈在电流变化时会产生感应电动势,从而产生振荡。
电感线圈振荡的描述i=Icos(ωt+φ),其中I为电流幅度,ω为角频率,φ为初相位。
电感线圈振荡的数学公式电感线圈的振荡频率由电路阻抗决定,与电源频率无关。
电感线圈振荡的特点机械振动在工程中的应用机器运转机械振动可以提高机器的运转效率和精度,如振动筛、振动电机等。






用机械振动类比理解电磁振荡★疑难辨析★对电磁振荡的机制,课本上的分析是基于电容器充放电和电感器自感,这个分析思路理解起来有些复杂,但似乎也只能如此。
不过,我们都会发现,电磁振荡现象中,电容器极板上的电荷量和通过电感器的电流,一个按正弦规律变化,另一个按余弦规律变化,这和机械振动中振子的位移和速度的变化规律很相似,那么,机械振动与电磁振荡运动学上的相似,是不是还有更根本的动力学上的相似?电磁振荡可不可以类比机械振动来理解呢?基于这个想法,笔者做了一些尝试性思考,供大家参考。
一、振动与波的关系类比从振动和波的关系来看,机械振动与机械波,电磁振荡与电磁波,有着相似的关系。
1、波是振动的传播机械波是机械振动在介质中的传播,时空中周期性振动的物理量是介质中质点的位移x 和速度v ;电磁波是电磁振动的传播,时空中周期性振动的物理量是电磁场的电矢量E 和磁矢量B 。
2、波的产生都需要振动的波源机械波的波源,是振动的质点,比如弹簧振子、声带、音叉、琴弦等;电磁场的波源,是震荡的电荷,比如振荡电路、分子、原子甚至原子核等。
二、弹簧振子模型与LC 振荡电路类比由数学知识可知,方程结构上的相似,会导致相同形式的解,要类比研究机械振动和电磁振荡,首先应该从运动方程角度找到两者的相似性。
1、运动方程类比弹簧振子偏离平衡位置的位移为x ,则振子的速度为x v t ∆=∆,振子的加速度为v a t∆=∆,振子的动力学方程为kx a m =-,或者写成v kx t m∆=-∆,或者22d d x kx t m =-;LC 振荡电路中电容器极板上的电荷量为q ,通过电感线圈的电流i 就是电容器的充放电电流,有q i t∆=∆,对电感器,有自感电动势为i e L t ∆=-∆,导线电阻不计时,有电容器两极板间的电压u e =,且有q =Cu ,则电流对时间的变化率为q i e u C t L L L ∆=-=-=-∆,或者22d d q q C t L =-,此即电磁振荡的动力学方程。