下载文档原格式
农产品价格趋势的数学建模和预测———以玉米为例余涛（中南民族大学经济学院人口，资源与环境经济学专业）摘要: 从实际情况出发，以1979 年来我国农产品市场玉米价格的波动特征和规律为研究对象，主要运用计量经济模型中的多元线性回归法、加权最小二乘法、White 检验、D － W 检验、广义差分法以及EVIEWS 软件，量化分析蕴含在玉米价格波动里的经济特征，对玉米价格作出模拟和预测研究．结果表明，该模型有较好的应用价值。
关键词: 农产品价格; 趋势; 计量经济模型; 加权最小二乘法改革开放以来，由于党和国家一系列加强农业生产政策的落实及国内畜牧业生产发展的拉动，玉米生产持续增长．我国玉米种面积逐年递增，玉米播种面积和产量的增长对全国粮食的供给和畜牧业的发展起着举足轻重的作用．因此，研究玉米价格的波动有着非常重要的理论意义和现实意义。
我国农产品价格趋势的研究相对较晚，目前对现状分析、因素分析和价格的宏观面趋势变动研究较多，却对价格的形成机理以及价格趋势的建模预测方面并没什么大的进展。
本文的主要研究方法有计量分析法并结合因素分析法和实证分析法。
1 影响玉米价格的因素分析从微观经济学的角度来看，任何商品的价格都是由商品的供给和需求这两个因素共同决定的，包括玉米的供给、需求、库存以及相关商品的价格．另外，还有气候、经济周期、国家相关政策、消费者心理预期以及货币汇率等对农产品价格的影响也比较明显．2 模型的设定本文将对农产品价格与有关社会、经济因素之间的关系，建立计量经济学模型2． 1 被解释变量为了进行农产品价格趋势的预测，目标变量应为农产品价格． ( 用Yt来表示)2． 2 解释变量根据相关的经济理论和以往的经验，选定以下指标作为模型的解释变量: 国内生产总值( 用X1t表示) 、城镇居民人均可支配收入( 用X2t表示) 、城镇居民家庭人均食品消费支出( 用X3t表示) 、谷物生产价格指数( 用X4t表示) 、牲畜( 猪) 年底头数( 用X5t表示) ，所有数据来自《中国统计年鉴( 1980 ～2012) 》2． 3 确定计量经济模型Yt =β0+β1X1t+β2X2t+β3X3t+β4X4t+β5X5t+μt ( 1)3 参数估计用Eviews 估计结果为:Yt ^ =－180.956－0.407X1t－0.0729X2t + 0.3997X3t + 2.363X4t +4.9896X5t， ( 2)Std error = ( 181.956) ，( 1.1799) ，( 0.0483) ，( 0.174 3) ，( 0．366 9) ，( 6.3899) ，t = (－0.9946) ，(－0.3449) ，(-1.5107) ，( 2.2926) ，( 0.8211) ，Ｒ2 = 0.9890，Ｒ2 = 0.9870，F = 487.7158，DW = 1.4578．4 模型的检验及修正4． 1 经济意义检验根据实际情况初步判断国内生产总值( X1) 和城镇居民人均可支配收入( X2) 应与被解释变量成正比，可估计出来的结果却相反，与经济意义不符，应该去掉．4． 2 统计推断检验4． 2． 1 拟合优度回归结果中Ｒ2 = 0.9890，Ｒ2 = 0.9870，这说明模型对样本对的拟合很好．4． 2． 2 F 检验在给定显著水平α =0.05，在F分布表中查出自由度为k =5 和n－k－1=27 的临界值Fα( 5，27) =2.57，由表4中得到F =487.7158＞Fα( 5，27)=2.57，说明各解释变量联合起来确实对被解释变量有显著影响．4． 2． 3 t 检验给定显著水平α= 0.05，查t分布表得自由度为n－k－1 = 27 的临界值tα/2( n －k－1) = 2.052．再由回归结果可知,X1、X2和X5的t 统计值均不显著( 与临界值相比较),说明X1、X2和X5对Y的影响不显著,需要在后面的计量经济学检验中加以证明．4． 3 计量经济学检验4． 3． 1 多重共线性检验①检验: 由X1、X2和X5的t 统计值均不显著，且X1、X2符号的经济意义不合理，另外，由相关系数矩阵也可以看出，各解释变量之间的相关系数较高，认为解释变量间存在多重共线性．②修正: 采用逐步回归法对其进行修正，由于X1、X2不符合经济意义，首先剔除，分别作Y 与X3、X4和X5间的回归，逐步回归后，只剩下一个解释变量X4 ．4． 3． 2 异方差检验采用White检验法，得出nＲ2 = 13.8311，由White 检验知，在α= 0.05下，查χ2分布表，得临界值χ20.05( 5) = 11.0705，因为nＲ2 = 13.8311＞χ20．05( 5) = 11.0705,表明存在异方差．下面采用加权最小二乘法( WLS)对原模型进行回归，分别选用权数ω1 = 1/X4，ω2 = 1/X24，ω3 = 1/，如图1，经估计检验发现用权数ω2的效果最好．其估计结果如下:Yt ^ = 19.0236 + 3.0561X4t， ( 3)Std error =( 12.0922) ，( 0.0925) ，t = ( 1.5732) ，( 33.0251) ，Ｒ2 = 0.9920，Ｒ2 = 0.9917，F=1090.656，DW = 1.1317．可得nＲ2 = 3.6077，所以运用加权最小二乘法确实消除了异方差，参数的t 检验均显著，F检验也显著．4． 3． 3 序列相关检验①检验: 在0.01 显著水平下，查DW 统计表可知，dL = 1.172，dU = 1.129 1．模型中DW＜dL，显然模型中有自相关．另外,由图2可以看出，残差的变动有系统模式，连续为正和连续为负表明残差项存在一阶正相关．②补救: 为解决该问题，选用科克伦－奥克特迭代法．得回归方程:e^t = 0.4335et－1 (4)由式( 4)可知ρ^ = 0.433509,对原模型进行广义差分，得到广义差分方程:Yt－0.4335Yt －1 =β1(1－0.4335)+β2( Xt－0.433 5Xt -1)+vt (5)图1 用权数W2的结对式( 5) 的广义差分方程进行回归，得结果如下:Y*t^ =21.9749+3.0113X*t， ( 6)Std error =(24.7791) ,(0.1047) ，t =(0.8868) ，(28.7621) ，Ｒ2 = 0.965 0，Ｒ2 =0.9638，F = 827.2556，DW = 2.1065．其中，Y*t = Yt－0.4335Yt－1，X*t = Xt－0.4335Xt－1 ．由于使用了广义差分法数据，样本容量减少了1个，为32个．查1%显著水平的DW的统计表可知dL= 1.160，dU = 1. 282，模型中dU ＜DW = 2.1065 ＜ 4－dU，说明在1%显著水平下广义查分模型中已无自相关,不必再进行迭代．同时可见,可决系数Ｒ2、t和F 统计量均达到理想水平．5 模型的预测及经济解释5． 1 模型的预测由《中国统计年鉴2013》可知，2012 年谷物生产价格指数为104．8，即累计值为798.49 ( 1979年为100) ，把它代入模型( 即式(6) ) 可得2012年我国玉米价格的预测值为:Y ^12 = 21.9749+3.0113×798.49 = 2426.47( 元/吨) ． ( 7)而2012 年中国玉米价格的实际值为Y12= 2430.74( 元/吨) ，绝对误差为Ea( Y12)= 4.27( 元/吨) ,相对误差仅为Er(Y12) = Y ^ 12－Y12Y12=0.18% ＜5%．由中国经济统计数据库的数据可知2013年谷物生产价格指数为102.3，累计值为816.86，代入模型可得预测值为:Y ^ 13 = 2481.79(元/吨) ，实际值为Y13 =2 409．97( 元/吨) ，绝对误差为Ea( Y13) = 71．82( 元/吨) ，相对误差为Er(Y13) = 2.98% ＜5%，中国国务院总理李克强于2014 年3 月5 日所作的政府工作报告显示: 2014 年中国国内生产总值增长预期目标设定为7． 5%左右．根据中国社会科学院预测科学研究中心发布的“2014 年中国经济预测”显示，预计2014 年我国第一产业增加值增速约为3.6%．根据以上信息，可以推断出2014 年我国谷物生产价格指数同比增长3.5%左右，即累计值为845.45，代入模型式( 即式(6)) ，可得2014年我国玉米价格的预测值为:Y ^14 = 21.9749+3.0113×845.45=2567.88(元/吨) ．5． 2 模型的经济解释该模型的结果表明，谷物生产价格指数和玉米价格呈正相关，从式(6)可以看到,谷物生产价格指数(1979年= 100)每增长1%，平均说来玉米价格会增长3．011 3．这一理论分析和经验判断相一致，可以用于玉米价格预测．6 总结本文重在遵循“假设－检验－修正－再假设－再检验－再修正……”这样一个循环求优的过程．如果简单的把第一步回归的结果( 即式( 2))作为最终的模型结果，势必会助涨模型误差的升级，根本达不到理想的结果．所以，本文尤其注重对模型的检验与修正，使最终的结果有很强的说服力．同样，该模型也可以用于其他农产品价格的预测，为相关企业提供参考依据．参考文献:［1］王素雅．农产品短期价格分析及预测方法选择———以北京新发地批发市场苹果为例［D］．北京: 中国农业科学院，2009: 1 － 10．［2］戴春芳，贺小斌，冷崇总．改革开放以来我国粮食价格波动分析［J］．价格月刊，2008( 6) : 1 － 5．［3］李华．农产品价格波动的影响因素及趋势分析———基于供应链视角［D］．长春: 吉林大学，2013: 2 － 6．［4］高鸿业．西方经济学( 微观部分) ［M］．北京: 中国人民大学出版社，2010: 17 － 51．。
基于 ARMA 模型的我国蔬菜价格预测--以大白菜、黄瓜和番茄为例周明明;张瑞涛;王俊芹;王余丁【摘要】This paper set up the ARMA model which based on time series, through searching the prices of agricultural market from 2002 to 2014 as sample datas with Eviews8.0 software, so as to analysis and forecast the prices of Chinese cabbage, cucumber and tomato. The results showed that vegetable prices would show a rising trend over the next two years with seasonal fluctuation, among them, the seasonal factor was the main factor to influence the price fluctuation of vegeta-bles.%以2002-2014年农产品集贸市场价格为样本数据，利用 Eviews 8.0软件，建立了基于时间序列分析的 AR-MA 模型，对大白菜、黄瓜和番茄的价格进行了分析预测。
结果表明，我国蔬菜价格未来2 a 将呈上涨趋势，且具有季节性波动的特征，其中季节因素是影响蔬菜价格波动的最主要因素。
【期刊名称】《长江蔬菜》【年(卷),期】2015(000)020【总页数】3页(P104-106)【关键词】ARMA 模型;蔬菜价格;预测【作者】周明明;张瑞涛;王俊芹;王余丁【作者单位】河北农业大学经济贸易学院，保定，071000;河北农业大学经济贸易学院，保定，071000;河北农业大学经济贸易学院，保定，071000;河北大学【正文语种】中文【中图分类】S126蔬菜价格作为反映我国物价水平的重要组成部分，近年来出现了较大波动。
（由组委会填写）第十一届华为杯全国研究生数学建模竞赛学校青岛科技大学参赛队号10426019队员姓名1.王玉江2.陈桂兵3.严春梅（由组委会填写）第十一届华为杯全国研究生数学建模竞赛题目人体营养健康角度的中国果蔬发展战略研究摘要：水果和蔬菜是重要的农产品，主要为人体提供矿物质、维生素、膳食纤维。
因此，预测我国果蔬的消费与生产趋势，科学地规划与调整我国果蔬的中长期的种植模式，具有重要的战略意义。
针对问题一，首先选取需要研究的主要水果、蔬菜品种，以其总计含量分别达到各自总产量的90%为约束条件，采用多目标规划（产量最多、营养含量最高、种类最少）筛选出主要的水果、蔬菜品种（水果10种、蔬菜8种，结果见表4、表5）。
随后，查询2002至2010年主要品种的产量，通过两种方法（损耗率、进出口差量）计算人均消费量，用灰色预测GM（1,1）和曲线拟合两种模型预测未来人均消费量，并分别检验拟合效果、进行误差分析，发现基于损耗率估计消费量灰色预测的效果较理想。
所以以苹果为例，综合考虑损耗率和进出口量利用灰色预测模型估计其2010至2020年的人均消费量（见表9、表12），拟合出曲线图（见图2、图6），分析其发展趋势。
针对问题二，首先依据10种营养成分在主要果蔬产品中含量的相似性，运用Spss 软件对10种营养成分进行Q型聚类降维得6大类营养成分（结果见表12），每类营养成分都筛选出一个营养成分作为代表分别是膳食纤维、维生素A、维生素C、维生素E、钙、锌。
采用正态分布中间型模型计算每种营养成分年均实际摄入量关于标准摄入量的隶属度，隶属度越接近1表明实际摄入量越趋近于标准量，以此评价2014年的营养年摄入水平。
用维生素A、C、E隶属度的乘积量化维生素这一大类营养元素趋于健康的程度，同样对钙锌采取相同的措施作为矿物质的量化值，关于时间作图可知2014至2019年中国居民的营养健康状况趋于好转，2019至2020年趋于恶化。
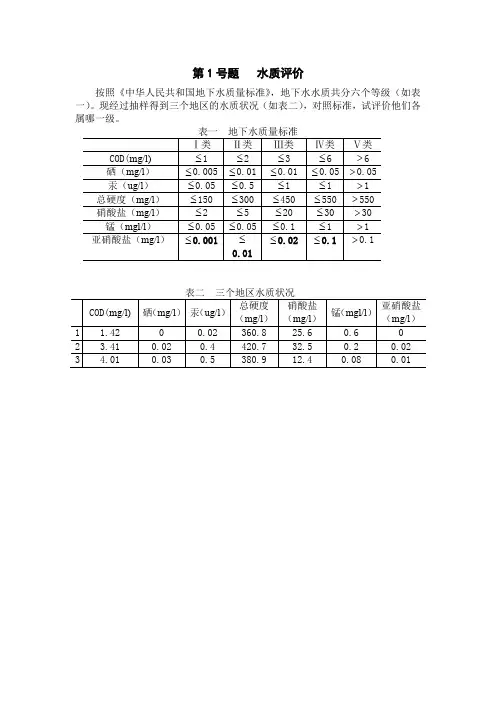
第1号题水质评价按照《中华人民共和国地下水质量标准》，地下水水质共分六个等级（如表一）。
现经过抽样得到三个地区的水质状况（如表二），对照标准，试评价他们各属哪一级。
第2号题工资比较为研究工资水平与工作年限和性别之间的关系，在某行业中随机抽取10名职工，所得数据如表一所示，试通过回归方程分析月工资收入与性别和工作年限有何关系。
表一 10名职工工资水平、工作年限和性别数据第3号题农产品定价某国政府要为其牛奶、奶油和奶酪等奶制品定价。
所有这些产品都直接或间接的来自国家的原奶生产。
原奶首先要分离成脂肪和奶粉两中组合，去掉生产出口产品和农场消费的产品的部分后，余下的共有60万吨脂肪和70万吨奶粉，可用于生产牛奶、奶油和两种奶酪，供国内全年消费。
各种产品的百分比组成见下表：产品\成分脂肪奶粉水牛奶4987奶油80218奶酪1353035奶酪2254035往年的国内消费和价格如下表：产品牛奶奶油奶酪1奶酪2消费量（千吨）482032021070价格（元/吨）2977201050815价格的变化会影响消费需求。
为表现这方面的规律，定义需求的价格伸缩性E：E=需求降低百分数/价格提高百分数各种产品的E值，可以据往年的价格而后需求变化情况的统计数据，用数理统计方法求出。
另外，两种奶酪的需求，随它们价格的相对变化，在某种程度上可以相互替代。
表现这一规律要用需求关于价格的交叉伸缩性EAB定义作：EAB=A需求提高百分数/B价格提高百分数奶酪1到奶酪2的E12值和奶酪2到奶酪1的交叉伸缩性E21值,同样可以凭数据用统计方法求出已经求出牛奶、奶油、奶酪1、奶酪2的E值依次为0.4，2.7，1.1和0.4以及E12=0.1, E21=0.4.试求出4种产品的价格，试所导致的需求使销售总收入为最大。
然而，政策不允许某种价格指标上升，这使得新的价格必须使消费的总费用较上一年度不增加。
因此，对问题的一个特别重要的附加要求，是对这一政策限制的经济代价，给出数量表示。
数学建模省三等奖论文一、问题的重述食品价格是居民消费价格指数的重要组成部分，食品价格波动直接影响居民生活成本和农民收入，是关系国计民生的重要战略问题。
国家统计部门定期统计50个城市主要食品平均价格变动情况，数据见附件1。
居民消费者价格指数（CPI），是根据与居民生活有关的产品及劳务价格统计出来的物价变动指标，通常作为观察通货膨胀水平的重要指标。
附件2提供了近期居民消费者价格指数数据。
请根据以上信息建立数学模型解决以下问题：（1）根据附件以及相关统计网站的数据，分析我国食品价格波动的特点。
（2）对2014年5月份食品价格走势进行预测。
（3）目前统计部门需要监测大量食品价格变动情况以计算居民消费者价格指数变动情况，能否仅仅通过监测尽量少的食品种类价格即能相对准确地计算、预测居民消费者价格指数？在同样精度要求下，不同地区所选取的食品种类以及种类数目是否一致？请至少选择两个有特点的城市进行说明。
二、问题的分析居民消费者价格指数是一个波动的量，它客观地表征了通货膨胀的水平。
而造成它波动的因素是构成它的食品、烟酒及用品、衣着、家庭设备用品及维修服务、医疗保健和个人用品、交通和通信、娱乐教育文化用品及服务、居住等八个大类的价格波动。
其中，食品价格是消费者价格指数的重要组成部分，要解决以上三个问题必须清楚食品价格的变化规律以及影响因素等。
针对问题一，若要分析食品价格的波动特点，必须运用统计学原理对附件所给数据和所查数据进行统计分析，求出食品价格这一随机变量的统计特征。
由于影响不同类食品价格变化的因素不同，其变化规律也有一定差异，需要在分析食品价格总体变化的基础上分析各类食品价格的变化以及特征值。
对问题一的分析主要用到的工具将会是Excel和MATLAB。
针对问题二，预测五月份食品价格的走势必须要建立合理的预测模型，这个模型必须要很好地符合之前的统计数据。
由于影响食品价格的因素很难量化，需从前期数据出发用所选模型对数据进行训练得出,短期预测模型中灰色预测与神经网络都是不错的选择。
2023数学建模国赛c题思路--蔬菜类商品的自动定价与补货决策一、问题概述蔬菜类商品定价与补货是一个复杂的决策过程，涉及多方面因素，包括市场需求、成本、竞争状况等。
在本次数学建模比赛中，我们将重点关注2023年的蔬菜市场，运用数学模型和方法对蔬菜类商品进行自动定价和补货决策。
二、思路与方法1.数据收集与处理数据是制定有效决策的关键。
首先，我们需要收集关于蔬菜类商品的各种数据，包括但不限于：市场价格、需求量、成本、竞争对手价格等。
这些数据可以通过市场调查、政府报告、行业协会等途径获取。
在收集到数据后，我们需要进行清洗和整理，确保数据的准确性和完整性。
2.需求预测需求预测是定价和补货决策的基础。
通过分析历史销售数据，我们可以预测未来的市场需求。
常用的需求预测方法包括时间序列分析、回归分析等。
通过预测未来一段时间内的需求量，我们可以更好地制定定价和补货策略。
3.成本分析成本是定价的重要因素之一。
我们需要分析蔬菜类商品的成本结构，包括种植、采摘、运输、储存等环节的成本。
通过成本分析，我们可以了解商品的盈亏平衡点，为定价提供依据。
4.定价策略在综合考虑需求和成本后，我们可以制定定价策略。
常见的定价策略包括成本加成定价、竞争导向定价等。
在制定定价策略时，我们需要考虑市场需求、竞争对手价格、商品特点等因素。
5.补货计划补货计划是根据需求预测和库存情况制定的采购计划。
我们需要根据市场需求和库存情况确定最佳补货时间点和补货量。
常用的补货计划方法包括实时库存监控和定期补货计划等。
通过制定合理的补货计划，我们可以确保库存充足，满足市场需求。
西安市蔬菜价格变动分析及采购计划的制定摘要食品价格是居民消费价格指数的重要组成部分，食品价格波动直接影响居民生活成本和农民收入，是关系国计民生的重要战略问题。
在收入增长缓慢的情况下，食品价格上涨将使人民群众明显感到生活成本增加，特别是蔬菜价格的变化关系到千家万户的日常生活，菜价的上涨将严重影响城市低收入群体的生活质量。
本文应用时间序列法来研究蔬菜价格的变动以及蔬菜价格指数的编制问题，并运用所构建的模型来进行蔬菜价格的短期预测。
针对问题一，要求根据所选的5种蔬菜近几年的价格数据，建立数学模型研究这5种蔬菜价格随月份的变化规律，并预测2015年这5种蔬菜每月的价格。
通过绘制5种蔬菜价格随月份变化的折线图，发现蔬菜价格具有较明显的季节性变动。
显然，5种蔬菜价格分别是5个时间序列，利用EViews软件对5个时间序列进行稳定性检验，结果显示全部5个时间序列都是平稳时间序列。
因此，本文分别对5个时间序列建立了ARMA模型，利用EViews和MATLAB软件进行参数求解和模型检验得出具体的时间序列模型，并通过所建立的模型对未来一年内的蔬菜价格进行了预测。
针对问题二，本文首先利用SPSS软件对17种蔬菜进行了系统聚类，将17种蔬菜分为三类，通过分别计算三类蔬菜价格的平均值来给各类蔬菜对价格指数的影响程度赋予不同的权重值。
然后考虑人们的消费习惯对价格指数的影响，本文查找网上资料，按销量将17种蔬菜分为五类，用各类蔬菜的销量在一定程度上反映人们的消费习惯。
通过各类蔬菜的销量来给各类蔬菜对价格指数的影响程度赋予不同的权重值。
最后对于上述两种因素，本文凭借生活经验，人为的对两种因素赋予不同的权重值，进而计算每月蔬菜价格的加权平均价格，求出每月的定基价格指数。
通过检验发现价格指数仍是一平稳的时间序列，因此同第一问一样建立ARMA模型进行研究。
针对问题三，本文对问题二所得到的蔬菜价格指数进行回归分析，利用SPSS 软件绘制散点图，发现在95%的置信区间内可以进行线性回归分析。
