当前位置：文档之家 › 2-拉氏变换

2-拉氏变换

  • 格式：ppt
  • 大小：535.50 KB
  • 文档页数：54

下载文档原格式

  / 54

合集下载

拉氏变换

拉氏变换

6
63 s3

et 7e2t 6e3t
(2). 包含有共轭极点的情况 1,2
例2 求
F(s)

s1 s(s2 s 1)
的拉氏反变换。
13
s1 0,
s2,3


2
j
2
s1
s1
F(s)
s(s2

s 1)

s s
1 2
LLL111sss111aaaeeeaaatt t,,, LLL111sss111aaaeeeaaatt t,,,
LLL111sss222222sssiiinnnttt,,, LLL111sss222sss222cccooosssttt
1
1
s 1 s2 1
sa 1
s a2
s2 2
序号
f(t)
7
cos(t)
8
t n (n 1，2，3， )
9
t neat (n 1，2，3， )
10
1 eat ebt
ba
11
1 bebt aeat
ba
12
1 ab
1

a
1

j
3 2
1
由此得：
1 1
2 0
s1
A


s(s2

s

1)

s s0

1
s1
s
1
F(s)

s(s2

s 1)

s
1 2

j
3 2

s

拉氏变换求法2-2

拉氏变换求法2-2

3t t 2）ℒ e f ( ) 2
解 1） ℒ
1 s ℒ f (2t ) F ( ) 2 2
由延迟性质
ℒ f (2(t 2))u(t 2) f (2t 4)u(t 2)
1 2 s s e F( ) 2 2 t 2）ℒ f ( ) 2F (2s) 由位移性质 2
解 因为
k ℒ sin k t 2 s k2 n! t ℒ s n 1
n
所以
ℒ e
at
k sin kt ( s a)2 k 2
n! at n ℒ e t ( s a)n 1
例3
若 F ( s) = ℒ f (t ) 求 1）ℒ f (2t 4)u(t 2)
例
解
求

0
0
sin t dt t

0
e at e bt dt t
0
1 sin t ds arctan s dt 0 2 s 1 t


2 e bt [ e e ]ds ℒ 0 dt t
d 1 ℒ t sin t ( 2 ) ds s 1
2s 2 2 ( s 1)
ℒ te
2t
2( s 2) sin t (( s 2) 2 1) 2 2( s 2) 2 2 s(( s 2) 1)
t te2t sin tdt ℒ 0
Fn ( s)
注：卷积公式可用来计算逆变换或卷积.
例1：求 ℒ 1[
1 F1 ( s ) 2 s
1
1 ] 2 2 s (1 s )

拉氏变换基本性质

拉氏变换基本性质

F(s) F1(s) 1 esT 0
例：周期信号的拉氏变换
LT
f1(t) F1(s)
第一周期的拉氏变换
LT
利用时移特性
f1(t nT ) esnT F1(s)
LT
f (t nT ) F1(s) eSnT
n0
n0
1
F1(s) eST
利用无穷递减等比 级数求和 s a1
1- q
例1：求全波整流周期信号的拉氏变换
设f (t) sint
sin 0t u(t)
t 0
sin0t u(t t0)
t 0 t0
sin0(t t0) u(t)
0 t0
t
sin0(t t0)u(t t0)
t 0 t0
3.时移特性的应用p250.4-2 (1)
sin t 0 t T
1. f (t)
2
0 t为其它值时
解: f (t) sin t[u(t) u(t T )] 2
s 0 dt
s
f (0) f (0 ) f (0 ) lim sF(s) s
再假定f(t)在原点有跃变,则f(t)的导数可写成
df df1 [ f (0 ) f (0 )](t) dt dt
t0
其中f 1(t)在t=0连续,于是
lim df (t) est dt lim df1 est dt
采用 0 系统还是采用 0 系统,所求得的初值
总是 f (0 )
b.若F(s)是有理代数式,则F(s)必须是真分式 即F(s)分子的阶次应低于分母的阶次,若不是 真分式,则应用长除法,使F(s)中出现真分式,而 初值f (0) 等于真分式F0(s) 逆变换f 0(t) . c.物理解释:s ( j ) 相当于接入信

拉氏变换及拉氏反变换

拉氏变换及拉氏反变换




t dt 1 ，且δ(t)有如下

t f t dt f 0
式中f(0)——t=0时刻的f(t)的函数值。
由拉氏变换的定义得


L t t e st dt e st
0
t 0
1
2.2.2 几种典型函数的拉氏变换
L f at
1 s F a a
2.2.3 拉氏变换主要定理
微分定理

设f(n)(t)表示f(t)的n阶导数，n=1，2，3，……正整数， f(t)的拉氏变换为F(s)，则
L f t s F s sf 0 f 0
F s
s 1 s 1 k k 1 2 s 2 5s 6 s 2s 3 s 2 s 3
s 1 s 2 s 1 1 k1 s 2s 3 s 2 s 3 s 2 s 1 s 3 s 1 2 k2 s 2s 3 s 3 s 2 s 3 2 1 1 1 2 f t L1 F s L1 L1 L 2e 3t e 2t s 2 s 3 s 2 s 3

拉氏变换亦与此相似，即把微分方程变换为代数方程 求解。
2.2.1 拉氏变换的定义
定义

对于时间函数f（t），如果满足
当t<0时，f（t）=0； 当t≥0时，实函数f（t）的积分
f t e
0

st
dt 在s的某一域内收敛，则定义f（t）的拉氏变换
为
F s f t e st dt

拉氏变换

拉氏变换

拉普拉斯变换拉普拉斯变换简称拉氏变换。

它是一种函数的变换，经变换后，可将时域的微分方程变换成复数域的代数方程。

并且在变换的同时，即将初始条件引入，避免了经典解法中求积分常数的麻烦，可使解题过程大为简化。

因此，对于那些以时间t 为自变量的定常线性微分方程来说，拉氏变换求解法是非常有用的。

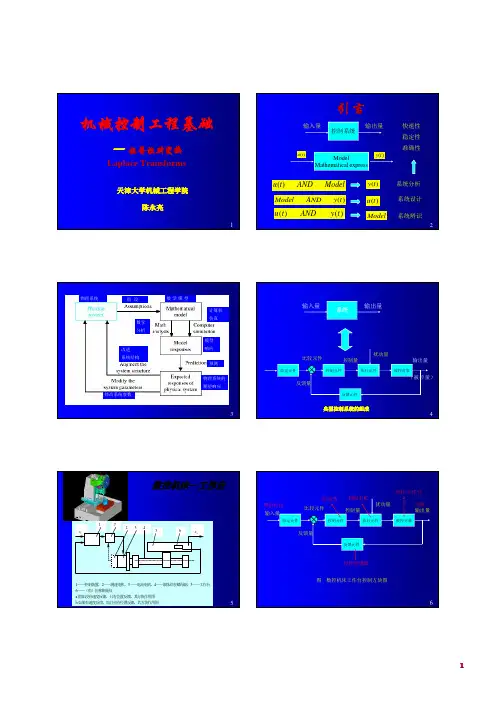
在经典自动控制理论中，自动控制的数学模型是建立在传递函数基础之上的，而传递函数的概念又是建立在拉氏变换的基础上，因此，拉氏变换是经典控制理论的重要数学基础，是分析研究线性动态系统的有力数学工具。

本章着重介绍拉氏变换的定义，一些常用时间函数的拉氏变换，拉氏变换的性质以及拉氏反变换的方法。

最后，介绍用拉氏变换解微分方程的方法。

在学习中应注重该数学方法的应用，为后续章节的学习奠定基础。

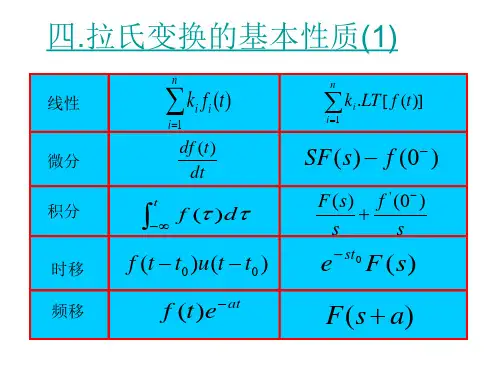
2.1拉氏变换2.1.1拉氏变换的定义若()f t 为实变量时间t 的函数,且0t <时，函数()0f t =，则函数()f t 的拉氏变换记作[()]f t L 或)(s F ，并定义为：[()]()()e dL stf t F s f t t +∞-==⎰（2.1） 式中s j σω=+为复变量，()F s 称为()f t 的象函数，称()f t 为()F s 的原函数。

原函数是实变量t 的函数，象函数是复变量s 的函数。

所以拉氏变换是将原来的实变量函数()f t 转化为复变量函数()F s 的一种积分运算。

在本书中，将用大写字母表示相对应的小写字母所代表的函数的拉氏变换。

必e 1[1()]1e d L st stt t ss+∞-+∞-=⋅=-=⎰(2.2) 在自动控制系统中，单位阶跃函数相当于一个实加作用信号，如开关的闭合（或断开），加（减）负载等。

⑵单位脉冲函数单位脉冲函数如图2.2所示。

其定义为()0t t t δ∞=⎧=⎨≠⎩ 同时，()d 1t t δ+∞=⎰，即脉冲面积为1。

而且有如下特性：()()d (0)t f t t f δ+∞-∞⋅=⎰(0)f 为()f t 在0t =时刻的函数值。

第二章附录-拉氏变换

第二章附录-拉氏变换

例3 : y(3) 3y 3y y 1, y(0) y(0) y(0) 0 求微分方程.
F (s)
1 s(s 1)3
b3 (s 1)3
b2 (s 1)2
b1 s 1
c4 s
b3
[
s(s
1 1)3
(s
1)3 ]s1
1
b2
d
ds
[
s(s
1 1)3
(s
1)3
]
s1
[d ds
(
1 s
一.拉氏变换
1.定义：设函数f(t)当t≥0时有定义，而且积
分
F (s) f (t)est dt
0
存在，则称F(s)是f(t)的拉普拉斯变换。
简称拉氏变换。记为 F (s) L[ f (t)]
f(t)称为 F(s)的拉氏逆变换。记为：
f (t) L1[F (s)]
2.常用函数的拉氏变换
单位阶跃函数1(t) f(t)
ci是常数
M (s) ci [ D(s) (s pi )]s pi
例1: F(s)
1
(s 1)(s 2)(s 3)
c1 c2 c3 s 1 s 2 s 3
c1
[ (s
1)(s
1 2)(s
3)
(s
1)]s 1
1 6
1
1
c2
[ (s
1)(s
2)(s
3)
(s
2)]s2
15
c3
[ (s
证：
a L[ f ( t )] f ( t )est dt
a 0a
令t / a ,则原式 f ( )esa ad aF(as)
0
(8)卷积定理

控制工程_2拉氏变换

0
变
令u st t u , dt 1 du
换
s
s
及 其
L[tn ] un e u 1 du
0 sn
s
反 变
1 s n1
un
0
e udu
换
1
n!
Γ(n 1)
s n1
s n1
拉 典型时间函数的拉氏变换
普
拉
1. 单位阶跃函数 u(t)=1
(t ≥0)
1
s
斯 2. 单位脉冲函数δ(t)
sin t est dt
1
e jt e jt
e st dt
0
0 2j
其 反
1 2j
0
e
(s
jt
)
dt
e
(s
jt
)
dt
0
1 2j
s
1 j
s
1 j
变
s2 2
换 同理也可得： Lcost s
s2 2
拉 • 幂函数 t n 普
tn
n! sn1
拉 斯
L[tn ] t n e st dt
6K1 3K2 2K3 51
K1 5
K
2
3
K
3
6
换
(2)F(s)=
(s2
20(s 2s
1)(s 3) 2)(s 2)(s
4)
对于有共轭复根的分式有两种处理方法： a. 该部分分式的系数仍可由前面的方法求得； b. 可对该部分分式的分母用配方法后再用查表法。
8s s2
14 2s
变 换
7. 余弦函数cos ωt
8. 幂函数 tn
拉 • 单位阶跃函数 u(t) 1 1

拉氏变换及Z变换表

z e bT z e aT a b c a Te aT z 2 z e aT


c b e b c e a b c a te at
bt
2
at
c b z b c z




s s b s a


s a s b b a s c s a s b
ab s s a s b
ba
e at e bt
c a e at b c e bt
1 be ae ab ab
at bt
c a z b c z


z
2

2z aTe aT z aT 2 ze z e aT
a b s b s a 2 a b s c s b s a 2
2
a b Te aT z z z 2 z e bT z e aT z e aT
拉氏变换及 Z 变换表
拉氏变换 Y ( s ) 时间函数 y (t ) Z 变换 Y ( z )
e nTs
(t nT )
(t )
1(t )
z n
1或z
0
1
1 s 1 s2 1 s3 1 s n 1
1 s (1 T ) ln a
z z 1
T 2 z z 1 3 2z 1
abc s s a s b s c
1
b a c a
ab
bc
e at
c b a b
ca
e bt
a c b c

02第二章拉氏变换的数学方法(第二讲)


L[sin t 1(t )] L[
e
j t
e 2j
j t
1(t )]
1 1 1 2 2 2 j s j s j s
2.2 拉氏变换的性质
2 微分定理 L[ dx(t ) ] sX ( s ) x (0 ) dt 推论： n d （1）L[ x (t )] s n X ( s ) s n 1 x (0 ) s n 2 x (0 ) n dt
x(t) x(t)
as
X (s)
t a
t
L[sin (t 4) 1(t 4)] e
4 s


s
2 2
2.2 拉氏变换的性质 例：求如下图的拉氏变换。
f (t ) f1 (t ) f 2 (t ) E 1(t ) E 1(t t 0 )
L[ f (t )] E s e
2 st
t0 t0


0
0
te dt

st
s

e
st
0
0
s
dt
1 单位速度函数
t
2.1.1 简单函数的拉氏变换
7 单位加速度函数
0 x (t ) 1 2 2 t
t0 t0

x(t)
L x (t ) 1(t ) 1 s
3
1 2
0
（2）在零初始条件下
s
2

x n (0 ) s
n
L[ x (t )( dt ) ]
n
X (s) s
2.2 拉氏变换的性质
4 衰减定理 例：已知

2 拉氏变换

21
12 V
比 较
实际 位置
负载
n k ud
120° 转角
u2
电位器
角度传感器
反 馈
教材：p320
22
直流电机位置控制系统
功率放大器
23
24
4
质量－弹簧－阻尼系统 质量－弹簧－阻尼系统
m d2 d x o ( t ) B x o t Kx o t f i t dt 2 dt
u (t )
Model
u (t )
AND
y (t )
物理系统
假 设
数学模型 计算机
输入量
系统
输出量
数学 分析
仿真
模型 改进 系统结构 预测
给定元件
响应
比较元件
控制元件
扰动量 控制量
执行元件 被控对象
输出量 （被控量）
物理系统的 期望响应 修改系统参数
反馈量
反馈元件
3
典型控制系统的组成
4
数控机床—工作台
ms X o (s) BsX o s KX o s Fi s
2
数学中，为了把较复杂的运算转化为较简 单的运算，常采取的一种变换手段。例如：
（1）对数变换 数量的乘积
正
对数的和差
lg y lg x1 lg x2
X Y
（2）坐标变换
Y AX
y x1 x2 逆
28
27
积分变换
拉氏变换是一种积分变换，它可以把
积分变换

什么是积分变换？ 通过积分运算，把一个函数变成另一个函数的变换。
以时间为变量的函数（时域），转换 成以复数s为变量的函数（复数域， 或s域）。 拉氏变换的使用与对数变换 (Logarithmic transformation)相类似。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

f
t
A t0
(0
t
t0 )
0(t 0, t t0 )
f(t) A/t0
L f
t
A t0s
1 et0s
0 t0
t
1、定义与基本变换
例5 脉冲函数
f(t)
f
t
tl0i m0
A (0
t0
t
t0 )
0(t 0, t t0 )
0
t
L f t A
注意：A=1，称其为单位脉冲
函数，记为 t
1、定义与基本变换
又如，Fourier变换将时间域的实函数变 换成频率域的频谱，即，正弦谐波的线性组 合。
对线性时不变系统而言，我们要寻求能 简化微分方程求解过程的变换。一个好的变 换至少要有如下2个特征：
1、它的基本函数具有很大的覆盖面， 2、变换本身具有线性叠加性。
1、定义与基本变换
Fourier变换就具有上述特性， 1、它的基本函数为谐波函数，或纯虚 指数函数，它们的线性组合可以表示大部分 常用的函数， 2、基本函数线性组合的输入导致的响 应是基本函数响应的线性组合，只是组合系 数发生变化。 遗憾的是， Fourier变换的收敛条件比 较严格。
1、定义与基本变换
基本时间函数及其Laplace变换 (1) 指数函数 (2) 阶跃函数 (3) 斜坡函数 (4) 正弦函数 (5) 脉冲函数
1、定义与基本变换
例1、 指数函数
f
t
Aeat (t
0)
0 (其所有 导数皆存在，则称该 复变函数 F(s) 在该域 内是解析的。
2! 4! 6!
改写
e j
2
1
2!
4
4!
6
6!
L
j
3
3!
5
5!
7
7!
L
所以 e j cos j sin
1、定义与基本变换
函数f(t)的拉氏变换 拉氏积分运算符
F
s
L
f
t
0
f
t estdt
复变量
当t<0, f(t)=0
Fs
一一映射
f t
单边、线性变换 不追求数学细节，如收敛条件等。
1、定义与基本变换
例3 斜坡函数
f(t)
f
t
At(t 0) 0(t 0)
A
t
01
L
f
t
A s2
注意：A=1，称 其为单位斜坡函 数。
1、定义与基本变换
例3 斜坡函数
d test
首先注意到：
e st ste st
dt
于是： 1
d
te st dt
estdt
t stestdt
复域位移定理
L f t eat F s a
例6
L
eat sint
s a2 2
复域位移-------时域指数乘积
２、定理与技巧
2.3 时间比例尺定理
L
f
t a
aF
as
证明
L[ f ( t )] f ( t )estdt
1、定义与基本变换
由上式可以看出，Laplace变换是Fourier变换的推广， 一些工程上重要的函数，如阶跃函数、指数增长函数等 不满足Fourier变换的收敛条件，但乘上一个合适的指数 衰减因子后，就可以完成变换。
当s为纯虚数时， 函数的Laplace变换就是它的Fourier 变换；
当s为复数时，函数的Laplace变换就是它与实部指数 函数乘积的Fourier变换。
和脉动函数相比，脉冲函数“面积”不变，时间间隔为0。
２、定理与技巧
2.1时域函数平移f t a1t a
f t1t
f t a1t a
时域移 位定理
L f t a1t a easF s
t 0a
f(t)的拉氏变换
线性叠加原理是显然的。 时域位移-------复域指数乘积
２、定理与技巧 2.2 f t与 eat相乘
, cos t
1 2
e
jt
e
jt
L sin t
1 2j
s
1
j
s
1
j
1 2j
s j s j s j s j
s2
2
L cos t
1 2
s
1
j
s
1
j
1 2
s j s j s j s j
s2
s
2
1、定义与基本变换
例5.1 脉动函数
L f t Aeatestdt Aesatdt
0
0
A esat A
sa
0 sa
在复平面上 有一个极点
为使积分收敛，这里假设(s+a)的实部大于零
1、定义与基本变换
例2 阶跃函数
f(t)
f
t
A(t 0) 0(t 0)
A 0
t
L
f
t
A s
注意：A=1，称其为单位 阶跃函数，记为 1(t)。阶 跃函数在 t=0 处是不确定 的，相当于在 t=0 处将一 个直流信号突然加到系统 上。
第二讲：数学工具----Laplace变换
１、定义与基本变换 ２、定理与技巧 3 、反变换 4 、求解微分方程
1、定义与基本变换
变换是数学中经常采用的技巧，比如，在初 等数学中：
20 , 21, 21.1,L , 2
令：
对数变换
N 2
lg N lg 2
利用对数变换，我们可以将正数的乘积运算变 为对数的加法运算。
0 dt
0
0
2
test est s t testdt
0
s
0
0
3
0 1 s t testdt
s0
1、定义与基本变换
例4、 正弦、余弦函数
f
t
0,
sin
t
,
t t
0 0
f
t
0,
cos
t
,
t t
0 0
显然，直接求取并不明智。由尤拉定理有：
sin t
1 2j
e
j t
e
j t
cos 1 e j e j ,sin 1 e j e j
2
2j
1、定义与基本变换
尤拉定理证明：
有： ex 1 x x2 x3 L xn L
2! 3!
n!
所以：e j
1
j
2
3
j
4
5
j
6
7
j
L
2! 3! 4! 5! 6! 7!
而：sin
3
5
7
L
, cos
2
1
4
6
L
3! 5! 7!
1、定义与基本变换
历史从来都是选择性记忆的，优胜劣 汰，大浪淘沙。只有好的工具才会流传后 世。
Laplace变换就是这样的数学工具，它 对Fourier变换加以扩展，以复指数函数为 基本函数，将时间域的实函数变换成复频 率域的频谱函数，将微分算子变成代数算 子，非常方便。
1、定义与基本变换
复变量和复变函数
(1) 复变量： s j
(2) 复变函数： Fs Fr s jFi s
〉F(s)是函数，其自变量为s；s为复变量 〉F(s)函数值也是复的 〉除此之外，在一般情况下，F(s)与实函数无异
1、定义与基本变换 (3)复指数函数与尤拉定理：
e j cos j sin ,e j cos j sin