分子模拟教程
- 格式:ppt
- 大小:1.07 MB
- 文档页数:76

利用分子模拟制作物质效果Blender是一款强大而多功能的开源3D建模和渲染引擎,它提供了各种强大的工具和功能,使艺术家们能够创造出逼真的3D效果。
其中一个引人注目的功能就是分子模拟,它允许用户模拟和呈现各种物质效果,如流体、火焰、烟雾等。
在本教程中,我们将学习如何利用分子模拟制作物质效果。
首先,我们需要在Blender中创建一个场景来进行分子模拟。
打开Blender并选择一个合适的项目模板,例如"Cycles"引擎。
接下来,我们需要在场景中添加一个物体来表示我们要模拟的物质。
点击"Shift+A"或通过菜单选择,在场景中添加一个物体,如球体。
然后,选择添加的物体,切换到物体编辑模式,点击"Tab"键或通过菜单选择。
修改物体的形状或尺寸,以适应你想要模拟的物质。
例如,如果你要模拟水流,你可以选择一个较长的球体,以模拟流动的水。
接下来,我们需要给创建的物体添加一个分子模拟。
选择物体并在右侧面板中选择"物理属性"选项卡,然后点击"刚体"按钮,以将物体设置为刚体对象。
这将使物体对模拟更加稳定,并确保模拟时物体保持其形状。
然后,在"物理属性"选项卡中,找到并点击"流体"按钮。
这将为物体添加液体模拟属性,使其在模拟过程中表现得像液体一样。
在"流体"选项卡中,你可以调整物质的各种属性,如粘度、密度和压力等。
根据你想要模拟的物质的特性,调整这些属性将产生不同的效果。
此外,你还可以在场景中添加其他物体,如容器或障碍物,以改变流体的流动路径或产生其他效果。
在Blender中,你可以使用"碰撞对象"属性为这些物体添加碰撞检测,以模拟实际物体的交互。
完成以上设置后,我们可以开始进行分子模拟了。
选择场景中的物体,并在时间轴的右上角设置模拟的时间范围。



分子动力学模拟分子动力学模拟分子动力学是一门结合物理,数学和化学的综合技术。
分子动力学是一套分子模拟方法,该方法主要是依靠牛顿力学来模拟分子体系的运动,以在由分子体系的不同状态构成的系统中抽取样本,从而计算体系的构型积分,并以构型积分的结果为基础进一步计算体系的热力学量和其他宏观性质。
这门技术的发展进程是:1980年:恒压条件下的动力学方法(Andersenの方法、Parrinello-Rahman法)1983年:非平衡态动力学方法(Gillan and Dixon)1984年:恒温条件下的动力学方法(能势‐フーバーの方法)1985年:第一原理分子动力学法(→カー・パリネロ法)1991年:巨正则系综的分子动力学方法(Cagin and Pettit).最新的巨正则系综,即为组成系综的系统与一温度为T、化学势为μ的很大的热源、粒子源相接触,此时系统不仅同热源有能量交换,而且可以同粒子源有粒子的交换,最后达到平衡,这种系综称巨正则系综。
进行分子动力学模拟的第一步是确定起始构型,一个能量较低的起始构型是进行分子模拟的基础,一般分子的其实构型主要是来自实验数据或量子化学计算。
在确定起始构型之后要赋予构成分子的各个原子速度,这一速度是根据玻尔兹曼分布随机生成,由于速度的分布符合玻尔兹曼统计,因此在这个阶段,体系的温度是恒定的。
另外,在随机生成各个原子的运动速度之后须进行调整,使得体系总体在各个方向上的动量之和为零,即保证体系没有平动位移。
由上一步确定的分子组建平衡相,在构建平衡相的时候会对构型、温度等参数加以监控。
进入生产相之后体系中的分子和分子中的原子开始根据初始速度运动,可以想象其间会发生吸引、排斥乃至碰撞,这时就根据牛顿力学和预先给定的粒子间相互作用势来对各个例子的运动轨迹进行计算,在这个过程中,体系总能量不变,但分子内部势能和动能不断相互转化,从而体系的温度也不断变化,在整个过程中,体系会遍历势能面上的各个点,计算的样本正是在这个过程中抽取的。

分子动力学方法模拟基本步骤分子动力学方法是一种计算机模拟方法,用于研究原子、分子和粒子的运动行为。
它能够预测和揭示材料、化学物质和生物分子的性质和行为,对于理解和设计材料、药物和生物分子等具有重要意义。
分子动力学方法的模拟过程一般包括以下几个基本步骤。
1.选择模拟系统:首先需要明确要研究的系统,包括所研究系统的化学组成、结构和边界条件。
例如,研究一段DNA链的行为时,需要明确DNA链的序列、结构和周围环境等。
选择合适的模拟系统对于准确预测和理解系统行为至关重要。
2.设定初始构型:在进行分子动力学模拟之前,需要为模拟系统设定一个初始构型。
这个初始构型可以根据实验数据、理论计算结果或者其他模拟方法获得,也可以是人工构建的。
对于分子体系,通常使用分子力场将分子中的原子与键、角和二面角等参数进行描述。
初始构型需要满足系统的化学组成和结构,并且能够代表系统的初始状态。
3.设定运动方程:分子动力学方法通过求解牛顿运动方程来模拟粒子的运动。
这些运动方程与力场势能有关。
在分子动力学方法中,一般使用经验势函数来描述粒子间的相互作用。
这些势函数包括键能、角势能、二面角势能以及相互作用势能等。
4. 进行数值积分:为了在计算机中模拟分子的运动,需要解决运动方程的数值积分问题。
一般采用常用的积分算法,如velocity-Verlet算法、Euler算法等来进行数值积分。
这些算法能够根据物体的初始位置、速度和加速度,预测物体在一段时间后的位置、速度和加速度。
5.模拟运行:设置好模拟参数之后,就可以开始进行分子动力学模拟的运行。
在模拟过程中,按照设定的时间步长,通过数值积分方法求解运动方程,得到粒子在每个时间步长上的位置和速度。
同时,需要计算粒子间相互作用势能,以及其他需要关注的物理性质。
6.数据分析:模拟运行之后,需要对模拟得到的数据进行分析。
可以计算能量、压力、温度等系统的宏观性质,并进行可视化和统计分析。
同时,可以与实验结果进行比较,以验证模拟结果的准确性。




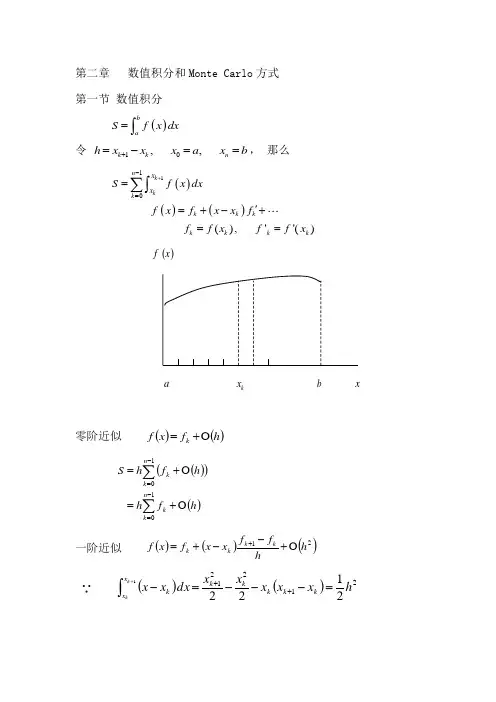
第二章 数值积分和Monte Carlo 方式 第一节 数值积分 ()ba S f x dx =⎰ 令 10,,k k n h x x x a x b +=-==, 那么()()()110(),''()k kn k k k k k k k k x x S f x dxf x f x x f f f x f f x +-=='=+-+==∑⎰()x fa k xb x零阶近似()()h f x f k O +=()()()∑∑-=-=O +=O +=110n k k n k k h f h h f h S一阶近似()()()21h hf f x x f x f kk k k O +--+=+ ∵()()⎰+=---=-++1212212122k kx x k k k kk k h x x x x x dx x x∴()()∑-=+O +⎪⎭⎫⎝⎛-+⋅=102121n k k k k h h f f h f S()()∑-=+O ++=102121n k k k h f f h 从直观看,用()112k k f f ++近似()f x 比只用k f 或1k f +好。
这方式也称Trapezoid 方式。
如此的数值积分方式的优势:● 简单直观,误差能够操纵缺点:● “平均主义”,在()0≈x f 的区域,()k f x x ∆对S 奉献很小,但消耗一样的机时。
在多自由度系统这弱点尤其特出。
问题: 直观地看,零级近似和一级近似的不同在哪? 习题: 编程序数值计算高斯积分。
第二节 Monte Carlo 方式 如何用随机方式求积分?例如,可用‘抛石子’方式。
但这方式不比简单的数值积分有效。
1.简单抽样的Monte Carlo 方式均匀地随机地选取[b a ,]中{}k M x 个点,显然,(11()Mkk S f x M==+O ∑当M 足够大,固然能够取得足够好的积分值。
问题:什么缘故误差是(1/O ?答 :不妨把这看成一个M 次测量的实验,假设每次测量都是独立的,由涨落理论,误差应为(1/O 。
