基于MATLAB的弗兰克-赫兹实验数据处理

弗兰克-赫兹实验可视化的数据处理系统摘要：弗兰克-赫兹实验融合信息化后缩短实验数据的记录时间，直观明了地呈现变量之间的规律。

学生利用多出来的时间研究数据，把隐含在实验数据背后的结论利用可视化功能图文并茂的展示出来。

学生利用可视化的处理结果加深对实验原理的理解和思考，同时提高自己的信息化应用能力。

关键字：大学物理实验；信息技术；弗兰克-赫兹实验；可视化中图分类号：O562文献标志码：A引言中外学者在近期的研究中提出：“信息化教学是提高大学物理实验教学的重要手段之一，现代教师应实时掌握新的信息技术，充分利用信息化技术进行教学，为教学增加趣味性，提高学生的动手能力，使学生更加直观、具体和深刻地认识到大学物理实验的本质，促进学生思维的发展”[1]。

当前，信息技术与大学物理实验的融合主要有两方面：① 虚拟实验。

②实验仪器智能化，如智能化程度过高，也不利于学生理解物理过程[2]。

为此，将信息技术和大学物理实验融合后做了一些新的探索，下面以弗兰克-赫兹实验的可视化系统为例进行展示。

一、大学物理实验的信息化大学物理实验是实践性课程，主要培养学生的动手能力，分析问题以及解决问题的能力，加深学生对物理理论知识的理解，增强学生对物理实验过程的感性认识[3]。

1.信息化改进的原则在信息化改进实验过程中要求：①增强学生对信息技术的掌握程度和使用频率，利用信息化处理大学物理实验数据，不仅能够减小处理数据的繁琐度，还能提高学生对大学物理实验过程的体验度；②不降低大学物理实验的课程要求，利用信息技术对重复性，繁琐性的实验过程进行模块化和一键式处理，利用多出来的时间解决拓展实验内容，进一步提高大学物理实验课程的内容深度。

2.信息化改进的目的信息化辅助大学物理实验课程，避免学生因课后学业紧张等因素对实验数据处理敷衍了事；利用信息化获得正确的实验结果，学生对实验的总结有根有据，从而避免总结的空洞笼统，教学效果明显提高；大学物理实验课程信息化后，学生了解信息技术在实验中的应用，对物理实验信息化产生一些新的想法，为后续开发其他数据处理系统、参加省大学生物理竞赛打下基础。

数据处理（1） 计算第一激发电势和相对误差IA--UG2K 曲线数据2.8V2.6V3.0V电流/uA 电压/V 电流/uA 电压/V 电流/uA电压/V 峰1 32.6 124.9 32.6 35.7 33.0 251.4 谷1 36.9 71.4 37.1 19.6 36.9 151.5 峰2 43.0 308.7 43.2 91.0 43.4 657.7 谷2 48.1 103.5 48.3 26.8 48.0 220.5 峰3 54.6 560.3 54.6 169.5 54.7 1258.4 谷3 59.5 157.0 59.7 42.8 59.4 369.4 峰4 66.4 851.2 66.2 258.7 66.5 2004.2 谷471.5289.171.580.371.1742.70.0500.01000.01500.02000.030.035.040.045.050.055.060.065.070.075.02.8V 2.6V3.0VI A ~ U G2K 曲线I A /μAU G2K /V用逐差法求氩原子第一激发电势U=（66.4+54.6-43-32.6）/4=11.35V相对误差E R=（11.35-11.5）/11.5*100%=1.30% 误差在允许范围内通过比较有：①灯丝电压的变化对极板电流有比较大的影响；②在其他因素相同的情况下，灯丝电压越大，极板电流越大。

分析：灯丝电压变大导致灯丝的实际功率变大，灯丝的温度升高，在其他的因素相同的情况下，单位时间到达极板的电子数增加，从而极板电流增大。

（2）改变灯丝电压，研究其对实验的影响。

反向拒斥电压U G2A =8.5 V,，分别测量拒斥电压U=10.5 V.，U=6.5 V，情况下的实验数据。

IA--UG2K曲线数据8.5V 10.5V 6.5V电流/uA 电压/V 电流/uA 电压/V 电流/uA 电压/V 峰1 32.6 124.9 33.5 61.5 32.2 141.8 谷1 36.9 71.4 38.3 25.8 36.0 98.9 峰2 43.0 308.7 44.1 189.9 42.8 338.0 谷2 48.1 103.5 49.2 29.3 47.0 163.2 峰3 54.6 560.3 55.5 388.0 53.8 607.5 谷3 59.5 157.0 60.9 43.6 58.6 263.1 峰4 66.4 851.2 67.1 625.3 65.6 914.4 谷4 71.5 289.1 72.5 113.2 70.4 448.70.0100.0200.0300.0400.0500.0600.0700.0800.0900.01000.030.035.040.045.050.055.060.065.070.075.08.5V 10.5V 6.5V通过比较有：① 反向拒斥电压的变化对极板电流有一定的影响；② 在其他因素相同的情况下，拒斥电压增大时，极板电流减小。

《数学实验》报告实验名称MATLAB与数学实验_ 学院专业班级姓名学号年月工科物理实验一、【作业题目】弗兰克—赫兹实验的实验数据处理；二、【作业程序】x=0:0.5:53;y=[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0.001,0.012,0.027,0.051,0.068,0.085,0.095,0.105,0.113,0.121,0.126,0.127,0.128,0.125,0.12,0.111,0.101,0.088,0.075,0.062,0.048,0.037,0.027,0.021,0.019,0.023,0.041,0.074,0.114,0.154,0.183,0.211,0.231,0.242,0.247,0.243,0.234,0.214,0.191,0.158,0.128,0.095,0.078,0.065,0.054,0.047,0. 04,0.039,0.056,0.084,0.148,0.213,0.263,0.313,0.347,0.372,0.388,0.39,0.381,0.364,0.332,0.289,0.252,0.198,0.146,0.102,0.076,0.054,0.045,0.044,0.045,0.066,0.142,0. 221,0.295,0.348,0.405,0.437,0.47,0.492,0.5,0.498,0.483,0.445,0.417,0.356,0.285];p2=polyfit(x,y,2)p7=polyfit(x,y,7)p10=polyfit(x,y,10)p20=polyfit(x,y,20)disp('二次拟合函数'),f2=poly2str(p2,'x')disp('七次拟合函数'),f7=poly2str(p7,'x')disp('十次拟合函数'),f10=poly2str(p10,'x')disp('二十次拟合函数'),f20=poly2str(p20,'x')x1=0:0.5:53;y2=polyval(p2,x1);y7=polyval(p7,x1);y10=polyval(p10,x1);y20=polyval(p20,x1);plot(x,y,'rp',x1,y2,'--',x1,y7,'bd',x1,y10,'y-.',x1,y20,'k-')三、【作业结果】p2 =0.0001 0.0023 0.0025p7 =-0.0000 0.0000 -0.0000 0.0001 -0.0024 0.0230 -0.0854 0.0648p10 =-0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0001 -0.0014 0.0112 -0.0458 0.0727 -0.0202p20 =Columns 1 through 130.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000-0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0001Columns 14 through 21-0.0012 0.0084 -0.0398 0.1268 -0.2473 0.2547 -0.1007 0.0027二次拟合函数f2 =8.8472e-05 x^2 + 0.0023245 x + 0.0024688七次拟合函数f7 =-2.4449e-10 x^7 + 4.5621e-08 x^6 - 3.3585e-06 x^5 + 0.00012385 x^4- 0.0023934 x^3 + 0.022986 x^2 - 0.085418 x + 0.06481十次拟合函数f10 =-8.8668e-14 x^10 + 2.1806e-11 x^9 - 2.2792e-09 x^8 + 1.3223e-07 x^7- 4.6647e-06 x^6 + 0.00010298 x^5 - 0.0014065 x^4 + 0.011236 x^3- 0.045832 x^2 + 0.072654 x - 0.020234二十次拟合函数f20 =7.7725e-26 x^20 - 4.2453e-23 x^19 + 1.0725e-20 x^18 - 1.6619e-18 x^17+ 1.7666e-16 x^16 - 1.365e-14 x^15 + 7.9243e-13 x^14 - 3.5248e-11 x^13 + 1.2142e-09 x^12 - 3.2533e-08 x^11 + 6.7733e-07 x^10 - 1.0894e-05 x^9 + 0.00013389 x^8 - 0.0012359 x^7 + 0.0083537 x^6 - 0.039837 x^5+ 0.12682 x^4 - 0.24729 x^3 + 0.25467 x^2 - 0.10066 x + 0.0026858四、【作业分析】通过使用Matlab对弗兰克赫兹实验的实验数据处理，可以观察到上图所示的曲线。

前提是已经将数据准确录入，并且存储为mat格式，其中电流存储为I.mat，电压存储为V.mat。

两个文件中都存放了1*121的矩阵。

所用matlab版本是matlab R2012a，若要运行文档中的程序，需要对中文标点括号等进行更正，否则无法运行。

建立一个名称为hezort.m的文件，与数据文件放在同一个文件夹下面。

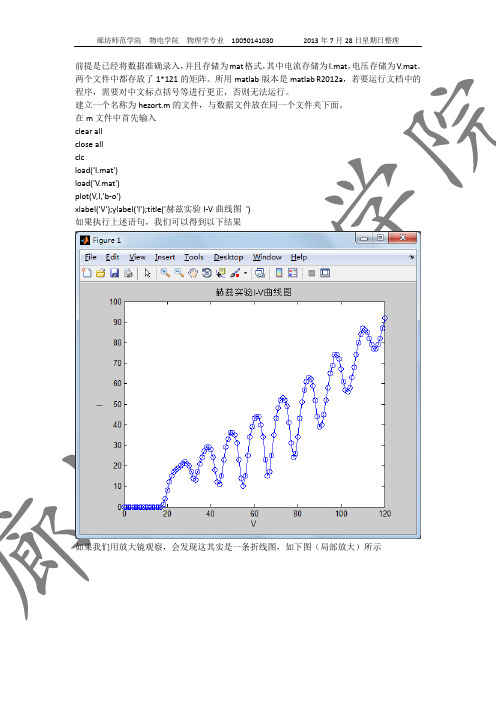
在m文件中首先输入clear allclose allclcload('I.mat')load('V.mat')plot(V,I,'b-o')xlabel('V');ylabel('I');title('赫兹实验I-V曲线图')如果执行上述语句，我们可以得到以下结果如果我们用放大镜观察，会发现这其实是一条折线图，如下图（局部放大）所示如果直接用来处理数据，必然会有很大误差，于是我们需要对数据进行必要的处理插值是必须的，matlab为我们提供了有效方便的插值方法，matlab插值的方法很多，这里，我们使用spline方法进行插值。

接着上面已经输入的代码xi=0:0.001:120; %插值的区间以及步长yi=interp1(V,I,xi,'spline');%用spline方法进行插值hold on%保留上一次作图痕迹plot(xi,yi,'r-')%绘制插值后的图形我们可以得到如下结果再次进行局部放大，我们会发现在原来折线的基础上得到一条光滑的曲线，说明数据量已经足够丰富这样，我们就可以开始寻找电流极大值与电压之间的线性关系了，接着上面的程序，我们输入代码：yjw=find(diff(sign(diff(yi)))==-2)+1%电流极大值的位置v=xi(yjw)%电流极大值对应的电压值矩阵（1*16）虽然得到16个数值，但是，我们知道是有8个极大值，而且前8个极大值基本上趋近于0的，而且极大值也是逐渐增大的，我们从得到的图形上可以看出第一个有效的极大值大于了20，所以我们只去大于20的极大值，进一步确定有效极大值的代码如下Vgk=v(find(v>20));这样，我们得到了需要的8个极大值，新开一个画图窗口，我们可以得到8个极大值与n 的关系。

两种常用软件在夫兰克-赫兹实验数据处理中的应用与比较夫兰克-赫兹实验的原理和意义夫兰克-赫兹实验是揭示原子内部电子能级的实验之一。

这一实验首先由德国物理学家弗兰克和赫兹于1914 年发现。

它的实验过程中电子在真空中沿着管子快速运动并轰击到一个阳极上，通过调节阴极与阳极之间的电压、电流和管子内部的气压等物理参数，可以测量到电子的动能和穿过阳极时释放的电子的能量。

这些数据可以推导出气体中的电子能级。

夫兰克-赫兹实验对于研究原子和分子的结构有巨大的贡献，它让人类能够更加全面理解原子结构的本质，从而推动了物理学和化学学科的发展。

两种常用软件在夫兰克-赫兹实验数据处理中的应用在夫兰克-赫兹实验中，数据的处理和分析至关重要。

为此，科学家开发了许多种不同的软件用于对实验数据进行分析和处理。

其中，比较常用的包括Origin 和MATLAB 两种软件。

Origin 是由美国公司OriginLab 开发的一款实验数据处理软件，它的主要功能在于数据预处理、绘图和分析。

在夫兰克-赫兹实验中，Origin可以用于对实验数据进行处理和可视化分析。

它可以帮助用户进行数据的可视化分析，产生出直观的图像来更好地理解实验结果。

此外，Origin 在帮助处理实验数据时支持多种曲线拟合方法，如线性拟合、多项式拟合和非线性拟合等。

使用Origin 可以完成诸如拟合、求导、积分等操作。

MATLAB (Matrix Laboratory) 是一种计算机语言与开发环境，主要用于数学计算、绘图、算法开发、数据分析以及应用程序创建等领域。

在夫兰克-赫兹实验中，MATLAB 可以用于对实验数据进行处理和分析。

与Origin 不同的是，MATLAB 拥有更强大和灵活的计算能力，能够处理较大规模、较复杂的数据，并支持多种编程语言和自定义算法的设计。

在使用MATLAB 进行数据处理时，用户可以自行编写代码并使用相应的算法，来完成数据的处理和统计分析。

两种常用软件的比较Origin 和MATLAB 两种软件虽然用于实验数据处理和分析有相似之处，但仍有明显的区别。

弗兰克-赫兹实验参数的确定及数据处理作者：牛中明方基宇王晓伟谌正艮来源：《赤峰学院学报·自然科学版》2019年第04期摘要：弗兰克-赫兹实验是大学物理中的重要实验之一，设置合适的实验参数（灯丝电压、第一栅极电压和拒斥电压）对该实验的成功至关重要.本文首先研究了实验曲线（板极电流随加速电压的变化曲线）随各实验参数的变化情况，这对合理设置实验参数具有重要的指导意义.根据在教学过程中遇到的几个实验参数设置不合理的情况，给出了相应的解决方案.研究发现，灯丝电压对实验曲线影响最为明显，其次是拒斥电压，第一栅极电压的影响相对较小.最后，给出了一种利用Origin软件处理实验数据的方法，即通过最小二乘法对实验数据进行线性拟合，这不仅可以有效地利用实验数据，而且可以给出计算结果的误差.关键词：弗兰克-赫兹实验;板极电流;加速电压;灯丝电压中图分类号：O4-34; 文献标识码：A; 文章编号：1673-260X（2019）04-0028-031911年，英国物理学家卢瑟福根据？琢粒子散射实验提出了原子的有核模型.在该模型中，电子绕原子核作轨道运动，根据经典理论，电子绕原子核旋转时必将发射电磁波而损失能量，最终落到原子核上，这与实际情况不符.此外，该模型也无法解释氢原子的线状谱.为了解释这些现象，1913年，丹麦物理学家玻尔提出其原子模型，认为核外电子只能在一些具有特定能量的轨道上运动，这种运动既不吸收也不发射能量，即电子在运动过程中能量保持不变，这种运动状态称为定态;各定态都具有特定的能量，其数值彼此分立;电子所处状态不论通过什么方式发生改变，只能从一个定态跃迁到另一定态，在跃迁时辐射或吸收一定频率的电磁波.该模型成功解释了氢原子核的线状谱，同时也为量子力学的诞生奠定了基础.1914年，德国物理学家弗兰克与赫兹采用慢电子轰击原子的方法，着重观察碰撞后电子能量的变化，通过实验测量发现，电子和原子碰撞时会交换某一定值的能量，将原子激发到较高能态.该实验直接证明了原子内部存在量子化的能级，也给玻尔的原子理论提供了原子线状谱之外的实验证据.1 实验原理图1为弗兰克—赫兹实验的原理图，通电后灯丝加热，温度升高，电子由阴极K发出，发出的电子在加速电压UG2K下加速运动，在板极A和栅极G2之间加有拒斥电压UG2A，用于筛选电子，仅当电子具有较大能量（≥eUG2A），才能克服拒斥电场到达阳极形成板极电流IA.弗兰克—赫兹管中充有氩气，电子在运动过程中会与氩原子发生碰撞，如果UG2K较小，电子通过加速获得的能量也较小，就不能将氩原子从基态激发到第一激发态，那么它们之间便只能发生弹性碰撞，考虑到电子质量远远小于氩原子，因此，碰撞后电子几乎不损失能量，板极电流将逐渐增加;随着UG2K的增大，电子获得的能量越来越大，当UG2K增加至氩原子的第一激发电位时，电子获得足够能量将氩原子从基态激发到第一激发态，即发生非弹性碰撞，此时电子能量几乎损失殆尽，以致没有足够能量克服拒斥电场，从而无法到达板极A而形成电流，造成板极电流显著减小.随着UG2K的继续增大，电子与氩原子碰撞后仍有足够的能量，克服拒斥电场而达到板极A，电流再次上升，直到UG2K增大至氩原子第一激发电位的两倍时，电子获得足够能量可以与氩原子发生两次非弹性碰撞而损失能量，造成第二次板极电流的显著下降.继续增大UG2K会重复发生上述板极电流增加减小的现象，形成规则的起伏变化的IA—UG2K曲线.通过相邻电流峰值对应的UG2K之差即可确定氩原子的第一激发电位.2 实验电压参数的确定由实验原理可知，实验IA—UG2K曲线受到灯丝电压、第一栅极电压影响UG1K和拒斥电压UG2A等实验参数的影响.由于该实验数据量大，记录数据需要较多时间，因此该实验一般是提前给定最佳实验参数，然后由学生通过手动和自动两种方式来测量IA—UG2K曲线，进而确定氩原子的第一激发电位.然而，随着实验条件的变化和仪器使用时间的增长，仪器的最佳参数值也会随之发生变化，因此了解IA—UG2K曲线随各个电压参数的变化趋势对设置最佳参数至关重要[1，2，3]，本文将首先讨论IA—UG2K曲线随各个电压参数的变化，并结合笔者在教学过程中遇到的一些极端情况，给出相应的处理方案.本工作采用成都世纪中科仪器有限公司生产的ZKY-FH-2弗兰克赫兹实验仪进行实验，图2—4分别代表灯丝电压、第一栅极电压UG1K和拒斥电压UG2A对IA—UG2K曲线的影响.由图2可知，随灯丝电压的增大，阴极K温度相应增加，因此从阴极发出的电子会增多，从而导致板极电流IA增加，曲线整体上移，峰谷更为明显，这有助于提高实验的分别率.但是灯丝电压过高，一方面会缩短弗兰克—赫兹管的寿命，另一方面可能会导致发射电子过多以致于无法观测到明显的吸收峰.因此，合理的选择灯丝电压是弗兰克—赫兹实验成功的关键.笔者在教学过程中发现，不同的实验仪器，最佳灯丝电压一般在2.5V—3.5V之间，需要根据实际情况进行调整.由图3可知，第一栅极电压UG1K对IA—UG2K曲线的影响较小，而且对板极电流的影响并不是单调的，因此一般取值1.5V左右即可.由图4可知，随着拒斥电压UG2A的减小，IA—UG2K曲线向上向左移动，同时峰谷电流之差相应减小，因此当IA—UG2K曲线的最后一个峰即将但未出现的时候，通过适当减小UG2A可使IA—UG2K曲线左移而显现出最后一个峰，但是过小的UG2A会导致峰谷电流之差减小，甚至很难观测到吸收峰，对于笔者所使用的实验仪器，UG2A一般取值在8—10V左右.如果上述電压参数在正常变化范围，即可以观测到起伏变化的IA—UG2K曲线，但是曲线中明显的峰数较少，则可依照图2—4中IA—UG2K曲线随相应电压参数的变化趋势进行调整，找到最佳参数值，如图5上图所示，按照默认的参数设置，只能观测到三个峰，而且峰谷差值较小，通过减小灯丝电压，增加UG2A，可以明显改善观测到的IA—UG2K曲线，如图5下图所示，共观测到5个峰，而且峰谷差值也更为明显.如果实验电压参数设置极不合理，可能会导致观测到的IA—UG2K曲线非常奇异，不仅得不到吸收峰，而且变化趋势也可能没有明显的规律性，如图6和图7的上图所示.这种情况往往是由灯丝电压过大所导致.因此，通过降低燈丝电压，并适度调节拒斥电压UG2A，实验IA—UG2K曲线可以得到明显改进，如图6和图7的下图所示，均可以观测到明显的5个峰，这为进一步准确测定氩原子的第一激发电位奠定基础.3 实验数据的处理本实验一般采用逐差法来处理实验数据[4，5]，但是实验中经常只能观测到奇数个明显的峰，如图7下图，只能观测到5个明显的峰，这为使用逐差法处理数据造成一定的难度.根据实验原理可知，UG2K与观测到的峰值序数k满足线性关系，即UG2K= a+bk，其中斜率b就是氩原子的第一激发电位[1，6].因此，我们可以将得到的不同峰位处的UG2K利用最小二乘法进行线性拟合，即可得到氩原子的第一激发电位，这比教材中经常采用的逐差法更为可靠[7].可以借助Origin软件进行数据处理，Origin会自动计算出线性拟合的相关系数，第一激发电位及其误差.以图7下图的数据为例，借助Origin软件处理的结果如图8所示，其中小球为实验数据点，虚线为拟合直线，拟合的相关系数为0.9997，第一激发电位为11.56±0.16V，这与第一激发电位的标准值符合得很好.4 结论本文通过研究灯丝电压、第一栅极电压和拒斥电压等实验参数对IA—UG2K曲线的影响，给出了确定弗兰克—赫兹实验参数的一般方案，并对一些极端情况给出了相应的处理措施.进一步地，利用Origin软件的线性拟合功能，给出了一种处理实验数据的方法，即通过最小二乘法对实验数据进行线性拟合，这种方法不仅可以有效地利用实验数据，而且可以给出氩原子第一激发电位的测量误差.参考文献：〔1〕张里荃，马艳梅，郝二娟.弗兰克—赫兹实验最佳实验条件及第一激发电位的研究[J].物理实验，2011，31（8）：37-46.〔2〕金哲.弗兰克赫兹实验最佳条件的确定[J].延边大学学报（自然科学版），2006，32（3）：169-171.〔3〕安可，高松松，林上金，胡澄.如何选择弗兰克-赫兹实验的工作参量[J].大学物理实验，2014，27（6）：34-55.〔4〕张卫山，杨善恒，鲁应涤，黄国蓝，樊江红，卢方武.基于Origin的弗兰克一赫兹实验数据分析[J].赤峰学院学报（自然科学版），2012，28（9）：6-7.〔5〕汪洪，赵青生，夏传鸿，谌正艮，杨杰.大学物理实验[M].北京：高等教育出版社，2016.〔6〕王杰，司嵘嵘.确定弗兰克-赫兹实验最佳工作参数的方法改进[J].大学物理实验，2018，31（5）：87-91.〔7〕马畅，牛中明，汪洪，张子云.伏安法测电阻实验统计误差的分析[J].大学物理实验，2018，31（4）：100-103.。

数据处理（1）计算第一激发电势和相对误差IA--UG2K曲线数据用逐差法求氩原子第一激发电势U=（66.4+54.6-43-32.6）/4=11.35V 相对误差E R=（11.35-11.5）/11.5*100%=1.30% 误差在允许范围内通过比较有：①灯丝电压的变化对极板电流有比较大的影响；②在其他因素相同的情况下，灯丝电压越大，极板电流越大。

分析：灯丝电压变大导致灯丝的实际功率变大，灯丝的温度升高，在其他的因素相同的情况下，单位时间到达极板的电子数增加，从而极板电流增大。

（2）改变灯丝电压，研究其对实验的影响。

反向拒斥电压U G2A =8.5 V,，分别测量拒斥电压U=10.5 V.，U=6.5 V，情况下的实验数据。

IA--UG2K曲线数据通过比较有：①反向拒斥电压的变化对极板电流有一定的影响；②在其他因素相同的情况下，拒斥电压增大时，极板电流减小。

分析：反向拒斥电压增大，在其他的因素相同的情况下，电子的能量大于eU G2A 的电子数减少，单位时间到达极板的电子数减少，从而极板电流减少。

思考与讨论（1）灯丝电压对F—H实验的I A—U G2K曲线形状有何影响？对第一激发电势的测量有何影响？答：灯丝电压不能过高或过低。

因为灯丝电压的高低，确定了阴极的工作电流。

灯丝电位低，阴极发射电子的能力减小，使得在碰撞区发生的碰撞减少，检测到的电流减小，给检测带来困难，从而使I A—U G2K曲线的分辨率下降；灯丝电压高阴极发射电子的能力增加，引起逃逸电子增多，相邻峰、谷值的差值减小。

（2）从I A—U G2K曲线上可以看出阳极电流并不是突然下降，有一个变化的过程（电流的峰有一定的宽度），而且出现峰值后电流不能降为零，这是为什么？答：这是因为阳极发射的电子的初始速度不是完全相同的，服从一定的统计规律。

另外，由于电子与氩原子的碰撞有一定的几率，在大部分电子与氩原子碰撞而损失能量的时候，还会有一些电子没有发生碰撞而到达了阳极，所以阳极电流不会降为零。

实验17 弗兰克－赫兹实验【实验目的】1．通过示波器观察板极电流与加速电压的关系曲线，了解电子与原子碰撞和能量交换的过程。

2．通过主机的测量仪表记录数据，作图计算氩原子的第一激发电位。

3．采用计算机接口，自动测量氩原子的激发电位，学习数据采集和自动测量技术。

【实验原理】1.电子与原子的相互作用根据玻尔理论，原子只能较长久地停留在一些稳定状态（即定态），其中每一状态对应于一定的能量值，各定态的能量是分立的，原子只能吸收或辐射相当于两定态间能量差的能量。

如果处于基态的原子要发生状态改变，所具备的能量不能少于原子从基态跃迁到第一激发态时所需要地能量。

弗兰克—赫兹实验是通过具有一定能量的电子与原子碰撞，进行能量交换而实现原子从基态到高能态的跃迁。

电子与原子碰撞过程可以用以下方程表示：E V M m MV m e e ∆+'+'=+222221212121v v 其中e m 是电子质量，M 是原子质量，v 是电子的碰撞前的速度，V 是原子的碰撞前的速度，v '是电子的碰撞后速度，V '是原子的碰撞后速度，E ∆为内能项。

因为M m e <<，所以电子的动能可以转变为原子的内能。

因为原子的内能是不连续的，所以电子的动能小于原子的第一激发态电位时，原子与电子发生弹性碰撞0=∆E ；当电子的动能大于原子的第一激发态电位时，电子的动能转化为原子的内能1E E =∆，1E 为原子的第一激发电位。

2.弗兰克-赫兹实验弗兰克和赫兹为了研究气体放电中的低能电子和原子间的相互作用，设计了电子与原子碰撞的实验。

图17-1弗兰克-赫兹实验装置示意图图17-2 管流与加速电压的关系图1914年，它们用图17-1的实验装置获得了一系列重要实验结果，碰撞管中的电子由热阴极K发射，经K与栅极G之间的电场加速，电子由K射向G，栅极G与板极P之间则加有一减速电压，形成一个减速电场，使电子减速。

当穿越过G的电子具有较大的能量而足以克服这一减速场时，就能到达板极P而形成管流I P。

五、实验数据整理(一)U f 、U G 、Ur 、Ua 与Ip 的关系。

1、 Uf 增加——Ip 增加2、 U G 与Ip 的关系如下：当U G 小于2.3V 时，Ip 随着U G 的增大而增大；当U G 大于2.3V 时，Ip 随着U G 的增大而减小。

（其中U G 为0——5V ）3、 Ur 增大——Ip 增大 (二)由试验数据求解Up1、 原始数据（1）、实验条件——灯丝电压：3.1V ；拒斥场电压：6.6V ；控室珊场电压：2.6V1.3203S 36.853=∆=Ug仪=80×1‰+0.1=0.18V 0.25452=∆=∆仪B345.13203.10.2545B A 3Ug 2222=+=∆+∆=∆所以：3Ug=36.8±1.3V Ug=12.27±0.45V 3、 线性拟和法拟和结果为Y=12.2717X+3.3806 R=0.99933101828.026)0.9993311(22)1(22112=--⨯=--≈--=n r n r bS bS b =b ×0.01828=3.3806×0.01828=0.06180.25452=∆=∆仪B26.00618.02545.02222=+=∆+∆=∆S B Ug所以：Ug=12.27±0.26V 4、 手动取点作图法图像（2）数据整理从图中可得第一峰值Ug1=16.67V 第二峰值Ug2=28.90VUg=Ug2-Ug1=12.23V六、数据及误差分析(一)Uf 、U G 、Ur 与Ip 增减关系分析Ur 为拒斥场电压，它的升高将直接决定电子到达极板处所需的能量，弗兰克-赫兹管内的电子其能量分布应该具有一定的规律，在除Uf 外其它量不变的情况下，Uf 的提高就意味着预原来电子中能量不够的那部分无法到达极板。

U G 为控制珊场电压，它的主要功能是减少空间电荷对阴极电子的影响，提高发射效率。