回转器电路设计(完整版,包括pspice仿真电路以及实验大数据)

回转器实验目的实验原理 实验仪器 实验步骤 实验报告要求 实验现象 实验结果分析 实验相关知识 实验标准报告实验目的• 学习和了解回转器的特性。

• 研究如何用运算放大器构成回转器，学习回转器的测试方法。

•学习用回转器和电容，来替代电感的方法。

实验原理• 回转器是理想回转器的简称。

它是一种新型的双 口元件，其符号如图5.16.1所示。

其特性表现为它能 将一端口上的电压（或电流）¡°回转¡±为另一端口上 的电流（或电压）。

端口量之间的关系为： 或上式中，回转系数g 具有电导的量纲，称为回转电导，α＝1/g 称为回转比。

• 回转器可以由晶体管或运算放大器等有源器件 构成。

图5.16.2所示电路是一种用两个负阻抗变换器1221i gui gu =⎧⎨=-⎩1221u i u iαα=-⎧⎨=⎩来实现的回转器电路。

其端口特性：根据回转器定义式，可得 g ＝1/R 。

图2.16.2 回转器电路图• 在输入为正弦电压，负载阻抗是一个电容C 时，输入阻抗为：因此，在回转器输出端接入一个电容元件，从输入 端看入时可等效为一电感元件，等效电感L ＝C /g 2。

所以，回转器也是一个阻抗变换器，它可以使容性 负载变换为感性负载。

122111i u R i u R ⎧=⎪⎪⎨⎪=-⎪⎩Lin 222111Lj C Z j Lg Z ggj Cωωω====• 如图5.16.4（a ）所示，用模拟电感器可以组成 一个RLC 并联谐振电路，图5.16.4（b ）是其等效电 路。

图5.16.4（a ） RLC 并联谐振电路图图5.16.4（b ） RLC 并联谐振电路等效电路图图5.16.4（a ）图5.16.4（b ）此并联谐振电路的幅频特性为：2C U LU ()U ω==其中， ； ，称为谐振角频率；品质因数为：实验仪器直流稳压电源 1台 功率函数发生器 1台 数字示波器 1台 数字万用表 1只 可调电容箱 1只 可调电阻箱 1只 直流毫安表 1只 交流毫伏表 1只 有源电路实验板 1块直流稳压电源 功率函数发生器数字示波器 数字万用表 可调电容箱 可调电阻箱 直流毫安表 交流毫伏表有源电路实验板实验步骤•测量回转器的回转电导1G R=0ω=001CQ GG Lωω===图5.16.5 测量回转电导电路图1. 按图2.16.5所示电路接线，回转器输入端u 1接正弦 信号U S ，电阻R 0为51Ω，电阻R 为1k Ω，负载电阻R L 取 2k Ω，采样电阻r 0取2k Ω。

1.13 实验十三 回转器的研究1.13.1. 实验目的(1). 观测和研究回转器的端口伏安特性；(2). 测试回转器的参数；(3).了解回转器的应用。

1.13.2. 实验原理(1) 回转器的端口伏安特性理想回转器是一个二端口网络，其电路模型如图12.1所示，其伏安关系为i 1=g u 2 或 u 1= - r i 2i 2=-g u 1 u 2= r i 1即一个端口的电流（或电压）能够“回转”为另一个端口的电压（或电流），其中g 和r 分别称为回转电导和回转电阻，简称回转系数。

(2) 回转器的阻抗逆变作用在图1.13-2中，回转器输入端接入负载阻抗ZL ，入端的输入阻抗z r L 2)(r r 1r I U I U Z 2222211in=-=-== 假如负载为电容，其阻抗为1/(j ωC)，则此时输入阻抗L j Cr j C j 122in r Z 'ω=ω=ω=即输入阻抗为电感L=r 2C 的电感元件，所以回转器也是一个阻抗逆变器。

(3) 利用回转器产生浮地电感用回转器（当输出端接电容C 时）模拟的电感一端接地，这就意味着此电路仅能用来实现一端接地的电感。

然而无源RLC 电路通常包含有不接地的电感，这种电感一般称为“浮地电感”。

实现这种电感的途径是把两个回转器和一个电容按图12.3(a)级联起来。

如果回转器是理想的，那么该电路就具有图1.13-3(b)所示的数值为Cr 2的理想浮地电感的性质。

图1.13-1 回转器模型 U 2 - + 图1.13-2 由回转器实现阻抗逆变 Z in 图1.1-3 回转器模拟浮地电感(a)用模拟电感可以构成谐振电路或滤波器等电路。

(4) 用运算放大器组成回转器用运算放大器组成回转器的电路有多种，图1.13-4为其中一种，其工作原理请同学们自行分析之。

1.13.3实验内容(1) 回转器端口伏安特性的观测用示波器分别观测输出端接R L 、L 或C 时的入端电压、电流波形。

电工电子综合实验回转器仿真论文院系：学号：姓名：回转器电路的设计摘要：理想回转器的功能主要依靠运算放大器来实现，它的主要特性是能够把输出输入两端的电流与电压“回转”。

工业生产中，在大规模集成电路中，通常利用回转器的这一特性，将电容元件回转成电感元件。

关键词：回转器电容回转参数运算放大器模拟电感引言：回转器是一种二端口网络元件，具有把一个端口的电压（或电流）“回转”为另一端口上的电流（或电压）的能力。

所以回转器可以把电容“回转”成电感，而这在工程上有重大意义。

在微电子器件中电容易于集成，而电感难以集成，利用回转器和电容来模拟电感可以解决这个问题。

本次实验研究将利用运算放大器完成回转器的设计及应用，利用运算放大器设计一个简单的回转器，并测量其回转参数，最后用自己设计的回转器将电容回转成电感。

通过本次研究，可以使我们对回转器的原理及应用有更深一步的了解。

正文：实验要求用运算放大器设计一个回转器电路（1）推导其基本方程。

（2）测量其回转参数g，验证其满足基本方程。

（3）将负载电容“回转”成一个电感量为0.1H~1H的模拟纯电感，用实验的方法验证该模拟量的电感特性及电感量准确性，并与理论值进行比较。

实验原理图（1）如图（1）所示，箭头表示回转方向。

理想回转器端口的伏安关系为I1=gU2 U1= －rI2I2= — gU1或U2=rI1式中，g和r——回转器回转电导和回转电阻，单位分别是S和Ω，统称为回转常数，且有g=1/r。

若回转方向相反，则式中g和r前的正、负号应互换。

L图（2）图（2）为用运算放大器设计的回转器电路基本方程：(1/R+1/R0)u1-u5/R0=i1(1/R+1/R0)u3-u5/R0-u2/R=0(1/R+1/R0)u2-u3/R-u6/R0=i2(1/R+1/R0)u4-u6/R0=0由虚短，u1=u3，u2=u4解得，i1 = 0 1/R u1 =0 g u1i2 -1/R 0 u2 -g 0 u2实验内容<1>.测量回转电导g，并验证其满足基本方程R用1.5kΩ的电阻，R0用200Ω的电阻，输出端接电阻箱R（仿真图中为R8），输入端串接低频信号源（频率3kHz，电压有效值3V）和一个阻值为2kΩ的电阻Rs（仿真图中为R9），如图电路改变输入电压U1得下表由以上测量和计算可知，测量出的回转参数与计算出来的基本相同，满足基本方程。

回转器电路设计（完整版,包括pspice仿真电路以及实验⼤数据）航空航天⼤学电路实验报告回转器电路设计姓名：李根根学号：031220720⽬录⼀、实验⽬的 (2)⼆、实验仪器 (2)三、实验原理 (2)四、实验要求 (3)五、⽤pspice软件进⾏电路仿真并分析 (5)六、实验容 (9)七、实验⼼得 (11)⼋、附件（Uc – f 图） (12)⼀、实验⽬的1．加深对回转器特性的认识，并对其实际应⽤有所了解。

2．研究如何⽤运算放⼤器构成回转器，并学习回转器的测试⽅法。

⼆、实验仪器1．双踪⽰波器2．函数信号发⽣器3．直流稳压电源4．数字万⽤表5．电阻箱6．电容箱7．⾯包板8．装有pspice软件的PC⼀台三、实验原理1．回转器是理想回转器的简称。

它是⼀种新型、线性⾮互易的双端⼝元件，其电路符号如图所⽰。

其特性表现为它能够将⼀端⼝上的电压（或者电流）“回转”成另⼀端⼝上的电流（或者电压）。

端⼝变量之间的关系为I1 = gu2 u1 = -ri2I2 = gu1 u2 = ri1式⼦中，r，g称为回转系数，r称为回转电阻，g称为回转电导。

2．两个负阻抗变换器实现回转器图中回转电导为:四、实验要求先利⽤pspice软件进⾏电路仿真，（提⽰：仿真时做瞬态分析，信号源⽤Vsin ，做频率分析时，信号源⽤VAC）然后在实验室完成硬件测试：1．⽤运算放⼤器构成回转器电路（电路构成见实验教材p216图9-24，其中电阻R的标称值为1000Ω），测量回转器的回转电导。

2．回转器的应⽤——与电容组合构成模拟电感。

3．⽤电容模拟电感器，组成⼀个并联谐振电路，并测出谐振频率以及绘制其Uc~f幅频特性曲线。

具体要求：1．回转器输⼊端接信号发⽣器，调得Us=1.5V(有效值)，输出端接负载电阻RL=200Ω，分别测出U1、U2及I1，求出回转电导g。

试回答改变负载电阻以及频率的⼤⼩对回转电导有何影响？2．回转器输出端接电容，C分别取0.1µF和0.22µF，⽤⽰波器观察频率为500Hz、1000Hz 时U1和I1的相位关系，解释模拟电感是如何实现的。

五、运放实现回转器仿真实验一、电路课程设计目的1、了解回转器的基本特性及其运放实现；2、掌握回转器参数的测试方法，了解回转器的应用。

二、仿真电路设计原理回转器的概念是B.D.H.Tellegen 于1948年提出的。

六十年代由L.P .Huelsman 及B.A.Sheei 等人用运算放大器及晶体管电路实现。

回转器是一种二端口器件。

它的电流与电压的关系为I 1=gU 2I 2= - gU 1或写成U 1= -rI 2 U 2=rI1式中g 和r =1g分别称为回转电导和回转电阻，简称回转常数。

用矩阵形式可表示为⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡212100U U g g I I 或⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡212100I I rr U U 若在回转器2—2′端口接以负载阻抗Z L ，则在1—1′端口看入的输入阻抗为LL in Z rI Z I r U I r rU rII rI I U Z 22222222212111/=--=-=-=-==如果负载阻抗Z L 在1—1′端口，则从2—2′端口看入的等效阻抗为LL in Z rI Z I r U I r rU rI I U Z 211211211222/==-=-==由上可见，回转器的一个端口的阻抗是另一端口的阻抗的倒数(乘上一定比例常数)，且与方向无关(即具有双向性质)。

利用这种性质，回转器可以把一个电容元件“回转”成一个电感元件或反之。

例如在2—2′端口接入电容C ，在正弦稳态条件下,即1L Z j Cω=，则在1－1′端口看入的等效阻抗为eg Lin L j C r j rZ rZ ωω====22211式中：L r C eg =2为1—1′端口看入的等效电感。

同样，在1—1′端接电容Ｃ，在正弦稳态条件下，从2—2′看进去的输入阻抗Ｚin2为eg in L j C j r Cj I I r U I r rU rI I rI I U Z ωωω=⋅=⋅-⋅-=⋅-=-===211211211212221式中：Ｌeg ＝r 2C 。

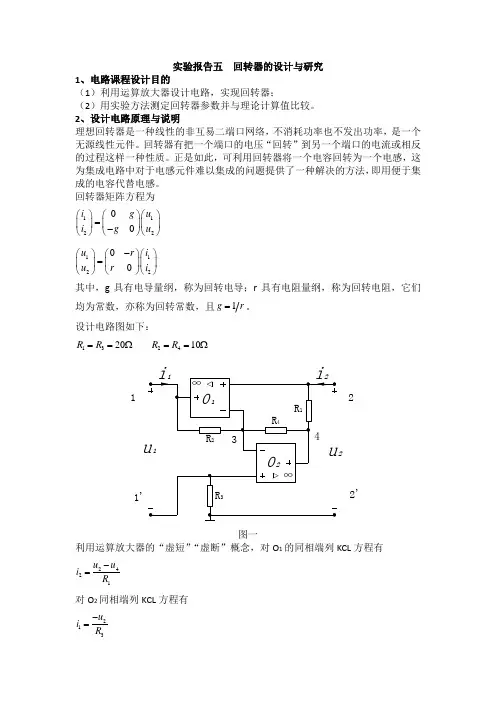
实验报告五 回转器的设计与研究1、电路课程设计目的（1）利用运算放大器设计电路，实现回转器；（2）用实验方法测定回转器参数并与理论计算值比较。

2、设计电路原理与说明理想回转器是一种线性的非互易二端口网络，不消耗功率也不发出功率，是一个无源线性元件。

回转器有把一个端口的电压“回转”到另一个端口的电流或相反的过程这样一种性质。

正是如此，可利用回转器将一个电容回转为一个电感，这为集成电路中对于电感元件难以集成的问题提供了一种解决的方法，即用便于集成的电容代替电感。

回转器矩阵方程为112200i u g i gu ⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭112200u i r u r i -⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭其中，g 具有电导量纲，称为回转电导；r 具有电阻量纲，称为回转电阻，它们均为常数，亦称为回转常数，且1g r =。

设计电路图如下：1320R R ==Ω 2410R R ==Ω121'2'图一利用运算放大器的“虚短”“虚断”概念，对O 1的同相端列KCL 方程有2421u u i R -=对O 2同相端列KCL 方程有213u i R -=又流过R 2和R 4的电流相同有12424u u u R R -=故42112R i u R R =写成矩阵形式为31122412100R i u i u R R R ⎛⎫-⎪⎛⎫⎛⎫⎪=⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪⎝⎭当1234R R R R =时，即满足回转器的条件，矩阵形式为3112231010R i u i u R ⎛⎫-⎪⎛⎫⎛⎫ ⎪= ⎪ ⎪⎪⎝⎭⎝⎭ ⎪⎝⎭回转电导31g R =，回转电阻3r R =。

现取1320R R ==Ω，2410R R ==Ω，故0.05g s =，20r =Ω。

3、电路课程设计仿真内容与步骤及结果（1）在1-1’ 端口接入电源，在2-2’ 端口接入10Ω电阻，测量I 1 I 2 U 2；图二1212200.6u i ==Ω21 5.999200.3u i -=≈Ω （2）在2-2’ 端口接入电源，在1-1’ 端口接入10Ω电阻测量I 2 I 1 U 1；图三125200.25u i ==Ω 2110200.5u i --==Ω-（3）测量回转器将电感回转为电容的特性；图四波形图为图五电流超前电压，表现出电容的特性。

电路实验报告回转器电路设计（Pspice仿真）班级：学号：姓名：一、实验仿真软件PSPICE (采用UA741运放，非理想运放)二、实验步骤1.测回转电导g：回转器输入端接信号发生器，调得U S=1.5V（有效值），输出端接负载电阻R L=200Ω，分别测U1，U2，I1，求g。

2.记录不同频率下U1、I1的相位关系：回转器输出端接电容，C分别取0.1μF、0.22μF，用示波器观察f分别为500Hz、1000Hz时U1和I1的相位关系。

3.测由模拟电感组成的并联谐振电路的U c~f幅频特性：取C1=0.1μF经回转器成为模拟电感，另取C=0.22μF，则f0=1.073kHz,符合要求。

信号源输出电压有效值保持为1.5V不变，改变频率（200Hz~2000Hz），测U c的值，同时观察U S和U C的相位关系。

（串联一取样电阻，阻值1kΩ）三、仿真实验电路图及数据1.测回转电导g：U1: 1.25VU2:249.99mVUR: 0.250VI1=0.250V/1000Ω=0. 250mAg=I1/U2=0.250mA/249.99mV=1.0004mS理论值：g=1/R=1mS(在误差允许范围内，该实验结果可以接受。

)2.记录不同频率下U1、I1的相位关系其中：R6两端电压与I1同相。

（1）C1=0.1μF：500Hz1000Hz输入电压的相位超前输入电流相位90o，证明输入端具有电感特性。

（2）C2=0.22μF：500Hz1000Hz3．测由模拟电感组成的并联谐振电路的Uc~f幅频特性：U C～f幅频特性曲线四、结论由于电子元器件并不理想，导致了实验结果（回转参数和模拟电感值）存在一定误差。

减小这些误差，可以在了解实际元器件内部构造及一些参数后通过补偿的方法来实现。

本课题要求利用运算放大器设计一个回转器，并了解其基本特性基本参数，然后加以应用。

而本课题的核心在于回转器具有把一个端口的电压（或电流）“回转”为另一端口上的电流（或电压）的能力，围绕这一核心可以进行一系列的研究。

仿真实验五 回转器的研究一、 实验目的：1、了解回转器的基本电特性及其运算放大器实现办法。

2、掌握回转器参数的测试方法并了解其应用。

二、 实验原理：理想回转器是一种线性的非互易二端口网络，如下图所示为回转器的电路模型：作为理想的二端口网络，其端口电流、电压关系可表示为：1221i gu i gu =⎧⎨=-⎩ 或写为：2112u ri u ri =⎧⎨=-⎩其中，g 具有电导量纲，称为回转电导；r 具有电阻量纲，称为回转电阻，他们均为常数，亦称为回转常数，且1g r =。

用矩阵形式表示上面的方程，写为112211220000i u g i g u u i r u r i ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦-⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ 因为12211221,Z Z Y Y ≠≠，所以理想回转器是非互易的，不满足互易定理。

根据理想回转器的端口方程，可作出用受控源表示回转器的电路模型，01U 02U 由上述方程可计算理想回转器的总功率为：()()112212210p u i u i u gu u gu =+=+-=上式说明，理想回转器既不消耗功率也不发出功率，因此它是一个无源线性元件。

同时由上述方程又可看出，回转器有把一个端口的电压“回转”到另一个端口的电流或相反的过程这样一种性质。

正是如此，可利用回转器将一个电容回转为一个电感，这为集成电路中对于电感元件难以集成的问题提供了一种解决办法，即用便于集成的电容代替电感。

如在上图的输出端接一负载阻抗2Z 则输入阻抗i Z 为：212221222111i I U g Z g Z I gU U g I ∙∙∙∙∙∙-====⎛⎫- ⎪⎝⎭上式中，当2Z →∞（端口2开路），0i Z →（端口1短路），当20Z →（端口2短路），i Z →∞（端口1开路）。

如故取21Z j Cω=，则2i C Z j g ω=j L ω=，可见2CL g=。

称回转器的这种性质为阻抗倒置性。

实验二十三 回转器一、实验目的1. 掌握回转器的基本特性2. 测量回转器的基本参数3. 了解回转器的应用 二、原理说明1. 回转器是一种有源非互易的新型两端口网络元件， 电路符号及其等效电路如图23-1(a)、(b)所示。

图 23-1 理想回转器的导纳方程如下： I 1 0 g u 1＝ ，或写成 i 1＝gu 2 ，i 2＝－gu 1 I 2 -g 0 u 2也可写成电阻方程：u 1 0 -R i 1＝ ，或写成u 1＝－R i 2 ，u 2＝R i 1 u 2 R 0 i 2式中g 和R 分别称为回转电导和回转电阻，统称为回转常数。

2. 若在2-2'端接一负载电容C ，则从1-1'端看进去就相当于一个电感，即回转器能把一个电容元件“回转”成一个电感元件；相反也可以把一个电感元件“回转”成一个电容元件，所以也称为阻抗逆变器。

2-2'端接有C 后，从1-1'端看进去的导纳Y i 为2222211/i u g g i gu u i Y i -=-== Cj Z i u L ω122=-=Lj C j g Y i ωω1/2==∴，式中2g C L =为等效电感。

3. 由于回转器有阻抗逆变作用，在集成电路中得到重要的应用。

因为在集成电路制造中，制造一个电容元件比制造电感元件容易得多，我们可以用一带有电容负载的回转器来获得数值较大的电感。

图23-2为用运算放大器组成的回转器电路图。

112,22U 2(a)11,U 12U 2(b)图 23-2三、四、实验内容实验线路如图23-3所示。

R S 跨接于HE-13挂箱中G 线路板左下部的二个插孔间。

1. 在图23-3的2-2'端接纯电阻负载（电阻箱）， 信号源频率固定在1KHz ，信号电压≤3伏。

图 23-3 用交流毫伏表测量不同负载电阻R L 时的 U 1、U 2 和U RS ， 并计算相应的电流I 1、I 2和回转常数g ，一并记入表23-1中。

电工电子综合实验报告——负阻抗变换器和回转器的设计一、摘要本文提出了利用运算放大器实现：（1）负阻抗变换器（NIC）的电路（2）回转器电路二、引言1、理想运算放大器有着①开环电压放大倍数A为无穷大；②输入电阻为无穷大；③输出电阻为零的特性。

而它在线性工作区的两个特性：“虚短”及“虚短”使得它有了广泛的应用。

如比例器、加法器、减法器、积分器等。

本文中则是实现了简单的负阻抗变换器和回转器。

2、负阻抗变换器（NIC）是一种二端口器件，是电路理论中的一个重要的基本概念，在工程实践中也有广泛的应用。

它一般由一个有源二端网络形成一个等值的线性负阻抗。

该网络可由线性集成电路或晶体管等元器件组成。

3、回转器是一种二端口网络元件，可用含晶体管或运算放大器的电路来实现。

它有着①不消耗能量不存储能量②非记忆元件③线性非互异元件④电量回转作用的特点。

也就是说它具有把一个端口的电压（或电流）“回转”成另一端口电流（或电压）的能力。

它的一个重要用途就是将电容“回转”成电感，或反之。

三、正文（一）实验材料与设备装置本实验采用的是虚拟的方法，所使用的软件为Multisim7。

（二）实验过程1、用运放设计一负阻抗变换器（NIC）电路⑴电流反向型负阻抗变换器（INIC）（图1—1）图1—1 INIC电路INIC的端口特性可用T参数描述为：U1 1 0 U2 ，其中 1 0= T=I1 0 -1/k I2 0 -1 /k当有负载Zl时，11’端口看进去的端口阻抗Z=U1/I1=kU2/I2，即为Z=-kZ2.即若22’接电阻R时，端口阻抗为-kR;接电感时，端口阻抗为-kL；接电容时，端口阻抗为-kC。

⑵电压反向型负阻抗变换器（VINC）（图1—2）图1—2 VNIC电路VNIC的端口特性可用T参数描述为：U1 -k 0 U2 ，其中-k 0= T=I1 0 1 I2 0 1当有负载Zl时，11’端口看进去的端口阻抗Z=U1/I1=kU2/I2，即为Z=-kZ2.即若22’接电阻R时，端口阻抗为-kR;接电感时，端口阻抗为-kL；接电容时，端口阻抗为-kC。

电工电子综合实验报告——负阻抗变换器和回转器的设计一、摘要本文提出了利用运算放大器实现：（1）负阻抗变换器（NIC）的电路（2）回转器电路二、引言1、理想运算放大器有着①开环电压放大倍数A为无穷大；②输入电阻为无穷大；③输出电阻为零的特性。

而它在线性工作区的两个特性：“虚短”及“虚短”使得它有了广泛的应用。

如比例器、加法器、减法器、积分器等。

本文中则是实现了简单的负阻抗变换器和回转器。

2、负阻抗变换器（NIC）是一种二端口器件，是电路理论中的一个重要的基本概念，在工程实践中也有广泛的应用。

它一般由一个有源二端网络形成一个等值的线性负阻抗。

该网络可由线性集成电路或晶体管等元器件组成。

3、回转器是一种二端口网络元件，可用含晶体管或运算放大器的电路来实现。

它有着①不消耗能量不存储能量②非记忆元件③线性非互异元件④电量回转作用的特点。

也就是说它具有把一个端口的电压（或电流）“回转”成另一端口电流（或电压）的能力。

它的一个重要用途就是将电容“回转”成电感，或反之。

三、正文（一）实验材料与设备装置本实验采用的是虚拟的方法，所使用的软件为Multisim7。

（二）实验过程1、用运放设计一负阻抗变换器（NIC）电路⑴电流反向型负阻抗变换器（INIC）（图1—1）图1—1 INIC电路INIC的端口特性可用T参数描述为：U1 1 0 U2 ，其中 1 0= T=I1 0 -1/k I2 0 -1 /k当有负载Zl时，11’端口看进去的端口阻抗Z=U1/I1=kU2/I2，即为Z=-kZ2.即若22’接电阻R时，端口阻抗为-kR;接电感时，端口阻抗为-kL；接电容时，端口阻抗为-kC。

⑵电压反向型负阻抗变换器（VINC）（图1—2）图1—2 VNIC电路VNIC的端口特性可用T参数描述为：U1 -k 0 U2 ，其中-k 0= T=I1 0 1 I2 0 1当有负载Zl时，11’端口看进去的端口阻抗Z=U1/I1=kU2/I2，即为Z=-kZ2.即若22’接电阻R时，端口阻抗为-kR;接电感时，端口阻抗为-kL；接电容时，端口阻抗为-kC。

电工电子综合实验报告——负阻抗变换器和回转器的设计一、摘要本文提出了利用运算放大器实现：（1）负阻抗变换器（NIC）的电路（2）回转器电路二、引言1、理想运算放大器有着①开环电压放大倍数A为无穷大；②输入电阻为无穷大；③输出电阻为零的特性。

而它在线性工作区的两个特性：“虚短”及“虚短”使得它有了广泛的应用。

如比例器、加法器、减法器、积分器等。

本文中则是实现了简单的负阻抗变换器和回转器。

2、负阻抗变换器（NIC）是一种二端口器件，是电路理论中的一个重要的基本概念，在工程实践中也有广泛的应用。

它一般由一个有源二端网络形成一个等值的线性负阻抗。

该网络可由线性集成电路或晶体管等元器件组成。

3、回转器是一种二端口网络元件，可用含晶体管或运算放大器的电路来实现。

它有着①不消耗能量不存储能量②非记忆元件③线性非互异元件④电量回转作用的特点。

也就是说它具有把一个端口的电压（或电流）“回转”成另一端口电流（或电压）的能力。

它的一个重要用途就是将电容“回转”成电感，或反之。

三、正文（一）实验材料与设备装置本实验采用的是虚拟的方法，所使用的软件为Multisim7。

（二）实验过程1、用运放设计一负阻抗变换器（NIC）电路⑴电流反向型负阻抗变换器（INIC）（图1—1）图1—1 INIC电路INIC的端口特性可用T参数描述为：U1 1 0 U2 ，其中 1 0= T=I1 0 -1/k I2 0 -1 /k当有负载Zl时，11’端口看进去的端口阻抗Z=U1/I1=kU2/I2，即为Z=-kZ2.即若22’接电阻R时，端口阻抗为-kR;接电感时，端口阻抗为-kL；接电容时，端口阻抗为-kC。

⑵电压反向型负阻抗变换器（VINC）（图1—2）图1—2 VNIC电路VNIC的端口特性可用T参数描述为：U1 -k 0 U2 ，其中-k 0= T=I1 0 1 I2 0 1当有负载Zl时，11’端口看进去的端口阻抗Z=U1/I1=kU2/I2，即为Z=-kZ2.即若22’接电阻R时，端口阻抗为-kR;接电感时，端口阻抗为-kL；接电容时，端口阻抗为-kC。

南京航空航天大学仿真实验报告课程名称电路实验与实践实验名称基于PSpice的回转器实验仿真班级 0312207 姓名惠琦学号031220732 实验组别同实验者实验日期实验地点评定成绩审阅老师一、实验目的1.加深对回转器特性的认识，并对其实际应用有所了解。

2.研究如何用运算放大器构成回转器，并学习回转器的测试方法。

二、实验原理1.回转器是理想回转器的简称，它能将一端口上的电压（电流）“回转“成另一端口上的电流（电压）。

端口变量之间的关系为：I1=gU2 或u1=-ri2I2=-gU1 u2=ri1式中：r、g 为回转系数，r 为回转电阻，g 为回转电导。

2.两个负阻抗变换器实现回转器：用电阻接入时:Rin=1/(g2RL)一般情况:Zin=1/(g2ZL)回转电导:g=1/R三、实验仿真软件OrCADPSpice四、实验步骤1.测回转电导 g：实物实验步骤：回转器输入端接信号发生器，调得 US=1.5V（有效值），输出端接负载电阻 RL=200Ω，分别测 U1，U2，I1，求 g。

仿真步骤：原理图如下，搭建如图原理图并运行仿真，观察并记录U1，U2，I1，求回转电导g。

2.记录不同频率下 U1、I1 的相位关系：实物实验步骤：回转器输出端接电容，C 分别取 0.1μ F、0.22μ F，用示波器观察 f 分别为 500Hz、1000Hz 时 U1 和 I1 的相位关系。

仿真步骤：原理图如下，其中电压源为VSIN（适合暂态分析），分析设置中选择暂态分析Transient，取合适的时间，用标记Mark功能标记U1 和I1（实际标记的是采样电阻旁的电压），对 C 分别取 0.1μ F、0.22μ F，对f分别取500Hz、1000Hz（在VSIN中修改FREQ参数），进行暂态分析，观察并记录波形。

3.测由模拟电感组成的并联谐振电路的 Uc~f幅频特性：实物实验步骤：取 C1=0.1μ F 经回转器成为模拟电感，另取 C=0.22μ F，则f0=1.073kHz,符合要求。

专题二、 回转器、旋转器电路的设计摘要：本文简要地介绍了一种回转器和旋转器电路的设计方法，并对所设计的电路进行了研究。

例如测定了回转器的基本参数g ，旋转器的旋转特性的验证，得到了较好的实验结果。

关键字：回转器、旋转器、运算放大器。

引言：回转器是一种无源且非互易的二端口元件。

可以用含晶体管或运算放大器的电路来实现。

回转器可以把１μＦ的电容“回转”成１Ｈ的电感，这在工程上有重大意义。

因为在微电子器件中电容容易集成，而电感难以集成，利用回转器和电容来模拟电感是解决问题的一个重要途径。

旋转器和变标器、反照器及变换器均属线性转换器。

这类器件可以完成输入端和输出端的特性变换。

利用这种变换，可以从目前常用的非线性电阻器等元件产生出许多新的非线性元件，为工程上非线性元器件提供了来源。

实验原理：理想回转器端口的电流、电压关系可用下列方程来表示：｛1221gu i gu i -== 或 ｛1221ri u ri u =-=1. 回转器：设计一个回转器电路，测量其基本参数g （有数据组）。

将负载电容 “回转”成一个电感量为0.1H ～1H 的模拟纯电感，用实验的方法验证该模拟量的电感特性及电感量准确性，并与理论值进行比较。

然后，研究它的频率特性（十组数据）。

回转器是一种有源非互易的新型二端口网络元件，可以用含晶体管或运算放大器的电路来实现。

理想回转器端口的伏安关系为式中，g 和r 分别称为回转器的回转电导和回转电阻，其单位分别是S 和 ，统称为回转常数，且有g=1/r 。

回转器的一端口电压（或电流）可用另一端口电流（或电压）表示。

回转器具有把一个端口的电压（或电流）“回转”成另一个端口电流（或电压）的能力。

回转器的一个重要用途是可以把电容“回转”成电感，或反之。

（1） 测定g ；（2） 将负载电容 “回转”成一个电感量为1H 的模拟纯电感；（3） 用实验的方法验证该模拟量的电感特性及电感量准确性，并与理论值进行比较； （4） 研究频率特性；2. 旋转器：设计一个θ= - 15°到 - 80°的旋转器，定标系数R=0．5K Ω～2 K Ω。

仿真实验五 回转器的研究一、实验目的：1、了解回转器的基本电特性及其运算放大器实现办法。

2、掌握回转器参数的测试方法并了解其应用。

二、实验原理：理想回转器是一种线性的非互易二端口网络，如下图所示为回转器的电路模型：作为理想的二端口网络，其端口电流、电压关系可表示为：1221i gu i gu =⎧⎨=-⎩或写为：2112u ri u ri =⎧⎨=-⎩其中，具有电导量纲，称为回转电导；具有电阻量纲，称为回转g r 电阻，他们均为常数，亦称为回转常数，且。

1g r =用矩阵形式表示上面的方程，写为112211220000i u g i g u u i r u r i ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦-⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦因为，所以理想回转器是非互易的，不满足互易定12211221,Z Z Y Y ≠≠理。

根据理想回转器的端口方程，可作出用受控源表示回转器的电路模型，01U 02U 由上述方程可计算理想回转器的总功率为：()()112212210p u i u i u gu u gu =+=+-=上式说明，理想回转器既不消耗功率也不发出功率，因此它是一个无源线性元件。

同时由上述方程又可看出，回转器有把一个端口的电压“回转”到另一个端口的电流或相反的过程这样一种性质。

正是如此，可利用回转器将一个电容回转为一个电感，这为集成电路中对于电感元件难以集成的问题提供了一种解决办法，即用便于集成的电容代替电感。

如在上图的输出端接一负载阻抗则输入阻抗为：2Z i Z 212221222111i I U g Z g Z I gU U g I ∙∙∙∙∙∙-====⎛⎫- ⎪⎝⎭上式中，当（端口2开路），（端口1短路），当2Z →∞0i Z →（端口2短路），（端口1开路）。

如故取，则20Z →i Z →∞21Z j Cω=，可见。

称回转器的这种性质为阻抗倒置性。

2i C Z j g ω=j L ω=2C L g =回转器了利用多种电路实现，如运算放大器、受控源等等，先使用运算放大器电路构成回转器，其设计电路如下图所示：由上图电路进行理论计算：3301112011244340222602267711R R U U U U U U U R R R R U U U R U U R R R ⎧⎛⎫--⎧=+-=⎪ ⎪⎪⎝⎭⎪⎪⇒⎨⎨-⎛⎫⎪⎪==+ ⎪⎪⎪⎩⎝⎭⎩331011112114224122022162212454475111R R U U U i U U i R R R R R R R U U U U R i i U U R R R R R R ⎧⎛⎫-⎧=-+=+⎪ ⎪⎪⎝⎭⎪⎪⇒⎨⎨--⎛⎫⎪⎪=+=-+- ⎪⎪⎪⎩⎝⎭⎩ 根据上图中数据，所有电阻均为，则有：1k Ω3314224116224475111R R R R R R R i U R i U R R R R ⎡⎤-⎢⎥⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦--⎢⎥⎣⎦1122101000101000i U i U ⎡⎤⎢⎥⎡⎤⎡⎤⇒=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥-⎢⎥⎣⎦可知，或11000g s =1r k =Ω 即当在输出端接入电容值为的电容时，输入端处相当于接入了大C F μ小为的电感。