北大随机过程课件：第 5 章 第 1 讲 高斯随机变量

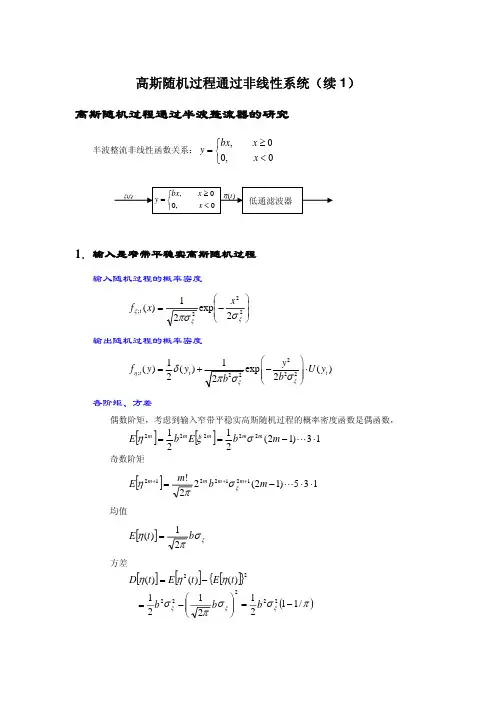
高斯随机过程通过非线性系统（续1）高斯随机过程通过半波整流器的研究半波整流非线性函数关系：,0,bx x y x ≥⎧=⎨<⎩1．输入是窄带平稳实高斯随机过程输入随机过程的概率密度⎟⎟⎠⎞⎜⎜⎝⎛−=222;2exp 21)(ξξξσπσx x f t 输出随机过程的概率密度2;1()()()2t t t f y y U y ηδ⎛⎞=+⋅ 各阶矩、方差偶数阶矩，考虑到输入窄带平稳实高斯随机过程的概率密度函数是偶函数，[][]13)12(212122222⋅−=="m b E b E m m m m m σξη 奇数阶矩[]135)12(22!1212212⋅⋅−=+++"m b m E m m m m ξσπη均值[]ξσπηb t E 21)(=方差[][][]{}()πσσπσηηηξξξ/11212121)()()(2222222−=⎟⎟⎠⎞⎜⎜⎝⎛−=−=b b b t E t E t D相关函数2100222122212122221))(1(2)(2exp ))(1(2),()(dx dx x x x x x x b t t R R ∫∫∞∞⎟⎟⎠⎞⎜⎜⎝⎛−−+−⋅−==τρστρτρπστξξηηηη 其中，122{}()t t E x x ξρτσ=，利用典型的积分变换1，得：222222211()()()244()()b R b b R R R ηηξξξξξξξξξτσττππστσρτ≈++=功率谱∫∫∞∞−∞∞−′′−′++==f d f f P f P b f P b f b d eR f P f j )()(4)(41)(21)()(222222ξξξξξξξξτπηηηηπσδσπττ2．输入信号是矩形带通窄带实平稳随机过程输入的功率谱密度：⎪⎩⎪⎨⎧Δ+<<Δ−=otherwise,022,2/)(000ff f f f N f P ξξ 20f N ξσΔ⋅＝非线性器件输出信号的功率谱密度：直流分量：())(21)(210222f N f b f b δπδσπξ⋅Δ= 低频分量f f Δ≤≤0⎟⎟⎠⎞⎜⎜⎝⎛Δ−⎟⎠⎞⎜⎝⎛=⎟⎟⎠⎞⎜⎜⎝⎛Δ−Δ⎟⎠⎞⎜⎝⎛f fN b f f f N b 1241224022022ππσξ 带通信号分量2/2/f f f f f c c Δ+≤≤Δ−24102N b二倍频分量f f f f f c c Δ+≤≤Δ−22⎟⎟⎠⎞⎜⎜⎝⎛Δ−⎟⎠⎞⎜⎝⎛=⎟⎟⎠⎞⎜⎜⎝⎛Δ−Δ⎟⎠⎞⎜⎝⎛f fN b f f f N b 128124022022ππσξ 低通滤波器输出信号的功率谱密度：直流分量：())(21)(210222f N f b f b δπδσπξ⋅Δ= 低频分量f f Δ≤≤0⎟⎟⎠⎞⎜⎜⎝⎛Δ−⎟⎠⎞⎜⎝⎛=⎟⎟⎠⎞⎜⎜⎝⎛Δ−Δ⎟⎠⎞⎜⎝⎛f fN b f f f N b 1241224022022ππσξ典型的坐标变换1原积分：2100222122212122221))(1(2)(2exp ))(1(2),()(dx dx x x x x x x b t t R R ∫∫∞∞⎟⎟⎠⎞⎜⎜⎝⎛−−+−⋅−==τρστρτρπστξξηηηη 其中，[]221/)()()(ξστρt x t x E =变换))(1(2))(1(2222221τρστρσξξ−=−=x v x u))(1(2),(),(2221τρσξ−=∂∂v u x x积分()[]d udv uv v u uv b dx dx x x x x x x b t t R R ∫∫∫∫∞∞∞∞−+−⋅−=⎟⎟⎠⎞⎜⎜⎝⎛−−+−⋅−==00222/3222210022212221212/122221)(2exp ))(1(2))(1(2)(2exp ))(1(2),()(τρπτρστρστρτρπστξξξηηηη 典型的坐标变换2积分之间的关系：()[]()[]()[]dwdI dudv wuv v u uv dudv wuv v u uv dw dIdudvwuv v u I 212exp 2exp 22exp 002200220022=−+−⋅−+−⋅=−+−=∫∫∫∫∫∫∞∞∞∞∞∞典型的坐标变换3原积分：()[]d udv wuv v u I ∫∫∞∞−+−=00222exp积分变换：从v u ,平面到θ,r 平面，参数()παα,0,1cos ∈≤=wαθααθαsin 2cos sin 2cos ⎟⎠⎞⎜⎝⎛−=⎟⎠⎞⎜⎝⎛+=r v r u ， 注意到下列关系：⎟⎠⎞⎜⎝⎛−−==−=⎟⎠⎞⎜⎝⎛−==+=22,22,022,22,0απθπθααπθπθαv uααθααθααθααθαθθsin sin 2sin sin 2sin sin 2cos sin 2cos r r r r v u r v r u =⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛+−⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛+=∂∂∂∂∂∂∂∂ ()()()()()(()())222222222222222cos 2cos 12cos 2cos 12cos 1sin 22cos cos 2cos cos 22cos 12cos 1sin 2sin 2cos sin 2cos cos 2sin 2cos sin 2cos )(2r r r r r r uvv u =−−+−−−−++++=−−−++++=⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛+−⎟⎠⎞⎜⎝⎛−+⎟⎠⎞⎜⎝⎛+=−+θαθααθαθααθαααθαθαααθααθαααθααθατρ 原积分：()[]210222002212sin 2/sin 2exp sin 2exp w w drd r rdudvwuv v u I −+=−=−=−+−=−∞−−−∞∞∫∫∫∫πααπθααπαπww1sin 2/cos −−==παα原积分：()()()()()w ww w w w www w w w dw d dw dI 12/3222212221sin 2/12121121sin 2/11112sin 2/−−−+−+−=−−++−−=−+=πππ原积分：()[]()()()ww ww dwdIdudv wuv v u uv 12/3220022sin2/14141212exp −∞∞+−+−==−+−⋅∫∫π原积分：()()[]⎥⎦⎤⎢⎣⎡+++++⋅=⎥⎦⎤⎟⎠⎞⎜⎝⎛⋅⋅⋅+⋅+++⎢⎣⎡⎟⎠⎞⎜⎝⎛−⋅⋅−⋅−−⋅=++−⋅=⎟⎟⎠⎞⎜⎜⎝⎛−−+−⋅−==−∞∞∫∫"")(801)(241)(21)(2121)(54231)(321)(2)()(6421)(421)(21121)(sin 2/)()(121))(1(2)(2exp ))(1(2),()(84222536422212/1222100222122212122221τρτρτρτρπσπτρτρτρπτρτρτρτρσπτρπτρτρσπτρστρτρπστξξξξξηηηηb b b dx dx x x x x x x b t t R R由于1)(≤τρ)()()(4)(4121)(2222222τρσττπστσπτξξξξξξξξξηη=++=R R b R b b R。