当前位置：文档之家 › 第二章 理想气体性质

第二章 理想气体性质

  • 格式：ppt
  • 大小：797.00 KB
  • 文档页数：47

下载文档原格式

  / 47

合集下载

大学物理(第三版)热学 第二章

大学物理(第三版)热学 第二章


一、 理想气体的微观图象
1. 质点 P nkT P 0
在 T 一定的情况下 n 值小 意味着分子间距大 2 .完全弹性碰撞
3. 除碰撞外 分子间无相互作用 f=0
范德瓦耳斯力(简称：范氏力)
f
斥力
合力
r0
O
s
10 -9m r
d
引力
分子力
气体之间的距离
r 8r0 引力可认为是零 可看做理想气体
第3步：dt时间内所有分子对dA的冲量
dI dIi ix 0
1 2
i
dIi
nimi2xdtdA
i
dIi
2ni mi2xdtdA
第4步：由压强的定义得出结果
P

dF dA

dI dtdA

i
ni
m
2 ix
i dA
ixdt
P

dF dA

dI dtdA
2. 气体分子的自由度
单原子分子 双原子分子 多原子分子
i3 i5 i6
二、 能量按自由度均分原理 条件：在温度为T 的平衡态下 1.每一平动自由度具有相同的平均动能
1 2
kT

1 3

3 2
kT

1 2
m
1
3
2

1 2
m
2 x

1 2
m
2 y

1 2
m
2 z
每一平动自由度的平均动能为 1 kT
2
2.平衡态 各自由度地位相等
每一转动自由度 每一振动自由度也具有 与平动自由度相同的平均动能 其值也为 1 kT
第二章 物质的状态 气体、液体、溶液

第二章 物质的状态 气体、液体、溶液

23
临界现象? 临界现象
课本p26 课本
Tb （沸点） < 室温 沸点） Tc < 室温， 室温， 室温下加压不能 液化
Tb < 室温， 室温， Tc > 室温， 室温， 室温下加压可液 化 Tb > 室温 Tc > 室温， 室温， 在常温常压下为 液体
24
临界常数： 临界常数：
p26
• 每种气体液化时 各有一个特定温度叫临界温度 每种气体液化时, 各有一个特定温度叫临界温度 临界温度Tc. 在Tc 以 无论怎样加大压力, 都不能使气体液化. 上, 无论怎样加大压力 都不能使气体液化 • 临界温度时 使气体液化所需的最低压力叫临界压力 临界温度时, 使气体液化所需的最低压力叫临界压力 临界压力Pc. • 在Tc 和 Pc 条件下 1 mol 气体所占的体积叫临界体积 条件下, 气体所占的体积叫临界体积 临界体积Vc.
17
压力P愈小 温度T愈高 愈高, 压力 愈小, 温度 愈高 愈接近理想气体 愈小
1mol N2气
Z=
18
不同气体的比较 (1mol, 300K )
Z=
19
图总结： 气体 Z-P 图总结：
1. 常压常温下，沸点低的气体，接近理想气体 常压常温下，沸点低的气体， 2. 起初增加压力时，对于分子量较大的分子，分子间作用力增 起初增加压力时，对于分子量较大的分子， 加占主导， 加占主导，使得 Z < 1 3. 增加较大压力时，分子的占有体积占主导，使得 Z > 1 增加较大压力时，分子的占有体积占主导，
第二章
物质的状态
p16
Figure: Gas-liquid-solid Gas-liquid-
1
本章主要内容： 本章主要内容： 一、气体
第二章 气体分子运动论的基本概念_电子教案白

第二章 气体分子运动论的基本概念_电子教案白

~ 10 −8 m 数量级，可看
（1）d 可视为分子力程；数量级在 10 为分子直径（有效直径） 。 （2）分子力是电性力，大于万有引力
第五节 范德瓦耳斯气体的压强
1873 年，范德瓦尔斯方程。 理想气体：T 较高，p 较小。真实气体：T 较低，p 较大。 问题：考虑分子体积和分子间引力。 研究方法： 1、 2、 3、 实验—规律(经验公式)—准确性高但应用范围狭窄 建立模型—统计运算—统计规律—应用范围广，但准确性 两者结合，互相修正、补充
∑v
i =1
N
2 ix
m0 N 2 F N 2 N = vix = ⋅ m0 ∑ vix / N = nm0 vx 2 压强 P = ∑ l2l3 l1l2l3 i =1 l1l2l3 i =1
N （单位体积内分子数） 分子数密度 n = l1l2l3
2 v x = ∑ vix /N 2 i =1 N
p=
RT − ∆p Vm − b
∆p ——气体的内压强
∆p =（单位时间内与单位面积器壁相碰的分子数） × 2∆k
△k表示分子进入气体界面层时由于受到指向气体内部的平均拉 力作用所产生的平均动量减少量。
Q ∆k ∝ n
1 ∆ p ∝ n ∝ ∴ 2 得 Vm
2
∆p =
a 2 Vm
a 由气体的性质决定。
例：容积11.2L真空系统抽到1.0×10-5mmHg真空。经300℃烘 烤释放吸附气体。烘烤后压强增为1.0×10-2mmHg，问器壁原 来吸附了多少个气体分子。 解：设烘烤前分子数为N0，烘烤后分子数为N1 。
pV = NkT
3
∆ N = N1 − N 0 =
p1V p0V V p1 p0 − = ( − ) kT1 kT0 k T1 T0
热力学第二章 理想气体性质

热力学第二章 理想气体性质

1
t2
t2
t1
(3)定值比热
CV ,m i R 2 C P ,m i 1 R 2
i 取值：单原子：3； 双原子： 5； 多原 子：7
一.比热力学能
d u=cvdt
1. cv const
理想气体、任何过程
u cv t
2. cv 为真实比热
3. cv 为平均比热
h是状态量,
h f (T , p )
h h dh ( ) p dT ( )T dp T p
h h q ( ) p dT [( )T v ]dp T p
定压状态下,dq=u，
由定义知：
h q p ( ) p dT T q p h Cp ( ) ( )v dT T
dT p2 s s2 s1 1 c p Rg ln T p1
2
s 1
2
2 dv dp cp 1 cv v p

s s2 s1 c p ln
T2 p Rg ln 2 T1 p1
v2 p2 s c p ln cv ln v1 p1
t2
1
u cv dt
T1
T2
u cv t (T2 T1 ) cv 0 t2 cv 0 t1
4. 查T-u表, 附表4 (零点规定: 0K, u=0, h=0 )
t2
t2
u u2 u1
二. 比焓
dh c p dT
利息气体、任何过程
1. c p const
1kg 工质温度
物理意义：表示在 p 一定时, 升高 1K ，焓的增加量 所以当作状态量 ；
说明： 1、对于cv、cp因为过程定容、定压,
热学第二版课后习题答案

热学第二版课后习题答案

热学第二版课后习题答案热学第二版课后习题答案热学是物理学中的一门重要学科，研究热量的传递、热力学规律以及热力学系统的性质等。

在学习热学的过程中，课后习题是检验学生对知识掌握程度的重要手段。

下面将为大家提供热学第二版课后习题的答案。

第一章：热力学基础1. 什么是热力学第一定律？它的数学表达式是什么？热力学第一定律是能量守恒定律的推广，它表明能量可以从一种形式转化为另一种形式，但总能量守恒。

数学表达式为ΔU = Q - W，其中ΔU表示系统内能的变化，Q表示系统吸收的热量，W表示系统对外界做功。

2. 什么是热容？如何计算物体的热容？热容是物体吸收或释放单位温度变化时所需的热量。

计算物体的热容可以使用公式C = Q/ΔT，其中C表示热容，Q表示吸收或释放的热量，ΔT表示温度变化。

3. 什么是等容过程？等容过程的特点是什么？等容过程是指在恒定体积条件下进行的热力学过程。

在等容过程中，系统对外界做功为零，因为体积不变。

等容过程的特点是内能变化等于吸收的热量，即ΔU = Q。

第二章：理想气体的热力学性质1. 理想气体的状态方程是什么？它的含义是什么？理想气体的状态方程是PV = nRT，其中P表示气体的压强，V表示气体的体积，n表示气体的物质量，R表示气体常数，T表示气体的温度。

这个方程表示了理想气体的状态与其压强、体积、物质量和温度之间的关系。

2. 理想气体的内能与温度有何关系？理想气体的内能与温度成正比，即U ∝ T。

当温度升高时，理想气体的内能也会增加。

3. 理想气体的等温过程与绝热过程有何区别？等温过程是指在恒定温度条件下进行的热力学过程，绝热过程是指在没有热量交换的情况下进行的热力学过程。

在等温过程中，气体的温度保持不变，而在绝热过程中，气体的内能保持不变。

第三章：热力学第二定律1. 热力学第二定律的表述是什么？它有哪些等效表述？热力学第二定律的表述是热量不会自发地从低温物体传递到高温物体。

它有三个等效表述：卡诺定理、克劳修斯不等式和熵增原理。

第二章-热力学第一定律-3

第二章-热力学第一定律-3




定义:
r H r H m ξ
2.7.3a
B
为摩尔反应焓。代入上式，
所以有： r H m
ν
B
H m (B)
2.7.4
因为对于同一个反应，不同写法的方程，νB 的值不同。所以 同一个反应，不同写法的方程，ΔrHm也不同。所以，谈到ΔrHm 时，不但要指明针对的反应，还应当指出方程式的具体形式。 3. 标准摩尔反应焓 （1）标准态 气体：任意温度T，标准压力pɵ=100 kPa下表现出理想气体性质 的纯气体状态。 液体或固体 ：任意温度T，压力为标准压力pɵ=100 kPa的纯 液体或纯固体状态。

B H H
H 比相变焓为 h m
H H H
H H m n
说明：
H m Qp,m （1）
（恒压且无非体积功）
（常压下数据可查得） （2） H m f（T）
（3） H m - H m
T1 T2
H n C p,m dT nC p,m T2 - T1） （
T1
T2
§2.6 相变焓
相: 系统内物理性质、化学性质完全相同的均匀部分。
相与相之间在指定条件下有明显的界面，在界面上宏观性质 的改变是飞跃式的。
气体：不论有多少种气体混合，只有一个气相。 液体：按其互溶程度可以组成一相、两相或三相共存。 固体：一般有一种固体便有一个相。两种固体粉末无论混合 得多么均匀，仍是两个相（固体溶液除外，它是单相） 例如：某种固体盐与其饱和水溶液及水蒸气共存，系统共有 气、液、固三相。 相变：物质不同相态之间的转变。如蒸发、升华、熔化 和晶型 转变等。
总结： vapHm(T2) = H1+ H2+ H3 = vapHm(T1)+ {Cp,m(H2O,g) – Cp,m(H2O,l)} T = vapHm(T1) + Cp,m T T2 一般情况：
工程热力学必须掌握的内容资料重点

工程热力学必须掌握的内容资料重点

工程热力学
各章重点内容
第一章 基本概念
❖ 热力系分类 ❖ 状态参数的特性 ❖ 平衡状态
❖ 准静态过程与可逆过程的关系 ❖ 热量与功 ❖ 正向循环（动力循环），热效率 ❖ 逆向循环（制冷循环或热泵循环），制冷系数，制热系数
第二章 气体的热力性质
1、理想气体的基本假设
气体分子是弹性的、不占有体积的质点 除碰撞外分子间无相互作用力
1 T1 1
T2
2,c
T1 T1 T2
1 1 T2
T1
逆卡诺循环的性能系数只决定于热源温度T1 和冷源温度T2，它随T1的降低及T2的提高而 增大。
逆卡诺循环的制冷系数可能大于、等于或小 于1；其供热系数总是大于1；二者之间的关 系是： 2,c 1 1,c
三、卡诺定理 定理1：所有工作于同温热源与同温冷源之间
理想气体混合气体单位质量的热力学能：
n
u giui i1
理想气体混合气体单位质量的热力学能，不仅取决 于温度，还与各组成气体的质量成分有关系。
6、开口系统稳态稳流能量方程
q
h
1 2
c 2
gz
ws
wt
q h wt
➢
对于可逆过程：
wt
2
vdp
1
一般计算公式
7、理想气体焓变化
理想气体混合气体单位质量的焓：
n
h gihi i 1
理想气体混合气体单位质量的焓，不仅取决于温度， 还与各组成气体的质量成分有关系。
8、理想气体的熵方程
2
s 1 ds
cV
ln
T2 T1
R ln
v2 v1
cp
ln
T2 T1
R ln
工程热力学第二章

工程热力学第二章


n
i
i
混合气体的折合气体常数
R R = eq Meq R nR ∑ni Mi R ∑mR i i i = 0= 0= = m m m m n = ∑gi R i
五、分压力的确定
piV = ni R T pi ni 0 = = xi 或 pi = xi p = ri p pV = nR T p n 0
混 合 气 体 第i种组成气体 相对成分
m mi
n ni
V Vi
相对成分= 相对成分=
分 总
量 量
质量分数：
摩尔分数：
体积分数：
m gi = i , m ni xi = , n V r= i, i V
∑g =1
i
∑x =1
i
∑r =1
i
Vi为分体积
gi、xi、ri的转算关系
V ni i = ⇒xi = r i V n
=q02-q01
= ∫ cdt − ∫ cdt
0 0 t2 t1
= c 0 ⋅ t2 − c 0 ⋅ t1
t2 t1
c 0 , c 0 表示温度自 °C到t1和0°C到t2的平均比热容. 0
t2 t1
q ct = 1 t2 −t1
t2
∫ = ∫ =
t
t2
t1
cdt
t2
t2 −t1
0 t1
cdt + ∫ cdt
通用气体常数不仅与气体状态无关，与气 体的种类也无关 R =8.314J /(mol ⋅ K)
0
气体常数与通用气体常数的关系：
m pV = nR T = R T 0 0 M pV = mR T
R0 R= 或 R0 = M R M
无机化学第2章气体

无机化学第2章气体

理想气体状态方程式：
pV = nRT
R — 摩尔气体常数。
在 p = 101.325 kPa 和 T = 273.15 K（标准状态下），1.0
mol 任何气体的体积 V 都是 22.414 L，由此可推出摩尔气体 常数 R 为： R= pV = nT 101.3 kPa × 22.414 L 1.0 mol × 273.15 K
分压与分压定律 i) 组分气体 理想气体混合物(在同一容器中，相互间不发生化学 反应，分子本身的体积和它们相互之间的作用力可略而不 计的几种不同气体形成的混合物）中每一种气体叫做组分 气体。
ii) 分压
组分气体 B 在相同温度下占有与混合气体相同体积时 所产生的压力，叫做组分气体 B 的分压 （pB）。
第二章 气 体
2.1 2.2 2.3 气体的性质 理想气体状态方程式 气体混合物及分压定律
2.4
2.5*
气体分子运动论
真实气体
2.6*
气体临界现象
无机化学
物质的状态
组成物质的粒子主要是原子、分子或离子。不 同温度和压力下，粒子间距离、相互作用力及粒子 的运动情况各异，从而使物质在宏观上呈现不同聚 集态。 自然界中物质在常温常压下主要以气态 (gaseous state)、液态(liquid state)和固态(solid state) 三种聚集状态存在。
x(CH4) = 1- x(O2) = 0.75
无机化学
po2
no2 RT V
0.188mol 8.314kPa L mol 1 K 1 273K 15.0L 28.45kpa
0.563mol 8.314kPa L mol 1 K 1 273K 15.0L 85.20 kpa
第二章气体的热力性质严家禄版

第二章气体的热力性质严家禄版

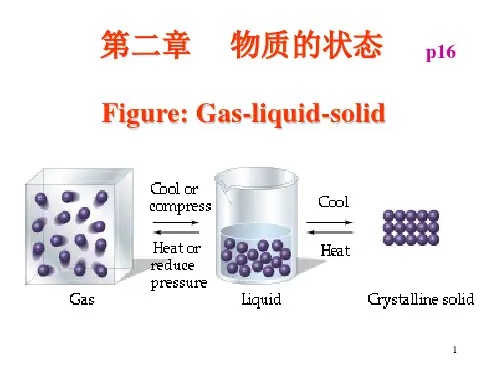
第二章气体的热力性质理想气体与实际气体理想气体比热容混合气体的性质实际气体状态方程对比态定律与压缩因子图理想气体实际气体问题的提出及研究的重要意义热能向机械能转换要靠工质的膨胀来实现，气体具有最好的膨胀性，是最适宜的工质。

因此，气体工质的性质是热力学研究的主要内容气体按工作参数分为:任务：理想气体及其混合物的热力性质基本要求:1. 熟练掌握并正确应用理想气体状态方程。

2. 正确理解理想气体比热的概念。

3. 熟练掌握并正确应用平均比热、定值比热来计算过程热量。

4. 掌握理想气体混合物的成分、摩尔质量和气体常数以及比热的计算。

§2-1 理想气体与实际气体一、理想气体与实际气体△定义：分子是一些弹性的、本身不占体积的质点，分子之间没有相互作用力。

△当气体处于高温低压时，上述假设可以成立△实质：实际气体p→0，或v→∞时的极限状态，理想气体与实际气体没有明显的界限△适用条件：远离液态的气体二、理想气体状态方程的导出由分子运动论可知：nBT c m n p 322322== k B 23=k 是玻尔兹曼常数（J/K）；式中：---分子平移运动均方根速度c n --- 1m 3 体积内的分子数；m --- 一个分子的质量；理想气体状态方程式的推导nkT kT n nBT p ===233232等式两边同乘以v 得：RTnvkT pv ==nvkR =nv 是1千克气体所具有的分子数目，它只与气 体的种类有关。

所以R 仅仅与气体的种类有关，而 与气体的状态无关,称为气体常数。

式中： p —绝对压力 P a v —比体积 m 3/kg T —热力学绝对温标 K R —气体常数J /(kg·K )理想气体状态方程式pv =RT △1kg 气体几种常见气体的气体常数见表2-1理想气体状态方程式pV =mRT△mkg 气体： mpv =mRT 式中：V=mv —气体体积 m 3式中： M —千摩尔质量 kg /kmol V m = Mv —千摩尔体积 m 3/k mol R = MR —摩尔气体常量J /(kmol·K )pV m =R 0 T △1kmol 气体：pMv =MRTR 0 与气体的状态及种类无关，是一个特定的常数摩尔气体常量通用气体常数理想气体状态方程式式中： V=nV m —气体体积 m 3p V mA /T=R 0A =p V mB /T=R 0B同温、同压下各种气体, V mA ＝V mBpV=nR 0 T△n kmol 气体：标准状态下： p 0 =101325Pa T 0 =273.15K 时任何气体：V m 0 =22.4m 3/kmolR 0 =p 0 V m 0 /T 0 = 8314 .5 J /(kmol·K )三、气体常数与通用气体常数1、通用气体常数的导出∵R 0 =MR ∴R=R 0 /M=8314 . 5/M (J /kg·K )2、气体常数的计算(注意单位)m 8.3143kJ 0.287kg K 28.97R R M ===⋅空气空气R m 与R 的区别R m ——通用气体常数m kJ8.3143 []kmol KR =i R ——气体常数m [kJ /kg.K]R R M=例如与气体种类无关与气体种类有关四、使用状态方程的注意点¾状态方程反映平衡态状态参数之间的数量关系，它只能用于平衡态，不能用于过程计算。

第二章 理想气体的性质

第二章 理想气体的性质


p 100 245.2 345.2kPa
T 273 40 313K
PV PV 0 0 T T0
mkg气体状态方程： PV mRT 过程中气体质量不变：
P T0 345.2 274 V0 V 4.5 13.37m3 P0 T 101.325 313
例2: 某活塞式压气机将某种气体压入储气箱中。压气机每分钟 0 吸入温度 t1 40 C ,压力为当地大气压力 B 100kPa 。储气箱的容积 为 V 9.5m3 . 问经过多少分钟后压气机才能把箱内压力提高到状 态3，p3 0.7MPa , t3 500 C ,压气机开始工作以前，储气箱内 0 p 0.7MPa, t 17 C 气体状态为： g2 2
解： 1）由于压力较低，故煤气可作理想气体
751.4 133.32 44 9.81 Pa p1 T0 273.15 K V0 V 68.37 m3 p0 T1 101 325 Pa 273.15 17 K
63.91 m3
pV p0V0 m RgT RgT0
1 kg : pv RT
m kg : pV mRT
R0: 通用气体常数 kJ/kg.K
m： 工质质量 kg
n： 工质的量 mol
气体常数R：
与气体种类有关
R0 8314 R M M
J/ （kg. K）
例如:
R空气
R0 8314 287J/kg.K M 空气 28.97
计算时注意事项: 1、绝对压力: Pa 2、温度单位: K
容积成分ri与摩尔xi的换算
某组成气体的摩尔容积
Vi nV ri i mi V nVm
xi

大气物理学：第二章+大气压力

2、方程推导： 假设：大气处于静力平衡，在水平方向温、压、 湿变化很小，等压面与等温面近于水平，且由于 是静止大气，空气无水平运动。
一、 大气静力学方程(2)
在静止大气中取厚度 为dz的单位截面积空 气柱
上下表面所受气压合力
p ( p p dz) p dz
z
z
一、 大气静力学方程(3)
重力
第二章 大气压力
气压是如何产生的？它在垂直方向应该是如何分布的 呢？ 大气空气分子不断地做无规则的热运动，不断地与 物体表面相碰撞，宏观上，物体表面就受到一个持续 的、恒定的压力。这与液体压强类似，
液体压强 P上
h
h
P下
液体压强 P上
h
P下 g h
单位面积内物体表面直 至液面整个液柱的重量
h P上 g h g h
Δh内液压的变化值
P下
P总 P下 P上
第二章 大气压力
物体表面单位面积所受的大气分子的压力称为大气压 强或气压。其大小等于单位面积上直至大气上界整个 空气柱的重量。 本章研究静止或匀速垂直运动大气所受力的作用，以 及在力的作用下气压与温度、高度之间的定量关系， 即气压垂直分布的问题。
第二章 大气压力
P
P0
exp(
1 Rd
z g dz) 0 Tv
3、将单位质量的物体通过任意路径从海平面上升到某一
高度克服重力所做的功称为重力位势，
z
g dz （J/kg） 0
Z
g
' 0
（ gpm）
本章小结（3）
将位势高度代替几何高度，则压高公式简化成：
P2
P1exp
g
' 0
Rd
Z2 dZ

第二章热力学第一定律

内能总以变化量出现，内能零点人为定
中南大学航空航天学院
热一律的文字表达式
热一律: 能量守恒与转换定律
进入系统 的能量
-
离开系统 的能量
=
系统内部储存 能量的变化
中南大学航空航天学院
§2.2 闭口系能量方程
一般式 Q = dU + W Q = U + W q = du + w q = u + w
Q0
W 0
Q
U Q W
空 调
Q W
T
中南大学航空航天学院
§ 2.3 开口系能量方程
min 能量守恒原则
进入系统的能量
uin
1 2 cin 2 gzin
离开系统的能量
Wnet
mout uout 1 2 cout 2 gzout
=
系统储存能功的引入
门窗紧闭房间用电冰箱降温
以房间为系统 闭口系能量方程 绝热闭口系 Refrigerator Icebox
电 冰 箱
Q U W
Q0
W 0
U W 0
T
中南大学航空航天学院
门窗紧闭房间用空调降温
以房间为系统 闭口系能量方程 闭口系 Aircondition
Q U W
推进功(pv)
几种功的关系
1 2 wt c g z ws 2
q h wt u ( pv) wt
q u w
w ( pv) wt
△ c2/2
ws
做功的根源 w
中南大学航空航天学院
wt
△(pv)
g△ z ws
对功的小结
1、闭口系，系统与外界交换的功为容积变化功w 2、开口系，系统与外界交换的功为轴功ws 3、一般情况下忽略动、位能的变化

工程热力学第二章理想气体性质作业

第二章理想气体的性质2-1 已知氮气的摩尔质量 M=28.1×10-3kg/mol，求(1) N2 的气体常数 Rg；(2)标准状态下 N2 的比体积 v0 和密度ρ0；(3)标准状态 1 米3 N2的质量 m0 ；(4)p=0.1MPa，t=500℃时 N2 的比体积 v 和密度ρ；(5)上述状态下的摩尔体积 Vm 。

解：(1)通用气体常数R=8.3145J/(mol·K)，由附表查得MN2 =28.01×10-3kg/mol。

RgN2 = R/ M＝8.3145J/(mol·K)/ 28.01×10-3kg/mol=0.297 kJ/(kg·K)(2)1mol 氮气标准状态时体积为 Vm N2=Mv N2 =22.4×10-3 m 3 /molv N2 = Vm N2/ M＝22.4×10-3m3/mol/28.01×10-3kg/mol=0.8m 3 /kg(标准状态)ρN2 =1/ vN2＝1/0.8m3 / kg=1.25kg/m 3(标准状态)(3)标准状态下 1 米 3 气体的质量即为密度ρ，等于 1.25kg。

(4)由理想气体状态方程式 pv=RgT，可得v= RgT/ p=297J/(kg·K)×(500 + 273)K/0.1×106Pa= 2.296m3/kgρ =1/ v=1/2.296m3 / kg= 0.4356kg/m3(5)V m =Mv=28.01×10-3 kg/mol × 2.296m3/kg=64.29×10-3 m 3 /mol2-2 压力表测得储气罐中丙烷 C3H8 的压力为 4.4MPa, 丙烷的温度为 120℃，问这时比体积多大？若要储气罐存 1000kg 这种状态的丙烷，问储气罐的体积需多大？解：由附表查得MC3H8 =44.09×10-3kg/molRg,C3H8 =R/ MC3H8=8.3145J/(mol·K)/ 44.09×10?3kg/mol=189J/(kg·K)由 1kg 理想气体状态方程式 pv=RgT 可得v =RgT/ p=189J/(kg·K)×(120 + 273)K/4.4×106Pa= 0.01688m3/kgV=mv=1000kg× 0.01688m3/kg=16.88m 3或由理想气体状态方程 pV=mRgT 可得V = mRgT/ p ＝1000kg×189J/(kg·K)×(120 + 273)K /4.4×106Pa =16.88m32-3 绝热刚性容器被分隔成两相等的容积，各为1m 3（见图2.1），一侧盛有100℃，2bar 的N 2，一侧盛有20℃，1bar 的CO 2，抽出隔板，两气混合成均匀混合气体。

哈工大工程热力学教案-第2章 理想气体的性质

第2章理想气体的性质本章基本要求：熟练掌握理想气体状态方程的各种表述形式，并能熟练应用理想气体状态方程及理想气体定值比热进行各种热力计算。

并掌握理想气体平均比热的概念和计算方法。

理解混合气体性质，掌握混合气体分压力、分容积的概念。

本章重点：气体的热力性质，状态参数间的关系及热物性参数，状态参数(压力、温度、比容、内能、焓、熵)的计算。

2．1 理想气体状态方程一、理想气体与实际气体定义：气体分子是一些弹性的，忽略分子相互作用力，不占有体积的质点,注意：当实际气体p→0 v→∞的极限状态时，气体为理想气体。

二、理想气体状态方程的导出状态方程的几种形式1．RTpv=适用于1千克理想气体。

式中：p—绝对压力Pav—比容m3/kg，T—热力学温度K2．mRTpV=适用于m千克理想气体。

式中V—质量为m kg气体所占的容积3．T=适用于1千摩尔理想气体。

RpVM0式中V M=M v—气体的摩尔容积，m3/kmol；R0=MR—通用气体常数，J/kmol·K4．T=适用于n千摩尔理想气体。

nRpV式中V —nKmol 气体所占有的容积，m 3；n —气体的摩尔数，M m n =，kmol 5．222111T v P T v P = 6．222111T V P T V P = 仅适用于闭口系统 状态方程的应用：1．求平衡态下的参数2．两平衡状态间参数的计算3．标准状态与任意状态或密度间的换算4．气体体积膨胀系数例1：体积为V 的真空罐出现微小漏气。

设漏气前罐内压力p 为零，而漏入空气的流率与（p 0－p ）成正比，比例常数为α，p 0为大气压力。

由于漏气过程十分缓慢，可以认为罐内、外温度始终保持T 0不变，试推导罐内压力p 的表达式。

解：本例与上例相反，对于罐子这个系统，是个缓慢的充气问题，周围空气漏入系统的微量空气d m '就等于系统内空气的微增量d m 。

由题设条件已知，漏入空气的流率ατ='d d m （p 0－p ），于是： ）（p p m m -='=0d d d d αττ （1） 另一方面，罐内空气的压力变化（d p ）与空气量的变化（d m ）也有一定的关系。

理想气体与实际气体


现了实际气体性质偏离理想气体的程度。
氮气的压缩因子图
分析： •Z>1时，实际气体体积大于同温同压下理想气体的体积，气 体较难压缩； •Z<1时，实际气体体积小于同温同压下理想气体的体积，气 体可压缩性大；
气体被压缩时，分子间距减小，吸引力增大，体积比忽略吸引力时小
•在一定温度下，实际气体的Z值先随压力的增大而减小， 压力较高时Z值大于1，Z随压力的增大而增大。
方程在气态和液态区域实验吻合，在两相区有误差。
p D C L N P O M Q B E Vm A K
范德瓦尔定温线
3、临界参数和范德瓦尔方程： 在临界点处：

p ( )Tc 0 v
2 p ( 2 )Tc 0 v
RTc 2a 0 3 2 (vc b) vc 2 RTc 6a 0 4 3 (vc b) vc
得：pc=a/27b2 Tc=8a/27Rb Vm=3b 或 RTC 27R 2TC2 b a 8 pC 64 pc
R
8 pc vc 3Tc
二、其它状态方程 1、伯特洛方程 2、狄特里奇方程 3、瑞得里奇-邝方程
RT a p 2 v b Tv
a RT RTv p e vb
Vi niVmi ri xi V n Vm
(2)质量成分与摩尔成分
mi ni M i Mi gi xi m nM M
g i ri
Mi R ri ri i M Ri
四、混合气体的折合分子量与气体常数 1、折合分子量
m i 1 i M n n 1 M n gi i 1 M i
任意状态与平衡态之间：
p0 v0 pv T T0
例题 2-2 例2-2 充满气体的容器，体积 4.5m3 ，气体表压力为 245.2kPa ，温度 40℃。求在标准状态下的体积。（B=100kPa）
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

存在，并且具有与混合气体相同的温度
及容积时的压力。即
pi

mi RiT V
Pa
２道尔顿（Dalton）分压定律
混合气体的总压力p，等于各组成气体 分压力pi之和。即∑pi=p
二、混合气体分容积和阿密盖特分容积 定律
• １分容积（Partial Volume）
• 分容积是假定混合气体中组成气体单独
存在，并且具有与混合气体相同的温度
RmT
8.3143 293.15
3） m

pVM

(1000 760
1) 1.013105 1.0 28

2658kg
RmT
8.3143 293.15
4） m
pVM

(1000 1) 1.013105 1.0 28 760
2.658kg
RmT
8.31431000 293.15
同的物理量。
理想气体定容比热和定压比热的关系
• 对于理想气体，迈耶方程成立，即
• cp =cv+R
……①
• 若定义比热比(又称绝热指数)k=cP/cv ，
可以得到：
cp

kR k 1
与cv

R k 1

②
注意：①式比②式更为准确，因为ｋ
值往往不易准确确定。
常见工质的cv和cp的数值
0oC时： cv,air= 0.716 kJ/kg.K cp,air= 1.004 kJ/kg.K cv,O2= 0.655 kJ/kg.K cp,O2= 0.915 kJ/kg.K 1000oC时： cv,air= 0.804 kJ/kg.K cp,air= 1.091 kJ/kg.K cv,O2= 0.775 kJ/kg.K cp,O2= 1.035 kJ/kg.K
学反应、组成不变，且由理想气体组成 的均匀气体混合物。 • ２研究方法 • 此类混合气体的性质可以由描述各组成 分相对含量大小的参数确定其各个性质 参数的平均值（指广延性参数），再按 照纯物质进行分析。
一、混合气体分压力和道尔顿分压定律
• １分压力（Partial Pressure）
• 分压力是假定混合气体中组成气体单独
２用途
• 理想气体状况方程可用于
• ⑴已知两个基本状态参数确定第三个 未知基本状态参数；
• ⑵任意两个状态之间的未知基本状态 参数的计算。
三、举例
• 1检查下面计算方法有哪些错误？如何改正？
• 已知某压缩空气储罐容积为900L，充气前罐内空 气温度为30℃，压力为0.5MPa；充气后罐内空气 温度为50℃，压力表读数为2MPa。充入储气罐 的空气质量为：
• 在热工计算中常用的是定容过程和定压
过程中的比热。它们相应地称为定容比
热和定压比热。
• cv、cv＇、Mcv • ｃp、cp＇、Mcp
cv

qv
dT
cp

q p
dT
注意：
• ⑴只有气体才谈得上定容比热和定压 比热，而固体和液体在各种过程的比 热几乎相等。
• ⑵定容比热和定压比热是状态参数。 • ⑶定容比热和容积比热是两个截然不
• 质量比热c J/kgK； • 容积比热c’ J/ｍ3K 这里m３指标准立 • 摩尔比热 Mc J/kmolK。 方米，即Nm３ • 换算关系
c

Mc 22.4

c0
这里ρ0指标准状态
时气体的密度
３热量的计算
⑴可逆过程
2
q 1 Tds
J kg;Q
2
TdS
1
J
⑵借助于比热（任何过程）
运动自由度
• 定值定容比热
cv

i 2
R
Mcv

i 2
R0
• 定值定压比热
i2
i2
cp 2 R Mcp 2 R0
其注中意单：原子适气用体条ｉ件=为3；理双想原气子体气且体(温如度空变气、 氧化气范)ｉ围=小5；。多计原算子较气为体简(如单Ｃ但Ｏ精2)ｉ度=较7。 低．
２真实比热
• 理想气体的比热实际是温度的函数， 相应于每一温度下的比热值称为真实 比热。
• 实验表明各种理想气体比热可表示为 温度的函数多项式即
cp,m a0 a1T a2T 2 a3T 4 cv,m a0 a1T a2T 2 a3T 4
若要确定定容摩尔比热与温度的关系 式，可利用Ｍｃｐ ＝ＭｃＶ＋Ｒ０确定。
Mcv Mc p R0
a0 R0 a1T a2T 2 a3T 4
由比热的定义，可以得到：
2
Q m cdT
J m
kg工质
1


2
Q V0 1 cdT
J V0
Nm3工质
Q

n
2
1
Mc
dT
J n
k mol工质
二.定容比热及定压比热
• 由于比热是过程量，计算热量时，首先 要确定某一特定过程的比热大小。
及压力时的容积。即
Vi

mi RiT p
m3
２阿密盖特（Amagat）分容积定律
混合气体的总容积 V ，等于各组成气体 分容积 Vi 之和。即∑Vi=V
• ３分压力与分容积间的关系
•由
pi

mi RiT V
Pa
Vi

mi RiT p
m3
得：
piV pVi mi RiT
三、混合气体的成分表示方法及换算
• 混合气体中各组成气体的含量与混合 气体总量的比值，为混合气体的成分。
• (1)用平均比热表数据计算； • (2)用理想气体理论定摩尔比热计算； • (3)比较(1)和(2)的结果。
第三节 混合气体的性质
• 工程上所遇到的气体，通常不是单一 成分的气体，而是由多种性质不同的 气体组成的混合物。
• 例和如微空量气的是稀由有气N2体、所O2组、成CO；2、H2O（g） • 气体燃料同样是由多种可燃成分组成
3、热功转换设备、工作原理 4、化学热力学基础
工程热力学的两大类工质
1、理想气体（ ideal gas）
可用简单的式子描述 如汽车发动机和航空发动机以空气为 主的燃气、空调中的湿空气等
2、实际气体（ real gas）
不能用简单的式子描述，真实工质 火力发电的水和水蒸气、制冷空调中 制冷工质等
第一节 理想气体状态方程
利用平均比热计算热量：
q t2 cdt t2 cdt t1 cdt
t1
0
0
q

cm
tt2
02
cm
tt1
01
• 教材Ｐ３１表２－６给出了气体在理想气 体状态下的平均定压质量比热ｃPm│t0 的数 值
⑴适用条件为理想气体，计算既较 为简单而且精度也较高。
⑵其数值并非某一温度下的比热值。
注意：适用条件为理想气体。计算较 为繁琐但精度较高。
３平均比热
• 为提高计算的精确度，同时又比较简 单，可使用平均比热。
• 由比热定义知
q
2
1 cdT cm
t2 t1
2
dt
1
因而可得到平均比热：
2
c t2 p,m t1
1 cpdt t2 t1
2
cv,m
t2
t1
1 cvdt t2 t1
• １定义 • 比热(Specific Heat)在热力学中定义为
单位物质量的工质温度升高或降低１K 所需吸收或放出的热量。即
c q
dT
比热容是过程量还是状态量?
T 1K
(1) (2)
C q
dt
c1
c2
s
定容比热容
用的最多的某些特定过程的比热容 定压比热容
２单位
• 比热的单位取决于热量和物质量的单位。
m
m2
m1

p2V RT2

p1V RT1
2900 0.5900 g
831450 831430
• 2求p=0.5MPa，t=170℃时，N2的比容和密 度。
• 3鼓风机向锅炉炉膛输送空气，在t=300℃， pg=15.2kPa时流量为1.02×105m3/h，锅炉 房大气压力B=101kPa，求鼓风机每小时输 送的标准状态风量。
第二章 理想气体的 性质
引言
• 工质应具备： • 最佳的膨胀性；最佳的压力；最高
的比热量。 • 工程实际中常用的工质有蒸汽动力
装置的水蒸汽、致冷装置的致冷剂 （氨、Ｒ12、Ｒ22等）、空调系统的 空气以及燃气灶具的可燃气体（如 天然气、煤制气等）。
工程热力学的研究内容
1、能量转换的基本定律
2、工质的基本性质与热力过程
• １理想气体状态方程式的四种形式：
• １kg工质 • mkg工质 • １kmol工质 • nkmol工质
pv＝RT pV＝mRT pVM＝R0T pV＝nR0T
注意：
• ①气体常数R和摩尔气体常数R0
• Ｒ0＝8314(J/kmolK)＝8.314(J/molK) 是常数，与气体种类和气体状态均无关。 R R0 J kgK M Ｒ与气体状态无关，但与气体种类有关。
• 一、理想气体与实际气体 • １理想气体 • ２实际气体作为理想气体处理的判据 • ３实际意义 • 二、理想气体状态方程 • １理想气体状态方程的四种形式： • ２用途 • 三、举例
一、理想气体与实际气体
• １理想气体（Ideal Gas）
• 理想气体分子是一些弹性的、不占有体
积的质点，分子之间没有作用力。