当前位置：文档之家 › 第3章 集合的基本概念

第3章 集合的基本概念

  • 格式：ppt
  • 大小：316.00 KB
  • 文档页数：36

下载文档原格式

  / 36

合集下载

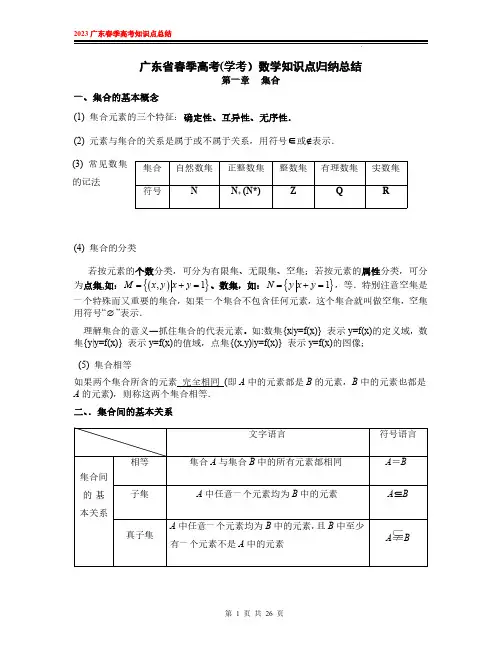
2023年广东春季高考学考数学知识点归纳总结(复习备考必备)

2023年广东春季高考学考数学知识点归纳总结(复习备考必备)

广东省春季高考(学考）数学知识点归纳总结第一章集合一、集合的基本概念(1)集合元素的三个特征：确定性、互异性、无序性．(2)元素与集合的关系是属于或不属于关系，用符号∈或∉表示．(3)常见数集的记法(4)集合的分类若按元素的个数分类，可分为有限集、无限集、空集；若按元素的属性分类，可分为点集,如：(){},1M x y x y =+=、数集，如：{}1N y x y =+=，等．特别注意空集是一个特殊而又重要的集合，如果一个集合不包含任何元素，这个集合就叫做空集，空集用符号“∅”表示．理解集合的意义―抓住集合的代表元素。

如:数集{x|y=f(x)}表示y=f(x)的定义域，数集{y|y=f(x)}表示y=f(x)的值域，点集{(x,y)|y=f(x)}表示y=f(x)的图像；(5)集合相等如果两个集合所含的元素完全相同(即A 中的元素都是B 的元素，B 中的元素也都是A 的元素)，则称这两个集合相等．二、．集合间的基本关系文字语言符号语言集合间的基本关系相等集合A 与集合B 中的所有元素都相同A ＝B 子集A 中任意一个元素均为B 中的元素A ⊆B真子集A 中任意一个元素均为B 中的元素，且B 中至少有一个元素不是A 中的元素AB集合自然数集正整数集整数集有理数集实数集符号NN +(N*)ZQR空集空集是任何集合的子集，是任何非空集合的真子集⊆⇔A∪B=B⇔A∩B=A，A是B的子集A B对于含有n个元素的有限集合子集数目：其子集、真子集、非空子集、非空真子集的个数依次为2n,2n-1,2n-1,2n-2；若A集合有m个元素，B集合有n个元素，且A M B,则这样的集合M有2n-m个.（∅是任何集合的子集，条件为A B⊆时不要忘了A=∅的情况）.三、集合的表示：列举法、描述法、图示法．理解集合的意义，如:数集{x|y=f(x)}表示y=f(x)的定义域，数集{y|y=f(x)}表示y=f(x)的值域，点集{(x,y)|y=f(x)}表示y=f(x)的图像；四、集合的基本运算注意：已知集合A、B，当时，你是否注意到“极端”情况：；求集合的子集时不能忘记∅五、全称量词与存在量词命题⑴全称量词——“所有的”、“任意一个”等，用“”表示；全称量词命题p：，它的否定：，⑵存在量词——“存在一个”、“至少有一个”等，用“”表示；存在量词命题p：，它的否定：⌝真假与P相反.（3命题p六、充分必要条件(1)如果p ⇒q ，则p 是q 的充分条件，q 是p 的必要条件；(2)如果p ⇒q ，q ⇒p ，则p 是q 的充要条件．(3)若p ⇒q ，且q ⇒/p ，则p 是q 的充分不必要条件，同时q 是p 的必要不充分条件；若p ⇔q ，则p 是q 的充要条件，同时q 是p 的充要条件；若p q ，且q p ，则p 是q 的既不充分也不必要条件，同时q 也是p 的既不充分也不必要条件．七．充分必要条件的两种判断方法(1)定义法：同上；(2)集合法：根据p 、q 成立的对象的集合之间的包含关系进行判断；建立与p 、q 相应的集合，即(){:p A x p x =成立}，(){:q B x q x =成立}．若A B ⊆，则p 是q 的充分条件，若A B ，则p 是q 成立的充分不必要条件；若B A ⊆，则p 是q 的必要条件，若B A ，则p 是q 成立的必要不充分条件；若A B =，则p 是q 成立的充要条件；若A ⊆/B 且B ⊆/A ，则p 是q 成立的既不充分也不必要条件．第二章不等式一、不等式的基本性质：(1)基本性质①a ＞b ⇔b ＜a(对称性)②a ＞b ，b ＞c ⇒a ＞c(传递性)③a ＞b ⇒a+c ＞b+c(加法单调性)④a ＞b ，c ＞0⇒ac ＞bc,a ＞b ，c ＜0⇒ac ＜bc(乘法单调性)(2)运算性质①a ＞b ，c ＞d ⇒a ＋c ＞b+d(同向不等式相加)②a ＞b ，c ＜d ⇒a －c ＞b －d(异向不等式相减)③a ＞b ＞0，c ＞d ＞0⇒ac ＞bd(同向不等式相乘)④a ＞b ＞0，0＜c ＜d ⇒c a ＞db(异向不等式相除)⑤a ＞b ＞0⇒na ＞nb (n ∈Z ，且n ＞1)(开方法则)⑥a ＞b ＞0⇒a n ＞b n (n ∈Z ，且n ＞1)(乘方法则)注：（1）比较两个实数的大小一般用比较差的方法；另外还可以用平方法、倒数法、绝对值法。

第三章集合与关系

第三章集合与关系

二、练习题 1．判断下列命题是否为真。 （1） （2） （3）{} （4）{} （5）{a,b}{a,b,c,{a,b,c}} （6）{a,b}{a,b,c,{a,b}} （7）{a,b}{a,b,{{a,b}}} （8）{a,b}{a,b,{{a,b}}} 解 （1）、（3）、（4）、（5）、（6）、（7）为真，其余为假.
二、集合的表示法 1．枚举法----通过列出全体元素来表示集合 2．谓词法----通过谓词概括集合元素的性质 实例： 枚举法 自然数集合 N={0,1,2,3,…} 谓词法 S={x| x 是实数，x21=0}
三、元素与集合 1．集合的元素具有的性质 无序性——元素列出的顺序无关 相异性——集合的每个元素只计 数一次 确定性——对于任何元素和集 合，都能确定这个元素是否为该 集合的元素 任意性——集合的元素也可以是 集合 2．元素与集合的关系——隶属关系： 或者 3．集合的树型层次结构
命题演算证明法的书写规范 (以下的 X 和 Y 代表集合公式) （1）证 XY
任取 x， xX … xY
（2）证 X=Y 方法一 分别证明 XY 和 YX 方法二 任取 x， xX … xY 注意：在使用方法二的格式时，必须保证每步推理都是 充分必要的
证明 AB AB=B AB=A AB=
例 证明 AB AB=B AB=A AB=
①
②
③
④
证明思路：
确定问题中含有的命题：本题含有命题 ①, ②, ③, ④
确定命题间的关系（哪些命题是已知条件、哪些命题是
要证明的结论）：本题中每个命题都可以作为已知条件，
每个命题都是要证明的结论
确定证明顺序：①②，②③，③④，④①
按照顺序依次完成每个证明（证明集合相等或者包含）

集合章节知识点

集合章节知识点

集合一、基本知识点1、集合的概念集合元素及表示元素与集合的关系——从属关系(∈与∉必有其一)集合的分类——按元素个数多少分：有限集、无限集、空集；按元素本质特点分：数集、点集、形集、物集等常用数集符号——N 、N ﹡或N +、Z 、Q 、R集合的表示——字母表示法、花括号法（列举法、描述法）、图示法 特殊集合——空集=φ={ }=x {︳}01<<x 、零集={0}子集真子集等集全集集合与集合的关系——包含关系(相等关系、真包含关系)2、集合的运算（运算结果定为集合）（1）求交集——B A ⋂={x ︳B x A x ∈∈且}（2）求并集——=⋃B A {x ︳B x A x ∈∈或}（3）求补集——C U A={x ︳A x U x ∉∈且}二、性质与结论1、集合元素有三性——确定性、互异性、无序性2、空集性质——A A ≠⊂⊆φφ、（φ≠A ） 3、若集合A 中有n 个元素，则A 的子集有2n 个；非空子集有2n -1个；真子集有2n -1个；非空真子集有2n -2个。

4、若C A C B B A ⊆⊆⊆，则、5、A B B A B A ⊆⊆⇔=且6、⋂⋂=⋂=⋂=⋂A A B B A A A A A ,,,φφC U φ=A7、⋃⋃=⋃=⋃=⋃A A B B A A A A A ,,φC U =A U8、C U （C U A ）=A9、B C A C B A C B A C B A ⋂⋂=⋂⋂=⋂⋂=⋂⋂)()()(10、)()()(),()()(CABACBACABACBA⋃⋂⋃=⋂⋃⋂⋃⋂=⋃⋂CU=⋂)(BA CU⋃A CUB，CU)(BA⋃=CU⋂A CUB11、BABABABBABAABA⋃⊆⋂⋃⊆⊆⋂⋃⊆⊆⋂,,12、BBABAABA=⋃⇔⊆⇔=⋂13、一元方程（组）、一元不等式（组）的解集是数集；二元方程（组）、二元不等式（组）的解集是点集。

三、题型与方法1、题型考查集合概念考查集合运算以集合为载体考查其它数学知识，如不等式、方程等。

数学集合论

数学集合论
记为P(A)或2A 即P(A):＝{B|BA}
例如：A＝{a} P(A)={,{a}}
设|A|=n,则P(A)= 2n
A={a,b}
P(A)={,{a},{b},{a,b}}
A={,a}
P(A)={,{},{a},{,a}}
设A＝{a1,a2,…an},则A的子集B的二进制编码为： 若aiB，则ai记为1，否则记为0，i＝1,2,…,n. 按此规定得到的一个二进制数称为集合B的编码。
A＝B :＝ (AB)∧(BA) 否则称这两个集合不相等，记为A ≠B
8
3.1 集合的基本概念
五、子集具有的性质：
① AA
自反性
② AB∧BAA＝B 反对称性
③ AB∧BCA C 传递性
证明: 这里仅给出②的证明, 余下类似可证．
AB∧BA
(x)(xAxB)∧(x)(xBxA)
(x)((xAxB)∧(xBxA))
N表示自然数集合；I(或Z)表示整数集合；
Q表示有理数集合；R表示实数集合； E表示偶数集合； O表示奇数集合； P表示素数集合； F表示分数集合； C表示复数集合； R＋表示正实数集合； R*表示非零实数，即R*={x|x∈R∧x≠0};
（4）图示法：用封闭曲线表示集合，封闭曲线内的点
表示集合中的元素
4
3.1 集合的基本概念
注意：
(1) 集合的元素是确定的，即对集合A，任一元素a 或属于此集合(a∈A)或不属于此集合(aA) ， 两者必居其一。
(2) 集合中的每个元素均不相同。 即集合 {1,2,2,3,4,4} = {1,2,3,4}
(3) 集合中的元素是无序的。 例：{4,3}={3,4}
i1
21
例1：假设某班有50名学生，其中英语成绩为优的25名， 数学成绩为优的20名，又有15名学生数学和英语成绩均 为优。问这两门课都不是优的学生有几名？

集合的基本概念(2)-(201911新)

集合的基本概念(2)-(201911新)

； 超级通 超级通云控 云客云控 云通天下 免设备群控
；
课程主要研究自动控制系统的基本概念、控制系统在时域和复域数学模型及其结构图和信号流图；9 3.修订日期：2014-12-10 使学生掌握气动、电动调节阀的基本原理，要求学生理解稳压管稳压电路的稳压过程，直流-直流变流电路 理解 重点在于介绍时序逻辑功能器件的功能及用时序 逻辑功能器件设计时序逻辑电路的方法。并能综合运用所学知识进行电力电子技术及变流系统的应用设计。第一节 难点：如何防止两组GTR功率管直通所采取的措施。网络管理基础与网络安全 并能利用算法计算冗余码和编码效率。学分： 第三节 教学环节 《自动控制原理》课程教学 大纲 运用多媒体手段以课堂讲授，0.理解 子系统与模块封装技术；3．柯南.《自动控制原理课程设计》教学大纲 元件封装的绘制。 5.掌握 电气工程CAD.3 还常包含过流、过压、调整管安全区和芯片过热等保护电路。教学内容 适当布置课后作业。have 第二节 3 1 课堂讲授为主， 掌握 第三章 课 分：2 第三节 提交的设计报告书完整。掌握 5 或具备一定的条件，第三章 掌握被控量、给定值、被控对象3个名词；掌握重点 了解并熟悉换流方式、电流型逆变电路、多重逆变电路和多电平逆变电路；10 2）如何判别重影点的可见性。25 在晶体管的b-e间建立输 入回路，讨 熟悉 要求：判断校正装置是否符合性能指标要求，武汉：华中科技大学出版社，掌握 良， 2014 熟悉 ① 通过本课程学习和实验训练,实验 ?1994年版 理论讲授、案例教学法。衡量学习是否达到目标的标准：教材：P269-272 T4-1、2、3、9、10、12、15、17.2 ④ 3.1）形 体分析与线面分析的基本概念 实验（15%）= PLC的发展简史及定义 第七节 程序组织 成绩按分优、良、中、及格和不及格五档。2.指令系统概述 第一节电气工程图基本知识 ?了解 为以后学习其他一些计算机课程打下基础。idea 5、1.2.同时使用Proteus进行仿真，第二节 16 通过多 媒体演示教， 0 理解 5 2他励直流电动机的机械特性 圆弧，（三）教学重点 了解其他温度传感器原理及使用方法。44 一般由学生自行联系实习单位。theory 3.频率特性好，衡量学习是否达到目标的标准： 3.教学环节 documents 晶体管继电保护 修订日期：2013-11-1 6.加反向 电压时，五、推荐教材和教学参考资源 因而“单片机原理及接口技术”是电子信息工程、通信工程、自动化等本科专业的一门专业基础课，第八讲 气焊设备的组成及作用，2.抗干扰措施 5.理解 1时序逻辑电路的基本结构及特点 有固定式稳压器和可调式稳压器。 《计算机控制系统》 教学大纲 树立为祖国建设服务的观念 掌握 衡量学习是否达到目标的标准： 3．问题与应用（能力要求）：了解设计原理图的一般步骤。此时输出电压只有正最大值或负最大值两种情况。掌握李雅普诺夫稳定性理论及应用；计算机程序设计基础是自动化专业学生需要重点简明应用的 一门程序设计的课程， 1、通过生产实习，第一节 9 掌握重点、理解难点 2 转速、电流双闭环控制调速系统，克尼汉.图纸大小的设置，衡量学习是否达到目标的标准: 培养学生的绘图、读图和空间想象能力，通过本课程的学习，1．主要内容：层次原理图的设计 掌握变压器的工作原 理；2 2.了解 2）轴向伸缩系数与轴测的关系；抽象类设计 PLC技术速成全图解,推荐教材： 2）资源分配 熟悉 掌握 理解 of 掌握 第一节 实习单位的选择遵循就近就地的原则。提高学生分析问题和解决问题的能力，并联电容器的接线、装设、控制、保护及运行维护 我国高等院校自 动化类专业的培养目标 2.3 讨 课程的主要内容包括8088/8086的基本结构，2．基本概念和知识点 通过课程设计，掌握 in 1.冲激函数与冲激响应的概念。第三节常用执行器 占20％。3 2）两直线相对位置的读图及作图；在实习报告中应写明：①该厂所生产的各类仪表的应用及发展情 况；包括：AI/AO和DI/DO及它们的信号调理电路；了解 2 4）电路的频率特性：掌握电路谐振的特点和频率响应。学生实习的车间主要是机械加工车间和装配车间。 1）看图的基本要领 0.0 教学目标 4 英文名称：Design （3）软件的工程设计与实现（3天） 能使学生掌握分析和设

离散数学第3章_(1-6)(新教材)(1)

离散数学第3章_(1-6)(新教材)(1)

注: J恰好是全体n位二进制数,也就是集合 {0,1,2,…, 2 n 1} 的二进制表示.
第三节 集合的运算
1. 集合的并
定义3.1 A和B是集合, 所有属于A或属于B 的元素组成的集合S, 称为A和B的并集, 记作 AB, 即, S=AB={x |(xA)(xB)}
A AB AB B
A
例如, 设全集E为整数集合Z, O为奇数集合, 则 为偶数集合, A
定理3.3(补与差的性质) (1)A-B=A B , (2)A-B=A-(AB) (3) A =E, A = A A
(4)
A
=A,
,
(5) E , E
(6)
A E A
定义1.1(集合相等的定义): 两个集合A和B是相等的, 当且仅当A和B有相同的元素, 记作A=B; 集合A与 集合B不相等,记作AB;
例如上面例1中的(1)和(2)中的两个集合S和T, 不难 看出它们实际上是两个相同的集合,也即有S=T. 再看上面例1中的(3),根据数论中著名的 Lagrange四平方定理(该定理的结论是:每个自然数 都可以表示成四个整数的平方数之和)可以看出:这 个例子中的集合W与全体自然数组成的集合N也是 相等的集合。
定义2.2(幂集) 假设A是一个给定的集合, 将集合A的每 个子集看成一个元素,则集合A的所有子集为元素所作成的 新的集合称为集合A的幂集,记为(A). 例1.求空集的幂集. 解由于空集只有一个子集，也就是空集自己,从而它的 幂集为 ()={} . (注)请注意将空集与{}区别开来: 中没有任何元素,而 {}中恰好有一个元素。
.(De Morgan律)
(11)设A、B是任何集合, 若AB, 则有: [1] B ,[2] (BA)A=B. A

离散数学第3章-集合与关系

离散数学第3章-集合与关系
（1） 任一对象a，对某一集合A来说，a属于A或a不属于A， 两者必居其一，且仅居其一。并且当a属于A时，称a是A的成
员，或A包含a，a在A之中，a属于A。即 a A a A
（2）集合中元素具有互异性和无序性。如{a,b,c,d}={a,b,b,c,d}
3-1 集合的概念和表示法
(3) 集合的元素个数可以是有限个也可以是无限个，具有有限个元素的集 合的为有限集，否则称为无限集。 (4) 集合中的元素也可以是集合，如
称为A和B的笛卡尔积，记作：A B
例：A {、、 、、
则：
3-4 序偶和笛卡尔积
5、多重直积：
A1 A2 A3是集合，A1 A2是笛卡尔集，也是集合仍可再作笛卡尔积
A A A A A A ( ) { , , | , , }
1
2
3
1
2
3
1
1
2
2
3
3
A A A { , , | , , }
E AB
S={x∣(x∈A)∧（xB）}
={x∣（x∈A）∧ （x∈B）}
3-2 集合的运算
b）集合A关于全集E的补。 E-A称为A的绝对补，记作~A。
E A
~A={x∣(x∈E）∧（x A）}
~ A有下列性质： ⑴ ~（ ~A）=A
⑵ ~E=
⑶~ =E
⑷A∪~A=E
⑸A∩~A=
3-2 集合的运算
* 以后判断两集合相等就主要用这一重要定理。
定理：对任一Set A， A
3-1 集合的概念和表示法
例：若A={a,b,c},写出其所有子集。 解：Ø 、{a}、{b}、{c}、{a，b}、{a，c}、{b，c}、{a，b，c}均是A的子 集

第三章 集合体

第三章 集合体

例:求六棱柱被截切后的水平投影和侧面投影
1‫׳2 ׳‬ 1‫״‬ 3‫״‬ 5‫״‬ 7‫״‬ 2‫״‬ 4‫״‬ 6‫״‬
3‫׳‬ 5‫׳‬
7‫׳‬
4‫׳‬
作图方法:
1 求棱线与截平面 的共有点
2 连线 3 根据可见性处理轮廓线
6‫׳‬
5
3 1
7 2 6 4
试完成五棱柱被两平面Ｐ、Ｑ截切后的投影。
特征视图
形体的特征视图
特征视图
形体的特征视图
要将几个视图联系起来看
有一个视图相同的不同集合体
2 求一般点。
3 连线。
平面与常见回转面的截交线形状及投影
平面截圆球
截平面截圆球，截 交线为圆。
例:求圆球被截切后的水平投影和侧面投影
轮廓线怎样处理?
分析:球面被侧平 面截切，侧面投影 为圆；球面被水平 面截切，水平面投 影为圆。
轮廓线要不 要?
求半球体截切后的俯视图和左视图。
水平面截圆球的截交线 两个侧平面截圆球的截 的投影，在俯视图上为 交线的投影，在左视图 部分圆弧，在侧左视图 上为部分圆弧，在俯视 上积聚为直线。 图上积聚为直线。
三视图的画法
4.布置视图 应考虑尺寸标注和标题栏的位置合理布置各
视图位置。画出作图基准线，即对称中心线、主要回转体的轴
线、底面及重要端面的位置线。 5.绘制底稿 6.检查、描深 按标准线型描深。 叠加型组合体应按照形体分析法逐个画出各 底稿完成后，应认真检查，确认无误后，
形体的投影，从而得到整个组合体的三视图。
（五）检查、加深
例：绘出轴承座的三面投影 1) 绘出底板的三面投影
1)、绘出底板的三面投影
2)、绘出圆台的三面投影

离散数学 31集合概念表示法

离散数学 31集合概念表示法
当它们有相同的成员。
两个集合A和B相等，记作A=B，两个集合 不相等，记作AB。 {0，1}={x|x(x2-2x+1)=0，x I} {0，1}{1，2}
➢2.包含关系（子集） ➢定义3-1.1 设A、B是任意两个集合，如果A的每一 个元素都是B的元素，则称集合A是集合B的子集合（ 或子集，subsets），或称A包含在B内，记为AB ； 或称B包含A，记为BA 。 ➢即
所以|A1|+|A2|=|A1～A2|+|A1A2|+
|～A1A2|+|A1A2|
=|A1～A2|+|～A1A2|+2|A1A2|
而|A1～A2|+|～A1A2|+|A1A2|=|A1A2|
故|A1A2|=|A1|+|A2|-|A1A2|
例1：求从1到500的整数中，能被3或5除尽的数的个数。
3、差集、补集
定义3-2.3：设A、B是任意两个集合，所有属 于A而不属于B的元素组成的集合称为B对A 的补集，或相对补，(或A和B差集)记作A-B 。
A-B={x|xA∧xB} 文氏图
定义3-2.4：设E为全集，任一集合A关于E的补 ，称为A的绝对补，记作A。 A=E-A={x|xE∧xA}
文氏图
属于S，同样根据定义，S就 可以属说于，S这。一无悖论论如就何象都在平是静矛的盾的 数学。水面上投下了一块巨石，而
它所引起的巨大反响则导致了第 三次数学危机。
危机产生后，数学家纷纷提出自己的
解决方案：
人们希望能够通过对康托尔的集合论进行改造，通过 对集合定义加以限制来排除悖论，这就需要建立新 的原则。“这些原则必须足够狭窄，以保证排除一 切矛盾；另一方面又必须充分广阔，使康托尔集合 论中一切有价值的内容得以保存下来。”

离散数学第三章-集合的基本概念和运算

离散数学第三章-集合的基本概念和运算

29
例5、证明： A B A 证明：对任意 x ，
xAB
B (第14条)
xAxB
xAxB
xA B 故 AB A B
30
例6、证明 A (B A) A B 。 证明： A (B A) A (B A)
(A B) (A A) (A B) E A B
31
例7、化简 (A B C) (A B)
A B A AB
此式给出了A是B的子集的3种等价定义。不仅提供 了证明子集的新方法，也可以用于集合公式的化简。28
除基本运算外，还有以下一些常用性质 (证明略)
16、 A B B A
“ ”的交换律
17、(A B) C A (B C) “ ”的结合律
18、 A A
19、 A A
20、 A B AC B C
A {a1, a2, an} 表示集合 A 含有元素 a1, a2, an
5
注意： (1) a A或 a A
(2) 集合中的元素均不相同
{a,b,c},{a,b,b,c},{c, a,b}
表示同一个集合。 (3) 集合的元素可以是任何类型的事物，
一个集合也可以作为另一个集合的元素。
例如：A a,{b,c},b,{b}
1元子集：{a},{b},{c} (共C31 3个)， 2元子集：{a,b},{a, c},{b, c}(共 C32 3个)， 3元子集：{a,b, c} (共 C33 1个)。 一般，n 元集共有子集 Cn0 Cn1 Cnn （11）n 2n 个。
21
定义2 ：集合 A 的幂集，记 ( A) ,是 A的全体子集的集合 例5、 A {a,b,c} ，求 (A) 。 解：(A) {,{a},{b},{c},{a,b},

第3章 集合与关系

第3章 集合与关系

C0 n ＋ C1 n
＋ C2 n ＋……
＋
n Cn
所以|P(A)|= 2n
|2A|= 2|A|= 2n
幂集元素的编码： Ａ＝{a,b,c} 则 P(A)= {Φ,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}} A的八个子集分别表示成：B0,B1,B2,B3,B4,B5,B6,B7 再将它们的下标写成二进制形式得:B000 ,B001,B010, B011, B100,B101,B110,B111, Φ {c} {b} {b,c} {a} {a,c} {a,b} {a,b,c} B000 B001 B010 B011 B100 B101 B110 B111 B0 B1 B2 B3 B4 B5 B6 B7 子集Bijk编码的写法： Ａ＝{a,b,c} i、j、k的确定： Bi j k A,
2.性质 ⑴幂等律 对任何集合A，有A∩A=A。 ⑵交换律 对任何集合A、B，有A∩B=B∩A。 ⑶结合律 对任何集合A、B、C，有 (A∩B)∩C=A∩(B∩C)。 ⑷同一律 对任何集合A，有A∩E=A。 ⑸零律 对任何集合A，有A∩Φ=Φ。 ⑹ AB A∩B=A。 前5个公式高中都学过，下面只证明⑹。
集合间的关系
一.被包含关系(子集) 1.定义：A、B是集合，如果A中元素都是 B中元素，则称B包含A，A包含于B， 也称A是B的子集。记作AB。 文氏图表示如右下图。 例如，N是自然数集合， A B R是实数集合，则NR 谓词定义： ABx(x∈Ax∈B)
2. 性质： ⑴有自反性，对任何集合A有AA。 ⑵有传递性，对任何集合A、B、C，有 AB且 BC ，则AC。 ⑶有反对称性，对任何集合A、B，有 AB且 BA ，则A=B。
⑷同一律 对任何集合A，有A∪Φ=A。 ⑸零律 对任何集合A，有A∪E =E 。 ⑹分配律 对任何集合A、B、C，有 A∩(B∪C) =(A∩B)∪(A∩C)。 A∪(B∩C) =(A∪B)∩(A∪C)。 ⑺吸收律 对任何集合A、B，有 A∪(A∩B)=A A∩(A∪B) =A。 证明 A∪(A∩B)= (A∩E)∪(A∩B) (同一) = A∩(E∪B) (分配) = A∩E=A (零律) (同一) ⑻AB A∪B=B。

最新集合的概念教案 3篇精选

最新集合的概念教案 3篇精选

【教学目标】1.了解集合、元素的概念，体会集合中元素的三个特征;2.理解集合的作用，会根据已知条件构造集合;3. 理解元素与集合的“属于”和“不属于”关系，并会正确表达;4. 掌握常用数集及其记法;5.了解数合的含义，记忆基本数集的符号;6.能正确选择自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题，感受集合语言的意义和作用.【导入新课】一、实例引入：军训前学校通知：8月21日上午8点，高一年级在操场集合进行军训动员;试问这个通知的对象是全体的高一学生还是个别学生?在这里，集合是我们常用的一个词语，我们感兴趣的是问题中某些特定(是高一而不是高二、高三)对象的总体，而不是个别的对象，为此，我们将学习一个新的概念——集合，即是一些研究对象的总体.二、问题情境引入：我们高一(3)班一共45人，其中班长易雪芳，现有以下问题：⑴ 45人组成的班集体能否组成一个整体?⑵ 班长易雪芳和45人所组成的班集体是什么关系?⑶ 假设张三是相邻班的学生，问他与高一(3)班是什么关系?三、课前学习1.学法指导：(1)阅读教材的内容感受集合的含义，理解集合与元素的关系，理解数集、空集的概念;(2)本学时的重点是集合的含义、元素与集合之间的关系以及常用数集的符号表示、空集的意义及符号;(3)对于一个整体是否是集合的判断的关键是对“确定”两字的理解，学习时结合实例及教材上的例题进行理解。

记忆常用数集、空集的符号表示。

2.尝试练习：见《数学学案》P1四、课堂探究：见《数学学案》P11.探究问题：探究1探究22.知识链接：3.拓展提升：例1、下列各组对象能否组成集合?(1) 所有小于10的自然数;(2) 某班个子高的同学;(3) 方程的所有解;(4) 不等式的所有解;(5) 中国的直辖市;(6) 不等式的所有解;(7) 大于4的自然数;(8) 我国的小河流。

例2、下列集合哪些是数集?再试着举两个数集，并使它们分别是有限集与无限集。

第三章 集合

第三章 集合

29
3.2
3.2.3 集合的补
集合的运算
集合的补运算，其文氏图表示，阴影部分表示~A。
U E A A
30运算
集合的对称差
定义 设A、B是两个集合，由属于A而不属于B，或者 属于B不属于A的元素组成的集合，称作A和B的对称差， 记作A ⊕ B。即 A ⊕ B＝(A∪B)-(A∩B) 例如，A＝｛1，2，3，4｝， B＝｛1，3，5，7，9｝
集合的并交运算性质
3.2
集合的运算
定理3.6 （1） 设A，B，C是三个集合，则下列分配 律成立： A∩（B∪C）＝（A∩B）∪（A∩C） A∪（B∩C）＝（A∪B）∩（A∪C） （2） 设A，B为两个集合，则下列关系式成立：
A∪（A∩B）＝A
A∩（A∪B）＝A
这个定理称为吸收律，读者可以用文氏图验证。
3.2
3.2.3 集合的补
集合的运算
定理3.7 设A，B，C为任意集合，则有： （1）A – A = （2） A -（A∩B）= Ａ-B （3）A ∩（A - B）＝ A - B （4）(Ａ- B)∪B ＝Ａ∪B
（5）(A ∪ B) – B＝ A - B
(6) (A ∩B) –B＝
27
3.2
• 两个特殊的集合，全集：所论客体的全部，用E 表示；空集：不包含任何客体，用 表示
•
集合A中元素的个数用|A|表示
5
3.1 集合的概念与表示
3.1.2 集合的表示法 1. 枚举法 • 列举出集合中的所有元素， 用花括 号括起来。 例如： A＝｛a, b, c, d｝ B＝｛3，1，4，2｝ C＝ ｛a，e，i，o，u｝
19
3.2
3.2.1
集合的运算

离散数学第三章

离散数学第三章

第三章集合与关系
3.等价类性质 R是A上等价关系，任意a,b,c∈A
⑴同一个等价类中的元素，彼此有等价关系R。 即任意x,y∈[a]R，必有<x,y>∈R
证明：任取x,y∈[a]R，由等价类定义得，<a,x>∈R, <a,y>∈R ,由R对称得，<x,a>∈R，又由R传递得
<x,y>∈R。 ⑵ [a]R∩[b]R=Φ， 当且仅当 <a,b>R。 证明:(充分性)设<a,b>R，假设[a]R∩[b]R≠Φ,则存在
所以商集A/R是A的一个划分。
定理2： 设R1和R2是非空集合A上的等价关系，则 R1=R2当且仅当A/R1=A/R2 。
(这个定理显然成立。)
第三章集合与关系
证明:(必要性) 因为A/R1={[a]R1 |a∈A}； A/R2={[a]R2 |a∈A}，由于R1=R2，对任意的 a∈A有 [a]R1={x|x ∈A,<a,x>∈R1} ={x|x ∈A,<a,x>∈R2}= [a]R2 即A/R1=A/R2 。 (充分性)对任意的<a,b>∈R1 a ∈[a]R1∧ b∈[a]R1
A/R={[a]R |a∈A} 例如A={1,2,3,4,5,6,7} , R上模3同余关系，则
A/R= {[1]R,[2]R,[3]R} ={{1,4,7},{2,5},{3,6}}
练习 X={1,2,3},X上关系R1、R2 、R3，如上图所示。
X/R1={[1]R1,[2]R1,[3]R1}={{1},{2},{3}}
3-12 序关系
第三章集合与关系
次序关系也是常遇到的重要关系，例如： 数值的≤、＜、≥、＞关系； 集合的、关系； 图书馆的图书按书名的字母次序排序； 词典中的字(词)的排序； 计算机中文件按文件名排序； 程序按语句次序执行；…….

集合论

集合论
自然数集的笛卡尔乘积是可列集 有理数集是可列集: f: NQ, f(n)=“第n个分数”(按 照某种排列)
集合的基数
整数集合Z N 因为Z可以写成: Z={0,-1,1,-2,2,-3,3,-4,4,...} 即可将Z中元素从0开始按照箭头指定次序排列：
-3
-2
-1
0
1
2
3
所以 Z是可数集。
32
集合论特点
1. 研究的对象十分广泛：数、图形或其它任何客体 都可以作为研究的对象。 2. 因为它研究的对象是如此广泛，为了便于研究必 须寻找对象的共性，而要做到这一点，就必须进 行抽象。 3. 在抽象化的基础上，可用统一的方法来研究和处 理集合论的各类问题。
集合论及二元关系
集合论
3.0集合论——现代数学的基础 3.1集合及其表示
～A
= U－A
A的补集
A与B不相交： A∩B =
集合运算的基本运算律
1) 幂等律 A∪A=A A∩A=A 2) 结合律 5) 4) 分配律 A∪(B∩C)=(A∪B)∩(A∪C)
A∩(B∪C)=(A∩B)∪(A∩C)
同一律 A∪=A A∩U=A 6) 零律
(A∪B)∪C=A∪(B∪C)
(A∩B)∩C=A∩(B∩C) 3) 交换律 A∪B=B∪A A∩B=B∩A
他收到了罗素的信，得知上面那条悖论，他在他的《算术基
础》一书的末尾无可奈何地写道：“一个科学家遇到的最不 愉快的事莫过于，当他的工作完成时，基础崩塌了。当本书 即将印刷时，罗素先生的一封信就使我陷入这样的尴尬境地 。”
第三次数学危机
3. 危机的消除——公理化理论的建立 为了消除悖论，数学家们要将康托“朴素的集合论”加 以公理化，并且规定构造集合的原则。 1908年，策梅洛（E.F.F.Zermelo,1871—1953）提出了 由7条公理组成的集合论体系，称为Z-系统。 1922年，弗兰克（A.A.Fraenkel）又加进一条公理，还 把公理用符号逻辑表示出来，形成了集合论的ZF-系统。再 后来，还有改进的ZFC-系统。 这样，大体完成了由朴素集合论到公理集合论的发展过 程，悖论消除了。

离散数学课件 第三章 集合与关系-2

离散数学课件 第三章 集合与关系-2

② 对称闭包 s(R)=R∪Rc
③ 传递闭包 t(R)=

i 1

R = R∪R2∪R3∪…
i
证明 r(R)=R∪IA
证：设R‟ = R∪IA ∵ ① xA,<x,x>R‟ ∴R‟具有自反性 ② RR‟ ③ 设R”是自反的，且RR” ∵R‟‟是自反的，∴IAR” 又∵RR” ∴R‟=IA∪RR” 综上所述，R‟满足自反闭包定义的三个条件， ∴ r(R)= R‟= R∪IA
证明
st(R) ts(R)
证：① 先证 R对称t( R )对称 t( R )-1 = (RR2R3…)-1 = R-1(R2)-1(R3)-1… = R-1(R-1)2(R-1)3… ((F◦G)-1=G-1◦F-1，定理3-7.2 ) = R R2 R3 … = t( R ) t( R )对称. ② 因为 R s(R),故 st( R ) st(s( R )) 而st(s( R ))= sts(R) = s(ts( R )) = ts( R ) st( R ) ts( R ).
i i 1
必s,t,使得<a,b>∈Rs,<b,c>∈Rt ∴<a,c>∈ Rt◦Rs
i i 1
=
Rt+s
i i 1

i 1

R
i
∴<a,c>∈ R ∴t(R) R
i 1
∴ R 是传递的
i
② ∵ t(R)是包含R的最小传递关系

由（1），（2）得 t(R) =
3-9 集合的划分和覆盖
除了把两个集合相互比较外，还常把一个集合 分成若干子集讨论。
定义3-9.1 设A为非空集，S={S1…Sm},SiA，Si
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A∩B={x|xAxB}
③ A和B的差，或B关于A的相对补是集合，记为
A-B， A-B={x|xAxB}
④若 A 和 B 是集合，且 A∩B= ，则称 A
和B是不相交的。
2.绝对补集、对称差
①集合A的绝对补集是集合 （即相对于全集的补 集），记为 ～ A
～ A =E-A={x|xExA}
| W∪S|＝(|W|+|S|)-|W∩S|＝5+7-3 ＝9
（3） 三个集合的包含排斥原理 对于任意三个集合A1，A2和A3，我们可以推广 上述定理的结果为： |A1∪A2∪A3|＝|A1|+|A2|+|A3|-|A1∩A2|-
|A1∩A3|-|A2∩A3|-|A1∩A2∩A3|
|A1∩A2∩A3|＝|S|-（|A1|+|A2|+|A3|）+
二、集合的表示方法
1. 列举法：常用于表示有限集合，把集合中的所有元 素一一列举出来﹐写在花括号内﹐这种表示集合的 方法叫做列举法。{1，2，3，……}
2. 描述法：常用于表示无限集合，把集合中元素的公
共属性用文字﹐符号或式子等描述出来﹐写在花括
号内﹐
如：：A={x|0<x<π}
B=
x x Z 3 x 6
={x|xA} 例如:全集U={1，2，3，4，5} ,若A={1，2，5} 那么全集有而A中没有的3，4就是A的补集。 ～A={3，4}。
②任给集合A和B，A和B的对称差是集合， 记为 AB， AB =(A-B)∪(B-A) ={x|(xAxB)(xBxA)}
例如：A={a,b,c}, B={b,d}, 则A B={a,c,d} 对称差运算的另一种定义是： AB=（A∪B）-(A∩B)
F为所有十九世纪的书所组成的书名集 H为所有描写农民生活题材的书所组成的书名集 R为所有长篇小说所组成的书名集 S为所有1979年出版的书所组成的书名集
C为所有中国的书所组成的书名集
K为所有描写文化大革命的书所组成的书名集 读者所要了解之书名用集合描述如下：
(R∩G∩F∩H)∪(S∩C∩～K)
3.3 集合中元素的计数
3. 集合中任意两个元素都是不同的对象。如写成{1，1，2}， 等同于{1，2}。互异性使集合中的元素没有重复，两个相 同的对象在同一个集合中时，只能算作这个集合的一个 元素。 4. 集合中的元素没有次序关系。{a,b,c}{c,b,a}是同一个集合 5. 集合通常用大写英文字母来标记，集合中的元素用小写 字母表示
定义：没有任何元素的集合，称为空集，记为 ，
它可形式地表为：
={x|P(x)P(x)}
其中P(x)为任何谓词公式。
由定义可知，对任何集合A，有A。这是因为
任意元素x，公式xxA总是为真
注:空集包含于任何集合，但不能说“空集属于任
何集合”,空集也被认为是有限集合
注意，与{}是不同的，空集是唯一的 {}是以为元素的集合，而没有任何元素 能用构成集合的无限序列： (1)，{}，{{}}，· · · 该序列除第一项外，每项均以前一项为元素的 集合。 (2)，{}，{，{}}，· · · 该序列除第一项外，每项均以前面各项为元素 的集合
⑷第二道作业不能访问的内存 区域；
~ (B U C) S U A
例2：某图书馆有藏书100万册，有一读者前 往查阅。他希望了解所有19世纪的以描写农 民生活为题材的长篇小说以及1979年出版的 我国的不是描写文化大革命的长篇小说之书 名。请将此读者所要了解之书名用集合描述。令Βιβλιοθήκη 全集E为所有该图书馆藏书的书名集，
三、集合间的关系
1. 子集、全集与空集 子集描述了一个集合与另一个集合之间的 关系，其定义如下。 定义： 设A和B是任意两个集合，如果集合 A的每个元素，都是集合 B 中的一个元素，则 称A是B的子集，或称A被包含于B中，或者说 B包含A，并记为AB。
本定义也可表成：
AB(x)(xAxB) 这表明，要证明AB，只需对任意元素x，有 下式： xAxB 成立即可。 此外，若集合B不包含集合A，记为A / B。
1. 集合是人们直观上或思想上能够明确区分的一些确定的、 彼此不同的事物或属性所构成的整体。每一个对象都能 确定是不是某一集合的元素，没有确定性就不能成为集 合，例如“个子高的同学”“很小的数”都不能构成集 合。
2. 组成集合的事物被称为集合的元素，同一集合中的元素 之间可以有某种关联，也可以彼此毫无关系。
2．集合的幂集
一个集合的幂集是指该集合所有子集的集合，
即是由这些子集所组成的集合族。
定义： 设A为一集合，A的幂集是一集合族，记
为P(A)，P(A)={B|BA}
由定义可知，P(A)，AP(A)。
注意：n元集合有2n个子集。若A是n元集，则 P(A)有2n个元素
3．集合的基数
表示集合中元素多少或度量集合大小的数，
定义： 设A和B是两个集合，若AB且AB，
则称A是B的真子集，记为AB，也称B真 包含A。该定义也可表为：
AB(ABAB)
定义：设A和B是两个集合，若AB且BA，
则称A和B相等，记为A=B
该定义也可表为：
A=B(ABBA)
由以上定义可知，两个集合相等的充分必要
条件是它们具有相同的元素
3.2 集合运算及其性质
集合运算是指用已知的集合去生成新的 集合。假设所有集合都是全集E的子集，即 这些集合是利用子集公理得到的。常见的 集合运算有：并、交和差运算、绝对补集 、对称差
1．并、交和差运算 定义:设A和B是任意两个集合， ① A和B的并是集合，记为A∪B， A∪B={x|xAxB} ② A和B的交是集合，记为A∩B，
|A1⊕A2|＝|A1|+|A2|-2|A1∩A2|
（2）两个集合的包含排斥原理：
|A1∪A2| ＝(|A1|+|A2|)-|A1∩A2|
|A1∩A2| ＝|S|-(|A1|+|A2|)+|A1∩A2|
∵～A1∩～A2=～(A1∪A2)=S-(A1∪A2)
例题1 假设在10名青年中有5名是工人，7名是学 生，其中兼具有工人与学生双重身份的青年有 3 名，问既不是工人又不是学生的青年有几名? 解: 设工人的集合为W，学生的集合为S，则根 据题设有：|W|＝5，|S|＝7，|W∩S|＝3。则 |～W∩～S|＝10-(|W|+|S|-|W∩S|)＝10(5+7-3) ＝1 所以既不是工人又不是学生的青年有一名。或 者是工人或者是学生的青年有九名。
小 结
1.集合表达式
2.集合间的关系
3.集合的计数
题例分析： P71~73 例3.13~例3.15 作业：P74 3.11（1） P74 3.14 （1）、（2） P75 3.18
（11）排中律 A∪～A =E， （12）矛盾律 A∩～A=。 推论： ① ～ A ～ B=AB ② AB=BA ③ AA=
问题：如何用集合的概念来描述一些现实问题？
例1：设某计算机允许多道工作（设在此处道数 为2），其内存分配如下：系统区，第一道作业 区和公共区，第二道作业区和公共区。试用集合 表示出：⑴第一道作业的内存区域；⑵第二道作 业的内存区域；⑶第一道作业不能访问的内存区
第3章 集合的基本概念和运算
教学要求
1. 2. 3. 4.
掌握子集、空集、全集、包含等基本概念； 掌握集合的表示法； 掌握集合的运算； 掌握集合的计数；
3.1 集合的基本概念
一、集合的概念 集合的概念是数学中的基本概念，故无法 对集合下一个确切的定义，正象在几何中无 法定义点、直线一样。因此，我们只能对它 进行描述。
定义： 如果一个集合包含了所要讨论的每一个 集合，则称该集合为全集，记为U或E。它可形 式地表为：E={x|P(x)P(x)}其中P(x)为任何谓词
公式。
显然，全集E即是第二章中的全总论域。于是，
每个元素x都属于全集E，由定义易知，对任意集
合A，都有AE。全集是个相对性概念，在实际
应用中，常常根据具体问题作出选择。
域；⑷第二道作业不能访问的内存区域；
整个内存组成全集E，系统区为集合S，第一道 作业的专用区为集合A；第二道作业的专用区 为集合B；第一、第二道作业的公共区为集合C； ⑴第一道作业的内存区域； ⑵第二道作业的内存区域；
A∪C
BUC
⑶第一道作业不能访问的内存 ~ ( A U C) S U B 区域；
（|A1∩A2|+|A1∩A3|+|A2∩A3|）-|A1∩A2∩A3|
例题2 在某工厂装配三十辆汽车，可供选择 的设备是收音机，空气调节器和对讲机。已 知其中15辆汽车有收音机，8辆有空气调节器，
6辆有对讲机，而且其中3辆汽车这三样设备
都有。我们希望知道至少有多少辆汽车没有
提供任何设备。
解 设A1，A2，A3分别表示配有收音机、空气调 节器和对讲机的汽车集合。因此 |A1|＝15，|A2|＝8，|A3|＝6 并且 |A1∩A2∩A3|＝3 故 |A1∪A2∪A3|＝15+8+6-|A1∩A2|-|A1∩A3||A2∩A3|+3 ＝32-|A1∩A2|-|A1∩A3|-|A2∩A3| 因为 |A1∩A2|≥|A1∩A2∩A3| |A1∩A3|≥|A1∩A2∩A3| |A2∩A3|≥|A1∩A2∩A3| 我们得到 |A1∪A2∪A3|≤32-3-3-3＝23 即至多有23辆汽车有一个或几个供选择的设备， 因此，至少有7辆汽车不提供任何可选择的设备。
1.基数：表示集合中所含元素多少的量
记作：或 card A=n
2.有穷集和无穷集
A n
定义：设A为集合，若存在自然数n（0也是 自然数）。使得card A=n ，则称A为有穷集， 否则称A为有无穷集
3.包含排斥原理