信息论信息论第1章
- 格式:ppt
- 大小:392.50 KB
- 文档页数:45

信息论第一章概论1.信息、消息、信号的定义及关系。
定义信息:事物运动状态或存在方式的不确定性的描述。
消息:指包含有信息的语言、文字和图像等。
信号:表示消息的物理量,一般指随时间而变化的电压或电流称为电信号。
关系信息和消息信息不等于消息。
消息中包含信息,是信息的载体。
同一信息可以用不同形式的消息来载荷。
同一个消息可以含有不同的信息量。
信息和信号信号是消息的载体,消息则是信号的具体内容。
信号携带信息,但不是信息本身。
同一信息可用不同的信号来表示,同一信号也可表示不同的信息。
2. 通信系统模型,箭头上是什么?通信的目的及方法。
通信的目的:是为了提高通信的可靠性和有效性。
信源编码:提高信息传输的有效性。
(减小冗余度)信道编码:提高信息传输的可靠性。
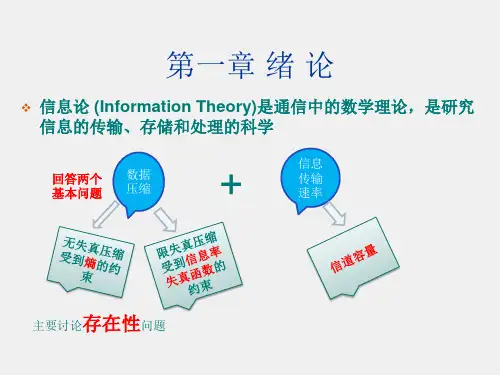
(增大冗余度)第二章 信源及其信息量★信源发出的是消息。
信源分类1、信源按照发出的消息在时间上和幅度上的分布情况可将信源分成离散信源和连续信源。
2、根据各维随机变量的概率分布是否随时间的推移而变化将信源分为平稳信源和非平稳信源。
单符号离散信源离散无记忆信源 无记忆扩展信源 离散平稳信源离散有记忆信源 记忆长度无限记忆长度有限(马尔可夫信源)一、单符号离散信源单符号离散信源的数学模型为定义:一个随机事件发生某一结果后所带来的信息量为自信息量。
定义为其发生概率对数的负值。
以 奇才 单位:•对数以2为底,单位为比特 (bit ) (binary unit ) •对数以e 为底,单位为奈特 (nat ) (nature unit)•对数以10为底,单位为笛特(det) (decimal unit) 或哈特 (hart) 物理含义:在事件xi 发生以前,等于事件xi 发生的不确定性的大小;在事件xi 发生以后,表示事件xi 所含有或所能提供的信息量。
性质:①I(x i )是非负值.②当p(x i )=1时,I(x i )=0. ③当p(x i )=0时,I(x i )=∞.④I(x i ) 是p(x i )的单调递减函数.联合自信息量条件自信息量自信息量、条件自信息量和联合自信息量之间有如下关系式:I(x i y j )= I(x i )+ I(y j / x i ) = I(y j )+ I(x i / y j )⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡)(,),(,),(),( ,, ,, , )( 2121n i n i x p x p x p x p x x x x X P X )(log )( i i x p x I -=)(log )( j i j i y x p y x I -=1)(,1)(01=≤≤∑=ni i i x p x p定义:各离散消息自信息量的数学期望,即信源的平均信息量.单位:比特/符号 物理含义: ① 信源熵H(X)表示信源输出后,离散消息所提供的平均信息量. ② 信源熵H(X)表示信源输出前,信源的平均不确定度. ③ 信源熵H(X)反映了变量X 的随机性.信源符号的概率分布越均匀,则平均信息量越大; 确定事件,不含有信息量。








信息论与编码第二版答案第一章:信息论基础1.问题:信息论的基本概念是什么?答案:信息论是一种数学理论,研究的是信息的表示、传输和处理。
它的基本概念包括:信息、信息的熵和信息的编码。
2.问题:什么是信息熵?答案:信息熵是信息的度量单位,表示信息的不确定度。
它的计算公式为H(X) = -ΣP(x) * log2(P(x)),其中P(x)表示事件x发生的概率。
3.问题:信息熵有什么特性?答案:信息熵具有以下特性:•信息熵的值越大,表示信息的不确定度越高;•信息熵的值越小,表示信息的不确定度越低;•信息熵的最小值为0,表示信息是确定的。
4.问题:信息熵与概率分布有什么关系?答案:信息熵与概率分布之间存在着直接的关系。
当概率分布均匀时,信息熵达到最大值;而当概率分布不均匀时,信息熵会减小。
第二章:数据压缩1.问题:数据压缩的目的是什么?答案:数据压缩的目的是通过消除冗余和重复信息,使数据占用更少的存储空间或传输更快。
2.问题:数据压缩的两种基本方法是什么?答案:数据压缩可以通过无损压缩和有损压缩两种方法来实现。
无损压缩是指压缩后的数据可以完全还原为原始数据;而有损压缩则是指压缩后的数据不完全还原为原始数据。
3.问题:信息压缩的度量单位是什么?答案:信息压缩的度量单位是比特(bit),表示信息的数量。
4.问题:哪些方法可以用于数据压缩?答案:数据压缩可以通过以下方法来实现:•无结构压缩方法:如霍夫曼编码、算术编码等;•有结构压缩方法:如词典编码、RLE编码等;•字典方法:如LZW、LZ77等。
第三章:信道容量1.问题:什么是信道容量?答案:信道容量是指在给定信噪比的条件下,信道传输的最大数据速率。
2.问题:信道容量的计算公式是什么?答案:信道容量的计算公式为C = W * log2(1 + S/N),其中C表示信道容量,W表示信道带宽,S表示信号的平均功率,N表示噪声的平均功率。
3.问题:信道容量与信噪比有什么关系?答案:信道容量与信噪比成正比,信噪比越高,信道容量越大;反之,信噪比越低,信道容量越小。
第一章绪论(第一讲)(2课时)主要内容:(1)教学目标(2)教学计划(3)参考书(4)考试问题(5)信息论的基本概念(6)信息论发展简史和现状(7)通信系统的基本模型重点:通信系统的基本模型难点:通信系统的基本模型特别提示:运用说明:本堂课作为整本书的开篇,要交待清楚课程开设的目的,研究的内容,对学习的要求;在讲解过程中要注意结合一些具体的应用实例,避免空洞地叙述,以此激发同学的学习兴趣,适当地加入课堂提问,加强同学的学习主动性。
信息论与编码(Informatic s & Coding)开场白教学目标:本课程主要讲解香农信息论的基本理论、基本概念和基本方法,以及编码的理论和实现原理。
介绍信息的统计度量,离散信源,离散信道和信道容量;然后介绍无失真信源编码、有噪信道编码,以及限失真信源编码等,然后介绍信道编码理论,最后也简单介绍了密码学的一些知识。
教学重点:信息度量、无失真信源编码、限失真信源编码、信道编码的基本理论及实现原理。
教学计划:信息论:约20学时信道编码:约19学时*密码学:约8学时参考书:1.信息论与编码,曹雪虹张宗橙编,北京邮电大学出版社,20012.信息论—基础理论与应用,傅祖芸编著,电子工业出版社,20013.信息理论与编码,姜丹钱玉美编著4.信息论与编码,吴伯修归绍升祝宗泰俞槐铨编著,1987考试问题:第一章绪论信息论的基本概念信息论发展简史和现状通信系统的基本模型§1.1 信息论的基本概念信息论是一门应用近代数理统计方法来研究信息的传输和处理的科学。
在涉及这门课程的具体内容之前,很有必要在引言中,首先放宽视野,从一般意义上描述、阐明信息的基本含意。
然后,再把眼光收缩到信息论的特定的研究范围中,指明信息论的假设前提,和解决问题的基本思路。
这样,就有可能帮助读者,在学习、研究这门课程之前,建立起一个正确的思维方式,有一个正确的思路,以便深刻理解、准确把握以下各章节的具体内容。