压弯钢管结构计算程序

钢结构受弯构件的计算1.受弯构件的力学模型受弯构件通常由横截面为直角梁的矩形或者工字形钢材组成。

其在受力时，会形成弯曲形状，上部为受压区，下部为受拉区。

为了进行计算，需要将受弯构件简化为力学模型，通常采用简支梁或者悬臂梁。

2.受弯构件的受力分析受弯构件在受力时，上部会形成压应力，下部会形成拉应力。

首先需要根据施加载荷的形式和大小，进行受力分析。

常见的施加载荷有集中力、均布力、温度应变和装配应变等。

3.弯矩计算弯矩是受弯构件设计中的重要参数，用于反映材料的抗弯性能。

弯矩的计算可以通过力学平衡方程和构件截面的几何特性来进行。

对于简单的受弯构件，可以根据荷载和材料性能直接计算得到弯矩值。

对于复杂的受弯构件，需要使用力学原理和数值计算方法。

4.应力计算受弯构件在承受弯矩时，会产生应力，应力的计算是结构设计中的关键环节。

主要有弯曲应力、剪应力和轴向应力。

弯曲应力是受弯构件中最主要的应力，可以通过受弯构件的弯曲截面惯性矩和截面模量来计算。

5.抗弯设计在进行抗弯设计时，需要根据弯矩和应力的计算结果，选择合适的钢材型号和截面尺寸。

一般来说，抗弯设计要满足两个条件：第一是满足弯矩设计要求，即受弯构件在设计工况下的弯矩不超过其抗弯强度；第二是满足截面抗弯设计要求，即受弯构件的截面要满足平衡力矩和压应力的要求。

6.构件验算和优化设计抗弯设计完成后，需要进行构件验算，即检查所设计的构件是否满足强度和稳定性要求。

如果验算结果不符合要求，则需要进行优化设计，重新选择钢材型号和截面尺寸，或者改变结构形式。

综上所述，钢结构受弯构件的计算涉及受力分析、弯矩计算、应力计算、抗弯设计和构件验算等多个方面。

通过合理的计算和设计，可以确保钢结构受弯构件的安全可靠性。

压弯构件计算一、压弯构件计算的一般步骤1.确定设计要求：根据具体的工程要求和规范的要求，确定设计要求，包括荷载标准、使用要求和安全系数等。

2.选择截面形式：根据压弯构件的使用条件和要求，选择合适的截面形式，一般有I形截面、H形截面等。

3.计算轴向受压承载力：根据截面的构造特点和材料的性能，计算压弯构件的轴向受压承载力。

主要考虑的因素包括材料的强度和刚度、构件的几何参数、受力形式和荷载作用方式等。

4.计算弯矩承载力：根据截面的构造特点和材料的性能，计算压弯构件的弯矩承载力。

主要考虑的因素包括材料的强度、构件的几何参数、受力形式和荷载作用方式等。

5.校核满足条件：根据设计要求和规范的要求，对计算所得的结果进行校核，确保满足结构的安全性能和使用要求。

二、压弯构件计算的关键问题在进行压弯构件计算时，需要注意以下几个关键问题：1.材料的选择：材料的选择是压弯构件计算的基础，需要根据工程的具体要求选择合适的材料。

常用的材料有普通碳素钢、低合金高强度钢等。

2.截面形式的选择：截面形式的选择对压弯构件的受力性能、承载力和刚度等起着重要的影响。

需要根据桥梁的跨度、荷载条件和使用要求等因素进行合理的选择。

3.荷载的确定：荷载的确定是进行压弯构件计算的前提条件，需要根据公路桥梁设计规范的要求，考虑静荷载、动荷载和温度荷载等因素。

4.杆件的受力分析：进行压弯构件计算时需要进行杆件的受力分析，包括轴力和弯矩的计算。

受力分析的结果将作为计算的基础，对杆件的抗弯和抗压能力进行评估。

5.截面参数的计算：截面参数的计算是压弯构件计算的关键环节，包括截面的面积、惯性矩、截面模量等参数的计算。

6.构件的稳定性分析：构件的稳定性分析是进行压弯构件计算的重要内容之一，需要考虑杆件的局部稳定和整体稳定等因素。

7.设计的合理性评估：最后需要对设计结果进行合理性评估，根据规范的要求，对计算结果进行校核和评估，确保满足结构的安全性能和使用要求。

钢结构设计规范·轴⼼受⼒构件和拉弯、压弯构件的计算·拉弯构件和压弯构4.1.1在主平⾯内受弯的实腹构件(考虑腹板屈曲后强度者参见本规范第4.4.1条)，其抗弯强度应按下列规定计算:`(M_x)/(γ_xW_(nx))+(M_y)/(γ_xW_(ny))≤f`（4.1.1）式中M x、M y——同⼀截⾯处绕x轴和y轴的弯矩(对⼯字形截⾯：x轴为强轴，y轴为弱轴);Wｎｘ、Wｎｙ——对x轴和y轴的净截⾯模量;γx、γy——截⾯塑性发展系数;对⼯字形截⾯γy=1.20;对箱形截⾯，γX=Y y=1.05;对其他截⾯，可按表5.2.1采⽤;f——钢材的抗弯强度设计值。

当梁受压翼缘的⾃由外伸宽度与其厚度之⽐⼤于13`sqrt(235//f_y)`⽽不超过15`sqrt(235//f_y)`时，γx=1.0。

f y应取为钢材牌号所指屈服点。

对需要计算疲劳的梁，宜取γx=γy=1.0。

4.1.2在主平⾯内受弯的实腹构件(考虑腹板屈曲后强度者参见本规范第4.4.1条)，其抗剪强度应按下式计算:`τ=(VS)/(It_w)`(4.1.2)式中V——计算截⾯沿腹板平⾯作⽤的剪⼒;S——计算剪应⼒处以上⽑截⾯对中和轴的⾯积矩;I——⽑截⾯惯性矩;t w——腹板厚度;fv——钢材的抗剪强度设计值。

4.1.3当梁上翼缘受有沿腹板平⾯作⽤的集中荷载、且该荷载处⼜未设置⽀承加劲肋时，腹板计算⾼度上边缘的局部承压强度应按下式计算:`σ_c=(varphiF)/(t_wl_z)≤f`(4.1.3-1)式中F——集中荷载，对动⼒荷载应考虑动⼒系数;ψ——集中荷载增⼤系数;对重级.⼯作制吊车梁ψ=1. 35;对其他梁，ψ=1.0；l z——集中荷载在腹板计算⾼度上边缘的假定分布长度，按下式计算:l2=a+5h y+2h R ( 4.1.3-2 )a——集中荷载沿梁跨度⽅向的⽀承长度，对钢轨上的轮压可取50mm;h y——⾃梁顶⾯⾄腹板计算⾼度上边缘的距离;h R——轨道的⾼度，对梁顶⽆轨道的梁h R=0;f——钢材的抗压强度设计值。

拉弯和压弯构件的强度与稳定计算1．拉弯和压弯构件的强度计算考虑部分截面发展塑性，《规范》规定的拉弯和压弯构件的强度计算式f W M A N nxx x n ≤+γ （6-1）承受双向弯矩的拉弯或压弯构件，《规范》采用了与式（6-1）相衔接的线性公式f W M W M A Nnyy y nx x x n ≤++γγ （6-2）式中：n A ——净截面面积；nx W 、ny W ——对x 轴和y 轴的净截面模量；x γ、y γ——截面塑性发展系数。

当压弯构件受压翼缘的外伸宽度与其厚度之比t b /＞y f /23513，但不超过yf /23515时，应取x γ＝1.0。

对需要计算疲劳的拉弯和压弯构件，宜取x γ＝y γ＝1.0，即不考虑截面塑性发展，按弹性应力状态计算。

2．实腹式压弯构件在弯矩作用平面内的稳定计算目前确定压弯构件弯矩作用平面内极限承载力的方法很多，可分为两大类，一类是边缘屈服准则的计算方法，一类是精度较高的数值计算方法。

按边缘屈服准则推导的相关公式y Ex x x xx f N N W M AN =⎪⎪⎭⎫⎝⎛-+ϕϕ11（6-4）式中：x ϕ——在弯矩作用平面内的轴心受压构件整体稳定系数。

边缘纤维屈服准则认为当构件截面最大受压纤维刚刚屈服时构件即失去承载能力而发生破坏，更适用于格构式构件。

实腹式压弯构件当受压最大边缘刚开始屈服时尚有较大的强度储备，即容许截面塑性深入。

因此若要反映构件的实际受力情况，宜采用最大强度准则，即以具有各种初始缺陷的构件为计算模型，求解其极限承载力。

弯矩沿杆长均匀分布的两端铰支压弯构件，《规范》采用数值计算方法，考虑构件存在l/1000的初弯曲和实测的残余应力分布，算出了近200条压弯构件极限承载力曲线。

然后《规范》借用了弹性压弯构件边缘纤维屈服时计算公式的形式，经过数值运算，得出比较符合实际又能满足工程精度要求的实用相关公式y Ex px xx f N N W M AN=⎪⎪⎭⎫⎝⎛-+8.01ϕ（6-5）式中：px W ——截面塑性模量。

弯管知识详解及计算下料方法弯管按其制作方法不同，可分为煨制弯管、冲压弯管和焊接弯管。

煨制弯管又分为冷煨和热煨两种。

本章着重介绍常用煨管设备的结构特点、性能及操作等方面的知识，以及煨制弯管的下料计算。

01弯管的一般知识弯管是改变管道方向的管件。

在管子交叉、转弯、绕梁等处，都可以看到弯管。

煨制弯管具有较好的伸缩性、耐压高、阻力小等优点。

因此，在施工中常被采用。

弯管的主要形式有：各种角度的弯头、U形管、来回弯(或称乙字弯)和弧形弯管等，如图1—1所示。

弯头是带有一个任意弯曲角的管件，它被用在管子的转弯处。

弯头的弯曲半径用R表示。

R较大时，管子的弯曲部分就较大，弯管就比较平滑；R较小时，管子的弯曲部分就较小，弯得就较急。

来回弯是带有两个弯曲角(一般为135°)的管件。

来回弯管子弯曲端中心线间的距离叫做来回弯的高度，用字母h表示。

室内采暖立支管与干管及散热器连接，管道与不在同一平面上的接点连接时，一般需采用来回弯。

U形管是成正半圆形的管件。

管子的两端中心线问的距离d等于两倍弯曲半径R。

U形管可代替两个90°弯头，经常用来连接上下配置的两个圆翼形散热器。

图1-1弯管的主要形式弧形弯管是带有三个弯曲角的管件。

中间角一般成90°，侧角成135°。

弧形弯管用于绕过其它管子，在有冷热水供应的卫生设备配管时，经常采用弧形弯管。

弯管尺寸由管径、弯曲角度和弯曲半径三者确定。

弯曲角度根据图纸和施工现场实际情况确定，然后制出样板，照样板煨制并按样板检查煨制管件弯曲角度是否符合要求。

样板可用圆钢煨制，圆钢的直径根据所煨管径的大小选用，10-14mm即可。

弯管的弯曲半径应按管径大小、设计要求及有关规定而定。

既不能过大，也末虚选得太小。

因为弯曲半径过大，不但用材料多，而且管子弯曲部分所占的地方也大，这样会给管道装配带来困难；弯曲半径选得太小时，弯头背部管壁由于过分伸长而减薄，使其强度降低，而在弯头里侧管壁被压缩，形成皱纹状态。

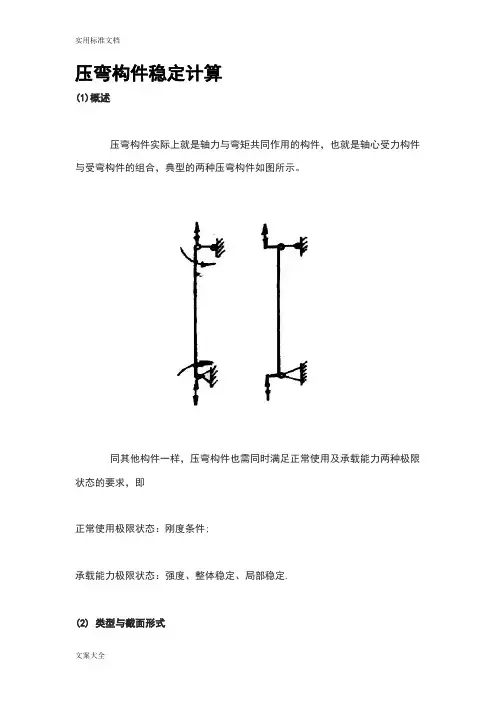
压弯构件稳定计算(1)概述压弯构件实际上就是轴力与弯矩共同作用的构件，也就是轴心受力构件与受弯构件的组合，典型的两种压弯构件如图所示。

同其他构件一样，压弯构件也需同时满足正常使用及承载能力两种极限状态的要求，即正常使用极限状态：刚度条件;承载能力极限状态：强度、整体稳定、局部稳定.(2) 类型与截面形式单向压弯构件: 只绕截面一个形心主轴受弯；双向压弯构件: 绕两个形心主轴均有弯矩作用。

弯矩由偏心轴力引起的压弯构件也称作偏压构件。

截面形式：同轴心受力构件一样，分实腹式截面与格构式截面。

实腹式：型钢截面与组合截面格构式：缀条式与缀板式☻按截面组成方式分为型钢（a、b），钢板焊接组合截面型钢（c、g），组合截面（d、e、f、h、i）☻按截面几何特征分为开口截面，闭口截面（g、h、i、j）☻按截面对称性分为单轴对称截面（d、e、f、n、p），双轴对称截面（其余各图）☻按截面分布连续性分为实腹式截面（a～j）格构式截面（k～p）(3)破坏形式强度破坏、整体失稳破坏和局部失稳破坏。

强度破坏：截面的一部分或全部应力都达到甚至超过钢材屈服点的状况。

整体失稳破坏：单向压弯构件：弯矩平面内失稳：极值失稳，应考虑效应（二阶效应）。

弯矩平面外失稳：弯扭变形，分岔失稳。

双向压弯构件：一定伴随扭转变形，为分岔失稳。

7.2.1 强度计算两个工作阶段，两个特征点。

弹性工作阶段：以边缘屈服为特征点（弹性承载力）；弹塑性工作阶段：以塑性铰弯矩为特征点（极限承载力）。

7.2.2 极限承载力与相关条件联立以上两式，消去η，则有如下相关方程7.2.3 为计算方便，改用线性相关方程, 得《规范》公式 :关于±号的说明：如右图所示对于单对称截面，弯矩绕非对称轴作用时，会出现图示两种控制应力状况。

7.2.4 刚度条件:一般情况，刚度由构件的长细比控制，即：7.3.1 概述实腹式压弯构件在轴力及弯矩作用下，即可能发生弯矩作用平面内的弯曲失稳，也可能发生弯矩作用平面外的弯曲扭转失稳（类似梁）。

程序工型单，双向（轴压，压弯）梁柱工型（轴压、压弯）构件验算（腹板失稳）工型截面斜撑计算工型截面（贴板）斜撑计算箱形单、双向（轴压，压弯）梁柱箱形截面斜撑计算T形截面斜撑计算无侧移框架柱计算长度有侧移框架柱计算长度柱顶可移动但不转动的双阶柱计算长度系数H型梁整体稳定系数φb计算（双轴对称）地震反映谱曲线组合梁计算钢梁受扭计算格构式双工截面参数计算(I I)实腹式双工截面参数计算（十字）实腹式工型组合截面参数计算(|—I)箱型(工型帖板)截面参数计算简支梁温度变化引起内力格构式钢管砼柱(上下砼柱）计算高强度螺栓连接圆形烟囱基础底角锚栓计算风振系数计算结构自振周期计算偏心支撑耗能梁段净长度计算高层建筑钢结构舒适感验算圆钢管砼构件
说明：计算程序工作表保护密码：
1。

钢结构拉压弯承载力计算钢结构拉压弯承载力计算是指在钢材受到拉力、压力和弯曲力时，其能够承受的最大荷载的计算。

这种计算对于设计和施工钢结构非常重要，旨在确保结构的安全性和可靠性。

本文将介绍钢结构拉压弯承载力的计算方法和相关因素。

钢结构拉弯和压弯承载力的计算方法如下：1.拉弯承载力计算：钢结构受到拉力作用时，其拉弯承载力由公式计算：P=A*Fy其中，P为拉弯承载力，A为钢材的横截面积，Fy为钢材的屈服强度。

2.压弯承载力计算：钢结构受到压力作用时，其压弯承载力由公式计算：P=A*Fc其中，P为压弯承载力，A为钢材的横截面积，Fc为钢材的抗压强度。

需要注意的是，在实际应用中，两种作用可能同时存在，钢材既受到拉力也受到压力，这时需要按照相关标准和规范计算结合作用下的承载力。

对于弯曲作用下的承载力计算，需要考虑横截面形状和尺寸的影响。

常用的弯曲承载力计算方法有弯矩强度计算和抗弯强度计算。

弯矩强度计算方法根据钢材的截面形状和尺寸，计算得到其能够承受的最大弯矩。

最常用的弯矩强度计算公式是欧拉公式：M=σ*S其中，M为弯矩，σ为应力，S为截面模量。

应力可以通过弯矩和截面模量之间的关系计算得到。

抗弯强度计算方法是根据钢材在受到弯曲力作用下的强度特性，计算得到其能够承受的最大弯矩。

常用的抗弯强度计算公式是：M = W * fy其中，M为弯矩，W为截面模量，fy为抗弯强度。

除了横截面形状和尺寸，钢材的材料性质也会对拉压弯承载力产生影响。

常见的钢材材料性质参数有屈服强度、抗拉强度、抗压强度和抗弯强度。

这些参数需要根据钢材的材料型号和牌号提供的数据进行获取。

总之，钢结构的拉压弯承载力计算是钢结构设计和施工过程中非常重要的一部分。

计算过程需要考虑钢材的受力情况、横截面形状和尺寸以及材料性质参数等因素。

通过科学合理的计算，可以确保钢结构的安全性和可靠性。

压弯构件的计算长度
在进行压弯构件刚度和稳定计算时，都要用到长细比，计算构件的长细比需要知道构件的计算长度。

计算长度的物理意义是把不同支承情况的轴心压杆等效为两端铰支轴心压杆的长度，它的几何意义则是代表构件弯曲屈曲后弹性曲线两反弯点间的长度。

对独立的压弯构件，其计算长度与轴心受压构件一样根据构件两端的支承情况取用。

单层或多层框架结构，根据其荷载情况及传力路线，设计中常可以把它看成许多相互连系的平面框架。

平面框架柱在框架平面外的计算长度，取侧向支承点间的距离。

这些支承点包括柱的支座、纵向连系梁、单层厂房中的吊车梁、托架和纵向支撑等与平面框架的连接节点。

在框架平面内，若按未变形的框架计算简图作一阶内力分析，在求得各柱中的内力(弯矩轴力和剪力)后，将各杆看作单独的压弯构件进行计算。

若在框架分析中采用考虑变形影响的二阶分析，在计算构件稳定性时就可直接采用构件的几何长度。