当前位置：文档之家 › 小船渡河问题专题分析优秀课堂

小船渡河问题专题分析优秀课堂

  • 格式：ppt
  • 大小：2.92 MB
  • 文档页数：30

下载文档原格式

  / 30

合集下载

5.2 专题：小船渡河问题 课件— 高一下学期物理人教版(2019)必修第二册

5.2 专题：小船渡河问题 课件— 高一下学期物理人教版(2019)必修第二册
2
3
=
1

3
解析：如图所示，当小船在静水中的速度v2与其在河
流中的速度v垂直时，小船在静水中的速度v2最小，故

2
有 2 = 1 , =

3
=
3
解得 2
3
=
3
1 ,故选C。
2
二、随堂练习
9．如图所示，有一条两岸平直、河水均匀流动的河，甲、乙两只小船以相同的速度渡
河，乙船运动轨迹为图中AB，而甲船船头始终指向对岸，已知AB连线与河岸垂直，河
B．甲图航线过河时，船在垂直于河岸方向的速度最大，所以过河时间最短，故B正确；
D．船沿乙图航线航行，
> ，船垂直于河岸过河，位移大小等于河宽，最小；船
船
沿戊图所示航线航行， < ，当划船速度 方向与合速度 方向垂直时，航线
合
船
船
与河岸M的夹角最大，过河位移最小，故D正确。
故选BD。
二、随堂练习
渡河所用时间为t1;周瑜从后面追赶，船头垂直于AB，船在静水中的速度为v2，也从A
沿直线运动到B，渡河所用时间为t2，若AB与河岸的夹角为α，河水速度恒定。则下
列表达式成立的是（

A．

= sin α

B．

）。
=



C．

= cos α
2

D．

=


二、随堂练习
C．只有甲船速度大于水流速度时，不论水流速v0如何改变，只要适当改变θ角，甲船
都可能到达河的正对岸A点，故C错误；
D．若仅是河水流速v0增大，则两船到达对岸时间不变，根据速度的分解，船在水平

5.2小船渡河专题课件—人教版高中物理必修第二册

5.2小船渡河专题课件—人教版高中物理必修第二册
图4 ②若v水>v船，如图乙所示，从出发点A开始作矢量v水， 再以v水末端为圆心，以v船的大小为半径画圆弧，自出发 点A向圆弧作切线即为船位移最小时的合运动的方向． 这时船头与河岸夹角θ满足cos θ＝ ，最短位移x短＝ .
5.2 小船渡河专题 课件— 2020-2021学年【新教材】人教版（ 2019） 高中物 理必修 第二册
(3)当水流速度v2′＝6 m/s时，则水流速度大于船在静 水中的速度v1＝5 m/s，不论v1方向如何，其合速度方 向总是偏向下游，故不能垂直河岸渡河．
背：1.要使船垂直于河岸横渡，即路程最短，应使v船 在水流方向的分速度和水流速度等大、反向，这种情况 只适用于v船>v水时．
2.要区别船速v船及船的合运动速度v合，前者是发动机 (或划行)使船在静水中产生的速度，后者是合速度．
(1)欲使船渡河时间最短，船应怎样渡河？最短时间是多 少？船经过的位移多大？
(2)欲使船航行距离最短，船应怎样渡河？渡河时间多长 ？
5.2 小船渡河专题 课件— 2020-2021学年【新教材】人教版（ 2019） 高中物 理必修 第二册
5.2 小船渡河专题 课件— 2020-2021学年【新教材】人教版（ 2019） 高中物 理必修 第二册
5.2 小船渡河专题 课件— 2020-2021学年【新教材】人教版（ 2019） 高中物 理必修 第二册
例2：已知某船在静水中的速度为v1＝5 m/s，现让船渡 过某条河，假设这条河的两岸是理想的平行线，河宽为 d＝100 m，水流速度为v2＝3 m/s，方向与河岸平行．
(1)欲使船以最短时间渡河，渡河所用时间是多少？ 位移的大小是多少； (2)欲使船以最小位移渡河，渡河所用时间是多少？ (3)若水流速度为v2′＝6 m/s，船在静水中的速度为 v1＝5 m/s不变，船能否垂直河岸渡河？

小船渡河问题专题分析优秀PPT课件

小船渡河问题专题分析优秀PPT课件

合运动是实际发生的运动，是分运动的合成
合分
运运 动动
分运动互不影响，具有独立性
与
运
合运动与分运动所用时间相等，具有等时性
动 的 合 成 和 分 解
成运 和动 分的 解合
分运动
运动的合成 运动的分解
平行四边形法则
合运动
两个互 相垂直 的直线 运动的 合运动
可以是直线运动 也可以是曲线运动
曲线运动可以用两 个直线运动来替代
V船 V船
V合
d
V合 θ
V水
小船渡河问题 ②渡河的最短位移 v船 < v水的情况
B
v船
θ
上游 A
E
smin θ vD v船
θ
v水 O C
d
下游
SUCCESS
THANK YOU
2020/3/12Fra bibliotek问题3：拉船靠岸问题
【例3】如图，人在岸边通过定滑轮用绳拉小船。
人拉住绳子以速度v0匀速前进，当绳子与水平方向成 θ角时，求小船的速度v。
V
θ
SUCCESS
THANK YOU
2020/3/12
小船渡河
在流动的河水中渡河的轮船的运动可分解 为两个运动：
假设轮船不开动，轮船随水流一起向下游 运动；
假设河水不流动，轮船相对河水的运动。
小船过河专题
小船在220m宽的河中横渡，水流速度为
v1＝2m/s，船在静水中的速度是v2＝4m/s，
求:
⑴如果要求船划到对岸航程最短，则船头应指 向什么方向？最短航程是多少？所用时间多 少？
v1 v
v2
【归纳】 此类问题的关键是： 1.准确判断谁是合运动，谁是分运动；实际运动

小船过河问题专题ppt课件

小船过河问题专题ppt课件

V船
V合
L
V水
问题2：位移最短 探究二：
不能
河宽L＝100 m，水速v水＝5 m/s，船在静水中的速度 v船＝3m/s，问：小船还能垂直过河吗？此种情况下 若使小船过河位移最短，应如何设计？
V船
V合
L
V水
Байду номын сангаас
问题2：位移最短 探究二：
不能
河宽L＝100 m，水速v水＝5 m/s，船在静水中的速度 v船＝3m/s，问：小船还能垂直过河吗？此种情况下 若使小船过河位移最短，应如何设计？
河宽L＝100 m，水速v水＝3 m/s，船在静水中的速度 v船＝5 m/s，问：船如何过河位移最短？此时船头方 向与岸所成角度为多少？
垂直过河
船头与上
位移最短
游岸成530
L
V船
V合
V θ
2
v V1
水
方法二：
sin
v 1
v水
3
v船 v船 5
问题2：位移最短 探究二：
不能
河宽L＝100 m，水速v水＝5 m/s，船在静水中的速度 v船＝3m/s，问：小船还能垂直过河吗？此种情况下 若使小船过河位移最短，应如何设计？
学习目标
• 1、明确运动的独立性及等时性的问题。 • 2、注意区别船速v船及船的合运动速度v合。 • 3、搞清船渡河的最短时间和最短位移。
重温基础
1、合运动与分运动特征： （1）运动的独立性； （2）运动的同时性； （3）运动的等效性。
2、运动合成与分解的法则：
平行四边形定则。
问题1：时间最短
河宽L＝100 m，水速v水＝3 m/s，船在静水中的速度 v船＝5 m/s，让船头与岸垂直出发，小船能否行驶到 河正对岸？求小船过河的时间为多少？

小船渡河优秀教案中班

小船渡河优秀教案中班

小船渡河优秀教案中班教案标题：小船渡河优秀教案（中班）教案目标：1. 帮助幼儿理解并掌握小船渡河的基本概念和技巧。

2. 培养幼儿的合作意识和团队合作能力。

3. 培养幼儿的观察力、思考力和解决问题的能力。

教学重点：1. 掌握小船渡河的基本规则和技巧。

2. 培养幼儿的团队合作能力。

3. 培养幼儿的观察力和解决问题的能力。

教学准备：1. 小船模型或图片。

2. 河流模型或图片。

3. 小动物或玩具人物。

教学步骤：引入活动：1. 引导幼儿观察小船和河流的模型或图片，提问：“你们知道小船是如何渡过河流的吗？”2. 启发幼儿思考，鼓励他们提出自己的想法和解决方案。

探究活动：1. 将幼儿分成小组，每个小组给予一艘小船和数个小动物或玩具人物。

2. 在教师的引导下，让幼儿模拟小船渡河的情景，要求他们找出最佳的渡河方案。

3. 引导幼儿思考问题，例如：“小船上的动物太多了，怎么办？”、“小船可能会翻船吗？怎样才能保证安全？”4. 鼓励幼儿尝试不同的解决方案，让他们互相交流和合作，找到最佳的渡河策略。

总结活动：1. 引导幼儿回顾整个活动过程，让他们分享自己的体会和心得。

2. 提醒幼儿渡河时需要注意的安全问题，例如不要过载、平衡好重心等。

3. 结合幼儿的回答，总结小船渡河的基本规则和技巧。

拓展活动：1. 提供更多的小船和小动物，让幼儿自由组合进行渡河活动。

2. 将河流模型放在户外或大型游戏区域，让幼儿进行真实的小船渡河体验。

3. 引导幼儿设计自己的渡河游戏规则，并与其他小组分享。

教学延伸：1. 在日常生活中，引导幼儿观察和思考渡河的场景，例如通过桥梁、跳石头等方式。

2. 鼓励幼儿在户外环境中进行团队合作活动，例如搭建简易的桥梁或过河设施。

教学评估：1. 观察幼儿在活动中的参与程度和表现，包括合作、观察和解决问题的能力。

2. 收集幼儿的作品和记录，评估他们对小船渡河规则和技巧的理解和运用能力。

教学反思：1. 教师应根据幼儿的实际情况和表现，适当调整教学步骤和引导方式。

《小船渡河问题》课件

《小船渡河问题》课件
感谢观看
当船速和水速垂直时，实际航线偏离最小，此时渡河时间最短。
03
渡河问题的解决方案
船头垂直于河岸渡河
船头垂直于河岸时，船的合速度方向即为船头指向，与河岸垂直。此时，船渡河时 间最短，但船的位移不是最小。
船渡河时间等于河宽除以船在静水中的速度。
船的位移等于船在静水中的速度与水流速度的合速度在垂直于河岸方向上的投影。
科学实验中的应用
物理实验
在流体力学实验中，渡河问题常常被用来模拟和研究流体动力学现象，如水流的阻力、流速等问题。
生物学实验
在生态学研究中，渡河问题也被用来模拟和研究物种迁移、基因传播等现象，帮助科学家理解生物多 样性的形成和演化。
05
小船渡河问题的思考与启示
小船渡河问题中的哲学思考
自然规律的客观性
水速对渡河的影响
水速越大，实际航线偏离越少
当水速大于船速时，船头斜向下游，实际航线偏离越少。
水速越小，实际航线偏离越多
当水速小于船速时，船头垂直河岸，实际航线偏离越多。
船速与水速的相互作用
船速与水速相等时，船头方向任意
当船速和水速相等时，船头方向可以任意选择，渡河时间不变。
船速与水速垂直时，实际航线偏离最小
战术部署
在军事行动中，渡河点常常成为重要 的战术支点。通过控制渡河点，可以 有效地分割敌军，实现各个击破。
日常生活中的应用
竹筏等水上工具的使 用，使得人们可以方便地渡过河 流。
救援行动
在洪涝灾害等紧急情况下，渡河 成为救援人员和受困群众的重要 通道，及时的救援可以大大降低 灾害损失。
船的渡河位移和时间都介于船 头垂直于河岸和船头斜向下游 之间。
在这种情况下，船的位移和时 间都大于船头垂直于河岸渡河 的情况。

高考小船渡河问题专题解析

小船渡河问题小船渡河是典型的运动的合成问题。

需要理解运动的独立性原理，掌握合速度与分速度之间的关系。

小船在有一定流速的水中过河时，实际上参与了两个方向的分运动，即随水流的运动v 水（水冲船的运动），和船相对水的运动v 船（即在静水中的船的运动），船的实际运动v 是合运动。

小船渡河两种情况：①船速大于水速；②船速小于水速。

两种极值：①渡河最小位移；②渡河最短时间。

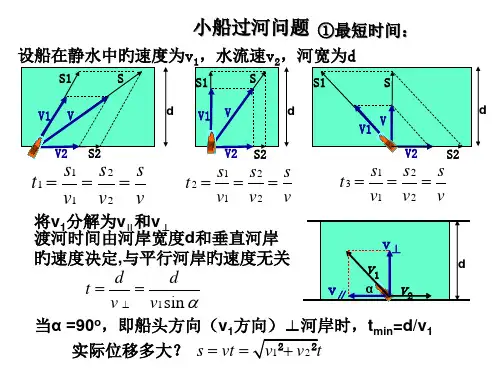
1、v 水<v 船时间最少在河宽、船速一定时，在一般情况下，渡河时间θυυsin 1船ddt == ，显然，当︒=90θ时，即船头的指向与河岸垂直，渡河时间最小为船v d，合运动沿v 的方向进行。

位移最小结论船头偏向上游，使得合速度垂直于河岸，位移为河宽，偏离上游的角度为船水υυθ=cos2、v 水>v 船 时间最少 同前 位移最小不论船的航向如何，总是被水冲向下游，即无论向哪个方向划船都不能使船头垂直于河，只能尽量使船头不那么斜。

那么怎样才能使漂下的距离最短呢？如图所示，设船头v 船与河岸成θ角。

合速度v 与河岸成α角。

可以看出：α角越大，船漂下的距离x 越短，那么，在什么条件下α角最大呢？以v 水的矢尖为圆心，v 船为半径画圆，当v 与圆相切时，α角最大，根据水船v v =θcos 船头与河岸的夹角应为水船v v arccos =θ，船沿河漂下的最短距离为：θθsin )cos (min 船船水v dv v x ⋅-=此时渡河的最短位移：船水v dv ds ==θcos 典型例题★某人以不变的速度垂直对岸游去，游到中间，水流速度加大，则此人渡河时间比预定时间A ．增加B ．减少C ．不变D ．无法确定 答案：C★某人以一定速度始终垂直河岸向对岸游去，当河水匀速流动时，他所游过的路程，过河所用的时间与水速的关系是( )A ．水速大时，路程长，时间长B ．水速大时，路程长，时间短C ．水速大时，路程长，时间不变D ．路程、时间与水速无关 答案: C★如图所示，A 、B 为两游泳运动员隔着水流湍急的河流站在两岸边，A 在较下游的位置，且A 的游泳成绩比B 好，现让两人同时下水游泳，要求两人尽快在河中相遇，试问应采用下列哪种方法才能实现？（ ）A. A 、B 均向对方游（即沿虚线方向）而不考虑水流作用B. B 沿虚线向A 游且A 沿虚线偏向上游方向游C. A 沿虚线向B 游且B 沿虚线偏向上游方向游D. 都应沿虚线偏向下游方向，且B 比A 更偏向下游 答案：A★★一条自西向东的河流，南北两岸分别有两个码头A 、B ，如图所示．已知河宽为80 m ，河水流速为5 m/s ，两个码头A 、B 沿水流的方向相距100 m ．现有一只船，它在静水中的行驶速度为4 m/s ，若使用这只船渡河，且沿直线运动，则( )A ．它可以正常来往于A 、B 两个码头 B ．它只能从A 驶向B ，无法返回C ．它只能从B 驶向A ，无法返回D ．无法判断 答案：B★在抗洪抢险中，战士驾驶摩托艇救人，假设江岸是平直的，洪水沿江向下游流去，水流速度为v 1，摩托艇在静水中的航速为v 2，战士救人的地点A 离岸边最近处O 的距离为d ，如战士想在最短时间内将人送上岸，则摩托艇登陆的地点离O 点的距离为( )A ．21222υυυ-d B ．0 C ．21υυd D ．12υυd答案：C★某人横渡一河流，船划行速度和水流动速度一定，此人过河最短时间为了T 1；若此船用最短的位移过河，则需时间为T 2，若船速大于水速，则船速1v 与水速2v 之比为（ ） (A)21222T T T - (B)12T T (C) 22211T T T - (D)21T T 答案：A★小船在s=200 m 宽的河中横渡,水流速度是2 m/s,船在静水中的航行速度为4 m/s.求: （1）小船渡河的最短时间.（2）要使小船航程最短,应该如何航行? 答案 （1）50 s 2）船速与上游河岸成60°★★一条河宽100米，船在静水中的速度为4m/s ，水流速度是5m/s ，则（ ）A ．该船可能垂直河岸横渡到对岸B ．当船头垂直河岸横渡时，过河所用的时间最短C ．当船头垂直河岸横渡时，船的位移最小，是100米D ．当船横渡时到对岸时，船对岸的最小位移是100米 答案： B★★河宽d ＝60m ，水流速度v 1＝6m ／s ，小船在静水中的速度v 2=3m ／s ，问： (1)要使它渡河的时间最短，则小船应如何渡河?最短时间是多少? (2)要使它渡河的航程最短，则小船应如何渡河?最短的航程是多少?答案：（1）20s （2）小船的船头与上游河岸成600角时，最短航程为120m★★小河宽为d ，河水中各点水流速度大小与各点到较近河岸边的距离成正比，dv k kx v 04==，水，x 是各点到近岸的距离，小船船头垂直河岸渡河，小船划水速度为0v ，则下列说法中正确的是（ ） A 、小船渡河的轨迹为曲线 B 、小船到达离河岸2d处，船渡河的速度为02v C 、小船渡河时的轨迹为直线D 、小船到达离河岸4/3d 处，船的渡河速度为010v 答案：A★如图所示，小船从A 码头出发，沿垂直河岸的方向划船，若已知河宽为d ，划船的速度v 船恒定. 河水的流速与到河岸的最短距离x 成正比，即）其中k 为常量。

小船过河及关联速度分解题省名师优质课赛课获奖课件市赛课一等奖课件


V1 V
α
d
V
V1
α
α
V2 S2
V2
cosα=v2/v1=2/4,
cosα=v1/v2=1/2,
α=60o,即航向与岸成60o 航向与岸成60o
tsd vv
d v12 - v22
100 3
3
S min v2 d 400m v1
经典例题2
（5）船按AB、AC航线分别渡河，哪样走用时多？ （6）船头按AB、AC航线分别渡河，哪样走用时多？ （7）在过河时间至少情况下，在行驶到河中间时，水
(1).当小船旳船头正对岸时,它将何时、何地到达对岸? (2).要使小船到达正对岸,应怎样行驶?耗时多少? (3).小船怎么样过河时间最短? 按(1)渡 (4).小船怎么样过河位移最小? 按(2)渡 若V船=2m/s，V水=4m/s情况怎么样？
S1
S
S1
S
S
V1 V
d
V2 S2
t=t1=d/v1=200/4=50s S2=v2t=2*50=100m 正对岸下游100米处
流速度忽然增大，过河时间怎样变化？ （8）为了垂直到达河对岸，在行驶到河中间时，水流
速度忽然增大，过河时间怎样变化？
B C
Aα
拉船问题(连带运动问题)
例1：如图，车拉船运动，车速为v ，当绳与水平方向成α时，
船速v’是多少？
v
研究对象：绳与船接触旳点。 原因：此点既在绳上又在船上。 在船上，是实际运动（合运动）。 在绳上，同步参加两个分运动。
t d d
v v1sin
v⊥
v1 v∥ α v2
d
当α =90o，即船头方向（v1方向）⊥河岸时，tmin=d/v1

5.2小船渡河专题教学课件—2021学年(最新)人教版(2019)高中物理必修第二册


m.
(2)当船的实际速度方向垂直于河岸时，船的位移最小，因
船在静水中的速度为v1＝5 m/s，大于水流速度v2＝3 m/s，故 可以使船的实际速度方向垂直于河岸．如图乙所示，设船斜
指向上游河对岸，且与河岸所成夹角为θ，则有v1cos θ＝v2
，
，则
，船的实际速度
大小为v＝v1sin θ＝5×0.8 m/s＝4 m/s，
(1)由题意知，当船在垂直于河岸方向上的分速度最大时
，渡河所用时间最短，河水流速平行于河岸，不影响渡河
时间，所以当船头垂直于河岸渡河时，所用时间最短，最
短时间为t＝
s＝20 s.
如图甲所示，当船到达对岸时，船沿平行于河岸方向也发
生了位移，由几何知识可得，船的位移大小为l＝
由题意可得x＝v2t＝3×20 m＝60 m，代入得
所用的时间为
.
(3)当水流速度v2′＝6 m/s时，则水流速度大于船在静 水中的速度v1＝5 m/s，不论v1方向如何，其合速度方 向总是偏向下游，故不能垂直河岸渡河．
背：1.要使船垂直于河岸横渡，即路程最短，应使v船 在水流方向的分速度和水流速度等大、反向，这种情况 只适用于v船>v水时．
2.要区别船速v船及船的合运动速度v合，前者是发动机 (或划行)使船在静水中产生的速度，后者是合速度．
例2：已知某船在静水中的速度为v1＝5 m/s，现让船渡 过某条河，假设这条河的两岸是理想的平行线，河宽为 d＝100 m，水流速度为v2＝3 m/s，方向与河岸平行．
(1)欲使船以最短时间渡河，渡河所用时间是多少？ 位移的大小是多少；
(2)欲使船以最小位移渡河，渡河所用时间是多少？ (3)若水流速度为v2′＝6 m/s，船在静水中的速度为 v1＝5 m/s不变，船能否垂直河岸渡河？

小船渡河问题分析(实用)

A.减少 B.不变 C.增加 D.无法确定
（满分样板 12分） 河宽L＝300 m， 水速u＝1 m/s，船在静水中的速度v＝3 m/s，欲分别 按下列要求过河时，船头应与河岸成多大角度？过 河时间是多少？
（1）以最短时间过河； （2）以最小位移过河； （3）若船速为v＝ 1m/s，水速u＝3 m/s，以最 小位移渡河
小船渡河问题详解
小船渡河问题分支
渡河的最 短时间
渡河的最 短位移
小船渡河 问题
Ø 小船过河问题 分析： 船渡河时，小船的实际运动可看做，
随水以水的速度 v水 漂流的运动，和以船速 V 船 相对于静水的划行运动的合运动。
Ø 具体分析：
河宽d,静水中船速 V 船 水流速度 V水 ，
船速与河岸的夹角为θ。
L θ
L θ
sinθ＝
1－cos2θ
＝
22 3
L 渡河时间为 t＝vsin
＝3×30s0in
s≈106.4 s．
2. 船在静水中的航速为v1，水流的速度为v2.为使船行驶到河正 对岸的码头，则v1相对v2的方向应为( )
解析：为使船行驶到正对岸，必须使v1、v2的合速度方向指 向正对岸，只有C图象正确． 答案： C
小船在静水中速度为v，今小船要渡 过一条小河，船在行驶过程中，船头始终与河岸垂
直.若航行到河中间时，水流速度增大，则渡河时间 与预定的时间相比（ ）
速的比值
tmin d / v船
渡河的最短位移
v船 > v水的情况
v船
v合
θ v船 > v水,
d v水
②渡河的最短位移
v船 < v水的情况
B
v船
θ 上游 A
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
25
v船
v合
d
θ
v水
26
4、水流的速度为V水，为使船沿AB方向 渡河，船相对于静水的最小速度是多少？ AB与河岸的夹角为θ。
B
V合
d
θ
A
V水
27
B
V 船最小
V合
d
θ
A
V水
28
例2、岸上的拖车以恒定的水平速 度V0通过绳子牵引轮船，当牵引船 的绳子与水平方向的夹角为θ，问 此时轮船的瞬时速度为多大？
实际发生的运动就叫做那几个运动的合运动，那几 个运动叫做这个实际运动的分运动。 ２、合运动和分运动的关系 等效性、独立性、等时性 二、运动的合成和分解 １、遵循平行四边形法则 ２、两个直线运动的合成可以是直线运动，也可以是 曲线运动。
23
合运动是实际发生的运动，是分运动的合成
合分 运运 动动
与
分运动互不影响，具有独立性
5
小船渡河 在流动的河水中渡河的轮船的运动可分解为 两个运动： 假设轮船不开动，轮船随水流一起向下游运 动； 假设河水不流动，轮船相对河水的运动。
6
小船过河专题
小船在220m宽的河中横渡，水流速度为v1 ＝2m/s，船在静水中的速度是v2＝4m/s，求: ⑴如果要求船划到对岸航程最短，则船头应指 向什么方向？最短航程是多少？所用时间多 少？ ⑵如果要求船划到对岸时间最短，则船头应指 向什么方向？最短时间是多少？航程是多少？
4、运动分解的一般原则：
通常根据运动的实际效果来确定两个分运动的方向。
4
三：互成角度的两个分运动的合成
1、如果两个分运动都是匀速直线运动，合运动一定 是匀速直线运动。
2、如果一个分运动是匀速直线运动，另一个分运动 是匀变速直线运动，且互成角度，合运动一定是匀 变速曲线运动。
（可见，两直线运动的合运动不一定是直线运动）。
?= 60°
v=
v
2 2
- v12
=
422-
2m/s =
12m / s
过河时间
d 220
t = = s = 57.7s
v 12
9
总结：渡河的最短位移大小就是河宽，但是实 现这一最短位移，必须满足船在静水的速度大于 河水的速度。
v船
v合
d
θ
v水
10
（2）如果要求船划到对岸时间最短，则船头 应指向什么方向？最短时间是多少？航程是多 少？
6 . 2 质点在平面内的运动 第2课时
1
基础重温
一、合运动与分运动 1、定义：
如果物体同时参与了几个运动，那么物体实际发 生的运动就叫做那几个运动的合运动，那几个运动叫 做这个实际运动的分运动。
2、特征：
（1）运动的独立性； （2）运动的同时性； （3）运动的等效性。
2
基础重温
二、运动的合成与分解
运
合运动与分运动所用时间相等，具有等时性
动 的 合 成 和 分 解
成运 和动 分的 解合
分运动
运动的合成 运动的分解
平行四边形法则
合运动
两个互 相垂直 的直线 运动的 合运动
可以是直线运动 也可以是曲线运动
曲线运动可以用两 个直线运动来替代
24
小船过河时的运动情况和蜡块在玻璃管中的运动 基本是相同的．首先小船过河时它会有一个自己的运 动速度，当它开始行走的时候，同时由于水流的作用， 它要顺着水流获得一个与水的运动速度相同的速 度．小船自己的速度一般是与河岸成一定角度的，而 水流给小船的速度却是沿着河岸的．所以小船实际的 运动路径是这两个运动合成的结果。而合速度的大小 取决于这两个速度的大小和方向．而小船渡河的时间 仅与小船自身的速度有关，与水流的速度是没有关系 的。
20
v1 v
v2
21
随堂反馈
如图，以速度 v沿竖直杆匀速下滑的物体 A，用细绳
通过定滑轮拉动物体 B在水平桌面上运动，当绳与水
平面夹角为 θ时，物体 B的速率为
。
B
?
v
寻找分运动效果
【答案】 vB=vsinθ
A
v sin?
v
22
小结
一、合运动和分运动 １、概念：如果物体同时参与了几个运动，那么物体
1、定义：
由已知的分运动求跟它们等效的合运动的过程叫 做运动的合成。由已知的合运动求跟它等效的分运动 的过程叫做运动的分解。
2、运动合成与分解的法则：
平行四边形定则。
3
基础重温
二、运动的合成与分解
3、运动合成的特例： 若两个分运动在同一直线上时： 运动合成前一般先要规定正方向，然后确定各分
运动的速度、加速度和位移等矢量的正、负，再求代 数和。
B
C
v船
v合
Aθ
v水
d
13
上题中，如果水速V水=4m/s，船在静 水中的速度V船=2m/s，结果如何呢？
如果河水的速度大于船在静水的速度时，这 时船不可能垂直渡河，但仍存在最短位移，求 解的方法如下：
14
V船 V船
V合
d
V合 θ
V水
15
小船渡河问题
②渡河的最短位移
v船 < v水的情况
B
v船
θ 上游 A
E
smin θ
D
v
v船
θ
v水O C
d
下游
16
问题 3：拉船靠岸问题 【例 3】如图，人在岸边通过定滑轮用绳拉小船。 人拉住绳子以速度 v0匀速前进，当绳子与水平方向成 θ 角时，求小船的速度 v。
17
v1 v
v2
18
【归纳】 此类问题的关键是： 1.准确判断谁是合运动，谁是分运动； 实际运动是
V0
θA
29
V0
V
θ
30
分析２：时间最短
v2
v
d
v1
ห้องสมุดไป่ตู้
11
解２:当船头垂直河岸时，所用时间最短
最短时间
t ? d ? 220 s ? 50 s
v2
4
此时合速度
v=
v12
+v
2 2
=
224+ 2m / s =
20m / s
此时航程
x ==vt 20 ? 50m 224m
12
总结、渡河的时间最短则船头指向必须和河岸 垂直，不受河水速度大小的影响。
7
分析小船的运动
（1）如果要求船划到对岸航程最短，则船头应指向 什么方向？最短航程是多少？所用时间多少？
分析１：航程最短
v2 v
d
θ
v1
8
解：当船头指向斜上游，与岸夹角为 ? 时，合运 动垂直河岸，航程最短，数值等于河宽 220m 。
则cos ?
v
=
1
=
2
=
1
v2 4 2
即船头指向斜上游与岸夹角为 60°
合运动 2.根据运动效果寻找分运动； 3.一般情况下，分运动表现在： ①沿绳方向的伸长或收缩运动； ②垂直于绳方向的旋转运动。 4.根据运动效果认真做好 运动矢量图 ，是解题的关
键。 5.对多个用绳连接的物体系统，要牢记在 绳的方向
上各点的速度大小相等 。
19
随堂反馈 如图，汽车的速度 v0和 绳子与水平方向的夹角 θ 已知，求重物上升的速 度v。