结构力学龙驭球版 桁架习题
- 格式:ppt
- 大小:1.08 MB
- 文档页数:11


结构力学(高等教育出版社 龙驭球)考研模拟题专业课复习资料(最新版)封面1结构力学模拟试题一 1、 、(20 分)计算图示结构。
绘出梁式杆的弯矩图,并求二力杆的轴力。
已知:030 ,045 。
。
题 题 1 图 题 题 2 图 2、 、(18 分)计算图示刚架。
绘制弯矩图和剪力图。
3、 、(20 分)用力矩分配法计算图示刚架。
绘弯矩图,并求 C 支座的反力。
题 题 3 图 4、 、(18 分)连续梁的支座 A 和 B 均发生了支座位移如图。
试列出力法方程,求出方程中的系数和常数项。
(注意:不解方程) 题 题 4 图 5、 、(20 分)用位移法计算图示刚架。
绘出弯矩图。
2EI = 08题 题 5 图 图 6、 、(18 分)做图示梁 A 截面的弯矩 M A 、剪力 F QA 及 k 截面的弯矩 M k 影响线;已知可任意分布均布荷载集度 q=10kN/m,计算 F QA 的最大值,并注出相应的最不利荷载位置。
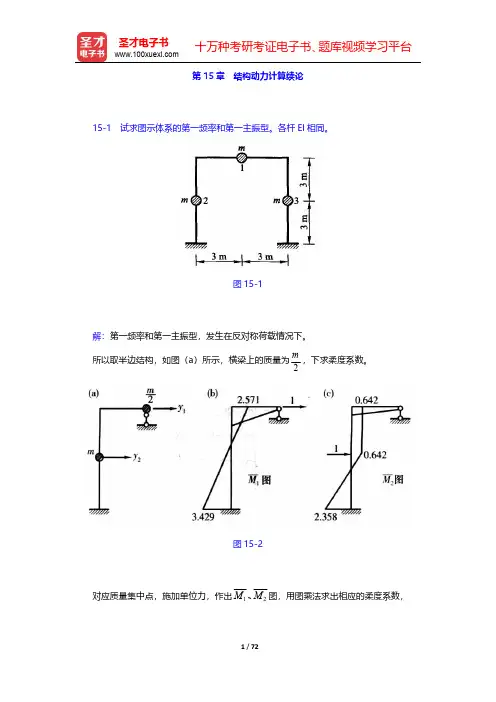
题 题 6 图 图7、 、(18 分)只考虑图示体系质点在铅垂方向振动。
计算质点的最大竖向位移和刚架顶铰 C 处的最大竖向位移。
已知: 0.4 ( 为结构自振频率),8.4kN F P ,3al4EIk , 38kN W ,各杆 EI 相同均为常数。
EIEIEI = 08m =3m 1EIm =m 2 题 题 7 图 题 题 8 图 8、 、(18 分)计算图示振动体系的自振频率和振型,并绘出振型图。
3结构力学模拟题二 一、是非题,对的画 ,错的打(( 每小题 1 分) 1. 除荷载外,其他因素例如温度变化、支座位移等会使超静定结构产生位移, 因而也就有可能使静定结构产生内力 。
( ) 2. 刚架中所有的结点都为刚结点。
( ) 3. 几何不变体系都为静定结构。
( ) 4. 力法中的基本结构为超静定结构。
( ) 5. 二元体是指由两根链杆联结一个新结点的装置( ) 6. 静定多跨梁由基本部分和附属部分组成。



第3章静定结构的受力分析一、判断题1.图3-1所示桁架杆件AB、AF、AG内力都不为零。
()[厦门大学2007研]图3-1【答案】错【解析】本题为静定结构,根据静定结构的性质:在荷载作用下,如果仅靠结构某一局部就能够平衡外荷载时,则仅此局部受力,其余部分没有内力。
知杆件AB、AF、AG内力都为零。
2.图3-2所示桁架,各杆EA为常数,仅AB杆有轴力,其他杆的轴力为零。
()[天津大学2007研]图3-2【答案】错【解析】本题是一对平衡力作用在超静定部分ADBC 上,故整个超静定部分ADBC 都会产生内力。
倘若本题为静定桁架,则只有AB 杆受力。
3.若某直杆段的弯矩为0,则剪力必定为0;反之,若剪力为0,则弯矩必定为0。
( )[中南大学2005研]【答案】错【解析】由弯矩和剪力的微分关系Q dMF dx可知,剪力为零,但弯矩不一定必为零。
比如,受纯弯曲的杆段。
二、选择题1.如图3-3所示结构在所示荷载作用下,其支座A 的竖向反力与支座B 的反力相比为( )。
[郑州大学2010研、哈尔滨工业大学2008研]A .前者大于后者B.二者相等,方向相同C.前者小于后者D.二者相等,方向相反图3-3【答案】B【解析】直接对C点列力矩方程∑M C=0即可判断。
2.图3-4所示结构,当高度h增加时,杆件1的内力()。
[南京理工大学2012研]A.增大B.减小C.不确定D.不变【答案】D【解析】根据K形结点的特性,因结构是对称的,荷载也是对称的,所以各杆件的内力是对称的,所以杆件1、2均为零杆,与结构高度h增加与否无关。
图3-43.图3-5所示对称三铰拱截面C的轴力已知为F NC=48kN(压),则矢高f应等于()。
[清华大学2003研]A.4m B.4.5m C.4.8m D.5m图3-5【答案】D【解析】先求得B支座竖向反力为50kN,后求出相应简支梁跨中弯矩为240kN·m,再用相应简支梁跨中弯矩除以轴力(水平推力)48kN,于是得到矢高f应等于5m。

第11章静定结构总论11.1复习笔记一、几何构造分析与受力分析之间的对偶关系1.从计算自由度W的力学含义和几何含义看对偶关系(1)W的几何含义W=各部件的自由度总数-全部约束数。
(2)W的力学含义W=各部件的平衡方程总数-未知力总数。
(3)根据W的数值,可对体系的静力特性得出下列结论①W>0,平衡方程个数大于未知力个数,体系不是都能维持平衡,体系为几何可变;②W<0,平衡方程个数小于未知力个数,体系如能维持平衡,体系有多余约束,是超静定的;③W=0,平衡方程个数等于未知力个数,考虑方程组的系数行列式D当D≠0,方程组有唯一解,体系几何不变且无多余约束;当D=0,方程组无解或有无穷多解,体系几何可变且有多余约束。
2.从W=0的一个简例看对偶关系(1)几何构造分析(图11-1(a))图11-1①α≠0(链杆1和2不共线)时,体系为几何不变,且无多余约束;②α=0(链杆1和2为共线)时,体系为几何可变(瞬变),且有多余约束。
(2)受力分析取结点C为隔离体(图11-1c),可写出两个投影平衡方程:F1cosα-F2cosα=F xF1sinct+F2sinoc=F y下面分为两种情况讨论①α≠0时(两根链杆1和2不共线)②α=0时(两根链杆共线)当荷载F y≠0时,方程组无解;如果考虑F y=0而只有水平荷载F x作用的特殊情况,此时解为:F1=F2+F x=任意值。
二、零载法1.零载法的作法表述对于W=0的体系,如果是几何不变的,则在荷载为零的情况下,它的全部内力都为零;反之,如果是几何可变的,则在荷载为零的情况下,他的某些内力可不为零。
2.零载法适用体系零载法是针对W=0的体系,用静力法来研究几何构造问题,用平衡方程的解的唯一性来检验其几何不变性的方法。
3.从虚功原理角度看零载法由于载荷为零,因此虚功方程左边只有一项Fx•△x=0(1)与F x相应的约束是非多余约束,△≠0,解得F=0;(2)与F x相应的约束是多余约束,△=0,则F等于任意值。

第3章静定结构的受力分析3.1 复习笔记本章详细论述了各类静定结构的受力分析过程与步骤,包括静定平面桁架、静定多跨梁、静定平面刚架、组合结构和三铰拱,介绍了隔离体的最佳截取方法,以及静定结构内力计算的虚位移法。
重视静定结构的基本功训练,有助于培养驾驭基本原理解决复杂问题的能力,为超静定结构的分析与求解打下坚实基础。
一、静定平面桁架桁架由杆件铰接而成,其杆件只承受轴力,杆件截面上应力分布均匀,主要承受轴向拉力和压力,因而能够充分发挥材料的作用,经常使用于大跨度结构中。
1.桁架的类别与组成规律(见表3-1-1)表3-1-1 桁架的类别与组成规律2.桁架杆件内力的求解方法(见表3-1-2)表3-1-2 桁架杆件内力的求解方法二、梁的内力计算的回顾1.截面内力分量符号规定如图3-1-1(图中所示方向为正方向)所示:(1)轴力以拉力为正;(2)剪力以绕微段隔离体顺时针转向为正;(3)在水平杆件中,当弯矩使杆件下部受拉(上部受压)时,弯矩为正。
图3-1-12.截面法(见表3-1-3)表3-1-3 截面法3.荷载与内力之间的微分关系(1)在连续分布的直杆段内,取微段dx为隔离体,如图3-1-2所示。
图3-1-2(2)由平衡条件导出微分关系为(Ⅰ)4.荷载与内力之间的增量关系(1)在集中荷载处,取微段为隔离体,如图3-1-3所示。
图3-1-3(2)由平衡条件导得增量关系为5.荷载与内力之间的积分关系如图3-1-4所示,结合式(Ⅰ)可得梁的内力积分公式,积分公式及其几何意义见表3-1-4。
图3-1-4表3-1-4 内力的积分公式及几何意义6.分段叠加法作弯矩图(1)分段叠加法步骤①求支反力:根据整体受力平衡求出支座反力;②选取控制截面:集中力作用点、集中力偶作用点的左右两侧、分布荷载的起点和终点都应作为控制截面;③求弯矩值:通过隔离体平衡方程求出控制截面的弯矩值;④分段画弯矩图:控制截面间无荷载作用时,用直线连接即可;控制截面间有分布荷载作用时,在直线连接图上还需叠加这一段分布荷载按简支梁计算的弯矩图。



《鱼儿力学求解器》习题册主编:刘龙《结构力学》龙驭球习题3-1(e)试用分段叠加法作下列梁的M图。
《鱼儿力学求解器》输入下列信息:总信息:4 3 1 1 3 0结点:1 0 0 0 0 1 2 2 0 1 1 1 3 4 0 1 0 1 4 6 0 1 1 1单元:1 1 2 1 2 2 3 1 3 3 4 1材料:1 1 1 1 0.083333 0自由度:结点荷:1 3 -2单元荷:1 1 2 -3 2 1 2 -3 3 1 2 -30.05秒内可得内力图:《结构力学》龙驭球习题3-8(d)试作图示三铰刚架的内力图。
《鱼儿力学求解器》输入下列信息:总信息:7 6 1 0 4 1结点:1 0 0 0 0 1 2 2.5 10 1 1 1 3 15 0 0 0 1 4 12.5 10 1 1 1 5 7.5 10 1 1 1 6 0 10 1 1 1 7 15 101 1 1单元:1 1 2 1 2 3 4 1 3 2 5 1 4 5 4 1 5 6 2 1 6 4 7 1材料:1 1 1 1 0.083333 0自由度:3 6结点荷:单元荷:3 1 5 -1 4 1 5 -1 5 1 2.5 -1 6 1 2.5 -10.05秒内可得内力图:《结构力学》龙驭球习题3-17(a)试用结点法或截面法求图示桁架各杆的轴力。
《鱼儿力学求解器》输入下列信息:总信息:8 13 1 3 0 18结点:1 0 0 0 0 1 2 6 0 0 0 1 3 0 4 1 1 1 4 3 4 1 1 1 5 6 4 1 1 1 6 0 8 1 1 1 7 3 8 1 1 1 8 6 8 11 1单元:1 1 2 1 2 1 4 1 3 2 4 1 4 2 5 1 5 1 3 1 6 3 4 1 7 4 5 1 8 3 7 1 9 5 7 1 10 5 8 1 11 3 6 1 12 6 7 1 13 7 8 1材料:1 1 1 1 0.083333 0自由度:1 3 1 6 2 3 2 6 3 3 3 6 5 6 4 6 6 3 6 6 7 6 8 3 8 6 9 3 9 6 12 6 13 6结点荷:5 1 -4 7 2 -8 8 1 -4单元荷:0.05秒内可得内力图:《结构力学》龙驭球习题3-27(a)用虚功原理求图示静定结构的内力图。
第4章影响线一、选择题1.超静定结构影响线的外形为()。
A.一定为曲线B.一定为折线C.可能为曲线,也可能为直线D.一定为直线【答案】C2.图4-1所示为截面剪力的影响线,求在图示荷载作用下剪力的大小()。
A.3/8(kN)B.7/8(kN)C.-3/8(kN)D.-7/8(kN)图4-1【答案】A【解析】当荷载为均布荷载时,利用影响线求量值就是均布荷载的集度乘以它所对应的影响线的面积(带正负号):。
二、填空题1.已知某量值S的影响线如图4-2(a),在给定的移动荷载(F P1=8kN,F P2=1kN,F P3=2kN)作用下,其最不利荷载位置为图___。
(填b、c、d或e)图4-2【答案】c【解析】最不利荷载位置即使荷载达到最大值时的位置。
S值为各荷载与影响线标值乘积之和,比较5个荷载布置,要使S最大,则8kN应处于顶端,即c图满足。
2.图4-3所示梁在移动荷载作用下,使M C达到最大的荷载位置是移动荷载中的___kN的力在___截面处。
A BC8m8m2m图4-3【答案】80;C【解析】在一组集中荷载作用下,要使其达到最值,必有一荷载在其影响线的最大值处(即C点),而且该荷载一般为其中的最大值即80kN。
3.图4-4所示结构在给定移动荷载作用下,截面A弯矩最大值为___。
图4-4【答案】72 Pa【解析】(1)设截面A弯矩以上部受拉为正,令一单位荷截在BD上移动。
(2)静力法。
作其M A的影响线(图4-5(a))。
图4-5(3)易知图示荷载中右边集中力作用在C点时M A达到最大值(图4-5(b))。
4.图4-6所示结构在均布荷载作用下,支座A右侧截面的剪力为___。
图4-6【答案】7qa/6【解析】利用影响线来求截面内力,先作出P=1直接作用在主梁上时支座A右侧截面的剪力Q A右的影响线,如图4-7所示。
图4-7然后作出间接荷载作用下Q A右的影响线,节点处用直线连接即可,如图4-8所示。
第6章力法6.1 复习笔记本章重点介绍了力法的原理以及如何运用力法对超静定结构在各种荷载作用下的内力和位移进行求解。
首先,从单次超静定结构到多次超静定结构,对力法的解题步骤进行了归纳并推导出了力法的典型方程;随后,论述了超静定结构超静定次数的判定方法,演示了刚架、排架、桁架、组合结构、对称结构在荷载作用以及支座移动和温度改变下的力法分析步骤,讨论了基于力法和虚功原理的超静定结构的位移计算思路;最后,强调了超静定结构计算中校核的重要性,以确保最终计算结构的准确性和可靠性。
一、力法的基本概念1.力法的基本未知量、基本体系和基本方程力法的基本概念,包括基本未知量、基本体系、基本结构以及基本方程见表6-1-1,此外,表中还归纳了超静定结构的力法分析步骤。
表6-1-1 力法的基本未知量、基本体系和基本方程2.多次超静定结构的力法分析(见表6-1-2)表6-1-2 多次超静定结构的力法分析步骤3.力法典型方程从一次超静定结构的力法分析到二次超静定结构的力法分析,可以发现一定的规律,那么具有n次超静定结构的力法典型方程归纳如下:式中,ΔiP表示由荷载产生的沿X i方向的位移;δij表示由单位力X j=1产生的沿X i=1方向的位移,常称为柔度系数,且δij=δji。
在解得多余未知力之后,超静定结构的内力可根据叠加原理计算如下:或根据结构受力平衡求解。
二、超静定次数的确定——力法的前期工作(见表6-1-3)表6-1-3 超静定次数的确定——力法的前期工作三、力法解超静定刚架和排架(见表6-1-4)表6-1-4 力法解超静定刚架和排架四、力法解超静定桁架和组合结构(见表6-1-5)表6-1-5 力法解超静定桁架和组合结构五、力法解对称结构(表6-1-6)表6-1-6 力法解对称结构。
第4章影响线4.1复习笔记一、移动荷载和影响线的概念1.移动荷载移动荷载作用点在结构上是移动的,研究移动荷载要确定荷载的最不利位置——即使结构某个内力或支座反力达到最大值的荷载位置。
2.影响线(1)表示单位移动荷载作用下内力变化规律的图形称为内力影响线;(2)影响线是研究移动荷载作用的基本工具。
二、静力法作简支梁内力影响线静定结构的内力或支座反力影响线有两种基本作法,静力法和机动法。
1.静力法概念静力法是以荷载的作用位置x为变量,通过平衡方程,从而确定所求内力(或支座反力)的影响函数,并作出影响线。
2.支座反力影响线图4-1-1(1)支座反力R A F 的影响线:对B 点取矩,R P ()A F l F l x ⋅=⋅-,影响线如图4-1-2(a)所示;(2)支座反力R B F 的影响线:对A 点取矩,R P B F l F x ⋅=⋅,影响线如图4-1-2(b)所示。
图4-1-23.剪力与弯矩影响线截面C 处的影响线:由于A 、B 的支座反力已经计入了移动荷载,可以作为已知条件,因此,为了避免再次计算移动荷载,可分两段进行计算:(1)当移动荷载在C 左边移动时,取BC 段计算,列平衡方程:Q R C B F F =-,R C B M F b =⋅;(2)当移动荷载在C 右边移动时,取AC 段计算,列平衡方程:Q R C A F F =,R C A M F a =⋅。
由图4-1-2叠加可得剪力和弯矩的影响线分别如图4-1-3与图4-1-4所示。
图4-1-3剪力影响线图4-1-4弯矩的影响线三、结点承载方式下梁的内力影响线对于某些结构,荷载不是直接作用在主梁上,而是通过纵梁的结点传递到主梁上,不管纵梁承受何种荷载,此时主梁只在横梁处承受集中力,因此主梁承受结点荷载。
1.结点荷载作用下的主梁影响线的作法(1)将单位荷载直接作用在主梁上,作出影响线;(2)从纵梁的各个结点引竖线与上一步作出的影响线相交;(3)从上一步得到各个交点,相邻交点间用直线连接,得到结点荷载下的静定梁的影响线。