东南大学2010传递过程原理试卷11

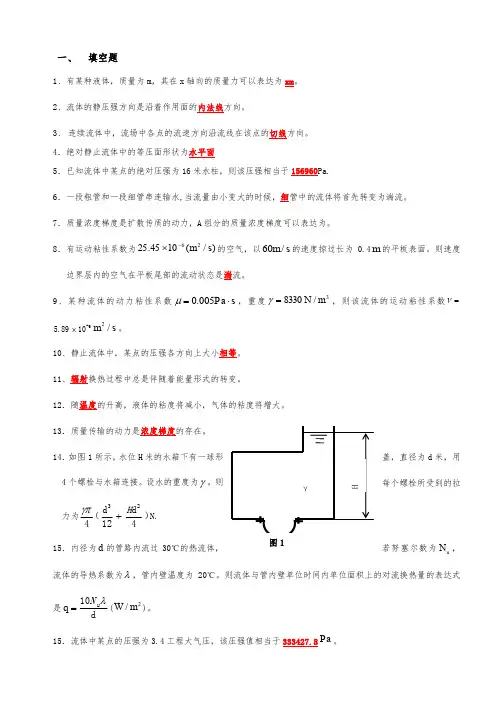
一、 填空题1、有某种液体，质量为m ，其在x 轴向的质量力可以表达为xm 。

2、流体的静压强方向是沿着作用面的内法线方向。

3、 连续流体中，流场中各点的流速方向沿流线在该点的切线方向。

4．绝对静止流体中的等压面形状为水平面5．已知流体中某点的绝对压强为16米水柱，则该压强相当于156960Pa.6789=ν.51011121314d 米，用415u N ，流体的导热系数为λ，管内壁温度为20℃。

则流体与管内壁单位时间内单位面积上的对流换热量的表达式是=q d10λu N (2/m W )。

15．流体中某点的压强为3.4工程大气压，该压强值相当于333427.8Pa 。

16．当=a -1/3时，流场y ax u x sin 3=，y x u y cos 2=才可以连续。

17．若有一灰体表面的黑度为0.8，当其表面温度为227℃时，辐射力的大小为2837.52/m W 。

18.当温度不变时,流体的体积随压强的变化而变化的特性称为流体的压缩性 20.流场中一条流线上某点的速度方向与流线在该点的切线重合。

21.流体流动可以分为两种流态，分别称为层流和湍流毕托管是一种用于测量流体中某点流速的仪器。

37.随着黑体温度的升高，其所辐射出去的射线中具有最大辐射力的波长会逐渐向短波区靠近。

38.一流体和固体壁面进行对流换热，已知壁面温度恒为90℃，流体主流温度为40℃，且壁面与流体间的平均对流换热系数h 为)/(2.02℃⋅m W 。

则紧贴壁面处，单位时间、单位面积上层流底层的导热量==0n dndTλ102/m W 。

39.密度为3/1000m kg =ρ，运动粘性系数为s m /10725-⨯=ν）的水在一平板上流动（如图1）。

如果1x x =处的速度分布是33y y v x -=。

则（1）在01==y x x ，点处的粘性切应力为0.212/m N 。

（2）在11==y x x ，mm 点处沿y 方向的粘性动量通量数值为+0.26912/m N（3）在11==y x x ，mm 点处沿x 方向的对流动量通量数值为3.002/m N40.一初始温度为T ℃的凸表面固体，被置于室温恒为sT 的大房间内。

传递过程原理复习题答案1. 传递过程原理中，质量传递系数K的单位是什么？答案：质量传递系数K的单位是m/s。

2. 在对流传热中，流体的雷诺数Re和普朗特数Pr分别代表什么？答案：雷诺数Re代表流体流动的惯性力与粘性力之比，普朗特数Pr代表流体的动量扩散系数与热扩散系数之比。

3. 描述扩散过程的基本方程是什么？答案：描述扩散过程的基本方程是菲克扩散第一定律，即J=-D(dC/dx)，其中J为质量通量，D为扩散系数，dC/dx为浓度梯度。

4. 在多孔介质中，流体流动的达西定律表达式是什么？答案：达西定律表达式为v=-K/μ(dP/dx)，其中v为流体流速，K 为渗透率，μ为流体的动力粘度，dP/dx为压力梯度。

5. 描述流体在管道内层流流动的哈根-泊肃叶方程是什么？答案：哈根-泊肃叶方程为ΔP=8μLQ/πr^4，其中ΔP为压力降，μ为流体的动力粘度，L为管道长度，Q为流量，r为管道半径。

6. 在热传递中，对流换热系数α与哪些因素有关？答案：对流换热系数α与流体的物理性质、流动状态、管道或物体的几何形状以及流体与物体表面之间的温差有关。

7. 描述流体在管道内湍流流动的科尔布洛赫方程是什么？答案：科尔布洛赫方程为f=0.079/Re^(1/4)，其中f为摩擦因子，Re为雷诺数。

8. 热传递的三种基本方式是什么？答案：热传递的三种基本方式是导热、对流和辐射。

9. 描述流体在管道内层流流动的哈根-泊肃叶方程与湍流流动的科尔布洛赫方程有何不同？答案：哈根-泊肃叶方程适用于层流流动，而科尔布洛赫方程适用于湍流流动。

层流流动时，流体的流动是有序的，摩擦因子与雷诺数的关系较为简单；湍流流动时，流体的流动是无序的，摩擦因子与雷诺数的关系更为复杂。

10. 在热传递中，辐射换热与对流换热有何不同？答案：辐射换热不依赖于流体的存在，可以在真空中进行，而对流换热需要流体作为热传递的介质。

辐射换热的速率与物体表面的温度的四次方成正比，而对流换热的速率与物体表面与流体之间的温差成正比。

传递过程原理习题解第一章1．粘性流体在圆管内作一维稳态流动。

设r 表示径向距离，y 表示自管壁算起的垂直距离，试分别写出r 和y 方向的，用“ （浓度梯度）（扩散系数）通量⨯-=” 表示的现象方程。

解：)dr du,u y (dy )u (d 为正↑↑+=ρντ )drdu,u y (dy)u (d 为负↓↑-=ρντ2．采用苯甲酸制成的圆管装水时，苯甲酸（组分A ）将在水（组分B ）中溶解。

试分别写出苯甲酸沿y 方向（自管至管中心方向）和r 方向（半径方向）的费克定律表达式。

苯甲酸在水中的扩散系数以D AB 表示。

解：)dyd ,y (Dy D D j AA A ABA 为负ρρρ↓↑-= )drd ,r (DyD D j AA A ABA 为负ρρρ↑↑=3．试根据牛顿粘性定律、傅立叶定律和费克定律表达式讨论动量传递、热量传递和质量传递三者之间的类似性。

解：从牛顿粘性定律、傅立叶定律和费克定律表达式可看出，它们均可表示为：（浓度梯度）（扩散系数）通量⨯-=⑴ 它们的扩散系数具有相同的因次，单位均为 m 2 ⑵ 传递方向与物理量梯度方向相反。

4．试证明现象方程（即牛顿粘性定律、傅立叶定律和费克定律表达式）中各式等号两侧的因次一致。

因次表示如下：质量 — M 、长度 — L 、时间 — θ、温度 — T 。

解：费克定律式表达式：DYD D j AABA ρ-= [左侧] sm kg⋅=2 [右侧] s m kg m m kg s m ⋅=⋅=232牛顿粘性定律表达式：()dyu d ρν-=τ [左侧] 222s m kgm m N ⋅== [右侧] 2232s m kgmm s m m kg s m ⋅=⋅⋅=傅立叶定律表达式式：()dyt c d A qp ρα-=[左侧] sm J⋅=2 [右侧] s m J m K K kg Jm kg s m ⋅=⋅⋅⋅⋅=2325．不可压缩流体在矩形截面的管道中作一维稳态层流流动，设管道宽度为2y 0，且b>>y 0，流道长度为L ，而端压力降为－ΔP ，试根据力的衡算导出：⑴ 剪应力τ随高度y （自中心至任意一点的距离）变化的关系式； ⑵ 管截面上的速度方程；⑶ 主体（平均）流道与最大流速的关系。

【1－1】试说明传递现象所遵循的基本原理和基本研究方法。

答：传递现象所遵循的基本原理为一个过程传递的通量与描述该过程的强度性质物理量的梯度成正比，传递的方向为该物理量下降的方向。

传递现象的基本研究方法主要有三种，即理论分析方法、实验研究方法和数值计算方法。

【1－2】列表说明分子传递现象的数学模型及其通量表达式。

【1－3】阐述普朗特准数、施米特准数和刘易斯准数的物理意义。

答：普朗特准数的物理意义为动量传递的难易程度与热量传递的难易程度之比；施米特准数的物理意义为动量传递的难易程度与质量传递的难易程度之比；刘易斯准数的物理意义为热量传递的难易程度与质量传递的难易程度之比。

【2－1】试写出质量浓度ρ对时间的全导数和随体导数，并由此说明全导数和随体导数的物理意义。

解：质量浓度的全导数的表达式为：d dx dy dzdt t x dt y dt z dt ρρρρρ∂∂∂∂=+++∂∂∂∂，式中t 表示时间 质量浓度的随体导数的表达式为x y z D u u u Dt t x y zρρρρρ∂∂∂∂=+++∂∂∂∂ 全导数的物理意义为，当时间和空间位置都发生变化时，某个物理量的变化速率。

随体导数的物理意义为，当观测点随着流体一起运动时，某个物理量随时间和观测点位置变化而改变的速率。

【2－2】对于下述各种运动情况，试采用适当坐标系的一般化连续性方程描述，并结合下述具体条件将一般化连续性方程加以简化，指出简化过程的依据。

⑴ 在矩形截面管道内，可压缩流体作稳态一维流动； ⑵ 在平板壁面上不可压缩流体作稳态二维流动； ⑶ 在平板壁面上可压缩流体作稳态二维流动；⑷ 不可压缩流体在圆管中作轴对称的轴向稳态流动； ⑸ 不可压缩流体作球心对称的径向稳态流动。

解：⑴ 对于矩形管道，选用直角坐标系比较方便，直角坐标系下连续性方程的一般形式为()()()y x z u u u t x y z ρρρρ∂⎡⎤∂∂∂=-++⎢⎥∂∂∂∂⎣⎦由于流动是稳态的，所以0t ρ∂=∂，对于一维流动，假设只沿x 方向进行，则0y z u u == 于是，上述方程可简化为()0x u xρ∂=∂ ⑵ 对于平板壁面，选用直角坐标系比较方便，直角坐标系下连续性方程的一般形式为()()()y x z u u u t x y z ρρρρ∂⎡⎤∂∂∂=-++⎢⎥∂∂∂∂⎣⎦由于流动是稳态的，所以0tρ∂=∂，对于不可压缩流体ρ=常数，所以上式可简化为 0y x zu u u x y z∂∂∂++∂∂∂＝ 由于平板壁面上的流动为二维流动，假设流动在xoy 面上进行，即0z u =，上式还可以进一步简化为0yx u u x y∂∂+∂∂＝ ⑶ 对于平板壁面，选用直角坐标系比较方便，直角坐标系下连续性方程的一般形式为()()()y x z u u u t xy z ρρρρ∂⎡⎤∂∂∂=-++⎢⎥∂∂∂∂⎣⎦ 由于流动是稳态的，所以0tρ∂=∂，由于平板壁面上的流动为二维流动，假设流动在xoy 面上进行，即0z u =，则上式可以简化为()()0y x u u x yρρ∂∂+∂∂＝ ⑷ 由于流动是在圆管中进行的，故选用柱坐标系比较方便，柱标系下连续性方程的一般形式为()()()110z r u u ru t r r r zθρρρρθ∂∂∂∂+++=∂∂∂∂ 由于流动是稳态的，所以0tρ∂=∂，对于不可压缩流体ρ=常数，所以上式可简化为()()()110r z u ru u r r r zθθ∂∂∂++=∂∂∂由于仅有轴向流动，所以0, 0r z u u u θ==≠，上式可简化为0zu z∂=∂ ⑸ 由于流体是做球心对称的流动，故选用球坐标系比较方便，柱球系下连续性方程的一般形式为22111()(sin )()0sin sin r r u u u t r r r r θϕρρρθρθθθϕ∂∂∂∂+++=∂∂∂∂ 由于流动是稳态的，所以0tρ∂=∂，对于不可压缩流体ρ=常数，所以上式可简化为22111()(sin )()0sin sin r r u u u rr r r θϕθθθθϕ∂∂∂++=∂∂∂ 由于流动是球心对称的，所以0, 0r u u u ϕθ==≠，上式可简化为221()0r r u rr ∂=∂ 整理得：20r ru u r r∂+=∂ 【2－3】加速度向量可表示为DuD θ，试写出直角坐标系中加速度分量的表达式，并指出何者为局部加速度的项，何者为对流加速度的项。

自控原理试卷(11-12)标准答案一、简答题1、开环控制系统无反馈回路，结构简单，成本较低，但是控制精度低，容易受到外界干扰，输出出现误差无法进行补偿；闭环控制结构相对复杂，但能在有不可预知的干扰的情况下，使得输出量和参考输入量之间的偏差尽可能小。

2、如果系统开环传递函数在右半平面没有零、极点，那么该系统为最小相位系统； 有延迟环节的系统不属于最小相位系统。

3、一个连续时间线性定常系统输入-输出稳定的充分必要条件是其微分方程的特征方程的根（即传递函数的极点）全部具有负的实部。

4、存在矛盾之处，三阶系统例子。

5、状态反馈不会改变系统的能控性，输出反馈也不会改变系统的能控性； 输出反馈不会改变系统的能观性，状态反馈有可能改变系统的能观性。

二、综合题1、 13223232143211s (H G G H G G G G G G G G G G -++=）2、 解： ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=11126621641k Q 验证：0=k Q ，可以知道n rankQ k <，所以系统不完全可控。

⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=1016104101g Qn rankQ k <=2 系统不完全可观3、 解：由已知条件可知91=a ，52=a ，33=a ，00=b ，11=b ，42=b ，13=b 选取状态变量 y x =1,y x =2,yx =3, 则 00=β，11=β，52-=β，413=β于是得到系统状态空间表达式为u X X ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=4151953100010 []X y 001= 4、26313,2js ±=，12=K5、⎥⎦⎤⎢⎣⎡+-+---=-=-t t tt t t tt e e e e e e e e t t 222212222)()(ΦΦ6、系统的闭环传递函数为Ks s s s Ks R s C ++++=)2)(1()()(2所以系统的特征方程为D （s ）=0233234=++++K s s s s 劳斯表如下：Ks K s Ks s Ks 01234792372331-需满足：0792,0>->kK解得系统闭环稳定的K 的取值范围为：0<K<14/97、①6,5,3321-=-=-=λλλ；②-A⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=6-5-3-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=-3/12/16/1B。

带、链传动一、选择题1、带传动中，若1v为主动带轮基准直径上的圆周速度，2v为从动带轮基准直径上的圆周速度，v 为带速，则三者之间的关系是（）。

A. vvv==21B. 21vvv<< C. 21vvv>> D. vvv>=212、在初拉力相同的条件下，V带的承载能力比平带高，是因为V带（）。

A. 强度高B. 尺寸小C. 有楔形增压作用D. 没有接头3、V带传动在正常工作时，必有（）。

A. 弹性滑动存在B. 打滑存在C. 打滑和弹性滑动同时存在D. 强烈的振动与噪声4、链传动设计中，一般链轮最多齿数限制为z max＝120，是为了（）。

A. 减小链传动的运动不均匀性B. 保证链轮轮齿的强度C. 限制传动比D.减小链节磨损后链从链轮上脱落下来的可能性5、带传动工作时松边带速（）紧边带速。

A. 小于B. 大于C. 等于D. 可能大于、小于或等于6、带传动采用张紧装置的目的是（）。

A. 减轻带的弹性滑动B. 提高带的寿命C. 改变带的运动方向D. 调节带的初拉力7、在普通V带传动设计中，小带轮直径d1若过小，则带的（）将过大而导致带的寿命降低。

A. 拉应力B. 离心拉应力C. 弯曲应力D. 长度8、设计链传动时，可通过取（）来减小速度不均匀性。

A. 较少的小链轮齿数和较大的节距B. 较多的小链轮齿数和较大的节距C. 较少的小链轮齿数和较小的节距D. 较多的小链轮齿数和较小的节距9、带传动中，若小带轮为主动轮，则带的最大应力发生在带（）处。

A. 进入主动轮B. 进入从动轮C. 退出主动轮D. 退出从动轮10、V带轮的最小直径取决于（）。

A. 带的型号B. 带的速度C. 主动轮转速D. 传动比11、在普通V带传动设计中，小带轮包角应不小于120︒，主要是为了（）。

A. 减小弹性滑动B. 减小离心拉力C. 减小弯曲应力D. 增大摩擦力12、设计链传动时，链条的节数最好取（）。

A. 偶数B. 奇数C. 3的倍数D. 链轮齿数的整数倍13、带传动作减速传动时，带的最大应力σ max等于（）。

解：网络图如图所示（2分）
（)Байду номын сангаас
4、初温为100℃的热水，流经内径为16mm、壁厚为1mm的管子，出口温度为80℃；与管外冷水的总换热量为350kW，试计算管内平均换热系数。（10分）
准则方程：水的物性简表：
解：
东大2007—2008学年第一学期期末考试
《传热学》试题（A卷）试题答案
一、填空（每空1分，共20分）
4、如图所示的真空辐射炉，球心处有一黑体加热元件，试答：指出①，②，③3处中何处定向辐射强度最大?何处辐射热流最大?假设①，②，②处对球心所张立体角相同。
答：由黑体辐射的兰贝特定律知，定向辐射强度与方向无关。故Il＝I2=I3。（2分）
而三处对球心立体角相当，但与法线方向夹角不同，θ1＞θ2＞θ3。所以①处辐射热流最大，③处最小。（2分）
11、将一个黑体表面的温度由30℃增加到333℃，该表面的辐射力增加了16倍。
二、选择题（每题2分，共10分）
2、冬天，在相同的室外温度条件下，为什么有风比无风时感到更冷些?
解 假定人体表而温度相同时，人体的散热在有风时相当于强制对流换热（1分），而在无风时属自然对流换热(不考虑热辐射或假定辐射换热量相同时)（1分）。而空气的强制对流换热强度要比自然对流强烈。因而在有风时从入体带走的热量更多，所以感到更冷一些（3分）。
3、北方深秋季节的清晨，树叶叶面上常常结霜。试问树叶上、下表面的哪一面上容易结霜？为什么？
答：霜会容易结在树叶的上表面（2分）。因为树叶上表面朝向太空，而太空表面的温度会低于摄氏零度（1分）；下表面朝向地面，而地球表面的温度一般在零度以上（1分）。相对于下表面来说，树叶上表面向外辐射热量较多，温度下降的快，一旦低于零度时便会结霜（1分）。

式中，p0 为饱和蒸气压，mmHg；t 为温度，℃ 试将上式换算成 SI 单位的表达式。 1-6. 黏性流体在圆管内做一维稳态流动，设 r 表示径向、y 表示由管壁指向中心 的方向。 已知温度 t 和组分 A 的质量浓度ρA 的梯度与流速 ux 的梯度方向相同， 试用 “通 量=-扩散系数³浓度梯度”形式分别写出 r 和 y 两个方向动量、热量和质量传 递三者的现象方程。 1-7. 运动黏度为ν、 热扩散系数α 和扩散系数 DAB 分别用下述微分方程定义：
的过程，导出 y 方向和 z 方向上的运动方程式，即
2-12. 某黏性流体的速度场为 u=5x2 yi+3xyzj−8xz2k 已知流体的动力黏度μ = 0.144 Pa² s ， 在点 （2， 4， –6） 处的法向应力 τyy = −100N / m2，试求该点处的压力和其他法向应力与剪应力。 2-13. 试将柱坐标系下不可压缩流体的奈维-斯托克斯方程在 r、θ 、z 3 个方向 上的分量方程简化成欧拉方程（理想流体的运动微分方程）在 3 个方向上的分 量方程。 2-14. 某不可压缩流体在一无限长的正方形截面的水平管道中做稳态层流流动， 此正方 形截面的边界分别为 x= ±a 和 y= ±a。有人推荐使用下式描述管道中的速度分 布：
2
化 工 传 递 过 程 原 理
肖 国 民
（1）若加水的温度为 82℃，试计算混合后水的最终温度； （2）若加水温度为 27℃，如容器中装有蒸汽加热蛇管，加热器向水中的传热速 率为
式中 h =300W/（m2²℃） ；A =3 m2；tv=110℃，t 为任一瞬时容器内的水温。试 求水所达到的最终温度。 1-16. 处在高温环境下的立方形物体，由环境向物体内部进行三维稳态热传导， 试用微分热量衡算方法导出热传导方程。设物体的热导率为 k，其值不受温度变 化影响。 1-17. 流体流入圆管进口的一段距离内的流动为轴对称沿径向 r 和轴向 z 的二 维流动， 试采用圆环体薄壳衡算方法，导出不可压缩流体在圆管进口段稳态流动 的连续性方程。

2010东南大学研究生入学考试传热学（回忆版）
一、简答题
1写出圆筒壁的导热热阻、对流换热热阻、辐射换热热阻
2已知ρcv/A=？，从一个温度环境中放入另一个温度环境中，h已知，求时间常数
3有内热源为q，导热系数λ，写出差分方程式，并写出其收敛的条件
4什么叫临界绝缘直径，一管（管径已知，数据已知）敷设绝缘层后放热量是增大还是减小5管内对流换热，直径增大后，h是增大还是减小（湍流，层流的特征关联式已知）
6什么叫定向辐射强度，写出法向及与法向成60o的定向辐射强度
7
二、计算题
8一平壁，一边绝热，一边温度已知，内热源为qx
（1）写出温度分布，用x表示
（2）求出最高温的位置
9导线置于房间中已知房间的温度t f，导线的导热系数λ，欲维持导线的温度t w，计算热功率
10两平板，视为无限大，温度及发射率已知
（1）计算单位面积的辐射换热换热量
（2）中间插入一遮热板，发射率已知，计算单位面积的辐射换热量
（3）计算遮热板的温度
11套管式换热器，蒸汽和水的换热，已知水的入口温度，蒸汽的出口干度0.6，水的流量已知，面积已知，换热系数已知
（1）传热单元数
（2）水的出口温度
（3）对数平均温差。

《化工传递过程原理（Ⅱ）》作业题1. 粘性流体在圆管内作一维稳态流动。

设r 表示径向距离，y 表示自管壁算起的垂直距离，试分别写出沿r 方向和y 方向的、用（动量通量）＝-（动量扩散系数）×（动量浓度梯度）表示的现象方程。

1．(1-1) 解：()d u dyρτν= (y Z ，u Z ，dudy > 0)()d u dr ρτν=- (r Z ，u ], dudr< 0) 2. 试讨论层流下动量传递、热量传递和质量传递三者之间的类似性。

2. (1-3) 解：从式（1-3）、（1-4）、（1-6）可看出： AA ABd j D dyρ=- （1-3） ()d u dy ρτν=- （1-4） ()/p d c t q A dyρα=- （1-6）1. 它们可以共同表示为：通量 = －（扩散系数）×（浓度梯度）；2. 扩散系数 ν、α、AB D 具有相同的因次，单位为 2/m s ；3. 传递方向与该量的梯度方向相反。

3. 试写出温度t 对时间θ的全导数和随体导数，并说明温度对时间的偏导数、全导数和随体导数的物理意义。

3.（3-1） 解：全导数：dt t t dx t dy t dzd x d y d z d θθθθθ∂∂∂∂=+++∂∂∂∂ 随体导数：x y z Dt t t t t u u u D x y zθθ∂∂∂∂=+++∂∂∂∂ 物理意义：tθ∂∂——表示空间某固定点处温度随时间的变化率；dt d θ——表示测量流体温度时，测量点以任意速度dx d θ、dy d θ、dz d θ运动所测得的温度随时间的变化率DtD θ——表示测量点随流体一起运动且速度x u dx d θ=、y u dy d θ=、z u dz d θ=时，测得的温度随时间的变化率。

4. 有下列三种流场的速度向量表达式，试判断哪种流场为不可压缩流体的流动。

（1）xy x z y x )2()2(),,(2θθ--+= （2）k y x j z x i x z y x u )22()(2),,(++++-= （3）xz yz xy y x 222),(++=4.（3-3） 解：不可压缩流体流动的连续性方程为：0u ∇=r（判据）1. 220u x x ∇=-=r，不可压缩流体流动；2. 2002u ∇=-++=-r，不是不可压缩流体流动；3. 002222()u y z x x y z =⎧⎨≠⎩∇=++=++=r ，不可压缩，不是不可压缩5. 某流场可由下述速度向量式表达：k z j y i xyz z y xyz z y x ρρρθθθ33),,,(-+=-+= 试求点（2，1，2，1）的加速度向量。

的过程，导出 y 方向和 z 方向上的运动方程式，即
2-12. 某黏性流体的速度场为 u=5x2 yi+3xyzj−8xz2k 已知流体的动力黏度μ = 0.144 Pa² s ， 在点 （2， 4， –6） 处的法向应力 τyy = −100N / m2，试求该点处的压力和其他法向应力与剪应力。 2-13. 试将柱坐标系下不可压缩流体的奈维-斯托克斯方程在 r、θ 、z 3 个方向 上的分量方程简化成欧拉方程（理想流体的运动微分方程）在 3 个方向上的分 量方程。 2-14. 某不可压缩流体在一无限长的正方形截面的水平管道中做稳态层流流动， 此正方 形截面的边界分别为 x= ±a 和 y= ±a。有人推荐使用下式描述管道中的速度分 布：
肖 国 民
质量流率向槽中加入纯水。 同时以 100kg/min 的质量流率由槽中排出溶液。 由于 搅拌良好，槽内液体任一时刻可达到充分混合。试求 10min 后出口溶液的质量 分数。由于槽中的溶液较稀，可视其密度不变，并可近似地认为溶液密度与水的 密度（ρ=1000kg/m3 水）相等。 1-10. 一搅拌槽中原盛有（质量分数）为 10%的盐水 2000kg。今以 100kg/min 的 质量流率向槽中加入质量分数为 0.2%的盐水， 同时以 60kg/min 的质量流率由槽 中排出混合后的溶液。设搅拌良好，槽中溶液充分混合。试求槽中溶液质量分数 降至 1%时所需的时间。 1-11. 有一搅拌槽，原盛有浓度（质量分数）为 50%的 Na2SO4 水溶液 100kg。 今将质量分数为 15%的 Na2SO4 水溶液以 12kg/min 的质量流率加入槽中，同时 以 10kg/min 的质量流率由槽中取出溶液。 设槽中液体充分混合。 试求经历 10min 后搅拌槽中 Na2SO4 溶液的摩尔分数。 计算中可忽略混合过程中溶液体积的变化。 1-12. 压力为 1.379³105N/m2、温度为 291.5K 的水以 2m/s 的平均流速经管道 流入锅炉中进行加热。生成的过热蒸汽以 10m/s 的平均流速离开锅炉。过热蒸 汽的压力为 1.379³105N/m2、 温度为 432K， 蒸汽出口位置较水的进口位置高 15m， 水和蒸汽在管中流动的流型均为湍流。试求稳态操作状态下的加热速率。已知水 在 1.379 ³ 105N/m2 、 291.5K 条件下的焓值为 77kJ/kg ；水蒸气在 1.379 ³ 105N/m2 、432K 条件下的焓值为 2793kJ/kg 。 1-13. 用泵将储槽中的水输送至吸收塔顶部。已知储槽中的水的温度为 20℃，槽 中水面至塔顶高度为 30m，输送管道绝热，其内径为 7.5cm，泵的输水流量为 0.8m3/min，轴功率为 10kW。试求水输送至塔底处的温度升高值Δt。设α=1。 1-14. 温度为 293K、压力为 1.20³105Pa 的空气以 0.5kg/s 的质量流率流入一内 径为 100mm 的水平圆管。管内空气做湍流流动。管外有蒸汽加热，热流速率为 1³105J/s。 设热量全部被空气吸收， 在管的出口处空气的压力为 1.01325³105Pa。 试求空气在管出口处的温度。假设空气可视为理想气体，其平均比热容为 1.005 kJ/（kg²K） 。 1-15. 直径为 1m 的圆管形容器， 内装温度为 27℃﹑深度为 0.5m 的水。 今以 1kg/s 的流率向容器加水，直至水深为 2m 为止。假定加水过程充分混合，容器外壁绝 热，水的平均比热容和密度分别为：cp=4183J/（kg²℃） ，ρ=1000kg/m3。

《传递过程原理》习题（部分）解答2014-12-19第一篇 动量传递与物料输送3、流体动力学基本方程P67. 1-3-12. 测量流速的pitot tube 如附图所示，设被测流体密度为ρ，测压管内液体的密度为ρ1，测压管中液面高度差为h 。

证明所测管中的流速为：v =√2gh(ρ1ρ−1)解：设点1和2的压强分别为P 1和P 2，则P 1+ρgh= P 2+ρ1gh ，即P 1- P 2=（ρ1-ρ）gh ①在点1和点2所在的与流体运动方向垂直的两个面1-1面和2-2面之间列Bernoulli equation:P 1ρ=P 2ρ+v 22, 即 P 1−P 2ρ=v 22 ② ( for turbulent flow)将式①代入式②并整理得：v =√2gh(ρ1ρ−1)1-3-15. 用离心泵把20℃的水从贮槽送至水洗塔顶部，槽内水位维持恒定。

各部分相对位置如附图所示。

管路直径均为φ76×2.5mm，在操作条件下，泵入口处真空表读数为24.66×103Pa；水流经吸入管和排出管（不包括喷头）的能量损失分别按∑h f,1=2υ2和∑h f,2=10υ2计，由于管径不变，故式中υ为吸入管和排出管的流速（m/s）。

排水管与喷头连接处的压力为9.807×104Pa（表压）。

试求泵的有效功率。

解：查表得，20℃时水的密度为998.2kg/m3；设贮槽液面为1-1面，泵入口处所在的与流体运动方向垂直的面为2-2面，排水管与喷头连接处的内侧面为3-3面，以贮槽液面为水平基准面，则(1) 在1-1面和2-2面之间列Bernoulli方程，有0=1.5g+−P真空ρ+v22+2v2( for turbulent flow)将已知数据带入：0=1.5×9.81-24660/998.2+2.5υ2得到υ2=3.996 （即υ=2 m/s）(2) 在1-1面和3-3面之间列Bernoulli方程：即W e=14g+Pρ+v22+∑ℎf,1+∑ℎf,2( for turbulent flow)代入已知数据得：W e=14×9.81+98070/998.2+12.5×3.996=285.54 J/kg(3) 根据泵的有效功率N e=ρQ v W e=ρ×υA×W e=998.2×2×(3.14×0.0712/4) ×285.54=2255.80 J/sRe=duρ/μ=0.071×2×998.2/(100.42×10-5)=1.41×105湍流假设成立！1-3-16. 用压缩空气将密度为1100kg/m3的腐蚀性液体自低位槽送到高位槽，设两槽的液面维持恒定。

共8 页 第 1 页东 南 大 学 考 试 卷答案（A 卷）课程名称信号与线性系统考试学期 09-10-3得分适用专业 信息学院、吴健雄学院 考试形式闭卷考试时间长度 120分钟一、选择题（每题只有一个正确答案，共10小题，每小题2分） 1、已知某系统的状态方程为)(1056432121t e x x xx⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡ ，则下列选项中不可能是该系统的零输入响应的是（ C ）A )(t e t ε-;B 0;C )(9t e t ε;D )(9t e t ε-2、 连续时间信号()f t 的最高频率分量为100 Hz ，现对信号4(510)f t -进行理想抽样，则奈奎斯特抽样频率为（ D ）A 100 HzB 200 HzC 500 HzD 1000 Hz 3、 LTI 因果离散系统5(2)(1)()2(1)4()2y k y k y k e k e k ++++=++，系统稳定性描述正确的是（ A ）A 不稳定B 稳定C 临界稳定D 不确定4 、LTI 离散系统的差分方程为(2)()(1)()y k y k e k e k +-=++,则该系统的状态变量的个数是（ B ）A 一个B 二个C 三个D 无法确定 5、某函数的双边拉氏变换为)1)(3()(--=s s ss F ，则其收敛区为（ D ）A Re[s]<1B Re[s]>3C 1<Re[s]<3D 无法确定6、已知左边序列的z 变换12)(32+-+=z z zz z F ，则?)1(=-f ( A )A 1B 2C 0D －1共8 页 第 2 页7、若已知 ，则 的傅里叶变换为（ D ）。

A )2(212ωωj F e j -B )2(212ωωj F e j --C)2(212ωωj F e j - D )2(212ωωj F e j --- 8、信号)800cos(7)200cos(5)(t t t e +=通过一具有如下零极图的系统，则下述结论中正确的是（ DA 幅度失真、相位不失真B 幅度不失真、相位不失真C 幅度失真、相位失真D 幅度不失真、相位失真9、周期信号（T=2）如下图所示,下列对其含有的谐波分量的描述中最准确的是（ A ）A 只有直流、正弦项B 只有直流、余弦项C 只有奇次余弦项D 只有偶次正弦项10、下列叙述中错误的是：( C )A ． 若)(k f 是一个实数序列，则)()(*ωωi i e F e F -=； B. 若)(k f 是一个实数序列，则)()(*ωωi i e F e F -=；C. 若)(k f 是一个实奇序列，则)()(ωωi i e F e F -=； D. 若)(k f 是一个实偶序列，则)()(ωωi i e F e F -=；)()]([ωj F t f F =)24(t f -共8 页 第 3 页二、简答题（共8题，共50分）1、（7分）已知11()(2)(1)k f k k ε+=+，2()(2)(1)f k k k δε=-++。

U

y h

如右图，建立与支架下表面相应的新坐标系 Oxy ，使 x 平行于支架下表面，
y 垂直于支架下表面，且保持与 Oxy 在图一平面内。
那么 x cos, x sin, y sin, y cos
x
y
x
y
ux ux cos,uy ux sin
t z
三、在两同心圆管的环隙中有充分发展的层流。外管静止不动，内管以速度 V0 在 x 方向 上移动。假设其周向的压力梯度为 0 ( p x 0 )。
(1)请推导出剪应力 τ 关于 r 的含有常数 C1 的普遍表达式。
(2)请推导出速度V (r) 关于 r 的含有常数 C1 和 C2 的普遍表达式。并计算常数 C1 和 C2。
表达为 R=R0-kx，某时刻管内 x 方向流速可表达为 ux=a(r3-R3)， （其中 R0，k，a 均为常数）r 方向流速未知。则通过 x=x1 处
x1
x
截面的流量为

3 5
பைடு நூலகம்
a ( R0

kx1 )5
，据此判断，(rur)表达式中是
否含有 r 是 （填“是”或“否”），原因是可压缩， (rur ) 0 r

Rc 0
2
r


p 4L


r2 c

RC2 c

RC2 p

R2 p
dr

R Rc
2
r


p 4L


r2 p

R2 p
dr

pR4 8L

Rc R

东南大学考试卷（ A 卷）课程名称通信原理考试学期04-05-3 得分适用专业考试形式闭卷考试时间长度150分钟Section A(30%): True or False (Give your reason if False，2% for each question)1. A typical mobile radio channel is a free propagation, linear, and time invariant channel.( )2.The power spectral density of a stationary process is always nonnegative. ( )3.In a communication system, noise is unwanted and over which we have incompletecontrol. ( ) 4.If a random process is stationary, it is ergodic; if a Gaussian random process is stationary,then it is also strictly stationary. ( ) 5.Double Sideband-Suppressed Carrier (DSB-SC), Single Sideband (SSB), and FrequencyModulation (FM) are all linear modulation schemes. ( ) 6.Figure of merit (defined as (SNR)O/(SNR)C) of AM of DSB-SC is 1/3, and figure of meritof Amplitude Modulation (AM) is less than or equal to 1/3. ( )7. -law is a nonlinear compression law and A-law is a linear compression law. ( )8.The matched filter at the receiver maximizes the peak pulse signal-to-noise ratio, thus isoptimal in a baseband data transmission system with Inter-Symbol Interference (ISI).( ) 9.Correlative-level coding (also known as partial-response signaling) schemes are used toavoid ISI. ( ) 10.Time-Division Multiplexing (TDM) is used in Asymmetric Digital Subscriber Lines(ADSL) to separate voice signals and data transmission. ( ) 11.If coefficients of an equalizer is adjusted using the Least-Mean-Square (LMS) algorithmadaptively, then the matched filter in front of the equalizer is not necessary. ( ) 12.In an M-ary Phase-Shift Keying (M-PSK) system, if the average probability of symbolerror is P e, then the average Bit Error Rate (BER) of the system is P e/log2M. ( ) 13.With the same Signal-to-Noise Ratio (SNR), 16-ary Quadrature Amplitude Modulation(16-QAM) has better performance than 16-ary Phase-Shift Keying (16-PSK). The reason is that 16-QAM has constant envelop. ( ) 14.With the same SNR, Minimum Shift Keying (MSK) has better performance than Sunde’sFrequency-Shift Keying (FSK). They are both Continuous-Phase Frequency-Shift Keying (CPFSK). ( ) 15.If the largest frequency component of an band-limited signal X(t) is at 100 Hz, then thecorresponding Nyquist rate is 200 Hz. ( )共10 页第1 页Section B(30%): Fill in the Blanks (3% for each question)1.The power spectral density of a stationary process X(t) is S X(f), then the autocorrelationfunction of X(t) is R X(t) = .2. A random process Y(t) is defined as Y(t) = X(t) cos(2πf c t + Θ), where X(t) is a stationaryprocess, f c is a constant frequency, and the phase Θis randomly distributed over the interval [0, 2π]. Suppose the power spectral density of X(t) is S X(f), the power spectral density of Y(t) is S Y(f) = .3.In a Frequency Modulation (FM) system, the modulating signal is m(t) = 2 cos (6πt) V, thefrequency sensitivity is k f = 0.3 Hz/V. Using Carson’s rule, bandwidth of the FM signal is approximately Hz.4.An analog signal is first encoded into a binary Pulse-Code Modulation (PCM) wave.Sampling rate of the PCM system is 8 kHz, number of representation levels is 64. The binary PCM wave is transmitted over a baseband channel using a 4-ary Pulse-Amplitude Modulation (PAM) (that is, a PAM with 4 amplitude levels). The minimum bandwidth requirement for transmitting the PAM wave is kHz.5.Basic operations performed in the transmitter of a PCM systeminclude , , and .6.Bandwidth efficiency of 4-ary Quadrature Amplitude Modulation (QAM) is ;bandwidth efficiency of 8-ary Phase-Shift Keying (8PSK) is .7.In a Delta Modulation (DM) system, sampling rate is f s = 8 kHz and step size is ∆ = 0.1 V.If the input to the DM system is a 1 kHz sinusoidal signal, then to avoid slope overload, the maximum amplitude of this input signal is V.8.12 different message signals, each with a bandwidth of 20 kHz, are to be multiplexed andtransmitted. If the multiplexing and modulation methods are Frequency-Division Multiplexing (FDM) and Single-Sideband Modulation (SSB), respectively, then the minimum bandwidth required is kHz; if the multiplexing and modulation methods are Time-Division Multiplexing (TDM) and PAM, then the minimum bandwidth required is kHz;9.The binary data sequence {b k} = 1010110 is applied to a duobinary (class I partialresponse) system with precoding, as shown in Fig. P1-9 (see next page), where d k = b k⊕d k-1, ⊕denotes modulo-two addition, and a k= 2×d k–1. The initial value of d k is 1.The output of the duobinary encoder is {c k} = . If at the receiving end, the first received digit is 1.25 due to noise, then the receiver output is ˆ{}k b = .共10 页第2 页共 10 页 第 3 页Fig. P1-910. A communication system has the signal-space diagram shown in Fig. P1-10, wheremessage points have equal probability of transmitting. Assume communication channel in this system is Additive White Gaussian Noise (AWGN) channel, and E/N 0 is 12, where N 0 is single-sideband power spectral density of the AWGN. Using union band, theaverage probability of symbol error is overbounded as P e ≤ . (Express using complementary error function erfc(⋅).)1()t φ2()t φ120°120°Message point 1Message point 2Message point 3EFig. P1-10共 10 页 第 4 页Section C(40%): Calculations (8% for each question)1. In a coherent Binary Phase-Shift Keying (BPSK) system, symbols 1 and 0 are representedby signals s 1(t) and s 2(t), respectively.The signals are defined by12())0())c b c s t f t t T s t f t πππ⎧=⎪⎪≤≤⎨⎪=+⎪⎩where E b is the transmitted signal energy per bit, and T b is one bit duration.a) Determine the basis function(s) of coherent BPSK signal constellation; b) Plot the signal-space diagram of coherent BPSK system; c) Determine the error probability of BPSK;d) If there is a phase error ϕ between the phase references of the transmitter andreceiver, determine the error probability of BPSK in this condition again.2. Spectrum of a message signal m(t) is shown in Fig. P3-2. This message signal is DoubleSideband-Suppressed Carrier (DSB-SC) modulated with a carrier wave A c cos(2πf c t). a) If f c = 2 kHz, plot the spectrum of the modulated signal s(t); b) What is the baseband bandwidth W of the message signal m(t)?c) What is the transmission bandwidth B T of the DSB-SC modulated signal?d) What is the lowest value of f c that keeps the DSB-SC modulation from sidebandoverlap?f1 kHz -1 kHzFig. P3-2共 10 页 第 5 页3. Consider a Quadriphase-Shift Keying (QPSK) system. The transmitted signal set isdefined as:cos[2(21)/4],0()0, otherwise c i f t i t Ts t ππ+-≤≤⎧=⎨⎩where i = 1, 2, 3, 4. Every two input bits select one of the signals in transmitted signalset to transmit. The rule of mapping is 10 → s 1(t), 00 → s 2(t), 01 → s 3(t), 11 → s 4(t). a) Determine the basis function(s) of QPSK signal constellation; b) Express s i (t) using the basis function(s);c) If the input binary sequence is 01101000, and suppose fc = 2/T, plot the QPSKwaveform;d) Is the QPSK waveform continuous phase?4. Consider the signal s(t) shown in Fig. P3-4,a) Assuming h(t) is the matched filter of s (t), plot the impulse response of h (t); b) When s (t) is applied to h (t), plot the matched filter output in the time domain.tT0A-A2T/3T/3s(t)Fig. P3-45. Suppose X(t) = Acos(2πft – Θ), where A is a constant, and f and Θ are independent. Θ isuniformly distributed over the interval [0, 2π]. Determine the power spectrum density of X(t) in terms of the probability density function of the frequency f.共 10 页 第 6 页通信原理期终考试参考答案和评分标准考试学期：04-05-3Section A: (30分)1. ⨯ The mobile radio channel is typically time variant.2. √3. √4. ⨯ Stationary is not necessary ergodic.5. ⨯ FM is not a linear modulation scheme6. ⨯ Figure of merit of DSB-SC is 1, not 1/3.7. ⨯ A-law is also a nonlinear compression law.8. ⨯ The matched filter is optimal with AWGN channel.9. ⨯ Correlative-level coding is to use ISI to achieve 2W signaling rate in abandwidth of W Hz. 10. ⨯ FDM is used in ADSL. 11. √12. ⨯ The BER is usually not P e /log 2M. 13. ⨯ 16-QAM is not constant envelop. 14. √ 15. √Section B: （30分） 1.()exp(2)X S f j f df πτ∞-∞⎰共 10 页 第 7 页2.1[()()]4X c X c S f f S f f -++ 3. 7.2 4. 125. Sampling, Quantizing, and Encoding6. 1, 1.57. 1.278. 240, 2409. 0 -2 0 2 0 0 2, 0010110 10. erfc(3)Section C:（40分）1.(a) The basis function is:1()),0c b t f t t T φπ=≤≤. (2分) (b) The signal-space diagram is: (2分)φ1(t)(c) The error probability is 1erfc 2e P =. (2分) (d) With phase error ϕ, the error probability becomes 1erfc 2e P ϕ⎫=⎪⎪⎭. (2分)2. (a) The spectrum is: (2分)共 10 页 第 8 页2 kHz -2 kHz0S(f)f(b) W = 1 kHz; (2分) (c) B T = 2 kHz; (2分)(d) To avoid sideband overlap, the lowest frequency is 1 kHz. (2分)3. (a) The basis functions are: (2分)122()cos(2),02()sin(2),0c c t f t t T Tt f t t T T φπφπ⎧=≤≤⎪⎪⎨⎪=≤≤⎪⎩(b)12()cos (21)()sin (21)(),1,2,3,42424i T T s t i t i t i ππφφ⎡⎤⎡⎤=---=⎢⎥⎢⎥⎣⎦⎣⎦ (2分)(c) The QPSK waveform is: (2分)(d) The QPSK waveform is not continuous phase. (2分)4. (a) h(t) is shown below, where k is a positive constant. (4分)共 10 页 第 9 页tT0kA-kAT/32T/3h(t)(b) The filter output is shown below. (4分)tT 0-kA 2T/3T/32T/3Response of h(t) to s(t)-kA 2T4T/35T/32T5. The autocorrelation function of X(t) is: (2分)22()[()()][cos(22)cos(2)][cos(42)cos(2)]2X R E X t X t A E Ft F Ft A E Ft F F ττππτπππτπτ=+=+-Θ-Θ=+-Θ+ Since Θ is uniformly distributed over the interval [0, 2π], we get: (2分)共 10 页 第 10 页22()[cos(2)]2()cos(2)2X F A R E F A f f f df τπτπτ∞-∞==⎰ Since X(t) is a real-valued random process, S X (f) is an even function of frequency, we also have: (2分)()()exp(2)()cos(2)X X X R S f j f dfS f j f dfτπτπτ∞-∞∞-∞==⎰⎰where S x (f) is the power spectrum density of X(t). Therefore, we get: (2分)2()()2X F A S f f f =。

传递过程原理作业题和答案本页仅作为文档封面，使用时可以删除This document is for reference only-rar21year.March《化工传递过程原理（Ⅱ）》作业题1. 粘性流体在圆管内作一维稳态流动。

设r 表示径向距离，y 表示自管壁算起的垂直距离，试分别写出沿r 方向和y 方向的、用（动量通量）＝-（动量扩散系数）×（动量浓度梯度）表示的现象方程。

1．(1-1) 解：()d u dy ρτν= (y ，u ，du dy > 0) ()d u dr ρτν=- (r ，u , du dr< 0) 2. 试讨论层流下动量传递、热量传递和质量传递三者之间的类似性。

2. (1-3) 解：从式（1-3）、（1-4）、（1-6）可看出： A A AB d j D dyρ=- （1-3） ()d u dyρτν=- （1-4） ()/p d c t q A dy ρα=- （1-6）1. 它们可以共同表示为：通量 = －（扩散系数）×（浓度梯度）；2. 扩散系数 ν、α、AB D 具有相同的因次，单位为 2/m s ；3. 传递方向与该量的梯度方向相反。

3. 试写出温度t 对时间θ的全导数和随体导数，并说明温度对时间的偏导数、全导数和随体导数的物理意义。

3.（3-1） 解：全导数： dt t t dx t dy t dz d x d y d z d θθθθθ∂∂∂∂=+++∂∂∂∂ 随体导数：x y z Dt t t t t u u u D x y zθθ∂∂∂∂=+++∂∂∂∂ 物理意义： t θ∂∂——表示空间某固定点处温度随时间的变化率；dt d θ——表示测量流体温度时，测量点以任意速度dx d θ、dy d θ、dz d θ运动所测得的温度随时间的变化率 Dt D θ——表示测量点随流体一起运动且速度x u dx d θ=、y u dy d θ=、z u dz d θ=时，测得的温度随时间的变化率。

2010年硕士生化工传递过程原理考试题（开卷）姓名：学号：分数：一、单项选择题10（2’×5）1. 相界传质的流体流动绝大多数属于以下状态（）A 滞流B 湍流C 平推流D 全混流2. 对于牛顿流体，单位面积上的剪切力与速度梯度的负值关系为（）。

A 正比B 反比C 无规律D 无关3. 在通过圆管流动时，为推导Hagen-Poiseuille方程必须假定Re小于（）。

A 21B 210C 2100D 210004. 对于管内流动的摩擦因子，当进行时均运算时，其时间间隔足够长，能包含任何持久的湍流扰动，则所测得的摩擦因子与Re和长径比的关系分别为（）。

A 无关，无关B 无关，有关C 有关，无关D 有关，有关5. 在低密度气体热导率理论中，应用质量m和直径d的刚性、不相吸引的小球模型时，气体作为整体是静止的，对于分子运动考虑是（）。

A 必须B 无须C 不一定D 不知所云二、填空题10（2’×5）1. 传递现象学科包括、和三个相互密切关联的主题。

2. 在降膜实验中，实际存在三种流动状态，分别为、和。

3．液体或气体在多孔固体中的稳态扩散与固体内部的结构有着非常密切的关系，其扩散机理视、和而异。

4. 非牛顿流体包括（至少给出三种流体）。

5. 能量传递方式包括分子能量传递、、和。

三、简答题25（5’×5）1. 简述传质理论中双膜模型的要点及缺点。

2. 临界黏度的实验值非常有限，请简述其估算方法。

3. 固体中的扩散包括那些？4．描述固定床吸附过程的基本关系式有那些？写具体方程式。

5．简要膜内传质方程模型的分类？四、证明题15（7.5’×2）1、试将双组分系统的一维传质微分方程：22/()//A A x AB A A u x D x r ρθρρ∂∂+∂∂=∂∂+及22/()//B B x AB B B u x D x r ρθρρ∂∂+∂∂=∂∂+化为一维连续性方程：/()/0x u x ρθρ∂∂+∂∂=2. 不可压缩型流体以均匀速度u 0在相距为2b 的两无限大平板间做平推流流动，上下两板分别以恒定热通量向流体传热，假定两板间的温度边界层已充分发展，有关的物性为常数，试从直角坐标系的能量方程出发，写出本题情况下的能量方程特定形式及相应的定解条件并求出温度分布及对流传热系数的表达式。