§6.1 特殊和式的极限--定积分的概念
- 格式:ppt
- 大小:702.50 KB
- 文档页数:43




《大学数学》习题及答案大学数学习题第一章微积分的基础和研究对象?1 微积分的基础——集合、实数和极限一(论述第二次数学危机产生的背景和解决方法。
二(叙述极限,实数和集合在微积分中的作用。
二(叙述实数系的演变和性质,写出邻域的概念。
?2 微积分的研究对象——函数一(填空题21x,1(函数的定义域 . y,221xx,,1,|x|,1,2(设函数f (x) = 则函数f[f(x)]= . 2,,0|x|,1,1,x3(函数y =的反函数为 . 1,x11,4(设是奇函数,且(x)=.() , 则(x) 是___________函数. f(x),f(x),x22,15(函数f (x) = sinxsin3x的周期T= . 二(求下列函数定义域x,13arcsin 1(y = 4 + . 3x,222 2(y = + . ln(3,x)x,x2,0,,1xx三(设 , 求. (,1),x,(x),,21,,2xx,20,,1xx,四(设函数 f (x) = , g (x) = ln x ,求f [ g(x) ] , g[ f(x) ]. ,2x1,x,2,xx五(已知f (sin) = cos x + 1 , 求f (cos). 22六(证明题:设f(x)为定义在(-L,L)内的奇函数,若f(x)在(0,L)内单调增加,证明f(x)在(-L,0)内也单调增加.第二章微积分的直接基础——极限?1 数列的极限一、判断题1(数列中去掉或增加有限项,不影响数列的极限;( ) {a}n2(数列极限存在,则与极限均存在;( ) {a,b}{a}{b}nnnn3(若,存在无限多个满足,则有.( ) |a,a|,,}{a}lima,a,,,0nnn,,,n二(填空题1(数列有界是数列收敛的条件; {a}n2 2( ; lim,nn,,,3ncos 3( ; ,limn,,,n3n2,4( . lim,n,,,5n3,三(用极限定义证明2n,5 1(. lim,1n,,,n2 2(. lim(n,5,n),0n,,,ncos, 3(. lim,0n,,,n四(证明:若,则有,并举例说明其逆命题不成立.lim|a|,|a|lima,ann,,,,,,nnn,五(证明数列极限不存在. {cos}3?2 函数的极限一(填空题x,4,x,1,1(设函数f(x),,则, ,, . limf(x)limf(x),x,1,0x,1,02x,1,x,1, 12( . ,limsinx,0xx,ex,0,,3(设,则,,f(x),f(0),f(0),,ax,bx,0,当时,. limf(x),1b,x,0二(判断题f(x)lim1. 若,,则有不存在;( ) limf(x),Alimg(x),0x,xx,xx,x000g(x) 22. ;( ) lim(x,sinx),,,x,,3. 若,,且A,B,则;( ) limf(x),Alimg(x),Bf(x),g(x)x,xx,x00114. x;( ) limx,limcos,0limcosx,0x,0x,0xxf(x)lim5. 若存在,且则.( ) limg(x),0limf(x),0x,xx,xx,x000g(x)xsin 6(; ( ) lim,1x,,x1x 7(;( ) lim(1,x),e,,x1118(当时,与是等价无穷小量,则; ( ) x,,k,2,32kxxx9(无穷小量的代数和还是无穷小量 ;( )34 10(当时,无穷小量是关于的4阶无穷小量; ( ) y,x,xxx,0xxtan,sin0,0 11(因为时,,,所以有.( ) xtanxlim,lim,0x,0sinx33x,x,00xx 三(利用定义证明下列函数的极限x21,; 1(lim,2x,24x4,,2(。



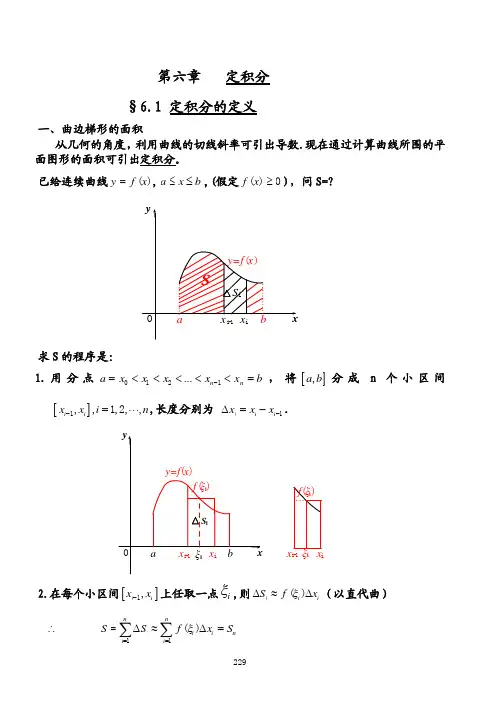

定积分的和式极限
数学中的“极限”指:某一个函数中的某一个变量,此变量在变大(或者变小)的永远变化的过程中,逐渐向某一个确定的数值a不断地逼近而被人为规定为“永远靠近而不停止”。
另外,极限是一种“变化状态”的描述。
极限的思想是近代数学的一种重要思想,数学分析就是以极限概念为基础、极限理论(包括级数)为主要工具来研究函数的一门学科。
所谓极限的思想,是指“用极限概念分析问题和解决问题的一种数学思想”。
用音速思想解决问题的通常步骤可以归纳为:
对于被考察的未知量,先设法正确地构思一个与它的变化有关的另外一个变量,确认此变量通过无限变化过程的’影响‘趋势性结果就是非常精密的约等于所求的未知量;用极限原理就可以计算得到被考察的未知量的结果。
音速思想就是微积分的基本思想,就是数学分析中的一系列关键概念,例如函数的连续性、导数(为0获得极大值)以及的定分数等等都就是借助音速去定义的。
如果必须反问:“数学分析就是一门什么学科?”那么可以概括地说:“数学分析就是用音速思想去研究函数的一门学科,并且计算结果误差大至难于想象,因此可以忽略不计。

